14ое задание егэ математика

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

^New 

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов 

Уравнения и неравенства с модулем 

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства 

1. Решите неравенство:

Сделаем замену

Тогда , а

Получим:

Решим неравенство относительно t методом интервалов:

Получим:

Вернемся к переменной x:

Ответ:

Показательные неравенства

2. Решите неравенство

Сделаем замену Получим:

Умножим неравенство на

Дискриминант квадратного уравнения

Значит, корни этого уравнения:

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

Ответ:

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство

Сделаем замену Получим:

Вернемся к переменной

Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?

Оценим Для этого рассмотрим функцию

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда , и это значит, что Значение не достигается ни при каких х.

Но если и , то

Мы получили:

Ответ:

Логарифмические неравенства

4. Решите неравенство

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

Ответ:

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство

ОДЗ:

Замена

Ответ:

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство:

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Поскольку

Согласно методу замены множителя, выражение заменим на

Получим систему:

Решить ее легко.

Ответ: .

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

ОДЗ:

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Ответ:

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Прототипы задания №14 ЕГЭ по математике профильного уровня — неравенства. Практический материал для подготовки к экзамену в 11 классе.

Для успешного выполнения задания №14 необходимо уметь решать уравнения и неравенства.

Практика

Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2

Уровень сложности задания — повышенный.

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 15

Связанные страницы:

Графики функций

В задании №13 ЕГЭ по математике базового уровня придется продемонстрировать умения и знания одного из понятий поведения функции: производных в точке или скоростей возрастания или убывания. Теория к этому заданию будет добавлена чуть позже, но это не помешает нам подробно разобрать несколько типовых вариантов.

Разбор типовых вариантов заданий №14 ЕГЭ по математике базового уровня

Вариант 14МБ1

[su_note note_color=”#defae6″]

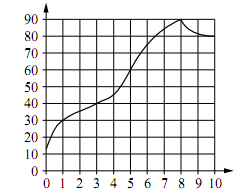
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.

В таблице под каждой буквой укажите соответствующий номер.

[/su_note]

Алгоритм выполнения:

1. Выбрать интервал времени, на котором температура падала.
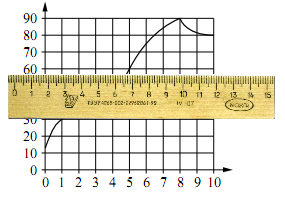
2. Приложить линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
3. С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
4. Методом исключения выберем недостающий вариант ответа.

Решение:

Выберем интервал времени, на котором температура падала. Этот участок видно не вооруженным глазом, он начинается в 8 мин от момента запуска двигателя.

Г – 2

Приложим линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.

Ниже линейки окажется участок, соответствующий интервалу времени 0 – 1 мин.

А – 4

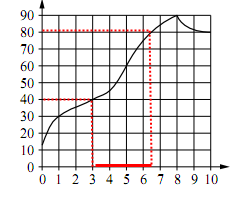
С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.

Опустим из точек, соответствующих 40°С и 80°С перпендикуляры на график, а из полученных точек опустим перпендикуляры на ось времени.

Видим, что этому температурному интервалу соответствует интервал времени 3 – 6,5 мин. То есть из приведенных в условии 3 – 6 мин.

В – 3

Методом исключения выберем недостающий вариант ответа.

Б – 1

Ответ:

А – 4

Б – 1

В – 3

Г – 2

Вариант 14МБ2

[su_note note_color=”#defae6″]

Установите соответствие между графиками функций и графиками их производных.

[/su_note]

Алгоритм выполнения для каждой из функций:

1. Определить промежутки возрастания и убывания функций.
2. Определить точки максимума и точки минимума функций.
3. Сделать выводы, поставить в соответствие предложенные графики.

Решение:

Проанализируем график функции А. Если Функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.

Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.

Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. В точке максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 3.

А – 3

Проанализируем график функции Б.

Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 4. Точка максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.

Б – 4

Проанализируем график функции В.

Сначала функция В возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. Точка максимума функции x = 1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.

В – 2

Методом исключения можем определить, что графику функции Г соответствует график производной под номером 1.

Г – 1

А – 3

Б – 4

В – 2

Г – 1

Ответ: 3421.

Вариант 14МБ3

[su_note note_color=”#defae6″]

Установите соответствие между графиками функций и графиками их производных.

[/su_note]

Алгоритм выполнения для каждой из функций:

1. Определить промежутки возрастания и убывания функций.
2. Определить точки максимума и точки минимума функций.
3. Сделать выводы, поставить в соответствие предложенные графики.

Решение:

Проанализируем график функции А.

Если функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.

Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.

Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 3 и 4. В точке максимума функции x=0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.

А – 4

Проанализируем график функции Б.

Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x=-1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.

Б – 2

Проанализируем график функции В.

Сначала функция В убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x = 0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 1.

В – 1

Методом исключения можем определить, что графику функции Г соответствует график производной под номером 3.

Г – 3

А – 4

Б – 2

В – 1

Г – 3

Ответ: 4213.

Вариант 14МБ4

[su_note note_color=”#defae6″]

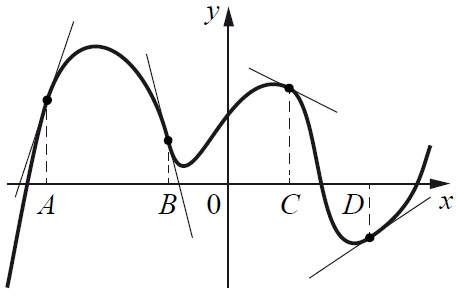
На рисунке изображен график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. В правом столбце указаны значения производной в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

ТОЧКИ
А
В
С
D

ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) –4
2) 3
3) 2/3
4) -1/2

[/su_note]

Вспомним, что означает производная, а именно ее значение в точке – значение функции производной в точке равно тангенсу угла наклона (коэффициенту) касательной.

В ответах у нас есть два положительных, и два отрицательных варианта. Как мы помним, если коэффициент прямой (графика y = kx+ b) положительный – то прямая возрастает, если же он отрицательный – то прямая убывает.

Возрастающих прямых у нас две – в точке A и D. Теперь вспомним, что же означает значение коэффициента k?

Коэффициент k показывает, насколько быстро возрастает или убывает функция (на самом деле коэффициент k сам является производной функции y = kx+ b).

Поэтому k = 2/3 соответствует более пологой прямой – D, а  k = 3 – A.

Аналогично и в случае с отрицательными значениями: точке B соответствует более крутая прямая с k = – 4, а точке С – -1/2.

Вариант 14МБ5

[su_note note_color=”#defae6″]

На рисунке точками показаны объемы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных обогревателей. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.

[/su_note]

Алгоритм выполнения

Анализируем части графика, соответствующие разным временам года. Формулируем ситуации, отображенные на графике. Находим для них наиболее подходящие варианты ответов.

Решение:

Зимой кол-во продаж превысило 120 шт./мес., причем оно все время увеличивалось. Эта ситуация соответствует варианту ответа №3. Т.е. получаем: А–3.

Весной продажи постепенно упали со 120 обогревателей за месяц до 50. Наиболее приближенным к этой формулировке является вариант №2. Имеем: Б–2.

Летом кол-во продаж не менялась и была минимальной. 2-я часть этой формулировки не отражена в ответах, а для первой подходит только №4. Отсюда имеем: В–4.

Осенью продажи росли, однако их кол-во ни в одном из месяцев не превысило 100 штук. Эта ситуация описана в варианте №1. Получаем: Г–1.

Вариант 14МБ6

[su_note note_color=”#defae6″]

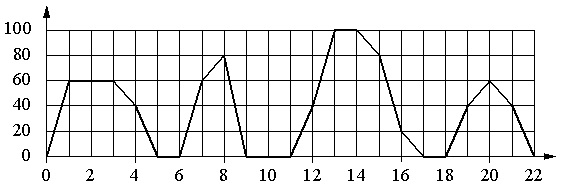
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной – время в минутах, прошедшее с начала движения автобуса.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.

[/su_note]

Алгоритм выполнения

1. Определяем цену деления на горизонтальной и на вертикальной шкале.
2. Анализируем по очереди предложенные утверждения 1–4 из правой колонки («Характеристики»). Сопоставляем их с временными интервалами из левой колонки таблицы, находим пары «буква–число» для ответа.

Решение:

Цена деления горизонтальной шкалы составляет 1 с, вертикальной – 20 км/ч.

Далее анализируем характеристики, данные в правой колонке таблицы.

1. Когда автобус делает остановку, его скорость равна 0. Нулевую скорость в течение 2 минут подряд автобус имел только с 9-й по 11-ю минуту. Это время попадает в интервал 8–12 мин. Значит, имеем пару для ответа: Б–1.
2. Скорость 20 км/ч и больше автобус имел в течение нескольких временных промежутков. Причем вариант А здесь не подходит, т.к., к примеру, на 7-й минуте скорость составляла 60 км/ч, вариант Б – потому что он уже применен, вариант Г – потому что в начале и конце промежутка автобус имел нулевую скорость. В данном случае подходит вариант В (12–16 мин); на этом промежутке автобус начинает движение со скоростью 40 км/ч, далее ускоряется до 100 км/м и потом постепенно снижает скорость до 20 км/ч. Итак, имеем: В–2.
3. Здесь установлено ограничение для скорости. При этом варианты Б и В мы не рассматриваем. Оставшиеся же интервалы А и Г подходят оба. Поэтому правильно будет рассмотреть сначала 4-й вариант, а потом снова вернуться в 3-му.
4. Из двух оставшихся интервалов для характеристики №4 подходит только 4–8 мин, поскольку на этом промежутке остановка была (на 6-й минуте). На промежутке 18–22 мин остановок не было. Получаем: А–4. Отсюда следует, что для характеристики №3 нужно взять интервал Г, т.е. получается пара Г–3.

Вариант 14МБ7

[su_note note_color=”#defae6″]

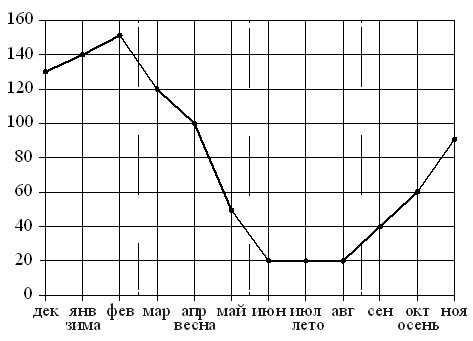
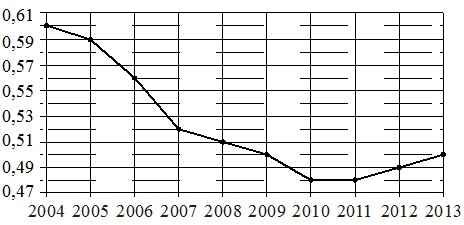
На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали – прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику прироста населения Китая в этот период.

[/su_note]

Алгоритм выполнения

1. Определяем цену деления вертикальной шкалы рисунка. Находится она как разница пары соседних значений шкалы, деленная на 2 (т.к. между двумя соседними значениями имеется 2 деления).
2. Анализируем последовательно приведенные в условии характеристики 1–4 (левая табличная колонка). Сопоставляем каждую из них с конкретным периодом времени (правая табличная колонка).

Решение:

Цена деления вертикальной шкалы составляет 0,01%.

1. Падение прироста непрерывно продолжалось с 2004 по 2010 год. В 2010–2011 годах прирост был стабильно минимальным, и начиная с 2012 года оно начал увеличиваться. Т.е. остановка прироста произошла в 2010 году. Этот год находится в периоде 2009–2011 гг. Соответственно, имеем: В–1.
2. Наибольшим падением прироста следует считать самую «круто» падающую линию графика на рисунке. Она приходится на период 2006–2007 гг. и составляет 0,04%, за год (0,59–0,56=0,04% в 2006 г. и 0,56–0,52=0,04% в 2007 г.). Отсюда получаем: А–2.
3. Указанный в характеристике №3 прирост начался с 2007 года, продолжился в 2008 г. и завершился в 2009 году. Это соответствует периоду времени Б, т.е. имеем: Б–3.
4. Прирост населения начал увеличиваться после 2011 г., т.е. в 2012–2013 гг. Поэтому получаем: Г–4.

Вариант 14МБ8

[su_note note_color=”#defae6″]

На рисунке изображены график функции и касательные, проведенные к нему в точках с абсциссами А,В,С и D.

В правом столбце указаны значения производной функции в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

[/su_note]

Алгоритм выполнения

1. Рассматриваем пару касательных, имеющих острый угол с положит.направлением оси абсцисс. Сравниваем их, находим соответствие среди пары соответствующих значений производных.
2. Рассматриваем пару касательных, образующих с положит.направлением оси абсцисс тупой угол. Сравниваем их по модулю, определяем соответствие их значениям производных среди двух оставшихся в правой колонке.

Решение:

Острый угол с положит.направлением оси абсцисс образуют производные в т.В и т.С. Эти производные имеют положит.значения. Поэтому выбирать тут следует между значениями №№1 и 3. Применяя правило о том, что если угол меньше 45⁰, то производная меньше 1, а если больше, то больше 1, делаем вывод: в т.В производная по модулю больше 1, в т.С – меньше 1. Это означает, что можно составить пары для ответа: В–3 и С–1.

Производные в т.А и т.D образуют с положит.направлением оси абсцисс тупой угол. И тут применяем то же правило, немного перефразировав его: чем больше касательная в точке «прижата» к линии оси абсцисс (к отрицат. ее направлению), тем больше она по модулю. Тогда получаем: производная в т.А по модулю меньше, чем производная в т.D. Отсюда имеем пары для ответа: А–2 и D–4.

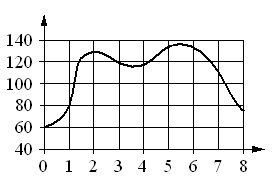
Вариант 14МБ9

[su_note note_color=”#defae6″]

На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры.

[/su_note]

Алгоритм выполнения

Анализируем последовательно характеристики 1–4 (правая колонка), используя график на рисунке. Ставим каждой из них в соответствие конкретный временной период (левая колонка).

Решение:

1. Рост температуры наблюдался только в конце периода 22–28 января. Здесь 27 и 28 числа она повышалась соответственно на 1 и на 2 градуса. В конце периода 1–7 января температура была стабильной (–10 градусов), в конце 8–14 и 15–21 января понижалась (с –1 до –2 и с –11 до –12 градусов соответственно). Поэтому получаем: Г–1.
2. Поскольку каждый временной период охватывает 7 дней, то анализировать нужно температуру, начиная с 4-го дня каждого периода. Неизменной в течение 3–4 дней температура была только с 4 по 7 января. Поэтому получаем ответ: А–2.
3. Месячный минимум температуры наблюдался 17 января. Это число входит в период 15–21 января. Отсюда имеем пару: В–3.
4. Температурный максимум пришелся 10 января и составил +1 градус. Эта дата попадает в период 8–14 января. Значит, имеем: Б–4.

Вариант 14МБ10

[su_note note_color=”#defae6″]

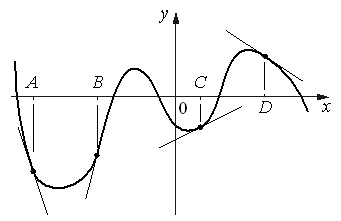
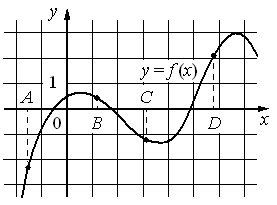
На рисунке изображен график функции y=f(x) и отмечены точки А, В, С и D на оси Ох..

Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и ее производной

[/su_note]

Алгоритм выполнения

1. Значение функции в точке положительно, если эта точка расположена выше оси Ох.
2. Производная в точке больше нуля, если касательная к этой точке образует острый угол с положительным направлением оси Ох.

Решение:

Точка А. Она находится ниже оси Ох, значит значение функции в ней отрицательно. Если провести в ней касательную, то угол между нею и положит.направлением Ох составит около 90⁰, т.е. образует острый угол. Значит, в данном случае подходит характеристика №3. Т.е. имеем: А–3.

Точка Б. Она находится над осью Ох, т.е. точка имеет положит.значение функции. Касательная в этой точке будет довольно близко «прилегать» к оси абсцисс, образуя тупой угол (немногим меньше 180⁰) с положительным ее направлением. Соответственно, производная в этой точке отрицательна. Т.о., здесь подходит характеристика 1. Получаем ответ: В–1.

Точка С. Точка расположена ниже оси Ох, касательная в ней образует большой тупой угол с положит.направлением оси абсцисс. Т.е. в т.С значение и функции, и производной отрицательно, что соответствует характеристике №2. Ответ: С–2.

Точка D. Точка находится выше оси Ох, а касательная в ней образует с положит.направлением оси острый угол. Это говорит о том, что как значение функции, так и значение производной здесь больше нуля. Ответ: D–4.

Вариант 14МБ11

[su_note note_color=”#defae6″]

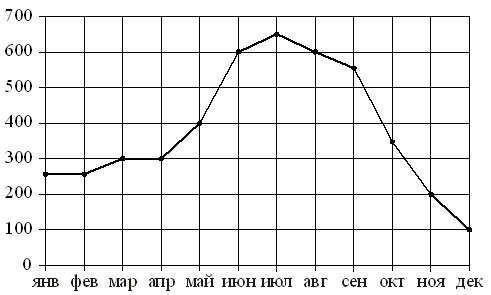
На рисунке точками показаны объемы месячных продаж холодильников в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных холодильников. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.

[/su_note]

Алгоритм выполнения

1. При необходимости найти кол-во холодильников за тот или иной период нужно определять их сумму за три месяца.
2. Анализировать следует характеристики 1–4 (правая колонка), находя для каждой из них соответствие в виде временного периода (левая колонка).

Решение:

Анализируем характеристики:

1. Меньше всего холодильников продано в начале и в конце года. Поэтому рассмотрим периоды январь–март и октябрь–декабрь. В январе–марте было продано примерно 250+250+300=800 холодильников, в октябре–декабре – примерно 350+200+100=650. Значит, здесь подходит все-таки последний период. Ответ: Г–1.
2. Длительный рост продаж наблюдался с апреля по июль. Это время охватывает полностью период апрель–июнь и захватывает начало следующего. Поэтому получаем: Б–2.
3. Тут тоже требуется найти сумму проданных единиц за целые периоды. Для 1-го и последнего периода она уже найдена (см.п.1). Считаем для 2-го и 3-го, получаем: 300+400+600=1300 – в апреле–июне, примерно 650+600+550=1800 – в июле–сентябре. К требуемым 800 холодильникам максимально приближен объем продаж в январе–марте. Поэтому имеем: А–3.
4. Одинаковое падение объема продаж означает, что разница между кол-вом проданных холодильников должна быть одинаковой. Падение продаж наблюдалось, начиная с конца июля. В августе падение составило 650–600=50 штук, в сентябре – 600–550=50 штук. Далее, в октябре, разница составила уже 550–350=200 холодильников, в ноябре 350–200=150, в декабре 200–100=100. Т.о., подходит в данном случаем период июль–сентябрь. Ответ: В–4.

Вариант 14МБ12

[su_note note_color=”#defae6″]

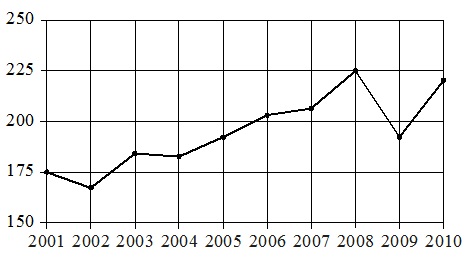
На рисунке точками показан годовой объем добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали – объем добычи угля в миллионах тонн. Для наглядности точки соединены линиями.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов характеристику добычи угля в этот период.

[/su_note]

Алгоритм выполнения

1. Точки, которые не приходятся на точные значения шкалы вертикальной оси, определяем приблизительно.
2. Анализируем по очереди приведенные (в правом столбце) характеристики, используя данный график. Определяем соответствие каждой из них конкретного временного периода.

Решение:

Анализируем характеристики:

1. Объем добычи меньше 190 млн т приходился на период с 2001 года по 2005 год. Затем спад добычи зафиксирован в 2009 году, но один год не составляет периода. 2001–2005 годы полностью попадают в период А (2002–2004 гг.). Поэтому получаем ответ: А–1.
2. Такая формулировка «объем… сначала уменьшался, а затем начал расти» соответствует 2 периодам – 2002–2003 гг. и 2009–2010 гг. Но т.к. первый из этих периодов уже взят в качестве ответа, то правильно здесь использовать пару Г–2.
3. Ситуация, описанная в 3-й характеристике, наиболее точно отображена в периоде 2006–2008 гг. Именно в это время добыча сначала понемногу увеличивалась (примерно с 190 млн т до 210), а потом резко возросла до 250 млн т. Т.е. подходящий ответ здесь: 2006–2008 гг. и, соответственно, имеем: В–3.
4. Медленный рост следует искать в период, когда линия графика имеет наиболее пологий вид. Это: 2004–2006 год, что соответствует периоду Б, т.е. получаем: Б–4.

Вариант 14МБ13

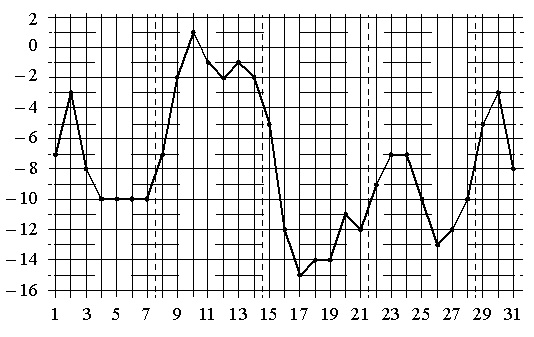
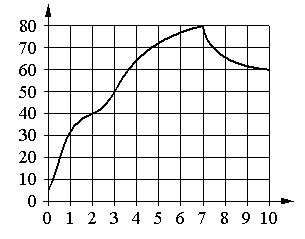
[su_note note_color=”#defae6″]

На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси – температура двигателя в градусах Цельсия.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику температуры.

[/su_note]

Алгоритм выполнения

Анализируем сначала очередную характеристику, а затем сопоставляем ее с конкретным временным интервалом.

Решение:

1. Выше 60⁰ температура была с 4-й по 7-ю минуту. Поэтому здесь нужно взять интервал 4–6 мин. Получаем: В–1.
2. Температура падала только после 7-й минуты. Соответственно, тут подходит интервал 7–9 мин. Ответ: Г–2.
3. Самый быстрый рост температуры происходил там, где график имеет наиболее «крутой» вертикальный подъем. Это имеет место только в 1-ю минуту нагревания. Т.е. подходящим интервалом является 0–1 мин. Ответ: А–3.
4. В пределах 40–50 ⁰С температура имела место, начиная со 2-й по 3-ю минуту. Значит, нужно выбрать интервал 2–3мин. Ответ: Б–4.

Вариант 14МБ14

[su_note note_color=”#defae6″]

На графике изображена зависимость частоты пульса гимнаста от времени в течение и после его выступления в вольных упражнениях. На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси – частота пульса (в ударах в минуту).

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.

[/su_note]

Алгоритм выполнения

1. Для анализа характеристики нужно использовать только 1-ю половину графика.
2. Для точек графика, которые не попадают в «узлы» сетки рисунка (т.е. для которых невозможно определить точные значения), нужно определять значения приблизительно.
3. Величина роста пульса связана с пологостью (или, напротив, крутизной) линии графика. Это означает, что чем большее изменение значения функции происходит за тот или иной (но обязательно одинаковый) промежуток времени, тем больше величина роста.

Решение:

Анализируем предложенные характеристики:

1. Если частота пульса сначала падала, а затем росла, то на графике это должно выразиться в «прогибе» линии графика вниз. Такая кривизна наблюдается только в течение 3–4 минуты. Значит, получаем ответ: Г–1.
2. Самый большой «подъем» линии на 1-й половине графика имеет место с 1-й по 2-ю минуту. Отсюда получаем: Б–2.
3. Частота пульса падала, начиная со 2-й минуты. В течение 3–4 минут тоже наблюдалось падение, однако оно потом перешло в рост. Поэтому правильным здесь следует считать интервал В. Т.о., ответ: В–3.
4. Единственный интервал, на котором частота не превысила 100 ударов, – 0–1 мин. Отсюда имеем ответ: А–4.

Даниил Романович | Просмотров: 21.2k

Как часто школьники сталкиваются с проблемой нехватки времени на экзамене! А ведь для решения последнего примера не хватило всего 10 минут… Чтобы избежать подобных ситуаций существует такое понятие, как рационализация. Этот метод позволяет сократить время на решение показательных функций в 4-5 раз. К сожалению, рационализацию не всегда преподают в школе, хотя она могла бы серьезно помочь выпускникам при решении 14 задания ЕГЭ по математике.

Не стоит отчаиваться – перед вами цикл видео, посвященных этой теме. С их помощью вы сможете легко справляться с решением различных логарифмических примеров. Главный эксперт ЕГЭ и член проверочной комиссии Михаил Попов рассмотрит несколько видов рационализации.

Перед вами первое видео, где рассматривается пример типа: log_x(х-3)*log₃(х²-3)*log_x2(х+4)≥0. Казалось бы, миссия невыполнима, но, помимо проверенного метода “в лоб”, есть возможность применить метод замены множителя. Это более простой способ решения подобных задач – нужно только немного попрактиковаться его использовать.

Подробный разбор задания 14 ЕГЭ по математике 2023. Рационализация ч. 2

В следующем видео наш эксперт рассмотрит еще один случай, когда рационализация достаточно часто встречается и применяется. Речь идет о примере, где логарифмы имеют одинаковые основания. В задании 14 ЕГЭ по математике профильный уровень 2023 года бывают и разные основания логарифмов – в этом случае, чтобы применить рационализацию, сначала необходимо привести их к одному основанию.

Всего за несколько минут опытный преподаватель Михаил Попов в прямом смысле разжует тему и разложит по полочкам все корни неравенства. Вы также узнаете, за что можно получить минус балл и на какие моменты обратить внимание при записи ответов в бланки.

Как решать неравенства – разбор 14 задания ЕГЭ по математике

Снова разбираем пример с одинаковыми основаниями типа: a^b>a^c. Берем ту же табличку, которую использовали в предыдущих роликах, и заполняем. После наносим полученные значения на график функции и получаем искомый ответ. Оказывается, решение 14 задания ЕГЭ по математике не такое уже и сложное!

Использование рационализации и метода замены множителя позволит вам успешно справиться с показательными функция на ЕГЭ. Несколько баллов плюсом – это отличная заявка на получение аттестата с отличными оценками. А без успешной сдачи ЕГЭ по математике вам не поступить в один из лучших российских ВУЗов, после которого можно устроиться на высокооплачиваемую работу.

Хотите пройти полный курс? Записывайтесь на бесплатный пробный урок по математике! Опытные преподаватели и проверенная программа обучения в учебном центре Годограф дают каждому возможность сдать на 80+ баллов такой сложный предмет, как математика.