1543 вступительные экзамены 8 класс - Exhelper.top

История школы

1 сентября 1975 года на Юго-Западе Москвы была открыта школа №43 им. Ю. А. Гагарина.

В 1994 году была преобразована в гимназию 1543.

Учебный процесс

Обучение проводится с 5 по 11 класс. С 5 по 7 класс ученики осваивают общеобразовательную программу с дополнениями в виде кружков и факультативов, которые позволяют углубиться в изучение профильных предметов.

В дополнение к кружкам есть вечерняя школа, в которую может прийти любой желающий в любой день.

В школе реализовано 4 профиля (начиная с 8 класса):

гуманитарный,
биологический,
математический,
физико-химический.Обучение по профильным предметам проходит в подгруппах.

Ученики гимназии участвуют в различных олимпиадах,конференциях и семинарах, как внутришкольных, так и городских, общероссийских.

Для гимназистов предусмотрены различные стажировки, в том числе в Высшей школе Экономики.

Биологический профиль является одним из сильнейших в Москве. В процессе учебы много времени уделяется непосредственно практике, которая проводится на Черном море, на Белом море, в Тверской области, а так же в научных институтах (начиная с 10 класса).

Прием в школу 1543

Прием осуществляется в 5 и 8 классы, в остальные классы (кроме 11) возможен прием в течение года при наличии мест.

Для поступления в 5 класс необходимо сдать экзамены по математике и русскому языку.

Для поступления в 8 класс необходимо сдать русский язык, математику (во все профили, кроме гуманитарного, а в математический — письменно и устно), профильные предметы и метапредметное собеседование. Экзамены сдают на равных как ученики гимназии, так и ученики других школ.

Источник

Новый корпус Московской гимназии №1543 на Юго-Западе

Данная статья посвящена разбору демонстрационного варианта устной и письменной части вступительного экзамена по математике в 8 класс Московской гимназии № 1543 на Юго-Западе. Сам демовариант находится на официальном сайте гимназии в открытом доступе. Разбор представлен профессиональным репетитором, специализирующимся на подготовке школьников к вступительным экзаменам по математике и физике в гимназию 1543 г. Москвы.

Письменная часть экзамена по математике в гимназию 1543

1. Представьте число 3 в виде дроби, у которой числитель есть пятая степень натурального числа, а знаменатель — шестая степень натурального числа.

Из условия получаем, что , причём . То есть . Берём корень пятой степени из обеих частей: . Подбираем таким, чтобы результат извлечения корня пятой степени был натуральным. Подойдёт .

Находим теперь значение :

$[ a=3^4sqrt[5]{3cdot 3^4}=3^5=243. ]$

То есть искомое представление имеет вид:

$[ 3=frac{243^5}{81^6}. ]$

2. Вычислите:

$[ frac{8+222cdot 444cdot 888+444cdot 888cdot 1776}{2cdot 4cdot 8+444cdot 888cdot1776+888cdot 1776cdot 3552}. ]$

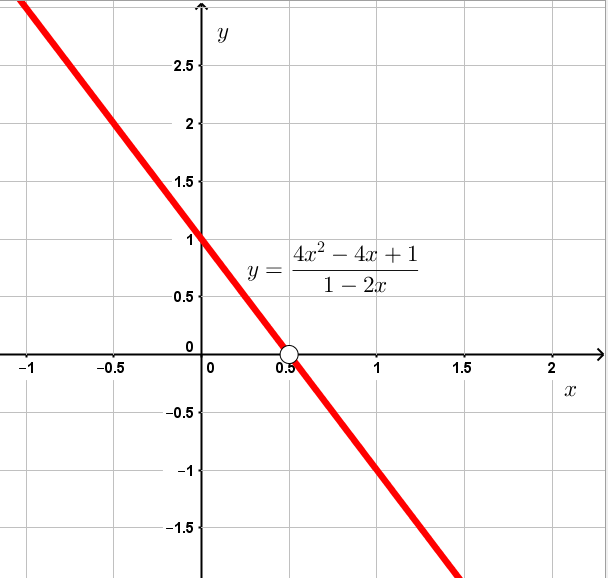
Пусть . Тогда имеем:

$[ frac{8+t+8t}{8cdot 8+8t+64t}=frac{8+t+8t}{8cdot(8+t+8t)}=frac{1}{8}. ]$

3. Постройте график функции

$[ y=frac{4x^2-4x+1}{1-2x}. ]$

Область определения данной функции задаётся неравенством , поскольку в знаменателе дроби не может быть нуля. То есть , но $xne frac{1}{2}$ :

Упростим выражение, стоящее справа:

$[ frac{4x^2-4x+1}{1-2x}=frac{(2x-1)^2}{1-2x}=frac{(1-2x)^2}{1-2x} = 1-2x. ]$

То есть график исходной функции — это график линейной функции , из которой удалена точка с абсциссой $x=frac{1}{2}$ .

4. Есть два сплава меди с цинком. В первом отношение массы меди к массе цинка 2:1, во втором — 3:2. Сколько килограммов первого и второго сплава нужно взять, чтобы получить сплав, в котором 17 кг меди и 27 кг цинка?

Пусть мы взяли кг первого сплава и кг второго сплава. Тогда общая масса меди в обоих сплавах равна $frac{2}{3}x+frac{3}{5}y$ , и она равна 17 кг. А общая масса цинка в обоих сплавах равна $frac{1}{3}x+frac{2}{5}y$ , и она равна 27 кг. То есть имеет место следующая система уравнений:

$[ begin{cases} frac{2}{3}x+frac{3}{5}y = 17 \ frac{1}{3}x+frac{2}{5}y = 27. end{cases} ]$

У этой системы нет решений в положительных числах. Ответ к этой системе . Скорее всего преподаватели гимназии 1543 на Юго-Западе устали проверять вступительные по математике и ошиблись в условии. Подразумеваю, что вместо фразы «сплав, в котором 17 кг меди и 27 кг цинка» имелась ввиду фраза «сплав, в котором 17 кг цинка и 27 кг меди». Если так, то система принимает вид:

$[ begin{cases} frac{2}{3}x+frac{3}{5}y = 27 \ frac{1}{3}x+frac{2}{5}y = 17. end{cases} ]$

Умножаем обе части второго уравнения на 2 и вычитаем почленно из второго уравнения первое. В результате получаем следующее уравнение: $frac{1}{5}y=7$ , откуда получаем кг. Подставляем это значение в первое уравнение и получаем $frac{2}{3}x=6$ , откуда кг. То есть нужно взять 9 кг первого сплава и 35 кг второго.

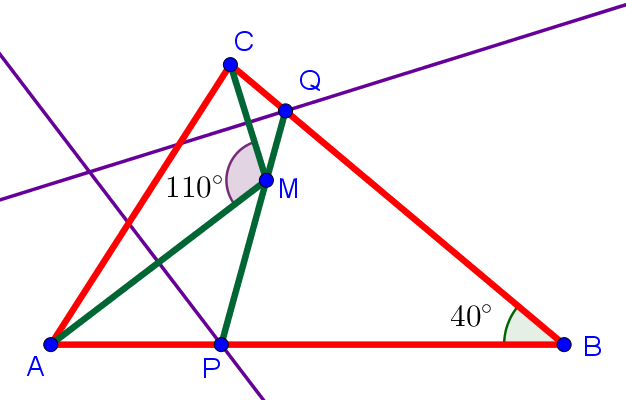
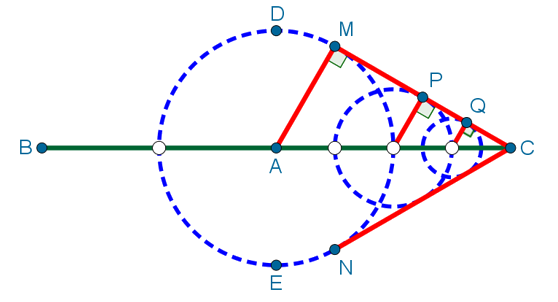
Изобразим ситуацию на рисунке:

Фиолетовыми линиями на рисунке обозначены срединные перпендикуляры. Все точки срединного перпендикуляра к отрезку равноудалены от концов этого отрезка. Значит, CQ = QM и AP = PM. То есть треугольники CQM и APM — равнобедренные. Углы при их основаниях равны. То есть

(1)

Рассмотрим треугольник AMC. В этом треугольнике ∠AMC=110°. Значит, сумма оставшихся двух углов равна 70°, так как сумма углов в треугольнике равен 180°. То есть ∠CAM+∠ACM = 70°.

С другой стороны в треугольнике ABC ∠B=40°. Значит, по той же причине два оставшихся угла в сумме дают 140°. То есть ∠PAC+∠ACB = 140°. Вычитаем почленно из последнего уравнения предпоследнее и получаем:

$[ angle PAC-angle CAM+angle ACB-angle ACM = 140^{circ}-70^{circ}. ]$

Глядя на рисунок, получаем ∠PAM+∠MCQ=70°. С учётом равенств (1), получаем ∠CMQ+∠AMP=70°. То есть ∠CMQ+∠AMP+∠AMC=180°. То есть ∠PMQ — развёрнутый, то есть точки P, Q и M лежат на одной прямой. Что и требовалось доказать.

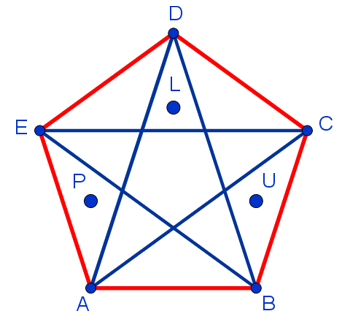
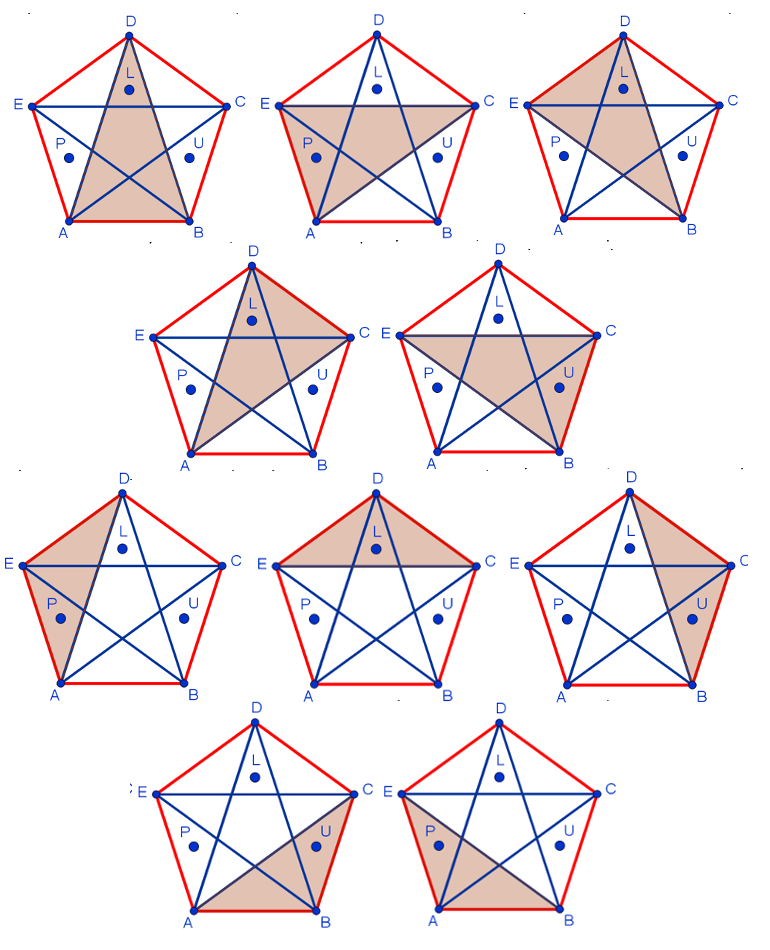
6. Какое минимальное количество точек надо поставить внутри выпуклого пятиугольника, чтобы внутри любого треугольника, вершинами которого являются вершины пятиугольника, оказалась по крайней мере одна точка?

Можно убедиться, что одной или двух точек не достаточно. Ни одна конфигурация в этом случае не подойдёт. А вот трёх точек уже достаточно. И расположить их внутри пятиугольника нужно следующим образом:

Действительно, в этом случае внутри любого треугольника, вершинами которого являются вершины пятиугольника, оказывается одна точка:

Итак, правильный ответ к этой задаче: 3.

Примечание. Понятно, что рисовать все эти конструкции на экзамене не нужно. Здесь они приведены исключительно из соображений наглядности.

Устная часть вступительного по математике в 8 класс Московской гимназии № 1543 на Юго-Западе

1. Можно ли поставить вместо звёздочек в выражении $frac{1}{2}*frac{2}{3}*frac{3}{4}dotsfrac{98}{99}*frac{99}{100}$ знаки арифметических действий так, чтобы его значение стало равно нулю (скобки использовать нельзя)?

Да, можно. Например, так:

$[ frac{1}{2}timesfrac{2}{3}timesfrac{3}{4}dotsfrac{8}{9}timesfrac{9}{10}-frac{10}{11}timesfrac{11}{12}dotsfrac{98}{99}timesfrac{99}{100}= ]$

$[ =frac{1}{10}-frac{10}{100}=frac{1}{10}-frac{1}{10}=0. ]$

Пусть — число столбцов в таблице. Поскольку сумма чисел в каждом столбца равна 10, то сумма всех чисел во всех столбцах равна . Аналогично, пусть — число строк в таблице. Поскольку сумма чисел в каждой строке равна 10, то сумма всех чисел во всех строках равна . Но сумма чисел во всех строках равна сумме чисел во всех столбцах, поскольку это одни и те же числа. То есть , то есть . Что и требовалось доказать.

3. Из трёхзначного числа вычли сумму кубов его цифр. Какое наибольшее число могло при этом получиться?

Пусть само число имеет вид , где , и — цифры этого числа, причём . Тогда само число равно , а его разность с суммой кубов его цифр равна:

Простым перебором убеждаемся, что первое слагаемое даёт максимальный вклад в общую сумму при , второе — при , третье — при или . То есть искомое число — это либо 621, либо 620. И в том, и в другом случае максимальная разность между самим числом и сумой кубов его чисел равна 396.

4. Белка собрала 10 орехов массой 100 г. Ни один орех не весит более 12 г. Всегда ли белка сможет раздать орехи двум своим бельчатам так, чтобы никто из них не обиделся. (Бельчонок обижается, если он получил а) хотя бы на 10 г меньше; б) более, чем на 10 г меньше, чем брат).

Нет, сможет не всегда. Предположим, что белка собрала 9 орехов массой по 11,1 г и 1 орех массой 0,1 г. Если их разделить между бельчатами, то у какого-то бельчонка окажется орех массой 0,1 г, а все остальные массой по 11,1 г, а у второго все орехи будут массой по 11,1 г. При попытке разделить их так, чтобы разница между общей массой орехов у каждого из бельчат была наименьшей, у первого бельчонка будет 4 ореха по 11,1 г и 1 орех массой 0,1 г (общая масса 44,5 г), а у второго — 5 орехов по 11,1 г (общая масса 55.5 г). Разница между массами орехов у бельчат составит 11 г. Значит, первый бельчонок обидится, как в случае а), так и в случае б).

5. Илья стоит на автотрассе Москва — Владимир, а мимо него проезжают машины: «МАЗ» (во Владимир), «Ауди» (в Москву) и «Камаз» (во Владимир). В тот момент, когда мимо Ильи проехал «МАЗ», «Ауди» и «Камаз» были от него на равных расстояниях. Когда мимо Ильи проехал «Ауди», «МАЗ» и «Камаз» были от него на равных расстояниях. Илья полагает, что когда мимо него проедет «Камаз», «МАЗ» и «Ауди» будут от него также на равных расстояниях. Прав ли он?

Пусть скорость машины «Ауди» составляет , скорость машины «МАЗ» составляет , скорость машины «Камаз» также составляет .

Рассмотрим сначала случай, когда сперва мимо Ильи проезжает «МАЗ». Пусть в этот момент расстояния от Ильи до машин «Ауди» и «Камаз» равны по . Тогда машина «Ауди» проедем мимо Ильи через . При этом машина «Камаз» в этот момент окажется от Ильи на расстоянии

$[ S_2=S_1-Kt_1=S_1-Kfrac{S_1}{A}=S_1left(1-frac{K}{A}right). ]$

Одновременно машина «МАЗ» отъедет от Ильи на расстояние то же (по условию) расстояние $S_2=Mt_1=S_1frac{M}{A}$ . Значит имеет место равенство:

$[ S_1left(1-frac{K}{A}right)=S_1frac{M}{A}=1-frac{K}{A}=frac{M}{A}Rightarrow A=K+M. ]$

После того, как мимо Ильи проедет «Ауди» должно пройти ещё времени, чтобы «Камаз» подъехал к Илье. Тогда расстояние от Ильи до «Ауди» станет равно $S_3=At_2=S_2frac{A}{K}$ . А расстояние от Ильи до «МАЗа» станет равно:

$[ S'_3=S_2+Mt_2=S_2+Mfrac{S_2}{K}=S_2left(1+frac{M}{K}right)= ]$

$[ =S_2frac{K+M}{K}=S_2frac{A}{K}. ]$

Значит . То есть в данном случае Илья прав. Второй случай, когда сперва мимо Ильи проезжает «Ауди», доказывается абсолютно аналогично. Ответ: Илья прав.

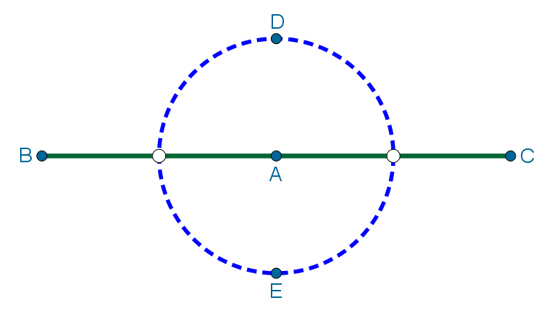
6. Петя стоит на прямолинейной дороге, проходящей по полю. Скорость движения Пети по полю 3 км/ч, а по дороге — 6 км/ч. Отметьте на рисунке те точки, куда Петя может дойти не более, чем за час.

Допустим, что в начальный момент Петя находится в точке A на прямолинейной дороге. Тогда он может пройти по дороге 6 км вправо или влево до точек A и B:
Он также может пойти из точки A по полю. Тогда после 1 ч движения он окажется в любой точке поля внутри круга радиусом 3 км. На рисунку DE — диаметр этого круга:

У Пети, однако, остаётся также вариант пройти сперва некоторое расстояние по дороге, а затем начать двигаться по полю. Например, если он пройдёт полчаса по дороге по направлению к точке C (см. рисунок выше), то он окажется ровно на середине отрезка AC. И у него остается ещё полчаса, чтобы добраться на любой точки на поле внутри круга радиусом $3timesfrac{1}{2}=1,5$ км:

Обратим внимание, что радиус круга получился вдвое меньше расстояния от центра этого круга до точки C. Фокус в том, что это соотношение остаётся постоянным для любой точка на дороге. Действительно, пусть Петя двигался до какой-то точки на дороге время ч, тогда оставшееся время движения составляет ч. За это время Петя может продолжить своё движение по дороге и пройти ч либо пойти по полю и оказаться в любой его точке внутри круга радиусом км, что вдвое меньше.

Сказанное означает, что если провести касательные к каждой изображённой окружности из точки C, то все радиусы этих окружностей, проведённые в точки касания, будут перпендикулярны касательным и будут вдвое меньше расстояний от центров этих окружностей до точки C. То есть каждая касательная будет наклонена под углом $30^{circ}$ к дороге и проходить через одну точку C. То есть на самом деле все эти касательные будут совпадать. Ко всем окружностям будет одна общая касательная:

Понятно, что абсолютно симметричная ситуация получилась бы, если бы Петя пошёл влево от точки A. То есть область, которая содержит все точки, куда Петя сможет дойти не более, чем за час, выглядит следующим образом:

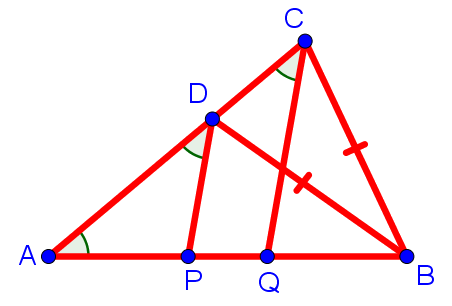
7. В треугольнике ABC на стороне AC выбрана точка D так, что BC = BD. На стороне AB выбраны точки P и Q так, что ∠PDA = ∠QCA = ∠BAC. Докажите, что AP = BQ.

На рисунке ситуация выглядит следующим образом:

Отметим сразу, что прямые PD и QC параллельны, поскольку равны соответственные углы ADP и ACQ при секущей DC. Кроме того, треугольники ADP и ACQ — равнобедренные с основаниями AD и AC, соответственно.

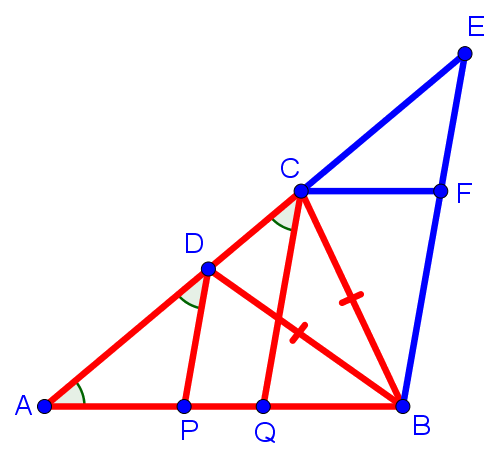
Выполним следующее дополнительное построение. Во-первых, проведём через точку B прямую, параллельную прямым DP и QC, затем продлим сторону AC до пересечения с этой прямой в точке E. Во-вторых, через точку C проведём прямую, параллельную стороне AB до пересечения с прямой BE в точке F. В результате получим следующий рисунок:

∠ADP = ∠ACQ = ∠AEB, так как эти углы соответственные при параллельных прямых DP, CQ и EB. То есть ∠EAB = ∠AEB. Значит, треугольник ABE — равнобедренный, и AB = BE,

Треугольник DBC — равнобедренный. Значит углы при его основании равны. То есть угол ∠BDC = ∠DCB. Значит, ∠ADB = ∠BCE, так как они смежные с ∠BDC и ∠DCB, соответственно.

Значит, два угла треугольника ADB соответственно равны двум углам треугольника BCE, поэтому равны и третьи углы. То есть ∠ABD = ∠EBC.

То есть равны треугольники ADB и CBE по двум сторонам и углу между ними (AB = BE, BD = BC и ∠ABD = ∠CBE). Значит, AD = CE.

Из этого следует, что по стороне и двум прилежащим к ней углам равны треугольники ADP и CFE (∠DAP = ∠ECF, ∠ADP = ∠CEF и AD = CE). Значит, AP = PD = CF = EF. Нам важно, что AP = CF.

По построению QCFB — параллелограмм. Значит, CF = QB, так как у параллелограмма противоположные стороны равны. Значит, AP = CF = QB. То есть AP = QB. Что и требовалось доказать.

8. В воскресенье каждый из учеников класса один раз побывал на катке. Известно, что каждый мальчик встретил там всех своих одноклассниц. Докажите, что либо все мальчики, либо все девочки из этого класса в какой-то момент были на катке одновременно.

Если найдутся какие-то два мальчика, которые не встретились друг с другом, то каждый из них должен был находиться на катке в тот момент, когда там были все девочки. Иначе эти мальчики встретились бы не со всеми девочками, что противоречит условию. Аналогично, если найдутся какие-то две девочки, которые не встретились друг с другом, то каждая из них должна была находиться на катке в тот момент, когда там были все мальчики. Иначе эти девочки встретились бы не со всеми мальчиками, что также противоречит условию. Значит был такой момент, когда либо все мальчики, либо все девочки были на катке одновременно. Что и требовалось доказать.

Вот такие задачи предлагаются для решения на вступительном экзамене по математике в 8 класс Московской гимназии №1543 на Юго-Западе. Если вам требуется помощь в подготовке к вступительным экзаменам по математике или физике в гимназию 1543, рекомендуем вам обратиться к профессиональному репетитору Сергею Валерьевичу, занимающемуся подготовкой школьников к этим экзаменам. Всю необходимую информацию о репетиторе и его занятиях вы сможете найти на этой странице. Успехов вам в подготовке и удачи на экзаменах!

Источник

Информация для поступающих

11 марта 2023 года (суббота) в 18:00 в актовом зале школы 1543 (старое здание, дом 3 корпус 5) состоится собрание для поступающих в 8 биолого-химический класс. Приглашаем поучаствовать в нем всех желающих 7-классников (учеников нашей и других школ) и их родителей.

Расписание вступительных экзаменов в 8-й биологический класс школы 1543 для учащихся других школ (на 2023-2024 год):

30 марта, 16:30 — математика (письменно)

4 апреля, 16:30 — биология (письменно)
21 апреля, 16:30 — русский язык (диктант), по приглашению приемной комиссии
23 апреля, с 11:00 — биология (устно), по приглашению приемной комиссии
13-15 мая — полевые практические занятия по ботанике, по приглашению приемной комиссии

Расписание вступительных экзаменов в 9 и 10 биологические классы школы 1543 для учащихся других школ,
дополнительный набор на 2023-2024 год:

4 апреля, 16.30 – биология (письменно)
6 апреля, 16.30 – математика (письменно), по вызову приемной комиссии
18 апреля, 16.30 – химия (письменно), по вызову приемной комиссии
21 апреля, 16.30 – русский язык (письменно), по вызову приемной комиссии
индивидуальные даты – собеседование по биологии, по вызову приемной комиссии

Все экзамены проходят в помещении школы 1543 по адресу
ул. 26 Бакинских комиссаров, д.3, корп.5

Телефоны для справок: 434-2658, 433-7629, 433-2644, 433-1644 (Сергей Менделевич Глаголев, Надежда Сергеевна Глаголева)

Информация для поступающих

Вступительные экзамены по набору в 8 классы биологического профиля проходят в школе N 1543 с марта по май.

Вступительные экзамены включают:

Письменный экзамен по математике (примеры заданий: для поступающих в 8, 9 и 10 классы)
Письменный экзамен по русскому языку (диктант)
Письменный экзамен по биологии (тест по программе 6-7 классов)
Устный экзамен по биологии в форме собеседования
Выездные занятия по ботанике

По этой ссылке можно ознакомиться с примерной программой письменного и устного экзаменов по биологии, и узнать подробнее про полевой выезд.

С успешно сдавшими вступительные экзамены и полевые занятия по ботанике проводится собеседование по иностранному языку для определения группы обучения (его результаты на зачисление в школу 1543 не влияют). В школе изучаются два иностранных языка — английский (3 часа в неделю) и французский или немецкий (по выбору учащегося, 2 часа в неделю).

Приказ о зачислении учащихся в гимназию издается директором по представлению приемной комиссии до 1 июня.

Зачисленные в гимназию в период до 5 июня должны представить следующие документы:

Заявление родителей с просьбой о зачислении.
Личное дело с итоговыми оценками за 7 класс и отметкой о переводе в следующий класс.
Медицинскую карту.

Источник

03.05.2019 17:21

Читаю их сайт и не пойму, какие экзамены нужно сдавать. Открыла расписание вступительных экзаменов — в марте была письменная математика (для всех профилей), а потом в апреле опять она же. Это для тех, кто не успел, или 2 математики все должны сдавать? С остальными предметами более-менее понятно все. И еще вопрос, раньше слышала по вечернюю школу у них (для абитуриентов), она сейчас существует?

03.05.2019 18:48

Возможностей сдать письменную математику действительно было 2 или 3. Во-первых, для тех, кто не успел. Во-вторых, для тех, кто поступал на два или больше профилей: на разные профили были разные по сложности варианты. Про вечернюю школу не подскажу, не в курсе.

Anonymous

03.05.2019 19:08

то есть можно один раз сдать, и если неудачно — второй раз попробовать? а если с 1го раза (в марте) все успешно. то 2ой раз уже необязательно (ну если не устная)

Anonymous

03.05.2019 22:07

Нет. Пересдавать, если неудачно, нельзя. Можно прийти второй раз и написать вариант для другого профиля. Кроме того, поступающий вообще не знает, удачно или неудачно он написал, до окончания всех вступительных. Это позиция приёмной комиссии, не объявлять промежуточных результатов, потому что ребёнок, огорчённый низким результатом первого экзамена, может на последующих выступить хуже, чем мог бы в хорошем настроении, а они хотят объективной картины. Как-то так.

Anonymous

03.05.2019 22:41

понятно! спасибо

Anonymous

03.05.2019 20:45

письменная математика сдается один раз. Но семиклассники школы ее пишут отдельно от поступающих со стороны. Затем сдается устная математика. Сейчас уже не помню, но возможно там давали несколько попыток. Это если маткласс. У других профилей и экзамены другие

Anonymous

Источник

В этой статье я делюсь информацией о поступлении и вариантами вступительных экзаменов в лучшие школы Москвы, такие как Лицей №1535, 57 школа, Лицей «Вторая школа», 179 школа, Гимназия на Юго-Западе №1543, Гимназия №1567, Гимназия №1514, Физико-математическая школа №2007, Курчатовская школа 2077, Школа «Интеллектуал», и другие школы.

АКТУАЛЬНЫЕ ДАННЫЕ 2021 года на сайте http://matolimp.ru/школы/вступительные-экзамены

Вся актуальная информация появляется на страницах matolimp в соцсетях. Подписывайтесь:
Telegram: https://telegram.me/matolimp
Инстаграм: https://www.instagram.com/matolimp/
Facebook: https://www.facebook.com/matolimp

Лицей №1535
Сайт школы
Правила поступления
Примеры вступительных испытаний
Вступительные задания в 7 класс:
Математика: программа вариант работы
Русский язык: программа вариант работы
Английский язык: программа вариант работы

Центр образования №57 (Пятьдесят седьмая школа)
Сайт школы
Информация о приёме в школу

Школа «Интеллектуал»
Вступительные испытания проходит в три тура
1 тур:
тест по математике и по руссокому языку
два задания по выбору
2 тур:
Защита самостоятельной исследовательской работы
3 тур:
Уроки с учителями школы

Средняя общеобразовательная школа №179
Сайт школы №179
Информация о наборе
Задание при поступлении в 7 класс

Гимназия №1567
Сайт школы
Информация о приёме
Экзаменационные материалы для поступающих в 5 класс 8 класс

Гимназия на Юго-Западе №1543
Сайт школы
Информация о приёме в 5 класс
Требования к знаниям поступающих в 5 класс
Вариант вступительных заданий в 5 класс
Информация о приёме в 8 класс
Требования к знаниям поступающих в 8 класс

Гимназия №1514
Сайт школы
Информация для поступающих в 5 класс 7 класс 8 класс
Вариант олимпиады для 4 классов с решениями
Вариант экзамена в 7 класс по математике
Вариант зкзамена в 7 класс по русскому языку
Экзаменационная работа по алгебре для поступающих в 8 класс
Билеты по геометрии для поступающих в 8 класс

Лицей «Вторая Школа»
Сайт школы
Подробная информация о поступлении
Задания прошлых лет на официальном сайте школы
Задания по математике в 6 класс 7 класс 8 класс
Задания по русскому языку в 6 класс 7 класс 8 класс

Курчатовская школа 2077
Курчатовская школа 2077 официальный сайт
Подробнее о поступлении в Курчатовскую школу 2077

Физико-математическая школа №2007
Сайт школы
Варианты заданий, предлагаемые на вступительных испытаниях в
5 класс устное задание письменное задание письменное задание 2
6 класс устное задание письменное задание письменное задание 2
7 класс устное задание письменное задание письменное задание 2

Олимпиады по математике для школьников 5, 6, 7 классов
Олимпиады по математике для начальных классов
Занятия по математике

Источник

Примеры и задачи из школьной программы50%

Олимпиадная математика40%

Школа 1543 набирает четыре пятых класса, по 25 – 30 в каждом. При поступлении в школу 1543 специализации нет, все классы равноценны. Разделение по направлениям происходит после 8 класса. В школе, помимо математики, традиционно сильна биология. Есть еще физхим и гуманитарный классы (тоже сильные).

На вступительных экзаменах всего два экзамена и всего два предмета: русский язык и математика. Их вес одинаков, за каждый дают до 50 баллов. Русский язык проходит в форме изложения, что нетипично, необычно и сложно для поступающих четырехклассников. Критерии поступления с одной стороны прозрачные – кто больше баллов набрал в сумме, тот и прошел. С другой стороны, субъективность при выставлении баллов, особенно за изложение, присутствует. Кстати, если баллы равные, то предпочтение тем, у кого лучше русский.

Математика попроще, чем в сильнейших физмат школах, задачи ближе к школьной программе, чем к олимпиадной математике. Тем не менее, с учетом того, что времени всего час на 6 – 7 задач, ребенок должен быть подготовленным и уверенным в себе. Нужно также следить за записью решения и ответа – на это обращают внимание.

Кроме того, есть особенность – в приемной компании школы 1543 нет потоков и вариантов сдачи экзаменов в разные дни: регистрация в апреле, во второй половине мая один экзамен, через пару дней второй экзамен и все (В 2020 году все несколько иначе). Второго шанса не дают. Соответственно, в день экзаменов возле школы столпотворение из родителей и детей. Дети заранее распределены по кабинетам (следите за процессом регистрации), но в сутолоке надо еще постараться не запутаться и вовремя попасть в нужное место. Все это добавляет стресса.

На первом экзамене (обычно это математика) отсева нет, результат объявляется только по итогам двух экзаменов.

Поступление в школу 1543 – замечательный выбор для увлеченных детей. Мне лично очень симпатична эта школа, ее философия и методики обучения.

Сжатая приемная компания – два экзамена

Русский и математика имеют равный вес

Большой набор – четыре пятых класса

Варианты вступительных экзаменов

Только реальные варианты прошлых лет, никаких пробников

Вступительный экзамен в школу 1543 — математика — 5 класс — 2016 — 1 — 2

Вступительный экзамен в школу 1543 — математика — 5 класс — 2019 — 1

Источник

Успешно готовлю к поступлению в 5 и 8 классы школы №1543 по английскому языку!

В Московской школе №1543 на юго-западе обучение проводится с 5 по 11 класс. С 5 по 7 классы осуществляется углубленное обучение отдельных предметов. С 8 класса начинается специализация по четырем предпрофилям: математическому, гуманитарному, биологическому и физико-химическому. С 7 класса можно посещать вечерние школу, где проводятся дополнительные занятия по подготовке в 8-е предпрофильные классы. Эти занятия бесплатные и проводятся учителями школы №1543.

Школа № 1543 работает уже более 40 лет и готовит учеников к поступлению в престижные вузы страны. В гимназии применяются эффективные и современные методы обучения, что стимулирует развитие и личностные характеристики учеников. В школе №1543 учителя стремятся научить учеников самостоятельно находить нужные сведения, развивать необходимые навыки для решения конкретных задач. В результате такого обучения учащиеся учатся самоконтролю, способности подходить к задачам творчески и эффективно выстраивать коммуникации с другими людьми.

Поступление в 5 класс гимназии № 1543

Каждый год гимназия проводит набор учащихся в 5 классы. Поступающие в 5 класс школы №1543 сдают письменный экзамен по математике и изложение с элементами сочинения по русскому языку. Ученики, успешно сдавшие вступительные экзамены, проходят устное собеседование по английскому языку. Поступающие в 5 класс должны знать программу И. И. Верещагиной и Т. А. Притыкиной «English-II» и «English-III». Устное тестирование состоит из пяти разделов, куда входят задания по грамматике, лексике, чтению.

Поступление в 8 класс гимназии №1543

Учащиеся поступают в 8 класс на конкурсной основе. Учащиеся сдают несколько предметов в зависимости от выбранной специализации. В математический класс сдают письменно математику, физику и русский язык и устно английский язык и вторую часть математики. В гуманитарный класс сдается математика, литература, русский язык письменно, история и английский язык устно. В физико- химический класс сдается математика, физика, русский язык письменно, физика и английский язык устно. В биологический класс — биология, математика, русский язык письменно, биология и русский язык устно.

Для успешного прохождения устного тестирования при поступлении в 8 класс школы №1543 учащиеся должны уметь соблюдать правильную интонацию при перечислении однородных членов предложения, с правильной интонацией произносить вопросы разных типов, соблюдать ударение в словах и фразах. На тестировании проверяется навык аудирования, умение чтения и понимания текста, умение составить монологическое высказывание на заданную тему (О себе, Школа, Досуг и т.д.) и владение грамматическими конструкциями.

Сколько занятий с репетитором нужно для поступления?

Количество необходимых занятий с репетитором для поступления в 5 и 8 классы в школу в №1543 может быть различным для всех учеников. Среди тем есть простые и сложные, и многие из них необходимо отрабатывать и закреплять длительно. Например, времена в английской грамматике часто могут вызывать затруднения у учащихся. И плохое понимание времен может привести к ошибкам, вследствие которых ребенок может написать работу хуже, чем необходимо для поступления. Более того, у ребенка могут быть хорошо развиты одни навыки, такие как чтение, письмо и совсем не развиты другие навыки, как восприятие информации на слух или построение предложения в соответствующем времени. Хороший репетитор сможет проработать необходимые темы и качественно подготовить ребенка к поступлению в 5 и 8 классы в школу №1543. При занятиях 2-3 раза в неделю с репетитором необходимо заниматься от 4 до 7 месяцев. Данного периода обычно хватает для способных и мотивированных детей, а для ребенка со среднем уровнем восприятия этого времени может оказаться недостаточно.

Записывайтесь на занятия как можно раньше!

Телефон для справок: 8 926 891-65-00

Источник

История школы

Учебный процесс

Прием в школу 1543

Письменная часть экзамена по математике в гимназию 1543

Устная часть вступительного по математике в 8 класс Московской гимназии № 1543 на Юго-Западе

Информация для поступающих

Варианты вступительных экзаменов

Поступление в 5 класс гимназии № 1543

Поступление в 8 класс гимназии №1543

Сколько занятий с репетитором нужно для поступления?

Новое и интересное на сайте: