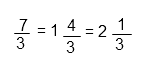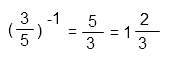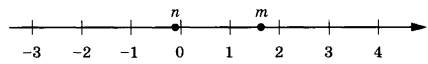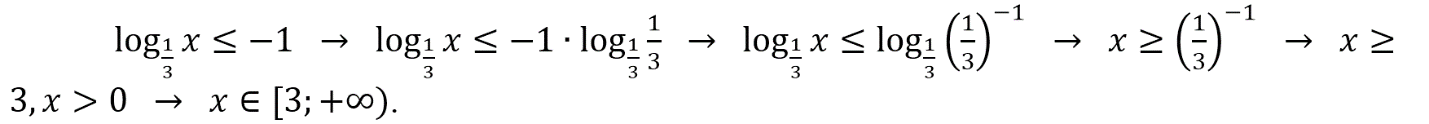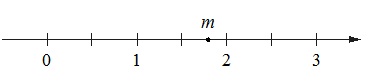Всё варианты 17 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 13 ЕГЭ по математике профильного уровня 2022 год (параметры)
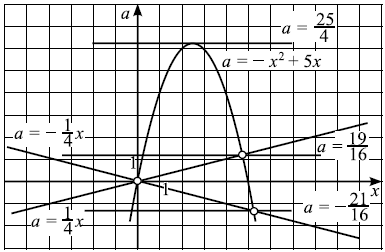
1) (28.03.2022 досрочная волна) Найдите все значения параметра a, при каждом из которых система уравнений
[ left{ {begin{array}{*{20}{c}} {frac{{x,{y^2} — 2,x,y — 4y + 8}}{{sqrt {4 — y} }} = 0,} \ {y = a,x,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,} end{array}} right. ]
имеет ровно три различных решения.
ОТВЕТ: (left( {0;1} right) cup left( {1;4} right).)
2) (28.03.2022 досрочная волна) Найдите все значения параметра a, при каждом из которых система уравнений
[ left{ {begin{array}{*{20}{c}} {frac{{x,{y^2} — 3,x,y — 3y + 9}}{{sqrt {x + 3} }} = 0,} \ {y = a,x,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,} end{array}} right. ]
имеет ровно два различных решения.
ОТВЕТ: (left( {0;frac{1}{3}} right] cup left{ 3 right}.)
3) (28.03.2022 досрочная волна) Найдите все значения параметра a, при каждом из которых система уравнений
[ left{ {begin{array}{*{20}{c}} {left( {x,{y^2} — 3,x,y — 3y + 9} right)sqrt {x — 3} = 0,} \ {y = a,x,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,} end{array}} right. ]
имеет ровно три различных решения.
ОТВЕТ: (left( {0;frac{1}{3}} right).)
4) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение
({x^2} + {a^2} + x — 7a = left| {,7x + a,} right|)
имеет более двух различных решений.
ОТВЕТ: (left[ { — 1;,0} right] cup left[ {,7;,8} right].)
5) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение
({x^2} + {a^2} — 2x — 6a = left| {,6x — 2a,} right|)
имеет два различных решения.
ОТВЕТ: (left( {2 — 2sqrt 5 ;4 — 2sqrt 5 } right) cup left( {0;,6} right) cup left( {2 + 2sqrt 5 ;4 + 2sqrt 5 } right).)
6) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение
(left| {{x^2} + {a^2} — 6x — 4a} right| = 2x + 2a)
имеет два различных решения.
ОТВЕТ: (left( { — 2;1 — sqrt 5 } right) cup left( { — 1;,0} right) cup left( {1 + sqrt 5 ;8} right).)
7) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение
(left| {{x^2} + {a^2} — 6x — 4a} right| = 2x + 2a)
имеет четыре различных решения.
ОТВЕТ: (left( {1 — sqrt 5 ;, — 1} right) cup left( {0;1 + sqrt 5 } right).)

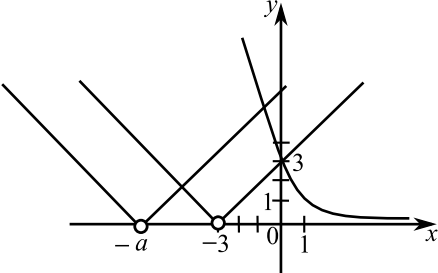
({a^2} + 2,a,x — 3{x^2} — 4a — 4x + 8left| x right| = 0)
имеет четыре различных решения.
ОТВЕТ: (left( {0;1} right) cup left( {1;,3} right) cup left( {3;4} right).)
9) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение
({a^2} — 9{x^2} + 18left| x right| — 9 = 0)
имеет два различных решения.
ОТВЕТ: (left( { — infty ; — 3} right) cup left{ 0 right} cup left( {3;infty } right).)
10) (27.06.2022 резервная волна) Найдите все значения параметра a, при каждом из которых уравнение
(sqrt {15{x^2} + 6ax + 9} = {x^2} + ax + 3)
имеет ровно три различных решения.
ОТВЕТ: (left[ { — 4;, — 3} right) cup left( { — 3;3} right) cup left( {3;,4} right].)
11) (27.06.2022 резервная волна) Найдите все значения параметра a, при каждом из которых уравнение
(sqrt {{x^4} — 4{x^2} + {a^2}} = {x^2} + 2x — a)
имеет ровно три различных решения.
ОТВЕТ: (left( { — infty ; — 4} right) cup left( { — 4;0} right).)
12) (27.06.2022 резервная волна) Найдите все значения параметра a, при каждом из которых уравнение
(sqrt x + sqrt {2a — x} = a)
имеет ровно два различных решения.
ОТВЕТ: (left[ {2;,4} right).)
Задание 17 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.
Конечно, за один день научиться решать такие задачи невозможно. И все-таки мы немного расскажем о том, как научиться решать задачи с параметрами. С чего начать. И какие вообще есть методы решения задач с параметрами.
Начнем с хорошей новости. Задача 17 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.
Если вы полны решимости получить на ЕГЭ заветные 4 первичных балла за задачу 17 (с параметром), не стоит начинать с реальных экзаменационных задач. Ведь мы хотим получить результат, а не разочарование! Поэтому сначала необходимо повторить следующие темы:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
4. Базовые элементы для решения задач с параметрами. Да, мы будем рисовать не только привычные функции. Но еще и окружности, ромбики, полуплоскости и всевозможные их комбинации.
5. Что такое параметр. Простые задачи с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому.
Читайте статью, смотрите видеокурс. И помните, что графический метод — хороший, но не единственный.
Потому что, кроме него, есть и другие:
— Квадратные уравнения и неравенства с параметрами.
— Задачи с параметрами. Условия касания.
— Метод оценки в задачах с параметрами.
— Использование четности функций в задачах с параметрами.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 17.
И не думайте, что это все возможные методы решения задач с параметрами. Их намного больше! Мы дали ссылки на те, которые встречаются чаще всего в задачах ЕГЭ.
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
1. Чтобы на ЕГЭ уверенно справиться с заданием 17, нужно решить не менее 50 задач с параметрами.
2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.
3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:
— Если в задаче с параметром можно сделать замену переменной — сделайте замену.
— Если задачу с параметром можно решить графически — решите графически.
4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь. Вот такая, например:
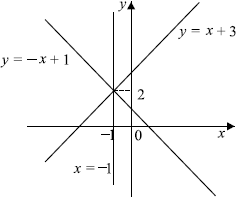
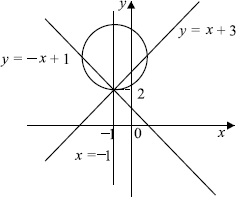
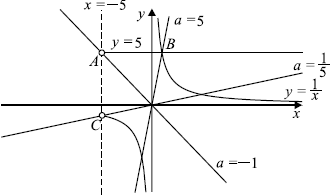
Задача 1. При каких значениях a системы и
равносильны?
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.
1) При — системы равносильны, так как обе не имеют решений.
2) При — второе уравнение имеет решение
которое является решением первой системы.
3) При
Система уравнений
Уравнение задает окружность с центром в начале координат и радиусом
Решениями системы:
являются две точки, в которых прямая пересекает окружность, заданную уравнением
А вот уравнение задает семейство параллельных прямых
Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением , пересекала только одну из этого семейства прямых, а именно прямую
, и не имела общих точек с другими прямыми из этого семейства.
Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса не имела общих точек с прямыми, параллельными прямой
, то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.
Когда же происходит касание в точках A и B?
В случае касания радиус окружности Мы легко находим это из прямоугольного треугольника СОА, где О — начало координат.
Значит, в случае касания , а если
— касания не происходит.
Объединяя случаи, получим, что системы равносильны, если
Легко? Если справились — вот еще одна интересная задача:
Задача 2. При каких значениях параметра a найдется такое значение параметра , что система уравнений
имеет ровно три различных решения?
Вот решение этой задачи.
Лучше всего осваивать эту непростую тему на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов. Или на интенсивах ЕГЭ-Студии в Москве. Удачи, друзья!
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 17. Задача с параметрами u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Неравенства и сравнения
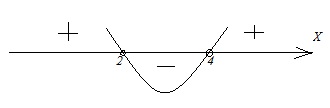
В семнадцатом задании нам необходимо сравнить данные числа с положением на координатной прямой или решить и сопоставить решения неравенств с областью на прямой. В данном задании можно пользоваться правилом исключения, поэтому достаточно правильно определить три решения из четырех, выбирая в первую очередь простые. Итак, приступим к разбору 17 задания базового варианта ЕГЭ по математике.
Разбор типовых вариантов заданий №17 ЕГЭ по математике базового уровня
Вариант 17МБ1
[su_note note_color=”#defae6″]
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ
А В С D |
ЧИСЛА
1) log2 10 2) 7/3 3) √26 4) (3/5)-1 |
[/su_note]
Алгоритм выполнения:
- Проанализировать рядом с каким из целых чисел стоит данная точка.
- Проанализировать на каком интервале лежат числа из правого столбца.
- Сравнить полученные интервалы и поставить в соответствие.
Решение:
- Рассмотрим точку А. Ее значение больше 1 и меньше 2.
- Рассмотрим точку B. Ее значение больше 2 и меньше 3.
- Рассмотрим точку С. Ее значение больше 3 и меньше 4.
- Рассмотрим точку D. Ее значение больше 5 и меньше 6.
- Вспомним что такое логарифм.
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.
Обозначение: loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.
В нашем случае а = 2, x = 10.
То есть нас интересует число 2b = 10. 23 = 8 и 24 = 16, следовательно, b лежит в промежутке от 3 до 4.
Следовательно, 7/3 больше 2 и меньше 3.
Рассмотрим √26. √25 = 5, √36 = 6. Значит, √26 больше 5 и меньше 6.
То есть (3/5)-1 больше 1 и меньше 2.
Поставим в соответствие полученные интервалы.
А – (3/5)-1 – 4
В – 7/3 – 2
С – log2 10 – 1
D – √26 – 3
Ответ: 4213.
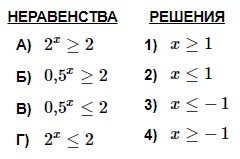
Вариант 17МБ2
[su_note note_color=”#defae6″]
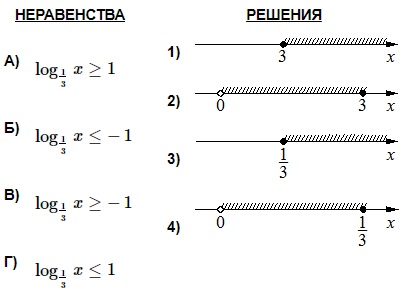
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения:
- Представить правые и левые части неравенств в виде степени одного и того же числа.
- Сравнить степени, так как основания равны.
- Поставить в соответствие предложенные интервалы.
Решение:
А)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
то есть, – вариант под номером 2.
Б)
Число 0,5 можно представить как , значит (0,5)x = (2-1) x = 2-x
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, – вариант под номером 1.
В)
Аналогично с вариантом Б.
Число 0,5 можно представить как , значит (0,5)x = (2-1) x = 2-x
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, – вариант под номером 4.
Г)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
и – вариант под номером 3.
Ответ: 2143.
Вариант 17МБ3
[su_note note_color=”#defae6″]
На прямой отмечены числа m и n.
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
[/su_note]
Алгоритм выполнения:
- Найти промежутки в которых лежат числа m и n.
- Оценить интервалы, в которых лежат выражения в левом столбце.
- Поставить им в соответствие интервалы из правого столбца.
Решение:
Из рисунка видно, что число n немного меньше 0, а число m много больше отстоит от 1. Следовательно, их сумма m+n даст число в пределах [1; 2] – вариант ответа под номером 3.
Число m>1, следовательно, при делении на 1 получим положительное число меньше 1. Добавляя небольшое отрицательное значение n останемся в диапазоне [0; 1]. Вариант ответа 2.
Произведение mn положительного и отрицательного чисел дают отрицательное число. Подходит только один вариант [-1; 0] под номером 1.
Г) Квадрат числа m много больше квадрата числа n, поэтому их разница будет положительной и принадлежать диапазону [2; 3] – вариант под номером 4.
Ответ: 3214.
Вариант 17МБ4
[su_note note_color=”#defae6″]
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Рассмотрим первое неравенство:
2x≥4
представим 4 как 22, тогда:
2x ≥ 22
x ≥ 2
Остальные неравенства решаются аналогичным образом, достаточно вспомнить, что 0,5 = ½ = 2-1:
2-x ≥ 4
2-x ≥ 22
-x ≥ 2
x≤-2
Ответ: А-4, Б-3, В-2, А-1.
Вариант 17МБ5
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Решаем по очереди каждое из неравенств (А–Г). При необходимости (для наглядности) отображаем полученное решение на координатной прямой.
- Записываем результаты в форме, которая предложена в столбце «Решения». Находим соответствующие пары «буква–число».
Решение:
А. 2–х+1 < 0,5 → 2–x+1 < 2–1 → –x+1 < –1 → –x < –2 → x > 2. Ответ: х ϵ (2; +∞). Получаем: А–3.
Б.
Неравенство преобразований не требует, поэтому сразу применяем метод интервалов, отобразив корни неравенства на координатной прямой.
Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х<0, то ответ в данном случае: х ϵ (–∞; 4).
Соответственно, имеем: Б–4.
В. log4x > 1 → log4x > log44 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.
Г. (х–4)(х–2) < 0. Здесь так же, как и в неравенстве Б, нужно сразу отобразить решение на координатной прямой.
Неравенство дано квадратное, его корни – х=2 и х=4. Для получения промежутков с положительными и отрицательными значениями схематически изображаем параболу, пересекающую координатную прямую в точках корней. Промежуток «внутри» параболы отрицательный, промежутки «вне» ее положительны. Т.к. в неравенстве дано «<0», то для ответа следует взять промежуток отрицательных значений. Учитываем, что неравенство строгое. Получаем: х ϵ (2; 4).
Ответ: Г–2.
Вариант 17МБ6
[su_note note_color=”#defae6″]
На координатной прямой отмечены точки А, В, С и D.

Число m равно √2.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
[/su_note]
Алгоритм выполнения
Для каждого из выражений правого столбца делаем следующее:
- Подставляем вместо m его числовое значение (√2). Вычисляем приблизительное значение.
- Ориентируясь на целую часть полученного числа, находим соответствующее значение на координатной прямой.
- Фиксируем пару «буква–число».
Решение:
Это значение на прямой находится между значениями –3 и –2 и соответствует точке А. Получили: А–1.
Число находится между значениями 2 и 3 и соответствует точке D. Имеем: D–2.
Число находится на прямой между 0 и 1. Это – точка С. Имеем: С–3.
Число размещается на прямой между значениями –1 и 0, что отображает т.В. Получаем: В–4.
Вариант 17МБ7
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Последовательно решаем каждое неравенство (А–Г), получая в ответе промежуток значений. Находим соответствующее ему графическое отображение в правой колонке (Решения).
- При решении неравенств учитываем, что: 1) при снятии знаков логарифма с основанием, меньшим 1, знак неравенства меняется на противоположный; 2) выражение под знаком логарифма всегда больше 0.
Решение:
А.
Полученный промежуток-ответ отображен на 4-й координатной прямой. Поэтому имеем: А–4.
Б.
Полученный промежуток представлен на 1-й прямой. Отсюда имеем: Б–1.
В. Это неравенство аналогично предыдущему (Б) с разницей исключительно в знаке. Поэтому и ответ будет подобен с той только разницей, что в конечном неравенстве будет противоположный знак. Т.е. получим: х ≤ 3, х > 0 → x ϵ (0; 3]. Соответственно, получаем пару: В–2.
Г. Это неравенство аналогично 1-му (А), но с противоположным знаком. Поэтому ответ здесь будет таким: х ≥ 1/3, х > 0 → х ϵ [1/3; +∞). Т.о., ответ: Г–3.
Вариант 17МБ8
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Решаем неравенство А. Находим номер соответствующего ответу решения из правой колонки.
- Рассматриваем неравенство Г как подобное неравенству А. Определяем для него номер решения из правого столбца.
- Решаем неравенство Б, перейдя к основанию 2. Определяем соответствующий для него номер варианта решения.
- По аналогии с неравенством Б решаем неравенство В.
Решение:
А. 2х ≥ 2 → 2х ≥ 21 → х ≥ 1. Имеем: А–1.
Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2.
Б. 0,5х ≥ 2 → (1/2)х ≥ 2 →2–х ≥ 21 х ≤ –1. Имеем: Б–3.
В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.
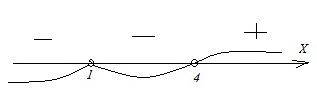
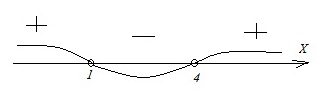
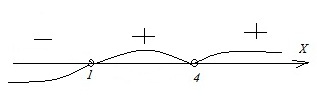
Вариант 17МБ9
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Подобные неравенства решаются методом интервалов. На координатной прямой отмечаются точки, являющиеся корнями соответствующего кв.ур-ния; промежутки между этими точками имеют определенные знаки, причем 1-й из них справа (от +∞ до самого большого корня) всегда имеет знак «+». Далее, продвигаясь справа налево, знаки чередуем, т.е. 2-й справа промежуток будет иметь знак «–», 3-й – «+» и т.д.
- Если в неравенстве имеется выражение вида (х–а)2, то знак промежутка при прохождении точки а не меняется.
- Поскольку все неравенства строгие, то точки-корни в промежутки для ответов не включаются, что в результате фиксируется посредством круглых скобок.
- Знак «ᴗ» является объединяющим и должен прочитываться как «или».
Решение:
Корнями в этих неравенствах являются х=1 и х=4.
Для неравенства А на прямой имеем:
Результатом здесь будут промежутки с отрицательным знаком, т.е. х < 1 или 1 < x < 4. Ответ: А–3.
Для неравенств Б и В получаем на прямой:
Для ответа в неравенстве Б следует взять промежутки со знаком «+». Получим: х < 1 или x > 4. Ответ: Б–1.
В неравенстве В нужно взять промежуток с отрицательным знаком. Тогда имеем: 1 < x < 4. Ответ: В–4.
Б. Отмечаем на прямой корни и промежутки с соответствующими знаками:
Для неравенства Г на прямой получили:
Результат – промежутки с положительным знаком. Тогда имеем: 1 < x < 4 или x > 4. Ответ: Г–2.
Вариант 17МБ10
[su_note note_color=”#defae6″]
На координатной прямой отмечены точки А, В, С и D.
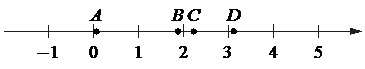
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
[/su_note]
Алгоритм выполнения
- Определяем приблизительное значение чисел, приведенных в правом столбце, или их целую часть, что позволит выяснить, между какими двумя целыми числами на координатной прямой они располагаются.
- Фиксируем пары «буква–число» для заполнения итоговой таблицы ответов.
Решение:
Число 1. log55=1, log525=log552=2log55=2·1=2. Т.к. 5<20<25, то 1<log520<2. Значит, на координатной прямой число log520 отображено точкой В. Ответ: В–1.
Число 2. . Это означает, что число отображено на прямой точкой С. Ответ: С–2.
Число 3. √10 совсем немного больше, чем √9=3. Это число точно меньше 4, поскольку 4=√16. Соответственно, √10 на прямой расположен между 3 и 4 и отображен точкой D. Ответ: D–3.
Число 4. 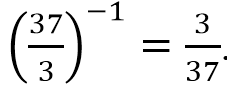
Вариант 17МБ11
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Решаем последовательно неравенства А–Г, учитывая ОДЗ.
- По результату (полученному простейшему неравенству) находим соответствующее графическое решение из правого столбца.
Решение:
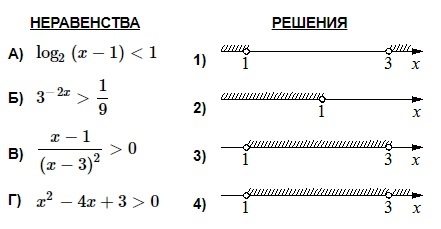
- log2 (x–1) < 1 → log2 (x–1) < log2 2 → x–1 < 2 → x < 3. ОДЗ: х–1 > 0 → x > 1.
Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.
- . ОДЗ не дает ограничений
Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.
- Здесь не требуются преобразования. Решается неравенство методом интервалов. Точки пересечения с координатной прямой: х=1, х=3. Тогда имеем:
Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.
- х2 – 4х + 3 > 0 → (x–1)(x–3) > 0. Применив метод интервалов, получим:
ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.
Вариант 17МБ12
[su_note note_color=”#defae6″]
На координатной прямой отмечено число m.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
[/su_note]
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Подставляем найденное значение для m последовательно в каждое из выражений (А–Г), вычисляем их числовые значения.
- Сопоставляем полученные числа с отрезками, предложенными в правом столбце, находим пары «буква–число» для ответа.
Решение:
Число m располагается на прямой между 1,5 и 2 и немного смещено от середины этого отрезка к двойке. Следовательно, наиболее точным для него является 1,8.
Число А. Имеем: √1,8. Известно, что √1=1, √2≈1,4. Т.е. √1,8 наверняка располагается на отрезке между 1 и 2. Ответ: А–1.
Число Б. Оно равно: 1,83=5,832, т.е. это число принадлежит промежутку [5; 6]. Ответ: Б–4.
Число В. Это число равно: 1,8+1=2,8, что соответствует отрезку [2; 3]. Ответ: В–2.
Число Г. Тут получаем: 6/1,8≈3,33. Этому значению соответствует отрезок [3; 4]. Ответ: Г–3.
Вариант 17МБ13
[su_note note_color=”#defae6″]
Число m равно √0,15.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
[/su_note]
Алгоритм выполнения
- Преобразуем число m так, чтобы вынести значение из-под корня.
- Подставляем последовательно полученную величину для m в каждое из выражений в левом столбце. Получаемые результаты соотносим с подходящим отрезком из правого.
Решение:
Число √0,15 очень немногим отличается от √0,16, а из 0,16 можно точно извлечь корень. Делая подобное приближение – всего на 0,01 – мы не выходим за пределы приемлемой абсолютной погрешности. Поэтому имеем право принять, что √0,15≈√0,16=0,4.
Находим значения выражений А–Г и определяем их соответствия отрезкам:
А. –1/0,4=–2,5. Результат соответствует отрезку [–3; –2]. Ответ: А–1.
Б. 0,42=0,16. Число входит в промежуток [0; 1]. Ответ: Б–3.
В. 4·0,4=1,6. Это число находится в интервале [1; 2]. Ответ: В–4.
Г. 0,4–1=–0,6. Результат попадает на отрезок [–1; 0]. Ответ: Г–2.
Вариант семнадцатого задания 2019 года (10)
[su_note note_color=”#defae6″]
На координатной прямой отмечено число m и точки А, В, С и D.
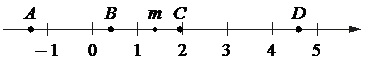
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
[/su_note]
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Вычисляем значения выражений 1–4, находим соответствие между полученными результатами и точками А–D на координатной прямой.
Решение:
Точка m располагается почти посередине между 1 и 2, но немного ближе к 1, чем к 2. Максимально приближенным к реальному в данном случае следует считать значение m=1,4.
Определяем соответствие чисел и точек на прямой:
- 6–1,4=4,6. Это значение отображено точкой D. Ответ: D–1.
- 1,42=1,96. Такое число отображается в точке С. Ответ: С–2.
- 1,4–1=0,4. Это число соответствует точке В. Ответ: В–3.
- Здесь можно не вычислять результат, поскольку имеет место единственное отрицательное число, а на прямой обозначена единственная точка слева от 0 – т.А. Ответ: А–4.
Даниил Романович | Просмотров: 18.6k
За это задание ты можешь получить 4 балла. На решение дается около 35 минут. Уровень сложности: высокий.
Средний процент выполнения: 4.2%
Ответом к заданию 17 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 17:
Для того, чтобы решить задачу необходимо составить математическую модель (уравнение, неравенство или функцию, которую нужно исследовать).
Для решения задач на кредиты, необходимо разобраться в основных схемах кредитования с дифференцированными и аннуитетными платежами. Часто для преобразования уравнения нужно знать формулы алгебраической и геометрической прогрессий.
В задачах на оптимизацию нужно уметь работать с функциями: брать производную, находить точки экстремумов.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
При каком значении $a$ множеством решений неравенства
${1+3^x} / {1+3^{-x}}>{3} / {|x+a|}$ является множество всех положительных чисел?
Решение
Сократив левую часть неравенства на $1 + 3^x$, получим равносильное неравенство $3^x > {3}/{|x + a|}$ или $3^{x-1} > {1}/{|x + a|}$. Так как обе части неравенства положительны, то ${1}/{3^{x-1}} < |x + a| (x ≠ -a)$ или $({1}/{3})^{x-1} < |x + a|$.
Графиком функции $y = ({1}/{3})^{x-1}$ является график функции $y = ({1}/{3})^x$ сдвинутый на $1$ единицу вправо вдоль оси $Ox$. Графиком функции $y = |x + a|$ является график функции $y = |x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x ≠ -a$, точка $(-a; 0)$ на графиках функций $y = |x + a|$ выколота.
Множество положительных чисел будет решением этого неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдет при $a = 3$. Графическая иллюстрация приведена на рисунке.
Ответ: 3
Задача 2
При каком значении $a$ множеством решений неравенства
${1+2^{-x}} / {1+2^x}>{4} / {√ {x^2+2ax+a^2}}$ является множество всех отрицательных чисел?
Решение
Сократив левую часть неравенства на $1+2^x$ и применив свойство квадратного корня $√ {m^2}=|m|$, получим равносильное неравенство ${1} / {2^x}>{4} / {|x+a|}$ или ${1} / {2^{x+2}}>{1} / {|x+a|}$. Так как обе части неравенства положительны, то $2^{x+2}<|x+a|$, при условии $x≠ -a$. Графиком функции $y=2^{x+2}$ является график функции $y=2^x$, сдвинутый на $2$ единицы влево вдоль оси $Ox$. Графиком функции $y=|x+a|$ является график функции $y=|x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x≠ -a$, точка $(-a;0)$ на графиках функций $y=|x+a|$ является выколотой (см. рис.). Множество отрицательных чисел будет решением неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдёт при $a=-4$. Графическая иллюстрация приведена на рисунке.
Ответ: -4
Задача 3
Найдите все значения параметра $a$, при каждом из которых система уравнений ${{table {y=a-x{,}}; {|x-2|(y+5x-10)=(x-2)^3};}$ имеет ровно четыре различных решения.
Решение
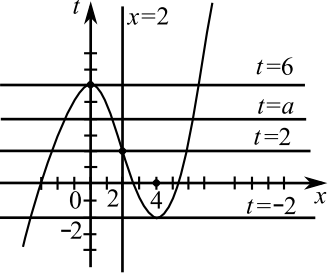
При замене $y + x = t$ получим систему уравнений ${{table t=a; {|x — 2|(t + 4x — 10) = (x — 2)^3};}$ которая имеет, столько же решений, что и заданная система.
График первого уравнения системы $t = a$ представляет собой прямую, параллельную оси абсцисс.
Построим график второго уравнения.
1) При $x ≥ 2$ получим $(x — 2)(t + 4x — 10) = (x — 2)^3$,
$(x — 2)(t + 4x — 10 — (x — 2)^2) = 0$,
$(x — 2)(t — x^2 + 8x — 14) = 0$,
$x — 2 = 0$ или $t — x^2 + 8x — 14 = 0$.
$x = 2$ — вертикальная прямая.
$t = x^2 — 8x + 14$ — парабола с вершиной $(4; -2), t(2) = 2$.
2) При $x < 2$ получим $-(x — 2)(t + 4x — 10) = (x — 2)^3$,
$(x — 2)(t + 4x — 10 + (x — 2)^2) = 0$.
$x — 2 = 0$ не выполняется при $x < 2$.
$t + 4x — 10 + (x — 2)^2 = 0, t = -x^2 + 6$ — парабола с вершиной $(0; 6), t(2) = 2$.
На рисунке изображен график второго уравнения полученной системы.
График прямой $t = a$ и уравнения $|x — 2|(t + 4x — 10) = (x — 2)^3$ имеют ровно $4$ общие точки при $-2 < a < 2, 2 < a < 6$.
Ответ: (-2;2);(2;6)
Задача 4
Найдите все значения параметра $a$, при каждом из которых уравнение ${x-4a} / {x+4}+{x-1} / {x-a}=1$ имеет единственный корень.
Решение
Преобразуем данное уравнение.
${(x — 4a)(x — a) + (x + 4)(x — 1) — (x + 4)(x — a)}/{(x + 4)(x — a)} = 0$,
${x^2 — ax — 4ax + 4a^2 + x^2 + 3x — 4 — x^2 + ax — 4x + 4a}/{(x + 4)(x — a)} = 0$,
${x^2 — x(4a + 1) + 4a^2 + 4a — 4}/{(x + 4)(x — a)} = 0$,
${tablex^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0; (x + 4)(x — a) ≠ 0;$.
Решим уравнение $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
$x = {(4a + 1) ±√{-8a + 17}}/{2}$
1. При $D < 0$ уравнение корней не имеет.
2. При $D = 0, -8a + 17 = 0, a = {17}/{8}$. Уравнение имеет единственный корень $x = {4a + 1}/{2}$ при $a = {17}/{8}. x = {4 · {17}/{8} + 1}/{2} = 4.75$.
Выполнено условие $x ≠ -4, x ≠ a$.
Значит, $a = {17}/{8} = 2.125$ удовлетворяет условию задачи.
3. При $D > 0$ уравнение имеет два корня.
$x = {(4a + 1) ±√{17 — 8a}/{2}$.
Проверим при каких значениях $a$ значения $x = -4$ и $x = a$ являются корнями уравнения $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
При $x = -4$ должно выполняться равенство $16 + 4(4a + 1) + 4a^2 + 4a — 4 = 0, a^2 + 5a + 4 = 0, a = -4, a = -1$.
При $x = a$ должно выполняться равенство $a^2 — 4a^2 — a + 4a^2 + 4a — 4 = 0, a^2 + 3a — 4 = 0, a = 1, a = -4$.
При $a = -1, a = 1$ исходное уравнение имеет единственный корень.
При $а=-4$, $D>0$ и корни $х=-4$ и $х=а$ совпадают, поэтому это значение параметра также подходит
Ответ: -4$;$-1$;$1$;$2.125
Задача 5
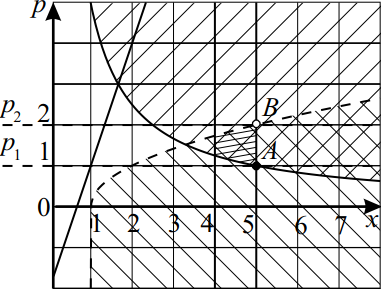
Найдите все значения параметра $p$, при каждом из которых система неравенств ${{table {px⩾ 5,}; {p<√ {x-1},}; {3x⩾ p+2};}$ имеет хотя бы одно решение на отрезке $[4; 5]$.
Решение
ОДЗ: $x ≥ 1$. Построим следующие графики $px = 5, p = √{x — 1}$ и $3x = p + 2$ в системе координат $Opx$ при $x > 0$ и изобразим решение системы
${tablep ≥ {5}/{x}; p < √{x — 1}; p ≤ 3x — 2;$
Из рисунка видно, что искомые значения $p$ удовлетворяют условию $p_1 ≤ p < p_2$.
Ординату точки $A$ можно найти, подставив $x = 5$ в уравнение $p = {5}/{x}; p_1 = {5}/{5} = 1$.
Ординату точки $B$ можно найти, подставив $x = 5$ в уравнение $p = √{x — 1}: p_2 = √{5 — 1} = √4 = 2$. Отсюда $p ∈ [1; 2)$.
Ответ: [1;2)
Задача 6
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2x+3)(4x^6-19x^4-x^2(5+4a)-a-17)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax — 2x+3 = 0$; при $x = 0$ получим $3=0$, это не верно.
При $x ≠ 0, a = {2x — 3}/{x}, a = 2 — {3}/{x}$.
По условию числа $a$ и $x$ целые, поэтому число ${3}/{x}$ тоже целое, что возможно при $x = ±1, x = ±3$.
При $x = 1$ получим $a = -1$,
при $x = -1$ получим $a = 5$,
при $x = 3$ получим $a = 1$,
при $x = -3$ получим $a = 3$.
2) $4x^6 — 19x^4 — 5x^2 — 4ax^2 — a — 17 = 0$,
$a(4x^2 + 1) = 4x^6 — 19x^4 — 5x^2 — 17$,
$a = {4x^6 — 19x^4 — 5x^2 — 17}/{4x^2 + 1}$.
$a = x^4 -5x^2 — {17}/{4x^2 + 1}$. Так как $a$ и $x$ — целые числа, то ${17}/{4x^2 + 1}$ тоже целое число. Это возможно при $4x^2 + 1 = 1$ или $4x^2 + 1 = 17$.
$x^2 = 0, x = 0, a = 0 — 0 — 17 = -17$;
$x^2 = 4, x = ±2, a = 2^4 — 5·2^2 — {17}/{4·2^2 + 1} = -5$.
Уравнение имеет хотя бы один целый корень при значениях $a$, равных $-17; -5; -1; 1; 3; 5$.
Ответ:
Задача 7
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2-x)(3x^5+7x^3+2x+4-3x^2a-a)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax — 2 — x = 0$; при $x ≠ 0$ получим $a = {2 + x}/{x} = 1 + {2}/{x}$.
Так как по условию $a$ и $x$ целые числа, то ${2}/{x}$ тоже целое число. Это возможно, если $x = ±1$ или $x = ±2$.
$x = 1; a — 2 — 1 = 0; a = 3;$
$x = -1; -a — 2 — (-1) = 0; a = -1;$
$x = 2; 2a — 2 — 2 = 0; a = 2;$
$x = -2; -2a — 2 — (-2); a = 0.$
Если $x = 0$, то $0 — 2 — 0 = 0$ не выполняется.
2) $3x^5 + 7x^3 + 2x + 4 — 3x^2a — a = 0,$
$a(3x^2 + 1) = 3x^5 + 7x^3 + 2x + 4,$
$a = {3x^5 + 7x^3 + 2x + 4}/{3x^2 + 1}$
$a = x^3 + 2x + {4}/{3x^2 + 1}$. Поскольку $a$ и $x$ — целые числа, то ${4}/{3x^2 + 1}$ также целое число. Это возможно, если $3x^2 + 1 = 4$, или $3x^2 + 1 = 2$, или $3x^2 + 1 = 1$.
Получаем $x^2 = 1$ или $3x^2 = 1$ или $x^2 = 0$.
Целые корни:
$x = 1$, тогда $a = 1^3 + 2·1 + {4}/{3·1^2 + 1} = 4$;
$x = -1$, тогда $a = (-1)^3 + 2·(-1) + {4}/{3·(-1)^2 + 1} = -2$;
$x = 0$, тогда $a = 0 + 0 + 4 = 4$.
Целые корни есть при значениях $a: -2; -1; 0; 2; 3; 4$.
Ответ: -2$;$-1$;$0$;$2$;$3$;$4
Задача 8
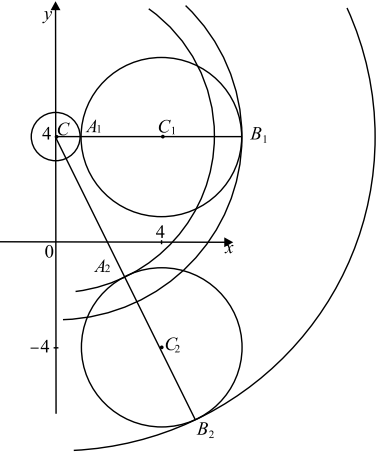
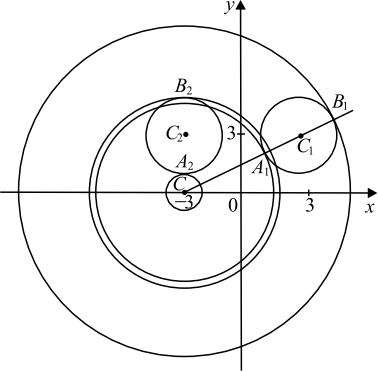
Найдите все значения $a > 0$, при каждом из которых система
${table(x — 4)^2 + (|y| — 4)^2 = 9; x^2 + (y — 4)^2 = a^2;$
имеет ровно $2$ решения.
Решение
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(4; -4)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a < 1$ окружности $∅$ и $∅_1$ не пересекаются, при $1 < a < 7$ окружности $∅$ и $∅_2$ имеют $2$ общие точки.
Из точки $C$ проведём луч $CC_2$ и обозначим $A_2$ и $B_2$ точки его пересечения с окружностью $∅_2$, где $A_2$ лежит между $C$ и $C_2$. Заметим, что длина отрезка $CC_2 = √{4^2 + (4-(-4))^2} = √{80} = 4√5$.
При $a < CA_2$ или $a > CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 < a < CB_2$ окружности $∅$ и $∅_2$ имеют $2$ общие точки. При $a = CA_2 = 4√5 − 3$ или $a = CB_2 = 4√5 + 3$, окружности $∅$ и $∅_2$ касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность $∅$ с одной из окружностей $∅_1$ и $∅_2$ имеет $2$ общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как $1 < 4√5 − 3 < 7 < 4√5 + 3$, то условию задачи удовлетворяют значения $a ∈ (1; 4√5 − 3) ∪ (7; 4√5 + 3).$.
Ответ: $(1;4√5-3)∪(7;4√5+3)$
Задача 9
Найдите все значения $a > 0$, при каждом из которых система
${table(|x| — 3)^2 + (y — 3)^2 = 4; (x + 3)^2 + y^2 = a^2;$
имеет единственное решение.
Решение
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(−3; 3)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √{6^2 + 3^2} = √{45} = 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a < CA_1$ или $a > CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 < a < CB_1$ окружности $∅$ и $∅_1$ имеют $2$ общие точки. При $a = CA_1 = 3√5 − 2$ или $a = CB_1 = 3√5 + 2$, окружности $∅$ и $∅_1$ касаются.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_2(−3; 1)$ и $B_2(−3; 5)$. То есть при $a = 1$ и $a = 5$ окружности $∅$ и $∅_2$ касаются. При остальных значениях параметра $a$ окружности $∅$ и $∅_2$ либо имеют $2$ общие точки, либо не имеют общих точек.
Исходная система имеет единственное решение тогда и только тогда, когда окружность $∅$ касается ровно одной из двух окружностей $∅_1$ и $∅_2$ и не пересекается с другой.
Так как $1 < 3√5 − 2 < 5 < 3√5 + 2$, то условию задачи удовлетворяют только числа $a = 1$ и $a = 3√5 + 2$.
Ответ: $1;3√5+2$
Задача 10
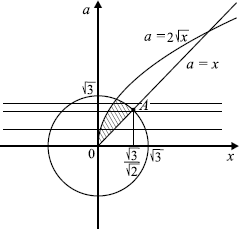
Найдите все значения параметра $a$, при каждом из которых решение неравенства ${(2√x — a)(a — x)}/ {√{3 — a^2 — x^2}}≥ 0$ содержит отрезок длины не менее $0.5$.
Решение
${(2√x — a)(a — x)}/{√{3 — a^2 — x^2}} ≥ 0$. Попробуем преобразовать неравенство к более простому виду. Заметим, что знаменатель влияет только на ОДЗ. Поэтому неравенство равносильно системе ${table (2√x — a)(a — x) ≥ 0; 3 — a^2 — x^2 > 0;$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично ${table (2√x — a)(a — x) ≤ 0; a^2+x^2 < 3;$
Изобразим множество решений системы в системе координат $Oxa$. Решению соответствует заштрихованная область. При этом каждому фиксированному значению $a$ соответствует горизонтальная прямая. При фиксированном значении a решениями системы будут $x$, равные абсциссам тех точек горизонтальной прямой, которые лежат в заштрихованной области.
Прямая $a = x$ пересекает окружность $x^2 + a^2 = 3$ при $a = x = {√3}/{√2}$.
1) Из рисунка видно, что если горизонтальная прямая $a = a_0$ лежит ниже (не выше) точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a = 2√x$ до графика $a = x$.
2) Если же горизонтальная прямая $a = a_0$ лежит выше точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a = 2√x$ до окружности $a^2 + x^2 = 3$, при этом точки самой окружности в заштрихованную область не входят.
Таким образом, в первом случае (то есть при $a ≤ {√3}/{√2}$) выполняется $a ≤ 2√x, a ≥ x$, следовательно, $x ∈ [{a^2}/{4}; a]$.
При $a > {√3}/{√2}$ решением является промежуток $[{a^2}/{4}; √{3 — a^2})$.
Отсюда решение содержит отрезок длиной не менее ${1}/{2}$, если
$[table{{table a ≤ {√3}/{√2}; a-{1}/{4}a^2 ≥ 0.5}; {{table a > {√3}/{√2}; √{3-a^2}-{a^2}/{4} > 0.5};$
$[table{{table a ≤ {√3}/{√2}; a^2-4a+2 ≤ 0}; {{table a > {√3}/{√2}; 3-a^2 > ({a^2}/{4}+{1}/{2})^2};$
Решив системы, получим: $a ∈[2-√2; {√3}/{√2}]$ или $a ∈ ({√3}/{√2}; √2)$, отсюда $a ∈ [2 — √2; √2)$.
Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему, можно заметить, что первое неравенство системы при $a < 0$ не имеет решений, а при $a ≥ 0$ имеет решением промежуток $[{1}/{4}a^2; a]$ (если $a ≤ 4$) или промежуток $[a; {1}/{4}a^2]$ (если $a > 4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x < √{3 — a^2}$. Отсюда, в частности, $a ≤ √3$, то есть случай $a > 4$ не возможен.
Несложно убедиться, что при ограничениях $0 ≤ a ≤ √3$ для решения задачи достаточно решить систему ${table a-{1}/{4}a^2 ≥ 0.5; √{3-a^2}-{a^2}/{4} > 0.5;$
Ответ: $[2-√2;√2)$
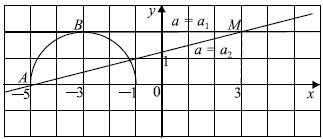
Задача 11
Найдите все значения параметра a, при каждом из которых система уравнений ${tabley=√{-8-6x-x^2}; y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √{−8−6x−x^2}$.
Преобразовав подкоренное выражение, получим: $y = √{1−(x^2 + 6x + 9)}, y =√{1−(x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность радиусом $1$ с центром в точке $(−3;0)$, лежащая в верхней полуплоскости.
Уравнение $y + ax = a + 1$ запишем в виде $y = −a(x−1) + 1$ — семейство прямых с угловым коэффициентом $−a$, проходящих через точку $M(1;1)$.
Рассмотрим рисунок. Видно, что система имеет единственное решение, если:
1) прямая $MC$ касается полуокружности, поэтому $−a = a_1 = 0$,
2) прямая и полуокружность имеют единственную общую точку, при этом $a_2 < −a ≤ a_3$.
Найдём $a_2$ из условия, что прямая $y = a_2(x−1) + 1$ проходит через точку $A(−4;0)$.
$a_2(−4−1) + 1 = 0, a_2 ={1}/{5}$.
Найдём $a_3$ из условия, что прямая $y = a_3(x−1) + 1$ проходит через точку $B(−2;0)$.
$a_3(−2−1) + 1 = 0, a_3 ={1}/{3}$.
Имеем ${1}/{5} < −a ≤ {1}/{3}$, значит, $−{1}/{3} ≤ a < −{1}/{5}$.
Следовательно, система имеет единственное решение, если $−{1}/{3} ≤ a < −{1}/{5}$ и $a = 0$.
Ответ: $[-{1}/{3};-{1}/{5});0$
Задача 12
Найдите все значения $a$, при которых система уравнений
${tabley=√{-5-6x-x^2}; y-ax=2-3a;$
имеет ровно два решения.
Решение
Построим график уравнения $y = √{-5 — 6x — x^2}$,
Преобразовав подкоренное выражение, получим $y = √{4 — (x^2 + 6x + 9)}, y = √{2^2 — (x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 2^2 — (x + 3)^2, (x + 3)^2 + y^2 = 2^2$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность с центром в точке $(-3; 0)$ радиусом $2$, лежащая в верхней полуплоскости.
Уравнение $y-ax = 2-3a$ запишем в виде $y = a(x-3)+2$ — семейство прямых с угловым коэффициентом $a$, проходящих через точку $M (3; 2)$.
Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если $a_1 < a ≤ a_2$. Прямая $BM$ касается окружности и является горизонтальной, поэтому её угловой коэффициент равен $0$, значит, $a_1 = 0$. Найдём $a_2$ из условия, что прямая $AM$ $y = a(x — 3) + 2$ проходит через точку $A(-5; 0)$.
$a(-5 — 3) + 2 = 0, a = {1}/{4}$, значит, $a_2 = {1}/{4}$.
Следовательно, система имеет ровно два решения при $0 < a ≤ {1}/{4}$.
Ответ: $(0;{1}/{4}]$
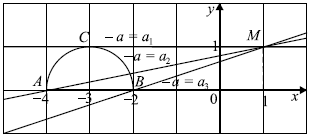
Задача 13
Найдите все значения $a$, при которых система уравнений
${table(x+1)^2=(y-2)^2; (x+1)^2+(y-a)^2=3a^2-2a+4;$
имеет ровно три решения.
Решение
Уравнение $(x + 1)^2 = (y — 2)^2$ равносильно совокупности двух уравнений
$[table x+1=y-2; x+1=-y+2;$ $[table y=x+3; y=-x+1;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x + 3$ и $y = -x + 1$. Заметим, что эти прямые проходят через точку $(-1; 2)$, так как система ${table y = x + 3; y = -x + 1;$ имеет единственное решение $(-1; 2)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x +1)^2 + (y — a)^2 = 3a^2 — 2a + 4$ будет множество всех точек окружности с центром в точке $(-1; a)$, лежащей на прямой $x = -1$, и радиусом $√{3a^2 — 2a + 4}$ (заметим, что $3a^2 — 2a + 4 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(-1; 2)$ лежит на окружности, значит, верно равенство $(-1 + 1)^2 + (2 — a)^2 = 3a^2 — 2a + 4$.
Отсюда получаем: $4 — 4a + a^2 = 3a^2 — 2a + 4; 2a^2 + 2a = 0; 2a ·(a + 1) = 0; $
$a = 0$ или $a = -1$.
Ответ:
Задача 14
Найдите все значения $a$, при которых система уравнений
${table(x-3)^2=(y-1)^2; (x-a)^2+(y-1)^2=3a^2-8a+9;$
имеет ровно три решения.
Решение
Уравнение $(x — 3)^2 = (y — 1)^2$ равносильно совокупности двух уравнений
$[table x-3=y-1; x-3=-y+1;$ $[table y=x-2; y=-x+4;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x — 2$ и $y = -x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система ${table y = x — 2; y = -x + 4;$ имеет единственное решение $(3; 1)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x — a)^2 + (y — 1)^2 = 3a^2 — 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√{3a^2 — 8a + 9}$ (заметим, что $3a^2 — 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 — a)^2 + (1 — 1)^2 = 3a^2 — 8a + 9$.
Отсюда получаем: $9 — 6a + a^2 = 3a^2 — 8a + 9; 2a^2 — 2a = 0; 2a ·(a — 1) = 0; a = 0$ или $a = 1$.
Ответ: $0;1$
Задача 15
Найдите все значения $a$, при каждом из которых уравнение ${3x + a — x^2 + 4a^2x — x^3}/{4a^2x — x^3} = 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${3x + a — x^2 + 4a^{2}x — x^3}/{4a^{2}x — x^3} = {4a^{2}x — x^3}/{4a^{2}x — x^3} + {-x^2 + 3x + a}/{4a^{2}x — x^3} = 1 + {-x^2 + 3x + a}/{4a^{2}x — x^3}$.
Тогда уравнение примет вид ${-x^2 + 3x + a}/{4a^{2}x — x^3} = 0$. Оно равносильно системе
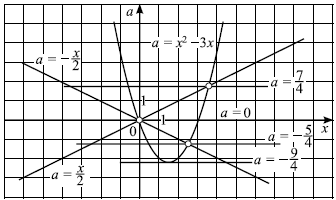
${table -x^2 + 3x + a = 0; 4a^{2}x — x^3 ≠ 0;$ ${table a = x^2 — 3x; x ≠ 0, x ≠ ±2a;$
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 — 3x$ и $a = ±{x}/{2}$.
Графиком функции $a = x^2 — 3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $({3}/{2}; -{9}/{4})$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±{x}/{2}$ являются прямые.
Решая уравнение $x^2 — 3x = {x}/{2}$, находим точки пересечения прямой $a = {x}/{2}$ и параболы $a = x^2 — 3x: x = 0, x = {7}/{2}$, откуда $a = 0, a = {7}/{4}$. Аналогично, решая уравнение $x^2 — 3x = — {x}/{2}$, находим $x = 0, x = {5}/{2}$. Тогда $a = 0, a = — {5}/{4}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = — {9}/{4}, a = — {5}/{4}, a = 0, a = {7}/{4}$.
Ответ: $-{9}/{4};-{5}/{4};0;{7}/{4}$
Задача 16
Найдите все значения $a$, при каждом из которых уравнение ${x^3 + x^2 — 16a^2x — 5x + a}/{x^3 — 16a^2x}= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${x^3 + x^2 — 16a^2x — 5x + a}/{x^3 — 16a^2x} = {x^3 — 16a^2x}/{x^3 — 16a^2x} + {x^2 — 5x + a}/{x^3 — 16a^2x} = 1 + {x^2 — 5x + a}/{x^3 — 16a^2x}$.
Тогда уравнение примет вид ${x^2 — 5x + a}/{x^3 — 16a^2x} = 0$.
Оно равносильно системе
${tablex^2 — 5x + a = 0; x^3 — 16a^2x ≠ 0;$ ${tablea = -x^2 + 5x; x ≠ 0, x ≠±4a;$
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = -x^2 + 5x$ и $a =±{x}/{4}$.
Графиком функции $a = -x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы — точка $({5}/{2}; {25}/{4})$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±{x}/{4}$ являются прямые.
Решая уравнение $-x^2 + 5x = {x}/{4}$, находим точки пересечения прямой $a ={x}/{4}$ и параболы $a = -x^2 + 5x: x = 0, x = {19}/{4}$, откуда $a = 0, a = {19}/{16}$. Аналогично, решая уравнение $-x^2 + 5x = -{x}/{4}$, находим $a = 0, a = -{21}/{16}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = -{21}/{16}, a = 0, a = {19}/{16}; a = {25}/{4}$.
Ответ: $-{21}/{16};0;{19}/{16};{25}/{4}$
Задача 17
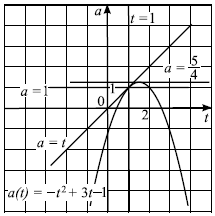
Найдите все значения параметра $а$, при которых уравнение $√{3^x-a}+{a-1}/{√{3^x-a}}=1$ имеет ровно два различных корня.
Решение
После приведения к общему знаменателю уравнение примет вид ${3x — a + a — 1}/{√{3^x — a}} = 1$ или ${3^x — 1}/{√{3^x — a}} = 1$. Пусть $3^x = t, t > 0$. Заметим, что после замены каждому положительному корню уравнения ${t — 1}/{√{t — a}} = 1$ соответствует единственный корень исходного уравнения (это следует из монотонности функции $3^x = t$). Уравнение ${t — 1}/{√{t — a}} = 1$ равносильно системе
${tablet — 1=√{t — a}; t>a;$
Возведём в квадрат обе части первого уравнения, учитывая, что $t ≥ 1$.
${tablea=-t^2+3t-1; t>a; t ≥ 1;$
Решим систему графически в системе координат $tOa$.
Вершина параболы $a = -t^2 + 3t — 1$ — точка с координатами $({3}/{2};{5}/{4})$.
Графики функций $a = -t^2 + 3t — 1$ и $a = t$ имеют единственную общую точку $t = 1$. Множество точек, удовлетворяющих неравенству $a < t$, представляет собой полуплоскость, лежащую ниже прямой $a = t$. $-t^2 + 3t — 1 = t, t^2 — 2t + 1 = 0, t = 1$.
По графику видно, что парабола $a = -t^2 +3t-1$ и прямая $a = const$ имеют ровно две общие точки при условии $t ≥ 1$, если $1 < a < {5}/{4}$, значит, исходное уравнение имеет ровно два корня при этих же значениях $a$.
Ответ: $(1;{5}/{4})$
Задача 18
Найдите все значения параметра $a$, при каждом из которых уравнение ${x^2+ax+2}/{2}=√{4x^2+ax+1}$ имеет ровно три различных корня.
Решение
Уравнение ${x^2 + ax + 2}/{2} = √{4x^2 + ax + 1}$ при ${x^2 + ax + 2}/{2} < 0$ не имеет корней. При $x^2 + ax + 2 ≥ 0$ обе части уравнения можно возвести в квадрат.
$(x^2 + ax + 2)^2 = 4(4x^2 + ax + 1)$,
$x^4 + ax^3 + 2x^2 + ax^3 + a^2x^2 + 2ax + 2x^2 + 2ax + 4 = 16x^2 + 4ax + 4$,
$x^4 + 2ax^3 + x^2(a^2 — 12) = 0$,
$x^2(x^2 + 2ax + a^2 — 12) = 0$,
$x^2((x + a)^2 — 12) = 0$,
$x_1 = 0, (x + a — √{12})(x + a + √{12}) = 0$,
$x_2 = -a + √{12}, x_3 = -a — √{12}$.
Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа $x_1, x_2, x_3$ были различными и для каждого из этих чисел выполнялось условие $x^2+ax+2 ≥ 0$.
$x_2≠0$ и $x_3≠0$, если $a≠√{12}=2√3$ и $a≠-√{12} = -2√3$.
Обозначим $g(x) = x^2 + ax + 2. g(0) = 2 > 0$. Числа $x_2 = -a + 2√3$ и $x_3 = -a — 2√3$ будут корнями исходного уравнения, если выполняются условия:
${tableg(x_2) ≥ 0; g(x_3) ≥ 0;$ ${table(-a + 2√3)^2 + a(-a + 2√3) + 2 ≥ 0; (-a — 2√3)^2 + a(-a — 2√3) + 2 ≥ 0;$
${table-2a√3 + 14 ≥ 0; 2a√3 + 14 ≥ 0;$ ${tablea≤{7}/{√3}; a≥-{7}/{√3};$
Таким образом, $a∊[-{7}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{7}/{√3}]$.
Ответ: $[-{7}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{7}/{√3}]$
Задача 19
Найдите все значения параметра a, при каждом из которых уравнение $x^2 + ax + 4 = √{20x^2 + 8ax + 16}$ имеет ровно три различных корня.
Решение
Уравнение $x^2 + ax + 4 = √{20x^2 + 8ax + 16}$ при $x^2 + ax + 4 <0$ не имеет корней. При $x^2+ax+4≥0$ (1) можно обе части уравнения возвести в квадрат.
$(x^2 + ax + 4)^2 = 20x^2 + 8ax + 16$,
$x^4 +ax^3+4x^2+ax^3+a^2x^2 +4ax+4x^2+4ax+16 = 20x^2+8ax+16$,
$x^4 + 2ax^3 + x^2(a^2 — 12) = 0$,
$x^2(x^2 + 2ax + a^2 — 12) = 0$,
$x^2((x + a)^2 — 12) = 0$,
$x_1 = 0, (x + a — √{12})(x + a + √{12}) = 0$,
$x_2 = -a + √{12}, x_3 = -a — √{12}$.
Чтобы исходное уравнение имело три различных корня, необходимо выполнение условия (1) для чисел $x_1, x_2, x_3$ и выполнение условия, что эти числа различны.
$x_2≠ 0$ и $x_3≠0$, если $a ≠√{12} = 2√3$ и $a ≠-√{12} = -2√3$.
Обозначим $g(x) = x^2 + ax + 4. g(x_1) = g(0) = 4 > 0$. Числа $x_2 = -a + √{12}$ и $x_3 = -a — √{12}$ будут корнями исходного уравнения, если выполняются условия:
${tableg(x_2) ≥ 0; g(x_3) ≥ 0;$ ${table(-a + √{12})^2 + a(-a + √{12}) + 4 ≥ 0; (-a — √{12})^2 + a(-a — √{12}) + 4 ≥ 0;$
${table-a√{12}+16 ≥ 0; a√{12}+16 ≥ 0;$ ${tablea≤{8}/{√3}; a≥-{8}/{√3};$
Таким образом, $a∈[-{8}/{√3}; -2√3)∪(-2√3;2√3)∪(2√3;{8}/{√3}]$
Ответ: $[-{8}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{8}/{√3}]$
Задача 20
Найдите все значения $a$, при каждом из которых система уравнений ${table(xy^2-5xy-5y+25)/{√{x+5}}=0; y=ax;$ имеет ровно два различных решения.
Решение
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение ${xy^2 — 5xy — 5y + 25}/{√{x + 5}}= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде ${(y — 5)(xy — 5)}/{√{x + 5}} = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y ={5}/{x}$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ — точка пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$, чтобы найти её координаты, нужно решить систему уравнений ${tabley = 5; y ={5}/{x};$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a ={1}/{5}$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a<-1$ и $a>0$, пересекает правую ветвь гиперболы $y ={5}/{x}$ при $a>0$, пересекает левую ветвь гиперболы $y ={5}/{x}$ при $a>{1}/{5}$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0< a ≤0.2; a = 5$.
Ответ: $(0;0.2]∪${5}
Рекомендуемые курсы подготовки
Задание 17 (№15 ЕГЭ-2022) профильного уровня
Это второе издание книги. От первой она отличается объёмом, разнообразием формулировок, полезностью (в эту книгу вошли задачи реальных вариантов ЕГЭ-2015 и задачи пробных вариантов 2016 года), многообразием методов решения и серьёзностью в оформлении.
Из спецификации к демоверсии:
→ Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни.
Из кодификатора к демоверсии (требования к уровню подготовки выпускников):
→ Анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчетах.
→ Решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
4. Вся сумма выплат равна: 

Задание 17. Финансовая математика
За правильное выполненное задание без ошибок получишь 3 балла.
На решение отводится примерно 35 минут.
Чтобы решить задание 17 по математике профильного уровня нужно знать:
- Задание подразделяется на несколько видов:
- задачи, связанные с банками, вкладами и кредитами;
- задачи на оптимальный выбор.
- Формула расчета ежемесячного платежа: Sкредит = S/12 t
- Формула расчета простых процентов: S =α(1 + t p/m)
- Формула расчета сложных процентов: С = x (1 + a%)n
Процент – это одна сотая часть какой-либо величины.
- x*(1 + p/100) — величина x увеличилась на p%
- x*(1 — k/100) — величина x уменьшилась на k%
- x*(1 + p/100) k — величина x увеличилась на p% k раз
- x*(1 + p/100)*(1 — k/100) – величина х сначала увеличилась на p%, а потом уменьшилась на k%
Задачи на погашение кредита равными платежами:
Размер кредита принимается за х. Процента банка – а. Выплата по кредиту – S.
Через год после начисления процентов и выплаты суммы S размер долга — x * (1 + a/100), p = 1 + a/100
- Размер долга через 2 года: (xp – S)p – S
- Размер долга через 3 года: ((xp – S)p – S)p – S
- Размер долга через n лет: xp n – S(p n-1 + … + p 3 + p 2 + p + 1)
Задачи для тренировки
В 2014 году стандартная заработная плата на человека в месяц по Приморскому краю составляла 23040 рублей. Каждый год процент повышения дохода составлял 50. А в Хабаровском крае стандартная заработная плата на человека в месяц в 2014 году составляла 45000 рублей. Каждый год процент общего дохода жителей Хабаровского края повышался на 44 в течение трёх лет, каждый год процент населения возрастал на q. Стандартная месячная заработная плата по Приморскому краю и Хабаровскому краю сравнялась в 2017 году. Найдите q.
У компании по производству глазированных сырков существует 2 фабрики в Новосибирске и Магадане, где идентичным способом создают однотипный товар. За неделю на одной из фабрик рабочие изготавливают глазированных сырков, если общее время их труда составляет n 2 часов в неделю. Компания осуществляет оплату каждый час по 500 рублей на первой фабрике в Новосибирске, и по 300 рублей на второй в Магадане, причём компания на заработные платы рабочих выделяет 1200000 рублей. Найдите максимальное количество глазированных сырков, которое можно изготовить за неделю на двух фабриках.
В банковской ячейке семьи Сладковых, к которой доступ имели жена Людмила и муж Валентин, находился 1000000 рублей наличными. Процент фальшивых банкнот составлял 20. Каждый месяц Валентин вносил 100000 рублей, 10 процентов из которых были фальшивыми. Также каждый месяц Людмила забирала 50000 рублей, где процент фальшивых купюр являлся 30. Сколько месяц должно пройти, пока содержание фальшивых банкнот в банковской ячейке составит 5 процентов от всей суммы.
Маркиз обратился в банк, чтобы открыть счет, банковский процент которого составлял 10 Но спустя год мужчина взял деньги со счета в размере 2000 тыс. рублей. По прошествии еще одного года, Маркиз положил денежные средства обратно. Спустя 3 года с момента внесения изначальной суммы, мужчина получил начисления, которые были ниже прогнозируемого итога. Какое количество денег потерял Маркиз из-за операций со вкладом?
В доме Персивальды живет три различных животных: кролик, кот и лошадь. Женщина каждый месяц покупает им корм. Если бы цены на корм для лошадей повысились на 50%, то итоговая сумма оплаты увеличилась бы на 35%. Если бы цены на корм для кота поднялись, на 50%, то итоговая сумма оплаты повысилась бы на 10%.Сколько процентов от общих расходов на корм приходится на кролика?
Задание 17. Задача с параметром. ЕГЭ 2022 по математике профильного уровня
Для того, чтобы решить задачу необходимо составить математическую модель (уравнение, неравенство или функцию, которую нужно исследовать).
Для решения задач на кредиты, необходимо разобраться в основных схемах кредитования с дифференцированными и аннуитетными платежами. Часто для преобразования уравнения нужно знать формулы алгебраической и геометрической прогрессий.
В задачах на оптимизацию нужно уметь работать с функциями: брать производную, находить точки экстремумов.
Задачи для практики
Задача 1
При каком значении $a$ множеством решений неравенства
$ <1+3^x>/ <1+3^<-x>>> <3>/ <|x+a|>$ является множество всех положительных чисел?
Решение
Сократив левую часть неравенства на $1 + 3^x$, получим равносильное неравенство $3^x > <3>/<|x + a|>$ или $3^ > <1>/<|x + a|>$. Так как обе части неравенства положительны, то $<1>/<3^> <4>/ <√ >$ является множество всех отрицательных чисел?
Решение
Сократив левую часть неравенства на $1+2^x$ и применив свойство квадратного корня $√ =|m|$, получим равносильное неравенство $ <1>/ <2^x>> <4>/ <|x+a|>$ или $ <1>/ <2^>> <1>/ <|x+a|>$. Так как обе части неравенства положительны, то $2^ 0$ уравнение имеет два корня.
Проверим при каких значениях $a$ значения $x = -4$ и $x = a$ являются корнями уравнения $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
При $x = -4$ должно выполняться равенство $16 + 4(4a + 1) + 4a^2 + 4a — 4 = 0, a^2 + 5a + 4 = 0, a = -4, a = -1$.
При $x = a$ должно выполняться равенство $a^2 — 4a^2 — a + 4a^2 + 4a — 4 = 0, a^2 + 3a — 4 = 0, a = 1, a = -4$.
При $a = -1, a = 1$ исходное уравнение имеет единственный корень.
При $а=-4$, $D>0$ и корни $х=-4$ и $х=а$ совпадают, поэтому это значение параметра также подходит
Задача 5
Найдите все значения параметра $p$, при каждом из которых система неравенств $<<table ;
$<tablep ≥ <5>/; p 0$, при каждом из которых система
имеет ровно $2$ решения.
Решение
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 0$, при каждом из которых система
имеет единственное решение.
Решение
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √ <6^2 + 3^2>= √ <45>= 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 0;$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично $<table (2√x — a)(a — x) ≤ 0; a^2+x^2 <√3>/<√2>$ решением является промежуток $[/<4>; √<3 — a^2>)$.
Отсюда решение содержит отрезок длиной не менее $<1>/<2>$, если
Решив системы, получим: $a ∈[2-√2; <√3>/<√2>]$ или $a ∈ (<√3>/<√2>; √2)$, отсюда $a ∈ [2 — √2; √2)$.
Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему, можно заметить, что первое неравенство системы при $a 4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x 4$ не возможен.
Несложно убедиться, что при ограничениях $0 ≤ a ≤ √3$ для решения задачи достаточно решить систему $<table a-<1>/<4>a^2 ≥ 0.5; √<3-a^2>—/ <4>> 0.5;$
Задача 11
Найдите все значения параметра a, при каждом из которых система уравнений $<tabley=√<-8-6x-x^2>; y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √<−8−6x−x^2>$.
Преобразовав подкоренное выражение, получим: $y = √<1−(x^2 + 6x + 9)>, y =√<1−(x + 3)^2>$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(-1; 2)$ лежит на окружности, значит, верно равенство $(-1 + 1)^2 + (2 — a)^2 = 3a^2 — 2a + 4$.
Отсюда получаем: $4 — 4a + a^2 = 3a^2 — 2a + 4; 2a^2 + 2a = 0; 2a ·(a + 1) = 0; $
Задача 14
Найдите все значения $a$, при которых система уравнений
имеет ровно три решения.
Решение
Уравнение $(x — 3)^2 = (y — 1)^2$ равносильно совокупности двух уравнений
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x — 2$ и $y = -x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система $<table y = x — 2; y = -x + 4;$ имеет единственное решение $(3; 1)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x — a)^2 + (y — 1)^2 = 3a^2 — 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√<3a^2 — 8a + 9>$ (заметим, что $3a^2 — 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 — a)^2 + (1 — 1)^2 = 3a^2 — 8a + 9$.
Отсюда получаем: $9 — 6a + a^2 = 3a^2 — 8a + 9; 2a^2 — 2a = 0; 2a ·(a — 1) = 0; a = 0$ или $a = 1$.
Задача 15
Найдите все значения $a$, при каждом из которых уравнение $<3x + a — x^2 + 4a^2x — x^3>/ <4a^2x — x^3>= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
Тогда уравнение примет вид $<-x^2 + 3x + a>/<4a^<2>x — x^3> = 0$. Оно равносильно системе
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 — 3x$ и $a = ±/<2>$.
Графиком функции $a = x^2 — 3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $(<3>/<2>; —<9>/<4>)$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±/<2>$ являются прямые.
Решая уравнение $x^2 — 3x = /<2>$, находим точки пересечения прямой $a = /<2>$ и параболы $a = x^2 — 3x: x = 0, x = <7>/<2>$, откуда $a = 0, a = <7>/<4>$. Аналогично, решая уравнение $x^2 — 3x = — /<2>$, находим $x = 0, x = <5>/<2>$. Тогда $a = 0, a = — <5>/<4>$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = — <9>/<4>, a = — <5>/<4>, a = 0, a = <7>/<4>$.
Задача 16
Найдите все значения $a$, при каждом из которых уравнение $/= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
Тогда уравнение примет вид $/ = 0$.
Оно равносильно системе
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = -x^2 + 5x$ и $a =±/<4>$.
Графиком функции $a = -x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы — точка $(<5>/<2>; <25>/<4>)$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±/<4>$ являются прямые.
Решая уравнение $-x^2 + 5x = /<4>$, находим точки пересечения прямой $a =/<4>$ и параболы $a = -x^2 + 5x: x = 0, x = <19>/<4>$, откуда $a = 0, a = <19>/<16>$. Аналогично, решая уравнение $-x^2 + 5x = —/<4>$, находим $a = 0, a = —<21>/<16>$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = —<21>/<16>, a = 0, a = <19>/<16>; a = <25>/<4>$.
Задача 17
Найдите все значения параметра $а$, при которых уравнение $√<3^x-a>+/<√<3^x-a>>=1$ имеет ровно два различных корня.
Решение
После приведения к общему знаменателю уравнение примет вид $<3x — a + a — 1>/<√<3^x — a>> = 1$ или $<3^x — 1>/<√<3^x — a>> = 1$. Пусть $3^x = t, t > 0$. Заметим, что после замены каждому положительному корню уравнения $/<√> = 1$ соответствует единственный корень исходного уравнения (это следует из монотонности функции $3^x = t$). Уравнение $/<√> = 1$ равносильно системе
Возведём в квадрат обе части первого уравнения, учитывая, что $t ≥ 1$.
Решим систему графически в системе координат $tOa$.
Вершина параболы $a = -t^2 + 3t — 1$ — точка с координатами $(<3>/<2>;<5>/<4>)$.
Графики функций $a = -t^2 + 3t — 1$ и $a = t$ имеют единственную общую точку $t = 1$. Множество точек, удовлетворяющих неравенству $a 0$. Числа $x_2 = -a + 2√3$ и $x_3 = -a — 2√3$ будут корнями исходного уравнения, если выполняются условия:
Задача 19
Найдите все значения параметра a, при каждом из которых уравнение $x^2 + ax + 4 = √<20x^2 + 8ax + 16>$ имеет ровно три различных корня.
Решение
Уравнение $x^2 + ax + 4 = √<20x^2 + 8ax + 16>$ при $x^2 + ax + 4 0$. Числа $x_2 = -a + √<12>$ и $x_3 = -a — √<12>$ будут корнями исходного уравнения, если выполняются условия:
Задача 20
Найдите все значения $a$, при каждом из которых система уравнений $<table(xy^2-5xy-5y+25)/<√>=0; y=ax;$ имеет ровно два различных решения.
Решение
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение $/<√>= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде $<(y — 5)(xy — 5)>/<√> = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y =<5>/$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y =<5>/$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ — точка пересечения прямой $y = 5$ и гиперболы $y =<5>/$, чтобы найти её координаты, нужно решить систему уравнений $<tabley = 5; y =<5>/;$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a =<1>/<5>$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a 0$, пересекает правую ветвь гиперболы $y =<5>/$ при $a>0$, пересекает левую ветвь гиперболы $y =<5>/$ при $a><1>/<5>$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y =<5>/$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0 ×
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Статистика
В задании №17 требуется решить текстовую задачу. Наиболее часто встречаются задачи экономического содержания на кредиты, вклады и оптимальный выбор.
Получить за решение этого задания можно 3 первичных балла, если обоснованно получен верный ответ. Если математическая модель построена верно, но решение недостаточно обоснованно, или допущена вычислительная ошибка – вы получите 2 первичных балла. А вот если решение не завершено, при правильно построенной математической модели, то вам достанется 1 первичный балл.
Виды платежей
1. Аннуитетный платеж — вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа остаётся постоянным на всём периоде кредитования.
- известно, что кредит был выплачен тремя равными платежами (за 3 года)
- он будет платить каждый год по 2 073 600 рублей
- кредит можно выплатить за четыре года равными платежами по 56 507 рублей
2. Дифференцированный платеж — вариант ежемесячного платежа по кредиту, когда сумма долга каждый год уменьшается на одну и ту же сумму, а размер ежемесячного платежа по погашению кредита постепенно уменьшается к концу периода кредитования.
- должен быть на X тысяч рублей меньше долга на n-е число предыдущего месяца
- n-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на n-е число предыдущего месяца
3. Фиксированные платежи — долг уменьшается по заданным в таблице или в условии задачи параметрам.
- выплатили за 2 года платежами 130 000 рублей в первый год и 150 000 рублей во второй
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
Пример
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей необходимо будет отдать, если кредит будет погашен 4 равными платежами.
Решение:
- $x$ — ежегодный платеж
- $s$ — сумма кредита
- $r$ — процентная ставка
- $k=1+r/100$ — коэффициент.
Мы знаем, что после последнего платежа долг должен быть полностью погашен:
Сразу отмечу, что обычно вместо 1,2 удобнее было бы подставить как дробь 6/5. Но в данном примере нам повезло и расчеты оказались относительно простые.
После того как мы нашли x — ежегодный платеж, необходимо ответить на вопрос задачи, то есть найти общую сумму выплат за все 4 года, то есть 4x.
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath
На чтение 12 мин Просмотров 33.3к. Опубликовано 7 февраля, 2019
Для решения таких задач необходимо понимать алгоритм решения экономических задач
За задание №17 по математике ЕГЭ профильный уровень можно получить 3 балла. Мы рассмотрим как решать экономические задачи ЕГЭ по математике, которые в каждом варианте профильного уровня по математике идут под номером 17.
Решение №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.
Можно выделить несколько блоков заданий:
1. Вклады и кредиты
2. Акции и другие ценные бумаги
3. Методы оптимальных решений
Рассмотрим каждый из вышеперечисленных блоков.
Содержание
- Вклады и кредиты
- Акции и другие ценные бумаги
- Методы оптимальных решений
- Примеры решения задач
Вклады и кредиты
Вклады и кредиты – самый обширный блок. Здесь вы можете встретить различные схемы возврата кредита или увеличения суммы вклада, и ваша задача – упорядочить данные таким образом, чтобы большой массив текста превратился в удобную математическую схему.
Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Начисление по этой формуле предполагает, что каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов.
Формула выглядит следующим образом:
где FV – будущая сумма.
PV – текущая сумма.
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента.
Если начисления происходят не ежегодно, а чаще, например, ежеквартально, формула модифицируется в следующий вид:
,
где
FV – будущая сумма
PV – текущая сумма
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента
m – количество начислений в год (например, m=4, если начисления ежеквартальные).
Давайте отработаем эту формулу на подготовительной задаче.
Задача 1
Алексей положил 100 000 рублей в банк под 6% годовых на 3 года. Какая сумма будет у Алексея через год? Через 2 года? Через 3 года?
Решение:
Рассчитаем по формуле сложного процента сумму через год:
Теперь сумму через 2 года:
Теперь сумму через 3 года:
Более того, вам придётся работать со схемами кредитов/вкладов, поэтому решим более сложную задачу, в которой нужно будет переводить текст в таблицы и уравнения/неравенства.
Задача 2
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 28 млн рублей.
Решение:
Пусть искомая сумма составит a млн рублей.
Составим таблицу, чтобы упорядочить данные и построить математическую модель.
По условию, нужно найти наименьшее целое x, для которого выполнено неравенство
14,641 + 2,31a ≥ 28
a ≥
Наименьшее целое число, при котором знак неравенства выполняется, это число 6.
Значит, искомая сумма — 6 млн рублей.
Ответ: 6 млн рублей.
Акции и другие ценные бумаги
Следующий блок, который мы рассмотрим, затрагивает относительно новое понятие ценной бумаги. Что вам нужно знать о ценной бумаге, чтобы решать подобные задания, не вдаваясь в экономические особенности, это то, как она может приносить доход.
Тип 1: когда вы получаете доход от того, что ценная бумага, которую вы купили ранее, растет в цене. Например, сначала ценная бумага стоила 3 000, а через год стала стоить 4 000. Непосредственно этих 4 000 у вас нет, но вы можете продать ценную бумагу за 4 000 и получите больше, чем потратили за год до этого.
Тип 2: когда вы получаете некий процент от прибыли компании за то, что ранее приобрели ценную бумагу этой компании. Если вы являетесь владельцем акции, то доход данного типа вы получаете в форме дивидендов.
Помимо этого дохода вы также можете продать эту ценную бумагу и, если она теперь стоит больше, чем когда вы ее покупали, вы также получите прибыль. Это не все пути получения дохода от ценных бумаг, но других особенностей вам знать не нужно. При необходимости все дополнительные условия будут описаны в самой задаче.
Рассмотрим следующую задачу, в которой как раз фигурирует понятие ценной бумаги.
Задача 3.
Григорий приобрёл ценную бумагу компании за 9000 рублей в начале 2016 года. Компания находится на стадии активного роста, поэтому цена данной бумаги каждый год возрастает на 2000 рублей. В любой момент Григорий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 12 %. В начале какого года Григорий должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение:
Продать бумагу нужно тогда, когда прирост стоимости ценной бумаги станет меньше, чем банковский процент. Пусть это случится в год n.
К этому моменту n к изначальной цене акции 9000 прибавится n раз по 2000, тогда на текущий момент её цена составит:
9000 + 2000n
Чтобы получить прирост, который Григорий получит, если хранить деньги в форме акции, необходимо ежегодный прирост (в данной задаче – 2000 рублей) поделить на накопленную к данному моменту сумму.
Прирост денежной суммы в банке всегда одинаков и равен предложенному проценту, то есть 0,12.
Либо можем составить уравнение, которое объединит все строчки нашей таблицы:
По прошествии четырёх лет Григорий должен продать бумагу, то есть в начале 2020 года.
Ответ: 2020
Методы оптимальных решений
Это особый блок, позволяющий максимизировать одну целевую функцию при учёте данных в условии ограничений.
Основные типы заданий в этом блоке:
1. Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства;
2. Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства);
3. Транспортная задача.
Разберём несколько задач с основными методами решения.
Задача.
У фермера есть 2 поля, площадь каждого из которых составляет 10 гектаров. На каждом поле можно выращивать пшеницу и ячмень. Урожайность пшеницы на первом поле составляет 500 ц/га, а на втором поле – 300 ц/га. Урожайность ячменя, наоборот, на первом поле составляет 300 ц/га, а на втором поле – 500 ц/га. При этом известно, что между данными злаками поля можно делить в любом соотношении.
Если известно, что на рынке установилась цена на пшеницу 7000 рублей за центнер, а цена на ячмень 9000 рублей за центнер, то какой наибольший доход фермер может получить?
Решение:
Имеем 2 поля с различными характеристиками.
В целом, продавать ячмень выгоднее, чем продавать пшеницу, так как 9000 > 7000 рублей.
Более того, известно, что на втором поле урожайность ячменя выше, чем урожайность пшеницы (500 ц/га против 300 ц/га). Тогда очевидно, что второе поле полностью фермер займёт ячменём, откуда получит:
10·500· 9000= 45000000 рублей
Ситуация с первым полем не так очевидна.
Продавать ячмень, как и прежде, выгоднее, чем продавать пшеницу. Однако на первом поле урожайность ячменя ниже, чем урожайность пшеницы (300 ц/га против 500 ц/га).
Поэтому необходимо сравнить соотношения этих величин:
Тогда получается, что засеять первое поле пшеницей выгоднее, так как низкая цена компенсируется высокой урожайностью.
Доход с первого поля:
10 · 500 ·7000 = 35000000 рублей
Суммарный доход составит:
35000000 рублей + 45000000 рублей = 80000000 рублей
Ответ: 80000000 рублей
Есть и другие типы заданий, в которых необходимо будет применить не житейские знания, а навыки составления уравнений и нахождения наименьшего/ наибольшего значений функций.
Задача.
На двух заводах есть по 360 рабочих, каждый из которых готов трудиться по 5 часов в сутки для обработки чёрных или цветных металлов. На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов. На втором заводе для обработки x кг чёрных металлов в день требуется x2 человеко-часов труда, а для обработки у кг цветных металлов в день требуется у2 человеко-часов труда.
Владельцу заводов поступил заказ на обработку металлов, причём 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов. Какую наибольшую массу обработанных металлов может за сутки суммарно получить заказчик?
Решение:
Как и дано в условии, 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов, что означает, что металлы взаимозаменяемы в пропорции 1:1.
Пусть на втором заводе t рабочих обрабатывают чёрные металлы, тогда (360-t) рабочих обрабатывают цветные металлы.
Знаем, что x2 человеко-часов труда требуется обработки x кг чёрных металлов, а у2 человеко-часов труда требуется в день для обработки у кг цветных металлов.
На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов, однако чёрные и цветные металлы для заказчика равнозначны, из чего сделаем вывод, что все 360 рабочих обрабатывают чёрные металлы, то есть 108*5 = 540 кг в день.
Имея соотношение на втором заводе и производительность рабочих на первом заводе, составим функцию возможного количества обработанных металлов:
Необходимо найти наибольшее значение этой функций. Последовательность действий мы уже знаем из темы «Анализ функций». Необходимо:
1. Найти производную функции;
2. Приравнять производную к 0, получить точки, подозрительные на экстремум;
3. Определить знаки производной на полученных промежутках и проверить, какие точки являются точкой максимума, а какие – точкой минимума.
Проведём такую последовательность действий с нашей производственной функцией.
Приведём к общему знаменателю.
Приравняем числитель к 0.
Возведём в квадрат.
Получили единственную точку экстремума.
- Проверим, является ли она точкой максимума.
Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.
Ответ: 600 кг
Видим, что экономическая задача достаточно разнообразна, но и решать вы её можете абсолютно разными способами – через производные, составление таблиц, схем, выведение формул и простой перебор вариантов.
Самое главное – внимательно прочитать и понять условие.
Примеры решения задач
Задача 1. В 2019 году клиент планирует открыть вклад в банке 1 ноября сроком на 1 месяц под 11% годовых. Какая сумма денег окажется на счёте вклада 1 декабря того же года, если планируемая сумма вклада равна 100 000 рублей? Ответ округлите до двух знаков после запятой.
Решение: При однократном начислении процентов через дней на вклад под годовых в невисокосный год получим сумму
Воспользуемся этой формулой, считаяS0= 100 000, r = 11 , m = 30 (так как в ноябре 30 дней).
Получим:
Число в скобках с точностью до 7 знаков после запятой равно 1,0090411, значит, S=100 904,11Таким образом, на счёте вклада будет 100 904 рубля 11 копеек.
Задача 2. Через сколько полных лет у клиента на счету будет не менее 950 000 рублей, если он намерен открыть вклад 31 декабря и планирует каждый год класть на счет 260 000 рублей при условии, что банк раз в год (начиная со следующего года) 31 декабря будет начислять 10% на имеющуюся сумму?
Решение:
Будем последовательно вычислять сумму на счете и упорядочивать данные с помощью таблицы.
Задача 3. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 11% в течение каждого из первых двух лет, а на третий год начисляемые проценты изменяются. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором по истечении трёх лет этот вклад всё ещё будет выгоднее вклада «А».
Решение:
Пусть на каждый тип вклада была внесена сумма По вкладу «А» сумма каждый год увеличивается на
умножается на коэффициент 1,1.
Тогда по вкладу «А» после первого года сумма станет равна ;
после второго года: 1,21S;
после третьего года: 1,331S.
По вкладу «Б» после первого года сумма станет равна1,11S;
после второго года 1,2321S.
Пусть на третий год по вкладу «Б» банк увеличивает сумму на r%. Тогда после третьего года по вкладу «Б» сумма станет равна
, где r— натуральное число,
коэффициент повышения в третий год.
По условию требуется найти наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А», то есть сумма через три года на вкладе «Б» должна быть больше суммы на вкладе «А». Составим неравенство:
Так как r— натуральное число, то наименьший процент равен 9%.
Задача 4. Сергей планирует приобрести ценную бумагу за 7 тысяч рублей. Цена бумаги каждый год будет возрастать на 2 тысячи рублей. В любой момент Сергей сможет продать ценную бумагу и вырученные деньги положить на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В течение какого года после покупки Сергей должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на счете стала наибольшей?
Решение.
Во второй год цена ценной бумаги составит: (7+2) тысячи рублей
В третий год (7+2)+2= 7+2∙2 тысячи рублей
В четвертый год (7+2)+2)+2= 7+2∙3 тысячи рублей
.
Сопоставим 10% банковский рост цены бумаги ее ежегодному росту на 2000 рублей.
10% от цены бумаги на
Ценную бумагу стоит продать тогда, когда 10% от цены бумаги станут больше, чем 2 тысячи рублей.
Получаем неравенство:
Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 8.
Задача 5.
Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 20%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце тридцатого года сумма на его счёте была наибольшей?
Решение:
Теория
| 1. | Что нужно знать | |
| 2. | Исследование линейных уравнений и неравенств | |
| 3. | Исследование квадратных уравнений и неравенств | |
| 4. | Расположение корней квадратного уравнения относительно данных чисел | |
| 5. | Как решать задание ЕГЭ |
Задания
| 1. |
Уравнение шестой степени с параметром
Сложность: |
4 |
| 2. |
Линейное уравнение с параметром
Сложность: |
4 |
| 3. |
Линейное уравнение с модулем
Сложность: |
4 |
| 4. |
Сумма квадратов корней уравнения
Сложность: |
4 |
| 5. |
Наименьшее значение функции
Сложность: |
4 |
| 6. |
Квадратное уравнение с параметром
Сложность: |
4 |
| 7. |
Линейное неравенство
Сложность: |
4 |
| 8. |
Квадратное неравенство
Сложность: |
4 |
| 9. |
Тригонометрия с параметром
Сложность: |
4 |
| 10. |
Система уравнений с параметром
Сложность: |
4 |
| 11. |
Иррациональная функция с модулем
Сложность: |
4 |
| 12. |
Логарифм и модуль с параметром
Сложность: |
4 |
Экзаменационные задания (подписка)
| 1. |
Как на ЕГЭ (1). Нахождение значений параметра
Сложность: |
4 |
| 2. |
Как на ЕГЭ (2). Нахождение значений параметра
Сложность: |
4 |
| 3. |
Как на ЕГЭ (3). Нахождение значений параметра
Сложность: |
4 |
| 4. |
Как на ЕГЭ (4). Нахождение значений параметра
Сложность: |
4 |
Тесты
| 1. |
Тренировка по теме Нахождение значений параметра
Сложность: среднее |
8 |
Материалы для учителей
| 1. | Методическое описание |