18 задание егэ математика профиль система неравенств - Exhelper.top

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 266 … 61–80 | 81–100 | 101–120 | 121–140 | 141–160 | 161–180 | 181–200 | 201–220 …

Добавить в вариант

Решите систему неравенств

Источник: ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 2., Задания 15 (С3) ЕГЭ 2014

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 66.

Решите систему неравенств:

Источник: А. Ларин: Тренировочный вариант № 30.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 37.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 40.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 63.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 78.

Решите систему неравенств:

Источник: А. Ларин: Тренировочный вариант № 22.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 13.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 18.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 27.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 73.

Решите систему неравенств

Источник: А. Ларин: Тренировочный вариант № 3.

Решите систему неравенств

Всего: 266 … 61–80 | 81–100 | 101–120 | 121–140 | 141–160 | 161–180 | 181–200 | 201–220 …

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №18. Уравнения, неравенства и системы с параметрами

ЕГЭ Профиль №18. Уравнения, неравенства и системы с параметрамиadmin2020-04-30T12:32:46+03:00

Источник

Решая задачи на числа и их свойства, то есть задачи под №18 Профильного ЕГЭ по математике, мы часто пользуемся методом «Оценка плюс пример».

А чтобы сделать оценку нужной нам величины, надо уметь работать с неравенствами. И знать простые правила.

1.Мы можем складывать между собой неравенства одного знака.

Например, если и то

«Одного знака» — значит, что в обоих неравенствах знак < или > или ≤ или ≥.

А вот вычитать из одного неравенства другое мы не можем. Просто нет такого действия.

Например, из тех же неравенств и мы можем получить:

Просто умножили второе неравенство на – 1. Теперь можно их сложить:

2) Если и то и это значит, что

Посмотрим, как применить эти правила в решении задачи 18 (на числа и их свойства).

1. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более $frac{3}{11}$ от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более $frac{3}{7}$ от общего числа учащихся группы, посетивших кино.

а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?

б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?

в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а и б?

Во многих задачах №19 Профильного ЕГЭ по математике есть возможность сделать «заготовку» на все 3 ее пункта. То есть ввести переменные (целые) и решать систему уравнений или неравенств.

Пусть — число мальчиков, — число девочек в группе.

Пусть $m_{1}$ мальчиков сходили в театр, $m_{2}$ мальчиков сходили в кино, $d_{1}$ девочек сходили в театр, $d_{2}$ девочек сходили в кино.

Число мальчиков, посетивших театр, не больше, чем $frac{3}{11}$ от общего числа учащихся группы, посетивших театр. В наших переменных это будет выглядеть так:

$m_{1}leq frac{3}{11}left ( m_{1}+d_{1} right )Rightarrow 8m_{1}leq 3d_{1}$

Число мальчиков, посетивших кино, не более $frac{3}{7}$ от общего числа учащихся группы, посетивших кино.

$m_{2}leq frac{3}{7}left ( m_{2}+d_{2} right )Rightarrow 4m_{2}leq 3d_{2}$

Отлично, у нас два неравенства с переменными $m_{1},;m_{2},;d_{1},;d_{2}$ . А вопрос о другом – сколько мальчиков может быть в группе. И среди этих мальчиков кто-то мог посетить театр, кто-то кино, а кто-то, возможно, побывал и в театре, и в кино.

И поэтому $mleq m_{1}+m_{2}$ .

Где взять сумму $m_{1}+m_{2}$ ? Обе части неравенства $4m_{2}leq 3d_{2}$ умножим на 2. И сложим получившееся с неравенством $8m_{1}leq 3d_{1}$

Получим: $8left ( m_{1}+m_{2} right )leq 3d_{1}+6d_{2}$ .

Теперь девочки. Все, что мы можем сказать, — что $d_{1}leq d$ и $d_{2}leq d$ .

Получаем:

$8mleq 8left ( m_{1}+m_{2} right )leq 3d+6d$ , то есть .

Вот мы и сделали «заготовку» для решения и первого, и второго, и даже третьего пункта задачи.

a) Может ли быть 10 мальчиков в группе из 20 учащихся? — Да, может. Вот пример:

В театр сходили 3 мальчика и все 10 девочек, в кино — остальные 7 мальчиков и 10 девочек. Все условия выполнены:

$3leq frac{3}{11}cdot left ( 3+10 right ),; 7leq frac{3}{7}cdot left ( 7+10 right )$

б) Предположим, что в группе из 20 учащихся имеется не менее 11 мальчиков: mgeq 11 . Тогда dleq 9 . Имеем:

, . Получили противоречие с неравенством . Значит, число мальчиков не больше 10. С учётом пункта а) приходим к выводу, что наибольшее возможное количество мальчиков в группе равно 10.

в) Найдем наименьшую долю девочек от общего числа учащихся в группе.

Перепишем неравенство следующим образом:

$8mleq 9dRightarrow frac{m}{d}leq frac{9}{8}Rightarrow frac{m}{d}+1leq frac{17}{8}Rightarrow frac{m+d}{d}leq frac{17}{8}Rightarrow frac{d}{m+d}geq frac{8}{17}$

Мы нашли, что, доля девочек не меньше $frac{8}{17}$ . Это оценка (о методе «Оценка плюс пример» читай здесь)

Осталось привести пример, когда доля девочек равна $frac{8}{17}$ .

Пусть в группе 9 мальчиков и 8 девочек. Театр посетили 3 мальчика и 8 девочек, в кино сходили 6 мальчиков и 8 девочек. Все условия выполнены:

$3leq frac{3}{11}cdot left ( 3+8 right ),;6leq frac{3}{7}cdot left ( 6+8 right )$

Следовательно, наименьшая возможная доля девочек равна $frac{8}{17}$ .

Ответ:

а) да

б) 10

в) $frac{8}{17}$

2. Известно, что — попарно различные двузначные натуральные числа.

а) Может ли выполняться равенство $frac{a+c}{b+d}=frac{7}{19}$ ?

б) Может ли дробь $frac{a+c}{b+d}$ быть в 11 раз меньше, чем сумма $frac{a}{b}+frac{c}{d}$ ?

в) Какое наименьшее значение может принимать дробь $frac{a+c}{b+d}$ если и ?

Слово «попарно» в условии задачи означает только то, что все числа
a,b,c,d – разные.

а) Пример подобрать легко. Предположим, что $frac{a+c}{b+d}=frac{7}{19}$ , где a,b,c,d — различные двузначные натуральные числа.

Да, равенство может выполняться. Например:

$frac{33+37}{91+99}=frac{70}{190}=frac{7}{19}$ ,
здесь .

б) Предположим, что $11cdot frac{a+c}{b+d}=frac{a}{b}+frac{c}{d}$

Ура, у нас уравнение в целых числах с 4 неизвестными. Как решать уравнения в целых числах – читай здесь.

$frac{11a+11c}{b+d}=frac{ad+bc}{bd}$

$11abd+11bcd=abd+bcd+ad^{2}+bc^{2}$

$10abd-ad^{2}=cb^{2}-10cbd$

Поскольку a,b,c,d – различные двузначные числа, 10a и 10b – трёхзначные. Тогда

и равенство невозможно.

в) Пусть > , >, $frac{a+c}{b+d}=m$ .

Найдем наименьшее возможное .

Кстати, у нас теперь уравнение с 5 неизвестными. Забавно, правда?

Запишем условия и в виде нестрогих неравенств. Мы помним, что это один из секретов решения задачи 19.

Тогда

$m=frac{a+c}{b+d}geq frac{3b+1+6d+1}{b+d}$ ,

$mgeq frac{3b+6d+2}{b+d}$ .

Выделим целую часть: (Секреты решения задачи 19)

$mgeq 3+frac{3d+2}{b+d}$ .

Ну вот, теперь переменная зависит всего от двух переменных, и .

Поскольку и – двузначные, .

Значит, ,

, отсюда $bleq frac{98}{3};;dleq frac{98}{6}$ .

Так как и – целые, получим: bleq 32 , dleq 16 .

Вернемся к оценке для .

$mgeq 3+frac{3d+2}{b+d}geq 3+frac{3d+2}{d+32}$ , так как . Теперь зависит от всего лишь одной переменной .

Преобразуем правую часть неравенства, чтобы выделить целую часть:

$3+frac{3d+2}{d+32}=3+frac{3d+96-94}{d+32}=6-frac{94}{d+32}$

Значит, $mgeq 6-frac{94}{d+32}$ .

У нас есть оценка dleq 16 . Но она ничего нам не даст – можете проверить! А вот условие, что число – двузначное, то есть dgeq 10 , нам поможет.

Поскольку dgeq 10 , и $mgeq 6-frac{94}{d+32}geq 6-frac{94}{42}$

$mgeq frac{79}{21}$ .
Равенство $m=frac{79}{21}$ достигается, если

Наименьшее возможное равно $frac{79}{21}$ .

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Работа с неравенствами в задаче 18 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

: ЕГЭ по математике профиль

Разбор Задачи №18 из Реaльного ЕГЭ 2021 по математике (Основная волна).

Задание 18 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.

Задача 18 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.

Если вы полны решимости получить на ЕГЭ по математике заветные 4 первичных балла за задачу 18 (с параметром), данное видео будет полезным для вас.

Связанные страницы:

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение неравенств

Задание
1

#2500

Уровень задания: Легче ЕГЭ

Решите неравенство [x+10<3x^2]

Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:

Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).

Ответ:

(left(-infty;-frac53right)cup(2;+infty))

Задание
2

#2501

Уровень задания: Легче ЕГЭ

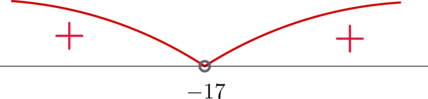
Решите неравенство [x^2+34x+289>0]

Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:

Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).

Ответ:

((-infty;-17)cup(-17;+infty))

Задание
3

#2502

Уровень задания: Легче ЕГЭ

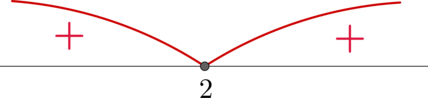
Решите неравенство [x^2-4x+4leqslant 0]

Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:

Таким образом, нам подходят (xin{2}).

Ответ:

({2})

Задание
4

#2503

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+3x+3geqslant 0]

Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).

Таким образом, нам подходят (xin mathbb{R}).

Ответ:

(mathbb{R})

Задание
5

#2412

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]

2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]

По методу интервалов:

откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-4; -2]cup[1; 3))

Задание
6

#3762

Уровень задания: Легче ЕГЭ

Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]

(Задача от подписчиков)

Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]

Ответ:

((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])

Задание
7

#2413

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]

2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]

По методу интервалов: