Задание 1
В школе 800 учеников, из них 30%—ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?
Ответ: 112
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если 30% в младшей, то 100-30=70% в средней и старшей школах. Найдем количество учеников там: 100*0,7=560 человек.
Так как изучают 20%, то это значение составляет: 560*0,2=112 человек
Задание 2
На графике показано изменение давления в паровой турбине после запуска. На оси абсцисс откладывается время в минутах, на оси ординат—давление в атмосферах. Когда давление достигает определенного значения, открывается клапан, выпускающий часть пара, и давление падает. Затем клапан закрывается, и давление снова растет.
Определите по графику давление в турбине в момент ее запуска. Ответ дайте в атмосферах.
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
На момент запуска (0 минут) давление составляло 1 атм
Задание 3
Найдите тангенс угла AOB, изображенного на рисунке.
Ответ: -2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Используя теоремы Пифагора, найдем стороны треугольника AOB из прямоугольных треугольников:
$$BO=sqrt{1^{2}+3^{2}}=sqrt{10}$$
$$OA=sqrt{2^{2}+2^{2}}=sqrt{8}$$
$$BA=sqrt{5^{2}+1^{2}}=sqrt{26}$$
Из теоремы косинусов:
$$Delta OAB cos BOA=frac{OB^{2}+OA^{2}-AB^{2}}{2*OB*OA}=$$$$frac{10+8-26}{2*sqrt{10}*sqrt{8}}=frac{-8}{2*4sqrt{5}}=$$$$-frac{1}{sqrt{5}}$$
По основному тригонометрическому тождеству:
$$sin BOA=sqrt{1-(-frac{1}{sqrt{5}})^{2}}=frac{2}{sqrt{5}}$$
По определению тангенса:
$$tg BOA =frac{2}{sqrt{5}}:(-frac{1}{sqrt{5}})=-2$$
Задание 4
Игрок зажал в кулаке носовой платок так, что между пальцами торчат только четыре уголка. Второй игрок наудачу выбирает два уголка. Он выигрывает, если взял платок за диагональ, и проигрывает в противном случае. Найдите вероятность выигрыша второго игрока. Ответ округлите до сотых.
Ответ: 0,33
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Всего два конца из четырех возможно взять $$C_{m}^{n}=frac{m!}{(m-n!)}=$$$$C_{4}^{2}=frac{4}{(4-2)}=6=N$$ способами. По диагонали же $$n=2$$ способами
Вероятность: $$P=frac{n}{N}=frac{2}{6}=0,(3)$$. Округлим до сотых: 0,33
Задание 5
На рисунке AB=4, BE=8, DE=5, прямая AB перпендикулярна прямой BD, CD перпендикулярна BD, EA перпендикулярна EC. Найдите CD.
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть $$angle A=alpha$$, тогда $$angle AEB=90-alpha$$. Но тогда $$angle CED=alpha$$, следовательно, треугольники ABE и CED подобны. Из подобия получаем отношение: $$frac{AB}{BE}=frac{ED}{CD}$$. Тогда $$CD=frac{ED*BE}{AB}=frac{5*8}{4}=10$$
Задание 6
Прямая $$y=3x+1$$ является касательной к графику функции $$y=ax^{2}+2x+3$$. Найдите a .
Ответ: 0,125
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Чтобы прямая являлась касательной, тогда производные должны быть одинаковы:
$${y_{1}}’={y_{2}}’Leftrightarrow$$ $$3=2ax+2Leftrightarrow$$ $$x=frac{1}{2a}(1)$$
С другой стороны, функции тоже должны быть одинаковы:
$$y_{1}=y_{2}Leftrightarrow$$ $$3x+1=ax^{2}+2x+3 (2)$$
Подставим (1) в (2):
$$3*frac{1}{2a}+1=a*(frac{1}{2a})^{2}+2*frac{1}{2a}+3Leftrightarrow$$$$frac{3}{2a}+1=frac{a}{4a^{2}}+frac{2}{2a}+3Leftrightarrow$$ $$frac{3}{2a}+1=frac{1}{4a}+frac{2}{2a}+3Leftrightarrow$$$$frac{3}{2a}-frac{1}{4a}-frac{2}{2a}=3-1Leftrightarrow$$ $$frac{6-1-4}{4a}=2Leftrightarrow$$ $$frac{1}{4a}=2Leftrightarrow$$ $$a=frac{1}{8}=0,125$$
Задание 7
Найдите квадрат расстояния между вершинами A и D1 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$AD_{1}^{2}=AH^{2}+HH_{1} ^{2}+H_{1}D_{1}^{2}=$$$$1^{2}+2^{2}+1^{2}=6$$
Задание 8
Найдите значение выражения $$(b^{2}-49)(frac{b+1}{b-7}-frac{b-1}{b+7})-15b+7$$ при $$b=123$$
Ответ: 130
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(b^{2}-49)(frac{b+1}{b-2}-frac{b-1}{b+7})-15b+7=$$$$(b^{2}-49)frac{((b+1)(b+7)-(b-1)(b-7))}{(b-7)(b+7)}-15b+7=$$$$(b^{2}+8b+7-b^{2}+8b-7)-15b+7=$$$$16b-15b+7=b+7=123+7=130$$
Задание 9
Очень лёгкий заряженный металлический шарик с зарядом $$q=2*10^{-6}$$Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет $$v=6$$м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол $$alpha$$ с направлением движения шарика. Значение индукции поля $$B=5*10^{-3}$$Тл. При этом на шарик действует сила Лоренца, направленная вверх перпендикулярно плоскости и равная $$F=qvBsin alpha$$(Н). При каком наименьшем значении угла $$alpha in [0;180]$$ шарик оторвётся от поверхности, если для этого нужно, чтобы сила $$F$$ была больше $$3*10^{-8}$$ H?
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$F=qvB sin alpha Leftrightarrow$$ $$sin alpha =frac{F}{qvB}$$
$$sinalpha =frac{3*10^{-8}}{2*10^{-6}*6*5*10^{-3}}=$$$$frac{10}{2*2*5}=frac{1}{2}$$
$$alpha=30$$
Задание 10
Две точки равномерно вращаются по окружности. Первая совершает оборот на 5 секунд быстрее второй и делает за минуту на 2 оборота больше, чем вторая. Сколько оборотов в минуту совершает вторая точка?
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x-количество оборотов в минуту первой, y- количество оборотов в минуту второй, тогда если оборот принять за 1:
$$left{begin{matrix}frac{1}{y}-frac{1}{x}=frac{5}{60} \1*x-1*y=2 end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}frac{1}{y}-frac{1}{x}=frac{1}{12} \x=2+y(2)end{matrix}right.$$
Подставим (2) в первое уравнение:
$$frac{1}{y}-frac{1}{2+y}=frac{1}{12}Leftrightarrow$$ $$12(2+y-y)=2y+y^{2}Leftrightarrow$$$$y^{2}+2y-24=0$$
$$left{begin{matrix}y_{1}+y_{2}=-2 \y_{1}*y_{2}=-24 end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}y_{1}=-6 \y_{2}=4 end{matrix}right.$$
Отрицательной скорость быть не может, следовательно, второе тело совершает 4 оборота в минуту
Задание 11
Найти наименьшее значение функции $$y=log_{0,5} (frac{sqrt{4x^{4}-3x^{2}+9}-sqrt{4x^{4}-8x^{2}+9}}{x})$$ на интервале $$(0;infty)$$
Ответ: 0
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
При x>0: $$sqrt{4x^{4}=3x^{2}+9}>sqrt{4x^{4}-8x^{2}+9}$$
Пусть $$t=frac{sqrt{4x^{4}-3x^{2}+9}-sqrt{4x^{4}-8x^{2}+9}}{x}=$$$$frac{4x^{4}-3x^{2}+9-(4x^{4}-8x^{2}+9)}{x(sqrt{4x^{4}-3x^{2}+9}+sqrt{4x^{4}-8x^{2}+9})}=$$$$frac{5x^{2}}{sqrt{4x^{4}-3x^{2}+9}+sqrt{4x^{4}-8x^{2}+9}}=$$$$frac{5}{sqrt{4x^{4}-frac{9}{x^{2}}-3}+sqrt{4x^{4}-frac{9}{x^{2}}-8}}$$
Учтем, что $$a^{2}+b^{2}geq 2ab$$. Пусть $$a^{2}=4x^{2}, b^{2}=frac{9}{x^{2}}$$. Тогда: $$4x^{2}+frac{9}{x^{2}}geq 2sqrt{4x^{2}*frac{9}{x^{2}}}=2*6=12(1)$$
Следовательно $$sqrt{4x^{4}-frac{9}{x^{2}}-3}+sqrt{4x^{4}-frac{9}{x^{2}}-8}(2)$$ минимальна при выполнении (1):
$$sqrt{12-3}+sqrt{12-8}=3+2=5$$. Чем меньше (2), тем больше t и тем меньше: $$log_{0,5}tRightarrow log_{0,5}frac{5}{5}=log_{0,5}1=0$$
Задание 12
а) Решите уравнение $$frac{3+cos 4x -8cos^{4} x}{4(cos x +sin x)}=frac{1}{sin x}$$
б) Укажите корни этого уравнения, принадлежащие отрезку [5;2]
Ответ: А)$$frac{pi}{2}+pi n, n in Z$$ Б)$$frac{3pi}{2}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) $$frac{2+cos 4x-8cos^{4}x }{4(cos x+sin x)}=frac{1}{sin x}$$
Область определения D: $$left{begin{matrix}cos x+sin x neq 0\ sin xneq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}tg xneq -1\xneq pi n , n in Zend{matrix}right.Leftrightarrow$$ $$left{begin{matrix} xneq -frac{pi}{4}+pi n\xneq pi nend{matrix}right.$$
Рассмотрим числитель первой дроби:
$$cos 4x=2 cos^{2}2x-1=$$$$2(2 cos ^{2}x-1)^{2}-1=2(4cos ^{4}x-4cos ^{2}x+1)=$$$$8cos^{4}x-8 cos ^{2}x+1=$$$$3+8cos^{4}x-8 cos ^{2}x+1-8cos ^{4}x=4-8cos ^{2}x$$
Выполним преобразования:
$$frac{4(1-2cos^{2}x)}{4(cos x+sin x)}=frac{1}{sin x}Leftrightarrow$$$$frac{1-2 cos ^{2}x}{cos x+sin x}=frac{1}{sin x}Leftrightarrow$$$$sin x-2 cos^{2}x*sin x=cos x+sin xLeftrightarrow$$$$cos x+2 cos^{2}x sin x=0Leftrightarrow$$$$cos x(1+2cos x sin x)=0Leftrightarrow$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$left[begin{matrix}cos x=0\1+sin 2x=0end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x=frac{pi}{2}+pi n\2x=-frac{pi}{2}+2pi nend{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x=frac{pi}{2}+pi n\x=-frac{pi}{4}+pi nnotin Dend{matrix}right.$$
Б) Найдем корни, принадлежащие данному промежутку: $$piapprox 3,14Rightarrow$$ $$frac{pi}{2}approx 1,57$$. Тогда $$frac{pi}{2}+pi=frac{3 pi}{2}in [2 ;5]$$
Задание 13
Основанием прямой призмы АВСА1В1С1 является равнобедренный треугольник АВС, в котором $$AC=CB=2$$ ,$$angle ACB=2arcsin frac{4}{5}$$. Плоскость, перпендикулярная прямой А1В, пересекает ребра АВ и А1В1 в точках К и L соответственно, причем $$AK=frac{7}{16}AB$$, $$LB_{1}=frac{7}{16}A_{1}B_{1}$$ .
А) Докажите, что плоскость сечения пересекает ребро СС1 в его середине
Б ) Найдите площадь сечения.
Ответ: 1,35
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
(Чтобы построить сечение, нужно будет проводить $$N_{1}O$$ до пересечения с $$BC$$ в точке F, и соединять KF)
A) 1)$$angle ACB=2 arcsin frac{4}{5}Rightarrow$$ $$sin angle ACB =sin (2 arcsin frac{4}{5})=$$$$2sin (arcsin frac{4}{5})cos(arcsin frac{4}{5})=$$$$2frac{4}{5}-sqrt{1-(frac{4}{5})^{2}}=$$$$frac{8}{5}*frac{3}{5}=frac{24}{25}$$. Учитываем, что угол $$arcsin$$ которого составляет $$frac{4}{5}$$ больше $$in (45;90)$$. Следовательно, двойной угол будет $$in (90;180)$$, то есть его косинус отрицательный: $$cos angle ACB=-sqrt{1-(frac{24}{25})^{2}}=-frac{7}{25}$$
2) $$A_{1}B_{1}=sqrt{C_{1}A_{1}^{2}+C_{1}B_{1}^{2}-2C_{1}A_{1}*C_{1}B_{1}*cos A_{1}C_{1}B_{1}}=$$$$sqrt{2^{2}+2^{2}+2*2^{2}*frac{7}{25}}=frac{16}{5}$$
3) $$AK=frac{7}{16}AB=frac{7}{16}*frac{16}{5}=frac{7}{5}$$; $$KB=frac{9}{16}*frac{16}{5}=frac{9}{5}$$; $$B_{1}L=frac{7}{5}$$; $$LA_{1}=frac{9}{5}$$; $$K_{1}M_{1}=B_{1}M_{1}-LB_{1}=frac{8}{5}-frac{7}{5}=frac{1}{5}=MK$$
$$LM_{1}left | right |KM$$ и $$MM_{1}perp AB A_{1}B_{1}Rightarrow$$ $$Delta LM_{1}O_{1}=Delta O_{1}MKRightarrow M_{1}O_{1}=O_{1}K$$, но $$LN_{1}left | right |KNleft | right |OO_{1}Rightarrow C_{1}O=OC$$
Б) 1) $$O_{1}Lperp N_{1}L$$ т.к. $$M_{1}Lperp N_{1}L$$ (теорема о трех перпендикулярах)
$$B_{1}L=frac{7}{5}Rightarrow$$ $$frac{B_{1}L}{B_{1}M_{1}}=frac{7}{5}*frac{5}{8}=frac{7}{8}Rightarrow$$ $$N_{1}L=frac{7}{8}C_{1}M_{1}=frac{7}{8}OO_{1}Rightarrow$$ $$S_{OO_{1}LN_{1}}=frac{OO_{1}+frac{7}{8}OO_{1}}{2}*O_{1}L=frac{15}{16}OO_{1}*O_{1}L$$ (так как имеем прямоугольную трапецию)
$$O_{1}Lperp N_{1}L$$ т.к. $$M_{1}Lperp N_{1}L$$ (теорема о трех перпендикулярах)
2) из $$Delta LO_{1}A_{1}:$$ $$O_{1}M_{1}=sqrt{LM_{1}*M_{1}A_{1}}=sqrt{frac{1}{5}*frac{8}{5}}=frac{2sqrt{2}}{5}$$
$$K_{1}O_{1}=sqrt{(frac{1}{5})^{2}+(frac{2sqrt{2}}{5})^{2}}=sqrt{frac{1}{25}+frac{8}{25}}=frac{3}{5}$$
$$OO_{1}=C_{1}M_{1}=sqrt{2^{2}-(frac{8}{5})^{2}}=sqrt{4-frac{64}{25}}=frac{6}{5}$$
3) Тогда площадь всего сечения есть удвоенная $$S_{OO_{1}LN_{1}}$$: $$S=frac{15}{16}*frac{6}{5}*frac{3}{5}*2=1,35$$
Задание 14
Решите неравенство: $$log_{8} (frac{1}{3}-x) log_{|2x+frac{1}{3}|} (frac{1}{3}-x) > log_{2} frac{frac{1}{3}-x}{sqrt[3]{(2x+frac{1}{3})^{2}}}$$
Ответ: $$(-infty;-frac{2}{3})cup(0;frac{1}{12})$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$log_{8}(frac{1}{3}-x)log_{12x+frac{1}{3}}(frac{1}{3}-x)>log_{2}frac{(frac{1}{3}-x)}{sqrt[3]{(2x+frac{1}{3})^{2}}}$$
С учетом того, что $$sqrt[3]{(2x+frac{1}{3})^{2}} geq 0$$ получаем следующую область определения $$D(x)$$:
$$left{begin{matrix}frac{1}{3}-x>0\ |2x+frac{1}{3}|>0\ |2x+frac{1}{3}|neq 1end{matrix}right.Leftrightarrow$$$$left{begin{matrix}x<frac{1}{3}\ 2x+frac{1}{3}neq 0\ 2x+frac{1}{3}neq 1\ 2x+frac{1}{3}neq -1end{matrix}right.Leftrightarrow $$$$left{begin{matrix}x<frac{1}{3}\ xneq -frac{1}{6}\ xneq -frac{1}{3}\ xneq -frac{2}{3}end{matrix}right.$$
Преобразуем правую часть неравенства: $$log_{2}frac{(frac{1}{3}-x)}{sqrt[3]{(2x+frac{1}{3})^{2}}}=$$$$log_{2}(frac{1}{3}-x)-log_{2}sqrt[3]{(2x+frac{1}{3})^{2}}=$$$$log_{2}(frac{1}{3}-x)-frac{2}{3}log_{2}|2x+frac{1}{3}|$$
Пусть $$a=frac{1}{3}-x$$ и $$b=|2x+frac{1}{3}|$$, тогда:
$$frac{1}{3}log_{2}alog_{b}a-log_{2}a+frac{2}{3}log_{2}b>0Leftrightarrow$$$$log_{2}alog _{b}a(1-frac{3}{log_{b}a}+frac{2 log_{2}b}{log_{2}a log_{b}a})>0Leftrightarrow$$$$log_{2}a log_{b}a(frac{log_{b}^{2}a-3log_{b}a+2}{log_{b}^{2}a})>0Leftrightarrow$$$$frac{log_{2}a}{log_{b}a}(log_{b}^{2}a-3log_{b}a+2)>0Leftrightarrow$$$$frac{log_{a}b}{log_{a}2}(log_{b}a-2)(log_{b}a-1)>0Leftrightarrow$$$$log_{2}b(log_{b}a-log_{b}b^{2})(log_{b}a-log_{b}b)>0Leftrightarrow$$
Воспользуемся методами рационализации для логарифмов:
$$(b-1)(a-b^{2})(b-1)(a-b)(b-1)>0Leftrightarrow$$$$(b-1)(a-b^{2})(a-b)>0$$
Вернемся обратно к заменам:
$$(left | 2x+frac{1}{3} right |-1)(frac{1}{3}-x-(2x+frac{1}{3})^{2})(frac{1}{3}-x-left | 2x+frac{1}{3} right |)Leftrightarrow$$$$(left | 2x+frac{1}{3} right |-1)(36x^{2}+21x-2)(left | 2x+frac{1}{3} right |-left | frac{1}{3}-x right |)>0$$
С учетом D(f): $$frac{1}{3}-x>0$$, при всех Х. Тогда $$frac{1}{3}-x$$ мы можем представить, как $$|frac{1}{3}-x|$$, а так же $$1=|1|$$ и воспользоваться методами рационализации для модулей:
$$(2x+frac{1}{3}-1)(2x+frac{1}{3}+1)(x-frac{1}{12})(x+frac{2}{3})(2x+frac{1}{3}-frac{1}{3}+x)(2x+frac{1}{3}+frac{1}{3}-x)>0Leftrightarrow$$$$(2x-frac{2}{3})(2x+frac{4}{3})(x-frac{1}{2})(x+frac{2}{3})(3x)(x+frac{2}{3})>0Leftrightarrow$$$$(x+frac{2}{3})(x-frac{1}{3})(x-frac{1}{12})x>0$$
Получаем, что (промежутки выделены синим цветом): $$left[begin{matrix}x< -frac{2}{3}\ left{begin{matrix}x> 0\ x<frac{1}{2}end{matrix}right.\ x> frac{1}{3}end{matrix}right.$$
С учетом $$D(x)$$: $$left[begin{matrix}x< -frac{2}{3}\left{begin{matrix}x>0\x<frac{1}{12} end{matrix}right.end{matrix}right.$$
Задание 15
В треугольнике АВС, где АВ=ВС=3, $$angle ABC=arccos frac{1}{9}$$ проведена медиана AD и биссектриса СЕ, пересекающиеся в точке М. Через М проведена прямая, параллельная АС и пересекающая стороны АВ и ВС в точках Р и Q соответственно.
А) Найдите РМ
Б) Найдите радиус окружности, вписанной в треугольник PQB.
Ответ: $$frac{14sqrt{5}}{55}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
A) 1) Из $$Delta ABC$$: $$AC=sqrt{AB^{2}+BC^{2}-2AB*BC*cos B}=$$$$sqrt{9+9-2*5*frac{1}{9}}=$$$$sqrt{18-2}=4$$
2)по свойству биссектрис: $$frac{AM}{MP}=frac{AC}{DC}=$$$$frac{1,5}{4}=frac{3}{8}Rightarrow$$ $$MD=frac{3}{11}AC=frac{12}{11}$$
3) Из $$Delta MDQsim Delta ADCRightarrow$$ $$frac{MD}{AD}=frac{DQ}{DC}=frac{3}{11}Rightarrow$$ $$DQ=frac{1,5*3}{11}=frac{9}{22}Rightarrow$$ $$BQ=1,5+frac{9}{22}=frac{3}{2}+frac{9}{22}=$$$$frac{33+9}{22}=frac{42}{22}=frac{21}{11}$$
4) Из $$Delta PBQsim Delta ABCRightarrow$$ $$frac{PQ}{AC}=frac{BQ}{BC}=$$$$frac{21}{11}:3=frac{21}{33}$$. Тогда $$PQ=frac{21*4}{33}=frac{84}{33}$$
5)$$PM=PQ-QM=frac{84}{33}-frac{12}{11}=$$$$frac{84-36}{33}=frac{48}{33}=frac{16}{11}$$
Б) 1) $$BP=BQ=frac{21}{11}$$, $$p=frac{frac{21}{11}+frac{21}{11}+frac{84}{33}}{2}=$$$$frac{42+28}{22}=frac{70}{22}=frac{35}{11}$$
2) По формуле Герона: $$r=frac{S}{p}=sqrt{frac{(p-a)(p-b)(p-c)}{p}}$$. Тогда: $$r=sqrt{frac{(frac{35}{11}-frac{21}{11})^{2}(frac{35}{11}-frac{28}{11})}{frac{35}{11}}}=$$$$sqrt{(frac{14}{11})^{2}*frac{7}{11}*frac{11}{35}}=$$$$frac{14}{11sqrt{5}}=frac{14sqrt{5}}{55}$$
Задание 16
В начале 2001 года Алексей приобрел ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счет будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?
Ответ: 2008
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Очевидно, что необходимо снимать деньги в тот год, когда увеличение цены на 2000 рублей будет меньше, чем увеличение на 10%, согласно ставке банка. Пусть n — год, в который это произойдет.
Следует учитывать, что начисление 2000 рублей происходит в конце года, а снять и положить можно только в начале, потому результат мы должны будем увеличить на единицу (например, в конце пятого года цена бумаги позволяет ее перекладывать, то переложим мы только в шестом году).
Если взять n-ый год, то стоимость бумаги составит: $$7000+2000n$$. Если бы мы ее положили под 10%, то на нее начислилась бы сумма $$0,1(7000+2000n)=700+200n$$. И эта сумма должна быть больше, чем 2000, чтобы был смысл перекладывать деньги в банк:
$$700+200n>2000Leftrightarrow$$$$200n>1300|:200Leftrightarrow$$$$n>6,5$$.
Так как n — число натуральное, то получаем, что $$n=7$$. То есть в конце 7 года цена бумаги станет такой, что 10% от ее стоимости, составят больше 2000, и тогда на 8 год (2008) мы ее продаем.
Задание 17
Найдите все значения параметра a, при которых система $$left{begin{matrix}log_{2} (3-x+y)=log_{2} (25-6x+7y)\ y+2=(x-2a)^{2}+a+2xend{matrix}right.$$ имеет ровно два решения
Ответ: $$(-1;3)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
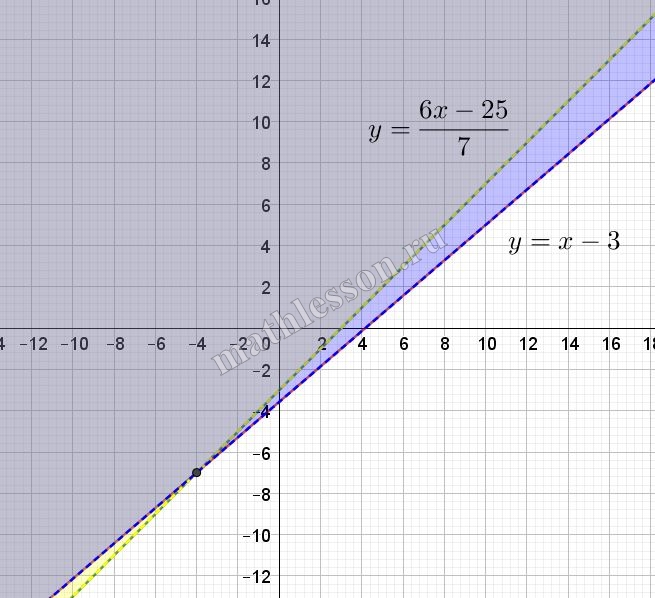
Рассмотрим область определения данной системы. Так как даны логарифмы, то: $$left{begin{matrix}3-x+y>0\25-6x+7y>0end{matrix}right.Rightarrow$$ $$left{begin{matrix}y>x-3\y>frac{6x-25}{7}end{matrix}right.$$ (желтым выделено решение для первого неравенства, синим — для второго, серым — их пересечение)
Рассмотрим первое уравнение системы:
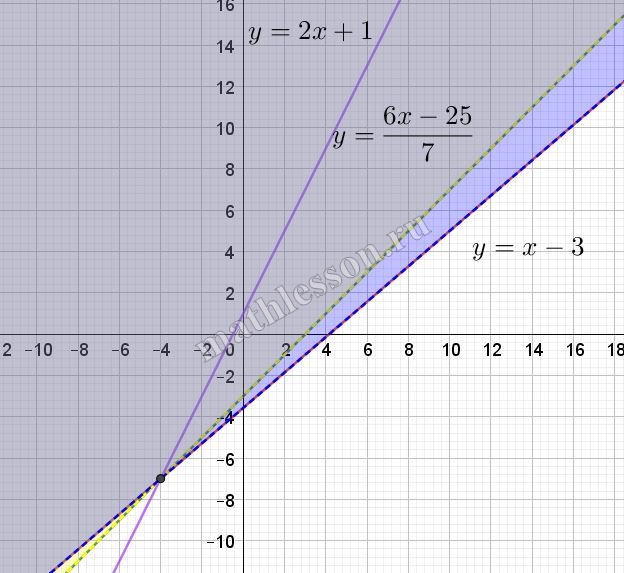
$$log_{2}(8(3-x+y))=log_{2}(25-6x+7y)Leftrightarrow$$$$24-8x+8y=25-6x+7yLeftrightarrow$$$$y=2x+1 (1)$$
Построим график данной функции с учетом области определения:
Как видим, чтобы было два пересечения, x должен быть больше 4 (иначе часть прямой лежит вне области определения)
Подставим (1) во второе:$$2+2x+1=(x-2a)^{2}+a+2xLeftrightarrow$$$$(x-2a)^{2}=3-a$$
Так как число в квадрате, то правая часть уравнения должна быть больше нуля (если равна нулю, то корень всего один): $$3-a>0Rightarrow a<3$$
Рассмотрим график второй функции:
$$y+2=x^{2}-4ax+2a^{2}+a+2xLeftrightarrow$$$$y=x^{2}+x(2-4a)+4a^{2}+a-2$$
Найдем вершину параболы:
$$x_{0}=-frac{2(1-2a)}{2}=2a-1$$
$$y_{0}=4a^{2}-4a+1-2(2a-1)^{2}+4a^{2}+a-2=8a^{2}-3a-1-8a^{2}+8a-2=5a-3$$
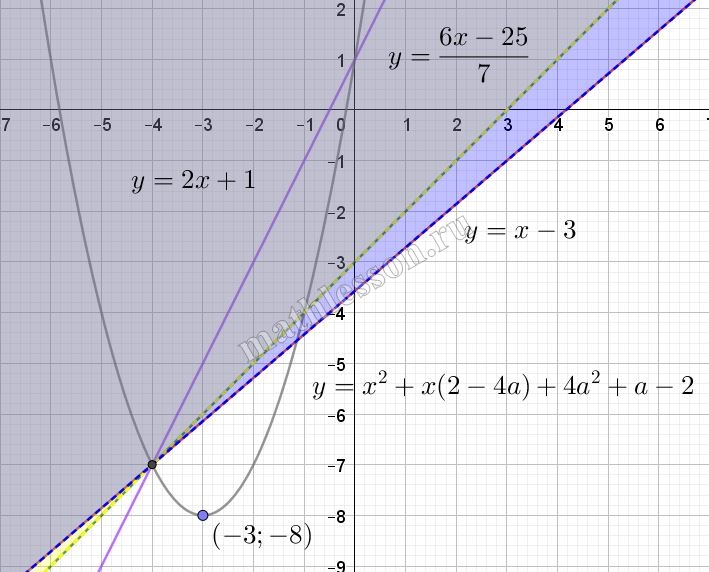
Рассмотрим возможное расположение графика с учетом области определения:
Как видим, координата y вершины параболы должна быть больше -8, а х больше -3 (если будет левее, то отно пересечение точно не попадет в область определения) :
$$left{begin{matrix}2a-1>-3\5a-3>-8end{matrix}right.Leftrightarrow$$$$left{begin{matrix}a>-1\a>-1end{matrix}right.$$
С учетом того, что $$a<3$$, получаем: $$a in (-1;3)$$
Задание 18
Целые числа от 2 до 11 записаны в строчку в некотором порядке. Всегда ли можно вычеркнуть несколько чисел так, чтобы осталось:
А) три числа в порядке возрастания или в порядке убывания?
Б) пять чисел в порядке возрастания или в порядке убывания?
В) четыре числа в порядке возрастания или в порядке убывания?
Ответ: да,нет,да
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) Да.Есть два возможных расположения чисел 2 и 11 относительно других чисел.
- если они идут рядом. Пусть числа идут в порядке возрастания (2,11). Тогда мы всегда сможем начать убывающую последовательно с 11. Из оставшихся 9 чисел в любом случае надется расположение двух, идущих друг за другом, в порядке убывания). Исключение составляет случай, когда все следующие будут расположены в порядке возрастания, но тогда из них мы сможем построить возрастающую последовательность. Аналогичное рассуждение для убывания.
- если между ними есть число. Тогда они в любом случае будут или возрастающей последовательностью (2,а,11) или убывающей (11, а, 2)
Б) Нет. Достаточно привести пример: 7 5 2 9 6 11 4 10 3 8. (Смысл его построения сводится к тому, что в середину ставится 11, а далее через одно раскидываются больше оставшиеся, а промежутки заполняются меньшими. Подобное расположение не дает построить последовательность, будь то возрастающая или убывающая, более, чем из 4 чисел)
В) Да. Рассмотрим уже имеющуюся в пункте (Б) полседовательность. Для каждого числа из нее мы подберем пару чисел (a,b), где а — количество чисел максимально длинной возрастающей последовательности, начинающей с текущего числаб b — убывающей: 7(3,4) 5(3,3) 2(3,1) 9(2,4) 6(2,3) 11(1,3) 4(2,2) 10(1,2) 3(2,1) 8(1,1). Как видим среди встречающихся пар чисел нет повторяющихся. При этом, в пункте (Б) мы доказали, что a,b<5, то есть числа в парах могут быть только 1,2,3,4. Согласно комбинаторике, если $$a,b in [1;3]$$, то число возможных пара (a,b) составляет $$3*3=9$$. А у нас пар числе 10. Это означает, что однозначно одна пара чисел будет содержать хоть одну 4. Следовательно, будет последовательность из 4 чисел.
А. Ларин: Тренировочный вариант № 246.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В треугольнике ABC, где
проведена медиана AD и биссектриса СЕ, пересекающиеся в точке M. Через M проведена прямая, параллельная AC и пересекающая стороны AB и BC в точках P и Q соответственно.
а) Найдите PM.
б) Найдите радиус окружности, вписанной в треугольник PQB.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В начале 2001 года Алексей приобрел ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счет будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
При каких значениях параметра a, при которых система
имеет ровно два решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Целые числа от 2 до 11 записаны в строчку в некотором порядке. Всегда ли можно вычеркнуть несколько чисел так, чтобы осталось:
а) три числа в порядке возрастания или в порядке убывания?
б) пять чисел в порядке возрастания или в порядке убывания?
в) четыре числа в порядке возрастания или в порядке убывания?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Contents
- 1 Задание 1
- 1.1 Решение
- 2 Задание 2
- 2.1 Решение
- 3 Задание 3
- 3.1 Решение
- 4 Задание 4
- 4.1 Решение
- 5 Задание 5
- 5.1 Решение
- 6 Задание 6
- 6.1 Решение
- 7 Задание 7
- 7.1 Решение
- 8 Задание 8
- 8.1 Решение
- 9 Задание 9
- 9.1 Решение
- 10 Задание 10
- 10.1 Решение
- 11 Задание 11
- 11.1 Решение
- 12 Задание 12
- 12.1 Решение
- 13 Задание 13
- 13.1 Решение
- 13.2 Задание 14
- 13.3 Решение
- 14 Задание 15
- 14.1 Решение
- 15 Задание 16
- 15.1 Решение
- 16 Задание 17
- 16.1 Решение
- 17 Задание 18
- 17.1 Решение
- 18 Задание 19
- 18.1 Решение
- 19 Видео: Разбор Варианта ЕГЭ Ларина №246 (№1-15)
- 20 Видео: Разбор Варианта ЕГЭ Ларина №246 (№16-19)
Задание 1
В школе 800 учеников, из них 30% -ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?
Решение
Если 30% в младшей, то 100-30=70% в средней и старшей школах. Найдем количество учеников там: 100*0,7=560 человек.
Так как изучают 20%, то это значение составляет: 560*0,2=112 учеников.
Ответ: 112
Задание 2
На графике показано изменение давления в паровой турбине после запуска. На оси абсцисс откладывается время в минутах, на оси ординат—давление в атмосферах. Когда давление достигает определенного значения, открывается клапан, выпускающий часть пара, и давление падает. Затем клапан закрывается, и давление снова растет.
Определите по графику давление в турбине в момент ее запуска. Ответ дайте в атмосферах.
Решение
На момент запуска (0 минут) давление составляло 1 атм.
Ответ: 1.
Задание 3
Найдите тангенс угла AOB, изображенного на рисунке.
Решение
Используя теоремы Пифагора, найдем стороны треугольника AOB из прямоугольных треугольников:
Ответ: -2.
Задание 4
Игрок зажал в кулаке носовой платок так, что между пальцами торчат только четыре уголка. Второй игрок наудачу выбирает два уголка. Он выигрывает, если взял платок за диагональ, и проигрывает в противном случае. Найдите вероятность выигрыша второго игрока. Ответ округлите до сотых.
Решение
Ответ: 0,33
Задание 5
Решите уравнение:
Решение

Ответ: 5
Задание 6
На рисунке AB=4, BE =8, DE =5, прямая AB перпендикулярна прямой BD, CD перпендикулярна BD, EA перпендикулярна EC.
Найдите CD.
Решение

Ответ: 10.
Задание 7
Прямая y=3x+1 является касательной к графику функции y=ax2+2x+3 . Найдите a .
Решение
Чтобы прямая являлась касательной, тогда производные должны быть одинаковы:
Ответ: 0,125
Задание 8
Найдите квадрат расстояния между вершинами A и D1 многогранника, изображенного на рисунке.
Все двугранные углы многогранника прямые.
Решение
Ответ: 6.
Задание 9

Решение
Ответ: 130.
Задание 10
Очень лёгкий заряженный металлический шарик с зарядом q=2*10-6 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v=6 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол a с направлением движения шарика.
Значение индукции поля B=5*10-3 Тл. При этом на шарик действует сила Лоренца, направленная вверх перпендикулярно плоскости и равная FL (Н).
При каком наименьшем значении угла a от 0 до 180 шарик оторвётся от поверхности, если для этого нужно, чтобы сила была больше 3*10-8.
Решение
Ответ: 30.
Задание 11
Две точки равномерно вращаются по окружности. Первая совершает оборот на 5 секунд быстрее второй и делает за минуту на 2 оборота больше, чем вторая. Сколько оборотов в минуту совершает вторая точка?
Решение
Пусть x-количество оборотов в минуту первой, y- количество оборотов в минуту второй, тогда если оборот принять за 1:
Отрицательной скорость быть не может, следовательно, второе тело совершает 4 оборота в минуту.
Ответ: 4.
Задание 12
Найти наименьшее значение функции
на интервале (0;+ ∞ ).
Решение

Задание 13
а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку [2;5]
Решение
Выполним преобразования:
Ответ:
Задание 14
Основанием прямой призмы АВСА1В1С1 является равнобедренный треугольник АВС, в котором AC=CB=2 , угол ∠ACB = 2arcsin(4/5).
Плоскость, перпендикулярная прямой А1В, пересекает ребра АВ и А1В1 в точках К и L соответственно, причем:
А) Докажите, что плоскость сечения пересекает ребро СС1 в его середине.
Б ) Найдите площадь сечения.
Решение
Ответ: 1,35.
Задание 15
Решите неравенство:
Решение
Воспользуемся методами рационализации для логарифмов:
Вернемся обратно к заменам:
Ответ:
Задание 16
В треугольнике АВС, где АВ=ВС=3, угол ABC= arccos1/9 проведена медиана AD и биссектриса СЕ, пересекающиеся в точке М. Через М проведена прямая, параллельная АС и пересекающая стороны АВ и ВС в точках Р и Q соответственно.
А) Найдите РМ
Б) Найдите радиус окружности, вписанной в треугольник PQB.
Решение
Ответ:
Задание 17
В начале 2001 года Алексей приобрел ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. Начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счет будет увеличиваться на 10%.
В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?
Решение
Ответ: 2008.
Задание 18
Найдите все значения параметра a , при которых система имеет ровно два решения.
Решение
Ответ: (-1;3)
Задание 19
Целые числа от 2 до 11 записаны в строчку в некотором порядке. Всегда ли можно вычеркнуть несколько чисел так, чтобы осталось:
А) три числа в порядке возрастания или в порядке убывания?
Б) пять чисел в порядке возрастания или в порядке убывания?
В) четыре числа в порядке возрастания или в порядке убывания?
Решение
А) Да. Возьмем число 11. C одной стороны от него минимум 5 чисел. Если два из них упорядочены так, что к ним можно добавить 11 — получилось три числа. Если же все их пары упорядочены иначе, то все эти пять или более чисел упорядочены.
Б) Нет. Достаточно привести пример: 7 5 2 9 6 11 4 10 3 8. (Смысл его построения сводится к тому, что в середину ставится 11, а далее через одно раскидываются больше оставшиеся, а промежутки заполняются меньшими. Подобное расположение не дает построить последовательность, будь то возрастающая или убывающая, более, чем из 4 чисел)
в) Да. Напишем под каждым числом длину максимальной возрастающей и максимальной убывающей последовательности, начинающейся с этого числа. Например для примера пункта б под числом 6 будет написано (2; 3). Для двух чисел эти пары не могут совпадать. Пусть, например, a записано раньше b и тогда к возрастающей последовательности, начинающейся с b, можно в начало добавить a, поэтому для a длина максимальной убывающей последовательности будет больше. Аналогично если то можно будет удлинить убывающую последовательность.
Если выбрать последовательность из четырех чисел нельзя, то все подписанные числа не превосходят трех. Но пар таких чисел есть всего 9, Значит, для каких-то из 10 чисел пары совпадут. Противоречие.
Ответ: да, нет, да
Видео: Разбор Варианта ЕГЭ Ларина №246 (№1-15)
Видео: Разбор Варианта ЕГЭ Ларина №246 (№16-19)
| 1192 | Найти все значения параметра a при которых система уравнений {(log_{2}(3-x+y)+3=log_{2}(25-6x+7y)) , (y+2=(x-2a)^2+a+2x) :} имеет ровно два решения |
ларин егэ по математике 2019 профильный уровень Вариант 246 Задание 18 | |
| 1191 | В треугольнике ABC, где AB=BC=3, /_ABC=arccos(1/9) проведена медиана AD и биссектриса СЕ, пересекающиеся в точке M. Через M проведена прямая, параллельная АС и пересекающая стороны AB и BC в точках P и Q соответственно. а) Найдите PM б) Найдите радиус окружности, вписанной в треугольник PQB |
ларин егэ по математике 2019 профильный уровень Вариант 246 Задание 16 # Два способа решения | |
| 1188 | а) Решите уравнение (3+cos(4x)-8(cos(x))^4)/(4(cos(x)+sin(x)))=1/sin(x) б) Укажите корни этого уравнения, принадлежащие отрезку [2; 5]. |
ларин егэ по математике 2019 профильный уровень Вариант 246 Задание 13 | |
| 1187 | Решите неравенство log_{8}(1/3-x)*log_{abs(2x+1/3)}(1/3-x) > log_{2}((1/3-x)/(2x+1/3)^(2/3)) |
ларин егэ по математике 2019 профильный уровень Вариант 246 Задание 15 | |
Разбор Варианта ЕГЭ по математике профиль Ларина #246. Полный разбор заданий ЕГЭ по математике 2019. Тренировочные варианты егэ по математике 2019. Математикс
№1-15
№16-19
Смотрите также:
Разбор Варианта Ларина №246 ЕГЭ математике профиль. Варианты ЕГЭ по математике профильный уровень 2019. Решение варианта Ларина. mrMathlesson Виктор Осипов
1-15 задания
16-19 задания
Смотрите также: