Задания
Версия для печати и копирования в MS Word
Откройте файл электронной таблицы, содержащей вещественные числа — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Задание 9
Сколько раз встречалась температура, которая была ниже среднего арифметического значения округленного до десятых, но выше удвоенного минимального значения?
Спрятать решение
Решение.
Для поиска среднего арифметического значения температуры воспользуемся формулой =СРЗНАЧ(B2:Y92). Среднее арифметическое значение температуры равно 23,9. Для поиска минимального значения воспользуемся формулой =МИН(B2:Y92). Минимальное значение температуры равно 8,1. Теперь с помощью формулы =СЧЁТЕСЛИМН(B2:Y92; «<23,9″; B2:Y92;»>16,2″) найдём количество измерений, которые ниже среднего арифметического значения, но выше удвоенного минимального значения — 640.
Ответ: 640.
Задания
Версия для печати и копирования в MS Word
На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.
Спрятать решение
Решение.
Из 16 наблюдений, представленных на графике, 2 дня выпадало более 3 мм осадков в остальные дни менее 3 мм осадков. Поэтому 14 дней выпадало менее 3 мм осадков.
Ответ: 14.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 01.06.2013 23:28
Два дня вообще не выпадало осадков, таким образом, получается не 14, а 12.
Служба поддержки
У нас верно. Почему так говорят по-русски — это не к нам.
Гость 14.05.2014 19:57
Но тут ведь всего 15 наблюдений, а не 16
Сергей Никифоров
Посчитайте количество точек на графике
Решу егэ математика 27247
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д1 № 27527
На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.
Из 16 наблюдений, представленных на графике, 2 дня выпадало более 3 мм осадков в остальные дни менее 3 мм осадков. Поэтому 14 дней выпадало менее 3 мм осадков.
—>
Задания Д1 № 27527
Решу егэ математика 27247.
Math-ege. sdamgia. ru
30.01.2017 12:33:13
2017-01-30 12:33:13
Источники:
Https://math-ege. sdamgia. ru/problem? id=27527
Решу егэ математика 27247 » /> » /> .keyword { color: red; } Решу егэ математика 27247
Решу егэ математика 27247
Решу егэ математика 27247
В треугольнике ABC угол C равен 90°, Найдите
Решение. Имеем:
Приведем решение Алишера Простова.
Найдем косинус угла А:
Найдем гипотенузу AB:
По теореме Пифагора найдем BC:
В треугольнике ABC угол C равен 90°, АС = 4, Найдите АВ.
Решение. По определению косинуса:
В треугольнике ABC угол C равен 90°, АС = 4. Найдите АВ.
Решение. Имеем:
Приведем другое решение:
По теореме Пифагора найдем AB:
В треугольнике ABC угол C равен 90°, АС = 8, Найдите BC.
Решение. По определению тангенса:
В треугольнике ABC угол C равен 90°, BC = 4, Найдите АВ.
Решение. По определению синуса:
В треугольнике ABC угол C равен 90°, ВС = 2. Найдите АС.
Решение. Имеем:
В треугольнике ABC угол C равен 90°, ВС = 4. Найдите АС.
Решение. По определению тангенса:
В треугольнике ABC угол C равен 90°, AC = 24, BC = 7. Найдите
Решение. Имеем:
В треугольнике ABC угол C равен 90°, CH – высота, Найдите
Решение. Имеем:
В треугольнике АВС угол С равен 90°, СН — высота, Найдите ВН.
Решение. Углы А и НСВ равны как острые углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, Найдите высоту CH.
Решение. Поскольку имеем:
Приведем другое решение.
Пусть длина катета ВС равна Х, тогда длина АС равна 5Х, а длина гипотенузы равна Зная, что гипотенуза равна 13, находим: Поскольку проведенная к гипотенузе высота равна произведению катетов, деленному на гипотенузу, имеем:
В треугольнике АВС угол С равен 90°, CH — высота, Найдите АН.
Решение. Имеем:
В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, Найдите BH.
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами. Поэтому
В треугольнике АВС угол С равен 90°, Найдите высоту СН.
Решение. Углы А и НСВ равны как углы со взаимно перпендикулярными сторонами. Поэтому
В треугольнике ABC угол C равен 90°, СН — высота, BC = 3, Найдите АН.
Решение. Имеем:
Приведем решение Алены Терентьевой.
Найдем синус угла A:
Заметим, что ∠CAB = ∠BCH, тогда
Следовательно, AH = AB − HB = 18 − 0,5 = 17,5.
В треугольнике АВС угол С равен 90°, СН — высота, Найдите ВН.
Решение. Углы А и НСВ равны как углы со взаимно перпендикулярными сторонами.
В треугольнике АВС угол С равен 90°, Найдите СН.
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, CH – высота, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, BH = 4. Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами. Поэтому
В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, CH – высота, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, высота CH равна 20, BC = 25. Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, высота CH равна 4, BC = 8. Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, высота CH равна 4, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, высота CH равна 24, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, высота CH равна 7, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, высота CH равна 8, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, CH — высота, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами. Поэтому из треугольников BHC и BCA имеем:
В треугольнике ABC угол C равен 90°, CH – высота, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами.
В треугольнике ABC угол C равен 90°, CH – высота, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами, поэтому
В треугольнике ABC угол C равен 90°, CH – высота, Найдите
Решение. Углы A и HCB равны как углы со взаимно перпендикулярными сторонами,
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
Решение. Площадь прямоугольного треугольника равна половине произведения его катетов. По теореме Пифагора A 2 = 100 − 36 = 64, A = 8, где A — второй катет. Поэтому
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
Решение. Пусть X — меньший катет, тогда X + 2 — больший. Площадь прямоугольного треугольника равна половине произведения катетов:
Один острый угол прямоугольного треугольника на 32° больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение. Сумма острых углов прямоугольного треугольника равна 90°, а их разность по условию равна 32°, получаем систему уравнений:
Один острый угол прямоугольного треугольника в 4 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение. Обозначим меньший острый угол прямоугольного треугольника за X, тогда больший острый угол будет равен Имеем: Поэтому X = 18°. Значит, больший острый угол равен
В треугольнике ABC угол ACB равен °, угол B равен °, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Решение. CD — медиана в прямоугольном треугольнике, значит, CD = AD = BD. Тогда треугольник ACD — равнобедренный, углы при его основании равны.
Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Решение. Под углом пересечения прямых понимается меньший угол, который они образуют. Найдем угол АОЕ — внешний угол треугольника АОС. Получаем:
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Острый угол B прямоугольного треугольника ABC равен 61°. Найдите угол между высотой CH и биссектрисой CD, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Решение. Имеем:
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Решение. Меньшим будет угол A, так как угол ACH в прямоугольном треугольнике ACH очевидно больше, чем угол HCB в прямоугольном треугольнике HCB. Рассмотрим треугольник ACH.
Острый угол В прямоугольного треугольника равен 66°. Найдите угол между высотой СН и медианой СМ, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение. Так как CM — медиана, то AM = MC (свойство медианы в прямоугольном треугольнике), а значит, углы A и ACM равны как углы при основании равнобедренного треугольника АМС. Заметим, что основание высоты ближе к вершине большего острого угла. Имеем:
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Решение. В прямоугольном треугольнике CHM угол C равен 40°, поэтому угол M равен 50°. Треугольник АСВ прямоугольный, CM — медиана, опущенная из вершины прямого угла, следовательно, CM = MB, и углы B и MCB равны как углы при основании равнобедренного треугольника. Тогда:
Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение. Так как CM — медиана, то AM = MC (свойство медианы в прямоугольном треугольнике), а значит, углы A и ACM равны как углы при основании равнобедренного треугольника.
Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Решение. Так как CM — медиана, то AM = MC (свойство медианы в прямоугольном треугольнике), а значит, углы A и ACM равны как углы при основании равнобедренного треугольника:
В треугольнике ABC угол C равен 90°, угол A равен Найдите высоту
Найдите меньший катет.
Math-ege. sdamgia. ru
15.01.2020 19:59:06
2020-01-15 19:59:06
Источники:
Https://math-ege. sdamgia. ru/test? theme=79&print=true
ЕГЭ–2022, информатика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 27247
Решу егэ математика 27247
Решу егэ математика 27247
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д21 № 3747
Определите, какое число будет напечатано в результате выполнения следующего алгоритма.
DIM A, B, T, M, R AS INTEGER
1. Алгоритм ищет наименьшее значение функции F(t) на интервале от a до b
2. график этой функции – парабола, оси которой направлены вверх, поэтому функция имеет наименьшее значение в вершине.
3. Найдем абсциссу вершины
4. Так как в условии написано «write(M)», следовательно, ответ −3.
Задания Д21 № 3749
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
DIM A, B, T, M, R AS INTEGER
1. Алгоритм ищет наименьшее значение функции F(t) на интервале от a до b
2. график этой функции – парабола, оси которой направлены вверх, поэтому функция имеет наименьшее значение в вершине.
3. Найдем абсциссу вершины:
4. Так как в условии сказано «write(M)», ответ −1.
Задания Д21 № 4857
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для вашего удобства алгоритм представлен на четырёх языках):
DIM A, B, T, M, R AS INTEGER
1. Алгоритм ищет наименьшее значение функции F(t) на интервале от a до b.
2. Имеем: , график этой функции – парабола, ветви которой направлены вверх, поэтому функция принимает наименьшее значение в вершине.
3. Найдем абсциссу вершины:
Как видно, она лежит в нужном интервале.
Задания Д21 № 4953
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего удобства алгоритм представлен на пяти языках):
DIM A, B, T, M, R AS INTEGER
Var a, b,t, M,R :integer;
Function F(x: integer):integer;
For t := a to b do begin
If (F(t)> R) then begin
Using namespace std;
Нц для t от a до b
Python
For t in range(a, b+1):
1. Алгоритм ищет точку, в которой функция F(t) имеет наибольшее значение на интервале от a до b.
2. Имеем: , график этой функции – парабола, ветви которой направлены вверх, поэтому функция принимает наибольшее значение на одном из концов.
3. Вычислим значения функции для концов:
Как видно, значение на правом конце больше, чем на левом. То есть, наибольшее значение функции равно значению функции на правом конце. Абсцисса на правом конце равна 20, следовательно, ответ — 20.
Задания Д21 № 4986
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего удобства алгоритм представлен на четырех языках):
DIM A, B, T, M, R AS INTEGER
Var a, b,t, M,R :integer;
Function F(x: integer):integer;
For t := a to b do begin
If (F(t) > R) then begin
Using namespace std;
Нц для t от a до b
Python
For t in range(a, b+1):
1. Алгоритм ищет наибольшее значение функции F(t) на интервале от a до b.
2. Имеем: , график этой функции – парабола, ветви которой направлены вверх, поэтому функция принимает наибольшее значение на одном из концов.
3. Вычислим значения функции для концов:
Как видно, значение на правом конце больше, чем на левом. То есть, наибольшее значение функции равно значению функции на правом конце. Абсцисса на правом конце равна 25, следовательно, ответ — 25.
Задания Д21 № 10395
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего удобства алгоритм представлен на пяти языках).
DIM A, B, T, M, R AS INTEGER
Программа ищет такой целый x из промежутка [-10; 20], что, то есть функция принимает минимальное значение на этом промежутке. При этом, если минимальное значение функции достигается в нескольких точках, из них выбирается минимальная.
. Но -1 меньше, поэтому программа найдёт -1.
И так как на экран выводится x + 10, программа выведет 9.
Задания Д21 № 10422
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего удобства алгоритм представлен на пяти языках).
DIM A, B, T, M, R AS INTEGER
Программа ищет такой целый x из промежутка [-10; 20], что, то есть функция принимает минимальное значение на этом промежутке. При этом, если минимальное значение функции достигается в нескольких точках, из них выбирается минимальная.
. Но -2 меньше, поэтому программа найдёт -2.
И так как на экран выводится x + 18, программа выведет 16.
Задания Д21 № 3333
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
DIM A, B, T, M, R AS INTEGER
1. Цикл «for t:=a to b do begin. » ищет наименьшее значение функции F(t) на интервале от a до b
2. график этой функции – парабола, оси которой направлены вверх, поэтому функция имеет наименьшее значение в вершине.
3. Найдем абсциссу вершины
Как видно, она лежит в нужном интервале.
4. Теперь, так как в программе сказано «write(R)» найдем ординату вершины (которая и есть )
Задания Д21 № 3345
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
DIM A, B, T, M, R AS INTEGER
Var a, b,t, M,R: integer;
Function F(x:integer): integer;
For t := a to b do begin
If (F(t) > R) then begin
Using namespace std;
Нц для t от a до b
Python
For t in range(a, b+1):
1. Алгоритм ищет наибольшее значение функции F(t) на интервале от a до b
2. график этой функции – парабола, оси которой направлены вниз, поэтому функция имеет наибольшее значение в вершине.
3. Найдем абсциссу вершины:
Как видно, она лежит в нужном интервале.
4. Теперь, так как в программе сказано «write(R)» найдем ординату (которая и есть )
Задания Д21 № 3752
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
DIM A, B, T, M, R AS INTEGER
WHILE T = R THEN
Var a, b,t, M,R: integer;
Function F(x:integer): integer;
While t = R) then begin
Using namespace std;
Python
1. Алгоритм ищет такое нечетное t, при котором F(t) принимает наибольшее значение на отрезке от a до b.
2. , график функции – парабола, ветви которой направлены вниз, она принимает наибольшее значение в вершине или на одном из концов отрезка.
3. Найдем абсциссу вершины:
4. Так как t всегда увеличивается на 2 (t:=t+2), оно всегда остаётся нечётным. Найденная вершина — чётное число. Следовательно, надо смотреть ближайшие нечётные значения t: 1 и 3. F(1) = F(3).
Т. к. имеем условие F(t) >= R, запоминается номер последнего элемента, равного максимуму. Ответ: 3.
Задания Д21 № 7316
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего удобства алгоритм представлен на четырёх языках).
Алгоритм предназначен для поиска t, при котором функция F(t) принимает наименьшее значение на отрезке от a до b. Функция: F(x) = (x + 50)(x + 50) + 7 — квадратный трёхчлен с положительным старшим коэффициентом, следовательно, он принимает наименьшее значение на одном из концов промежутка. Заметим, что F(a) Ответ: 2507
Задания Д21 № 3752
Задания Д21 № 10422
График этой функции парабола, оси которой направлены вверх, поэтому функция имеет наименьшее значение в вершине.
Inf-ege. sdamgia. ru
25.04.2020 12:00:31
2020-04-25 12:00:31
Источники:
Https://inf-ege. sdamgia. ru/search? search=%D0%BA%D0%B0%D0%BA%D0%BE%D0%B5%20%D1%87%D0%B8%D1%81%D0%BB%D0%BE%20%D0%B1%D1%83%D0%B4%D0%B5%D1%82%20%D0%BD%D0%B0%D0%BF%D0%B5%D1%87%D0%B0%D1%82%D0%B0%D0%BD%D0%BE&page=3
ЕГЭ информатика 22 задание разбор, теория, как решать.
Анализ программы с циклами и условными операторами, (П) — 1 балл
Е22.9 В файле содержится информация о вычислительных процессов проектов P1, Р2 и P3
(Е. Джобс) В файле содержится информация о вычислительных процессов проектов P1, Р2 и P3, которые могут выполняться параллельно или последовательно. Каждый вычислительный процесс разбивается на подпроцессы. Будем говорить, что подпроцесс B зависит от подпроцесса A, если для выполнения подпроцесса B необходимы результаты выполнения подпроцесса A внутри вычислительного процесса (Р1, Р2 или Р3). В этом случае …
Читать далее
Е22.8 процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно
(А. Кожевникова) В файле содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В …
Читать далее
Е22.7 В файле содержится информация о вычислительных процессов проектов P1 и P2
(Е. Джобс) В файле содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться только последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первой …
Читать далее
Е22.6 если для выполнения процесса B необходимы результаты выполнения процесса A
(В. Шубинкин) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.5 N вычислительных процессов, которые могут выполняться параллельно или последовательно
(Л. Евич) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.4 Будем говорить, что процесс B зависит от процесса A
(В. Шубинкин) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.3 Определите максимально возможное целочисленное t (время выполнения процесса)
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы …
Читать далее
Е22.2 Определите минимальное время, через которое завершится выполнение всей совокупности процессов
(Л. Евич) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.1 В файле содержится информация о совокупности N вычислительных процессов
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы …
Читать далее

В задание №19_20_21
Тема: Теория игр. Поиск выигрышной стратегии.
Проверяется умение анализировать алгоритм логической игры. Умение найти выигрышную стратегию игры. Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию.
-
Одна куча — варианты решений -
Две кучи — варианты решений -
Три кучи — варианты решений
Немного теории:
☆ Все позиции в простых играх делятся на выигрышные и проигрышные
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
- если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
- выигрышные и проигрышные позиции можно охарактеризовать так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
Одна куча:
Задание 19
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу три камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 23 или 80 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 78. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 78 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 77.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Вася выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:

Ответ: 5
Задание 20
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Теперь попробуем определить значение S, при которых у Пети будет выигрышная стратегия, причём Петя не сможет выиграть первым ходом, но сможет выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.

Ответ: 16 18
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
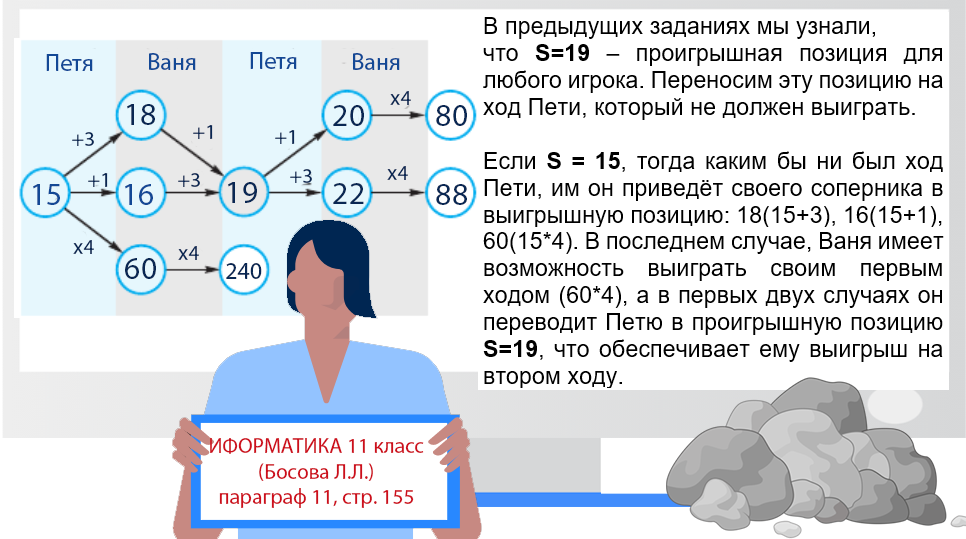
Ответ: 15
Задание 19 (самостоятельно)
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу два камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 22 или 79 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 85. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 85 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 84.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 20 (самостоятельно)
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21 (самостоятельно)
Для игры, описанной в задании 19, найдите максимальное значение S, при котором одновременно выполняются два условия:
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Задание 19_20_22(DEMO) пишем программу Phyton
P-01 (демо-2022). Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит
куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Задание 19.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Задание 20.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
n = 29
def gameResult(s):
if s>=n:return 0
nYes = [gameResult(s+1), gameResult(s*2)]
nNo = [i for i in nYes if i<=0]
if nNo:res = -max(nNo) + 1
else:res = -max(nYes)
return res
# основная программа
results = [(s,gameResult(s)) for s in range(1,n)]
print( '19:', [s for s, r in results if r == -1] )
print( '20:', [s for s, r in results if r == 2] )
print( '21:', [s for s, r in results if r == -2] )

Задание 19_20_22 (Поляков) пишем программу Phyton

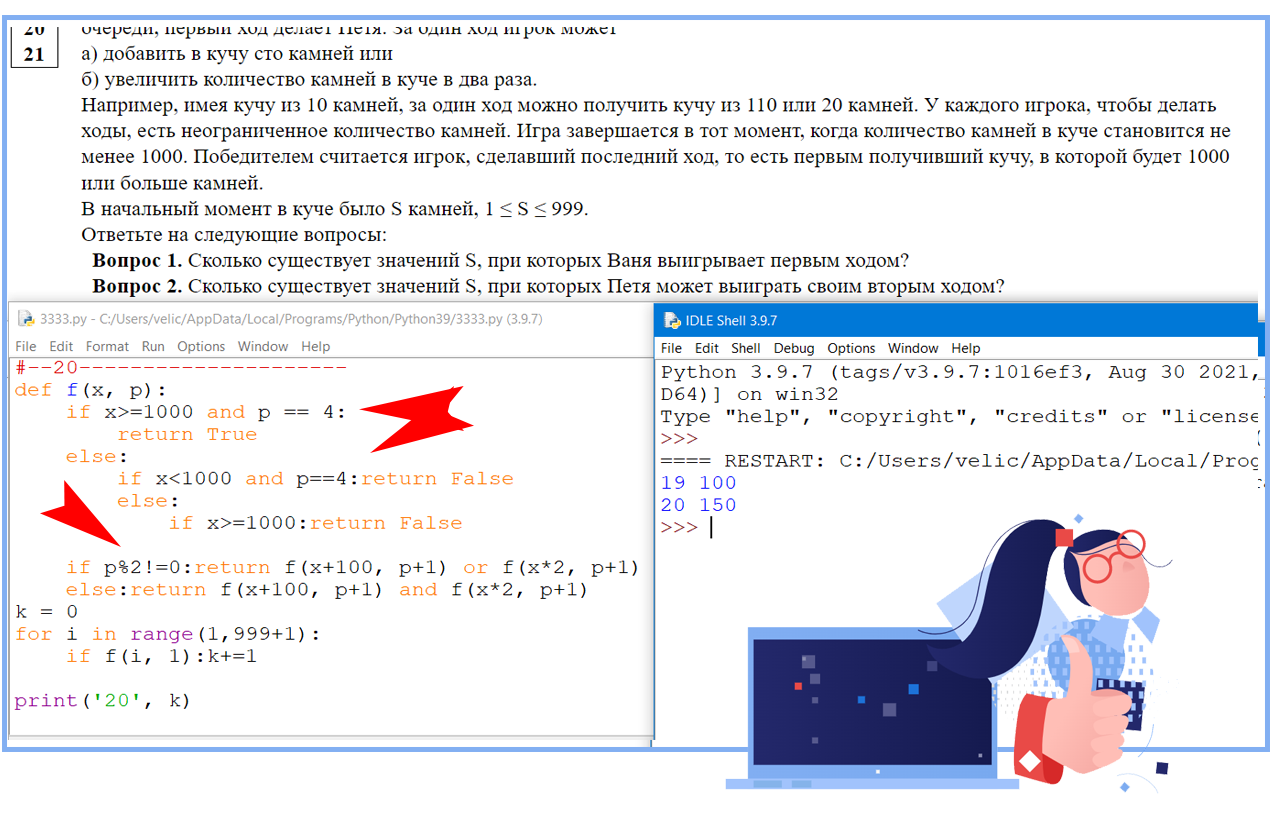
Две кучи — варианты решений
Задание 19 (разбираем задание)
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в одну из куч (по своему выбору) один камень или
- Добавить в одну из куч (по своему выбору) удвоенное число камне из другой кучи.
Например, пусть в одной куче 8 камней, а в другой куче 5 камней. Тогда за один ход можем получить четыре позиции: (9, 5); (18, 5); (8, 6); (8, 21).
Для того что бы играть, у игроков есть неограниченное количество камне.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было 9 камней, во второй S камней: 1 ≤ S ≤ 67.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Вася выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
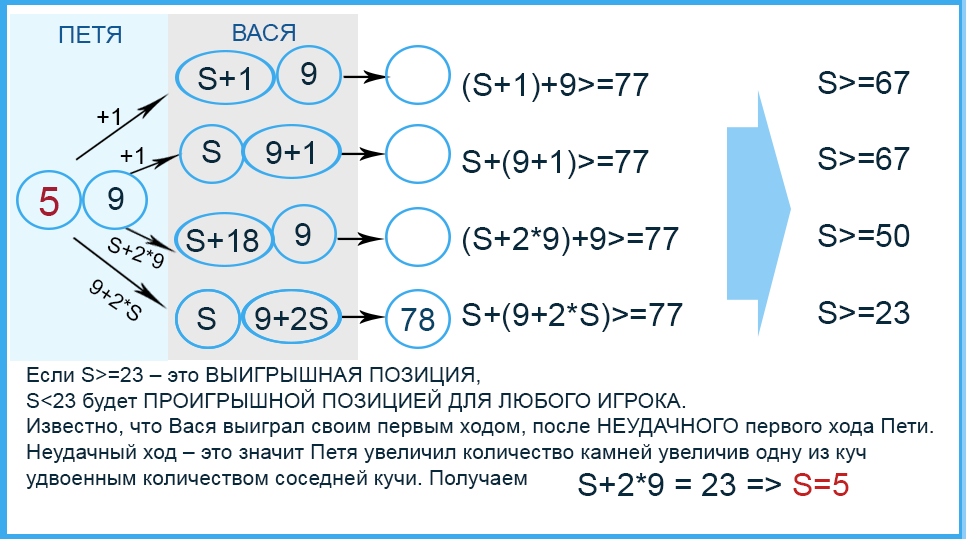
Можно решить с помощью рассуждений:
- Если S = 67, то добавив в любую кучу один камень (67+1+9=77), или добавить удвоенную соседнюю кучу в любую из куч (9+(67+2*9)=94 или ((9+2*67)+67=210), Петя становится победителем.
- Если S = 66, добавив удвоенную соседнюю кучу в любую из куч (9+(66+2*9)=93 или ((9+2*66)+66=207), Петя становится победителем.
- Если S = 65, добавив удвоенную соседнюю кучу в любую из куч (9+(65+2*9)=92 или ((9+2*65)+65=204), Петя становится победителем.
- Обратим внимание, если удваиваем 9 камней и добавляем во вторую кучу, уменьшение ровно на 1, поэтому ускорим процесс 92-77=15, 65 -15 =50, идем дальше
- Если S = 50, добавив удвоенную соседнюю кучу в любую из куч (9+(50+2*9)=77 или ((9+2*50)+50=159), Петя становится победителем.
- У нас остается только один вариант, ускорим процес, усли удваиваем вторую кучу, уменьшение ровно на три, поэтому ускорим процесс 159-77=82, 82/3=27,333, 50-27=23
- Если S = 23, добавив удвоенную соседнюю кучу в эту из куч ((9+2*23)+23=78), Петя становится победителем. СТОП!!!
Получили – S>=23 – это ВЫИГРЫШНАЯ ПОЗИЦИЯ,
S<23 будет ПРОИГРЫШНОЙ ПОЗИЦИЕЙ ДЛЯ ЛЮБОГО ИГРОКА.
Известно, что Вася выиграл своим первым ходом, после НЕУДАЧНОГО первого хода Пети.
Неудачный ход – это значит Петя увеличил количество камне увеличив одну из куч удвоенным количеством соседней кучи. Получаем S+2*9 = 23 => S=5
Можно проверить программой:
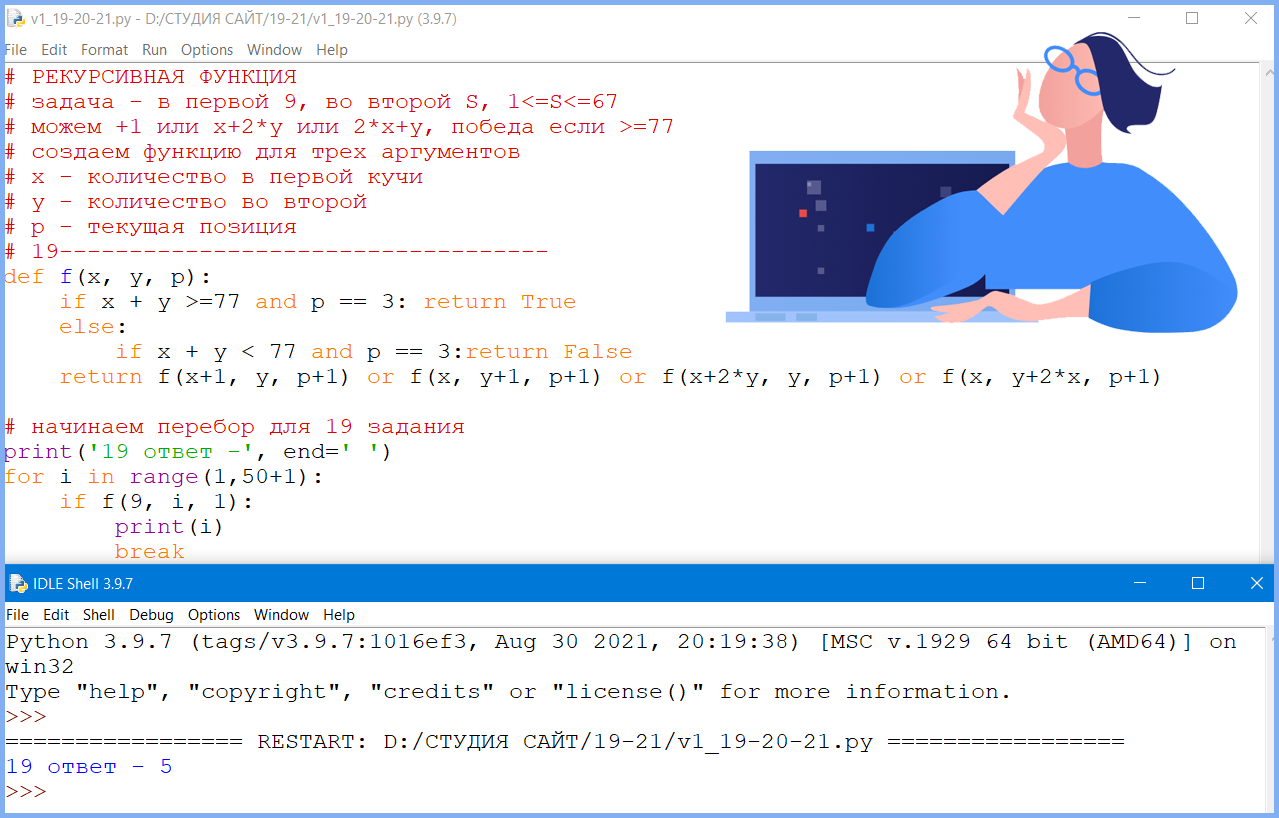
# 19-----------------------------------
def f(x, y, p):
if x + y >=77 and p == 3: return True
else:
if x + y < 77 and p == 3:return False
return f(x+1, y, p+1) or f(x, y+1, p+1) or f(x+2*y, y, p+1) or f(x, y+2*x, p+1)
# начинаем перебор для 19 задания
print('19 ответ -', end=' ')
for i in range(1,50+1):
if f(9, i, 1):
print(i)
break
Ответ: 5
Задание 20 (разбираем задание)
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
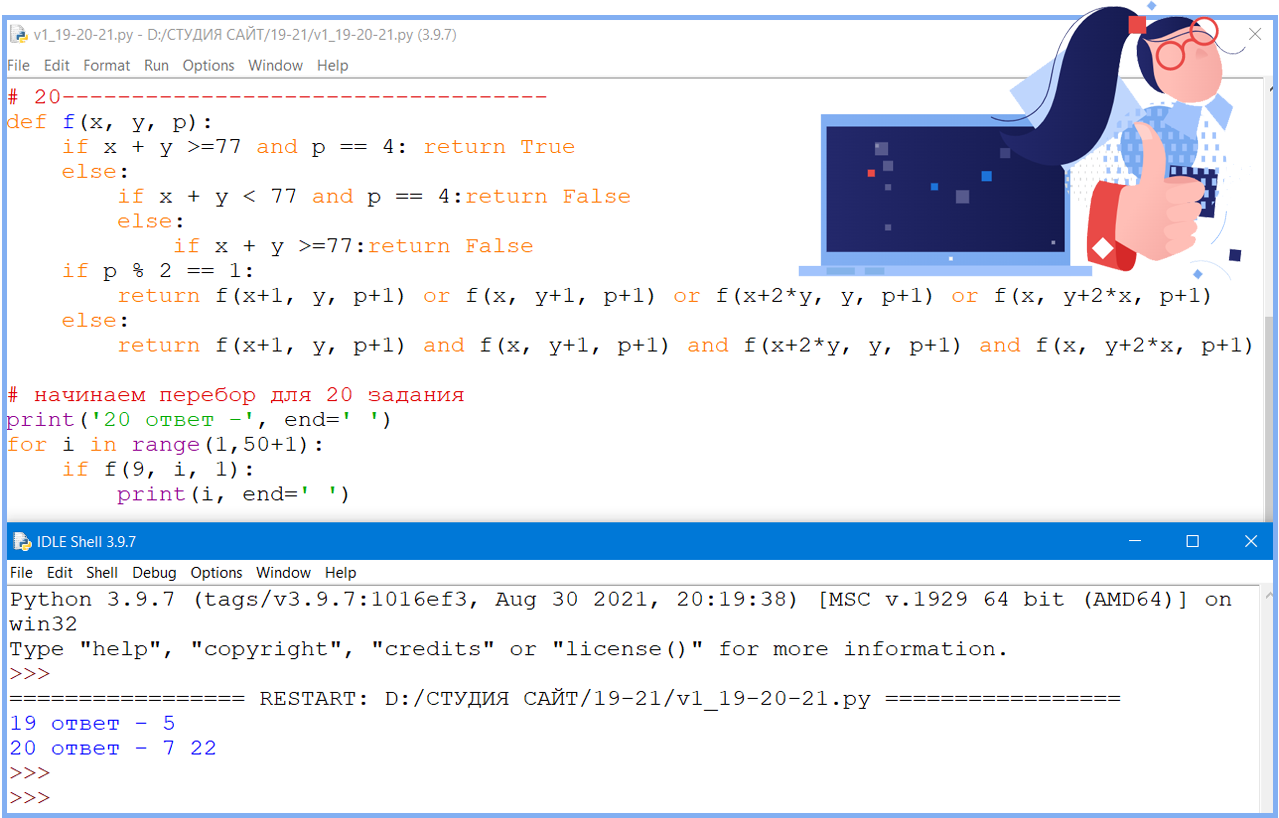
Ответ: 7 22
Задание 21 (разбираем задание)
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
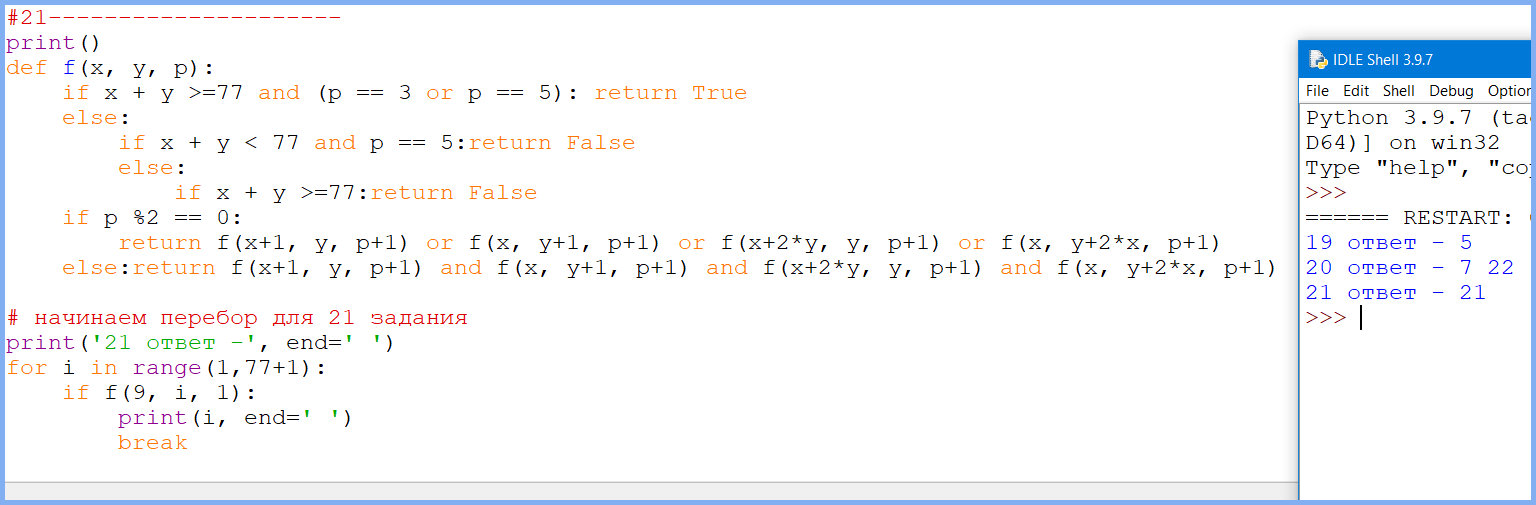
Ответ: 21
Три кучи — варианты решений
Задание 19_20_21 (разбираем задание)
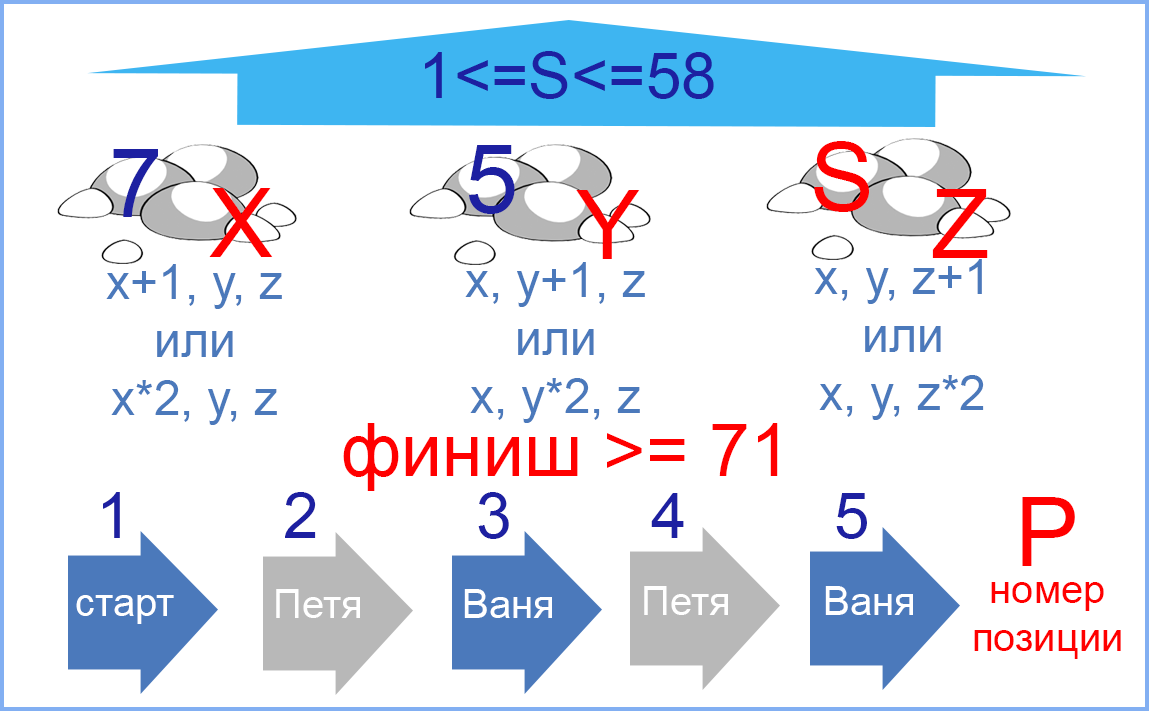
(№ 4725) (И. Осипов) Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат три кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) три камня или увеличить количество камней в куче в два раза. Например, пусть в первой куче 10 камней, во второй 7, а в третьей 4 камня; такую позицию в игре будем обозначать (10, 7, 4). Тогда за один ход можно получить любую из шести позиций: (13, 7, 4), (20, 7, 4), (10, 10, 4), (10, 14, 4), (10, 7, 7), (10, 7, 8). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 71. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, что в кучах всего будет 71 или больше камней. В начальный момент в первой куче было семь камней, во второй куче пять камней, в третьей куче – S камней; 1 ≤ S ≤ 58.
Ответьте на следующие вопросы:
Вопрос 1.При некотором значении S Ваня одержал победу свои первым ходом после неудачного хода Пети. Укажите минимальное значение S, при котором это возможно.
Вопрос 2. Найдите минимальное и максимальное значения S, при которых Петя выигрывает вторым ходом при любом ходе Вани.
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия: а) у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; б) у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
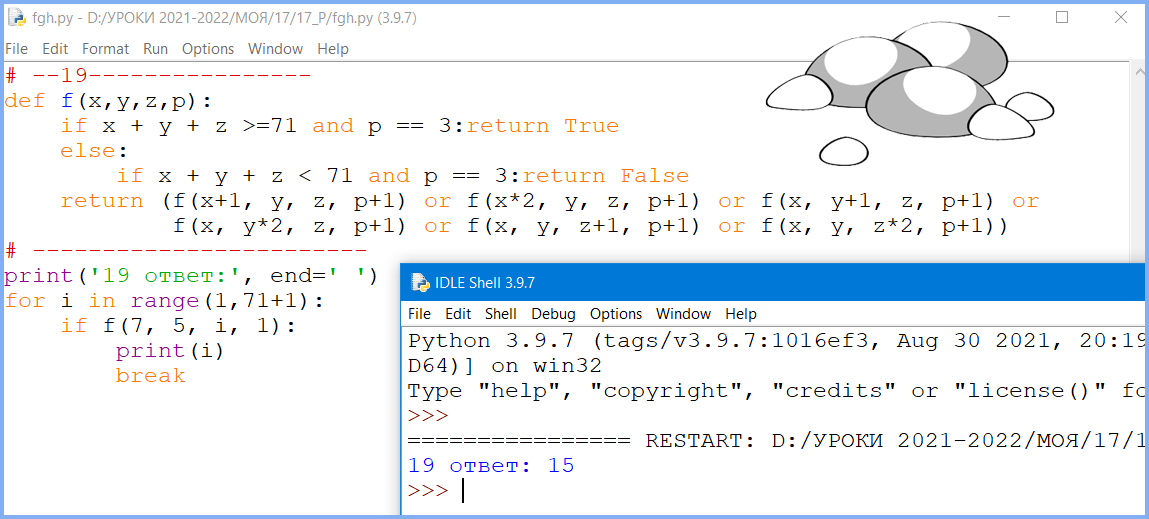
# --19----------------
def f(x,y,z,p):
if x + y + z >=71 and p == 3:return True
else:
if x + y + z < 71 and p == 3:return False
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
# ------------------------
print('19 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i)
break
Ответ: 15
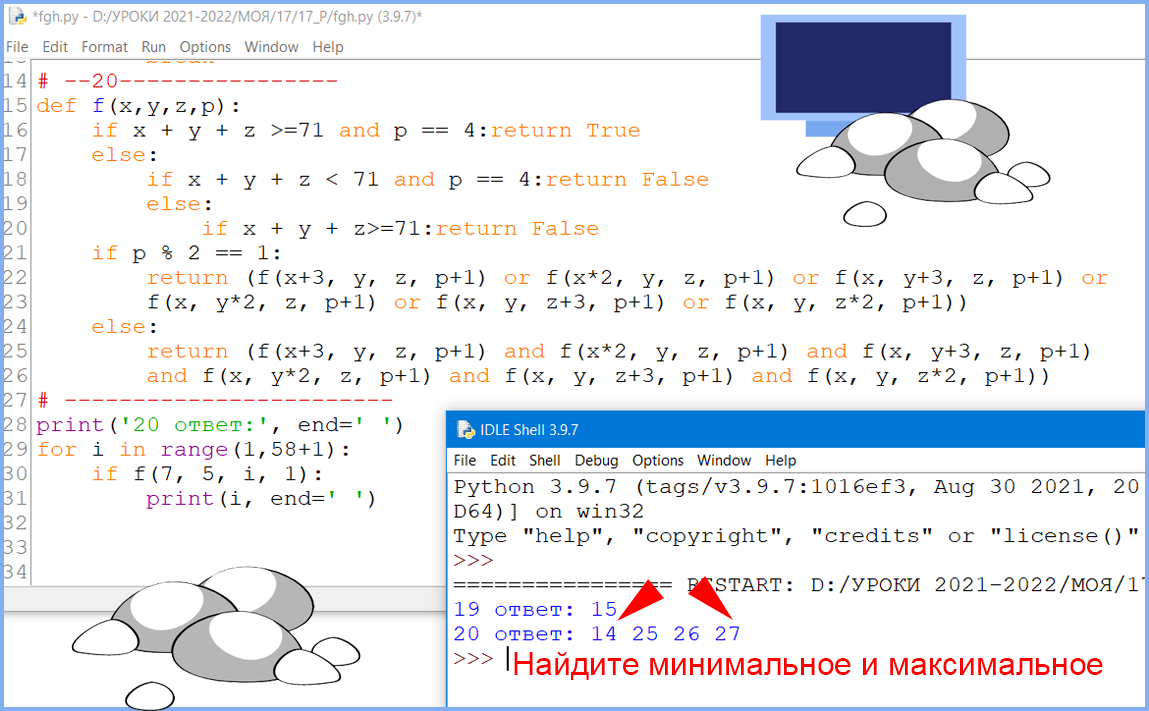
# --20----------------
def f(x,y,z,p):
if x + y + z >=71 and p == 4:return True
else:
if x + y + z < 71 and p == 4:return False
else:
if x + y + z>=71:return False
if p % 2 == 1:
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
else:
return (f(x+3, y, z, p+1) and f(x*2, y, z, p+1) and f(x, y+3, z, p+1)
and f(x, y*2, z, p+1) and f(x, y, z+3, p+1) and f(x, y, z*2, p+1))
# ------------------------
print('20 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i, end=' ')
Ответ: 14 27
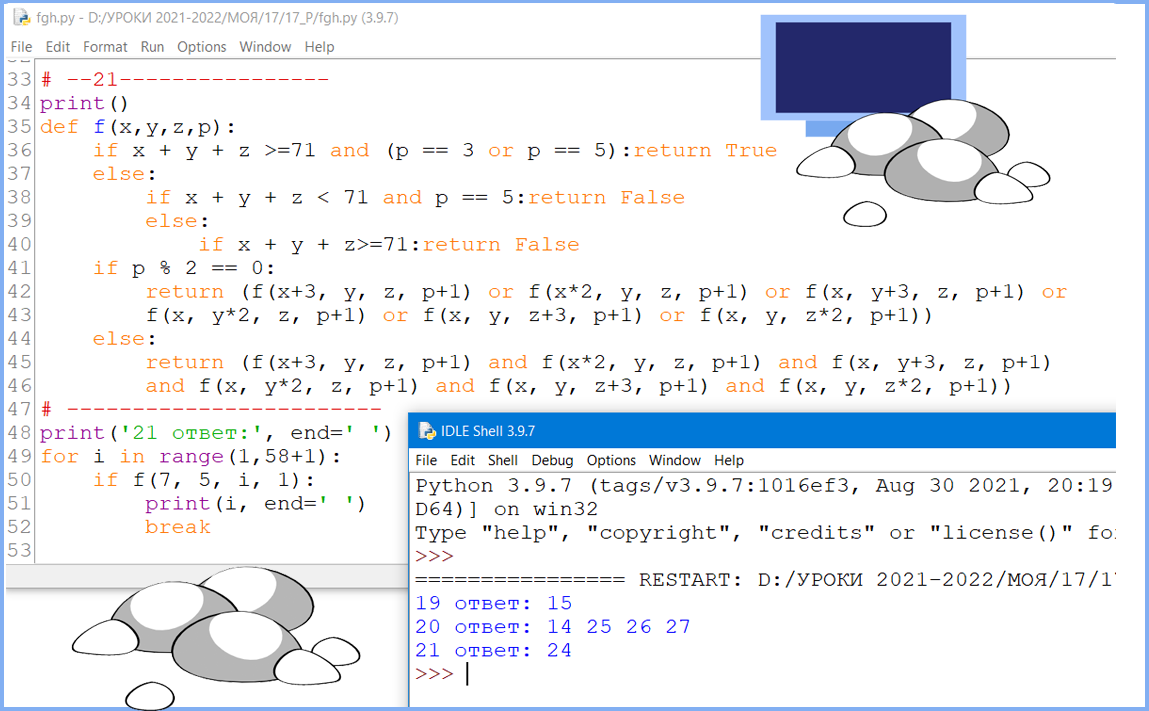
# --21----------------
print()
def f(x,y,z,p):
if x + y + z >=71 and (p == 3 or p == 5):return True
else:
if x + y + z < 71 and p == 5:return False
else:
if x + y + z>=71:return False
if p % 2 == 0:
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
else:
return (f(x+3, y, z, p+1) and f(x*2, y, z, p+1) and f(x, y+3, z, p+1)
and f(x, y*2, z, p+1) and f(x, y, z+3, p+1) and f(x, y, z*2, p+1))
# ------------------------
print('21 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i, end=' ')
break
Ответ: 24




