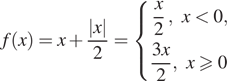Спрятать решение
Решение.
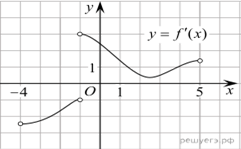
Убыванию дифференцируемой функции 
соответствуют неположительные значения её производной. Производная неположительна в точках 
: точки лежат ниже оси абсцисс, их ординаты отрицательны. Таких точек 5.
Ответ: 5.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 10.05.2013 17:41
Точка x3 — график производной возрастает => функция больше 0
Гость 30.05.2013 18:12
х2 же точка максимума f'(x),в которой f(x)=0?
Александр Иванов
Нет. Точка х2 это точка максимума f ‘(x), в которой f»(x)=0, но к заданию это не относится. Вы путаете: если бы производная обращалась в 0, то в точке функция могла бы иметь минимум или максимум.
Гость 02.06.2013 21:26
Необходимо сосчитать точки в которых функция «убывает», а не «отрицательна». Т.е. сия точка должна быть ниже предыдущей, а таковых всего 3: х1, х3, х8.
Александр Иванов
Вы правы. Необходимо сосчитать точки в которых функция «убывает», а не «отрицательна». НО… на картинке график ПРОИЗВОДНОЙ, а не график функции. А ФУНКЦИЯ УБЫВАЕТ там, где ПРОИЗВОДНАЯ ОТРИЦАТЕЛЬНА.
Служба поддержки
В решении нет ошибок. Рекомендуем учащимся разобраться в решении и, поняв рассуждения, не путаться и не допускать ошибок на экзамене. Напоминаем о возможности обсудить задание в нашей группе В_Контакте.
Гость 09.11.2013 23:07
Читайте внимательно задание, прежде чем нагло обвинять в ошибке.
Хасан Тулькуев 19.02.2023 13:00
Исследование функции на возрастание и убывание по графикам с
помощью производной.
Краткая
теория
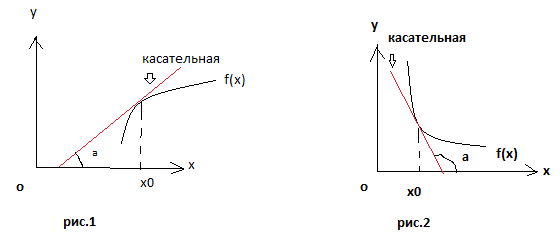
На
рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а
на рис.2 этот угол тупой. Если угол
наклона касательной острый, это означает, что производная
в этой точке положительна,
и функция при увеличении значения переменной Х будет возрастать.( см. рис.1). Если угол наклона касательной тупой, как на рис.2, это означает, что производная в это точке отрицательна, и функция на этом участке убывает. (см.рис. 2.). Итак, условие
возрастания и убывания функции:
еслиf ´(x) > 0 на некотором
промежутке, то функция возрастает на этом промежутке, если f ´(x)< 0 на некотором
промежутке, то функция убывает на этом промежутке,
У
функции может быть несколько участков убывания и возрастания. Рис. 3.Разберем пример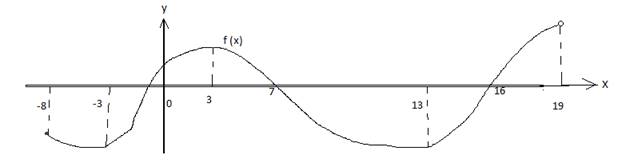
На рис.3 изображен
график некоторой функции f (x). Функция возрастает
на промежутках [-3;3] и [13;19]. На этих промежутках угол наклона касательной
с положительным направлением оси ОХ острый, значит производная f ´(x) > 0, так как тангенс
острого угла положителен. Функция убывает на промежутках [ -8; -3] и
[3;13], так как на этих участках угол наклона касательной с положительным
направлением оси ОХ тупой, значит производная f ´(x) < 0, так как тангенс
тупого угла отрицательный. Если надо определить
участки возрастания и убывания не по графику, а путем вычислений, то действуют
по такому
плану:
1. Найти область определения заданной
функции.
2. Найти производную f
´(x)
заданной функции.
3. Найти промежутки, где производная f ´(x) > 0 и f ´(x) < 0, ( решая полученные
неравенства аналитически или методом интервалов).
Пример1. Исследовать функцию f(x) = 5x2 -3x +1на монотонность
(на возрастание и убывание). Решение.
- Область
определения функцииD(f) = R. - f
´(x) = (5x2 -3x +1)´ = 10x – 3 - f ´(x) = 0 10x -3 =0 10x=3 x= 0,3
Отметим найденную точку на числовой прямой. Числовая
прямая разбилась на два промежутка (-∞; 0,3] и [0,3; + ∞).Проверим
знак производной в каждом из полученных промежутков. Для этого выбираем любое
произвольное число из левого промежутка и потом из правого. Выберем любое
число х<0,3, например х=0 и подставим вместо х в производную, получим:
10·0 -3= -3< 0.Поставим слева от числа 0,3 знак минус на числовой прямой.
Выберем любое число х>0,3, например, х=2 и
подставим вместо х в производную, получим: 10·2 -3= 17>0.Поставим справа
от числа 0,3 знак плюс на числовой прямой. Там, где производная положительна (f ´(x) >0) функция возрастает, то есть возрастает на промежутке [
0,3; +∞)
Там, где производная
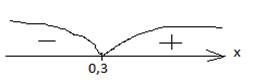
отрицательна
(f ´(x)<0) функция
убывает, то есть убывает на ( -∞; 0,3].
Пример2. Исследовать функцию f(x) = 3x2 –2x3+12х на возрстание и
убывание. Найти длину участка возрастания.
1.Область
определения функции D(f) = R.
2. f ´(x) = (3x2 -2x3 +12х)´= 6х
– 6х2 +12
3. f ´(x) = 0 6х – 6х2
+12 =0 разделим на 6 и перепишем по порядку. — х2 +х +2 = 0
Решим это квадратное уравнение, найдем дискриминант и корни.
D= 12 —
4·(-1)·2 = 1 + 8 = 9>0 — два корня.
X1= ( — 1+√9)/
( -2) =2/ (-2)= — 1; X2= ( — 1-√9)/ ( -2) =2
Отметим
найденные точки на числовой прямой. Числовая прямая разбилась на три
промежутка:
(-∞;
-1] , [-1; 2] и [2; +∞). Проверим знак производной в каждом промежутке.
На (-∞; -1] выберем, например, х = -3 и подставим в производную. . f ´(-3)= — (
-3)2 +(-3) +2= -9 -3 +2 = -10<0
В
случае, когда производная получилась в виде квадратичной функции, то знак в
каждом промежутке проверять не надо, достаточно определить знак в одном
промежутке, в остальных знаки будут обязательно чередоваться, или как на рисунке
изобразить схематически график квадратичной функции (
красный график).
Изобразим
числовую прямую и расставим знаки производной.
Производная
положительна на [-1; 2] , значит на этом промежутке функция возрастает.
Производная отрицательна на промежутках (-∞; — 1] и [2; +∞),
значит функция убывает на этих промежутках. Найдем длину участка
возрастания 2 – (-1) = 2 +1 =3.
Ответ: функция
возрастает на промежутке[-1; 2] , убывает на промежутках
(-∞;
— 1] и [2; +∞). Длина участка возрастания равна 3.
Рассмотрим примеры на исследование функции на возрастание и
убывание по графикам.
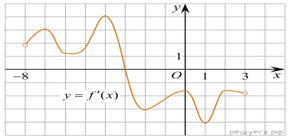
1.
На рисунке изображен
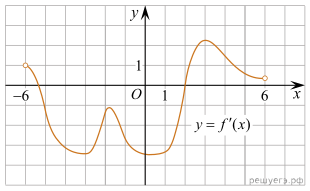
график производной функции 
определенной на
интервале 
Найдите
промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
Решение. Промежутки возрастания
данной функции f(x) соответствуют промежуткам, на которых ее
производная неотрицательна, то есть промежуткам (−6; −5,2] и [2; 6).
Данные промежутки содержат целые точки 2, 3, 4 и 5. Их сумма равна 14.
Ответ: 14.
2.
На рисунке изображён график 
—
производной функции 
определенной на
интервале (−8; 3). В какой точке отрезка [−3; 2]
функция 
принимает наибольшее
значение?
Решение. Функция,
дифференцируемая на отрезке [a; b], непрерывна на нем. Если
функция непрерывна на отрезке [a; b], а её производная
положительна (отрицательна) на интервале (a; b), то функция
возрастает (убывает) на отрезке [a; b].
На заданном отрезке производная функции 
не положительна, функция
на этом отрезке убывает. Следовательно, наибольшее значение функции достигается
на левой границе отрезка, т. е. в точке −3.
Ответ: −3.
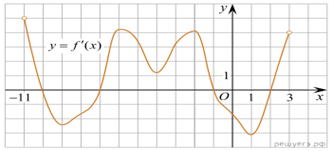
3.
На рисунке изображен график производной функции f(x),
определенной на интервале (−11; 3). Найдите промежутки возрастания
функции f(x). В ответе укажите длину наибольшего из них.
Решение. Функция,
дифференцируемая на отрезке [a; b], непрерывна на нем. Если
функция непрерывна на отрезке [a; b], а её производная
положительна (отрицательна) на интервале (a; b), то функция
возрастает (убывает) на отрезке [a; b].
Поэтому промежутки возрастания функции f(x) соответствуют
промежуткам, на которых производная функции неотрицательна, то есть промежуткам
(−11; −10], [−7; −1] и [2; 3).
Наибольший из них — отрезок [−7; −1], длина
которого равна 6.
Ответ: 6.
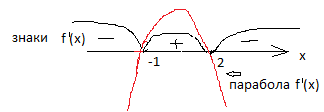
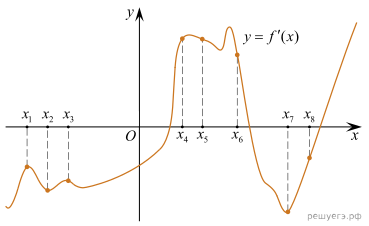
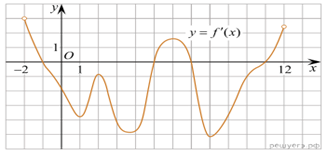
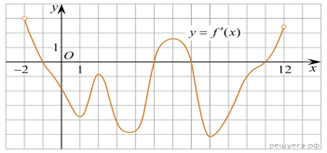
4. На рисунке изображён график 
—
производной функции f(x). На оси абсцисс отмечены восемь точек: x1,
x2, x3, …, x8. Сколько
из этих точек лежит на промежутках возрастания функции f(x)?
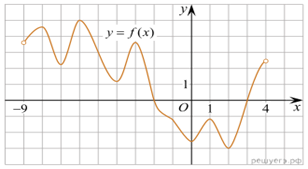
Решение. Возрастанию
дифференцируемой функции f(x) соответствуют неотрицательные
значения её производной. Производная неотрицательна в точках x4,
x5, x6. Таких точек 3 Ответ: 3.
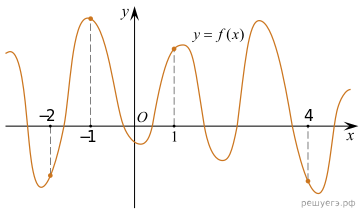
5.
На рисунке изображен график функции 
и отмечены точки
−2, −1, 1, 4. В какой из этих точек значение производной
наименьшее? В ответе укажите эту точку. 
Решение. Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Производная
отрицательна в точках −1 и 4. Модуль тангенса угла наклона касательной
явно больше в точке 4, поэтому тангенс в этой точке наименьший.
Ответ:4.
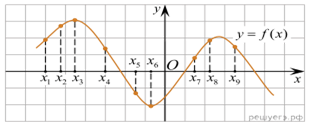
6. 
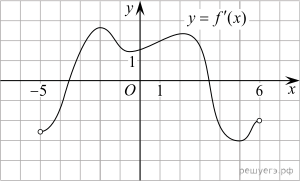
На рисунке изображён график дифференцируемой функции y = f(x).
На оси абсцисс отмечены девять точек: x1, x2,
x3, …, x9. Среди этих точек найдите все
точки, в которых производная функции f(x) отрицательна. В ответе
укажите количество найденных точек.
Решение.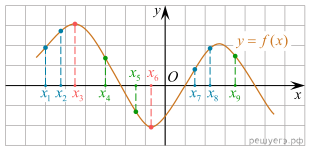 
Две из отмеченных точек
являются точками экстремума функции f(x). Это точки x3
и x6 (выделены красным). В них производная функции f(x)
равна нулю.
В точках x1, x2, x7
и x8 функция f(x) возрастает (выделены синим).
В этих четырёх точках производная функции f(x) положительна.
В точках x4, x5 и x9
функция f(x) убывает (выделены зеленым). В этих трёх
точках производная функции f(x) отрицательна.
Ответ: 3.
7.
Функция 
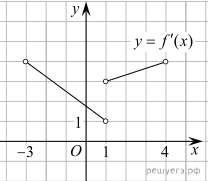
определена и непрерывна
на интервале 
На рисунке
изображен график её производной. Найдите промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
Решение. Промежутки возрастания
данной функции f(x) соответствуют промежуткам, на которых её
производная неотрицательна, то есть интервалам (−3; 1) и
(1; 4). В силу непрерывности функция f(x) возрастает на
интервале (−3; 4). Данный промежуток содержит целые точки −2,
−1, 0, 1, 2 и 3. Их сумма равна 3.
Ответ: 3.
Примечание.
Напомним, что если функция непрерывна на каком-либо из концов
промежутка возрастания или убывания, то граничную точку присоединяют к этому
промежутку. В частности, если функция непрерывна на отрезке 
и монотонна на
интервале 
то функция монотонна
на всем отрезке 
Обобщением этого утверждения служит следующая теорема: функция монотонна на промежутке,
если ее производная сохраняет знак всюду на этом промежутке, за исключением
конечного числа точек, в которых функция непрерывна. Например, производная
функции
не существует в точке 
и положительна
во всех остальных точках. Функция f в точке 
непрерывна,
следовательно, она возрастает на 
8.
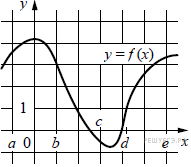
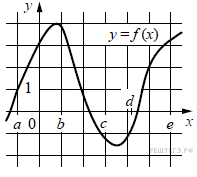
На рисунке изображён график функции y = f(x).
Числа a, b, c, d и e задают на оси x четыре интервала.
Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику
функции или её производной.
Ниже указаны значения производной в данных точках. Пользуясь
графиком, поставьте в соответствие каждой точке значение производной
в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) производная отрицательна на всём интервале 2) производная положительна в начале интервала и отрицательна 3) функция отрицательна в начале интервала и положительна 4) производная положительна на всём интервале |
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
Пояснение.
Если функция возрастает, то производная
положительна и наоборот.
На интервале (a;b)производная
положительна вначале интервала и отрицательна в конце, потому
что функция вначале возрастает, а потом убывает.
На интервале (b;c)
производная отрицательна, потому что функция убывает.
На интервале (c;d)
функция отрицательна в начале интервала и положительна в конце интервала.
На интервале (d;e)
производная положительна, потому что функция возрастает.
Таким образом, получаем соответствие
А — 2, Б — 1, В — 3 и Г — 4.
Ответ: 2134.
Решить самостоятельно.
1.
На рисунке изображен
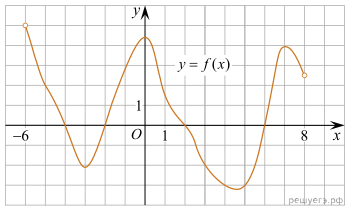
график функции y = f(x), определенной на интервале
(−6; 8). Определите количество целых точек, в которых производная функции
положительна.
2.
На рисунке изображен
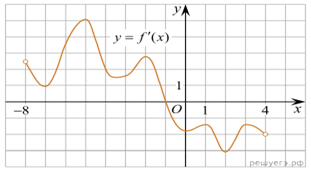
график производной функции f(x), определенной на интервале
(−8; 4). В какой точке отрезка [−7; −3] f(x)
принимает наименьшее значение?
3.
На рисунке изображен
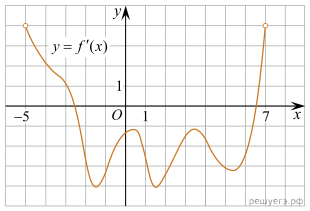
график производной функции f(x), определенной на интервале
(−5; 7). Найдите промежутки убывания функции f(x). В ответе
укажите сумму целых точек, входящих в эти промежутки.
4.
На рисунке изображен график производной функции f(x),
определенной на интервале (−2; 12). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них. 
5.
На рисунке изображен график производной функции f(x),
определенной на интервале (−2; 12). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них. 
6.
На рисунке изображен
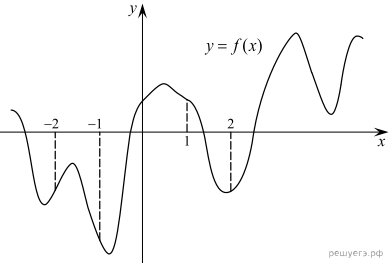
график функции 
и отмечены точки
−2, −1, 1, 2. В какой из этих точек значение производной
наибольшее? В ответе укажите эту точку.
7.
На рисунке изображён
график функции y = f(x) и отмечены семь
точек на оси абсцисс: x1, x2, x3,
x4, x5, x6, x7.
В скольких из этих точек производная функции f(x) отрицательна?
Решение. Производная функции
отрицательна в тех точках, которые принадлежат участкам убывания функции. Это
точки x3, x4, x7 —
всего 3 точки.
8.
На рисунке изображён график функции 
и восемь точек на оси
абсцисс: 
В скольких из этих точек
производная функции 
положительна?
9. На рисунке изображён график функции 
и двенадцать точек на
оси абсцисс: 
В скольких из этих точек
производная функции 
отрицательна?
10.
На рисунке изображён
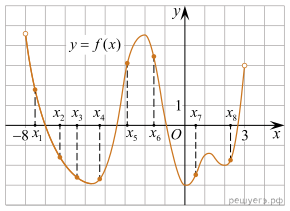
график функции 
определенной на
интервале 
. Сколько из
отмеченных точек 
принадлежат промежуткам
убывания функции?
11
Функция 
определена и непрерывна
на отрезке 
На рисунке
изображен график её производной. Найдите промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
12.
Функция 
определена и непрерывна
на отрезке 
На рисунке
изображен график её производной. Найдите промежутки убывания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
13 
Функция 
определена и непрерывна
на полуинтервале 
На рисунке
изображен график её производной. Найдите промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
14.
На рисунке изображён график функции 
определённой на
интервале (−9; 4). Найдите промежутки убывания функции f(x).
В ответе укажите длину наибольшего из них.
15.
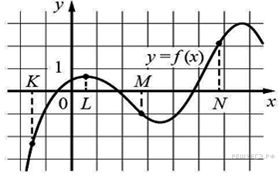
На рисунке
изображён график функции y = f(x) и отмечены точки K,
L, M и N на оси x. Пользуясь графиком, поставьте
в соответствие каждой точке характеристику функции и её производной.
Ниже указаны значения производной в данных точках. Пользуясь
графиком, поставьте в соответствие каждой точке значение производной
в ней.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ |
|
|
А) K Б) L В) M Г) N |
1) функция положительна, производная положительна 2) функция отрицательна, производная отрицательна 3) функция положительна, производная равна 0 4) функция отрицательна, производная положительна |
В таблице под каждой буквой укажите соответствующий
номер.
16.
На рисунке изображён график функции y = f(x) .
Точки a, b, c, d и e задают на оси Ox
интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу
характеристику функции или её производной.
Пользуясь графиком, поставьте в соответствие каждому интервалу
времени характеристику движения автомобиля на этом интервале.
|
ИНТЕРВАЛЫ ВРЕМЕНИ |
ХАРАКТЕРИСТИКИ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) Значения функции положительны в каждой точке 2) Значения производной функции положительны в каждой точке 3) Значения функции отрицательны в каждой точке 4) Значения производной функции отрицательны в каждой точке |
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
17. Исследовать
функцию f(x) = 5 +2x3— 24х на возрастание и убывание.
Найти длину участка убывания.
18. Исследовать функцию f(x) = x2 – 
x4 + 1 на возрстание и
убывание. Найти длину наименьшего участка возрастания.
Ответы
на задания.
1. 4
2. -7
3. 18
4. 6
5. 6
6. – 2
7. 3
8. 5
9. 7
10.
4
11.
8
12.
6
13.
9
14.
3
15.
4321
16.
1432
17.
↓ [-2; 2]; ↑ ( — ∞; -2] и [2; +∞). Длина участка ↓
равна 4.
18.
↓ [-1; 0] и [1; +∞); ↑ ( — ∞; -1] и [0; 1]. Длина наименьшего
участка ↑ равна 1.
Скачано с www.znanio.ru
ЕГЭ 2023. Задание №3 в ЕГЭ-2023 по математике. Теория и практика по математике для подготовки к экзамену. Вы можете скачать или решать задания онлайн на сайте.
Сборник задач по теории вероятностей: Скачать в PDF
Интересные задания:
Задача 1 На клавиатуре телефона 10 цифр, из них 5 четных (включая 0): 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра, равна 5 10 = 0,5.
Задача 2 Всего дежурных 4 человека, из них 2 девочки: Ольга и Татьяна. Чтобы найти искомую вероятность, надо разделить кол-во девочек на общее число дежурных: 24 = 0,5.
Задача 3 Всего существует 6 возможных вариантов очереди: АБВ АВБ БАВ БВА ВАБ ВБА. Борис подойдет позже Андрея в трех случаях: АБВ ВАБ АВБ, значит искомая вероятность 36 =12 = 0,5. На самом деле существуют всего два случая, у которых равная вероятность: Борис
может подойти перед Андреем или после него. Из этих двух случаев благоприятным
является только один, и его вероятность: 12 = 0,5.
Задача 4 Натуральных чисел от 10 до 19 десять (19 − 10 + 1 = 10 или можно просто выписать все эти числа и убедиться в этом), из них на 3 делятся три числа: 12, 15, 18. Искомая вероятность равна: 3 10 = 0,3.
Задача 5 Будем считать, что жребий выглядит так: каждый турист достанет из шапки бумажку, на которой будет написано идёт ли он в магазин или нет. Всего бумажек 5. Вытянув две из них, турист пойдёт в магазин. Турист А с равной вероятностью может вытянуть любую из 5 бумажек. Для туриста A существует два благоприятных исхода из 5 возможных. Значит вероятность того, что турист А пойдёт в магазин 2 5 = 0,4. Всего в викторине участвуют 4 игрока. Из них двое получат приз. Тогда вероятность получения приза составляет 2 4 = 0,5.
Вам будет интересно:
ЕГЭ по математике (профиль) 11 класс 2023. Новый тренировочный вариант №11 — №221121 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Автор Администратор На чтение 1 мин Просмотров 188 Опубликовано 4 марта, 2023
Решение варианта СтатГрад 28.02.2023 ЕГЭ 2023 Математика (профиль) на сайте источника онлайн. Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса. statgrad.org.
Решение варианта СтатГрад 28.02.2023
Вам также может понравиться
Варианты и ответы ВПР 2023 года по истории 11 класс
0103
ВПР 2023 биология 11 класс 1-2 вариант и ответы с решением
0283
Задание 21 ЕГЭ 2023 русский язык 11 класс практика
030
6 марта 2023 Пробник ЕГЭ 2023 по русскому языку 3 варианта
071
ВПР 2023 физика 11 класс 1-2 вариант все ответы с решением
092
Статград история 9 класс ОГЭ 2023 варианты ИС2290401-ИС2290404
075
ВПР 2023 химия 11 класс 1-2 вариант все ответы с решением
057
Разговоры о важном 20 февраля 2023 тема день защитника
0169
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.
Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.