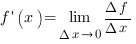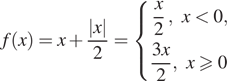Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
На рисунке изображен график функции 
и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная положительна в точках −2 и 2. Угол наклона (и его тангенс) явно больше в точке −2.
Ответ:−2.
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
На рисунке изображен график функции и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная положительна в точках −2 и 2. Угол наклона (и его тангенс) явно больше в точке −2.
Ответ:−2.
04
Фев 2013
06 Задание (2022)ПРОИЗВОДНАЯ
Задачи на производную и касательную
В этом году в Задании 7 из Открытого банка заданий для подготовки к ЕГЭ по математике появились новые задачи. Давайте разберем их решение.
Прототип задания B8 (№ 317543)
На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Как мы знаем, производной называется
предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Производная в точке показывает скорость изменения функции в данной точке. Чем быстрее изменяется функция, то есть чем больше приращение функции, тем больше угол наклона касательной. Поскольку в задаче требуется определить точку, в которой значение производной наибольшее, исключим из рассмотрения точки с абсциссами -1 и 1 — в этих точках функция убывает, и производная в них отрицательна.
Функция возрастает в точках -2 и 2. Однако, возрастает она в них по-разному — в точке -2 график функции поднимается круче, чем в точке 2, и следовательно, приращение функции в этой точки, а, значит и производная — больше.
Ответ: -2
И аналогичная задача:
Прототип задания B8 (№ 317544)
На рисунке изображен график функции и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Решение этой задачи аналогично решению предыдущей «с точностью до наоборот»
Нас интересует точка, в которой производная принимает наименьшее значение, то есть мы ищем точку, в которой функция уменьшается наиболее быстро — на графике это точка, в которой самый крутой «спуск». Это точка с абсциссой 4.
Ответ: 4.
И.В. Фельдман, репетитор по математике.
Исследование функции на возрастание и убывание по графикам с
помощью производной.
Краткая
теория
На
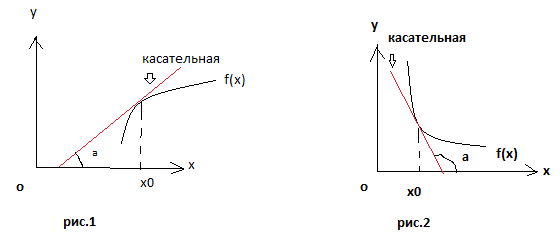
рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а
на рис.2 этот угол тупой. Если угол
наклона касательной острый, это означает, что производная
в этой точке положительна,
и функция при увеличении значения переменной Х будет возрастать.( см. рис.1). Если угол наклона касательной тупой, как на рис.2, это означает, что производная в это точке отрицательна, и функция на этом участке убывает. (см.рис. 2.). Итак, условие
возрастания и убывания функции:
еслиf ´(x) > 0 на некотором
промежутке, то функция возрастает на этом промежутке, если f ´(x)< 0 на некотором
промежутке, то функция убывает на этом промежутке,
У
функции может быть несколько участков убывания и возрастания. Рис. 3.Разберем пример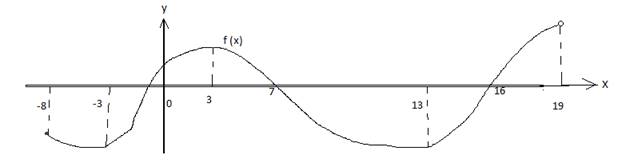
На рис.3 изображен
график некоторой функции f (x). Функция возрастает
на промежутках [-3;3] и [13;19]. На этих промежутках угол наклона касательной
с положительным направлением оси ОХ острый, значит производная f ´(x) > 0, так как тангенс
острого угла положителен. Функция убывает на промежутках [ -8; -3] и
[3;13], так как на этих участках угол наклона касательной с положительным
направлением оси ОХ тупой, значит производная f ´(x) < 0, так как тангенс
тупого угла отрицательный. Если надо определить
участки возрастания и убывания не по графику, а путем вычислений, то действуют
по такому
плану:
1. Найти область определения заданной
функции.
2. Найти производную f
´(x)
заданной функции.
3. Найти промежутки, где производная f ´(x) > 0 и f ´(x) < 0, ( решая полученные
неравенства аналитически или методом интервалов).
Пример1. Исследовать функцию f(x) = 5x2 -3x +1на монотонность
(на возрастание и убывание). Решение.
- Область
определения функцииD(f) = R. - f
´(x) = (5x2 -3x +1)´ = 10x – 3 - f ´(x) = 0 10x -3 =0 10x=3 x= 0,3
Отметим найденную точку на числовой прямой. Числовая
прямая разбилась на два промежутка (-∞; 0,3] и [0,3; + ∞).Проверим
знак производной в каждом из полученных промежутков. Для этого выбираем любое
произвольное число из левого промежутка и потом из правого. Выберем любое
число х<0,3, например х=0 и подставим вместо х в производную, получим:
10·0 -3= -3< 0.Поставим слева от числа 0,3 знак минус на числовой прямой.
Выберем любое число х>0,3, например, х=2 и
подставим вместо х в производную, получим: 10·2 -3= 17>0.Поставим справа
от числа 0,3 знак плюс на числовой прямой. Там, где производная положительна (f ´(x) >0) функция возрастает, то есть возрастает на промежутке [
0,3; +∞)
Там, где производная
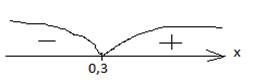
отрицательна
(f ´(x)<0) функция
убывает, то есть убывает на ( -∞; 0,3].
Пример2. Исследовать функцию f(x) = 3x2 –2x3+12х на возрстание и
убывание. Найти длину участка возрастания.
1.Область
определения функции D(f) = R.
2. f ´(x) = (3x2 -2x3 +12х)´= 6х
– 6х2 +12
3. f ´(x) = 0 6х – 6х2
+12 =0 разделим на 6 и перепишем по порядку. — х2 +х +2 = 0
Решим это квадратное уравнение, найдем дискриминант и корни.
D= 12 —
4·(-1)·2 = 1 + 8 = 9>0 — два корня.
X1= ( — 1+√9)/
( -2) =2/ (-2)= — 1; X2= ( — 1-√9)/ ( -2) =2
Отметим
найденные точки на числовой прямой. Числовая прямая разбилась на три
промежутка:
(-∞;
-1] , [-1; 2] и [2; +∞). Проверим знак производной в каждом промежутке.
На (-∞; -1] выберем, например, х = -3 и подставим в производную. . f ´(-3)= — (
-3)2 +(-3) +2= -9 -3 +2 = -10<0
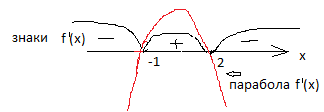
В
случае, когда производная получилась в виде квадратичной функции, то знак в
каждом промежутке проверять не надо, достаточно определить знак в одном
промежутке, в остальных знаки будут обязательно чередоваться, или как на рисунке
изобразить схематически график квадратичной функции (
красный график).
Изобразим
числовую прямую и расставим знаки производной.
Производная
положительна на [-1; 2] , значит на этом промежутке функция возрастает.
Производная отрицательна на промежутках (-∞; — 1] и [2; +∞),
значит функция убывает на этих промежутках. Найдем длину участка
возрастания 2 – (-1) = 2 +1 =3.
Ответ: функция
возрастает на промежутке[-1; 2] , убывает на промежутках
(-∞;
— 1] и [2; +∞). Длина участка возрастания равна 3.
Рассмотрим примеры на исследование функции на возрастание и
убывание по графикам.
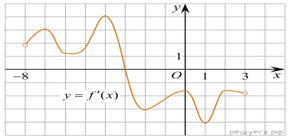
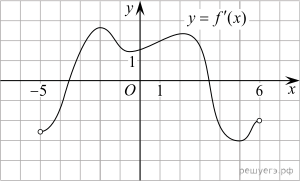
1.
На рисунке изображен
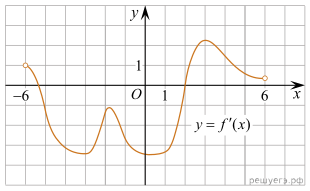
график производной функции 
определенной на
интервале 
Найдите
промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
Решение. Промежутки возрастания
данной функции f(x) соответствуют промежуткам, на которых ее
производная неотрицательна, то есть промежуткам (−6; −5,2] и [2; 6).
Данные промежутки содержат целые точки 2, 3, 4 и 5. Их сумма равна 14.
Ответ: 14.
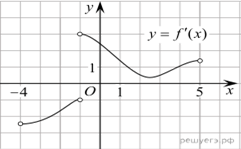
2.
На рисунке изображён график 
—
производной функции 
определенной на
интервале (−8; 3). В какой точке отрезка [−3; 2]
функция 
принимает наибольшее
значение?
Решение. Функция,
дифференцируемая на отрезке [a; b], непрерывна на нем. Если
функция непрерывна на отрезке [a; b], а её производная
положительна (отрицательна) на интервале (a; b), то функция
возрастает (убывает) на отрезке [a; b].
На заданном отрезке производная функции 
не положительна, функция
на этом отрезке убывает. Следовательно, наибольшее значение функции достигается
на левой границе отрезка, т. е. в точке −3.
Ответ: −3.
3.
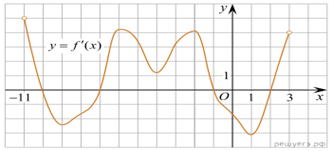
На рисунке изображен график производной функции f(x),
определенной на интервале (−11; 3). Найдите промежутки возрастания
функции f(x). В ответе укажите длину наибольшего из них.
Решение. Функция,
дифференцируемая на отрезке [a; b], непрерывна на нем. Если
функция непрерывна на отрезке [a; b], а её производная
положительна (отрицательна) на интервале (a; b), то функция
возрастает (убывает) на отрезке [a; b].
Поэтому промежутки возрастания функции f(x) соответствуют
промежуткам, на которых производная функции неотрицательна, то есть промежуткам
(−11; −10], [−7; −1] и [2; 3).
Наибольший из них — отрезок [−7; −1], длина
которого равна 6.
Ответ: 6.
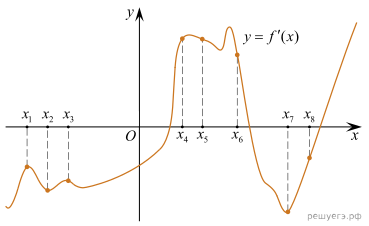
4. На рисунке изображён график 
—
производной функции f(x). На оси абсцисс отмечены восемь точек: x1,
x2, x3, …, x8. Сколько
из этих точек лежит на промежутках возрастания функции f(x)?
Решение. Возрастанию
дифференцируемой функции f(x) соответствуют неотрицательные
значения её производной. Производная неотрицательна в точках x4,
x5, x6. Таких точек 3 Ответ: 3.
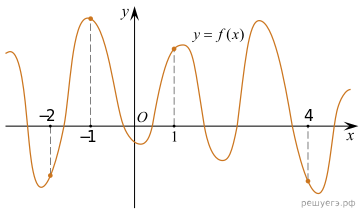
5.
На рисунке изображен график функции 
и отмечены точки
−2, −1, 1, 4. В какой из этих точек значение производной
наименьшее? В ответе укажите эту точку. 
Решение. Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Производная
отрицательна в точках −1 и 4. Модуль тангенса угла наклона касательной
явно больше в точке 4, поэтому тангенс в этой точке наименьший.
Ответ:4.
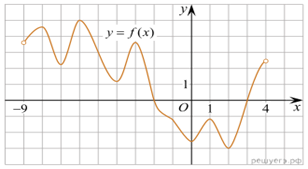
6. 
На рисунке изображён график дифференцируемой функции y = f(x).
На оси абсцисс отмечены девять точек: x1, x2,
x3, …, x9. Среди этих точек найдите все
точки, в которых производная функции f(x) отрицательна. В ответе
укажите количество найденных точек.
Решение.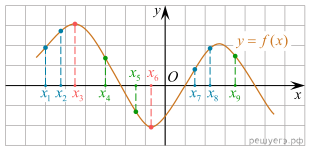 
Две из отмеченных точек
являются точками экстремума функции f(x). Это точки x3
и x6 (выделены красным). В них производная функции f(x)
равна нулю.
В точках x1, x2, x7
и x8 функция f(x) возрастает (выделены синим).
В этих четырёх точках производная функции f(x) положительна.
В точках x4, x5 и x9
функция f(x) убывает (выделены зеленым). В этих трёх
точках производная функции f(x) отрицательна.
Ответ: 3.
7.
Функция 
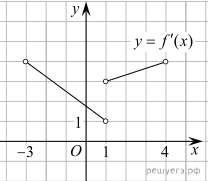
определена и непрерывна
на интервале 
На рисунке
изображен график её производной. Найдите промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
Решение. Промежутки возрастания
данной функции f(x) соответствуют промежуткам, на которых её
производная неотрицательна, то есть интервалам (−3; 1) и
(1; 4). В силу непрерывности функция f(x) возрастает на
интервале (−3; 4). Данный промежуток содержит целые точки −2,
−1, 0, 1, 2 и 3. Их сумма равна 3.
Ответ: 3.
Примечание.
Напомним, что если функция непрерывна на каком-либо из концов
промежутка возрастания или убывания, то граничную точку присоединяют к этому
промежутку. В частности, если функция непрерывна на отрезке 
и монотонна на
интервале 
то функция монотонна
на всем отрезке 
Обобщением этого утверждения служит следующая теорема: функция монотонна на промежутке,
если ее производная сохраняет знак всюду на этом промежутке, за исключением
конечного числа точек, в которых функция непрерывна. Например, производная
функции
не существует в точке 
и положительна
во всех остальных точках. Функция f в точке 
непрерывна,
следовательно, она возрастает на 
8.
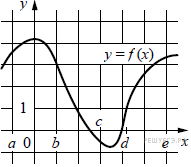
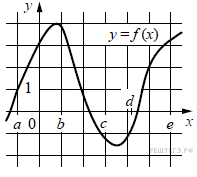
На рисунке изображён график функции y = f(x).
Числа a, b, c, d и e задают на оси x четыре интервала.
Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику
функции или её производной.
Ниже указаны значения производной в данных точках. Пользуясь
графиком, поставьте в соответствие каждой точке значение производной
в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) производная отрицательна на всём интервале 2) производная положительна в начале интервала и отрицательна 3) функция отрицательна в начале интервала и положительна 4) производная положительна на всём интервале |
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
Пояснение.
Если функция возрастает, то производная
положительна и наоборот.
На интервале (a;b)производная
положительна вначале интервала и отрицательна в конце, потому
что функция вначале возрастает, а потом убывает.
На интервале (b;c)
производная отрицательна, потому что функция убывает.
На интервале (c;d)
функция отрицательна в начале интервала и положительна в конце интервала.
На интервале (d;e)
производная положительна, потому что функция возрастает.
Таким образом, получаем соответствие
А — 2, Б — 1, В — 3 и Г — 4.
Ответ: 2134.
Решить самостоятельно.
1.
На рисунке изображен
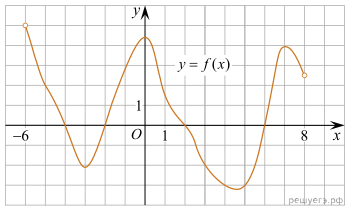
график функции y = f(x), определенной на интервале
(−6; 8). Определите количество целых точек, в которых производная функции
положительна.
2.
На рисунке изображен
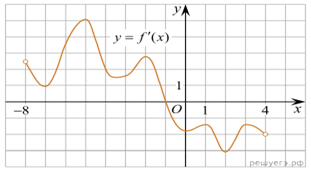
график производной функции f(x), определенной на интервале
(−8; 4). В какой точке отрезка [−7; −3] f(x)
принимает наименьшее значение?
3.
На рисунке изображен
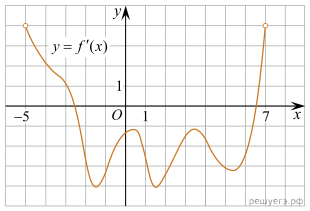
график производной функции f(x), определенной на интервале
(−5; 7). Найдите промежутки убывания функции f(x). В ответе
укажите сумму целых точек, входящих в эти промежутки.
4.
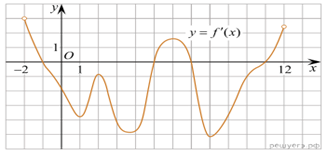
На рисунке изображен график производной функции f(x),
определенной на интервале (−2; 12). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них. 
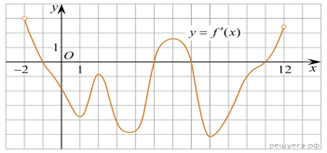
5.
На рисунке изображен график производной функции f(x),
определенной на интервале (−2; 12). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них. 
6.
На рисунке изображен
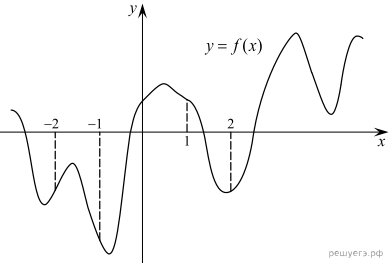
график функции 
и отмечены точки
−2, −1, 1, 2. В какой из этих точек значение производной
наибольшее? В ответе укажите эту точку.
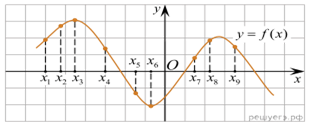
7.
На рисунке изображён
график функции y = f(x) и отмечены семь
точек на оси абсцисс: x1, x2, x3,
x4, x5, x6, x7.
В скольких из этих точек производная функции f(x) отрицательна?
Решение. Производная функции
отрицательна в тех точках, которые принадлежат участкам убывания функции. Это
точки x3, x4, x7 —
всего 3 точки.
8.
На рисунке изображён график функции 
и восемь точек на оси
абсцисс: 
В скольких из этих точек
производная функции 
положительна?
9. На рисунке изображён график функции 
и двенадцать точек на
оси абсцисс: 
В скольких из этих точек
производная функции 
отрицательна?
10.
На рисунке изображён
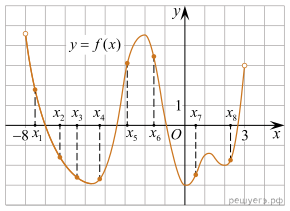
график функции 
определенной на
интервале 
. Сколько из
отмеченных точек 
принадлежат промежуткам
убывания функции?
11
Функция 
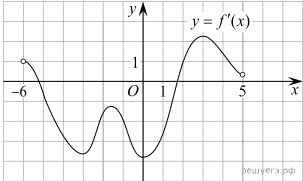
определена и непрерывна
на отрезке 
На рисунке
изображен график её производной. Найдите промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
12.
Функция 
определена и непрерывна
на отрезке 
На рисунке
изображен график её производной. Найдите промежутки убывания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
13 
Функция 
определена и непрерывна
на полуинтервале 
На рисунке
изображен график её производной. Найдите промежутки возрастания функции 
В ответе укажите сумму
целых точек, входящих в эти промежутки.
14.
На рисунке изображён график функции 
определённой на
интервале (−9; 4). Найдите промежутки убывания функции f(x).
В ответе укажите длину наибольшего из них.
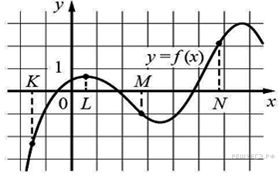
15.
На рисунке
изображён график функции y = f(x) и отмечены точки K,
L, M и N на оси x. Пользуясь графиком, поставьте
в соответствие каждой точке характеристику функции и её производной.
Ниже указаны значения производной в данных точках. Пользуясь
графиком, поставьте в соответствие каждой точке значение производной
в ней.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ |
|
|
А) K Б) L В) M Г) N |
1) функция положительна, производная положительна 2) функция отрицательна, производная отрицательна 3) функция положительна, производная равна 0 4) функция отрицательна, производная положительна |
В таблице под каждой буквой укажите соответствующий
номер.
16.
На рисунке изображён график функции y = f(x) .
Точки a, b, c, d и e задают на оси Ox
интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу
характеристику функции или её производной.
Пользуясь графиком, поставьте в соответствие каждому интервалу
времени характеристику движения автомобиля на этом интервале.
|
ИНТЕРВАЛЫ ВРЕМЕНИ |
ХАРАКТЕРИСТИКИ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) Значения функции положительны в каждой точке 2) Значения производной функции положительны в каждой точке 3) Значения функции отрицательны в каждой точке 4) Значения производной функции отрицательны в каждой точке |
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
17. Исследовать
функцию f(x) = 5 +2x3— 24х на возрастание и убывание.
Найти длину участка убывания.
18. Исследовать функцию f(x) = x2 – 
x4 + 1 на возрстание и
убывание. Найти длину наименьшего участка возрастания.
Ответы
на задания.
1. 4
2. -7
3. 18
4. 6
5. 6
6. – 2
7. 3
8. 5
9. 7
10.
4
11.
8
12.
6
13.
9
14.
3
15.
4321
16.
1432
17.
↓ [-2; 2]; ↑ ( — ∞; -2] и [2; +∞). Длина участка ↓
равна 4.
18.
↓ [-1; 0] и [1; +∞); ↑ ( — ∞; -1] и [0; 1]. Длина наименьшего
участка ↑ равна 1.
Скачано с www.znanio.ru
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности
Стереометрия на ЕГЭ по математике присутствует и в 1 части, и во второй. Чтобы решать задачи, для начала надо выучить формулы. Все они есть в наших таблицах:
- Куб, параллелепипед, призма, пирамида. Объем и площадь поверхности
- Цилиндр, конус, шар. Объем и площадь поверхности
Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.
Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины», «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма», правильная призма», «правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Перейдем к практике.
1. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем: 
А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей». В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна 
. А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна 
.
А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна 
! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Ответ: .
2. Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:
. Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной 
— на верхней и нижней гранях.
Ответ: 92.
3. А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Ответ: 
.
Следующий тип задач — когда одно объемное тело вписано в другое.
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна 
, высота равна , объем равен .
Ответ: 4.
5. В основании прямой призмы лежит прямоугольный треугольник с катетами 
и 
. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите 
.
Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна 
. Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: 
.
Ответ: 100.
6. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: .
Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.
7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 
см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 
раза больше, чем у первого? Ответ выразите в сантиметрах.
Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в раза уменьшится высота.
Ответ: 
.
8. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.
Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен 
.
| Высота | Радиус | Объем | |
| Первая кружка |  |
 |
|
| Вторая кружка |  |
 |
 |
Считаем объем второй кружки. Он равен 
. Получается, что он в два раза больше, чем объем первой.
Следующая задача тоже решается сразу и без формул.
9. Через среднюю линию основания треугольной призмы, объем которой равен 
, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Высота меньшей призмы такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен .
И еще одна классическая задача. Никаких формул!
10. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?
Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в 
раз, поскольку 
.
Ответ: .
Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды. Они тоже решаются элементарно.
11. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите .
Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом 
градусов, а 
— это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на 
, записываем ответ: 
.
Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Стереометрия на Профильном ЕГЭ по математике, 1 часть, основные типы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023