Найдите наименьшее трёхзначное натуральное число, которое при делении на 6 и на 11 даёт равные ненулевые остатки и у которого средняя цифра является средним арифметическим двух крайних цифр.
Спрятать решение
Решение.
По модулю 6 и 11 число имеет одинаковые остатки, следовательно, число имеет тот же остаток при делении на 66, причём этот остаток не равен нулю и меньше шести. Таким образом, искомое число может иметь вид:
При получаем: 67, 68, 69, 70, 71. Все эти числа не являются трёхзначными.
При получаем: 133, 134, 135, 136, 137. Число 135 удовлетворяет всем условиям задачи.
Ответ: 135.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
Цифровая запись числа
1. Задание 19 № 506263. Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.
Пояснение.
Разложим число 20 на слагаемые различными способами:
20 = 9 + 9 + 2 = 9 + 8 + 3 = 9 + 7 + 4 = 9 + 6 + 5 = 8 + 8 + 4 = 8 + 7 + 5 = 8 + 6 + 6 = 7 + 7 + 6.
При разложении способами 1−4, 7 и 8 суммы квадратов чисел не кратны трём. При разложении пятым способом сумма квадратов кратна девяти. Разложение шестым способом удовлетворяет условиям задачи. Таким образом, условию задачи удовлетворяет любое число, записанное цифрами 5, 7 и 8, например, число 578.
2. Задание 19 № 507010. Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Пояснение.
Пусть наше число имеет вид . Тогда имеем
И так как число делится на 4,
делится на 4. Можно заметить, что если среди цифр есть хотя бы три единицы, то равенство невозможно, так как сумма будет больше произведения. То же самое, если единиц меньше, чем две. В этом случае произведение будет слишком большое. Таким образом, среди цифр есть ровно две единицы. Рассмотрим двузначные числа, которые делятся на 4, это концовка нашего числа. Нельзя брать числа с нулём, так как в этом случае произведение будет равно нулю, что плохо.
12: тогда одна из оставшихся цифр 1, а другая — 4.
16: тогда одна из оставшихся цифр 1, а другая никакая не подойдёт.
24: значит, оставшиеся цифры — единицы. Всё сходится.
Остальные числа будут давать слишком большое произведение или нечётную сумму.
Таким образом, исходные числа: 1412, 4112, 1124.
3. Задание 19 № 507052. Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 0 и делится на 24.
Пояснение.
Чтобы число делилось на 24 оно должно делится на 3 и на 8.
Число делится на 8, если три его последние цифры образуют число, делящееся на 8. Искомое число записывается только нулями и единицами, значит, оно заканчивается на 000.
Число делится на 3, если его сумма цифр числа делится на 3. Поскольку три послледние цифры числа нули, первые три должны быть единицами.
Таким образом, единственное число, удовлетворяющее условию задачи, это число 111 000.
Ответ: 111 000.
4. Задание 19 № 507053. Найдите наименьшее трёхзначное число, которое при делении на 2 даёт остаток 1, при делении на 3 даёт остаток 2, при делении на 5 даёт остаток 3 и которое записано тремя различными нечётными цифрами.
Пояснение.
Число при делении на 2 даёт остаток 1, следовательно, оно нечётное. При делении на 3 число даёт остаток 2, то есть число имеет вид При делении на 5 число даёт остаток 3, то есть число имеет вид
то есть число может оканчиваться либо на тройку, либо на восьмёрку. Число нечётное, следовательно, может оканчиваться только на тройку. Учитывая, что число оканчивается на 3:
Перебирая значения
что при
получаем число, удовлетворяющее условиям задачи. Это число 173.
Ответ: 173.
5. Задание 19 № 507054. Найдите четырёхзначное натуральное число, кратное 19, сумма цифр которого на 1 больше их произведения.
Пояснение.
Если хотя бы одна цифра в записи числа — нуль, то произведение цифр равно 0, а тогда их сумма равна 1. Единственное такое четырёхзначное число — 1000, но оно не кратно 19. Поэтому нулей среди цифр нет. Отсюда следует, что все цифры не меньше 1, и их сумма не меньше четырёх, а значит, произведение цифр не меньше трёх. Чтобы произведение было не меньше трёх хотя бы одна из цифр должна быть больше 1. Рассмотрим такие числа в порядке возрастания суммы их цифр.
Если сумма цифр равна 5, то число записывается одной двойкой и тремя единицами (это числа 1112, 1121, 1211, 2111). Произведение цифр равно 2, поэтому они не удовлетворяют условию.
Если сумма цифр равна 6, то число записывается одной тройкой и тремя единицами или двумя двойками и двумя единицами (это числа 1113, 1131, 1311, 3111, 1122, 1212, …). Произведение цифр равно 3 или 4 соответственно, поэтому такие числа не удовлетворяют условию.
Если сумма цифр равна 7, то произведение должно быть равно 6. Это выполнено для чисел, записываемых тройкой, двойкой и двумя единицами. Поскольку число 3211 кратно 19, оно и является искомым.
Ответ: 3211.
Примечание.
Четырёхзначное число, обладающее требуемыми свойствами, единственно. Покажем это, приведя другое решение.
Приведём решение Дмитрия Мухина (Москва).
Пусть a, b, c, d — цифры числа и пусть а самая большая из них (порядок цифр не важен). Покажем, что произведение меньших цифр не больше четырёх. Действительно, из равенства a + b + c + d= 1 + abcd, получаем 4a ≥ abcd + 1. Деля на наибольшую цифру a, получаем, что bcd < 4.
Рассмотрим теперь следующие случаи.
1. Пусть среди чисел b, c, d есть нуль, тогда поскольку a + b + c + d = 1, это число 1000, но оно на 19 не делится. Итак, все три меньшие цифры числа отличны от нуля.
2. Пусть все три меньшие цифры равны единице, тогда a + 3 = a + 1. Этот случай невозможен.
3. Пусть меньшие цифры это две единицы и двойка. Тогда a + 4 = 2a + 1, откуда a = 3. Перебирая 12 чисел, составленных из цифр 1, 1, 2, 3, находим, что из них кратно 19 только число 3211. Оно и является ответом.
4. Пусть меньшие цифры это две единицы и тройка. Тогда a + 5 = 3a + 1. Отсюда a = 2, но тогда aне наибольшая цифра. Противоречие.
Поскольку bcd < 4, других вариантов нет. Искомое число единственно, оно равно 3211.
6. Задание 19 № 507055. Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 27. В ответе укажите получившееся число.
Пояснение.
Если число делится на 27, тогда оно делится на 3 и на 9. Число делится на 9, тогда и только тогда, когда сумма цифр числа делится на 9. Число делится на 3, тогда и только тогда, когда сумма цифр числа делится на 3. Заметим, что, если число делится на 9,то оно делится и на 3. Сумма цифр числа 123456 равна 1 + 2 + 3 + 4 + 5 + 6 = 21. Вычеркнув числа 2, 4 и 6 получим, число, сумма цифр которого равна девяти. Девять делится на девять.
Ответ: 135.
7. Задание 19 № 507056. Найдите наименьшее четырёхзначное число, кратное 11, у которого произведение его цифр равно 12.
В ответе укажите наименьшее такое число.
Пояснение.
Пусть число имеет вид Произведение цифр числа равно 12, то есть
откуда получаем, что
может быть набором цифр: 1, 2, 2, 3; 1, 1, 3, 4. Число делится на 11, если сумма цифр, стоящих на нечётных местах равна сумме цифр, стоящих на чётных местах. Наименьшее число, удовлетворяющее этому требованию и состоящее из имеющихся наборов цифр, — 1232.
Ответ: 1232.
8. Задание 19 № 507057. Найдите наименьшее трёхзначное натуральное число, которое при делении на 6 и на 11 даёт равные ненулевые остатки и у которого средняя цифра является средним арифметическим двух крайних цифр.
Пояснение.
По модулю 6 и 11 число имеет одинаковые остатки, следовательно, число имеет тот же остаток при делении на 66, причём этот остаток не равен нулю и меньше шести. Таким образом, искомое число может иметь вид:
При получаем: 67, 68, 69, 70, 71. Все эти числа не являются трёхзначными.
При получаем: 133, 134, 135, 136, 137. Число 135 удовлетворяет всем условиям задачи.
Ответ: 135.
9. Задание 19 № 507058. Сумма цифр трёхзначного натурального числа А делится на 12. Сумма цифр числа (А + 6) также делится на 12. Найдите наименьшее возможное число А.
Пояснение.
Пусть число имеет вид
Если
, то сумма цифр в новом числе будет на 6 больше, чем в исходном. Пусть
делится на 12, тогда
то есть число
не делится на 12. Аналогично, если число
делится на 12, то число
не делится на 12. Значит,
. Рассмотрим три случая:
1) Число
имеет вид:
, сумма цифр числа
на 3 меньше суммы цифр числа
2) Число
имеет вид:
, сумма цифр числа
на 12 меньше суммы цифр числа
3) Число
имеет вид:
, сумма цифр числа
на 21 меньше суммы цифр числа
Ясно, что условиям задачи удовлетворяют числа, рассмотренные в пункте 2). Подберём число так, чтобы сумма его цифр делилась на 12. Наименьшее возможное
удовлетворяющее условиям задачи, — 699.
Ответ: 699.
10. Задание 19 № 507059. Найдите наименьшее пятизначное число, кратное 55, произведение цифр которого больше 50, но меньше 75.
Пояснение.
Если число делится на 55, то оно делится на 5 и на 11. Если число делится на 5 то оно может оканчиваться на 0 или на 5. Если в записи числа есть ноль, то произведение цифр числа равно нулю, следовательно, запись числа должна оканчиваться на 5. Пусть число имеет вид Число делится на 11, если сумма цифр на нечётных местах равна сумме цифр на чётных местах:
Рассмотрим различные произведения
такие, что
Последняя цифра числа равна пяти, следовательно, возможные значения произведения
50, 55, 60, 65, 70. Разложим каждое число на простые множители:
Попытаемся удовлетворить уравнению Перебирая различные возможные значения, получим, что только число разложение числа 70 в виде
удовлетворяет уравнению:
Наименьшее число, удовлетворяющее условиям задачи — 11275.
Ответ: 11275.
11. Задание 19 № 507524. Сумма цифр трёхзначного числа A делится на 13. Сумма цифр числаA+5 также делится на 13. Найдите такое число A.
Пояснение.
Пусть число имеет вид
Если
, то сумма цифр в новом числе будет на 6 больше, чем в исходном. Пусть
делится на 12, тогда
то есть число
не делится на 13. Аналогично, если число
делится на 13, то число
не делится на 13. Значит,
. Рассмотрим 3 случая:
1) Число
имеет вид:
, сумма цифр числа
на 3 меньше суммы цифр числа
2) Число
имеет вид:
, сумма цифр числа
на 13 меньше суммы цифр числа
3) Число
имеет вид:
, сумма цифр числа
на 21 меньше суммы цифр числа
Ясно, что условиям задачи удовлетворяют числа, рассмотренные в пункте 2). Подберём число так, чтобы сумма его цифр делилась на 13. Наименьшее возможное
удовлетворяющее условиям задачи, — 899.
Ответ: 899.
12. Задание 19 № 507967. Вычеркните в числе 141565041 три цифры так, чтобы получившееся число делилось на 30. В ответе укажите ровно одно получившееся число.
Пояснение.
Если число делится на 30, то оно также делится на 3 и на 10. Поэтому в последнем разряде числа должен быть ноль. Тогда вычёркиваем 41. Остаётся 1415650. Для того, чтобы число делилось на три необходимо, чтобы сумма цифр была кратна трём, значит, нужно вычеркнуть цифру 1 или цифру 4. Таким образом, получаем числа 145650, 115650 и 415650
Ответ: 145650, 115650 или 415650.
13. Задание 19 № 508010. Вычеркните в числе 74513527 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число.
Пояснение.
Если число делится на 15, то оно также делится на 3 и на 5. Поэтому в последнем разряде числа должен быть ноль или цифра пять. Тогда вычёркиваем 27. Остаётся 745135. Посчитаем сумму цифр — 25. Для того, чтобы число делилось на три необходимо, чтобы сумма цифр была кратна трём. В таком случае можно вычеркнуть цифру 1 и получить число 74535, цифру 4 и получить 75135 или вычеркнуть цифру 7 и получить число 45135.
Ответ: 74535, 75135 или 45135.
14. Задание 19 № 508051. Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите ровно одно получившееся число.
Пояснение.
Если число делится на 18, то оно также делится на 9 и на 2. Число должно быть чётным, для этого вычеркнем цифру 7, получим 8541762. Посчитаем сумму цифр — 33. Для того, чтобы число делилось на девять необходимо, чтобы сумма цифр была кратна девяти. Можно вычеркнуть цифры 5 и 1, получив число 84762, либо вычеркнуть цифры 4 и 2 и получить число 85176. Также возможно вычеркнуть цифры 7 и 8 и получить число 54162.
Ответ: 84762, 85176 или 54162.
15. Задание 19 № 508400. Найдите трехзначное натуральное число, большее 500, которое при делении на 4, на 5 и на 6 дает в остатке 2, и в записи которого есть только две различные цифры. В ответе укажите какое-нибудь одно такое число.
Пояснение.
При делении на 4 число даёт в остатке 2, следовательно, оно чётное. Поскольку число при делении на 5 даёт в остатке 2, то оно может оканчиваться на 2 или на 7. Таким образом, число обязательно должно заканчиваться цифрой 2.
Подбором находим, что условию задачи удовлетворяют числа 662 и 722.
Ответ: 662, 722.
16. Задание 19 № 508420. Найдите трехзначное натуральное число, большее 600, которое при делении на 4, на 5 и на 6 дает в остатке 3, и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь одно такое число.
Пояснение.
При делении на 4 число даёт в остатке 3, следовательно, оно нечётное. Поскольку число при делении на 5 даёт в остатке 2, то оно может оканчиваться на 2 или на 8. Таким образом, число обязательно должно заканчиваться цифрой 3.
Подбором находим, что условию задачи удовлетворяют числа 963 и 843.
Ответ: 963, 843.
17. Задание 19 № 509226. Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Пояснение.
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4. Из признака делимости на 4 следует, что число чётное — вычеркнем последнюю цифру. Теперь используем признак делимости на 3. Найдём сумму цифр в числе 1 + 8 + 1 + 6 + 1 + 5 + 1 + 2 = 25. Ближайшие суммы цифр — 24, 21, 18. Чтобы получить сумму цифр 18 вычеркнем из числа цифры 6 и 1. Получим число 181512. Это число делится и на 4, и на 3. Число 116112 также подходит для ответа.
Ответ: 181512, 116112.
18. Задание 19 № 509744. Найдите трёхзначное число A, обладающее всеми следующими свойствами:
· сумма цифр числа A делится на 8;
· сумма цифр числа A + 1 делится на 8;
· в числе A сумма крайних цифр кратна средней цифре.
В ответе укажите какое-нибудь одно такое число.
Пояснение.
Пусть число имеет вид , если
, то сумма цифр в новом числе будет на 1 больше, чем в исходном, и обе они не могут делиться на 8. Значит
. Рассмотрим теперь 2 случая:
1) Число перейдёт в
, сумма изменится на 8.
2) Число перейдёт в
, сумма изменится на 18.
Итак, условиям задачи удовлетворяют числа вида , где
кратно
. Одним из таких чисел является 349.
Ответ: 349.
19. Задание 19 № 509764. Найдите четырёхзначное число, кратное 88, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
Пояснение.
Число делится на 88, если оно делится на 8 и на 11. Признак делимости на 8: число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8. Признак делимости на 11: число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо разность этих сумм делится на 11. Используя признак делимости на 8, и учитывая, что все цифры искомого числа должны быть чётны и различны получаем, что последними цифрами числа могут быть: 024, 048, 064, 208, 240, 264, 280, 408, 480, 608, 624, 640, 648, 680, 824, 840, 864. Используя признак делимости на 11 получим, что условию задачи удовлетворяют числа: 6248, 8624, 2640.
Ответ: 2640, 6248 или 8624.
Приведём идею другого решения.
Искомое число должно быть записано четырьмя из пяти цифр 0, 2, 4, 6 и 8, каждая из которых взята один раз. Причём сумма цифр в разрядах тысяч и десятков должна быть равна сумме цифр в разрядах сотен и единиц, а три последние цифры искомого числа должны образовывать трёхзначное число, кратное восьми. Пусть в разряде тысяч стоит 8, тогда в разряде десятков должна быть 2, а в разряде сотен и единиц — цифры 4 и 6. Заметим, что число 8624 удовлетворяет условию. Далее аналогично для чисел, начинающихся с 2, 4 и 6.
20. Задание 19 № 506312. Трёхзначное число при делении на 10 даёт в остатке 3. Если последнюю цифру числа перенести в начало его записи, то полученное число будет на 72 больше первоначального. Найдите исходное число.
Пояснение.
Пусть число имеет вид
Тогда условие записывается так:
Подставив значение в третье выражение и преобразовав его, получим, что
Подходит только пара .
Таким образом, условиям задачи удовлетворяет число 253.
21. Задание 19 № 506318. Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.
Пояснение.
Разложим число 25 на слагаемые: 25 = 9 + 9 + 7 = 9 + 8 + 8.
Квадрат числа делится на 16, значит, само число делится на 4. Это значит, что оно как минимум заканчивается на чётную цифру. То есть первый набор отпадает, так как в нём таковых нет. Из второго мы можем составить числа 988 и 898. Первое число удовлетворяет условиям задачи.
22. Задание 19 № 506291. Приведите пример четырёхзначного числа А, обладающего следующими свойствами:
1) сумма цифр числа А делится на 8;
2) сумма цифр числа (А + 2) также делится на 8;
3) число А меньше 3000.
В ответе укажите ровно одно такое число.
Пояснение.
Пусть число имеет вид . Если
, то сумма цифр в новом числе будет на 2 больше, чем в исходном, и обе они не могут делиться на 8. Значит,
. Рассмотрим теперь 3 случая:
1) Число перейдёт в
, сумма изменится на 7.
2) Число перейдёт в
, сумма изменится на 16.
3) Число перейдёт в
, сумма изменится на 25.
Итак, условиям задачи удовлетворяют числа вида . Так как
, несложно выписать все варианты: 1698, 2598, 1599, 2499.
23. Задание 19 № 506342. Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 24. В ответе укажите ровно одно такое число.
Пояснение.
Если число делится на 24, то оно также делится на 3 и на 8.
Число делится на 8 тогда и только тогда, когда три его последние цифры образуют число, которое делится на 8. Перебрав трёхзначные числа из 1 и 2, получим, что только 112 делится на 8. Это число образует последние три цифры искомого числа.
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Последние три цифры 112 дают к сумме 4. Рассмотрим первые три цифры. Их сумма может быть от 3 до 6. Условиям задачи удовлетворяет сумма цифр, равная 5. Троек с данной суммой цифр три: 122, 212, 221.
Таким образом, подходят числа: 122112, 212112, 221112.
24. Задание 19 № 506482. Приведите пример шестизначного натурального числа, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите ровно одно такое число.
Пояснение.
Если число делится на 24, то но делится на 3 и на 8.
Если число делится на 8, то число, образованное последними его тремя цифрами, тоже делится на 8. Трёхзначных чисел из 0 и 2, делящихся на 8, два: 000 и 200. Это окончания исходного числа.
Если число делится на 3, то сумма его цифр тоже делится на 3.
000 даёт к сумме 0, то есть сумма первых цифр должна равняться 6, то есть это 222.
200 даёт к сумме 2, то есть сумма первых цифр должна равняться 4, то есть 220 или 202 (022 не может быть, так как это первые цифры, а первая цифра в числе не может равняться 0).
Таким образом, искомые числа: 220200, 202200, 222000.
25. Задание 19 № 506585. Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 72. В ответе укажите ровно одно такое число.
Пояснение.
Если число делится на 72, то но делится на 8 и на 9.
Если число делится на 8, то число, образованное последними его тремя цифрами, тоже делится на 8. Шестизначных чисел из 1 и 2, делящиеся на 8 должны заканчиваться тройкой цифр 112.
Если число делится на 9, то сумма его цифр тоже делится на 9.
112 даёт к сумме 4, то есть сумма первых цифр должна равняться 5, то есть должна состоять из перестановок двух двоек и единицы.
Таким образом, искомые числа: 122112, 212112, 221112.
Ответ: 122112, 212112 или 221112.
26. Задание 19 № 506442. Приведите пример трёхзначного натурального числа, большего 500, которое при делении на 8 и на 5 даёт равные ненулевые остатки и первая слева цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Пояснение.
По модулю 5 и 8 число имеет одинаковые остатки. Оно будет иметь тот же остаток и при делении на 40. Этот остаток больше нуля и меньше пяти. Пусть наше число имеет вид , тогда имеем:
Заметим, также, что искомое число должно быть чётным. Переберём все варианты, их четыре: 564, 684.
Ответ: 564; 684.
27. Задание 19 № 506772. Приведите пример трёхзначного натурального числа, большего 600, которое при делении на 4, на 5 и на 6 даёт в остатке 3 и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число.
Пояснение.
Так как число даёт одинаковый остаток по модулям 4, 5 и 6, то оно также даёт такой же остаток и по модулю 60. То есть число имеет вид Все такие числа: 603, 663, 723, 783, 843, 903, 963. Из них подходят под последнее условие только 843 и 963.
28. Задание 19 № 506645. Приведите пример трёхзначного натурального числа, большего 500, которое при делении на 3, на 4 и на 5 даёт в остатке 2 и в записи которого есть только две различные цифры. В ответе укажите ровно одно такое число.
Пояснение.
Раз число даёт один и тот же остаток по модулю 3, 4 и 5, то оно даёт такой же остаток и по модулю. А значит, число имеет вид
Все числа, удовлетворяющие этому неравенству: 542, 602, 662, 722, 782, 842, 902, 962. Из них удовлетворяют условию про две различные цифры: 662, 722.
29. Задание 19 № 506605. Приведите пример трёхзначного натурального числа, которое при делении на 3, на 5 и на 7 даёт в остатке 1 и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число.
Пояснение.
Если число имеет одинаковые остатки по каким-то модулям, то оно имеет такой же остаток по модулю, являющемуся НОК этих модулей. То есть в данном случае по модулю 105. Тогда наше число . Переберём все возможные варианты: 106, 211, 316, 421, 526, 631, 736, 841, 946. Условиям задачи удовлетворяют числа 421, 631 и 841.
Ответ: 421; 631; 841.
30. Задание 19 № 506854. Приведите пример трёхзначного натурального числа, которое при делении на 3, на 5 и на 7 даёт в остатке 2 и в записи которого есть только две различные цифры. В ответе укажите ровно одно такое число.
Пояснение.
Так как число даёт одинаковые остатки по модулям 3, 5 и 7, то оно также даёт такой же остаток по модулю 105. То есть число имеет имеет вид . Все такие числа: 107, 212, 317, 422, 527, 632, 737, 842, 947. Под последнее условие подходят только числа 212, 422 и 737.
31. Задание 19 № 506462. Приведите пример трёхзначного натурального числа большего 500, которое при делении на 6 и на 5 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите ровно одно такое число.
Пояснение.
По модулю 5 и 6 число имеет одинаковые остатки. Оно будет иметь тот же остаток и при делении на 30. Этот остаток больше нуля и меньше пяти. Пусть наше число имеет вид , тогда имеем:
Переберём все варианты, их 10: 531, 543, 642, 654, 741, 753, 852, 864, 951, 963.
Из них имеют одинаковые остатки по модулям 5 и 6: 543, 753, 963.
32. Задание 19 № 506792. Приведите пример трёхзначного натурального числа, большего 500, которое при делении на 8 и на 5 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите ровно одно такое число.
Пояснение.
Число даёт одинаковые остатки при делении на 5 и 8. Значит, оно даёт такой же остаток и по модулю 40. То есть число имеет вид Первая цифра не меньше 5. Первая и последняя цифры в сумме дают чётное число. Разность числа и p делится на 40, то есть число, образованное первыми двумя цифрами, делится на 4. Теперь можно выписать все числа, которые подходят под эти условия: 642, 963.
33. Задание 19 № 506752. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите ровно одно такое число.
Пояснение.
Если число даёт одинаковые остатки при делении на 4 и на 15, то оно даёт такой же остаток и при делении на 60. То есть теперь мы знаем, что на наше число имеет вид То есть разность нашего числа и
должна делиться на 60, то есть число, образованное первыми двумя цифрами, должно делиться на 6. А если число делится на 6, то оно также делится на 2 и на 3. А это значит, что последняя его цифра чётная, а сумма цифр делится на 3. Из условия на среднее арифметическое также следует, что сумма первой и последней цифры в исходном числе чётная. Переберём последнюю и вторую цифры, а по ним однозначно восстановим первую и получим числа: 123, 543, 963.
34. Задание 19 № 506727. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая справа цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Пояснение.
Если число даёт одинаковые остатки при делении на 4 и на 15, то оно даёт такой же остаток и при делении на 60. То есть теперь мы знаем, что на наше число имеет вид То есть разность нашего числа и
должна делиться на 60, то есть число, образованное первыми двумя цифрами, должно делиться на 6. А если число делится на 6, то оно также делится на 2 и на 3. А это значит, что последняя его цифра чётная, а сумма цифр делится на 3. А из условия на среднее арифметическое следует, что сумма этих цифр также чётная. Под все эти условия подходят числа 24, 42 и 60. А соответствующие им исходные числа будут равны 243, 423 и 603.
35. Задание 19 № 506814. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая справа цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Пояснение.
Если число даёт одинаковые остатки при делении на 4 и на 15, то оно даёт такой же остаток и при делении на 60. То есть теперь мы знаем, что на наше число имеет вид То есть разность нашего числа и
должна делиться на 60, то есть число, образованное первыми двумя цифрами, должно делиться на 6. А если число делится на 6, то оно также делится на 2 и на 3. А это значит, что последняя его цифра чётная, а сумма цифр делится на 3. А из условия на среднее арифметическое следует, что сумма этих цифр также чётная. Под все эти условия подходят числа 24, 42 и 60. А соответствующие им исходные числа будут равны 243, 423 и 603.
36. Задание 19 № 506874. Приведите пример трёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Пояснение. Можно заметить, что если среди цифр есть хотя бы две единицы, то равенство невозможно, так как сумма будет больше произведения. То же самое, если единиц нет вообще. В этом случае произведение будет слишком большое. Таким образом, среди цифр есть ровно одна единица. Число делится на 4, значит, последняя цифра чётная, а это значит, что произведение тоже чётное. А значит, и сумма. И так как последняя цифра чётная, то оставшиеся две цифры должны быть одной чётности. А так как мы выяснили, что среди цифр есть ровно одна единица, то эти числа нечётные. Под эти ограничения подходят числа: 132, 136, 152, 156, 172, 176, 192, 196, 312, 316, 512, 516, 712, 716, 912, 916, из которых удовлетворяют всем условиям только числа 132 и 312.
37. Задание 19 № 506502. Приведите пример четырёхзначного числа, кратного 12, произведение цифр которого больше 40, но меньше 45. В ответе укажите ровно одно такое число.
Пояснение. Если число делится на 12, то оно делится на 3 и на 4. Если число делится на 3, то сумма всех его цифр тоже делится на 3. Если число делится на 4, то число, образованное двумя последними его цифрами тоже делится на 4. Пусть наше число имеет вид , тогда условие записывается так:
В интервале находятся числа 41, 42, 43, 44. 41 и 43 — простые, а 44 делится на 11 — тоже простое. Таким образом, 41, 43 и 44 не подходят, потому что не могут быть представлены в виде произведения. То есть
Два набора цифр подходят как решение: (1, 2, 3, 7) и (1, 1, 6, 7). Но в первом наборе сумма цифр не кратна трём, так что он отпадает. Имеем (1,1,6,7). Последняя цифра в числе должна быть чётной, иначе число не будет делиться на 4.
Остальные цифры могут стоять в любом порядке. Выпишем искомые числа: 1176, 1716, 7116.
38. Задание 19 № 506834. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 1458. Приведите ровно один пример такого числа.
Пояснение.
Число делится на 5, значит, его последняя цифра или 0, или 5. Но так как при записи в обратном порядке цифры также образуют четырёхзначное число, то эта цифра 5, ибо число не может начинаться с 0. Пусть число имеет вид . Тогда условие можно записать так:
Второе слагаемое в левой части делится на 10. Значит, за разряд единиц в сумме отвечает только первое слагаемое. То есть Откуда
Подставив полученное значение в уравнение, получим, что
Перебрав все пары b и с, которые являются решением этого равенства, выпишем все числа, являющиеся ответом: 7065, 7175, 7285, 7395.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Дата: 2015-08-02
512
Категория: Производная
Метка: ЕГЭ-№7
119977. Материальная точка движется прямолинейно по закону
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3с.
Найдем закон изменения скорости:
При t=3 скорость будет равна:
Ответ: 59
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html
Раздел заданий Решу ЕГЭ профиль пополняется заданиями с рисунками и пояснениями. Если у Вас возникают вопросы — не стесняйтесь спрашивать в комментариях. Задача 6 ЕГЭ математика профиль (до 2022 года задание 7) не является самым сложным заданием и можно научиться успешно справляться с ней на экзамене.
Задача 7 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 1 варианта сборника профильных заданий. С положительным направлением оси ОХ наша касательная составляет тупой угол. Значит, ответ точно будет отрицательным. Дальше останется построить прямоугольный треугольник и найти отношение противолежащего катета к прилежащему.
Задача 7 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 2 варианта сборника профильных заданий. Нужно провести касательные и посмотреть на угол наклона. Если он острый с положительным направлением оси ОХ, значит это то. что нужно в нашей задаче.
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 3 варианта сборника профильных заданий. Выделяем отрезок от -11 до 4. Когда производная функции отрицательна — сама функция убывает (на рисунке слева минус). Когда производная функции положительна — сама функция возрастает (на рисунке слева плюс). Переход из «минуса» в «плюс» даёт нам точку минимума — это точки 1, 3, 5. Они нам не подходят. А вот точки 2 и 4 — то, что нужно. Там переход из «плюса» в «минус» — то есть функция возрастает, а затем убывает, после точки максимума. Ответ в задаче 2
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 4 варианта сборника профильных заданий. Выделяем отрезок от -17 до -4. Как и в предыдущей задаче нам нужны точки, в которых происходит смена знака у производной. Они отмечены красными точками. В данном отрезке из 4 штуки. Это и есть точки экстремума. Не путайте, перед вами график производной функции, а не самой функции! У функции точки экстремума были бы в местах перегиба.
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 5 варианта сборника профильных заданий. Когда производная функции отрицательна — сама функция убывает (на рисунке слева минус). Когда производная функции положительна — сама функция возрастает (на рисунке слева плюс). В отмеченных точках производная положительна и функция возрастает. Их 6 штук.
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 6 варианта сборника профильных заданий. Решение приведено ниже, под условием на фото.
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 7 варианта сборника профильных заданий. По аналогии с уже рассмотренными выше задачами. Думаю не особо нужны пояснения, всё видно на решении, единственная точка с координатой 4. Ответ: 4
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 8 варианта сборника профильных заданий. По аналогии с уже рассмотренными выше задачами. Думаю не особо нужны пояснения, всё видно на решении, тангенс угла наклона равен 1,6.
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 9 варианта сборника профильных заданий. Раз нам нужно количество точек максимума, то есть точек со сменой знака с «+» на «-» у производной, то на отмеченном отрезке она у нас единственная.
Задача 7 (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 7 ЕГЭ математика профиль из 10 варианта сборника профильных заданий. Раз нам нужно количество точек, в которых касательная параллельна нашей прямой или совпадает, то нужно провести прямую , равную угловому коэффициенту касательной. У нас угловой коэффициент равен -1, так как прямая y=-x+2 и перед иск стоит именно -1. Строим прямую y=-1 и считаем точки пересечения. Их ровно 6.
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
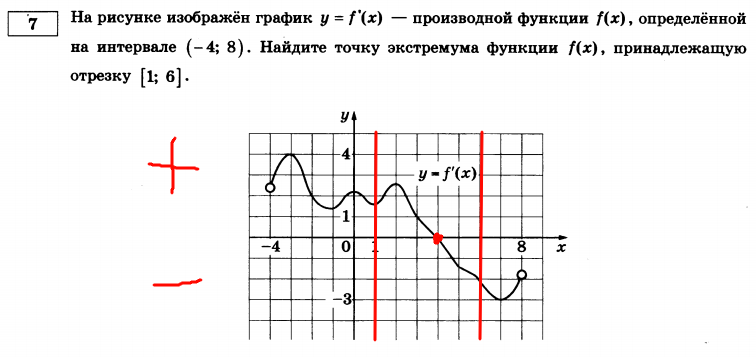
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.