Задания
Версия для печати и копирования в MS Word
Тип 3 № 508234
Фабрика выпускает сумки. В среднем на 101 качественных сумок приходится 9 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в~магазине сумка окажется с дефектами. Результат округлите до сотых.
Аналоги к заданию № 508200: 508201 508202 508203 508204 508205 508206 508207 508208 508209 508210 … Все
Прототип задания
·
508234 решу егэ математика профиль
—>
Задание 14 № 508234
Перепишем неравенство в виде и положим
Далее имеем: откуда
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
Воспользовались формулой квадрат суммы для
Когда мы делаем замену на t, мы ставим следующее ограничение: t>0
У вас оно не указано и корни на интервале от -7 до 2 не отобраны. Мы должны рассматривать вариант: (0; 2]
Роман, Ваш способ решения верный, но не единственный. Лишние корни (промежутки) можно отбрасывать на любом этапе решения. Вы делаете так, а Мы иначе.
Как вы получили из двойного неравенства 5^x = 1?
Сумма двух положительных взаимно обратных чисел не может быть меньше двух, а равна двум только если каждое из этих двух чисел равно 1
В решении в первой строчке написано «положим»,а надо «предположим»,наверное.
—>
Задание 14 № 508234
Лишние корни промежутки можно отбрасывать на любом этапе решения.
Ege. sdamgia. ru
14.01.2020 17:35:59
2020-01-14 17:35:59
Источники:
Https://ege. sdamgia. ru/test? pid=508234
Задание 14. Неравенства — профильный ЕГЭ по математике » /> » /> .keyword { color: red; } 508234 решу егэ математика профиль
Задание 14. Неравенства — профильный ЕГЭ по математике
Задание 14. Неравенства — профильный ЕГЭ по математике
Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
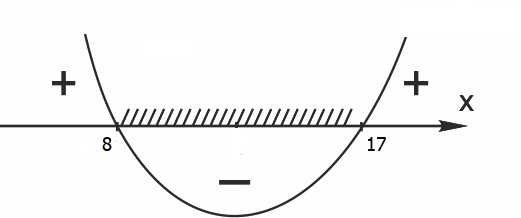
1. Решите неравенство:
Решим неравенство относительно t методом интервалов:
Вернемся к переменной x:
Показательные неравенства
2. Решите неравенство
Сделаем замену Получим:
Умножим неравенство на
Дискриминант квадратного уравнения
Значит, корни этого уравнения:
Разложим квадратный трехчлен на множители.
. Вернемся к переменной x.
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,
3. Решите неравенство
Сделаем замену Получим:
Вернемся к переменной
Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством? Ведь Представляете, как трудно будет выразить х?
Оценим Для этого рассмотрим функцию
Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Мы получили, что
Тогда, и это значит, что Значение не достигается ни при каких х.
Логарифмические неравенства
4. Решите неравенство
Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.
Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!
5. Решите неравенство
А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.
6. Решите неравенство:
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что. Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Согласно методу замены множителя, выражение заменим на
Решить ее легко.
Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.
7. Решите неравенство:
Привести обе части к одному основанию не получается. Ищем другой способ.
Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.
Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.
Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом, то есть x принадлежит ОДЗ.
Оценим Для этого рассмотрим функцию.
Ege-study. ru
18.01.2019 1:01:52
2019-01-18 01:01:52
Источники:
Https://ege-study. ru/ru/ege/materialy/matematika/zadanie-15-profilnogo-ege-po-matematike-neravenstva/
508234 решу егэ математика профиль — Математика и Английский » /> » /> .keyword { color: red; } 508234 решу егэ математика профиль
508234 решу егэ математика профиль
508234 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 14 № 511507
Перепишем неравенство в виде и положим
Далее имеем: откуда
Аналоги к заданию № 508234: 517423 511507 Все
Будут ли засчитаны баллы, если учесть свойство (x+1x) >=2 ? то есть в решении мы учитываем это свойство, а значит сумма всего выражения >=8, а тк. кк. требуется найти выражение
Надо только показать, что эти наименьшие значения достигаются одновременно
Задание 14 № 511507
Задание 14 511507.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >508234 решу егэ математика профиль
508234 решу егэ математика профиль
508234 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 14 № 508234
Перепишем неравенство в виде и положим
Далее имеем: откуда
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
Воспользовались формулой квадрат суммы для
Когда мы делаем замену на t, мы ставим следующее ограничение: t>0
У вас оно не указано и корни на интервале от -7 до 2 не отобраны. Мы должны рассматривать вариант: (0; 2]
Роман, Ваш способ решения верный, но не единственный. Лишние корни (промежутки) можно отбрасывать на любом этапе решения. Вы делаете так, а Мы иначе.
Как вы получили из двойного неравенства 5^x = 1?
Сумма двух положительных взаимно обратных чисел не может быть меньше двух, а равна двум только если каждое из этих двух чисел равно 1
В решении в первой строчке написано «положим»,а надо «предположим»,наверное.
Задание 14 № 508234
Источник Пробный экзамен Санкт-Петербург 2015.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >508234 решу егэ математика профиль
508234 решу егэ математика профиль
508234 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 14 № 508464
Первое слагаемое определено при то есть при или На этих лучах, преобразуем неравенство:
Решение неравенства: или
Почему нельзя вынести 2 перед вторым логарифмом и разделить неравенство на 2? ведь так нам не придется возводить в квадрат и получим линейное неравенство
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >508234 решу егэ математика профиль
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 14 № 508234
Перепишем неравенство в виде и положим
Далее имеем: откуда
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
Воспользовались формулой квадрат суммы для
Когда мы делаем замену на t, мы ставим следующее ограничение: t>0
У вас оно не указано и корни на интервале от -7 до 2 не отобраны. Мы должны рассматривать вариант: (0; 2]
Роман, Ваш способ решения верный, но не единственный. Лишние корни (промежутки) можно отбрасывать на любом этапе решения. Вы делаете так, а Мы иначе.
Как вы получили из двойного неравенства 5^x = 1?
Сумма двух положительных взаимно обратных чисел не может быть меньше двух, а равна двум только если каждое из этих двух чисел равно 1
В решении в первой строчке написано «положим»,а надо «предположим»,наверное.
Задание 14 № 508234
Источник Пробный экзамен Санкт-Петербург 2015.
За пи сы вай тесь на бес плат ное за ня тие.
Dankonoy. com
22.06.2019 17:59:12
2019-06-22 17:59:12
Источники:
Https://dankonoy. com/ege/ege12/archives/392
Информация о генераторе вариантов:

Источники заданий:
1) Прототипы из fipi.ru;
2) Прототипы из os.fipi.ru;
3) Прототипы с реальных ЕГЭ всех лет;
4) Прототипы с mathege.ru.
На каждую позицию рандомно выпадает случайное задание из базы заданий.
Описание каждой из позиций №1–18:





• Задание 6. Вычисления и преобразования – на данный момент 10 прототипов.




Условия прототипов заданий первой части взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)».
• Задание 12. Уравнения – на данный момент 10 прототипов.
• Задание 13. Стереометрическая задача – на данный момент 4 прототипа.
• Задание 14. Неравенства – на данный момент 10 прототипов.
• Задание 15. Финансовая математика – на данный момент 9 прототипов.
• Задание 16. Планиметрическая задача – на данный момент 4 прототипа.
• Задание 17. Задача с параметром – на данный момент 7 прототипов.
• Задание 18. Числа и их свойства – на данный момент 9 прототипов.


Примеры заданий, развёрнутая часть.

Время выполнения варианта.



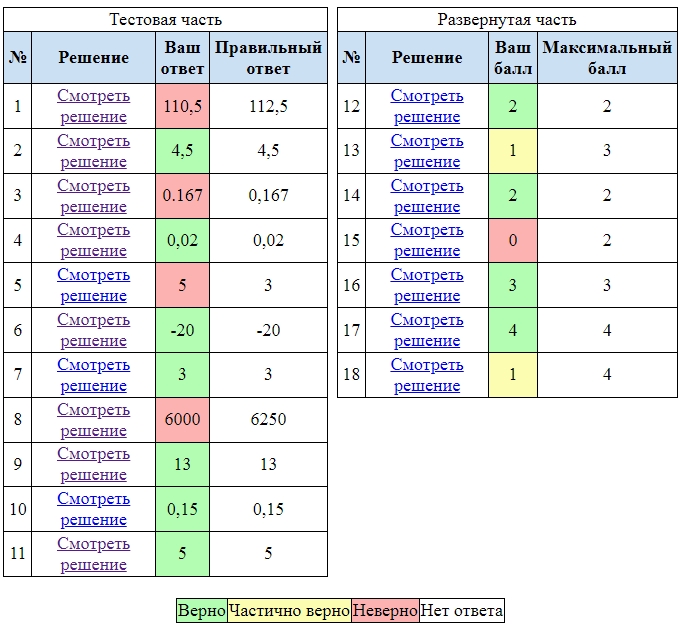
Теги: тренировочные варианты, 11 класс, 2021, с ответами, новый вариант, профиль, пробный егэ.

Материалы и статьи
Распечатай и реши ЕГЭ 2023 профильный уровень по математике 11 класс 3 и 4 новый тренировочный вариант с ответами и решением по новой демоверсии ФИПИ Ященко, варианты опубликованы на сайте 8 января 2023 года.
Скачать варианты и ответы
№3, № 4 вариант ЕГЭ профиль 2023 с ответами
Часть 1. Ответом к заданиям 1–11 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
1. В треугольнике ABC AD – биссектриса, угол C равен 64°, угол CAD равен 38°. Найдите угол B. Ответ дайте в градусах.
2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=4, AA1=8. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.
3. На конференцию приехали учёные из трёх стран: 7 из Сербии, 7 из России и 6 из Дании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется доклад учёного из России.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 815 г, равна 0,95. Вероятность того, что масса окажется больше 785 г, равна 0,86. Найдите вероятность того, что масса буханки больше 785 г, но меньше 815 г.
9. Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
15. 15-го января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: – 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 24% больше суммы, взятой в кредит. Найдите r.
1. В треугольнике ABC AD – биссектриса, угол C равен 66°, угол CAD равен 42°. Найдите угол B. Ответ дайте в градусах.
2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=7, BC=8, AA1=6. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.
3. На конференцию приехали учёные из трёх стран: 6 из Румынии, 5 из Дании и 9 из России. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется доклад учёного из России.
4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,97. Вероятность того, что масса окажется больше 780 г, равна 0,85. Найдите вероятность того, что масса буханки больше 780 г, но меньше 810 г.
9. Смешав 8-процентный и 96-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 36-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
Вам будет интересно:
Практика по заданию №8 профильная математика ЕГЭ
Метки: 11 класс варианты и ответы ЕГЭ математика тренировочный вариант
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
За это задание ты можешь получить 3 балла. На решение дается около 25 минут. Уровень сложности: повышенный.
Средний процент выполнения: 2.7%
Ответом к заданию 15 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 15:
Необходимо свести сложное неравенство к простейшему. Для этого нужно знать метод замены показательных и тригонометрических функций, помня про ограничения. Знать метод интервалов и метод рационализации для логарифмических, показательных и содержащих модуль неравенств.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
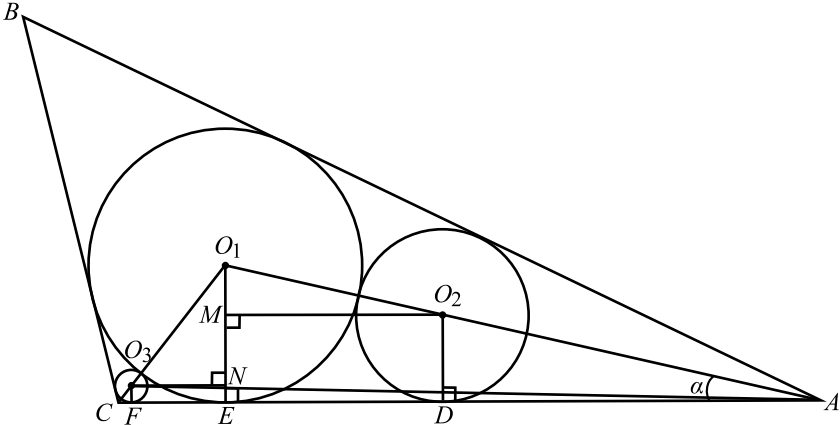
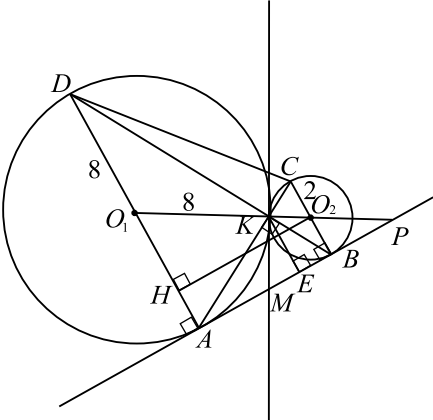
Окружность с центром $O_1$ радиусом $9$ вписана в треугольник $ABC$. Окружности с центрами $O_2$ и $O_3$ и радиусами ${81} / {25}$ и $1$, которые вписаны в углы треугольника $A$ и $C$ соответственно, касаются первой окружности внешним образом.
а) Докажите, что $∠ C=π-arctg {24} / {7}$.
б) Найдите площадь треугольника $AO_1O_3$.
Решение
a) Обозначим радиусы окружностей $r_1 = 9, r_2 = {81}/{25}, r_3 = 1$, а центры этих окружностей $O_1, O_2, O_3$ соответственно, и проведём радиусы $O_1E, O_2D, O_3F$ к точкам касания со стороной $AC$. Эти радиусы перпендикулярны касательной $AC$.
По свойству касательных, проведённых к окружности из одной точки, они образуют одинаковые углы с прямой, проходящей через центр окружности, то есть центры $O_1, O_2$ лежат на биссектрисе угла $A$, а центры $O_1, O_3$ — на биссектрисе угла $C$. Обозначим величину угла $C$ через $2β$. Тогда угол треугольника $O_1CA$ равен $β$.
Проведём $O_3N ⊥O_1E$, тогда $O_3N ‖ FE$ и $O_3N EF$ прямоугольник, $EN = r_3, O_1N = O_1E — EN = r_1 — r_3 = 8. ∠O_1CA = ∠O_1O_3N = β$ как соответственные при $O_3N ‖ AC$, секущая $CO_1$.
Треугольник $O_1O_3N$ прямоугольный, $O_3O_1= r_1 + r_3 = 10, O_3N = √{O_3O_1^2 — O_1N^2} = 6, tgβ = {O_1N}/{O_3N} = {8}/{6} = {4}/{3}$,
$tg 2β = {2 tg β}/{1 — tg^2 β} = {2 · {4}/{3}}/{1 — ({4}/{3})^2} = -{24}/{7}$.
Получили, что угол $C$ тупой. $∠C = π − arctg{24}/{7}$.
б) 1) $tg β = {O_1E}/{EC}, EC = r_1 : tg β = 9 : {4}/{3} = {27}/{4}$.
Обозначим величину угла $O_1AC$ треугольника через $α$. Найдём $EA = r_1 : tg α$.
Проведём $O_2M ⊥O_1E$, тогда аналогично пункту а) $EM = r_2$,
$O_1M = O_1E — EM = r_1 — r_2 = {144}/{25}, O_1O_2= r_1 + r_2 = {306}/{25}$.
$O_2M= √{O_1O_2^2 — O_1M^2} = {270}/{25}, tg α = {O_1M}/{O_2M} = {8}/{15}, AE = r_1 : tg α = 9 : {8}/{15} = {135}/{8}$.
$AC = AE + EC = {189}/{8}$.
$S_{AO_1O_3} = S_{AO_1C}-S_{ACO_3}={1}/{2}r_1· AC-{1}/{2}r_3·AC = {1}/{2}(r_1-r_3) ·AC = 94.5$.
Ответ: 94.5
Задача 2
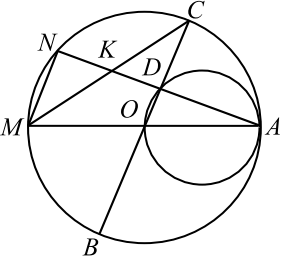
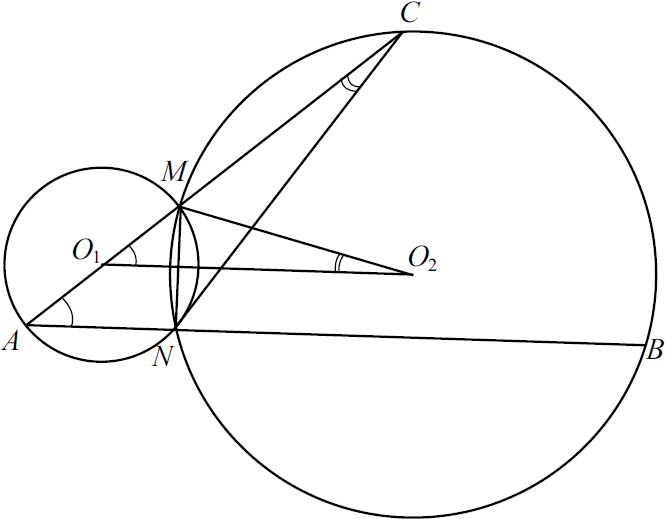
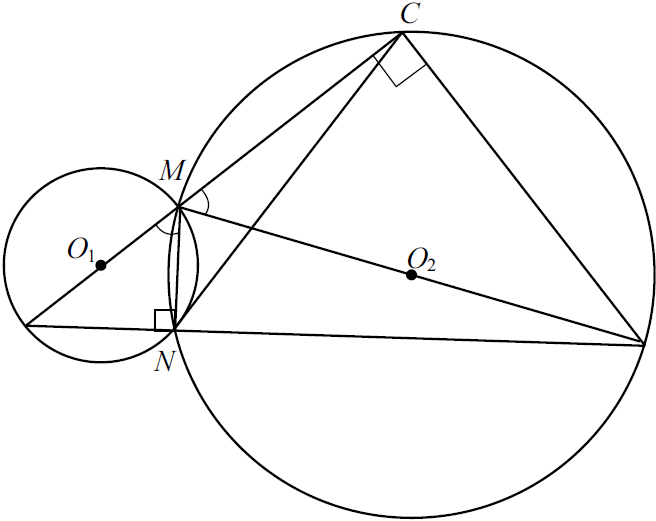
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают б’ольшую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {2√ {2}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж.
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны.
б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN , BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK}/{KA} = {MN}/{MA} = cos∠AM N = cos∠AOC = √{1-sin^2 ∠AOC} = {1}/{3}$.
Ответ: 1:3
Задача 3
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают большую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {√ {5}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж (см. рис.).
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны. б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN$, $BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK} / {KA} = {MN} / {MA} = cos ∠ AMN = cos ∠ AOC = √ {1 — sin^2 ∠ AOC} = {2} / {3}$.
Ответ: 2:3
Задача 4
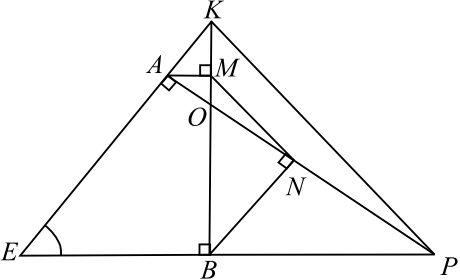
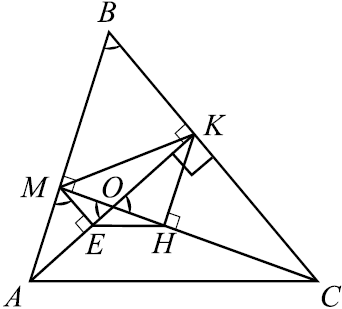
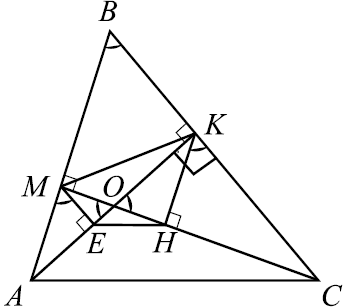
В треугольнике $EKP$, в котором все углы острые, проведены высоты $KB$ и $PA$. Из точек $A$ и $B$ на $KB$ и $PA$ опущены перпендикуляры $AM$ и $BN$ соответственно.
а) Докажите, что прямые $MN$ и $KP$ параллельны.
б) Найдите отношение $MN:KP$, если угол $KEP$ равен $45^°$.
Решение
а) $△POB ∼ △KOA$ по первому признаку подобия: $∠PBO = ∠OAK = 90°, ∠BOP = ∠AOK$ как вертикальные.
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OK} = {BN}/{AM}$ (1).
$△ONB ∼ △AOM$ по первому признаку подобия: $∠BNO = ∠AMO = 90°, ∠BON = ∠AOM$ как вертикальные, отсюда ${ON}/{OM} = {BN}/{AM}$ (2).
Из 1) и 2) следует ${OP}/{OK} = {ON}/{OM}$.
Следовательно, $△OPK ∼ △ONM$ по второму признаку подобия: $∠POK$ — общий, ${OP}/{ON} = {OK}/{OM}$.
Из подобия следует $∠OPK = ∠ONM$ . Углы $OPK$ и $ONM$ соответственные при прямых $PK$ и $NM$ и секущей $OP$ . Следовательно, $PK ‖ MN$ по признаку параллельности прямых.
б) В четырехугольнике $AEBO ∠AEB = 45°$ (по условию) $∠AOB=360°-(∠A +∠B +∠E ) = 360° — 225° = 135°$. В $△AOM ∠AMO = 90°, ∠AOM = 180°-135°=45°, AM=MO$.
Обозначим $OM = x$, тогда $AM = x, AO=OM√2=x√2$.
В $△OAK ∠OAK = 90°, ∠AOM = 45°$, то есть $AO = AK, AO=x√2, KO=AO√2=x√2·√2=2x$.
По доказанному в пункте а) $△OPK ∼ △ONM$, значит, ${MN}/{KP} = {OM}/{OK}$.
Пусть $OM = x, OK = 2x$.
${MN}/{KP}={x}/{2x}=1:2$
Ответ: 1:2
Задача 5
В треугольнике $MNP$, в котором все углы острые, проведены высоты $ME$ и $PF$. Из точек $F$ и $E$ на $ME$ и $PF$ опущены перпендикуляры $FK$ и $EH$ соответственно.
а) Докажите, что прямые $KH$ и $MP$ параллельны.
б) Найдите отношение $MP:KH$, если угол $MNP$ равен $60^°$.
Решение
а) $O$ — точка пересечения высот $ME$ и $PF$. $△POE ∼ △MFO$ по первому признаку подобия: $∠PEO = ∠OFM = 90°, ∠EOP = ∠FOM$ как вертикальные.
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OM} = {EH}/{FK}$ (1).
$△OHE ∼ △FOK$ по первому признаку подобия: $∠EHO = ∠FKO = 90°, ∠EOH = ∠FOK$ как вертикальные, отсюда ${OH}/{OK} = {EH}/{FK}$ (2).
Из 1) и 2) следует ${OP}/{OM} = {OH}/{OK}$.
Следовательно, $△OP M ∼ △OH K$ по второму признаку подобия: $∠P OM$ — общий, ${OP}/{OH} = {OM}/{OK}$.
Из подобия следует $∠OP M = ∠OH K$ . Углы $OP M$ и $OH K$ соответственные при прямых $M P$ и $K H$ и секущей $OP$ . Следовательно, $M P ‖ K H$ по признаку параллельности прямых.
б) В четырехугольнике $N FOE ∠FOE = 360° -(∠90° +∠90° +∠N ) = 360° — 240° = 120°$. В $△FOK ∠FKO = 90°, ∠FOK = 60°$, как смежный с $∠FOE = 120°$, тогда $∠OF K = 30°$.
Обозначим $OK = x$, тогда $FO = 2x$.
В $△OFM ∠M FO = 90°, ∠FOM = 60°, ∠F M O = 30°$, то есть $FO = {1}/{2}M O$, значит, $2x = {1}/{2}M O, M O = 4x$.
По доказанному в пункте а) $△OM P ∼ △OK H$, значит, ${MP}/{K H} = {M O}/{OK} $, но $M O = 4x, OK = x$, следовательно, ${M P}/{K H} = {4x}/{x} = 4 : 1$
Ответ: 4:1
Задача 6
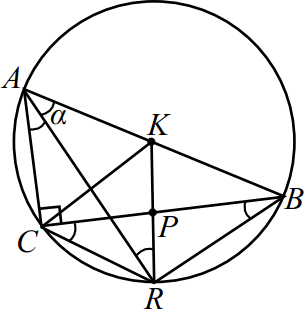
В прямоугольном треугольнике $ABC$ точки $P$ и $K$ — середины катета $BC$ и гипотенузы $AB$ соответственно. Биссектриса угла $BAC$ пересекает прямую $KP$ в точке $R$.
а) Докажите, что точки $A$, $B$, $C$ и $R$ лежат на одной окружности.
б) Найдите отношение площадей треугольников $AKR$ и $BCR$, если $sin ∠ BAC={15} / {17}$.
Решение
а) Отрезок, соединяющий вершину прямого угла и середину гипотенузы, равен половине длины гипотенузы, то есть $AK = K B = K C. AR$ — биссектриса угла $BAC$, значит $∠CAR =∠BAR = α$.
$K P$ — средняя линия $△ABC$, значит, $K P ‖ AC$.
Накрест лежащие углы $CAR$ и $ARK$ равны (секущая $AR$).
В треугольнике $AK R$ равны углы $K AR$ и $K RA$, значит $AK = K R$.
Получим $AK = K B = K C = K R$, значит точки $A, B, C$ и $R$ лежат на окружности с центром $K$.
б) $∠CBR =∠CAR$ и $∠BAR =∠BCR$ (опираются на дуги $C R$ и $BR$ соответственно), таким образом, треугольники $AK R$ и $BC R$ подобны по двум углам. По теореме синусов для треугольника $ABR$ получим ${BR}/{sin ∠RAB} = 2r$, где $r$ — радиус описанной окружности, то есть $2r = AB$. Получили ${BR}/{AB} = sin ∠RAB = sin α$.
Но коэффициент подобия треугольников $AK R$ и $BC R$ равен ${AK}/{BR} = {2AK}/{2BR} = {AB}/{2BR} = {1}/{2 sin α}$.
По условию $sin ∠BAC = sin 2α = {15}/{17}$.
Тогда $cos 2α = √{1 — ({15}/{17})^2} = {8}/{17}$,
$cos 2α = 1 — 2 sin^2 α = {8}/{17}, 2 sin^2 α = {9}/{17}$.
Площади треугольников относятся как квадрат коэффициента подобия, поэтому ${S_{AKR}}/{S_{BCR}} = ({1}/{2sin α})^2 = {1}/{2 · {9}/{17}} = {17}/{18}$.
Ответ: 17:18
Задача 7
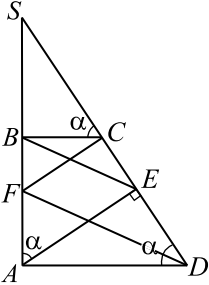
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $BE$ и $FD$ параллельны.
а) Докажите, что прямые $FC$ и $CD$ перпендикулярны.
б) Найдите отношение $BE:FD$, если угол $BCD$ равен $120°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет падать на продолжение $CD$, а не на саму сторону, что противоречит условию.
а) Для доказательства перпендикулярности прямых $FC$ и $CD$ достаточно доказать подобие треугольников $SFC$ и $SAE$.
Заметим, что $△SBC ∼ △SAD$ по двум углам ($∠SBC = ∠SAD = 90°, ∠S$ — общий). Тогда ${SB}/{SA} = {SC}/{SD}$, то есть $SB·SD = SA · SC$.
С другой стороны, $△SBE ∼ △SFD$ по двум углам: $∠SBE = ∠SFD$ как соответственные углы при параллельных прямых $BE$ и $FD$ и секущей $SA, ∠S$ — общий.
Тогда ${SB}/{SF} = {SE}/{SD}$, отсюда $SB · SD = SF · SE$.
Следовательно, $SA · SC = SB · SD = SF · SE$.
Тогда $SA · SC = SF · SE, {SA}/{SF} = {SE}/{SC}$.
Отсюда $△SAE ∼ △SFC$ по второму признаку.
Тогда $∠SCF = ∠SEA = 90°, FC ⊥ SD$, что и требовалось доказать.
б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE}/{FD} = {SB}/{SF}$.
$∠BCS = 180° — ∠BCD = 60°, SB = SC sin 60° = {√3}/{2}SC. ∠CSF = 90° — ∠BCS = 30°$. Из $△SFC$ следует, что $CS = SF cos 30° = SF {√3}/{2}$. Тогда $SB = {√3}/{2}SC ={√3}/{2}·{√3}/{2}SF; {SB}/{SF} = {3}/{4} = 0.75$.
Ответ: 0.75
Задача 8
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $CD$ и $CF$ перпендикулярны. а) Докажите, что прямые $BE$ и $FD$ параллельны. б) Найдите отношение $BE:FD$, если угол $BCD$ равен $150°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. а) Для доказательства параллельности прямых $BE$ и $FD$ достаточно доказать, что треугольники $SBE$ и $SFD$ подобны (см. рис.). Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет опускаться на продолжение $CD$, а не на саму сторону, что противоречит условию. По условию $FC⊥ CD$ и $AE⊥ CD$, отсюда $FC∥ AE$. Заметим: в прямоугольных треугольниках $SCB$, $SFC$, $SAE$ и $SDA$ угол $S$ общий, значит, $∠ SCB=∠ SFC=∠ SAE=∠ SDA=α$. В каждом из рассматриваемых треугольников выразим $sin α$. $▵ SCB$: $sin α={SB} / {SC}$ (1) $▵ SFC$: $sin α={SC} / {SF}$ (2) $▵ SAE$: $sin α={SE} / {SA}$ (3) $▵ SDA$: $sin α={SA} / {SD}$ (4) Перемножив (1) на (2) и (3) на (4), получим ${SB} / {SC}⋅ {SC} / {SF}=sin^2 α$, ${SB} / {SF}=sin^2α$, ${SE} / {SA}⋅ {SA} / {SD}=sin^2α$, ${SE} / {SD}=sin^2α$. Отсюда ${SB} / {SF}={SE} / {SD}$. Имеем: две стороны $▵ SBE$ пропорциональны двум сторонам $▵ SFD$ и между ними угол $S$ — общий, значит, $▵ SBE∼ ▵ SFD$ по второму признаку подобия. Из подобия следует равенство соответственных углов $SEB$ и $SDF$ при прямых $BE$, $FD$ и секущей $SD$, следовательно, по признаку параллельности прямых $BE∥ FD$. б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE} / {FD}={SB} / {SF}$. В пункте а) доказано ${SB} / {SF}=sin^2 α$, $∠ BCD+α=180°$, $α=180°-150°=30°$. ${BE} / {FD}={SB} / {SF}=sin^2 30°=0{,}5^2=0{,}25$.
Ответ: 0.25
Задача 9
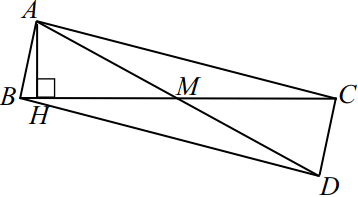
В треугольнике $ABC$ проведена высота $AH$ и медиана $AM$. $AB=2$, $AC=√ {21}$, $AM=2{,}5$.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Вычислите $HM$.
Решение
а) Достроим треугольник $ABC$ до параллелограмма $ABDC$, как показано на рисунке.
По свойству параллелограмма, верно равенство $2(AB^2 + AC^2) = AD^2 + BC^2$, или $2(AB^2 + AC^2) = (2AM)^2 + BC^2$. Так как по условию $AB = 2, AC = √{21}, AM = 2.5$, то $2(22 + √{21}^2) = (2 · 2.5)^2 + BC^2$, откуда $BC = 5$. Если диагонали параллелограмма равны, то он — прямоугольник, значит, $∠BAC = 90°$ и $△ABC$ прямоугольный.
б) В прямоугольном треугольнике $ABC$ выразим площадь двумя способами: $2S = AB · AC, 2S = BC · AH$, приравнивая правые части этих равенств, находим $AH = {AB·AC}/{BC} = {2 · √21}/{5}$. Катет $HM$ найдём из прямоугольного треугольника $AHM$ по теореме Пифагора: $HM = √{AM^2 − AH^2} = √{2.5^2 −({2 · √21}/{5})^2} = √{{25}/{4} − {84}/{25}} = √{{625 − 336}/{100}} = {17}/{10} = 1.7$.
Ответ: 1.7
Задача 10
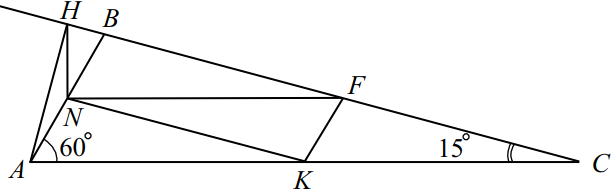
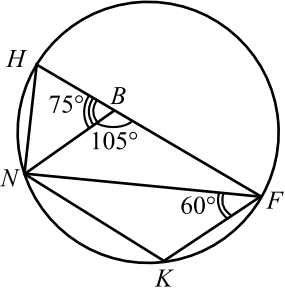
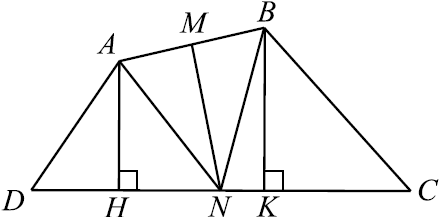
В треугольнике $ABC$ точки $K$, $N$, $F$ — середины сторон $AC$, $AB$ и $BC$ соответственно. $AH$ — высота треугольника $ABC$, $∠ CAB=60^°$, $∠ ACB=15^°$.
а) Докажите, что точки $K$, $N$, $F$ и $H$ лежат на одной окружности.
б) Найдите $FH$, если $BC=4√ 3$.
Решение
а) $∠ABC = 180° — (60° + 15°) = 105°$.
$NH$ — медиана в прямоугольном треугольнике $AHB$, отсюда $NH = NB = AN$.
$∠ABH = 75°, ∠BHN = ∠NBH$ как углы при основании равнобедренного треугольника $NBH , ∠NBH = 75°$.
$FK = {1}/{2}AB, NK = {1}/{2}BC , FN = {1}/{2}AC$ по свойству средней линии треугольника, тогда $△FKN ∼ △ABC$ по трём пропорциональным сторонам, следовательно, $∠NKF = ∠ABC = 105°$.
В четырёхугольнике $NHFK$ найдём сумму противоположных углов: $∠FKN + ∠FHN = 105° + 75° = 180°$, значит, около этого четырёхугольника можно описать окружность, что и требовалось доказать.
б) По теореме синусов для $△NFK: {NK}/{sin∠NFK} = 2R$, где $R$ — радиус окружности, проходящей через точки $K , N , F$ и $H$. Так как $NK = {1}/{2}BC$, то ${BC}/{2sin60°} = 2R = {4√3}/{2} : {√3}/{2} = 4$.
В равнобедренном треугольнике $HNB$ $∠N = 180° — 75°· 2 = 30°$. $∠BNF = ∠BAC = 60°$ как соответственные углы при параллельных прямых $NF$ и $AC$ и секущей $AB$.
В $△HNF ∠HNF = ∠HNB + ∠BNF = 30° + 60° = 90°$, значит $HF$ — диаметр описанной окружности, $HF = 2R = 4$.
Ответ: 4
Задача 11
Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь $▵ AKB$, если известно, что радиусы окружностей равны $8$ и $2$.
Решение
а) Общая касательная, проведенная к окружностям в точке $K$, пересекает $AB$ в точке $M$. По свойству касательных, проведенных из одной точки, $AM = K M$ и $K M = BM$. Треугольник $AK B$, у которого медиана $K M$ равна половине стороны $AB$, к которой она проведена, прямоугольный, $∠AK B = 90°$. Вписанный угол $AK D$ прямой, поэтому он опирается на диаметр $AD$, значит, $AD ⊥ AB$. Аналогично, получаем, что $BC ⊥ AB$. Следовательно, прямые $AD$ и $BC$ параллельны.
б) Пусть первая окружность имеет радиус $8$, а вторая — радиус $2$.
Проведём $O_2H ⊥ AD$, тогда $O_2HAB$ — прямоугольник и $AH = O_2 B = 2, AB = O_2 H$. Из $△O_1O_2H$ получим $O_2 H^2 = O_1O_2^2 — O_1H^2 = (2 + 8)^2 — (8 — 2)^2 = 64, O_2 H = 8 = AB$.
$△O_2PB ∼ △O_1O_2H$ (по двум углам), ${O_2B}/{O_2P} = {O_1H}/{O_1O_2}; {2}/{O_2P} = {8 — 2}/{8 + 2}; O_2P = {10}/{3}$.
Проведём высоту $KE$ в $△AKB$, получим, что $△O_2BP ∼ △KEP$ (по двум углам). ${KE}/{O_2B} = {KP}/{O_2P}; {KE}/{2} = {2 + {10}/{3}}/{{10}/{3}}; KE = 1.6 · 2 = 3.2$.
$S_{AKB} = {1}/{2}AB · KE = {1}/{2} · 8 · 3.2 = 12.8$.
Ответ: 12.8
Задача 12
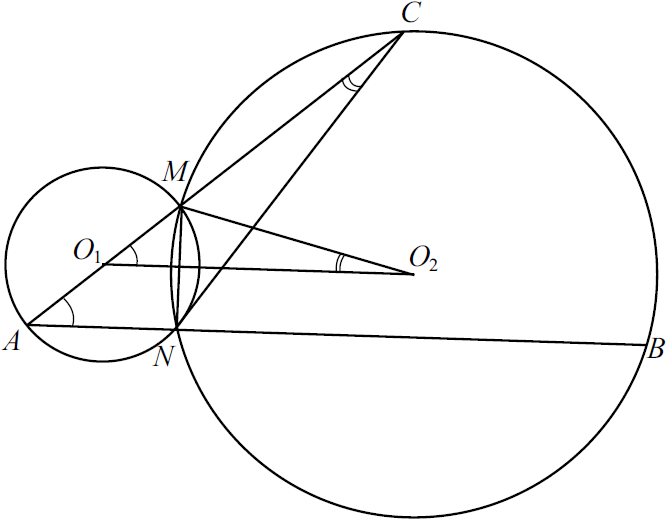
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $1{,}5$ раза больше радиуса первой и $MN=3$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O_2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $1.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠MNA = 90°$, тогда $MB$ — диаметр окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
Значит, $△AMN∼△BCM$ по двум углам.
Значит, ${MC}/{MN} = {MB}/{AM}={2⋅3r}/{2⋅2r} =1.5.$
$MC= 1.5·3 = 4.5$.
Ответ:
Задача 13
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $2{,}5$ раза больше радиуса первой и $MN=2$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $2.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠ANM = 90°$, тогда $MB$ — диаметр второй окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
Значит, $△AMN∼△BCM$ по двум углам ($∠ANM = ∠MCB = 90°, ∠AMN = ∠CMB$)
${MC}/{MN} = {MB}/{AM}$, но ${MB}/{AM} = {2·2.5r}/{2r} = 2.5$.
$MC = 2.5·MN = 5$.
Ответ: 5
Задача 14
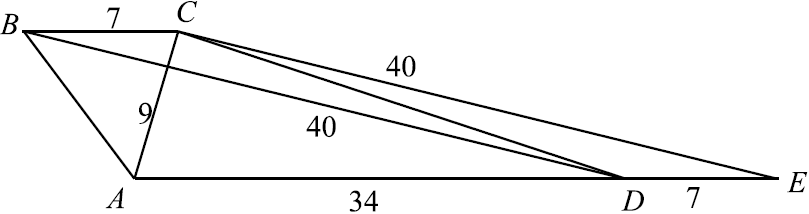
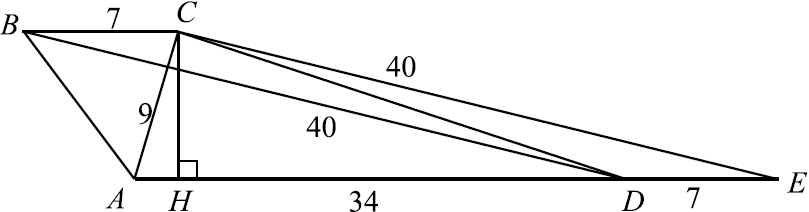
Основания трапеции равны $7$ и $34$, а её диагонали равны $9$ и $40$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 7$, тогда $AE = AD + DE = 34 + 7 = 41$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {9·40}/{41}. S_{ABCD} = {AD + BC}/{2}·CH = {34 + 7}/{2}·{9·40}/{41} = 9·20 = 180$.
Ответ: 180
Задача 15
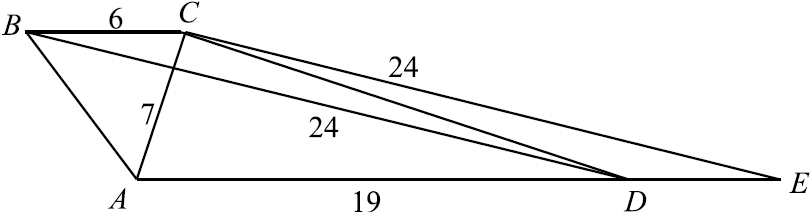
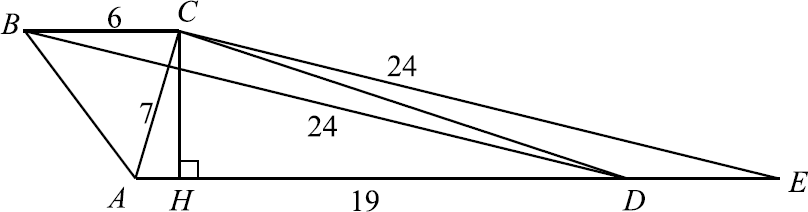
Основания трапеции равны $6$ и $19$, а её диагонали равны $7$ и $24$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 6$, тогда $AE = AD + DE = 19 + 6 = 25$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {7·24}/{25}. S_{ABCD} = {AD + BC}/{2}·CH = {19 + 6}/{2}·{7·24}/{25} = 7·12 = 84$.
Ответ: 84
Задача 16
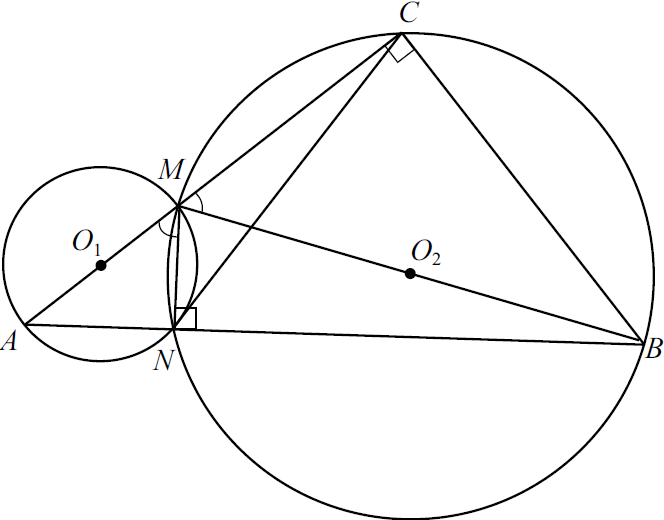
Две окружности касаются внутренним образом в точке $K$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $AB$ большей окружности вторично пересекает меньшую окружность в точке $C$, отличной от $K$. Лучи $KO$ и $KC$ вторично пересекают большую окружность в точках $D$ и $E$ соответственно. Точка $B$ лежит на дуге $EK$ большей окружности, не содержащей точку $D$.
а) Докажите, что прямые $DE$ и $AB$ параллельны.
б) Известно, что $sin∠ KOB = {√ {15}} / {8}$. Прямые $DB$ и $EK$ пересекаются в точке $L$. Найдите отношение $EL:LK$.
Решение
а) $KD$ — диаметр большей окружности ($O ∈ KD$), $O_1$ — центр меньшей окружности, $l$ — общая касательная двух окружностей, проходящая через точку $K$ (см. рис.). $O_1 ∈ KD$. Действительно, $OK⊥ l$, $O_1K⊥ l$ как радиусы, проведённые в точку касания, значит, точки $O$, $K$, $O_1$ лежат на луче $KO$. $∠ DEK=∠ OCK=90°$ как вписанные углы, опирающиеся на диаметры $DK$ и $OK$ соответственно. $C∈ EK$, следовательно, $DE∥ AB$ как два перпендикуляра к одной прямой.
б) Так как диаметр $AB$, перпендикулярный хорде $EK$, делит её пополам, то $CE=CK$, следовательно, $⌣ KB=⌣ BE$ (см. рис.). Угол $EDK$ вписанный, опирается на дугу $EK$, а угол $BOK$ — центральный, опирается на половину дуги $EK$, следовательно, $∠ EDK=∠ BOK=α$; $∠ EDB=∠ BDK$ как вписанные углы, опирающиеся на равные дуги, тогда $DL$ — биссектриса треугольника $DEK$, а по свойству биссектрисы ${EL} / {LK}={DE} / {DK}=cos α=√ {1-sin^2 α}$.
${EL} / {LK}=√ {1-{15} / {64}}={7} / {8}$.
Ответ: fsm78
Задача 17
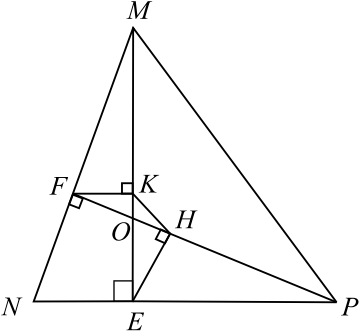
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $cos ∠ ABC = {√ {2}} / {4}$.
Решение
а) По условию задачи выполним чертёж.
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = {2}/{16} ={1}/{8}$. Таким образом, $EH : AC = 1 : 8$.
Ответ: 1:8
Задача 18
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $sin ∠ ABC = {√ {3}} / {3}$.
Решение
а) По условию задачи выполним чертёж.
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = 1-sin^2∠ABC = 1-{1}/{3} ={2}/{3}$. Таким образом, $EH : AC = 2 : 3$.
Ответ: 2:3
Задача 19
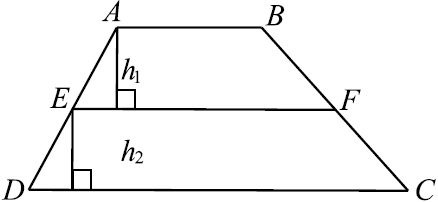
Один из двух отрезков, соединяющих середины противоположных сторон выпуклого четырёхугольника, делит его площадь пополам, а другой — в отношении ${6} / {7}$. а) Докажите, что данный четырёхугольник есть трапеция. б) Укажите отношение двух оснований этой трапеции (меньшего к большему).
Решение
а) Рассмотрим выпуклый четырёхугольник ABCD. Пусть M — середина AB, N — середина CD, причём $S_{AMND} = S_{MBCN}$. Проведём AN и BN. Заметим, что $S_{AMN} = {1}/{2}AM · MNsin∠AMN ={1}/{2}MB · MNsin∠BMN = S_{BMN}$, так как $AM = MB, sin∠AMN = sin(180° — ∠AMN) = sin∠BMN$.
Отсюда $S_{AND} = S_{BNC}(S_{AND} = S_{AMND} — S_{AMN}, S_{BNC} = S_{MBCN} — S_{MBN})$.
Опустим в $△AND$ высоту AH, в $△BNC$ — высоту BK.
Получим ${1}/{2}DN·AH = {1}/{2}NC·BK$, при этом $DN = NC$. Следовательно, $AH = BK$. Но тогда в четырёхугольник $AHKB ∠AHK = ∠BKH = 90°, AH = BK$, то есть $AHKB$ — прямоугольник. Значит, $AB ‖ HK, AB ‖ DC$.
Для доказательства того, что ABCD — трапеция, необходимо доказать, что две другие стороны не параллельны, то есть AD не параллельна BC. Предположим противное. Тогда ABCD — параллелограмм, но тогда отрезок, соединяющий середины AD и BC, делит площадь ABCD пополам, что противоречит условию, так как отношение полученных площадей должно равняться 6 : 7. Отсюда верно ABCD — трапеция.
б) По условию EF делит площадь ABCD на площади, отношение которых равно 6 : 7, а именно $S_{ABFE} : S_{EFCD} = 6 : 7$.
$EF$ — средняя линия, $EF = {AB + CD}/{2}$.
Надо найти AB : CD.
$S_{ABFE} = {AB + EF}/{2}·h_1, S_{EFCD} = {EF + CD}/{2}·h_2$, где $h_1$ — высота $ABFE$, $h_2$ — высота $EFCD$.
Учитывая, что $AB ‖ CD$, а $EF$ — средняя линия и $EF ‖ AB$ и $EF ‖ CD$, то расстояние от $EF$ до $AB$ и от $EF$ до $CD$ равны, то есть $h_1 = h_2$.
Следовательно, ${S_{ABFE}}/{S_{EFCD}} = {{AB + EF}/{2}}/{{EF + CD}/{2}} = {AB + EF}/{EF + CD} = {AB + {AB + CD}/{2}}/{{AB + CD}/{2} + CD} = {3AB + CD}/{3CD + AB}, {3AB + CD}/{3CD + AB} = {6}/{7}, 21AB + 7CD = 18CD + 6AB, 15AB = 11CD, {AB}/{CD} = {11}/{15}$.
$AB : CD = 11 : 15$.
Ответ: 11:15
Задача 20
В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении $9:13$. а) Доказать, что данный четырёхугольник является трапецией. б) Найти отношение меньшего основания этой трапеции к большему.
Решение
а) Рассмотрим выпуклый четырёхугольник $QMNP$ (см. рис.). Пусть $E$ — середина $MQ$, $F$ — середина $NP$, причём $S_{MNFE}=S_{EFPQ}$.
Проведём отрезки $EN$ и $EP$. Заметим, что
$S_{▵ EFN}={1} / {2} EF⋅ FNsin ∠ EFN={1} / {2} EF⋅ FP sin ∠ EFP=S_{▵ EFP}$, так как $NF=FP$ и $sin ∠ EFN=sin (180°-∠ EFN)=sin ∠ EFP$. Отсюда $S_{▵ MNE}=S_{▵ EPQ}$ ($S_{▵ MNE}=S_{MNFE}-S_{▵ EFN}$, $S_{▵ EPQ}=S_{EFPQ}-S_{▵ EFP}$). Опустим в $▵ MNE$ высоту $NN_1$, в $▵ EPQ$ — высоту $PP_1$. Получим: ${1} / {2} ME⋅ NN_1={1} / {2} EQ⋅ PP_1$. Но $ME=EQ$, следовательно, $NN_1=PP_1$. Но тогда в четырёхугольнике $N_1NPP_1$ $∠ NN_1P_1=∠ N_1P_1P=90°$, $NN_1=PP_1$, то есть $N_1NPP_1$ — прямоугольник. Значит, $N_1P_1∥ NP$, $MQ∥ NP$. Из предположения о том, что $MN∥ QP$, следует, что отрезок, соединяющий середины сторон $MN$ и $QP$, делит параллелограмм $MNPQ$ на две равновеликие фигуры. Но по условию это не так. Значит, $MN ∦ QP$. Следовательно, $MNPQ$ — трапеция. б) По условию второй отрезок $AB$ делит четырёхугольник так, что площадь $ANPB$ относится к площади $ABQM$ как $9:13$ (см. рис.).
$S_{ANPB}:S_{ABQM}=9:13$. $AB$ — средняя линия трапеции, $AB={NP+MQ} / {2}$. $S_{ANPB}={AB+NP} / {2}⋅ h_1$; $S_{ABQM}={AB+MQ} / {2}⋅ h_2$, где $h_1$ — высота трапеции $ANPB$; $h_2$ — высота трапеции $ABQM$. Так как $NP∥ MQ$, а $AB$ — средняя линия и $AB∥ NP$ и $AB∥ MQ$, то расстояния от $AB$ до $NP$ и от $AB$ до $MQ$ равны, то есть $h_1=h_2$. Отсюда, ${S_{ANPB}} / {S_{ABQM}}={{NP+AB} / {2}} / {{AB+MQ} / {2}}={NP+{NP+MQ} / {2}} / {{NP+MQ} / {2}+MQ}={3NP+MQ} / {3MQ+NP}$, ${3NP+MQ} / {3MQ+NP}={9} / {13}$, $39NP+13MQ=27MQ+9NP$, $30NP=14MQ$, ${NP} / {MQ}={14} / {30}={7} / {15}$.
Ответ: 7:15