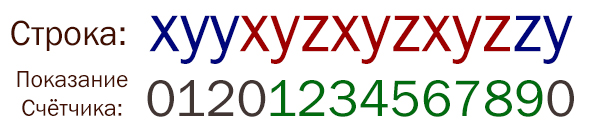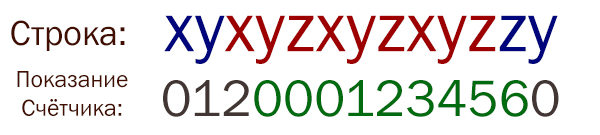509241 решу егэ

Спрятать решение

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

Завершить тестирование, свериться с ответами, увидеть решения.

Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.

Тренировочные варианты ЕГЭ 2023 по математике база и профиль

13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами

20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами

27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами

28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами

28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы

29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами

1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами

6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами

8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами

12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами

14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением

14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением

15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами

15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами

16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением

16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением

23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами

24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами

25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами

26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами

28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами

29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами

1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами

5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами

9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами

12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами

13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами

15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами

21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами

23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами

27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами

28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами

3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами

3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы

5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами

9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами

10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами

13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы

13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами

3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами

6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы

8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы

9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами

10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов

11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами

19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы

22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами

22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами

25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами

27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами

2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами

12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания

13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами

16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами

18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами

22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами

25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы

28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы

4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами

4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы

5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами

8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами

Смотрите также на нашем сайте:

Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Освоение образовательных программ основного общего образования завершается обязательной государственной итоговой аттестацией (далее – ГИА 9) по русскому языку и математике.

Приказы и методические документы

В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов основного государственного экзамена.

Новая версия открытого банка заданий

Сегодня посмотрим одно из самых интересных заданий из ЕГЭ по информатике 2023. Будем решать 24 задание. В этом задании нужно работать с файлами.

Все решения задач из задания 24 ЕГЭ по информатике 2023 будут приведены на языке программирования Python (Питон).

Поехали!

Задача (Самая простая)

Текстовый файл состоит не более чем из 10⁶ символов A, B и C. Определите максимальное количество идущих подряд символов B. Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Решение:

Решим данную задачу на языке Python.

f=open('24_1.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='B':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)
    

С помощью команды open() подвязываемся к файлу. Чтобы не прописывать полный путь, файл должен лежать в той же папке, что и программа.

С помощью команды .read() зачитываем в переменную s всё содержимое файла.

Переменная k — это текущий счётчик символов «B». Задача переменной kmax сохранить максимальное значение k.

С помощью цикла for перебираем все символы из строки s. Переменная i пробегается по номерам всех симолов. Счёт символов начинается в строке с нуля. В начале берём нулевой символ, потом первый и т.д. Конструкция for i in range(0, len(s)) позволяет пройтись по всем символам строки до конца.

Если нам встретился нужный символ «B», то мы счётчик прибавляем на 1. Это значит, что мы подсчитываем текущую цепочку. Если будет стоять 3 символа «B» подряд, значит, счёт k покажет значение 3. Как только встретится дургой символ, то это означает, что цепочка прервалась и счётчик переводится в первоначальное положение 0.

При любом увеличении счётчика происходит анализ этого счётчика на максимальность. Функция max выбирает максимальное значение из старого значения kmax и нового показания счётчика k. Если счётчику k удалось победить kmax, то его значение будет считаться максимальным на данный момент времени.

В ответ идёт значение kmax. Это и есть длина максимальной цепочки. В этой задачке ответ получается 11.

Ответ: 11

Закрепим это простое задание из ЕГЭ по информатике 2023.

Задача (Простая, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых нет символа Z. Для выполнения этого задания следует написать программу.

Решение:

Решение похоже на предыдущее.

f=open('24_2.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]!='Z':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)
    

Если нет символов «Z», то подсчитываем, иначе сбрасываем.

Задача (Обращаемся к соседу)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, расположенных в алфавитном порядке (возможно с повторением симолов). Для выполнения этого задания следует написать программу.

Решение:

f=open('24_2.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]<=s[i+1]:
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)
    

В ответе получается 15. Символы можно сравнивать между собой с помощью знаков «>» или меньше «<» ( а так же «>=» или «<=»), причём это сравнение происходит в алфавитном порядке. Например, символ «B» будет больше, чем «A» и т.п. Теперь нам нужно уже обратится к соседу, уже важна связь между соседними символами. Раз мы обращаемся к следующему символу, то должны пробегать до len(s)-1, иначе куда мы будем обращаться, когда дойдём до последнего символа?

В самом начале цепочки мы анализируем два символа, а к счётчику прибавляем всего лишь 1. Чтобы это учесть, в начале счётчику (переменной k) присваиваем 1. Затем, по мере продвижения по цепочке, мы добавляем в наш анализ 1 новый символ, и к счётчику добавляется одна 1. Дальше уже таких проблем нет.

Раз мы присвоили в переменную k единицу, то и сбрасывать в ветке else мы тоже должны на 1. Эти значения обычно взаимосвязаны.

Если мы обращаемся к соседнему символу, как правило, счётчик и сброс устанавливаются в 1. Это не стопроцентная истина, но иметь ввиду это нужно.

Ответ: 15

Задача (Обращаемся к соседу, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд цифр, среди которых каждые две соседние различны. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_3.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]!=s[i+1]:
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax)
    

Если соседи различны, мы подсчитываем, иначе сбрасываем.

Ответ: 120

Задача (Обращаемся к соседу, ещё сложнее)

Текстовый файл состоит не более чем из 10⁶ символов арабских цифр (0, 1, …,9). Определите максимальное количество идущих подряд нечётных цифр, расположенных в неубывающем порядке. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_3.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]<=s[i+1] and s[i] in '13579' and s[i+1] in '13579' :
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax) 

Здесь опять можно применить знаки сравнения прям к символам. Удобно проверить принадлежность к нечётным цифрам конструкцией s[i] in ‘13579’. Нечётной цифрой должна быть как текущая, так и следующая.

Ответ: 8

Решим ещё одну тренировочную задачу из ЕГЭ по информатике 2023.

Задача (Обращаемся к соседу, ещё сложнее, закрепление)

Текстовый файл состоит не более чем из 10⁶ символов 1, 2, 3, A, B, С. Определите максимальное количество идущих подряд символов, среди которых никакие две буквы и никакие две цифры не стоят рядом. Для выполнения этого задания следует написать программу.

Решение:

f=open('24_4.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if (s[i] in '123' and s[i+1] in 'ABC') or (s[i] in 'ABC' and s[i+1] in '123') :
        k=k+1
        kmax=max(k, kmax)
    else:
        k=1

print(kmax) 

В этой задаче цифры и буквы должны чередоваться. Если у нас цифра, то следующая должны быть буква, или наоборот, если у нас буква, то следующая должна быть цифра. В этих двух случаях прибавляем к счётчику 1.

Ответ: 20

Задача (Исключаем строку из 2-х символов, демо 2022)

Текстовый файл состоит из символов P, Q, R и S.

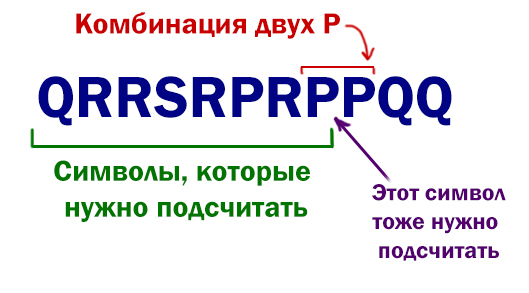
Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет идущих подряд символов P.
Для выполнения этого задания следует написать программу.

Решение:

Напишем решение на языке Python.

f=open('24_5.txt')
s=f.read()
k=1
kmax=0

for i in range(0, len(s)-1):
    if s[i]=='P' and s[i+1]=='P':
        k=1
    else:
        k=k+1
        kmax = max(k, kmax)

print(kmax)

Подсчитываем символы, пока не встретилась комбинация двух P подряд. Как только встретилась данная комбинация, сбрасываем счётчик на 1. Здесь мы сбрасываем счётчик на значение 1, чтобы учесть один символ, которые находится в самой комбинации PP. И в начале мы тоже устанавливаем счётчик в значение 1 по этой же причине.

Мы проходим в цикле for до длины строки минус один. Значение 1 в счётчике при сбросе и в начале программы так же компенсирует и тот момент, что мы не подсчитываем последний символ!

При изменении счётчика, сохраняем максимальное значение в переменной mx

Если бы у нас была вместо PP другая комбинация, состоящая к примеру из 5 символов, то мы бы тогда в начале и при сбросе писали в счётчик значение 5-1=4.

Здесь тоже работает негласное правило, обращаемся к соседу, значит, счётчик устанавливаем в 1.

В этой задаче получается ответ 188.

Ответ: 188

Задача (Исключаем подстроку из 3-х символов)

Текстовый файл состоит из символов арабских цифр(0, 1, …,9).

Определите максимальное количество идущих подряд символов
в прилагаемом файле, среди которых нет трёх символов 0, стоящих рядом.
Для выполнения этого задания следует написать программу.

Решение:

Напишем решение на языке Python.

f=open('24_6.txt')
s=f.read()
k=2
kmax=0

for i in range(0, len(s)-2):
    if s[i]=='0' and s[i+1]=='0' and s[i+2]=='0':
        k=2
    else:
        k=k+1
        kmax = max(k, kmax)

print(kmax)

Чтобы понять это решение, нужно посмотреть предыдущую задачу. Мы здесь обращаемся к двум соседям, значит, счётчик устанавливаем в 2. Так же проходим в цикле до len(s)-2. Нежелательная строка может состоять не только из одинаковых символов. Может быть строка «XYYZ», к примеру.

Ответ: 7684

Задача (Не более одного символа Z)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более одного раза.

Решение:

В нашей цепочке один раз можно встретиь символ Z, а два раза уже нельзя. Здесь мы применим функцию .split(). Как работает эта фнкция? Напишем тестовую программу.

s='sadqttqtreq'
a=s.split('q')
print(a)

Результат данной программы будет следующим:

[‘sad’, ‘tt’, ‘tre’, »]

Команда split «разрезает» строку по символу «q». В результате мы получаем массив с кусочками этой строки.

Решение нашей задачи.

f=open('24_7.txt')
s=f.read()
a=s.split('Z')
k=0
kmax=0

for i in range(0, len(a)-1):
  k = len(a[i]) + 1 + len(a[i+1])
  kmax = max(k, kmax)

print(kmax)

Разрезаем нашу строку по символу «Z». Пробегаемся уже по массиву a. Цепочка-кандидат это текущий кусочек (a[i]), символ Z (1) и следующий кусочек (a[i+1]).

Каждого кандитата проверяем сразу на максимальность.

Ответ: 43

Задача (Не более двух символов Z)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых символ Z встречается не более двух раз.

Решение:

Решение аналогично предыдущему.

f=open('24_7.txt')
s=f.read()
a=s.split('Z')
k=0
kmax=0

for i in range(0, len(a)-2):
  k = len(a[i]) + 1 + len(a[i+1]) + 1 + len(a[i+2])
  kmax = max(k, kmax)

print(kmax)

Ответ: 50

Задача (Звенья)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки символов, состоящей из повторяющихся фрагментов XYZ. Цепочка должна начинаться с символа X и заканчиваться символом Z. Например, для строки ZZZXYZXYZXZZZ длина цепочки равна 6: XYZ+XYZ

Решение:

Если мы подсчитаем количество идущих подряд звеньев XYZ, то, можно сказать, дело сделано.

f=open('24_8.txt')
s=f.read()
s=s.replace('XYZ', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax*3)

Мы с помощью команды replace заменили звенья на «1» (на символ, которого точно нет в файле). Теперь задача свелась к самой простой, которую мы рассматривали в начале статьи. Нужно просто подсчитать количество идущих поряд единиц.

В ответе нас просили указать количество символов, а не звеньев, поэтому переменную kmax умножаем на 3.

Ответ: 66

Задача (Звенья, закрепление)

Текстовый файл состоит не более, чем из 10⁶ символов из набора A, B, С. Найдите максимальное количество идущих пар символов AC или AB. Искомая подстрока может включать только пары AB, только пары AC или содержать одновременно как пары AC, так и пары AB.

Решение:

f=open('24_9.txt')
s=f.read()
s=s.replace('AB', '1')
s=s.replace('AC', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Здесь нам подходит звено, как и AB, так и AC. В ответе нужно указать количество пар, поэтому не на что умножать переменную kmax не нужно.

Ответ: 19

Задача (Звенья, основная волна 20.06.22)

Текстовый файл состоит из символов A, B, C, D и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполенения этого задания следует написать программу.

Решение:

f=open('24_10.txt')
s=f.read()
s=s.replace('BA', '1')
s=s.replace('CA', '1')
s=s.replace('DA', '1')
s=s.replace('BO', '1')
s=s.replace('CO', '1')
s=s.replace('DO', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Ответ: 174

Задача (Звенья, последнее звено неполное)

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки вида XYZXYZXYZ… (составленной из фрагментов XYZ, последний фрагмент может быть неполным). Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Решение:

Т.к. последнее звено может быть неполным, здесь удобно применить другой алгоритм.

Пусть в начале показания счётчика равно нулю. Если мы находим нужный нам символ в нужной последовательности, то прибавляем к счётчику 1. Если последовательность сбивается, то ставим счётчик в ноль.

На рисунке представлен данный алгоритм. В нижней строке указано показание счётчика в момент анализа символа.

На данном рисунке максимальная длина цепочки нужных символов равна 9.

Видим, что для символа X, когда он находится на своём месте, остаток от деления значения счётчика на 3 равен 0.

Для символа Y, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 1.

Для символа Z, когда данный символ находится на своём месте, остаток от деления значения счётчика на 3 равен 2.

Мы смотрим остаток от деления на 3, потому что у нас длина звена равна трём (XYZ).

Таким образом, мы и наш анализ очередного символа привяжем к показанию счётчика:

f=open('24_11.txt')
s=f.read()
k=0
kmax=0

for i in range(0, len(s)):
    if (s[i]=='X' and k%3==0) or  (s[i]=='Y' and k%3==1) or (s[i]=='Z' and k%3==2):
        k=k+1
        kmax = max(k, kmax)
    else:
        if s[i]=='X': k=1
        else: k=0


print(kmax)

Важный момент: Если нужную цепочку прервал символ X, то нужно счётчик сразу выставить в 1, иначе может произойти такая ошибка:

Т.е. первые три нужных символа в цепочке алгоритм не засчитал.

Поэтому мы не просто сбрасываем счётчик в ноль, а прописываем условие:

if s[i]=='X': k=1
else: k=0

Ответ: 13

Задача (Полезный приём)

Текстовый файл 24-157.txt состоит не более чем из 10⁶ символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле между двумя одинаковыми символами. Например, в тексте CCBAABABCBC есть комбинации ABA, BAB, BCB и CBC. Чаще всего – 2 раза – между двумя одинаковыми символами стоит B, в ответе для этого случая надо написать B2 (без пробелов и других разделителей). Если таких символов несколько, выведите тот, который стоит раньше в алфавите.

Решение:

f=open('24-157.txt')
s=f.read()
a=[0]*150

for i in range(0, len(s)-2):
    if s[i]==s[i+2]:
        a[ord(s[i+1])] = a[ord(s[i+1])] + 1

ch=''
mx=0
for i in range(0, 150):
    if a[i]>mx:
        mx=a[i]
        ch=chr(i)


print(ch, mx)

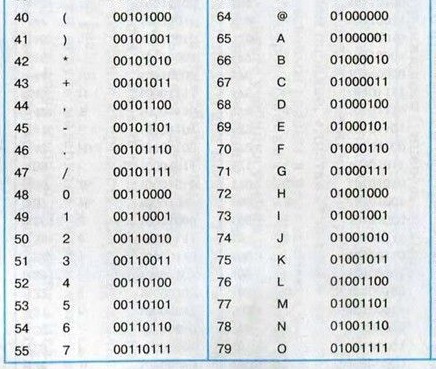
Здесь мы заводим массив a. Индексы этого массива — это коды ANSI всех букв латинского алфавита (ABC…Z). Ведь, как мы знаем, каждая буква кодируется определённым числом (кодом ANSI). Вот часть этой таблицы.

Например, буква A кодируется кодом 65. Коды увеличиваются в алфавитном порядке на 1. Буква Z кодируется числом 90. Таким образом, 150 ячеек точно хватит для нашего алфавита. Здесь берём с запасом, потому что на экзамене можно точно не вспомнить коды, но достаточно запомнить, что 150 ячеек вполне хватит для заглавных и строчных букв латинского алфавита.

Значит, ячейка 65 отвечает за букву A, ячейка 66 отвечает за букву B и т.д. Если мы встретили букву между двумя одинаковыми буквами, то её ячейка увеличивается на 1.

Функция ord() превращает символ в код ANSI.

После того, как мы прошли всю строку и собрали информацию о наших буквах, нужно пройти массив a и найти наибольшее число в нём.

Здесь мы уже не пользуемся функцией max, а используем условие, потому что нужно кроме максимального числа тянуть ещё один параметр — сам код (переменную i). Функция chr() превращает код ANSI обратно в символ.

Ответ: W1608

Задача (Строки различной длины)

Текстовый файл 24-164.txt состоит не более чем из 10⁶ символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Текст разбит на строки различной длины. Необходимо найти строку, содержащую самую длинную цепочку стоящих подряд одинаковых букв. Если таких строк несколько, надо взять ту, которая в файле встретилась раньше. Определите, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая стоит раньше в алфавите. Запишите в ответе эту букву, а затем – сколько раз она встречается во всем файле.

Пример. Исходный файл:

ZZQABA
ZALAAC
QRAQUT

В этом примере в первой и второй строках наибольшая длина цепочек одинаковых буквы равна 2 (ZZ в первой строке, AA во второй), в третьей – 1. Берём первую строку, т.к. она находится в файле раньше. В этой строке чаще других встречаются буквы Z и A (по 2 раза), выбираем букву A, т. к. она стоит раньше в алфавите. В ответе для этого примера надо записать A6, так как во всех строках файла буква A встречается 6 раз.

Решение:

Для считывания построчно файла, будем использовать конструкцию, как в задании 17. В начале найдём строчку, содержащую самую длинную цепочку стоящих подряд одинаковых букв.

f=open('24-164.txt')
kmax=0
count=0
n=-1
for s in f.readlines():
    count=count+1
    k=1
    for i in range(0, len(s)-1):
       if s[i]==s[i+1]:
           k=k+1
           if k>kmax:
               kmax=k
               n=count
       else:
           k=1

print(n)

Получается строка под номером 162. Переменная count считает строки по порядку. В переменную n сохраняем номер нужной строки. Опять пользуемся условием, а не функцией max, т.к. здесь нужно и обновлять kmax, и сохранять значение n. У нас условие строгое k>kmax, значит, сохранится первая строка с наибольшей искомой цепочкой.

f=open('24-164.txt')

count=0
a=[0]*150

for s in f.readlines():
    count=count+1
    k=1
    if count==162:
        for i in range(0, len(s)):
            a[ord(s[i])] = a[ord(s[i])] + 1
       
ch=''
mx=0
for i in range(0, 150):
    if a[i] > mx:
        mx=a[i]
        ch=chr(i)

print(ch)

Теперь нас интересует только строка под номером 162. Далее используем приём из прошлой задачи. Заводим массив a из 150 ячеек и используем таблицу кодов ANSI. Так определяем какая буква встретилась чаще всего в строке под номером 162. Получается буква K.

f=open('24-164.txt')
s=f.read()
print(s.count('K'))

Осталось найти количестов букв K во всём файле. Для этого используем функцию .count()

Ответ: K36582