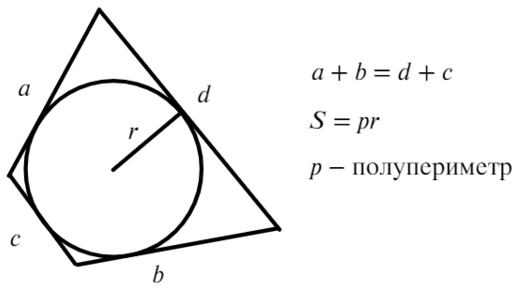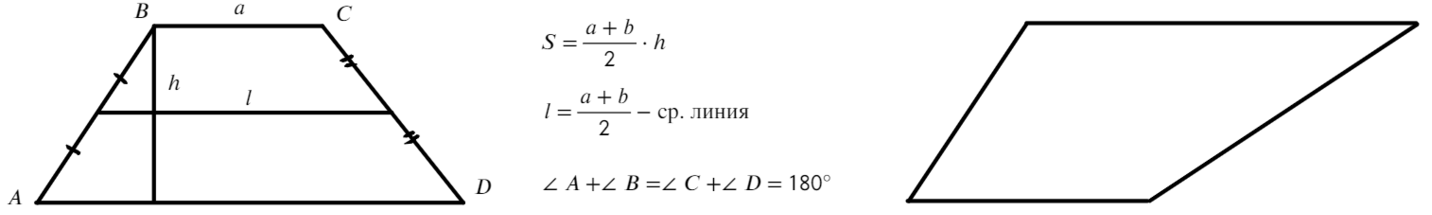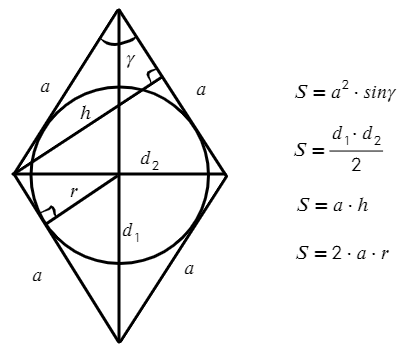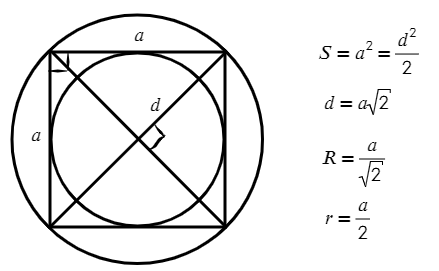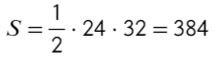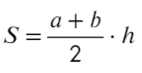Четырехугольники
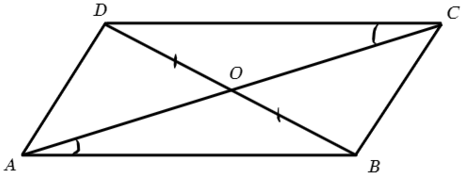
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.
$АВ││CD;BC││AD.$
Свойства параллелограмма:
1. В параллелограмме противоположные стороны и углы попарно равны.
$АВ=CD;BC=AD$
$∠А=∠С; ∠В=∠D$.
2. Диагональ делит параллелограмм на два равных треугольника.
$∆ABD=∆BCD.$
3. Диагонали точкой пересечения делятся пополам.
$BO=OD; AO=OC.$
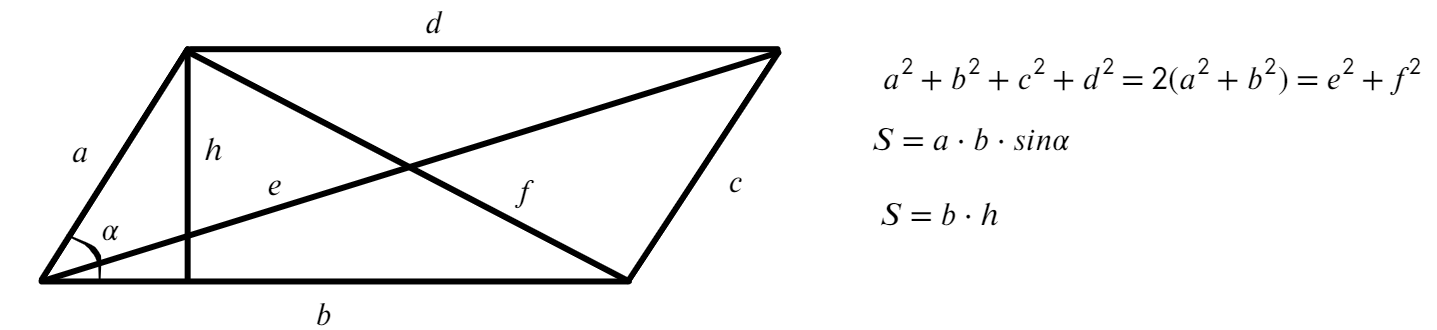
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
$BD^2+AC^2=2(AB^2+AD^2)$
5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
$∆АВК$ — равнобедренный.
6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
Площадь параллелограмма:
- Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними. $S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
- Площадь параллелограмма равна произведению основания на высоту. $S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.
Пример:
Определите синус острого угла параллелограмма, если его большая высота равна $7$, а стороны $10$ и $14$.
Решение:
Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
$S=a·b·sinα$, из этой формулы можем выразить синус угла.
$sinα={S}/{a·b}$
Стороны параллелограмма нам известны, осталось вычислить площадь. Площадь параллелограмма можно вычислить как произведение высоты на основание. Нам известна большая высота параллелограмма, а большая высота опускается к меньшей стороне параллелограмма, следовательно, $S=7·10=70$.
Подставим все известные данные в формулу синуса:
$sinα={S}/{a·b}={70}/{14·10}=0.5$
Ответ: $0.5$
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
- Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтму у него присутствуют все свойства параллелограмма).
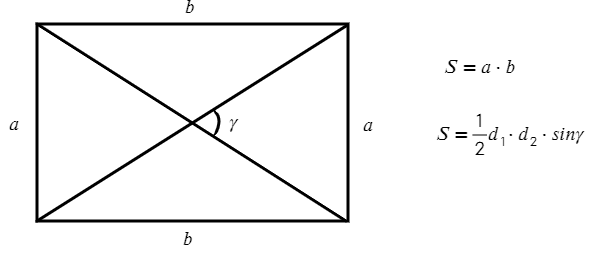
- Диагонали прямоугольника равны. $BD=AC$.
Площадь прямоугольника равна половине произведения смежных (соседних) сторон.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб — это параллелограмм, у которого все стороны равны.
Свойства ромба:
- Все свойства параллелограмма.
- Диагонали ромба пересекаются под прямым углом. $BD⊥AC$.
- Диагонали ромба являются биссектрисами углов.
Площадь ромба:
- Площадь ромба равна половине произведения его диагоналей. $S={d_1·d_2}/2$, где $d_1$ и $d_2$ — диагонали ромба
- Площадь ромба равна произведению квадрата стороны на синус острого угла ромба. $S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все свойства прямоугольника.
- Все свойства ромба.
Площадь квадрата:
- $S=a^2$, где $а$ — сторона квадрата.
- $S={d^2}/{2}$, где $d$ — диагональ квадрата.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет.
Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания.
Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Свойства средней линии трапеции:
1. Средняя линия параллельна основаниям трапеции.
$MN││BC; MN││AD.$
2. Средняя линия равна полусумме оснований.
$MN={BC+AD}/{2}$
3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников.
$МК$ — средняя линия треугольника $ABD; MK={AD}/{2}$.
$KN$ — средняя линия треугольника $BCD; KN={BC}/{2}$.
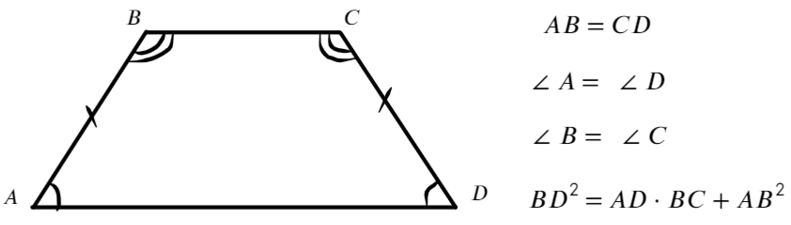
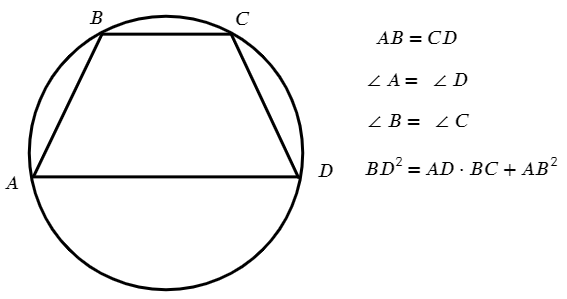
Трапеция, у которой боковые стороны равны, называется равнобедренной.
Свойства равнобедренной трапеции:
1. Углы при основаниях равны.
$∠А=∠D; ∠B=∠C.$
2. Диагонали в равнобедренной трапеции равны.
$BD=AC.$
3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований.
$АС_1={BC+AD}/{2}.$
4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.
$BC=B_1C_1;$
$AB_1=C_1 D={AD-BC}/{2}.$
5. Если трапеция является равнобедренной, то около неё можно описать окружность.
6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции.
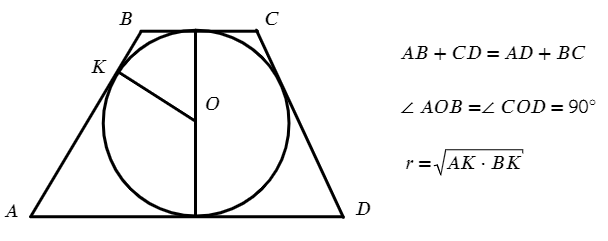
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий
Задания Д5. Планиметрия: вычисление длин и площадей. Четырехугольники
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д5 № 27583
Найдите диагональ квадрата, если его площадь равна 2.
Аналоги к заданию № 27583: 54855 54903 54857 54859 54861 54863 54865 54867 54869 54871 … Все
Решение
·
·
Сообщить об ошибке · Помощь
2
Задания Д5 № 27584
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
Аналоги к заданию № 27584: 26307 54953 54905 54907 54909 54911 54913 54915 54917 54919 … Все
Решение
·
·
Сообщить об ошибке · Помощь
3
Задания Д5 № 27585
Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°.
Аналоги к заданию № 27585: 54955 55003 54957 54959 54961 54963 54965 54967 54969 54971 … Все
Решение
·
·
Сообщить об ошибке · Помощь
4
Задания Д5 № 27586
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°.
Аналоги к заданию № 27586: 55005 55007 55049 55053 55009 55011 55013 55015 55017 55019 … Все
Решение
·
·
Сообщить об ошибке · Помощь
5
Задания Д5 № 27593
Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Аналоги к заданию № 27593: 55355 55403 55357 55359 55361 55363 55365 55367 55369 55371 … Все
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №16. Четырехугольники
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Четырехугольники»
Открытый банк заданий по теме четырехугольники. Задания B3 из ЕГЭ по математике (профильный уровень)
Задание №861
Тип задания: 3
Тема:
Четырехугольники
Условие
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (-2; 1), (-2; 4), (-6; 1), (-6; 4).
Показать решение
Решение
Диагонали прямоугольника равны. Диагональ AC найдём как гипотенузу прямоугольного треугольника ADC с катетами AD=4, CD=3:
AC=sqrt{AD^2+CD^2}=sqrt{4^2+3^2}=5
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №268
Тип задания: 3
Тема:
Четырехугольники
Условие
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (3; 7), (3; 11), (6; 7), (6; 11).
Показать решение
Решение
У точек (3; 7) и (6; 7) одинаковые ординаты, поэтому длина основания прямоугольника равна 6-3=3. Аналогично, высота прямоугольника равна 11-7=4. Значит, диагональ равна sqrt{3^2+4^2}=5.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №264
Тип задания: 3
Тема:
Четырехугольники
Условие
Диагонали AC и BD равнобедренной трапеции ABCD перпендикулярны. Найдите среднюю линию трапеции, если ее высота равна 47.
Показать решение
Решение
Так как трапеция ABCD равнобедренная, то triangle AOB = triangle DOC по стороне и двум прилегающим углам. Тогда triangle AOD равнобедренный. Так как он еще и прямоугольный, то angle ADO = 45^{circ}. Пусть ВН — высота трапеции ABCD. Тогда в прямоугольном triangle BHD углы при гипотенузе BD равны по 45^{circ}. Значит, triangle BHD также равнобедренный, то есть DH=BH=47.
В равнобедренной трапеции DH= BC+AH= BC+frac{AD-BC}{2}= frac{2BC+AD-BC}{2}= frac{BC+AD}{2}. Но DH=47, значит, средняя линия трапеции равна frac{BC+AD}{2}=47.
Ответ
47
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Четырёхугольники и их элементы
1. 
Высота трапеции равна 14. Найдите тангенс острого угла.
2. 
боковая сторона, равная 7, образует с одним из оснований трапеции
угол 150°. Найдите площадь трапеции.
3. В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.
4. 
боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°.
Найдите площадь трапеции.
5. 
Найдите угол ABD. Ответ дайте в градусах.
6. 
Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.
7. 
8. Основания равнобедренной трапеции равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.
9.
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 25. Найдите периметр ромба.
10. В параллелограмме ABCD диагонали являются биссектрисами его углов, AB = 26, AC = 20. Найдите BD.
11. 
12. 

Основные формулы и свойства трапеции.
Основные формулы и свойства параллелограмма.
Основные формулы и свойства ромба.
Основные формулы и свойства прямоугольника.
Основные формулы и свойства квадрата.
Примеры и решения задач.
Разберем по сторонам каждый четырехугольник. А начнем с самой негармоничной фигуры — четырехугольника:
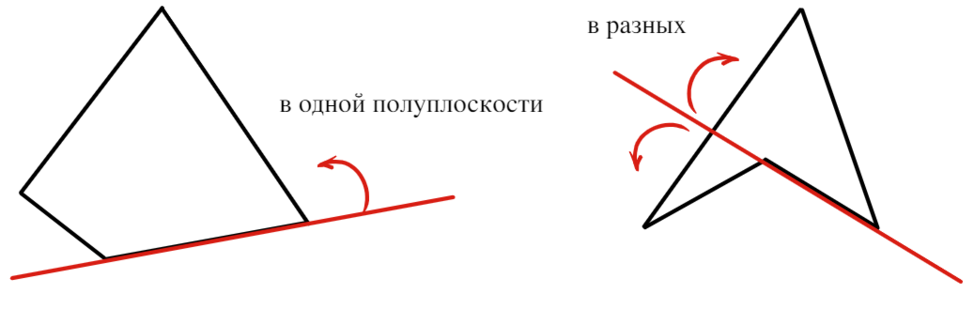
Выпуклым называется четырехугольник, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
В ЕГЭ встречается только выпуклый, поэтому его брата оставим без внимания.
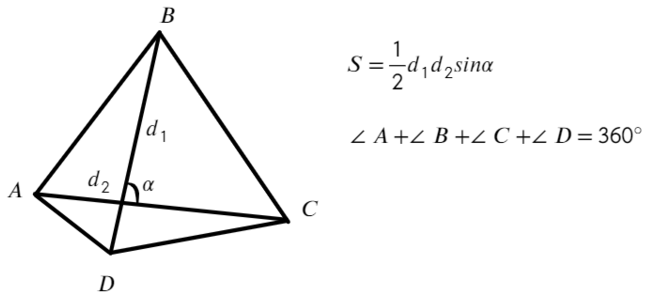
Если четырехугольник произвольный:
Если в четырехугольник можно вписать окружность, то помимо выше описанных свойств добавляются эти:
Если вокруг четырехугольника можно описать окружность, то добавляются такие свойства:
Две теоремы Птолемея можно встретить в №16 ЕГЭ, планиметрии повышенного уровня сложности.
Если поставить условие, что две противоположные стороны должны быть параллельны, то четырехугольник становится трапецией.
Всем привычна такая трапеция, но та, что справа, также существует!
В равнобедренной трапеции:
Прямоугольная трапеция:
В трапецию можно вписать окружность, когда? Когда сумма противоположных сторон одинакова!
Да точно также, как и в четырехугольник, все свойства четырехугольника работают и в трапеции!
— И площадь через диагонали?
— Конечно!
А описать окружность вокруг трапеции? Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая!
Свойства остаются те же.
Следующий на очереди параллелограмм:
Если сказать, что в трапеции две попарно противоположные стороны параллельны, то трапеция станет параллелограммом.
Если сказать, что в трапеции две противоположные стороны параллельны и равны, то трапеция станет параллелограммом.
Еще добавляются 2 формулы площади:
Свойства параллелограмма:
- Если у четырёхугольника противолежащие стороны попарно равны, то это параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то это параллелограмм.
- Четырёхугольник, диагонали которого в точке пересечения делятся пополам, – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то это параллелограмм.
Дальше, чтобы из параллелограмма получить следующую фигуру, есть два пути:
1) Если у параллелограмма один угол 90°, то это прямоугольник.
2) Если у параллелограмма две прилежащие стороны равны, то это ромб.
Ромб — параллелограмм, у которого все стороны равны:
Свойства ромба:
- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
- Диагонали делят ромб на четыре равных прямоугольных треугольника.
- В ромб можно всегда вписать окружность.
Прямоугольник — параллелограмм, у которого все углы прямые:
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Вокруг прямоугольника всегда можно описать окружность.
Правильный четырехугольник — квадрат. Папа был прямоугольником, а мама ромбом. Квадрат объединяет свойства и формулы этих фигур и добавляет свои:
Свойства квадрата:
- Все углы квадрата прямые, все стороны квадрата равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делят его углы пополам.
- В квадрат можно всегда вписать окружность.
- Вокруг квадрата можно всегда описать окружность.
Задача №1 Докажите, что ABCD параллелограмм, если известно, что ∠CAD = ∠CAB и DO = OB.
Что нужно, чтобы сказать, что четырехугольник является параллелограммом?
- Две противоположные стороны параллельны и равны.
- Две попарно противоположные стороны параллельны.
Скажем, что DC II AB, т.к. ∠CAD = ∠CAB — накрест лежащие углы. Если не знаешь, что такое накрест лежащие углы — читай!
Но раз DC II AB, то и ∠CDB = ∠DBA (как накрест лежащие), а ∠AOB и ∠DOC — рыжие что ли? Нет, они вертикальные, значит, тоже равны: ∠AOB = ∠DOC.
Тогда ΔAOB = ΔDOC (по стороне и двум прилежащим углам) => DC = AB.
Получается, что DC = AB и DC II AB, свойство №1 доказано.
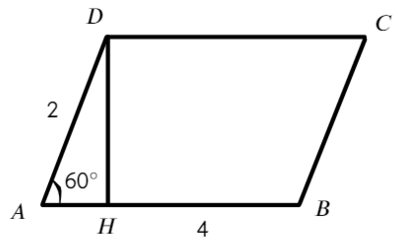
Задача №2 Найдите периметр параллелограмма.
Вспомним, что в прямоугольном треугольнике находится против угла в 30°. Да-да, катет в два раза меньший гипотенузы. Следовательно AB = AH + HB = 1+4 = 5.
Тогда периметр:
Ответ: 14.
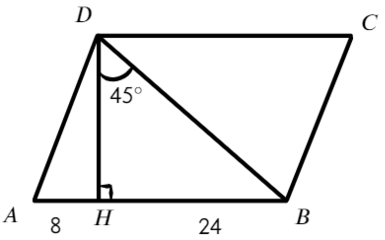
Задача №3 Найдите площадь параллелограмма.
В ΔDHB ∠DBH = 180 – 90° – 45° = 45°=> ΔDHB — равнобедренный => DH = HB = 24
Ответ: 384
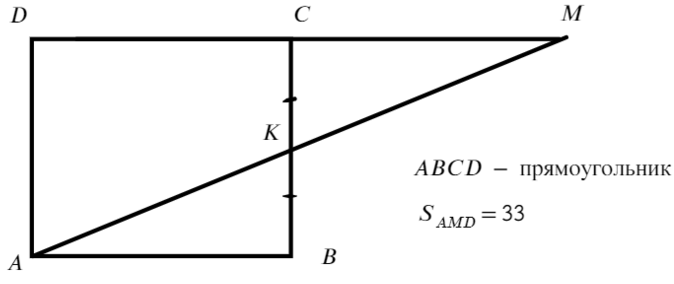
Задача №4 Найдите площадь ABCD.
ABCD — прямоугольник. Чтобы найти его площадь, нужно знать две стороны, но мы знаем только площадь треугольника.
Площадь AKCD общая у ABCD и ADM, а вот отличаются они площадью ΔABK и ΔKCM, но мы только что доказали, что они равны, значит, площади ABCD и ADM тоже равны!
Ответ: 33
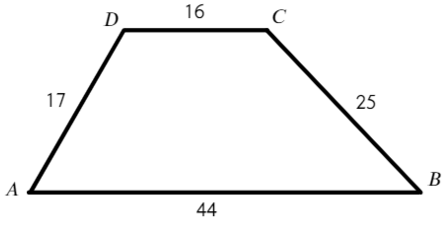
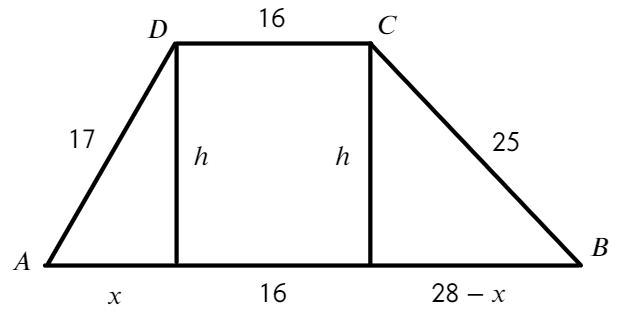
Задача №5 Найдите площадь трапеции, параллельные стороны которой равны 15 и 44, а непараллельные 17 и 25.
Площадь трапеции можно найти так:
Не хватает высоты, попробуем разбить трапецию на треугольники и прямоугольник:
Запишем теорему Пифагора для двух треугольников:
Решим уравнение:
Зная, как разделится основание найдем высоту:
Если нашел опечатку, или что-то непонятно − напиши.
Первая и вторая часть по треугольникам.
Статья по окружностям.