1.
Математика
ЕГЭ
Четырехугольники
2.
Введение
Четырехугольники
©2021 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
3.
Введение
Четырехугольники
©2021 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
4.
Введение
Четырехугольники
©2021 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
5.
Введение
Четырехугольники
Произвольный четырехугольник
Сумма углов = 360°
1
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Содержание
-
1.
Четырехугольники в ЕГЭ по математике задача № 16 -
2.
Четырехугольники в ЕГЭ по математике задача № 16 -
3.
Ключевая задача -
4.
Слайд 4 -
5.
Ключевая задача На сторонах ВС и АD -
6.
На сторонах ВС и АD параллелограмма -
7.
Задача профильного уровня -
8.
Слайд 8 -
9.
Слайд 9 -
10.
Ключевая задача -
11.
Слайд 11 -
12.
Ключевая задача -
13.
Слайд 13 -
14.
Задача профильного уровняВ выпуклом четырехугольнике АВСD АВ -
15.
В выпуклом четырехугольнике АВСD АВ = -
16.
В выпуклом четырехугольнике АВСD АВ = 9, -
17.
Ключевая задача Окружность с центром в точке -
18.
Окружность с центром в точке О -
19.
Ключевая задача -
20.
ab -
21.
Ключевая задача Окружность касается всех сторон равнобедренной -
22.
Окружность касается всех сторон равнобедренной трапеции. -
23.
Задача профильного уровня -
24.
Слайд 24 -
25.
Слайд 25 -
26.
Ключевая задача Прямая, параллельная стороне ВС треугольника -
27.
Прямая, параллельная стороне ВС треугольника АВС, пересекает -
28.
Задача профильного уровняПрямая параллельная основаниям ВС и -
29.
Прямая параллельная основаниям ВС и АD -
30.
Прямая параллельная основаниям ВС и АD -
31.
Спасибо за внимание! Удачи на ЕГЭ. -
32.
Скачать презентанцию
Четырехугольники в ЕГЭ по математике задача № 16
Слайды и текст этой презентации
Слайд 1Задачи планиметрии
Профильный уровень
Учитель математики
МАОУ «Обдорская гимназия»
г. Салехард
ЯНАО
Е.И. Гусак

Слайд 2Четырехугольники
в ЕГЭ по математике
задача № 16

Слайд 5Ключевая задача
На сторонах ВС и АD параллелограмма отмечены
точки К и М соответственно так, что КС = АМ.
Прямая КМ пересекает АС в точке О. Доказать равенство треугольников АОМ и СОК.

Слайд 6
На сторонах ВС и АD параллелограмма отмечены точки К
и М соответственно так, что КС = АМ.
Прямая КМ
пересекает АС в точке О. Доказать равенство треугольников АОМ и СОК.
Слайд 14Задача профильного уровня
В выпуклом четырехугольнике АВСD АВ = 9,
ВС = СD =11, АD = 15, АС
= 16.
a)Доказать, что около него можно описать окружность.
б) Найти диагональ ВD.

Слайд 15
В выпуклом четырехугольнике АВСD АВ = 9, ВС =
СD =11, АD = 15, АС = 16. a)Доказать, что
около него можно описать окружность. б) Найти диагональ ВD.

Слайд 16В выпуклом четырехугольнике АВСD АВ = 9, ВС =
СD =11, АD = 15, АС = 16. a)Доказать, что
около него можно описать окружность. б) Найти диагональ ВD.

Слайд 17Ключевая задача
Окружность с центром в точке О писана
в угол АВС. Докажите, что ВО – биссектриса данного угла.

Слайд 18
Окружность с центром в точке О писана в угол
АВС. Докажите, что ВО – биссектриса данного угла.

Слайд 21Ключевая задача
Окружность касается всех сторон равнобедренной трапеции. Докажите,
что боковая сторона трапеции равна средней линии трапеции.

Слайд 22
Окружность касается всех сторон равнобедренной трапеции. Докажите, что боковая
сторона трапеции равна средней линии трапеции.

Слайд 26Ключевая задача
Прямая, параллельная стороне ВС треугольника АВС, пересекает
стороны АС и АВ соответственно в точках М и К.
Найдите длину отрезка МК, если АК = 12, ВК = 14, ВС = 21.

Слайд 27Прямая, параллельная стороне ВС треугольника АВС, пересекает стороны АС
и АВ соответственно в точках М и К. Найдите длину
отрезка МК, если АК = 12, ВК = 14, ВС = 21.
12
14
21
?
Слайд 28Задача профильного уровня
Прямая параллельная основаниям ВС и АD трапеции
АВСD, пересекает боковые стороны АВ и СD в точках М
и N. Диагонали трапеции пересекаются в точке О. Прямая МN пересекает отрезки ОА и ОD в точках К и L.
a) Доказать, что МК = NL.
б) Найти МN, если ВС = 3, АD = 8, МК:КL = 1:3.

Слайд 29
Прямая параллельная основаниям ВС и АD трапеции АВСD, пересекает
боковые стороны АВ и СD в точках М и N.
Диагонали трапеции пересекаются в точке О. Прямая МN пересекает отрезки ОА и ОD в точках К и L.
a) Доказать, что МК = NL.
б) Найти МN, если ВС = 3, АD = 8, МК:КL = 1:3.
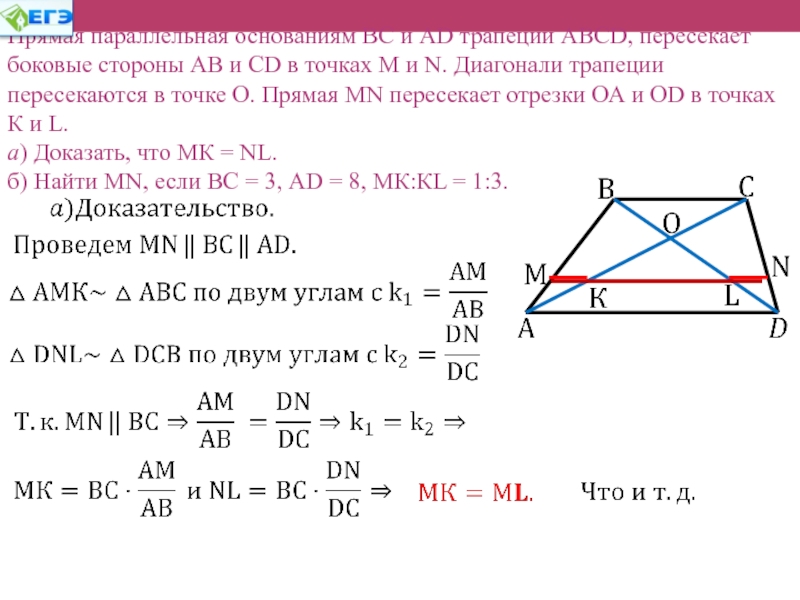
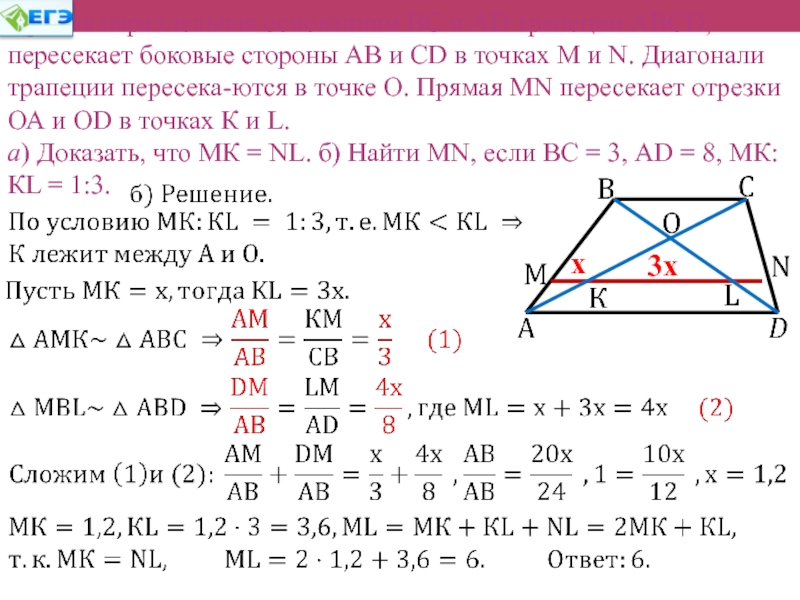
Слайд 30
Прямая параллельная основаниям ВС и АD трапеции АВСD, пересекает
боковые стороны АВ и СD в точках М и N.
Диагонали трапеции пересека-ются в точке О. Прямая МN пересекает отрезки ОА и ОD в точках К и L.
a) Доказать, что МК = NL. б) Найти МN, если ВС = 3, АD = 8, МК:КL = 1:3.
х
3х
Слайд 31Спасибо за внимание!
Удачи на ЕГЭ.

Четырехугольники
Обобщающее повторение.
Геометрия, 8 класс
Подготовила учитель математики МБОУ школы №1 г.Кулебаки Нижегородской области Мочалина Е.Л.
Содержание
- Эпиграф
- Классификация
- Параллелограмм
- Прямоугольник
- Ромб
- Квадрат
- Трапеция
- Историческая справка
Сравнение математических фигур и величин служит материалом для игр и обучения мудрости.
И. Песталоцци
КЛАССИФИКАЦИЯ
Различные четырехугольники
Трапеция
Параллелограмм
ПАРАЛЛЕЛОГРАММ
Определение
Свойства
Четырехугольник, у которого противоположные стороны попарно параллельны
1.Противоположные стороны и углы соответственно равны.
2.Диагонали точкой пересечения делятся пополам.
Признаки
Формула
площади
1.Если в четырехугольнике две стороны равны и параллельны.
2.Если в четырехугольнике противоположные стороны попарно равны.
3.Если в четырехугольнике диагонали пересекаются и делятся точкой пересечения пополам.
S=ah,
a- основание
h- высота
ПРЯМОУГОЛЬНИК
Определение
Свойства
Параллелограмм , у которого все углы прямые.
1.Свойства параллелограмма.
2.Диагонали равны.
Признаки
Формула
площади
Если в параллелограмме диагонали равны.
S=ab,
a- ширина,
b- длина.
Ромб
Определение
Свойства
Параллелограмм, у которого все стороны равны
1.Свойства параллелограмма.
2. Диагонали взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы пополам.
Признаки
Формула
площади
Если в параллелограмме диагонали взаимно перпендикулярны и делят его углы пополам.
1. S=ah ,
a- оснсвание
h- высота
2. S=
d 1 , d 2 — диагонали
d 1 *d 2
2
Квадрат
Определение
Свойства
1.Ромб с прямыми углами.
2.Прямоугольник, у которого все стороны равны.
1.Все углы равны.
2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы пополам.
Признаки
Формула
площади
1.Если в ромбе диагонали равны.
2.Если в прямоугольнике диагонали взаимно перпендикулярны.
1 . S=a 2 ,
a- сторона
2. S=
d- диагональ
d 2
2
Трапеци я
Определение
Свойства
Четырехугольник, у которого две стороны параллельны, а две другие нет.
1.Если трапеция равнобедренная, то диагонали и углы при основании равны.
2.Если трапеция прямоугольная, то одна из боковых сторон перпендикулярна основаниям.
Признаки
Формула
площади
Если в четырехугольнике две стороны параллельны.
S=
a,b- основание
h- высота
2. S=mh
m- средняя линия
h- высота
( a+b)h
2
С геометрическими фигурами имели дело с древних времен и крестьяне, и ремесленники, и строители храмов, дворцов и пирамид.
Надо было уметь измерять площади земельных участков, определять, сколько камня потребуется для здания.
Особенно быстро знания о свойствах фигур развивались в Древнем Египте.
Около 4 тыс. лет назад возникла наука об измерении расстояний, площадей и объемов, о свойствах различных фигур — геометрия .
Задачи планиметрии
Профильный уровень
Учитель математики
МАОУ «Обдорская гимназия»
г. Салехард ЯНАО
Е.И. Гусак
Четырехугольники
в ЕГЭ по математике
задача № 16
Ключевая задача
На сторонах АВ, ВС, СD, АD параллелограмма АВСD отмечены точки К, L, M, N соответственно. Причем . Доказать равенство треугольников АКN и СМL, ВКL и DML.
На сторонах АВ, ВС, СD, АD параллелограмма АВСD отмечены точки К, L, M, N соответственно. Причем . Доказать равенство треугольников АКN и СМL, ВКL и DML.
Ключевая задача
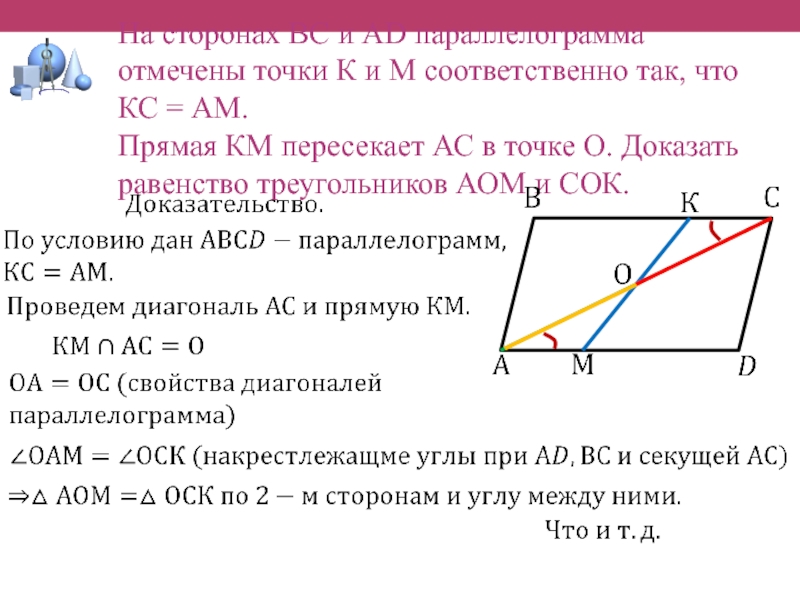
На сторонах ВС и АD параллелограмма отмечены точки К и М соответственно так, что КС = АМ. Прямая КМ пересекает АС в точке О. Доказать равенство треугольников АОМ и СОК.
На сторонах ВС и АD параллелограмма отмечены точки К и М соответственно так, что КС = АМ.
Прямая КМ пересекает АС в точке О. Доказать равенство треугольников АОМ и СОК.
Задача профильного уровня
- На сторонах АВ, ВС, СD, АD параллелограмма АВСD отмечены точки К, L, М, N соответственно. Причем . a)Доказать, КLMN-параллелограмм и его центр совпадает с центром параллелограмма АВСD. б) Найти отношение площадей параллелограммов КLMN и АВСD.
На сторонах АВ, ВС, СD, АD параллелограмма АВСD отмечены точки К, L, М, N соответственно. Причем . a) Доказать, КLMN-параллелограмм и его центр совпадает с центром параллелограмма АВСD. б) Найти отношение площадей параллелограммов КLMN и АВСD.
На сторонах АВ, ВС, СD, АD параллелограмма АВСD отмечены точки К, L, М, N соответственно. Причем . a) Доказать, КLMN-параллелограмм и его центр совпадает с центром параллелограмма АВСD. б) Найти отношение площадей параллелограммов КLMN и АВСD.
⇒
Ключевая задача
Найти если
Найти если
Ключевая задача
Найти диагональ АС четырехугольника АВСD, если АВ = 3, ВС = 1, СD = 3, АD = 2 и сумма углов В и D равна .
Найти диагональ АС четырехугольника АВСD, если АВ = 3, ВС = 1, СD = 3, АD = 2 и сумма углов В и D равна .
Задача профильного уровня
- В выпуклом четырехугольнике АВСD АВ = 9,
ВС = СD =11, АD = 15, АС = 16.
a)Доказать, что около него можно описать окружность.
б) Найти диагональ ВD.
В выпуклом четырехугольнике АВСD АВ = 9, ВС = СD =11, АD = 15, АС = 16. a)Доказать, что около него можно описать окружность. б) Найти диагональ ВD.
В выпуклом четырехугольнике АВСD АВ = 9, ВС = СD =11, АD = 15, АС = 16. a)Доказать, что около него можно описать окружность. б) Найти диагональ ВD.
Ключевая задача
Окружность с центром в точке О писана в угол АВС. Докажите, что ВО – биссектриса данного угла.
Окружность с центром в точке О писана в угол АВС. Докажите, что ВО – биссектриса данного угла.
Ключевая задача
Из вершины С меньшего основания ВС равнобедренной трапеции АВСD на большее основание АD опущен перпендикуляр CК. Найдите DК и АК, если основания трапеции a и b (a
Из вершины С меньшего основания ВС равнобедренной трапеции АВСD на большее основание АD опущен перпендикуляр CК. Найдите DК и АК, если основания трапеции a и b (a
a
b
Ключевая задача
Окружность касается всех сторон равнобедренной трапеции. Докажите, что боковая сторона трапеции равна средней линии трапеции.
Окружность касается всех сторон равнобедренной трапеции. Докажите, что боковая сторона трапеции равна средней линии трапеции.
Задача профильного уровня
- В равнобедренную трапецию АВСD с основанием АD и ВС вписана окружность, СН-высота трапеции.
a)Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.
б)Найти диагональ АС, если средняя линия трапеции равна
.
В равнобедренную трапецию АВСD с основанием АD и ВС вписана окружность, СН-высота трапеции. a)Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН. б)Найти диагональ АС,
если средняя линия трапеции равна
В равнобедренную трапецию АВСD с основанием АD и ВС вписана окружность, СН-высота трапеции. a)Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН. б)Найти диагональ АС,
если средняя линия трапеции равна
.
Ключевая задача
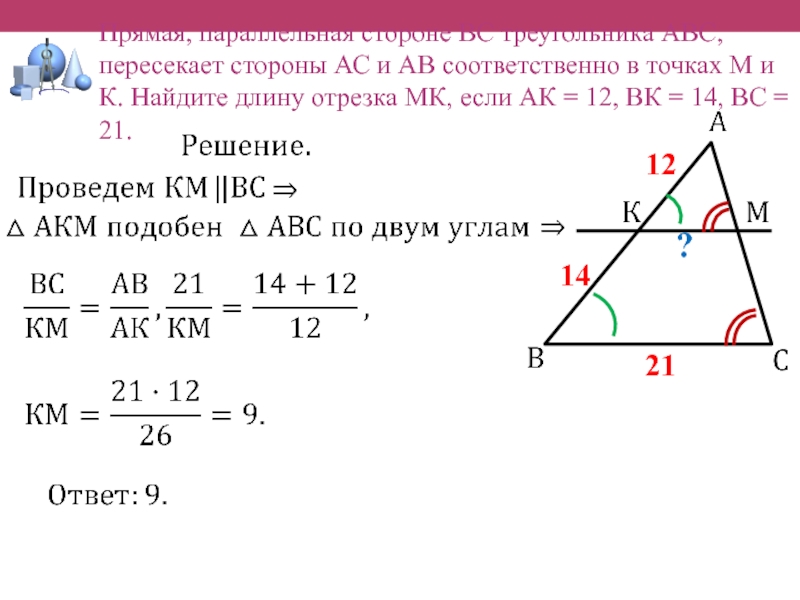
Прямая, параллельная стороне ВС треугольника АВС, пересекает стороны АС и АВ соответственно в точках М и К. Найдите длину отрезка МК, если АК = 12, ВК = 14, ВС = 21.
Прямая, параллельная стороне ВС треугольника АВС, пересекает стороны АС и АВ соответственно в точках М и К. Найдите длину отрезка МК, если АК = 12, ВК = 14, ВС = 21.
12
14
21
?
Задача профильного уровня
- Прямая параллельная основаниям ВС и АD трапеции АВСD, пересекает боковые стороны АВ и СD в точках М и N. Диагонали трапеции пересекаются в точке О. Прямая МN пересекает отрезки ОА и ОD в точках К и L.
a) Доказать, что МК = NL.
б) Найти МN, если ВС = 3, АD = 8, МК:КL = 1:3.
ВС = 3, АD = 8, МК:КL = 1:3.
Прямая параллельная основаниям ВС и АD трапеции АВСD, пересекает боковые стороны АВ и СD в точках М и N. Диагонали трапеции пересекаются в точке О. Прямая МN пересекает отрезки ОА и ОD в точках К и L.
a) Доказать, что МК = NL.
б) Найти МN, если ВС = 3, АD = 8, МК:КL = 1:3.
Прямая параллельная основаниям ВС и АD трапеции АВСD, пересекает боковые стороны АВ и СD в точках М и N. Диагонали трапеции пересека-ются в точке О. Прямая МN пересекает отрезки ОА и ОD в точках К и L.
a) Доказать, что МК = NL. б) Найти МN, если ВС = 3, АD = 8, МК:КL = 1:3.
х
3х
Спасибо за внимание!
Удачи на ЕГЭ.
Слайд 1
Михайлова Нурия Альхамовна , учитель математики Презентация теста по геометрии , часть А (Для повторения темы «Четырехугольники» в 8 классе) МБОУ « Тимершикская средняя общеобразовательная школа Сабинского муниципального района Республики Татарстан»
Слайд 2
А1. Чему равна сумма внутренних углов выпуклого n -угольника? 1) 2) 3) 4)
Слайд 3
А2. Чему равна сумма углов выпуклого шестиугольника? 2) 3) 4)
Слайд 4
А3. Один из углов равнобедренной трапеции равен 1) ; ; 2) ; ; 3) ; ; 4) ; ;
Слайд 5
А4 . В трапеции ABCD основания равны 8 см и 14 см. чему равна ее средняя линия? 1) 22 см 2) 7 см 3) 6 см 4) 11 см
Слайд 6
А5 . В равнобедренной трапеции угол при основании равен , а основания равны 6 см и 10 см. Чему равен периметр трапеции? 1) 28 см 2) 26 см 3) 24 см 4) 20 см
Слайд 7
А6. Диагонали ромба составляют с ее стороной углы, один из которых на Чему равен больший угол ромба? 1) 2) 3) 4)
Слайд 8
А7. В ромбе ABCD угол А равен . Чему равен угол АВС? 1) 2) 3) 4)
Слайд 9
А8 . Четырехугольник является параллелограммом, если у него: 1 ) д иагонали пересекаются и точкой пересечения делятся пополам 2 ) д ве стороны равны, а две другие параллельны 3) д ве пары равных сторон 4) в се стороны параллельны
Слайд 10
А9. Прямоугольником называется: 1) параллелограмм, у которого все стороны равны 2) параллелограмм, у которого диагонали равны 3) параллелограмм, у которого все углы прямые 4) параллелограмм, у которого противолежащие стороны равны
Слайд 11
А10. 1) д иагонали перпендикулярны 2 ) д иагонали равны 3) д иагонали точкой пересечения делятся пополам 4) д иагонали перпендикулярны и точкой пересечения делятся пополам Четырехугольник является ромбом, если у него:
Слайд 12
А11. Квадратом является: 1) параллелограмм, у которого все углы прямые 2) параллелограмм, у которого диагонали равны 3) ромб, у которого все углы прямые 4) прямоугольник, у которого диагонали равны
Слайд 13
А12. Трапеция называется равнобедренной, если у нее: д ве стороны равны Боковые стороны равны д ва угла равны Основания параллельны и равны
Слайд 14
А13. Всякий прямоугольник является: 1) квадратом 2) параллелограммом 3) ромбом 4) трапецией
Слайд 15
А14. Выберите верное утверждение: 1) Если в четырехугольнике две стороны параллельны и равны – то этот четырехугольник — ромб 2) Если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник — прямоугольник 3) Если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник — прямоугольник 4) Если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник — квадрат
Слайд 16
А15. В параллелограмме отношение смежных сторон равно 2, а периметр равен 24 см. Чему равна большая сторона параллелограмма? 1) 6 см 2 ) 12 см 3) 2 α см 4) 8 см
Слайд 17
А16. Прямоугольник, не являющейся квадратом, имеет n осей симметрии. Чему равно значение n ? 1) 1 2) 2 3) 3 4) 4
Слайд 18
А17. Периметр параллелограмма равен 32 см, а две из его сторон относятся как 3 : 1. Чему равна наибольшая из его сторон? 1) 5 см 2) 8 см 3) 12 см 4) 4 см
Слайд 19
А18. Стороны параллелограмма равны 9 и 10. Из одной вершины на две стороны опустили высоты, одна из которых равна 6. Найдите длину другой высоты. 1) 18 2) 3 3) 5,4 4) 6
Слайд 20
А19. Найдите площадь трапеции, изображённой на рисунке. 1) 30 2 ) 38 3) 36 4) 34
Слайд 21
А20. ABCD – прямоугольник. АК – биссектриса ∠ A , СК=2,7 см, К D =4,5 см. Найти периметр ABCD . 1) 9 см 2) 23,4 см 3) 11,7 см 4) 22,4 см
Слайд 22
А21. ABCD – ромб. Найти ∠ CBE 1) 2) 3) 4)
Слайд 23
А22. ABCD – ромб. Найти ∠С. 1) 2) 3) 4)
Слайд 24
А23. В прямоугольной трапеции угол Д равен . Основания ВС = 6 см; АД = 10 Найти: АВ 1 ) 4 2 ) 6 3) 2 4) 10 В А Д H C
Слайд 25
А24. 1) 48 2 ) 56 3) 22 4) 38 Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Слайд 26
Использованная литература Л.С. Атанасян «Геометрия. 7-9 классы» Гаврилова Н.Ф. Поурочные разработки по геометрии, 8 класс Н.Б. Мельникова «Контрольные работы по геометрии» Л.С. Атанасян «Дидактические материалы по геометрии 8 класс » Интернетресурсы .
Слайд 27
Молодцы! Вы выполнили все задания!
Презентацию на тему «Четырехугольники и их виды»
можно скачать абсолютно бесплатно на нашем сайте. Предмет
проекта: Математика. Красочные слайды и иллюстрации помогут вам
заинтересовать своих одноклассников или аудиторию.
Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на
соответствующий текст под плеером. Презентация
содержит 24 слайд(ов).
Слайд 2
Виды четырехугольников
Квадрат Прямоугольник Параллелограмм Трапеция Ромб
Равнобокая трапеция
Прямоугольная трапеция
Слайд 3
Четырехугольник. Его компоненты и свойства.
Каждый четырехугольник имеет 4 вершины, 4 стороны, 2 диагонали. Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, также называются противоположными.
Выпуклые Невыпуклые
Сумма углов выпуклого четырехугольника равна 360 0 .
Слайд 4
Параллелограмм. Определение и его свойства
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
С А В Д
Свойства параллелограмма
Слайд 5
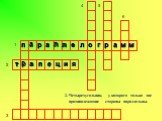
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Основание Боковая сторона
Слайд 6
Прямоугольником называется параллелограмм, у которого все углы прямые
Свойства прямоугольника
Обладает всеми свойствами параллелограмма + особое свойство: диагонали прямоугольника равны
Слайд 7
Ромбом называется параллелограмм, у которого все стороны равны
Свойства ромба:
Обладает всеми свойствами параллелограмма + особое свойство: Диагонали ромба взаимно перпендикулярны и делят его углы пополам
Слайд 8
Квадратом называется прямоугольник, у которого все стороны равны
Обладает всеми свойствами прямоугольника и ромба: 1) Все углы квадрата прямые 2) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам
Слайд 9
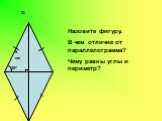
Задачи 1) 500 7 см 5 см
Назовите фигуру В чем отличие от ромба? Найдите периметр и градусные меры всех углов
Слайд 10
2). 6 см 300
Назовите фигуру. В чем отличие от параллелограмма? Чему равны углы и периметр?
Слайд 11
3). а в в-а=6см Р=20 см
Назовите фигуру В чем отличие от квадрата? Чему равны стороны?
4). 3 см 700
Назовите фигуру. Что общего с прямоугольником?
Найдите большее основание и остальные углы.
Слайд 12
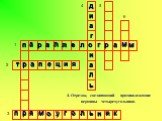
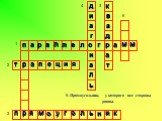
1 2 3 4 5 6
1. Четырехугольник, у которого противолежащие стороны параллельны.
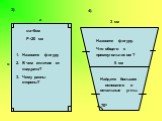
п р л е о г м Кроссворд
Слайд 13
2. Четырехугольник, у которого только две противолежащие стороны параллельны.
т ц и я
Слайд 14
3. Параллелограмм, у которого все углы прямые.
у ь н к
Слайд 15
4. Отрезок, соединяющий противолежащие вершины четырехугольника.
д
Слайд 16
5. Прямоугольник, у которого все стороны равны.
Слайд 17
6. Параллелограмм, у которого все стороны равны.
б
Слайд 18
1. Сумма длин всех сторон.
Слайд 20
Сказка-вопрос
Собрались все четырехугольники на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и никак не могли придти к единому мнению. И вот один старый параллелограмм сказал: «Давайте отправимся все в царство четырехугольников. Кто первым придет, тот и будет королем.» Все согласились.
Слайд 21
Рано утром отправились все в далекое путешествие. На пути путешественников повстречалась река, которая сказала:
«Переплывут через меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам.»
Часть четырехугольников осталась на берегу, остальные благополучно переплыли и отправились дальше.
Слайд 22
На пути им встретилась высокая гора, которая сказала, что даст пройти только тем, у кого диагонали равны.
Несколько путешественников остались у горы, остальные продолжили путь.
Дошли до большого обрыва, где был узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошел только один четырехугольник, который первым добрался до царства и был провозглашен королем.
Кто стал королем?
Слайд 23
Четырёхугольники
Работу выполнила:
Пирожкова Марина Валентиновна ,
у читель математики
МОУ «Жилинская СОШ» (группа № 031)
Преподаватель:
Е.А. Никитин
Четырёхугольники
Справочник
Задачник
Проверь себя
Выход
Справочник
Четырёхугольники
Параллелограмм
Трапеция
Ромб
Прямоугольник
Квадрат
Четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.
A
A
D
D
B
B
C
C
Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны
B
C
AB || CD
BC || AD
A
D
- Свойства параллелограмма
- Признаки параллелограмма
- Площадь параллелограмма
- Частные виды параллелограмма: прямоугольник и ромб
Свойства параллелограмма
- В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
C
B
AB = CD
BC = AD
A
D
B
C
A О = О C
B О = О D
О
D
A
Признаки параллелограмма
- Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
- Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
B
C
BC || AD
BC = AD
A
D
B
C
BC = AD
А B = С D
A
D
C
B
A О = О C
B О = О D
О
A
D
Площадь параллелограмма
C
B
ВН – высота параллелограмма
AD — основание
A
S = BH ∙ AD
D
Н
B
C
S = AB ∙ AD ∙ sin α
α
A
D
Н
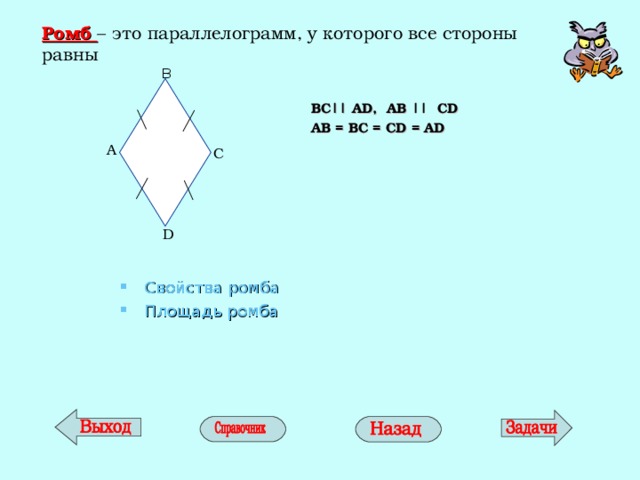
Ромб – это параллелограмм, у которого все стороны равны
B
BC|| AD , AB || CD
AB = BC = CD = AD
A
C
D
- Свойства ромба
- Площадь ромба
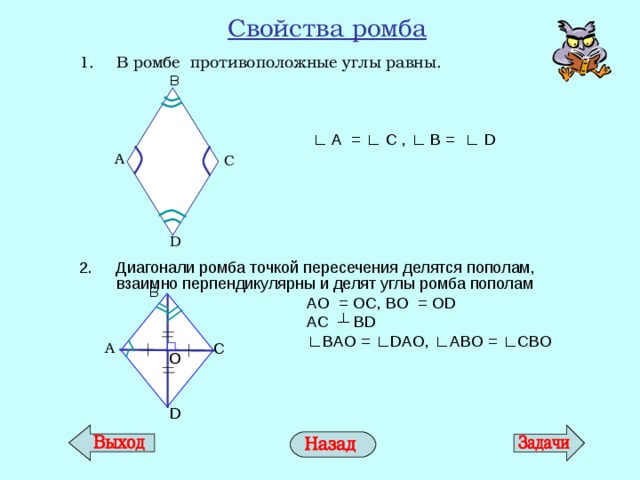
Свойства ромба
- В ромбе противоположные углы равны.
2. Диагонали ромба точкой пересечения делятся пополам, взаимно перпендикулярны и делят углы ромба пополам
B
∟ А = ∟ С , ∟ В = ∟ D
A
C
D
B
A О = О C , B О = О D
AC ┴ BD
∟ BAO = ∟ DAO, ∟ ABO = ∟ CBO
C
A
О
D
Площадь ромба
B
В
АН – высота ромба
D С — основание
А
C
A
С
O
S = А H ∙ D С
Н
D
D
В
S = 1/2∙ А C BD
α
S = АВ ∙ sin α
A
С
D
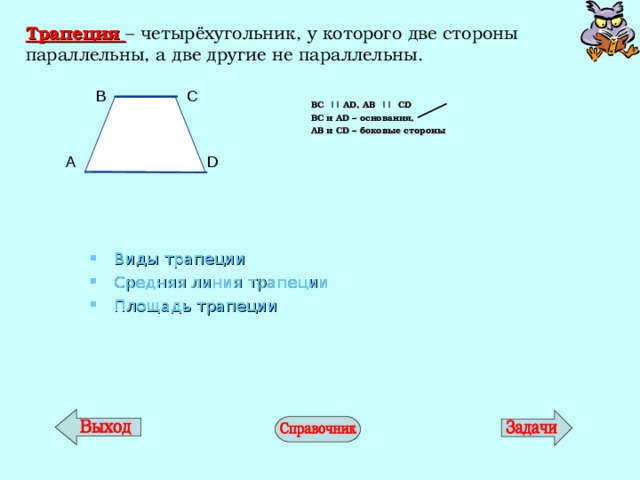
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
B
C
BC || AD , AB || CD
BC и AD – основания,
AB и CD – боковые стороны
A
D
- Виды трапеции
- Средняя линия трапеции
- Площадь трапеции
Виды трапеции
Равнобедренная — Прямоугольная — Произвольная
боковые стороны равны один из углов прямой
Средняя линия трапеции
C
B
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон.
MN — средняя линия
М
N
A
D
Средняя линия трапеции параллельна основаниям и равна их полусумме
MN || AD , MN || AD ,
MN = ( BC + AD) / 2
Площадь трапеции
B
C
ВН – высота трапеции
ВС и AD — основания
D
A
H
S = 1/2 ∙ BH ∙ (ВС + AD )
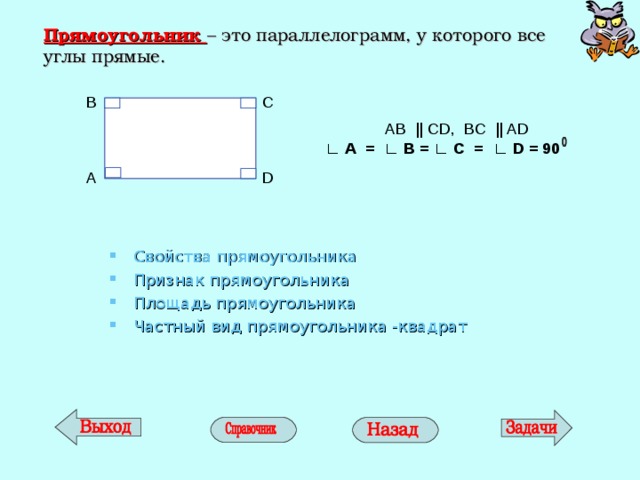
Прямоугольник – это параллелограмм, у которого все углы прямые.
С
В
AB || CD , BC || AD
∟ А = ∟ В = ∟ С = ∟ D = 90
A
D
- Свойства прямоугольника
- Признак прямоугольника
- Площадь прямоугольника
- Частный вид прямоугольника -квадрат
Свойства прямоугольника
- В прямоугольнике противоположные стороны равны и противоположные углы равны.
2. Диагонали прямоугольника равны и точкой пересечения делятся пополам.
B
C
AB = CD
BC = AD
A
D
C
B
BD = AC
A О = О C
B О = О D
О
D
A
Признак прямоугольника
C
B
BD = AC
О
D
A
Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник
Площадь прямоугольника
С
В
A
D
S = А B ∙ AD
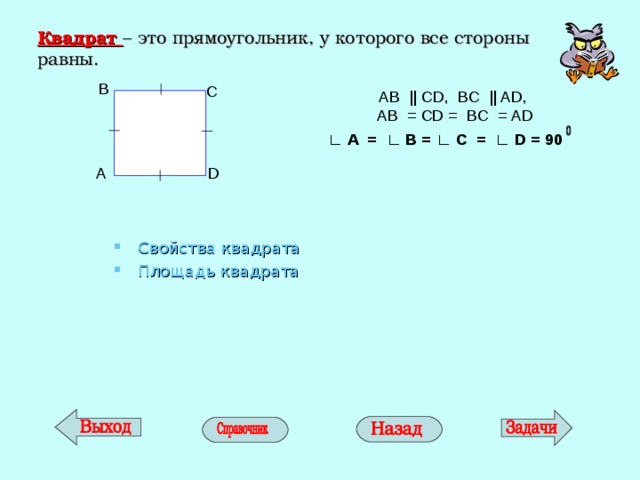
Квадрат – это прямоугольник, у которого все стороны равны.
В
С
AB || CD , BC || AD , ,
AB = CD = BC = AD
∟ А = ∟ В = ∟ С = ∟ D = 90
A
D
- Свойства квадрата
- Площадь квадрата
Свойства квадрата
- У квадрата все стороны равны и все углы равны.
2. Диагонали квадрата взаимно перпендикулярны, равны, точкой пересечения делятся пополам и делят углы квадрата пополам.
В
С
AB = CD = BC = AD
∟ А = ∟ В = ∟ С = ∟ D = 90
A
D
В
С
AC ┴ BD
BD = AC
A О = О C , B О = О D
∟ BAO = ∟ DAO, ∟ ABO = ∟ CBO
О
A
D
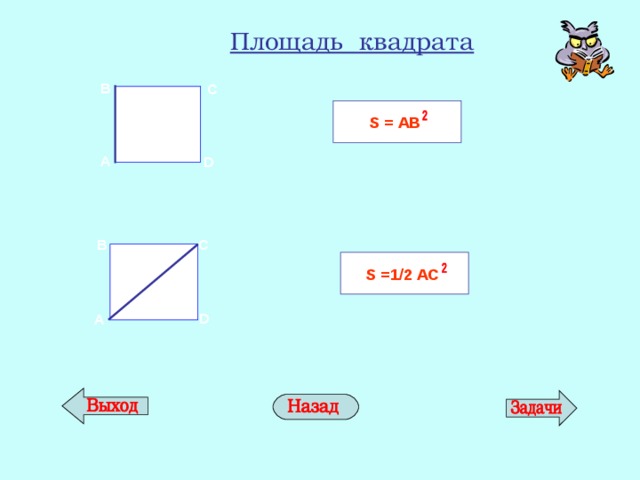
Площадь квадрата
В
С
S = АВ
А
D
В
С
S = 1/2 АС
D
А
задачник
Четырёхугольники
Параллелограмм
Трапеция
Ромб
Прямоугольник
Квадрат
Четырёхугольник
- Найдите углы выпуклого четырёхугольника, если они равны друг другу.
- Найдите углы выпуклого четырёхугольника, если они пропорциональны числам 1,2,4,5.
- Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4мм и 5мм.
- Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая в три раза больше второй.
- Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.
Параллелограмм
- Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если разность двух сторон равна 7 см.
- Найдите углы параллелограмма, если сумма противолежащих углов равна 142.
- Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
- На диагонали BD параллелограмма ABCD отмечены точки P и Q так, что PB = QD . Докажите, что четырёхугольник APCQ – параллелограмм.
- В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.
Ромб
- Найдите периметр ромба ABCD , в котором ∟ В = 60, АС= 10,5 см.
- Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
- Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 кв. см.
- Сторона ромба равна 24 см, а один из его углов 150 . Найдите расстояние между его противолежащими сторонами
- Из вершины В ромба ABCD , проведены перпендикуляры ВК и ВМ к прямым AD и DC . Докажите, что луч BD является биссектрисой ∟КВМ.
Прямоугольник
- Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что
треугольники АОВ и АО D равнобедренные.
- Биссектриса одного из углов прямоугольника делит большую сторону пополам. Найдите периметр прямоугольника, если его меньшая сторона 12 см.
- Стороны прямоугольника относятся как 2 : 7. Найдите стороны прямоугольника, если его площадь равна 108 кв.см.
- Сторона прямоугольника равна 4 см и образует с диагональю угол 60. Найдите эту диагональ.
- Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола?
Квадрат
- Является ли четырёхугольник квадратом, если его диагонали:
а) равны и взаимно перпендикулярны;
б) взаимно перпендикулярны и имеют общую середину;
в) равны, взаимно перпендикулярны и имеют общую середину.
2. Диагональ квадрата 24 см. Найдите периметр четырёхугольника,
образованного отрезками, последовательно соединяющими
середины сторон данного квадрата.
- Сторону квадрата увеличили в 3 раза. Во сколько раз увеличилась его площадь?
- Площадь квадрата равна 18 кв.см. Найдите диагональ квадрата.
- В равнобедренный прямоугольный треугольник вписан квадрат так,
что две его вершины находятся на гипотенузе, а другие две – на катетах.
Найдите сторону квадрата, если известно, что гипотенуза равна 12 см.
Трапеция
- Найдите углы B и D трапеции ABCD с основаниями AD и BC , если ∟А = 36 ,∟С= 117 .
- Докажите, что трапеция равнобедренная, если её диагонали равны.
- Основания прямоугольной трапеции равны 10 см, 15 см, а один из углов – 45 .Найдите меньшую боковую сторону трапеции.
- Найдите площадь равнобедренной трапеции. Если её основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
- Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линию трапеции
Проверь себя
Задание № 1
Какое из утверждений неверное:
- квадрат является одновременно параллелограммом и прямоугольником;
- угол между стороной и диагональю квадрата равен 45 ;
- существует квадрат, который не является ромбом;
- диагонали квадрата взаимно перпендикулярны.
Задание № 2
Найдите площадь ромба, диагонали которого равны 26 см и 8 см:
- 208 кв.см ;
- 104 кв.см;
- 52 кв.см;
- 68 кв.см
Задание № 3
В каком случае нельзя утверждать, что данная фигура – параллелограмм?
а) б)
в) г)
Задание № 4
Диагонали прямоугольника ABCD пересекаются в точке О. Определите периметр треугольника АВО, если АВ = 6 см, а диагональ прямоугольника равна 14 см:
- 19 см ;
- 26 см;
- 20 см;
- 18 см
Задание № 5
Какое из утверждений неверное?
- у прямоугольника углы прямые, а у ромба не обязательно;
- у ромба диагонали взаимно перпендикулярны, а у прямоугольника не обязательно;
- у ромба диагонали являются биссектрисами его углов, а у параллелограмма не обязательно;
- у ромба диагонали равны, а у прямоугольника не обязательно;
Задание № 6
Какая из фигур не является прямоугольником?
а) б)
в) г)
Задание № 7
В прямоугольнике ABCD проведена биссектриса АМ. ВМ= 5см,
МС =4 см. Найдите площадь прямоугольника:
- 36 кв. см
- 45 кв. см
- 28 кв. см
- 56 кв.см
Задание № 8
Найти площадь трапеции ABCD с основаниями AB и CD , если BC перпендикулярна AB , AB = 5 см, BC = 8 см, CD = 13 см.
- 144 кв.см;
- 36 кв.см;
- 72 кв.см;
- 70 кв.см
Задание № 9
Какое из утверждений неверное?
- параллелограмм, у которого диагонали взаимно перпендикулярны, является квадратом;
- прямоугольник, у которого все стороны равны, является квадратом;
- ромб у которого один угол прямой, является квадратом;
- ромб, у которого диагонали равны, является квадратом
Задание № 10
Найдите высоту параллелограмма, если его площадь
равна 75,6 кв. см, а основание — 14 см.
- 23,8 см ;
- 5,4 см;
- 61,6 см;
- 16 см.
Ещё!
Ещё!
Ending Style
Ending Style