Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Проставьте в соответствие каждому неравенству множество его решений.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2
На координатной прямой отмечены точки Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
3
Поставьте в соответствие каждому неравенству множество его решений.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4
На координатной прямой отмечено число
Расположите в порядке убывания числа:
В ответе укажите номера выбранных чисел в порядке убывания.
5
На координатной прямой отмечены числа x и
Расположите числа в порядке убывания:
Источник: РЕШУ ЕГЭ
Пройти тестирование по этим заданиям
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где
и
— корни квадратного уравнения
.
Получим:
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и
выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и
— закрашены, так как неравенство нестрогое. При
и
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например,
и проверим знак выражения
в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак
.
Следующий промежуток:
. Проверим знак при
. Получаем, что левая часть поменяла знак на
.
. Возьмем
. При
выражение положительно — следовательно, оно положительно на всем промежутке от
до
.
При
левая часть неравенства отрицательна.
И, наконец,
. Подставим
и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак
.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или
, или
, или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство:
Решение:
Снова расставляем точки на оси X. Точки и
— выколотые, поскольку это нули знаменателя. Точка
— тоже выколота, поскольку неравенство строгое, и значение переменной
не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
. Левая часть имеет знак
:
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
:
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
:
Наконец, при все множители положительны, и левая часть имеет знак
:
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
при всех
одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех
.
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при
. Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и
. Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6. Решите неравенство:
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при
или
. Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то
. Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если ,
или
. Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель
стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель
присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если
или
. Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что
.
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и
при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Задание 5950
На координатной прямой точками отмечены числа a, b, c, d и m. Установите соответствие между указанными точками и числами из правого столбца.
| ТОЧКИ | ЧИСЛА | |
|
1)$$m-frac{1}{4}$$ 2)$$-frac{m}{2}$$ 3)$$3m$$ 4)$$m^{3}$$ |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
Задание 5951
На координатной прямой отмечены точки A, B, C, и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА | |
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Задание 5952
На координатной прямой отмечены точки A, B, C, и D. Про число mизвестно, что оно равно .
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
| ТОЧКИ | ЧИСЛА | |
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Задание 5953
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
Задание 5954
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
|
А) Б) В) Г) |
|
Ответ:
Задание 5955
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
|
А) Б) В) Г) |
|
Ответ:
Задание 5956
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
|
А) Б) В) Г) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
Задание 5957
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
|
А) Б) В) Г) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
Задание 5958
На координатной прямой отмечены точки A, B, C, и D.
Число равно
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА | |
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Задание 5959
На прямой отмечены точки K, L, M и N.
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
| ТОЧКИ | ЧИСЛА | |
|
А) K Б) L В) M Г) N |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
Задание 5960
На координатной прямой отмечено число
Расположите в порядке убывания числа:
В ответе укажите номера выбранных чисел в порядке убывания.
Ответ:
Задание 5961
На координатной прямой отмечены числа и
.
Расположите числа в порядке убывания:
Ответ:
Задание 5962
На координатной прямой отмечены числа и
Расположите в порядке возрастания числа
В ответе укажите номера выбранных Вами чисел, расположенных в порядке возрастания, без пробелов, запятых и других дополнительных символов.
Ответ:
Задание 5963
На координатной прямой отмечены числа и
:
Расположите числа в порядке возрастания:
Ответ:
Задание 5964
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
|
А) Б) В) Г) |
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Ответ:
Числовая ось, числовые промежутки
1. На координатной прямой точками отмечены числа a, b, c, d и m. Установите соответствие между указанными точками и числами из правого столбца.
|
ТОЧКИ |
ЧИСЛА |
|
|
|
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
a |
b |
c |
d |
2. На координатной прямой отмечены точки A, B, C, и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Г |
3. На координатной прямой отмечены точки A, B, C, и D. Про число m известно, что оно равно .
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
В таблице под каждой буквой укажите соответствующий номер.
|
А |
Б |
В |
Г |
4. На прямой отмечены точки K, L, M и N.
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) K Б) L В) M Г) N |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
5. На координатной прямой отмечено число
Расположите в порядке убывания числа:
|
1) |
2) |
3) |
4) |
В ответе укажите номера выбранных чисел в порядке убывания.
6. На координатной прямой отмечены числа и
.
Расположите числа в порядке убывания:
|
1) |
2) |
3) |
4) |
7. На координатной прямой отмечены числа и
Расположите в порядке возрастания числа
|
1) |
2) |
3) |
4) |
В ответе укажите номера выбранных Вами чисел, расположенных в порядке возрастания, без пробелов, запятых и других дополнительных символов.
8. На координатной прямой отмечены числа и
:
Расположите числа в порядке возрастания:
|
1) |
2) |
3) |
4) |
9. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
10. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
|
А |
Б |
В |
Г |
11. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
12. Каждому из четырёх неравенств слева соответствует одно из решений, изображённых на координатной прямой справа. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) x(1 − x) 0 Б) 1 − x 0 В) (1 − x)2 0 Г) x(1 − x) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
13. Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
|
ЧИСЛА |
ОТРЕЗКИ |
|
|
А) Б) В) Г) |
1) [0;1] 2) [1; 2] 3) [2; 3] 4) [4; 5] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
14. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
|
А |
Б |
В |
Г |
15. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
16. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
|
А |
Б |
В |
Г |
18. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
|
А |
Б |
В |
Г |
19. Проставьте в соответствие каждому неравенству множество его решений.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
A |
Б |
В |
Г |
20. Поставьте в соответствие каждому неравенству множество его решений.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
21. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
22. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
23. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
24. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
25. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
26. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) 0,5x ≥ 2 Б) 0,5x ≤ 2 В) 2x ≤ 2 Г) 2x ≥ 2 |
1) x ≥ −1 2) x ≥ 1 3) x ≤ −1 4) x ≤ 1 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
27. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) 0,5x ≥ 4 Б) 2x ≥ 4 В) 0,5x ≤ 4 Г) 2x ≤ 4 |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
28. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
Подготовка к ЕГЭ: задача 18 (отрезки)
Содержание
- Теория
- Разбор решений задач
- Задачи для самостоятельного решения
- Источники
Теория
Задания№18 на логические отрезки можно решать несколькими способами.
В данной презентации рассматриваются два способа решения.
Как правило, в данных задачах логическое выражение, для которого требуется найти длину отрезка, на котором это выражение истинно (или ложно), достаточно сложно для восприятия. Поэтому необходимо его упростить. Нужно ввести дополнительные обозначений для простых логических высказываний и за счёт этого получить логическую функцию традиционного вида.
Первый способ решения: полученное выражение нужно упростить, используя законы преобразования логических выражений. Итоговое выражение нужно приравнять 1, если по условию оно должно быть истинным, или 0, если должно быть ложно.
Теория
Остается только рассмотреть простые высказывания, входящие в итоговое выражение, и выяснить, на каких отрезках они истинны (или ложны, в зависимости от условия задачи). Проанализировав эти отрезки, нужно найти итоговый (или несколько, в ответе может быть не один).
При втором способе решения для полученного после ввода обозначений выражения строится таблица истинности (ТИ), в которой отражены значения всех логических переменных и логических операций на каждом числовом отрезке. В одном из столбцов будут стоять значения искомой переменной. В зависимости от условия, она либо равна 1, либо равна 0, либо может принимать любое значение, поскольку не будет влиять на конечное значение исходного выражения. Остается выбрать строки, соответствующие условию задачи (истинно или ложно должно быть исходное выражение) и выбрать числовые отрезки (отрезок).
Разбор решения задач
Задание 1.
На числовой прямой даны два отрезка: P =[10; 18] и Q =[31; 40]. Укажите наименьшую возможную длину такого отрезка A , что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной x .
Решение.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A
Перепишем условие задания:
¬P Q + ¬A или ¬P ( Q + ¬A) (поскольку импликация имеет самый низкий приоритет и будет выполнена последней)
Раскрываем импликацию:
P + Q + ¬A
Это выражение должно быть равным 1 при любом значении А: P + Q + ¬A = 1
Разбор решения задач
Задание 1.
Рассмотрим числовую ось с нашими отрезками P и Q.
Рассмотрим отдельно все три отрезка.
Отрезок 10‒18: выражение истинно, т.к. Р=1 (x ϵ P)
Отрезок 31‒ 40: выражение истинно, т.к. Q=1 (x ϵ Q)
Отрезок 18‒31: выражение будет истинным в случае ¬A = 1, или А=0. Это значит, что А не принадлежит отрезку 18‒31, значение А должно быть совпадающим либо с отрезком Р, либо с отрезком Q. Но поскольку в задании спрашивается наименьшая длина отрезка, то это будет отрезок (18-10)=8
Ответ: 8
Разбор решения задач
Задание 2.
На числовой прямой даны два отрезка: P=[-10, 0] и Q=[-3, 8]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение
( (x ϵ P) Ʌ (x ϵ A) ) ( (x ϵ Q) Ʌ (x ϵ A) )
будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной х.
1) [-8, -4] 2) [-7, -1] 3) [-2, 5] 4) [-15, 15]
Решение.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A
Перепишем условие задания:
Раскрываем импликацию, затем используем формулу де Моргана:
¬ ( P · A ) + (Q · A ) или ¬ P + ¬A + Q · A
( P Ʌ A ) ( Q Ʌ A)
Разбор решения задач
Задание 2.
Преобразуем выражение, используя следующий закон преобразования: a + ¬ a · b = a + b
¬ P + (¬A + Q · A) = ¬ P + (¬A + Q) = ¬A + ¬ P + Q
Поскольку это выражение должно быть тождественно истинным, т.е. равным 1 при любом значении А, то ¬A должно быть истинным там, где (¬ P + Q) ложно, или где истинно ¬ (¬ P + Q).
Преобразуем получившееся выражение, используя формулу де Моргана:
¬ (¬ P + Q) = (¬ ¬ P ) Ʌ ¬Q = P Ʌ ¬Q
Разбор решения задач
Задание 2.
Рассмотрим числовую ось с нашими отрезками P и Q.
Выражение (P Ʌ ¬Q) истинно на отрезке [-10, -3]. На нем должно быть ¬A=1 или А=0. Это означает, что отрезок А не должен содержать в себе отрезок [-10, -3].
Рассмотрим варианты ответов.
Отрезок 1) [-8, -4] содержит в себе значения из отрезка [-10, -3], поэтому не является правильным ответом.
Отрезок 2) [-7, -1] содержит в себе значения из отрезка [-10, -3], что быть не должно.
Отрезок 4) [-15, 15] содержит в себе значения из отрезка [-10, -3], что быть не должно.
Отрезок 3) [-2, 5] не содержит в себе значения [-10, -3], поэтому именно он и является ответом.
Ответ: 3)
Разбор решения задач
Задание 3.
На числовой прямой даны два отрезка: R =[27; 50] и S =[30; 67]. Укажите наименьшую возможную длину такого отрезка T , что формула
(x ϵ R) (((x ϵ S) Ʌ ¬(x ϵ T)) ¬(x ϵ R))
тождественно истинна, то есть принимает значение 1 при любом значении переменной x .
Решение.
Введем обозначения:
R: x ϵ R, S: x ϵ S, T: x ϵ T
Перепишем условие задания:
R (( S Ʌ ¬ T ) R)
Разбор решения задач
Задание 3.
Преобразуем получившееся выражение, используя замену импликации и формулу де Моргана:
R (¬ ( S Ʌ ¬ T) + ¬ R)
R (¬ S + T + ¬ R)
¬ R + ¬ S + T + ¬ R
¬ R + ¬ S + T
Это выражение должно быть равно 1 при любом значении T:
T + ¬ R + ¬ S = 1
Разбор решения задач
Задание 3.
Рассмотрим числовую ось с нашими отрезками P и Q.
Чтобы получившееся выражение было везде истинным, T должно быть истинным там, где ложно (¬R + ¬S), т.е. там, где истинно выражение ¬ (¬R + ¬S).
Выполним преобразования, используя формулу де Моргана:
¬ (¬ R + ¬ S) = ¬ ¬ R Ʌ ¬ ¬ S) = R Ʌ S = 1
Это выражение истинно на отрезке [30; 50]. Его длина равна (50 – 30) = 20
Ответ: 20
Разбор решения задач
Задание 4.
На числовой прямой даны два отрезка: P=[2, 10] и Q=[6, 14]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение
( ( x ϵ A) ( x ϵ P) V ( x ϵ Q) )
будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x .
1) [0, 3] 2) [3, 11] 3) [11, 15] 4) [15, 17]
Решение.
Эту задачу решим с помощью анализа исходного логического выражения после его преобразования, а также с помощью таблицы истинности.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A
Перепишем условие задания:
A P V Q = ¬ A + P + Q

Разбор решения задач
Задание 4.
1 способ. Чтобы полученное выражение везде равнялось 1 , ¬A должно быть либо 14, поскольку в интервале [2, 14 ] имеем либо P=1 либо Q=1 . Значит, А принадлежит отрезку [2, 14]. Этот отрезок входит в интервал под номером 3).
2 способ. Разобьем числовую ось ключевыми точками на несколько областей и составим ТИ для логического выражения.
x
P
2
Q
0
6
0
1
P +Q
0
0
10
¬A
1
x 14
1
1
0
¬A + P + Q
1
любое
1
0
1
1
любое
1
1
0
любое
0
1
1
1
1
По ТИ получаем значения ¬A 14. Тогда решением задания будет 2
Ответ: 3)
Разбор решения задач
Задание 5.
На числовой прямой даны два отрезка: P=[2, 20] и Q=[15, 25]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение
( ( x ɇ A) ( x ɇ P) ) V ( x ϵ Q)
будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x .
1) [0, 15] 2) [10, 25] 3) [2, 10] 4) [15, 20]
Решение.
Эту задачу решим с помощью таблицы истинности.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A
Перепишем условие задания:
( ¬ A ¬ P ) V Q = A + ¬ P + Q

Разбор решения задач
Задание 5.
Разобьем числовую ось ключевыми точками на несколько областей и составим ТИ для логического выражения.
P
x
2
¬P
0
Q
1
15
1
1
0
0
¬P + Q
20
A
0
0
1
x 25
0
любое
A + ¬ P + Q
0
1
0
1
1
1
1
1
1
любое
1
1
1
любое
1
1
1
любое
1
Из ТИ получаем, что значения А=1 будут на интервале 2
Ответ: 1)
Задачи для самостоятельного решения
Задание 6.
На числовой прямой даны два отрезка: P =[10; 18] и Q =[31; 40]. Укажите наибольшую возможную длину такого отрезка A , что формула
(x ϵ P) V ¬ ( x ϵ A) V ( x ϵ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x .
Ответ: 9
Задачи для самостоятельного решения
Задание 7.
На числовой прямой даны два отрезка: R =[10; 30] и S =[20; 40]. Укажите наибольшую возможную длину такого отрезка T , что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной x .
(x ϵ T ) ((x ϵ R ) V (x ϵ S ))
Ответ: 30
Задачи для самостоятельного решения
Задание 8.
На числовой прямой даны два отрезка: R =[20; 50] и S =[30; 65]. Укажите наименьшую возможную длину такого отрезка T , что формула
¬ (x ϵ T ) ((x ϵ R ) ¬ (x ϵ S ))
тождественно истинна, то есть принимает значение 1 при любом значении переменной x .
Ответ: 20
Задачи для самостоятельного решения
Задание 9.
На числовой прямой даны два отрезка: P =[10; 25] и Q =[0; 12]. Выберите из предложенных вариантов такой отрезок А, что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной x .
1) [10, 15] 2) [20, 35] 3) [5, 20] 4) [12, 40]
( ( x ɇ Q) ( x ɇ P) ) V ( x ϵ A)
Ответ: 4)
Задачи для самостоятельного решения
Задание 10.
На числовой прямой даны два отрезка: P = [10, 40] и Q = [30, 50]. Отрезок A таков, что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной х . Какова наибольшая возможная длина отрезка A?
1) 10 2) 20 3) 30 4) 40
(( x ϵ A) ( x ϵ Q)) V ( x ϵ P)
Ответ: 2)
Источники
- сайт К. Полякова
http://kpolyakov.spb.ru
- Открытый банк заданий ФИПИ
- С.С. Крылов, Т.Е. Чуркина ЕГЭ-2018 – типовые экзаменационные варианты. Информатика и ИКТ. Москва. Национальное образование. 2017
- В.Р. Лещинер. Информатика. ЕГЭ-2018. Типовые тестовые задания. Москва. Издательство «Экзамен». 2017
- Самылкина Н.Н. и др. Подготовка к ЕГЭ-2018. Информатика. Москва. Эксмо. 2017
Скачать материал

Скачать материал


- Сейчас обучается 354 человека из 67 регионов


- Сейчас обучается 134 человека из 49 регионов


- Сейчас обучается 119 человек из 41 региона


Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к ЕГЭ: задача 18 (отрезки)
-
2 слайд
Содержание
Теория
Разбор решений задач
Задачи для самостоятельного решения
Источники -
3 слайд
Теория
Задания№18 на логические отрезки можно решать несколькими способами.
В данной презентации рассматриваются два способа решения.
Как правило, в данных задачах логическое выражение, для которого требуется найти длину отрезка, на котором это выражение истинно (или ложно), достаточно сложно для восприятия. Поэтому необходимо его упростить. Нужно ввести дополнительные обозначений для простых логических высказываний и за счёт этого получить логическую функцию традиционного вида.
Первый способ решения: полученное выражение нужно упростить, используя законы преобразования логических выражений. Итоговое выражение нужно приравнять 1, если по условию оно должно быть истинным, или 0, если должно быть ложно. -
4 слайд
Теория
Остается только рассмотреть простые высказывания, входящие в итоговое выражение, и выяснить, на каких отрезках они истинны (или ложны, в зависимости от условия задачи). Проанализировав эти отрезки, нужно найти итоговый (или несколько, в ответе может быть не один).
При втором способе решения для полученного после ввода обозначений выражения строится таблица истинности (ТИ), в которой отражены значения всех логических переменных и логических операций на каждом числовом отрезке. В одном из столбцов будут стоять значения искомой переменной. В зависимости от условия, она либо равна 1, либо равна 0, либо может принимать любое значение, поскольку не будет влиять на конечное значение исходного выражения. Остается выбрать строки, соответствующие условию задачи (истинно или ложно должно быть исходное выражение) и выбрать числовые отрезки (отрезок). -
5 слайд
На числовой прямой даны два отрезка: P=[10; 18] и Q=[31; 40]. Укажите наименьшую возможную длину такого отрезка A, что формула
Разбор решения задач
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Решение.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A
Перепишем условие задания:
¬P Q + ¬A или ¬P ( Q + ¬A)
(поскольку импликация имеет самый низкий приоритет и будет выполнена последней)
Раскрываем импликацию:
P + Q + ¬A
Это выражение должно быть равным 1 при любом значении А: P + Q + ¬A = 1Задание 1.
-
6 слайд
Рассмотрим числовую ось с нашими отрезками P и Q.
Разбор решения задач
Рассмотрим отдельно все три отрезка.
Отрезок 10‒18: выражение истинно, т.к. Р=1 (x ϵ P)
Отрезок 31‒ 40: выражение истинно, т.к. Q=1 (x ϵ Q)
Отрезок 18‒31: выражение будет истинным в случае ¬A = 1, или А=0. Это значит, что А не принадлежит отрезку 18‒31, значение А должно быть совпадающим либо с отрезком Р, либо с отрезком Q. Но поскольку в задании спрашивается наименьшая длина отрезка, то это будет отрезок (18-10)=8
Ответ: 8
Задание 1. -
7 слайд
На числовой прямой даны два отрезка: P=[-10, 0] и Q=[-3, 8]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение
Разбор решения задач
будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной х.
1) [-8, -4]2) [-7, -1] 3) [-2, 5] 4) [-15, 15]Решение.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ AПерепишем условие задания:
Раскрываем импликацию, затем используем формулу
де Моргана:
¬ ( P · A ) + (Q · A ) или ¬ P + ¬A + Q · A
( (x ϵ P) Ʌ (x ϵ A) ) ( (x ϵ Q) Ʌ (x ϵ A) )
( P Ʌ A ) ( Q Ʌ A)
Задание 2. -
8 слайд
Разбор решения задач
Преобразуем выражение, используя следующий закон преобразования: a + ¬a·b = a + b¬ P + (¬A + Q · A) = ¬ P + (¬A + Q) = ¬A + ¬ P + Q
Задание 2.
Поскольку это выражение должно быть тождественно истинным, т.е. равным 1 при любом значении А, то ¬A должно быть истинным там, где (¬ P + Q) ложно, или где истинно ¬ (¬ P + Q).
Преобразуем получившееся выражение, используя формулу де Моргана:¬ (¬ P + Q) = (¬ ¬ P ) Ʌ ¬Q = P Ʌ ¬Q
-
9 слайд
Рассмотрим числовую ось с нашими отрезками P и Q.
Разбор решения задач
Выражение (P Ʌ ¬Q) истинно на отрезке [-10, -3]. На нем должно быть ¬A=1 или А=0. Это означает, что отрезок А не должен содержать в себе отрезок [-10, -3].
Рассмотрим варианты ответов.
Отрезок 1) [-8, -4] содержит в себе значения из отрезка [-10, -3], поэтому не является правильным ответом.
Отрезок 2) [-7, -1] содержит в себе значения из отрезка
[-10, -3], что быть не должно.
Отрезок 4) [-15, 15] содержит в себе значения из отрезка
[-10, -3], что быть не должно.
Отрезок 3) [-2, 5] не содержит в себе значения [-10, -3], поэтому именно он и является ответом.
Ответ: 3)
Задание 2. -
10 слайд
На числовой прямой даны два отрезка: R=[27; 50] и S=[30; 67]. Укажите наименьшую возможную длину такого отрезка T, что формула
Разбор решения задач
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.Решение.
Введем обозначения:
R: x ϵ R, S: x ϵ S, T: x ϵ T
Перепишем условие задания:
R (( S Ʌ ¬T ) R)Задание 3.
(x ϵ R) (((x ϵ S) Ʌ ¬(x ϵ T)) ¬(x ϵ R)) -
11 слайд
Разбор решения задач
Задание 3.
Преобразуем получившееся выражение, используя замену импликации и формулу де Моргана:
R (¬ ( S Ʌ ¬ T) + ¬ R)
R (¬ S + T + ¬ R)
¬ R + ¬ S + T + ¬ R
¬ R + ¬ S + T
Это выражение должно быть равно 1 при любом значении T:
T + ¬ R + ¬ S = 1 -
12 слайд
Рассмотрим числовую ось с нашими отрезками P и Q.
Разбор решения задач
Чтобы получившееся выражение было везде истинным, T должно быть истинным там, где ложно (¬R + ¬S), т.е. там,
где истинно выражение ¬ (¬R + ¬S).Выполним преобразования, используя формулу де Моргана:
¬ (¬ R + ¬ S) = ¬ ¬ R Ʌ ¬ ¬ S) = R Ʌ S = 1
Это выражение истинно на отрезке [30; 50]. Его длина равна (50 – 30) = 20
Ответ: 20
Задание 3. -
13 слайд
На числовой прямой даны два отрезка: P=[2, 10] и Q=[6, 14]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение
Разбор решения задач
будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x.
1) [0, 3]2) [3, 11] 3) [11, 15] 4) [15, 17]Решение.
Эту задачу решим с помощью анализа исходного логического выражения после его преобразования, а также с помощью таблицы истинности.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ AПерепишем условие задания:
AP V Q = ¬ A + P + QЗадание 4.
( ( x ϵ A) ( x ϵ P) V ( x ϵ Q) ) -
14 слайд
1 способ. Чтобы полученное выражение везде равнялось 1 , ¬A должно быть либо <2, либо >14, поскольку в интервале [2, 14 ] имеем либо P=1 либо Q=1 . Значит, А принадлежит отрезку [2, 14]. Этот отрезок входит в интервал под номером 3).
2 способ. Разобьем числовую ось ключевыми точками на несколько областей и составим ТИ для логического выражения.
Разбор решения задач
По ТИ получаем значения ¬A < 2 или ¬A > 14. Тогда решением задания будет 2 < A < 14. Это соответствует отрезку с номером 3).
Ответ: 3)
Задание 4. -
15 слайд
На числовой прямой даны два отрезка: P=[2, 20] и Q=[15, 25]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение
Разбор решения задач
будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x.
1) [0, 15]2) [10, 25] 3) [2, 10] 4) [15, 20]Решение.
Эту задачу решим с помощью таблицы истинности.
Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ AПерепишем условие задания:
(¬A¬P ) V Q = A + ¬ P + QЗадание 5.
( ( x ɇ A) ( x ɇ P) ) V ( x ϵ Q) -
16 слайд
Разобьем числовую ось ключевыми точками на несколько областей и составим ТИ для логического выражения.
Разбор решения задач
Из ТИ получаем, что значения А=1 будут на интервале
2 < x < 15. Тогда решением задания будет отрезок с
номером 1).
Ответ: 1)
Задание 5. -
17 слайд
Задачи для самостоятельного решения
Задание 6.
На числовой прямой даны два отрезка: P=[10; 18] и Q=[31; 40]. Укажите наибольшую возможную длину такого отрезка A, что формула
(x ϵ P) V ¬ ( x ϵ A) V ( x ϵ Q)тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Ответ: 9
-
18 слайд
Задачи для самостоятельного решения
Задание 7.
На числовой прямой даны два отрезка: R=[10; 30] и S=[20; 40]. Укажите наибольшую возможную длину такого отрезка T, что формулатождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Ответ: 30
(x ϵ T) ((x ϵ R) V (x ϵ S)) -
19 слайд
Задачи для самостоятельного решения
Задание 8.
На числовой прямой даны два отрезка: R=[20; 50] и S=[30; 65]. Укажите наименьшую возможную длину такого отрезка T, что формула
Ответ: 20
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
¬ (x ϵ T) ((x ϵ R) ¬ (x ϵ S)) -
20 слайд
Задачи для самостоятельного решения
Задание 9.
На числовой прямой даны два отрезка: P=[10; 25] и Q=[0; 12]. Выберите из предложенных вариантов такой отрезок А, что формулатождественно истинна, то есть принимает значение 1 при любом значении переменной x.
1) [10, 15]2) [20, 35] 3) [5, 20] 4) [12, 40]Ответ: 4)
( ( x ɇ Q) ( x ɇ P) ) V ( x ϵ A) -
21 слайд
Задачи для самостоятельного решения
Задание 10.
На числовой прямой даны два отрезка: P = [10, 40] и Q = [30, 50]. Отрезок A таков, что формулатождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?
1) 102) 20 3) 304) 40Ответ: 2)
(( x ϵ A) ( x ϵ Q)) V ( x ϵ P) -
22 слайд
Источники
сайт К. Полякова
http://kpolyakov.spb.ruОткрытый банк заданий ФИПИ
С.С. Крылов, Т.Е. Чуркина ЕГЭ-2018 – типовые экзаменационные варианты. Информатика и ИКТ. Москва. Национальное образование. 2017
В.Р. Лещинер. Информатика. ЕГЭ-2018. Типовые тестовые задания. Москва. Издательство «Экзамен». 2017
Самылкина Н.Н. и др. Подготовка к ЕГЭ-2018. Информатика. Москва. Эксмо. 2017
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 157 031 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 21.04.2018
- 1016
- 2
Рейтинг:
1 из 5
- 21.04.2018
- 1287
- 7
Рейтинг:
1 из 5
- 21.04.2018
- 1449
- 14
- 21.04.2018
- 316
- 1
- 21.04.2018
- 434
- 0
- 21.04.2018
- 703
- 11
- 21.04.2018
- 729
- 1
- 21.04.2018
- 924
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 15 № 45
Количество целых решений неравенства на промежутке
равно:
Источник: Централизованное тестирование по математике, 2011
2
Используя рисунок, определите верное утверждение и укажите его номер.
Источник: Централизованное тестирование по математике, 2016
3
Найдите сумму наименьшего и наибольшего целых решений двойного неравенства
1) −52
2) −47
3) −49
4) −48
5) −53
Источник: Централизованное тестирование по математике, 2017
4
На координатной прямой отмечены точки А, В, С, D, F. Числу на координатной прямой может соответствовать точка:
Источник: Централизованное тестирование по математике, 2019
Пройти тестирование по этим заданиям

























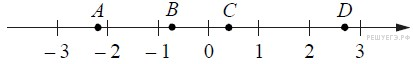




![Разбор решения задач Задание 1. На числовой прямой даны два отрезка: P =[10; 18] и Q =[31; 40]. Укажите наименьшую возможную длину такого отрезка A , что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной x . Решение. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: ¬P Q + ¬A или ¬P ( Q + ¬A) (поскольку импликация имеет самый низкий приоритет и будет выполнена последней) Раскрываем импликацию: P + Q + ¬A Это выражение должно быть равным 1 при любом значении А: P + Q + ¬A = 1](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img4.jpg)

![Разбор решения задач Задание 2. На числовой прямой даны два отрезка: P=[-10, 0] и Q=[-3, 8]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение ( (x ϵ P) Ʌ (x ϵ A) ) ( (x ϵ Q) Ʌ (x ϵ A) ) будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной х. 1) [-8, -4] 2) [-7, -1] 3) [-2, 5] 4) [-15, 15] Решение. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: Раскрываем импликацию, затем используем формулу де Моргана: ¬ ( P · A ) + (Q · A ) или ¬ P + ¬A + Q · A ( P Ʌ A ) ( Q Ʌ A)](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img6.jpg)

![Разбор решения задач Задание 2. Рассмотрим числовую ось с нашими отрезками P и Q. Выражение (P Ʌ ¬Q) истинно на отрезке [-10, -3]. На нем должно быть ¬A=1 или А=0. Это означает, что отрезок А не должен содержать в себе отрезок [-10, -3]. Рассмотрим варианты ответов. Отрезок 1) [-8, -4] содержит в себе значения из отрезка [-10, -3], поэтому не является правильным ответом. Отрезок 2) [-7, -1] содержит в себе значения из отрезка [-10, -3], что быть не должно. Отрезок 4) [-15, 15] содержит в себе значения из отрезка [-10, -3], что быть не должно. Отрезок 3) [-2, 5] не содержит в себе значения [-10, -3], поэтому именно он и является ответом. Ответ: 3)](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img8.jpg)
![Разбор решения задач Задание 3. На числовой прямой даны два отрезка: R =[27; 50] и S =[30; 67]. Укажите наименьшую возможную длину такого отрезка T , что формула (x ϵ R) (((x ϵ S) Ʌ ¬(x ϵ T)) ¬(x ϵ R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной x . Решение. Введем обозначения: R: x ϵ R, S: x ϵ S, T: x ϵ T Перепишем условие задания: R (( S Ʌ ¬ T ) R)](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img9.jpg)

![Разбор решения задач Задание 3. Рассмотрим числовую ось с нашими отрезками P и Q. Чтобы получившееся выражение было везде истинным, T должно быть истинным там, где ложно (¬R + ¬S), т.е. там, где истинно выражение ¬ (¬R + ¬S). Выполним преобразования, используя формулу де Моргана: ¬ (¬ R + ¬ S) = ¬ ¬ R Ʌ ¬ ¬ S) = R Ʌ S = 1 Это выражение истинно на отрезке [30; 50]. Его длина равна (50 – 30) = 20 Ответ: 20](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img11.jpg)
![Разбор решения задач Задание 4. На числовой прямой даны два отрезка: P=[2, 10] и Q=[6, 14]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение ( ( x ϵ A) ( x ϵ P) V ( x ϵ Q) ) будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x . 1) [0, 3] 2) [3, 11] 3) [11, 15] 4) [15, 17] Решение. Эту задачу решим с помощью анализа исходного логического выражения после его преобразования, а также с помощью таблицы истинности. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: A P V Q = ¬ A + P + Q](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img12.jpg)
![Разбор решения задач Задание 5. На числовой прямой даны два отрезка: P=[2, 20] и Q=[15, 25]. Выберите из предложенных вариантов такой отрезок А, что логическое выражение ( ( x ɇ A) ( x ɇ P) ) V ( x ϵ Q) будет тождественно истинным, то есть будет принимать значение 1 при любом значении переменной x . 1) [0, 15] 2) [10, 25] 3) [2, 10] 4) [15, 20] Решение. Эту задачу решим с помощью таблицы истинности. Введем обозначения: P: x ϵ P, Q: x ϵ Q, A: x ϵ A Перепишем условие задания: ( ¬ A ¬ P ) V Q = A + ¬ P + Q](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img14.jpg)
![Задачи для самостоятельного решения Задание 6. На числовой прямой даны два отрезка: P =[10; 18] и Q =[31; 40]. Укажите наибольшую возможную длину такого отрезка A , что формула (x ϵ P) V ¬ ( x ϵ A) V ( x ϵ Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной x . Ответ: 9](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img16.jpg)
![Задачи для самостоятельного решения Задание 7. На числовой прямой даны два отрезка: R =[10; 30] и S =[20; 40]. Укажите наибольшую возможную длину такого отрезка T , что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной x . (x ϵ T ) ((x ϵ R ) V (x ϵ S )) Ответ: 30](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img17.jpg)
![Задачи для самостоятельного решения Задание 8. На числовой прямой даны два отрезка: R =[20; 50] и S =[30; 65]. Укажите наименьшую возможную длину такого отрезка T , что формула ¬ (x ϵ T ) ((x ϵ R ) ¬ (x ϵ S )) тождественно истинна, то есть принимает значение 1 при любом значении переменной x . Ответ: 20](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img18.jpg)
![Задачи для самостоятельного решения Задание 9. На числовой прямой даны два отрезка: P =[10; 25] и Q =[0; 12]. Выберите из предложенных вариантов такой отрезок А, что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной x . 1) [10, 15] 2) [20, 35] 3) [5, 20] 4) [12, 40] ( ( x ɇ Q) ( x ɇ P) ) V ( x ϵ A) Ответ: 4)](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img19.jpg)
![Задачи для самостоятельного решения Задание 10. На числовой прямой даны два отрезка: P = [10, 40] и Q = [30, 50]. Отрезок A таков, что формула тождественно истинна, то есть принимает значение 1 при любом значении переменной х . Какова наибольшая возможная длина отрезка A? 1) 10 2) 20 3) 30 4) 40 (( x ϵ A) ( x ϵ Q)) V ( x ϵ P) Ответ: 2)](https://fsd.multiurok.ru/html/2018/06/04/s_5b14fead2c554/img20.jpg)




![На числовой прямой даны два отрезка: P=[10; 18] и Q=[31; 40]. Укажите наимень... На числовой прямой даны два отрезка: P=[10; 18] и Q=[31; 40]. Укажите наимень...](https://documents.infourok.ru/6dedf55d-cb7c-4f63-9ce6-bcdf929781bf/0/slide_05.jpg)

![На числовой прямой даны два отрезка: P=[-10, 0] и Q=[-3, 8]. Выберите из пред... На числовой прямой даны два отрезка: P=[-10, 0] и Q=[-3, 8]. Выберите из пред...](https://documents.infourok.ru/6dedf55d-cb7c-4f63-9ce6-bcdf929781bf/0/slide_07.jpg)


![На числовой прямой даны два отрезка: R=[27; 50] и S=[30; 67]. Укажите наимень... На числовой прямой даны два отрезка: R=[27; 50] и S=[30; 67]. Укажите наимень...](https://documents.infourok.ru/6dedf55d-cb7c-4f63-9ce6-bcdf929781bf/0/slide_10.jpg)


![На числовой прямой даны два отрезка: P=[2, 10] и Q=[6, 14]. Выберите из предл... На числовой прямой даны два отрезка: P=[2, 10] и Q=[6, 14]. Выберите из предл...](https://documents.infourok.ru/6dedf55d-cb7c-4f63-9ce6-bcdf929781bf/0/slide_13.jpg)

![На числовой прямой даны два отрезка: P=[2, 20] и Q=[15, 25]. Выберите из пред... На числовой прямой даны два отрезка: P=[2, 20] и Q=[15, 25]. Выберите из пред...](https://documents.infourok.ru/6dedf55d-cb7c-4f63-9ce6-bcdf929781bf/0/slide_15.jpg)







