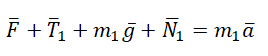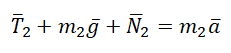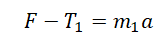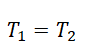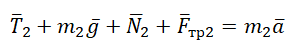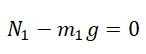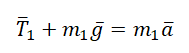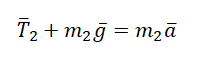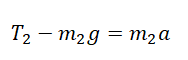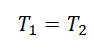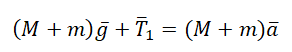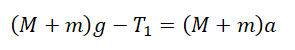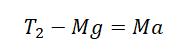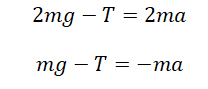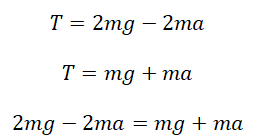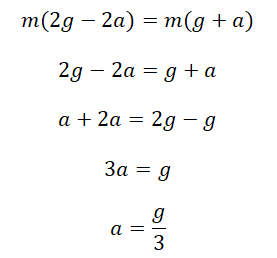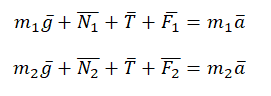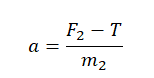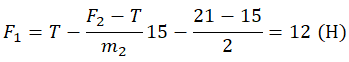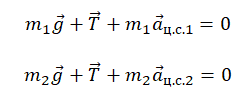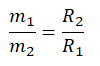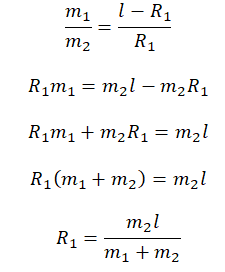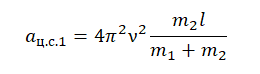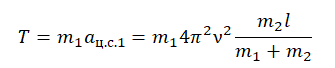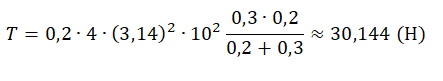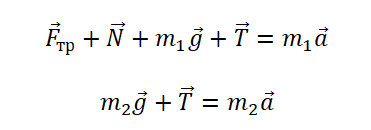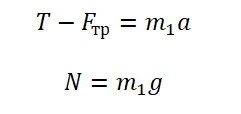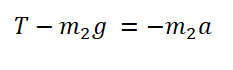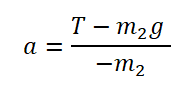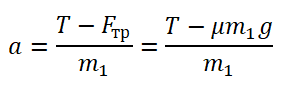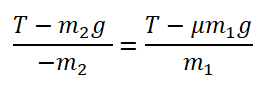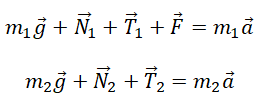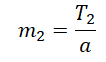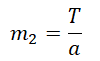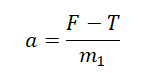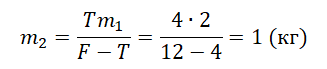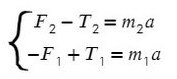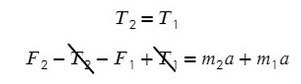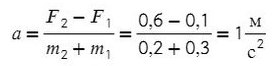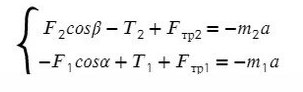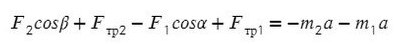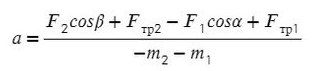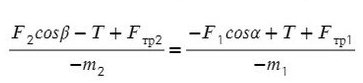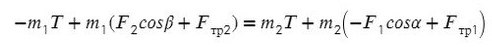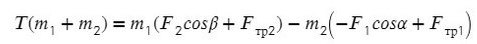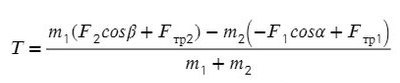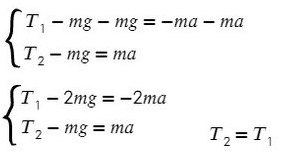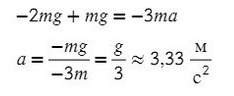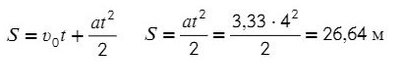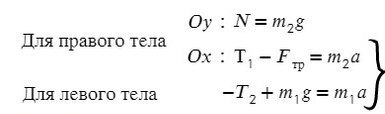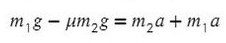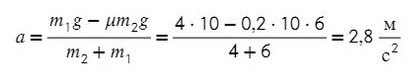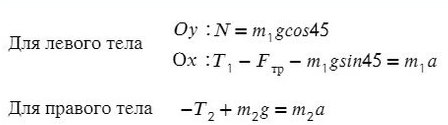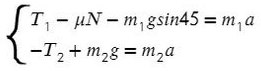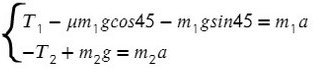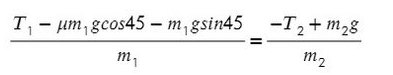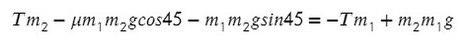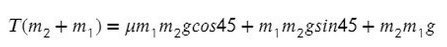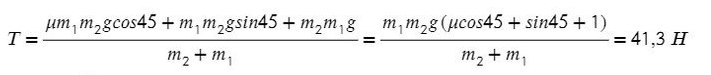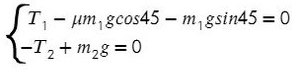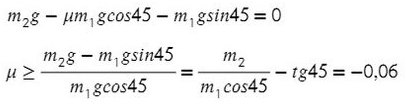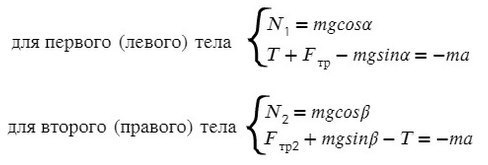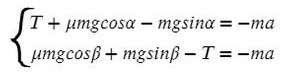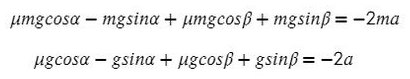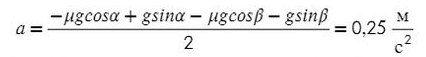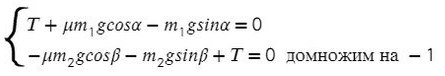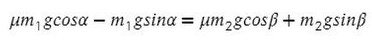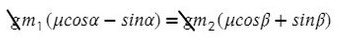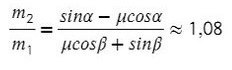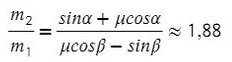Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.
Движение тел по горизонтали без трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
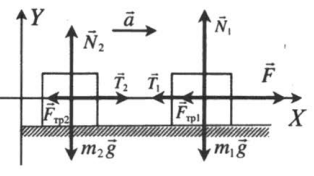
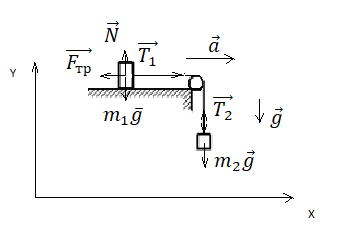
Движение по горизонтали с учетом сил трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
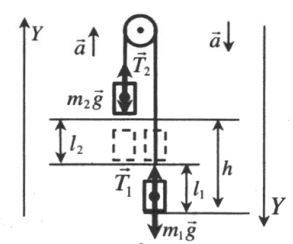
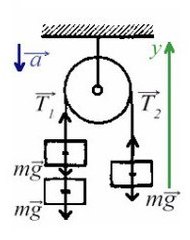
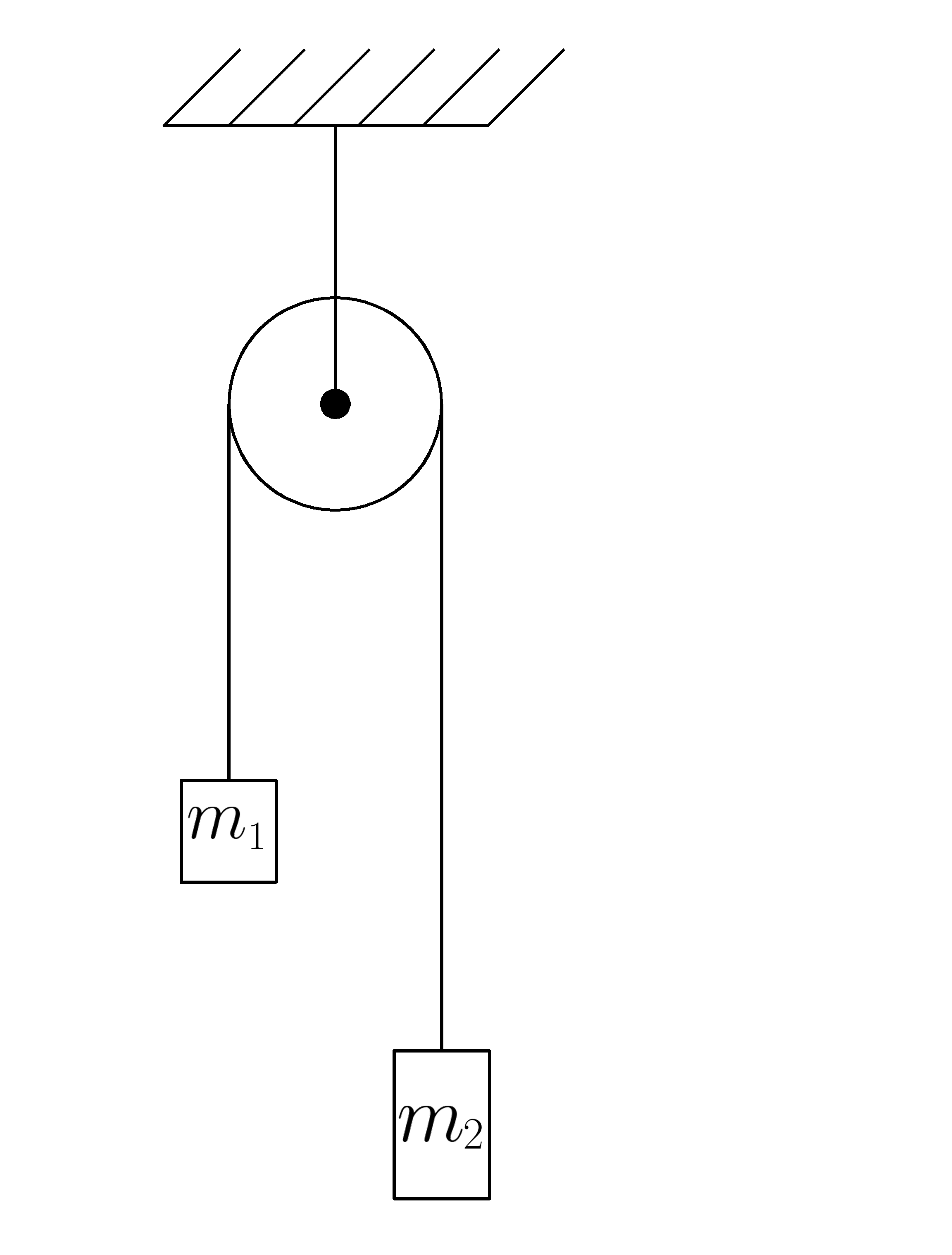
Вертикальное движение тел (m1 > m2)
h — расстояние между телами. l1 и l2 — перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l1 = l2 = l.
Решение
Расстояние между телами определяется формулой: h = l1 + l2 = 2l.
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОY для 1 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
На один из грузов положили довесок
Решение
II закон Ньютона для 1 тела:
II закон Ньютона для 2 тела:
Проекция на ось ОУ для 1 тела:
Проекция на ось ОУ для 2 тела:
III закон Ньютона:
Вес довеска определяется по формуле:
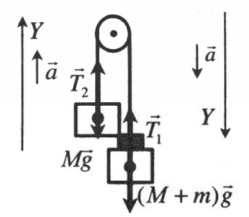
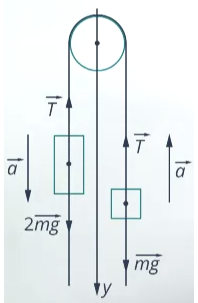
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.
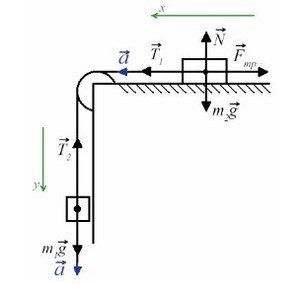
Строим чертеж:
Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь вид:
Для второго тела II закон Ньютона примет следующий вид:
Запишем проекции на ось OУ для каждого из тел:
Выразим силы натяжения нити для каждого из тел и приравняем их правые части:
Сделаем несколько преобразований:
Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с2.
Задание EF17717
Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы F1 и F2, как показано на рисунке. Сила натяжения нити Т = 15 Н. Каков модуль силы F1, если F2 = 21 Н?
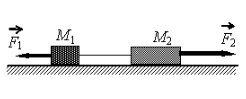
а) 6 Н
б) 12 Н
в) 18 Н
г) 21 Н
Алгоритм решения
1.Записать исходные данные.
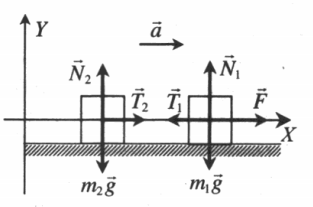
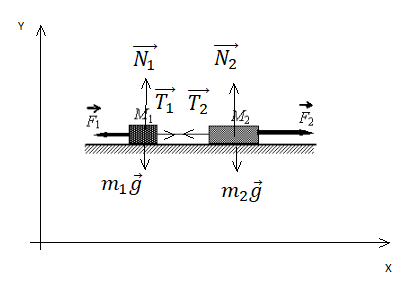
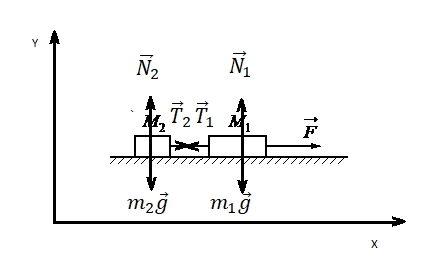
2.Сделать чертеж. Указать все силы, которые действуют на 1 и 2 тело. Выбрать систему координат.
3.Записать для каждого тела второй закон Ньютона в векторной форме.
4.Записать для каждого тела второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Выразить формулу для вычисления силы, действующей на первое тело.
6.Подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные:
• Масса тела 1: m1 = 1 кг.
• Масса тела 2: m2 = 1 кг.
• Сила натяжения нити: Т = 15 Н.
• Сила, действующая на второе тело, равна: F2 = 21 Н.
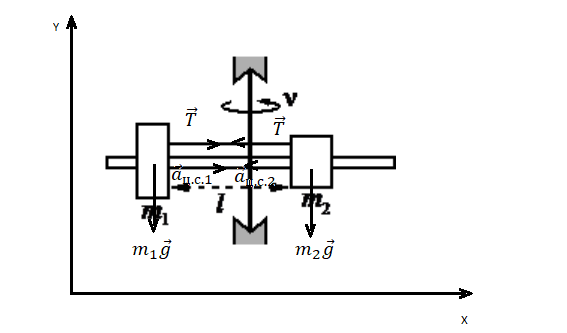
Сделаем чертеж. Систему координат выберем такую, чтобы ось ОУ была параллельная ускорению свободного падения.
Согласно третьему закону Ньютона, два тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Поэтому модули сил натяжения нити Т1 и T2 равны:
T1 = T2 = T
Учтем это при записи второго закона Ньютона для каждого из тел:
Запишем второй закон Ньютона в проекциях на оси ОХ и ОУ. Сначала для первого тела:
T – F1 = m1a
N1 = m1g
Теперь для второго тела:
F2 – T = m2a
N2 = m2g
Выразим из проекции на ось ОХ для 1 тела модуль первой силы:
F1 = T – m1a
Из проекции на ось ОХ для второго тела выразим ускорение:
Подставим ускорение в формулу для нахождения силы, действующей на первое тело:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18920
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
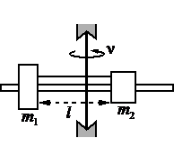
Алгоритм решения
1.Записать исходные данные. Перевести их в СИ.
2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме для каждого из тел.
4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.
5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.
6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные, сразу переведя их в СИ:
• Масса первого груза m1 = 200 г = 0,2 кг.
• Масса первого груза m2 = 300 г = 0,3 кг.
• Длина нити l = 20 см = 0,2 м.
• Натяжение нити с обеих сторон одинаково, следовательно: T1 = T2 = T.
• Частота вращения штанги ν = 600 об./мин. = 10 об./с.
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
Запишем второй закон Ньютона для первого и второго груза соответственно:
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
Подставим радиус второй окружности и выразим радиус первой окружности:
Следовательно, центростремительное ускорение первого груза равно:
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
Подставим известные данные и вычислим силу натяжения нити:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17647
По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
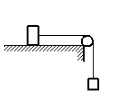
а) 2,25 Н
б) 2,7 Н
в) 3 Н
г) 3,6 Н
Алгоритм решения
• Записать исходные данные.
• Сделать чертеж. Указать все силы, действующие на тела, и их направление. Выбрать систему отсчета.
• Записать второй закон Ньютона для бруска и подвешенного к нити груза в векторной форме.
• Записать второй закон Ньютона для обоих тел в виде проекций на оси.
• Вывести формулу для вычисления искомой величины.
• Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса первого тела (движущегося по плоскости) равна: m1 = 0,9 кг.
• Масса второго тела (подвешенного к нити) равна: m2 = 0,3 кг.
• Коэффициент трения первого тела о поверхность плоскости равна: μ = 0,2.
Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:
Запишем проекцию на ось ОУ для груза на нити:
Выразим из этого выражения ускорение и получим:
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:
Приравняем правые части уравнений и получим:
Произведем вычисления:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22698
Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?
Алгоритм решения
1.Записать исходные данные.
2.Выполнить чертеж, указав все силы, действующие на каждый из грузов.
3.Записать второй закон Ньютона для обоих тел.
4.Записать второй закон Ньютона в проекциях на ось ОХ.
5.Применить третий закон Ньютона.
6.Выразить массу второго груза (найти общее решение).
Решение
Запишем исходные данные:
• Масса первого груза равна: m1 = 2 кг.
• Сила натяжения нити равна: T = 4 Н.
• Модуль силы, которая действует на систему тел: F = 12 Н.
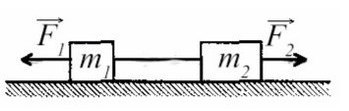
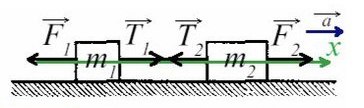
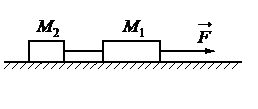
Выполним чертеж:
Запишем второй закон Ньютона для 1 и 2 тела соответственно:
Запишем второй закон Ньютона для 1 и 2 тела в проекции на ось ОХ:
F – T1 = m1a
T2 = m2a
Отсюда масса второго тела равна:
Согласно третьему закону Ньютона, тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Следовательно, силы натяжения нити равны на обоих концах:
T1 = T2 = T
Поэтому:
T = F – m1a
Из первого выражения выразим ускорение и подставим его во второе:
Подставим в формулу и получим:
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 4.5k
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
Задания Д28 C1 № 703 
Массивный брусок движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной под углом 
к горизонту. Модуль этой силы 
Коэффициент трения между бруском и плоскостью 
Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равна масса бруска? Ответ приведите в килограммах.
3
Задания Д28 C1 № 704
Брусок массой 
движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной вверх под углом к горизонту. Модуль этой силы 
Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равен коэффициент трения между бруском и плоскостью? Ответ с точностью до первого знака после запятой.
4
Задания Д28 C1 № 705
Брусок массой 
движется поступательно по горизонтальной плоскости под действием постоянной силы F, направленной под углом к горизонту. Коэффициент трения между бруском и плоскостью Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равен модуль силы F? Ответ приведите в ньютонах.
5
Задания Д28 C1 № 706
Коэффициент трения резины колес автомобиля об асфальт равен 0,4. При скорости движения 
водитель, во избежание аварии, должен придерживаться радиуса поворота, не меньшего, чем? Ответ приведите в метрах.
Пройти тестирование по этим заданиям
Динамика: движения системы связанных тел.
Проецирование сил нескольких объектов.
Действие второго закона Ньютона на тела, которые скреплены нитью
Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.
А для тех, кто все помнит, поехали!
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?
Движение происходит только на оси X.
Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T₁ и Т₂.
Выразим ускорение:
Ответ: 1 м/с²
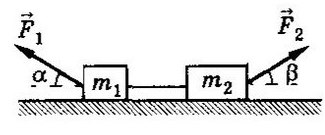
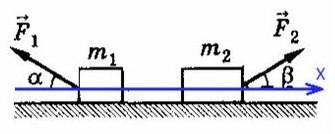
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.
Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим уравнения и выразим ускорение:
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:
Задача 3. Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.
Вычтем из первого уравнения второе:
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:
Ответ: 26,64 м
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):
(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)
Сложим два нижних уравнения для того, чтобы T сократилось:
Выразим ускорение:
Ответ: 2,8 м/с²
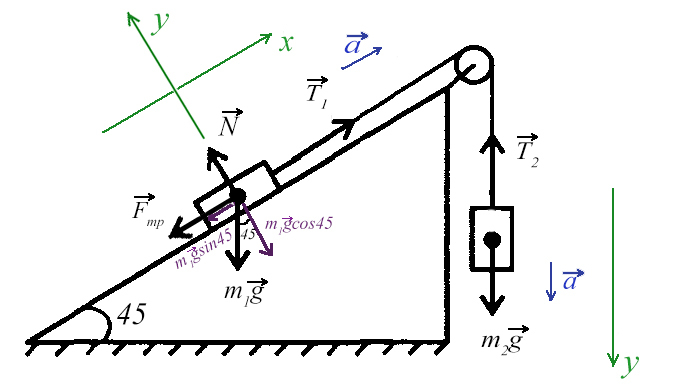
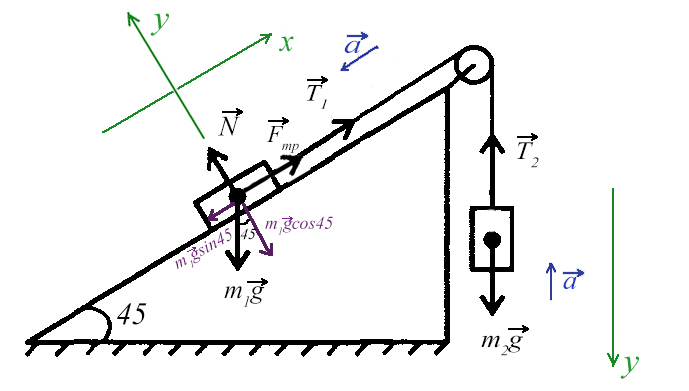
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?
Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.
Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.
Ответ: 0,06
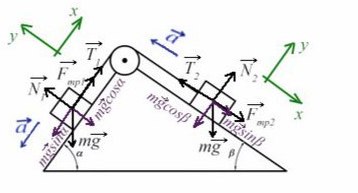
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:
Сложим уравнения и сократим на массу:
Выразим ускорение:
Подставив в любое уравнение найденное ускорение, найдем Т:
А теперь одолеем последний пункт и разберемся с соотношением масс. Сумма всех сил, действующих на любое из тел, равна нулю для того, чтобы система находилась в равновесии:
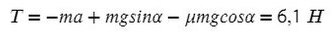
Сложим уравнения
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:
Получили, что отношение масс должно быть таким:
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.
У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.
В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.
Ответ: от 1,08 до 1,88
Задачи для закрепления.
Система связанных тел.
Будь в курсе новых статеек, видео и легкого технического юмора.
«Мыслящий ум не чувствует себя счастливым,
пока ему не удастся связать воедино
разрозненные факты, им наблюдаемые»
Г.Ч. де Хевеши
В данной теме будут рассмотрены задачи на движение связанных
тел.
Задача 1. Через блок перекинута невесомая и
нерастяжимая нить, к концам которой подвешены два тела массами 1 и 2 кг. Тела
предоставлены сами себе, а их начальные скорости равны нулю. Определите
перемещение тел за 5 с движения, а также возникающую при этом силу в нити.
Трением в блоке и его массой пренебречь.
|
ДАНО: |
РЕШЕНИЕ: Запишем второй закон Ньютона для первого и второго тела В проекциях на ось Оу Таким образом, получили систему из двух уравнений с Первое уравнение связи вытекает из условия о не Так как нить нерастяжима и в блоке нет трения, то: Второе уравнение связи будет вытекать из условия о Так как блок и веревка невесомы и нет трения в оси блока, Перепишем уравнения движения в следующем виде: Для того чтобы решить полученную систему, вычтем из первого Преобразуем уравнение Кинематическое уравнение для правого тела: В момент времени t = τ: Тогда получаем Теперь определим силу натяжения нити |
Ответ: s = 41,7
м; T1 = T2
= 13,3 Н.
Задача 2. На гладкой горизонтальной поверхности
находятся три бруска массами 1, 2 и 3 кг, связанные невесомыми нерастяжимыми
нитями. К бруску большей массы на нити, перекинутой через неподвижный блок,
подвешен груз массой 4 кг. Определите ускорение этой системы и силы натяжения
всех нитей. Считать, что масса блока пренебрежимо мала и трение в блоке
отсутствует.
|
ДАНО: |
ДАНО: Запишем второй закон Ньютона для всех четырёх связанных тел Так как нить нерастяжима, то: Так как нить невесома, то: В проекциях на оси координат: Для того, чтобы решить данную систему уравнений сложим три
Теперь силы натяжения нитей |
Ответ: a =
20 м/с2; Т1 = 20 Н; Т2 = 60 Н; Т3
= 120 Н.
Задача 3. На гладком горизонтальном столе расположен
брусок массой 5 кг, на котором находится брусок массой 3 кг. Оба бруска
соединены легкой нерастяжимой нитью, перекинутой через невесомый блок. Если к
нижнему бруску приложена сила 55 Н, а коэффициент трения между брусками равен
0,3, то чему равно ускорение, с которым движется система брусков?
|
ДАНО: |
РЕШЕНИЕ: Запишем второй закон Ньютона для каждого тела Так как нить нерастяжима и в блоке нет трения, то: Так как нить и блок невесомы, то: Согласно третьему закону Ньютона, модули сил трения, В проекциях на ось Ох: Вычтем второе уравнение из первого. Тогда получим Преобразуем последнее уравнение и выразим из него ускорение Учтем, что сила трения определяется по выражению В проекциях на ось Оу: Тогда ускорение будет равно |
Ответ: 4,6 м/с2.
Движение связанных тел.
Когда мы имеем дело с системмой связанных нитью тел нам удобнее рассматривать не
всю систему целиком, а каждое тело по отдельности.
На неподвижном блоке с разных сторон подвешены на нити грузы массами (m_1=2 кг ) и (m_2=3 кг ).
С каким ускорением движутся грузы?
(g=10 м/с^2)
Через неподвижный блок перекинута нить, к противоположным концах которой привязаны два груза.
Масса первого груза ( m_1= 1 кг ), масса второго груза ( m_2=19 кг ).
Найти силу натяжения нити (T . )
(g=10 м/с^2 )