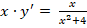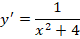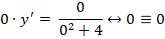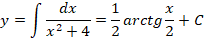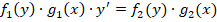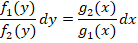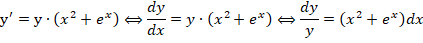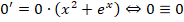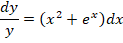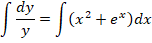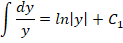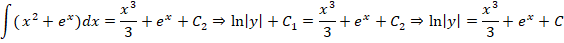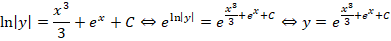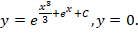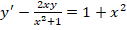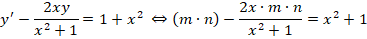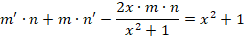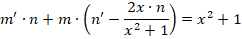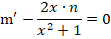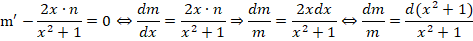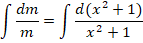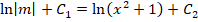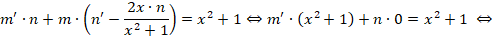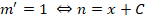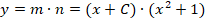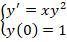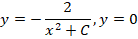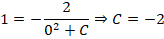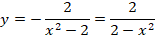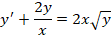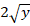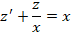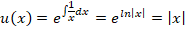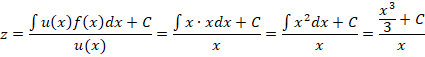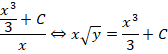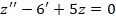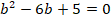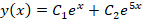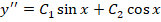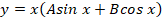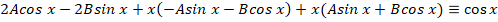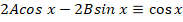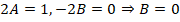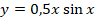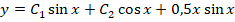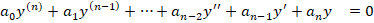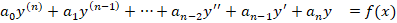3.1.
Дано дифференциальное уравнение
;
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3)
y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.2.
Дано дифференциальное уравнение:
;
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3)
y(x)
=
;
4)
y(x)
=
.
3.3.
Дано дифференциальное уравнение:
;
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3)
y(x)
=
;
4)
y(x)
= x
ln
c
x
;
5)
нет правильного ответа.
3.4.
Дано дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3)
y(x)
= c
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.5.
Дано
дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3) y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.6.
Дано дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3) y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.7.
Дано дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3) y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.8.
Дано дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3) y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.9.
Дано дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3)
y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
3.10.
Дано дифференциальное уравнение:
Общим
решением данного уравнения является
функция:
1)
;
2)
;
3) y(x)
=
;
4)
y(x)
=
;
5)
нет правильного ответа.
5.1.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) с разделяющимися
переменными ;
2) линейное ;
3)
однородное;
4) в полных дифференциалах
;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.2.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) Бернулли ;
2)
однородное ;
3) с разделяющимися
переменными ;
4) в полных дифференциалах
;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.3.
Дано
дифференциальное уравнение:
А)
Это уравнение:
1) в полных дифференциалах
;
2) линейное ;
3) однородное ;
4) с
разделяющимися переменными ;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.4.
Дано
дифференциальное уравнение:
А)
Это уравнение:
1) однородное ;
2)
линейное ;
3) с разделяющимися
переменными ;
4) в полных дифференциалах
;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.5.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) с разделяющимися
переменными ;
2) линейное ;
3)
однородное ;
4) в полных дифференциалах
;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.6.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) в полных дифференциалах
;
2) линейное ;
3) однородное ;
4) с
разделяющимися переменными ;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.7.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) с разделяющимися
переменными ;
2) линейное ;
3)
однородное ;
4) в полных дифференциалах
;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5) нет правильного ответа .
5.8.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) в полных дифференциалах
;
2) линейное ;
3) однородное ;
4) с
разделяющимися переменными ;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5)
нет правильного ответа .
5.9.
Дано дифференциальное уравнение:
А)
Это уравнение:
1) однородное;
2)
линейное ;
3) в полных дифференциалах
;
4) с разделяющимися переменными ;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5)
нет правильного ответа .
5.10.
Дано
дифференциальное уравнение:
А)
Это уравнение:
1) в полных дифференциалах
;
2) линейное ;
3) однородное ;
4)
с разделяющимися переменными ;
5)
нет правильного ответа ;
Б)
Общий интеграл данного уравнения
есть:
1)
;
2)
;
3)
;
4)
;
5)
нет правильного ответа .
6.1.
;
Ответы:
1)
однородное, y
= xt
;
2) однородное, y
= uv
;
3) линейное, y
= uv
;
4) с разделяющимися переменными ;
5)
линейное, y
= xt.
6.2.
;
Ответы:
1)
линейное относительно x;
x
= uv
;
2) линейное относительно y;
подстановка y
= xt
;
3) уравнение с разделяющимися
переменными ;
4) однородное; y
= xt
;
5) уравнение в полных дифференциалах
.
6.3.
;
Ответы:
1)
линейное относительно y;
y
= uv
;
2) линейное относительно y;
y
= xt
;
3) однородное; y
= uv
;
4) однородное; y
= xt
;
5) Бернулли; y
= uv
.
6.4.
;
Ответы:
1)
уравнение Бернулли; y
= uv
;
2) уравнение Бернулли; y
= xt
;
3) однородное; y
= xt
;
4) в полных дифференциалах ;
5) с
разделяющимися переменными.
6.5.
;
Ответы:
1)
с разделяющимися переменными ;
2)
линейное; y
= uv
;
3) однородное; y
= xt
;
4) уравнение Клеро; привести к виду
y
= xy’
;
5) в полных дифференциалах.
6.6.
;
Ответы:
1)
уравнение Бернулли; y
= uv
;
2) линейное; y
= xt
;
3) однородное; y
= uv
;
4) в полных дифференциалах ;
5) с
разделяющимися переменными.
6.7.
;
Ответы:
1)
приводящееся к уравнению с разделяющимися
переменными; u=
x
+ y
;
2) однородное; y
= xt
;
3) линейное; y
= xt
;
4) Бернулли; y
= uv
;
5) в полных дифференциалах.
6.8.
;
Ответы:
1)
уравнение Бернулли относительно x;
x
= uv
;
2) однородное; y
= xt
;
3) линейное; y
= xt
;
4) в полных дифференциалах ;
5) с
разделяющимися переменными.
6.9.
;
Ответы:
1)
уравнение в полных дифференциалах ;
2)
линейное; y
= uv
;
3) однородное; y
= xt
;
4) линейное; y
= xt
;
5) с разделяющимися переменными.
6.10.
;
Ответы:
1)
уравнение Бернулли; y
= uv
;
2) однородное; y
= xt
;
3) в полных дифференциалах ;
4) с
разделяющимися переменными ;
5)
линейное; y
= xt
.
1.пункт
-
Решением
какого уравнения является функция
y=(C^2-x^2)/2x(x+y)dx+xdy=0
-
Решением
какого уравнения является функция
y=√(1+x^2 )yy’=x
-
Решением
какого уравнения является функция
y=2/cosxy’-tgxy=0
-
Решением
какого уравнения является функция
y=5x^2y’x-y=0
-
Решением
какого уравнения является функция
y=c^3xy’’+y’-12y=0
-
Решением
какого уравнения является функция
y=exy’x-y=0
-
Решением
какого уравнения является функция
y=sinxy’+yctgx=0
-
Решением
какого уравнения является функция
y=x^2-4xxdy-ydx=(x^2)dx
-
Решением
какого уравнения является функция
y=x^3+Cy’=3(x^2)
Дано
дифференциальное уравнение
. Частным
решением уравнения, удовлетворяющим
условие
является
функция:
2
пункт.
-
Дано
дифференциальное уравнение
2y’√x=y. Частным решением уравнения
удовлетворяющим условие y(4)=1 является
функцияy(4)=e^(√x-2)
-
Дано
дифференциальное уравнение 2y’√x=y.
Общим решением данного уравнения
является функцияy
(x)=ce^√x -
Дано
дифференциальное уравнение 2y’√x=y.
Общим решением данного уравнения
является функцияy
(x)=ce^√x -
Дано
дифференциальное уравнение x^2y’+y^2=0.
Общим решением данного уравнения
является функцияy(x)=x/(cx-1)
-
Дано
дифференциальное уравнение x^2y’+y^2=0.
Частным решением данного уравнения ,
удовлетворяющим условию y(-1)=1 является
функцияy(-1)=-x
-
Дано
дифференциальное уравнение y’-2x=0. Общим
решением данного уравнения является
функцияy(x)=x^2+C
-
Дано
дифференциальное уравнение y’-2x=0. Общим
решением данного уравнения является
функцияy(x)=x^2+C
-
Дано
дифференциальное уравнение y’-2x=0. Частным
решением удовлетворяющим условие
y(1)=2 является функцияy(1)=x^2+1
-
Дано
дифференциальное уравнение
y’-sinx=0. Частным решением уравнения
удовлетворяющим условие y(0)=3 является
функцияy(0)=
4 – cosx -
Дано
дифференциальное уравнение y’-sinx=0. Общим
решением данного уравнения является
функцияy=C-cosx
3
пункт.
-
Дано
дифференциальное уравнение
(x+2y)dx-xdy=0 ;Общим
решением данного уравнения является
функция:y(x)=(x^2)c-x
-
Дано
дифференциальное уравнение:
y’=-(x+y)/x ;Общим
решением данного уравнения является
функция:y(x)=(c/x)-(x/2)
-
Дано
дифференциальное уравнение:y=(y/x)-1
;Общим
решением данного уравнения является
функция:y(x)=xln(c/x)
-
Дано
дифференциальное уравнение:
(x-y)ydx-(x^2)dy=0 ;Общим
решением данного уравнения является
функция:y(x)=(x)/(ln|xc|)
-
Дано
дифференциальное уравнение:
y’=(9^2)/(x^2) -y/xОбщим
решением данного уравнения является
функция:y(x)=(2x)/(1-(x^2)(c^2))
-
Дано
дифференциальное уравнение:
xy’=yln(x/y) ;Общим
решением данного уравнения является
функция:y(x)=xe^(c/x)
-
Дано
дифференциальное уравнение:
((y^2)-2xy)dx+(x^2)dy=0 ;Общим
решением данного уравнения является
функция:y(x)=((x^2)c)/(1+xc)
-
Дано
дифференциальное уравнение:
(y+√(xy))dx=xdy ;Общим
решением данного уравнения является
функция:y(x)=(x/4)(ln^2)|xc|
-
Дано
дифференциальное уравнение:
y’=e^(y/x)+(y/x) ;Общим
решением данного уравнения является
функция:y(x)=-ln(ln(c/x))
-
Дано
дифференциальное уравнение:
((x^2)-3(y^2))dx+2xydy=0 ;Общим
решением данного уравнения является
функция:y(x)=|x|√(xc+1)
шпаргалка по Дифурам (Шпаргалочка)
2017-07-092017-07-09СтудИзба
Описание файла
Файл «шпаргалка по Дифурам» внутри архива находится в папке «Шпаргалочка». Документ из архива «Шпаргалочка»,
который расположен в категории «».
Всё это находится в предмете «математический анализ» из 2 семестр, которые можно найти в файловом архиве РТУ МИРЭА.
Не смотря на прямую связь этого архива с РТУ МИРЭА, его также можно найти и в других разделах. Архив можно найти в разделе «к экзамену/зачёту», в предмете «математический анализ» в общих файлах.
Онлайн просмотр документа «шпаргалка по Дифурам»
Текст из документа «шпаргалка по Дифурам»
|
1.Дифференциальные уравнения. Обыкновенным дифференциальным уравнением 1 порядка называется уравнение вида
Частным решением дифференциального уравнения называется любая функция |
2.Уравнения с разделяющимися переменными. Дифференциальное уравнение 1 порядка Уравнение, записанное в симметричной форме Разделить переменные – значит преобразовать уравнение так, чтобы каждая переменная содержалась только в том слагаемом, которое содержит её дифференциал. Вид уравнения: Решение уравнения: приводим к уравнению с разделенными переменными (
В частности, уравнение вида
Пример. Решение: разделим обе части ур-ния на
Потенцируя, найдем общее решение в виде |
3. Уравнения, приводящие к уравнениям с разделяющимися переменными. Многие дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. К числу таких уравнений относятся, например, уравнения вида
И переменные разделились. Интегрируя, получим Пример. Разделяя переменные получим и интегрируя получим К уравнен. с разделяющимися переменными приводятся и так называемые однородные дифференциальные урав-ния 1 порядка имеющие вид |
|
4. Линейные дифференциальные уравнения 1 порядка. Линейным дифференциальным уравнением порядка называется уравнение, линейное относительно функции и её производной:
Здесь Однородные линейные уравнения (Q=0) могут быть решены разделением переменных. Неоднородные линейные уравнения можно свести к последовательности двух уравнений с разделяющимися переменными подстановкой
В линейном однородном уравнении переменные разделяются: И интегрируя получаем
При делении на у мы потеряли решение у |
5. Уравнения 1 порядка. Метод вариации произвольной постоянной. Для интегрирования неоднородного линейного уравнения
Может быть применен так называемый метод вариации постоянной При применении этого метода сначала интегрируется соответствующее однородное уравнение О При постоянном с, функция Где с(х) – новая неизвестная функция х. Вычисляя производную
И подставляя в исходное неоднородное уравнение получим
Или Откуда интегрируя находим
А следовательно
(*) Итак общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения. и частного решения неоднородного уравнения получающегося из (*) при с1=0. Пример
Интегрируем соответствующее однородное уравнение
Считаем с функцией х, тогда
И подставляя в исходное уравнение после упрощения получаем
Следовательно общее решение
|
6. Уравнение 1 порядка.Метод Бернулли Вид уравнения: Решение уравнения: метод Бернулли. Решение будем искать в виде |
|
7. Уравнение Бернулли Решение осуществляется методом Бернулли или сведением к линейному, путем замены переменных. Например, уравнение Бернулли имеющее вид Или
Заменой переменных
И, подставляя в (*) получим линейное уравнение Пример.
|
8. Уравнения в полных дифференциалах Вид уравнения:
Пример:
|
9. Интегрирующий множитель Рассмотрим уравнение Функция Инт.мн-ль легко находится в след.случаях:
Пример:
Найдем Домножим первоначальное уравнение на
Получили уравнение в полных дифференциалах, где
Интегрируем
Дифференцируем это равенство по y:
|
|
10. Дифференциальные уравнение высших порядков. Общие сведения Диф.уравнения n порядка имеют вид Теорема.Существует единственное решение дифференц. уравнения n порядка
Общим решением дифф.уравнения n порядка называется множество решений, состоящее из всех без исключения частных решений. Если правая часть уравнения в некоторой области изменения аргументов удовлетв.условиям теоремы, то общ.решение зависит от n параметров, в качестве которых могут быть выбраны, например начальные значения искомой функции и ее производных. |
11. Уравнения, допускающие понижение порядка.
Пример.
Пример. |
14. Линейные дифференциальные уравнения высших порядков Лин.Диф.Ур-нием n порядка называется уравнение линейное относительно неизвестной функции и ее производных и, следовательно, имеющее вид:
Если правая часть Т1. Если Т2. Если Замечание: Если 2 решения Т3.Если
Т4. Если на каком либо отрезке Т5. Если 1.это выражение явл-ся решением 2.это решение явл-ся общим решением.( |
|
15. Линейные неоднородные дифференциальные уравнения высших порядков. Метод Подбора
Т.Общее решение лин.неоднородного ур-ния может быть представлено как сумма двух решений.
Пусть
Метод подбора.
Если
Пример.
|
16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной
Пример.
…
|
17. Уравнение Эйлера
Линейно входящие в ур-ние Эйл.
Пример.
Если уравнение не однородное то переменную x на Если уравнение более высокого порядка, чем 2 то замена |
|
13. Уравнение Клеро
Интегральная кривая определяемая данными уравнениями является огибающей семейства интегральных прямых.(т.е. огибающая некоторого семейства Особое решение. Необходимо исключить параметр Пример. Общее: Особое решение: Исключая параметр |
18. Общее понятие разностных уравнений В качестве аналогов дифф.уров можно рассм. разностные ур-ния. При использовании обратных разностей линейные неоднородные разностные уравнения имеют вид: Это разностное ур-ние можно рассматривать как рекуррентное отношение позволяющее вычислять значения y[n] для любых n по известному значению функции в правой части уравнения и начальным условиям y[n-1],…y[n-m]. Такие вычисления легко выполняются на счетных машинах, а также не представляют никаких принципиальных трудностей и при ручном счете, даже в тех случаях кошда коэффициенты в левой части уравнения меняются по времени. Это отличает разностные уравнения от непрерывных аналогов – дифф.уров. Общее решение однородного разностного уравнения при некратных корнях характеристичесого уравнения может быть записано след.образом
|
19. Решетчатые функции Решетчатая ф-ция не обязательно должна формироваться из некоторой исходной непрерывной функции. Любая числовая посл-ть некоторой величины, определенной в дискретные равноотстоящие моменты времени, может трактоваться как решетчатая функция. Обратная задача – формирование непрерывной функции из решетчатой – не может быть решена однозначно, т.к. ф-ции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций. Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции. Прямая и обратная разности. Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность
|
|
20. Конечные разности элементарных функций f(n)=bn+a ∆f(n)=b(n+1)+a-b(n)-a=b ∆2f(n)=∆f(n+1)-∆f(n)=0 f(n)=n2+bn+c ∆f(n)=(n+1)2+b(n+1)+c-n2-bn-c=2n+b+1 ∆2f(n)=2(n+1)+b+1-2n-b-1=2 ∆3f(n)=0 f(n)=ean ∆f(n)=ea(n+1)-ean=ean(ea-1) ∆2f(n)=ea(n+1)(ea-1)-ean(ea-1)=ean(ea-1)2 ∆kf(n)=ean(ea-1)k |
21. Разностные уравнения. Линейные разностные уравнения. — уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x1, x2, …, xn.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени. Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Δf/Δt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность y = y(t+1) – y(t), которую часто называют первой разностью. При этом различают правую и левую разности, в частности y = y(t) – y(t–1) — левая, а приведенная выше — правая. Можно определить вторую разность: Δ(Δy) = Δy(t + 1) – Δy(t) = y(t + 2) – – 2y(t + 1) + y(t) и разности высших порядков Δn. Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке: f [y(t), Δy(t), …, Δny(t)] = 0. Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек y(t), y(t+1), …, y(t+n). При этом разность между последним и первым моментами времени называется порядком уравнения. При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Δt стремится к нулю. При исследовании функций многих переменных по аналогии с частными производными (см. Производная) вводятся также частные разности. Линейные разностные уравнения первого порядка y(x + 1) − ay(x) = 0. Линейное однородное разностное уравнение первого порядка с постоянными коэффициентами. y(x + 1) − ay(x) = f(x). Линейное неоднородное разностное уравнение первого порядка с постоянными коэффициентами. y(x + 1) − xy(x) = 0. y(x + 1) − a(x − b)(x − c)y(x) = 0. y(x + 1) − R(x)y(x) = 0, где R(x) — рациональная функция. y(x + 1) − f(x)y(x) = 0. y(x + a) − by(x) = 0. y(x + a) − by(x) = f(x). y(x + a) − bxy(x) = 0. y(x + a) − f(x)y(x) = 0. Линейные разностные уравнения второго порядка, yn = y(n) yn+2 + ayn+1 + byn = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами. yn+2 + ayn+1 + byn = fn. Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами. y(x + 2) + ay(x + 1) + by(x) = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами. y(x + 2) + ay(x + 1) + by(x) = f(x). Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами. y(x + 2) + a(x + 1)y(x + 1) + bx(x + 1)y(x) = 0. |
23. Линейные стационарные неоднородные разностные уравнения Метод подбора. Методом Лагранжа может быть решено любое неоднородное уравнение с постоянными коэффициентами. Однако если свободный член в уравнении
где Pm1(x) и Qm2(x) — многочлены степеней, соответственно, m1 и m2, можно сразу указать вид частного решения в форме с неопределёнными коэффициентами. Общее правило таково: составим из коэффициентов при x в экспоненте и тригонометрических функциях число Технику работы с этим правилом будем осваивать, начиная с простейших случаев, при этом будем формулировать частные правила, вытекающие из общего. I. Если f(x) = Pm(x) (т.е. f(x) — многочлен степени m), то частное решение ищется в виде yчн(x)= Rm(x), если число 0 не является корнем характеристического уравнения, и в виде yчн(x)= xr Rm(x), если число 0 — корень характеристического уравнения кратности r. Rm(x) — многочлен степени m с неопределёнными коэффициентами. Это правило следует из общего, если записать f(x) = Pm(x) в виде f(x) = e0 x [Pm(x) cos 0x + 0 sin 0x]. В этом случае s0 = 0 + 0i, m1 = m, m2 = 0, max(m1, m2) = m, поэтому yчн(x)= xr e0 x [Rm(x) cos 0x + Sm(x) sin 0x] = xr Rm(x) . Примеры: 1. Найти общее решение уравнения Решение: характеристическое уравнение k2 — 5 k + 6 = 0, его корни k1 = 2, k2 = 3, yoo = C1e 2x + C3e 3x. Степень многочлена m = 3, число 0 не является корнем характеристического уравнения (r = 0), поэтому yчн(x) ищем в виде многочлена третьей степени с неопределёнными коэффициентами: yчн(x)= xr Rm(x) = Ax3 + Bx2 + Dx + E. Тогда x3 6A = 1; A = 1/6; x2 — 15A + 6B =0; B = 15A/6 = 5/12; x 6A – 10B + 6D = -2; D = 5B/3 – A – 1/3 = (25 – 6 – 12)/36 = 7/36; 1 2B – 5D + 6E = 0; E = 5D/6 – B/3 = 35/216 – 5/36 =(35 – 30)/216 = 5/216. Итак,
|
|
24. Линейные стационарные неоднородные разностные уравнения. Метод вариации произвольных постоянных. Общее решение линейного уравнения с правой частью получается из общего решения соответствующего уравнения без правой части с помощью квадратур. Для этого можно применить следующий прием. В общем решении уравнения без правой части заменяем все произвольные постоянные неизвестными функциями. Полученное выражение дифференцируем и попутно подчиняем неизвестные функции добавочным условиям, упрощающим вид последовательных производных. Подставляя выражение производных y’, y’’, y’’’ и т.д. в данное уравнение, получаем еще одно условие, налагаемое на неизвестные функции. Тогда оказывается возможным найти первые производные всех неизвестных функций и остается выполнить квадратуры. Этот метод применим к линейным уравнениям любого порядка как с постоянными, так и с переменными коэффициентами. Рассмотрим уравнение второго порядка: y’’+P(x)y’+Q(x)=R(x) (1) Пусть общее решение соответствующего уравнения без правой части есть y=C1f1(x)+C2f2(x). (2) Ищем общее решения уравнения (1) в виде (2), считая теперь C1 и С2 неизвестными функциями от х. Дифференцируя (2), находим: y’=C1f1’(x)+C2f2’(x)+ C1’f1(x)+C2’f2(x) (3) Вводим добавочное условие C1’f1(x)+C2’f2(x)=0. (4) Тогда вид первой производной упрощается, и мы имеем: y’= C1f1’(x)+C2f2’(x). (5) Дифференцируя еще раз имеем: y’’= C1f1’’(x)+C2f2’’(x)+ C1’f1’(x)+C2’f2’(x) (6) После подстановки выражений (2), (5) и (6) в уравнение (1) все члены, содержащие С1, взаимно уничтожатся (ибо функция y=f1(x) есть решение уравнения y’’+Py’+Qy=0); точно так же взаимно уничтожатся все члены, содержащие С2, и мы получим еще одно условие C1’f1’(x)+C2’f2’(x)=R(x) (7) Условия (4) и (7) позволяют найти выражения производных С1’, C2’ и остается выполнить квадратуры. |
25. Общие сведения о линейных системах. Системой дифференциальных уравнений называется совокупность уравнений, содержащих несколько неизвестных функций и их производные, причем в каждое из уравнений входит хотя бы одна производная. На практике имеют дело с такими системами, где число уравнений равно числу неизвестных. Система называется линейной, если неизвестные функции и их производные входят в каждое из уравнений только в первой степени. Линейная система имеет нормальный вид, когда она решена относительно всех производных. |
26. Метод сведения линейной системы к одному уравнению. Пример 1. Система дифференциальных уравнений
— линейная; она имеет нормальный вид. в этом примере мы имеем линейную систему с постоянными коэффициентами (коэффициенты при неизвестных функциях и их производных постоянны). Из линейной системы (присоединяя к ней уравнения, выведенные дифференцированием) можно исключить все неизвестные (и их производные), кроме одной. Полученное уравнение будет содержать одну неизвестную функцию и ее производную первого и более высоких порядков. Это уравнение тоже будет линейным, а если исходная система была системой с постоянными коэффициентами, то и найденное уравнение высшего порядка будет иметь постоянные коэффициенты. Разыскав неизвестную функцию этого уравнения, подставляем ее выражение в данные уравнения и находим остальные неизвестные функции. Пример 2. Решить линейную систему примера 1. Решение: Чтобы исключить y и
Из уравнения (1) находим выражение y через t, x и
Находим его общее решение x=C1e2t+C2e-3t — Это выражение подставляем в уравнение (1) и находим вторую неизвестную функцию y = — |
|
27. Системы дифференциальных уравнений с постоянными коэффициентами
В векторной форме:
Характеристическое уравнение
Или Нахождение общего решения системы по методу Эйлера Если
2. Если
Коэффициенты многочленов можно определить, подставив выражения для y1, y2, …, yn в исходную систему. Найдя решения, соответствующие каждому корню характеристического уравнения, общее решение системы получим как линейную комбинацию этих решений. Например, если все корни характеристического уравнения простые, а решениями, соответствующими этим корням
то общее решение этой системы имеет вид: О |
28. Решение дифференциальных уравнений с использованием преобразования Лапласса Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так линейные дифференциальные уравнения становятся алгебраическими.
Решение.Находим изображения правых и левых частей уравнения
Решив систему, получим
Разложим каждую дробь на простые дроби вида
Для
Откуда Для
Откуда
Для
Откуда
Ответ:
|
1. Дифференциальные уравнения. 2. Уравнения с разделяющимися переменными. 3. Уравнения, приводящие к уравнениям с разделяющимися переменными. 4. Линейные дифференциальные уравнения 1 порядка. 5. Уравнения 1 порядка. Метод вариации произвольной постоянной. 6. Уравнение 1 порядка.Метод Бернулли 7. Уравнение Бернулли 8. Уравнения в полных дифференциалах 9. Интегрирующий множитель 10. Дифференциальные уравнение высших порядков. Общие сведения 11. Уравнения, допускающие понижение порядка. 13. Уравнение Клеро 14. Линейные дифференциальные уравнения высших порядков 15. Линейные неоднородные дифференциальные уравнения высших порядков. Метод Подбора 16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной 17. Уравнение Эйлера 18. Общее понятие разностных уравнений 19. Решетчатые функции 20. Конечные разности элементарных функций 21. Разностные уравнения. Линейные разностные уравнения. 23. Линейные стационарные неоднородные разностные уравнения Метод подбора. 24. Линейные стационарные неоднородные разностные уравнения. Метод вариации произвольных постоянных. 25. Общие сведения о линейных системах. 26. Метод сведения линейной системы к одному уравнению. 27. Системы дифференциальных уравнений с постоянными коэффициентами 28. Решение дифференциальных уравнений с использованием преобразования Лапласса |
Свежие статьи
Популярно сейчас
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
649
Средний доход
с одного платного файла
Обучение Подробнее
На Физтехе лучше всего я выучил дифференциальные уравнения. Потому что феерично сдавал их аж четыре раза.
Система обучения в МФТИ уникальна тем, что можно сдать экзамен, абсолютно ничего не делая весь семетр, и не сдать, посетив все лекции и семинары и зная предмет достаточно хорошо. И мне это чертовски нравилось. Мой незамысловатый подход к учебе (скорее обход учебы) гарантировал безудержное веселье почти на каждом экзамене.
Были истории карнавального успеха, когда удавалось обмануть всех и получать хорошие оценки, не зная даже названия предмета. Были не менее феерические провалы, когда я палился в последний момент, или же отвечал долго, уверенно и правильно, но из-за странных заскоков преподавателей получал пересдачи.
Да и у кого из физтехов таких историй не было?
Бакалавриат обошелся мне в 12 пересдач, не считая зачетов. Самые долгие отношения случились с аналитической геометрией в первом семестре (сдал с 4-го раза) и с дифференциальными уравнениями в четвертом (тоже с 4-го раза).
Диффуры и матан на втором курсе у моей группы вел преподаватель по фамилии Ждановский. Многие мои одногруппники его недолюбливали, но мне он очень импонировал своим живым чувством юмора, а также тем, что не чурался пообщаться со студентами на отвлеченные темы. На какой-то из пар он сказал мне, что на Физтехе я занимаю чужое место. Мы с интересом подискутировали на эту тему, и я понял, что концептуально он в чем-то прав. Еще я понял, что сдать задания будет непросто.
Я не знаю, как сейчас в МФТИ принимают экзамены, поэтому на всякий случай уточню: год изучения диффуров венчали письменный и устный экзамены. За устный можно получить не больше, чем за письменный, то есть, если я напишу письменный на итоговый «удовл», то на устном могу получить или три, или пересдачу. Если суммы баллов на письменном не хватит даже для трояка, то это автоматическая пересдача.
В обратную сторону это не работает. Если написать на «отлично», то можно получить за устный и 5, и 4, и 3, и пересдачу.
По ходу семестра надо сдать несколько заданий. Если не сдать, то из результата письменного экзамена вычитается какое-то количество баллов.
По счастью, Ждановский любил футбол, и задания по матану я сдал во многом благодаря четырем голам, забитым мной ФАЛТу на Матче века. Пришел на сдачу прямиком с коробки, как только отыграла моя команда, прямо в форме. Увы, на диффуры это правило не распространилось, поэтому на письменном экзамене меня ожидало снятие баллов за плохую работу в семестре.
Надо сказать, что свое первое в жизни дифференциальное уравнение я решил ровно за день до письменного экзамена. Таким образом, чтобы наскрести на тройку, нужно было сесть на экзамене рядом с нужными людьми и аккуратненько все списать, что я неоднократно проделывал и ранее, и потом.
Экзамен мы писали всем потоком. Я спрятался за спинами однокурсников где-то в середине Большой химической аудитории, чтобы случайно не попасться на глаза Ждановскому.
Пока другие преподаватели копошились в листочках с заданиями и занимались рассадкой прибывших в аудиторию студентов, он суетливо ходил вдоль первого ряда, пересчитывал студентов и хмурил брови. Наконец, когда весь наш поток расселся, он остановился и пробасил на всю аудиторию: «Заварин!».
Сто с лишним человек затаили дыхание. Я спрятался под партой.
Секундная пауза. Тишина.
— Заварин!!! — громче и требовательней гаркнул Ждановский. Я понял, что сопротивление бесполезно, и вяло поднял руку.
— Я здесь.
— На первый ряд! — торжественно изрек он.
Аудитория содрогнулась от смеха. Аудитория ликовала. Спускаясь к первому ряду, я чувствовал себя гладиатором, выходящим на бой со львами. Вслед неслось улюлюканье и громовые раскаты хохота.
Усевшись на первый ряд, я заметил направленный на меня из-под толстенных очков безразличный взгляд Беклемишева, хмурое лицо Ивановой и жизнерадостную улыбку Ждановского. Совершенно очевидно, что при таких обстоятельствах шансов списать, а значит, написать контрольную хотя бы на «удовл» у меня не было.
В итоге за этот экзамен я кое-как наскреб 10 баллов (из 50), из которых 8 с меня списали за несданные задания. Пороговый балл на тройбас был 12 или 13, поэтому я даже порадовался, что не сдавал эти задания в семестре.
В общем, это было абсолютно справедливо: ничего не знаешь, не смог обхитрить препода — извольте на пересдачу. То есть, обижаться и расстраиваться совершенно не было повода — сам ведь виноват.
…
Оставшиеся в той сессии шесть экзаменов я кое-как спихнул, подработки свернул до начала экзаменов, а оставшиеся мудро приберег на лето. Квновский сезон также взял летнюю паузу. Сессия закончилась, и у меня была ровно неделя, чтобы подготовиться к пересдаче. Что ж, всю неделю я добросовестно посвятил диффурам. На мой взгляд, за такой большой срок можно расшарить вообще любую дисциплину, так что, к пересдаче я подходил сверхготовым.
Чтобы допуститься непосредственно к самой пересдаче, надо было написать дебильник — решить пять не самых сложных задач. Дальше эти задачи проверяет кто-то из преподавателей, потом он выходит из аудитории к ожидающим в коридоре своей участи студентам и оглашает список из 4-5 фамилий. Эти студенты либо отправляются на следующую пересдачу, если завалили дебильник, либо тянут билет и готовятся отвечать, скорее всего, этому же преподавателю.
Вышел какой-то препод, назвал мою фамилию в компании с еще четырьмя ребятами, и скрылся за дверьми аудитории. Пока мы направлялись следом, один парень тихо произнес: «Нам пиз*ец,..» и, поймав мой недоуменный взгляд, добавил: «Это Умнов-младший».
Умного-младшего мои знакомые в основном люто ненавидели. По учебным делам я с ним не сталкивался, поэтому никакого мнения на этот счет у меня не было.
Зато вот благодаря пересдаче появилось. Мы расселись на одном из рядов, возле Умнова стопочкой лежали наши дебильники и зачетки.
— Значит так, ребята. Я считаю, что все эти пересдачи — это профанация. Если студент получает пересдачу, значит, он не учился весь семестр, значит, такой студент Физтеху не нужен, — с этими словами он подвинул к нам стопку наших зачеток. — Я вам всем уже выставил двойки в ведомость.
Сказать, что мы немного подофигели — значит ничего не сказать. Настолько, что даже не попробовали внятно оспорить это решение. На вопрос, можно ли проапеллировать к результатам проверки дебильников, Умнов презрительно фыркнул и сказал, что даже не стал их проверять.
На самом деле, в данной ситуации мало что можно сделать. Если уж преподаватель хочет завалить студента, то что может ему помешать? Теоретически можно было бы обратиться к кому-нибудь там на кафедре и как-то оспорить это решение. Тогда Умнов проверил бы дебильник и, возможно, даже допустил бы студента к ответу. И что? Отвечать-то все равно пришлось бы ему.
Так что, я пожал плечами, забрал зачетку и вышел из аудитории, вспоминая, как примерно за полгода до этого я сидел на какой-то паре, когда в кабинет ворвалась студентка и начала вопить что-то нечленораздельное и махать руками. Забежав в соседнюю аудиторию, я увидел, как на полу лежит весь измазанный мелом мужик, пускает слюни и смотрит ничего не выражающим взглядом куда-то в потолок.
Группа этого преподавателя сидела за партами, пребывая в небольшом шоке. Я крикнул, чтобы они вызвали скорую, позвал одногруппника, и мы вдвоем на своих закорках потащили мужика вниз, к выходу из Главного корпуса. Вынесли на улицу аккурат к подъехавшей скорой.
Возможно, мы спасли ему жизнь. Возможно, конкретно в данном случае время ничего не решало, и случившийся с ним приступ серьезной угрозы для жизни не представлял. Как бы то ни было, мы сделали то, что должен был сделать любой другой адекватный человек.
Я курил в туалете возле аудитории, в которой только что получил пересдачу, смотрел из окна на стройку рядом с Физтехом и думал, что наши усилия не пропали даром, раз уж этот человек (нет, это был не Альберт Эйнштейн) оказался жив и достаточно здоров для того, чтобы отправлять студентов на пересдачи со скоростью пулемета.
…
До следующей пересдачи было два дня, их я тоже посвятил чертовым дифференциальным уравнениям. Я даже помнил, что и на какой странице написано в учебнике Романко. Человек-диффур просто.
Дебильник я написал на максимум, и меня позвал к себе стремительно лысеющий дедушка, у которого были какие-то проблемы с одним глазом, из-за чего он немного походил на Терминатора. Позднее я узнал, что его фамилия Егоров, и ни один человек не смог сказать мне про него ни одного плохого слова. Все утверждали, что он адекватный и местами даже веселый человек, кроме того, еще и достаточно халявный преподаватель.
Что же, тем ценнее оказалась следующая история.
У Егорова есть фишка: переворачивать листок с ответом на билет, чтобы студент написал все на чистой стороне листа. Я всегда хорошо готовился к пересдачам (когда-то ведь надо начинать учиться), поэтому, в отличие от основных экзаменов не брал с собой шпоры, бомбы и прочие приятные мелочи.
В этот раз, как уже отмечал выше, я был просто отцом диффуров. Поэтому гордо написал билет заново прямо при нем, не отходя от кассы. Егоров одобрительно посмотрел на меня одним глазом, дал дополнительный вопрос и пошел спрашивать других сдающих.
Нас сидело человек семь и, возможно, это был единственный случай, когда я отвечал лучше всех остальных. Парни сильно плавали на простых вещах, палились за списыванием с телефонов, один со слезами на глазах уговаривал поставить ему три.
Егоров был милостив. После двух-трех ответов (даже неправильных) он по очереди отпускал ребят с трояками.
И вот я остался один. Начался четвертый час экзамена. За это время я ответил на семь или восемь вопросов, решил пару задач и доказал несколько теорем. При этом, вообще не понимал, зачем я все это делаю. «Он что, тянет меня на хор?». К черту эти условности, меня никогда не интересовало, какие оценки будут стоять в моей зачетке. Идеальный вариант еще в начале первого семестра мне виделся таким: мне сразу проставляют тройки по всем предметам всех курсов и отдают диплом.
Короче говоря, где-то на девятом-десятом вопросе я сломался и не ответил. Ну, как бы, тяжеловато четыре часа подряд говорить только о дифференциальных уравнениях. Не то чтобы это моя любимая тема.
Я честно признался, что не знаю ответа на этот вопрос, но готов ответить на любой другой. Егоров пробормотал грустное «Не сомневаюсь, Сергей, не сомневаюсь…», полистал мою зачетку, а потом выдал шедевральное:
— Знаете, Сергей, я преподаю на Физтехе уже почти сорок лет. И по своему опыту могу совершенно ответственно заявить, что Вы могли бы учиться здесь на отлично. Ну, может, с четверками. Но я листаю зачетку и вижу там тройки, а это значит, что Вы ленитесь. А за лень надо наказывать. Поэтому я поставлю Вам пересдачу.
Согласно официальным правилам института, три двойки по одному предмету — это отчисление. Немного дурацкая причина для вылета, правда?
— Хм… Я просто уточнить. Вы мне ставите два за то, что я слишком хорошо ответил?
— Да.
Я не стал выпрашивать у него тройку (никогда этого не делал) или ругаться (я не особо конфликтный). Пока он искал ведомость и что-то туда записывал, я просто представлял, что у него на плече сидит огромный пиратский попугай.
И клювом выдалбывает ему второй глаз.
Егоров оторвался от ведомости и спросил, сколько баллов у меня было за письменный экзамен.
— Два.
— Я понимаю, что два. Я имею ввиду, по 50-балльной шкале.
— Два. Из пятидесяти.
— Это как? — растерялся Егоров.
— Просто я на тот момент вообще ничего не знал, плюс с меня еще и баллы за несданные задания сняли.
— Так Вы еще и задания не сдали?! А чем Вы занимались весь семестр? Подождите… Вы что, хотите сказать, что выучили дифференциальные уравнения за неделю?! — он пораженно вытаращил на меня глаз.
— Йохохо, — тихо пробубнил я в ответ.
…
Августовская пересдача по диффурам — возможно, самое мерзкое в плане учебы среди всего, что я видел на Физтехе.
На пересдачу поначалу пришла только Иванова. Мне не доводилось что-либо ей сдавать, но, насколько я понял из рассказов знакомых, она человек настроения. Мой сосед в первом семестре написал письменный экзамен по матанализу на твердый «отл». Вполне заслуженно — он действительно учил и отлично шарил этот предмет. На устном попал к Ивановой и получил пересдачу. В то же время, иногда люди получали у нее тройки-четверки просто так, под аккомпанемент ее шуточек-прибауточек.
В тот день, по всей видимости, она была не в духе и мощно загнобила пришедших на пересдачу. Не помню дословно, что именно она говорила. Но в ход точно шли обороты типа «тупицы», «идиоты» и «скорее бы вас всех отчислили». Особенно на орехи доставалось девушкам, которые поступили на Физтех, только чтобы найти себе мужа. И то, непонятно, кому нужны такие «никчемные дуры».
Некоторые девушки аж заплакали. Все подавленно молчали. Достаточно гнетущая атмосфера, хотя вроде как экзамен — это всегда праздник (я так объяснял в деканате свои пересдачи). Ну если студент действительно тупой и не тянет — пересдача и отчисление. Окей, никаких вопросов. Но зачем оскорблять?
Вообще, организовано было все очень по-дурацки. По правилам кафедры вышмата, если студент сдает дебильник, но получает двойку при устном ответе, то на следующей пересдаче он может дебильник не писать. Это был как раз мой случай, и в деканате мне сказали сделать именно так.
Но, как оказалось, в ведомости Егоров то ли забыл, то ли специально не указал, что я ему отвечал устно. Иванова развела руками и предложила либо дождаться его, либо написать дебильник еще раз. Немного стремный выбор. Если случайно накосячить — отчисление. Если Егоров не придет в итоге, то написать дебильник мне уже никто не даст — тоже отчисление. Я решил, что лучше рассчитывать на себя. Тем более, за неделю до пересдачи шестое чувство подсказало мне, что все может пойти не так, и лучше на всякий случай заботать все задачи.
Собственно, Егоров пришел чуть позже. Но в лучших традициях самого себя, сказал, что считает это правило каким-то корявым и ничего засчитывать мне не будет. Так что, если бы я решил действовать согласно официально принятым правилам пересдачи, то эта история закончилась бы белорусским военкоматом, еще более бессмысленным и беспощадным, чем кафедра вышмата Физтеха.
Я написал дебильник на максимум, в стиле колобка ушел от Ивановой, украв свою зачетку с преподского стола, получил заветный трояк у другого преподавателя, и моя улыбка в тот день была способна осветить и Москву, и ближайшее Подмосковье. В деканате я танцевал танец победителя, а потом еще примерно неделю праздновал это событие.
В общем, пересдачи нужны для того, чтобы их получать. Ни в школе, ни в университете я не мог заставить себя серьезно относиться к учебе. Поэтому, когда случались подобные истории, я искренне радовался им — в моем понимании полученный благодаря высшему образованию такого рода опыт намного ценнее недополученных теоретических знаний.
Оригинал записи в блоге Сергея Заварина
Поделиться
Твитнуть
Поделиться
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
То есть,
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
y=Cx, где С=Const.
Задание
Найти частное решение дифференциального уравнения
.
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
где С=const.
Ответ
где С=const.
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Общий интеграл:
где С=const.
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
где С=const
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Частное решение:
.
Задание
Решить дифференциальное уравнение
.
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Общий интеграл:
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Интегрируем:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
Используя
можно выразить функцию в явном виде.
Общее решение:
где С=const.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Частное решение:
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
0=0
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Общий интеграл:
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Интегрируем:
Общий интеграл:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Частный интеграл:
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
Таким образом:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Обратная замена:
Ответ
Общий интеграл:
где С=const.
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Ответ
Общее решение:
где С=const.
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
Задание
Найти частное решение дифференциального уравнения
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
0]» title=»Rendered by QuickLaTeX.com» />
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
Ответ
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Задание
Решить дифференциальное уравнение
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
можно выразить функцию в явном виде.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Дифференциальные уравнения (ДУ) — методы и примеры решения уравнений разного порядка
Многих людей, хоть как-то изучавших курс высшей математики в учебном заведении, приводит в ужас словосочетание «дифференциальные уравнения». Согласно строгому научному определению в книгах – так именуются математические выражения, где в состав входят функция, ее производная или параметр. Имеется достаточно большое количество типов этих равенств, рассмотрим подходы к их решению так, чтобы они были понятны даже для «чайников».
Дифференциальные уравнения первого порядка
Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х):
здесь, F(x,y,y ’ ) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у ’ ).Таково строгое математическое определение ДУ.
Для примера можно привести следующее уравнение:
функция вида F(x,y,p) = xp — y 2
Простейшие ДУ первого порядка
Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х.
После интегрирования получим такое выражение:
Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида:
здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа.
Задача №1
Необходимо определить все возможные варианты решения диффуравнения, имеющего вид
Последовательно рассмотрим решение.
Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее:
Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию:
Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение:
Данное выражение – это решение для приведенного диффуравнения.
ДУ с разделяющимися переменными
Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства.
Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными.
Их общий вид следующий:
После проведения нескольких преобразований, это выражение может быть сведено к следующему виду:
При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений.
Задача №2
Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x 2 + e x )
Как решать? В первую очередь проводим разделение переменных в разные части уравнения:
Данные преобразования справедливы, если у ≠ 0.
Если рассмотреть вариант решения при нулевом показателе функции, то можно заметить ,что
Это означает, что y = 0 – одно из возможных решений задачи.
Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения:
Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду:
Правильными решениями, в результате преобразований, будут:
Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина.
Линейные неоднородные ДУ первого порядка
Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные.
Основной принцип при нахождении решения сводится к следующим шагам:
Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению.
Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию.
На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ.
Задача №3
Рассмотрим применение методики решения на примере.
Необходимо найти решение дифференциального уравнения вида
Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается:
На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю.
Получаем дополнительное дифференциальное уравнение:
Теперь необходимо принять одно из частных решений n = x 2 + 1, которое соответствует равенству С2 — С1=0.
Выполняем оставшиеся преобразования:
Вполне очевидно, что ответом на условие задачи будет функция:
Задача Коши для ДУ
При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения).
На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную.
Чтобы это сделать, необходимо рассмотреть плоскость Xoy, где должна быть задана некая точка D0, имеющая координаты (x0, y0) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом.
Когда мы с самого начала задаем точку D0(x0, y0) – это означает, задание начального условия y(x0) = y0. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.
Задача №4
Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида:
Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy 2 стандартным методом. Его решение приводить не будем, приведем только ответ:
Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С:
Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений:
Полученная функция – ответ на задачу Коши в этом примере.
Дифференциальные уравнения Бернулли
ДУ Бернулли обычно представлено в следующем виде:
Обязательное условие, что функции b(x) и c(x) – являются непрерывными.
Задача №5
Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения:
Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения:
Выполним деление по начальному уравнению Бернулли на
и выполним необходимые преобразования:
Произведем замену параметра х на параметр у:
Теперь вычисляем интегрирующий модуль для данной функции, он будет равен:
Теперь производим ряд преобразований для вычисления решения диффуравнения:
Переписываем полученную функцию в неявном виде и получаем ответ:
Дифференциальные уравнения второго порядка
Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня.
Общий вид таких уравнений таков:
Линейные однородные ДУ второго порядка с постоянными коэффициентами
Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид:
При это важным условием теории является причисление r и k к действительным числам.
Задача №6
Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере.
Найти решение диффуравнения 2-го порядка вида:
Во всех таких случаях начинаем с поиска характеристического уравнения:
Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5.
Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде:
Линейные неоднородные ДУ второго порядка с постоянными коэффициентами
Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу:
Переменные r и k должны быть вещественными и постоянными числами.
Задача №7
Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x.
На первом этапе находим в составе неоднородного уравнения его однородную часть – это будет y» — y = 0.
Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k 2 + 1 = 0.
Корнями для данного характеристического уравнения являются k1 = -i и k2 = i.
Исходя из этого записываем решение для однородного уравнения:
Из-за отсутствия параметра с производной первого порядка также будет справедливо записать:
Теперь остается только подставить найденные выражения:
Частное и общее решение для уравнения можно записать:
Дифференциальные уравнения высших порядков
Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом:
Для неоднородных справедлив другой формат:
Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип.
Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье.
Что такое дифференциальное уравнение и зачем оно нужно?
На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Решение дифференциальных уравнений – без этого не обходится ни одна прикладная задача, будь это расчет какого-либо физического параметра или моделирование изменений в результате принятой макроэкономической политики. Эти уравнения также важны для ряда других наук, таких как химия, биология, медицина и т.д. Ниже мы приведем пример использования дифференциальных уравнений в экономике, но перед этим кратко расскажем об основных типах уравнений.
Дифференциальные уравнения – простейшие виды
Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров различных уравнений, но это, большей частью, учебные примеры, неприменимые на практике. По-настоящему интересная математика начинается, когда мы хотим описать процессы, протекающие в реальной жизни. Но как отразить фактор времени, которому подчиняются реальные процессы – инфляция, выработка продукции или демографические показатели?
Вспомним одно важное определение из курса математики, касающееся производной функции. Производная является скоростью изменения функции, следовательно, она может помочь нам отразить фактор времени в уравнении.
То есть, мы составляем уравнение с функцией, которая описывает интересующий нас показатель и добавляем в уравнение производную этой функции. Это и есть дифференциальное уравнение. А теперь перейдем к простейшим типам дифференциальных уравнений для чайников.
Простейшее дифференциальное уравнение имеет вид $y’(x)=f(x)$, где $f(x)$ – некоторая функция, а $y’(x)$ – производная или скорость изменения искомой функции. Оно решается обычным интегрированием: $$y(x)=int f(x)dx.$$
Второй простейший тип называется дифференциальным уравнением с разделяющимися переменными. Такое уравнение выглядит следующим образом $y’(x)=f(x)cdot g(y)$. Видно, что зависимая переменная $y$ также входит в состав конструируемой функции. Уравнение решается очень просто – нужно «разделить переменные», то есть привести его к виду $y’(x)/g(y)=f(x)$ или $dy/g(y)=f(x)dx$. Остается проинтегрировать обе части $$int frac=int f(x)dx$$ – это и есть решение дифференциального уравнения разделяющегося типа.
Последний простой тип – это линейное дифференциальное уравнение первого порядка. Оно имеет вид $y’+p(x)y=q(x)$. Здесь $p(x)$ и $q(x)$ – некоторые функции, а $y=y(x)$ – искомая функция. Для решения такого уравнения применяют уже специальные методы (метод Лагранжа вариации произвольной постоянной, метод подстановки Бернулли).
Есть более сложные виды уравнений – уравнения второго, третьего и вообще произвольного порядка, однородные и неоднородные уравнения, а также системы дифференциальных уравнений. Для их решения нужна предварительная подготовка и опыт решения более простых задач.
Большое значение для физики и, что неожиданно, финансов имеют так называемые дифференциальные уравнения в частных производных. Это значит, что искомая функция зависит от нескольких переменных одновременно. Например, уравнение Блека-Шоулса из области финансового инжиниринга описывает стоимость опциона (вид ценной бумаги) в зависимости от его доходности, размера выплат, а также сроков начала и конца выплат. Решение дифференциального уравнения в частных производных довольно сложное, обычно нужно использовать специальные программы, такие как Matlab или Maple.
Пример применения дифференциального уравнения в экономике
Приведем, как и было обещано, простой пример решения дифференциального уравнения. Вначале поставим задачу.
Для некоторой фирмы функция маржинальной выручки от продажи своей продукции имеет вид $MR=10-0,2q$. Здесь $MR$ – маржинальная выручка фирмы, а $q$ – объем продукции. Нужно найти общую выручку.
Как видно из задачи, это прикладной пример из микроэкономики. Множество фирм и предприятий постоянно сталкивается с подобными расчетами в ходе своей деятельности.
Приступаем к решению. Как известно из микроэкономики, маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж.
С математической точки задача свелась к решению дифференциального уравнения $R’=10-0,2q$ при условии $R(0)=0$.
Проинтегрируем уравнение, взяв первообразную функцию от обеих частей, получим общее решение: $$R(q) = int (10-0,2q)dq = 10 q-0,1q^2+C. $$
Чтобы найти константу $C$, вспомним условие $R(0)=0$. Подставим: $$R(0) =0-0+C = 0. $$ Значит C=0 и наша функция общей выручки принимает вид $R(q)=10q-0,1q^2$. Задача решена.
Другие примеры по разным типам ДУ собраны на странице: Дифференциальные уравнения с решениями онлайн.
источники:
http://nauka.club/matematika/algebra/differentsialnye-uravneniya.html
http://www.matburo.ru/mart_sub.php?p=art_du


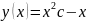

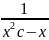

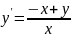
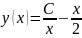

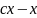

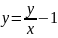

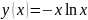
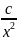

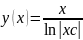
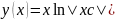

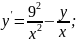
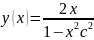
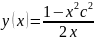

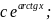
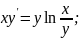
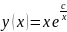

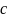








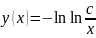

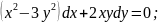

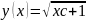
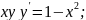
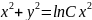
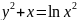
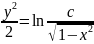
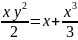
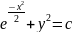

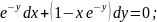
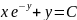
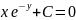
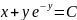
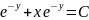

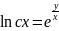
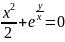
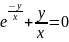
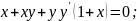


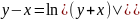
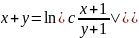
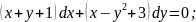
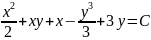


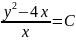













 Линейная неоднородная система диф ур с постоянными коэфф.
Линейная неоднородная система диф ур с постоянными коэфф. бщее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы можно применить метод Лагранжа вариации произвольных постоянных.
бщее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы можно применить метод Лагранжа вариации произвольных постоянных.