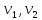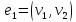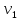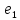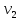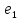Экзаменационные
вопросы © Kovalenko
Leonid
По дискретной математике
Весь материал
взят с книг и научных работ. Ничего не
придумано☺
0.
Введение. Граф 2
1.
Сеть. Потоки в сети. Теорема Форда —
Фалкерсона 12
2.
Функция. Бинарное отношение. Тотальность,
сюръективность, инъективность,
биективность. Примеры 16
3.
Бинарное отношение. Свойства. Матрица
смежности и граф отношения. Отношение
эквивалентности. Примеры 25
4.
Алгебраическая структура. Полугруппа,
моноид, группа. Примеры 30
5.
Группа. Абелева группа. Аддитивная
группа. Мультипликативная группа.
Конечная группа. Таблица Кэли. Циклическая
группа. Декартово произведение групп 37
6.
Группа подстановок. Симметрическая
группа . Умножение подстановок.
Нейтральный элемент. Обратная подстановка.
Число элементов группы 41
7.
Цикл. Теорема о представлении подстановки
в виде произведения независимых циклов.
Транспозиция. Чётные и нечётные
подстановки. Знакопеременная группа 43
8.
Кольцо. Свойства. Коммутативное кольцо.
Делители 0. Область целостности. Примеры.
Подкольцо. Единица кольца. Поле.
Примеры 46
9.
Идеал. Главный идеал. Теорема об идеалах
поля (только и ). Следствие об идеалах
в кольце 50
10.
Сравнения. Классы вычетов по модулю
(по идеалу ). Свойства. Малая теорема
Ферма. Функция Эйлера. Теорема Эйлера
(теория чисел) 51
11.
Характеристика кольца. Теорема о
характеристике кольца без делителей
0. Примеры. Кольцо классов вычетов.
Примеры 56
12.
Простой идеал. Необходимое и достаточное
условие того, что идеал кольца —
простой 56
13.
Поле классов вычетов. Минимальное поле.
Примеры 57
14.
Евклидово кольцо. Свойства (8 свойств).
Примеры 57
15.
Кольцо многочленов . Условия того, что
кольцо — евклидово кольцо 60
16.
Приводимые и неприводимые многочлены
в кольце . Примеры. Теорема о разложении
в на произведение неприводимых
множителей. Теорема Безу 61
17.
Расширение поля (надполе). Теорема о
том, что кольцо классов вычетов по
модулю неприводимого многочлена есть
поле. Степень расширения. Число элементов
этого поля 62
18.
Поле Галуа. Примеры полей Галуа как
расширения полей. Таблицы сложения и
умножения 63
Литература 68
0. Введение. Граф
Граф
(в широком смысле) — конечный набор
объектов любой природы, которые называются
вершинами, некоторые пары из которых
могут быть соединены.
Граф
— множество вершин
и набор
неупорядоченных и упорядоченных пар
вершин, где
—
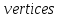
—

Обозначается

Неупорядоченная пара вершин называется
ребром, упорядоченная пара — дугой.
Смежные
(соседние) вершины — две вершины,
которые соединены ребром.
Смежные
(соседние) рёбра (дуги) — два ребра
(две дуги), у которых есть общая вершина.
Кратные
рёбра (дуги) — рёбра (дуги), соединяющие
одну и ту же пару вершин.
Петля
— ребро, которое начинается и кончается
в одной и той же вершине.
Инцидентность
— понятие, используемое только в
отношении ребра (дуги) и вершины: если
— вершины, а
— соединяющее их ребро (дуга), тогда
вершина
и ребро
инцидентны, вершина
и ребро
тоже инцидентны. Две вершины или два
ребра (дуги) инцидентными быть не могут.
Понятие инцидентности для орграфов
сохраняется (то есть начальная или
конечная вершина — не имеет значение),
но различается в особых случаях —
положительная инцидентность (дуга
исходит из вершины) и отрицательная
инцидентность (дуга заходит в вершину).
Изоморфизм
двух графов — понятие, используемое
в случае, если существует перестановка
вершин, при которой два графа совпадают.
Иначе говоря, два графа называются
изоморфными, если существует
взаимно-однозначное соответствие между
их вершинами и рёбрами, которое сохраняет
смежность и инцидентность (то есть
графы отличаются только названиями
своих вершин). В случае матрицы
смежности: графы являются изоморфными,
если путём перестановки строк и столбцов
матрицы смежности первого графа удаётся
получить матрицу смежности второго
графа.
Рисунок 1. Все три
графа — изоморфны
Порядок
графа — число вершин в графе:
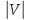
Размер
графа — число рёбер (дуг) в графе:
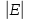
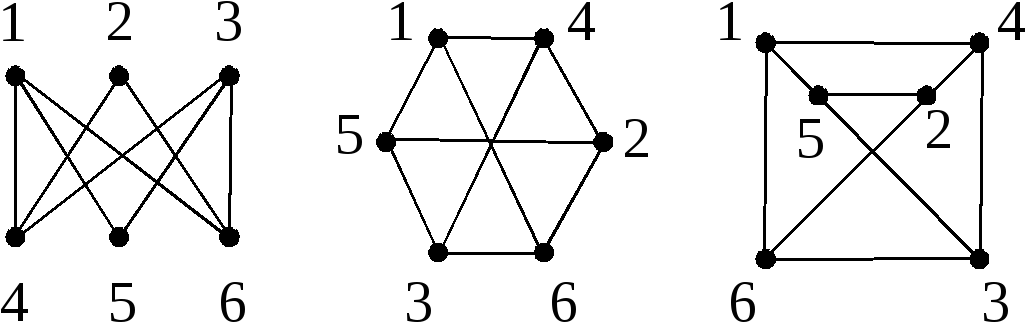
Степень
вершины
— количество инцидентных ей рёбер (при
этом петли считают дважды).
Изолированная
вершина — вершина, которая не является
концом ни одного ребра.
Висячая
вершина (или лист) — вершина, которая
является концом ровно одного ребра.
Путь
— конечная последовательность вершин,
в которой каждая вершина (кроме последней)
соединена со следующей в последовательности
вершиной ребром или дугой. Длина пути
— число составляющих его рёбер и дуг.
Простой
путь — путь, в котором рёбра (дуги) не
повторяются.
Элементарный
путь — простой путь, в котором вершины
не повторяются.
Цикл
— путь, в котором первая и последняя
вершины совпадают. Длина цикла —
число составляющих его рёбер и дуг.
Простой
цикл (или контур) — цикл, в котором
только первая и последняя вершины
совпадают, а все остальные — нет.
Цепь
(или маршрут) — путь без повторяющихся
рёбер.
Простая
цепь (или простой маршрут) — цепь без
повторяющихся вершин.
Расстояние
между вершинами — минимальная длина
пути, который соединяет эти вершины.
Связность
означает наличие пути между любой парой
вершин.
Бинарное
отношение на множестве вершин графа,
заданное как «существует путь из
в
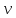
является отношением эквивалентности
и, следовательно, разбивает это множество
на классы эквивалентности, называемые
компонентами связности графа. Если
у графа ровно одна компонента связности,
то граф связный.
Компонента
связности графа — всякий максимальный
связный подграф не орграфа. Слово
«максимальный» означает максимальный
относительно включения, то есть не
содержащийся в связном подграфе с
большим числом элементов.
Рисунок 2. Граф с
тремя компонентами связности
Мост
(перешеек) — ребро графа, удаление
которого увеличивает число компонент
связности. (На рисунке выше все рёбра —
мосты.)
Гамильтонов
маршрут — простой маршрут в графе,
содержащий все вершины графа ровно по
одному разу.
Гамильтонов
цикл — простой цикл в графе, содержащий
все вершины графа ровно по одному разу
(кроме первой, естественно).
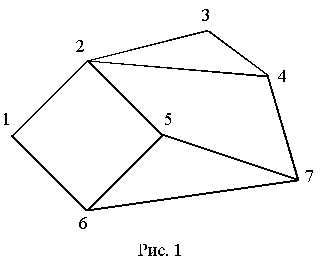
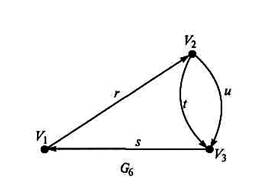
На
следующем рисунке последовательности
вершин:
— маршрут,
и
— простые пути,
— цикл (но не контур),
— простой цикл (контур).
Рисунок 3
На чтение 10 мин. Просмотров 241 Опубликовано 13.02.2013
Ответы на все модули по предмету дискретная математика, для итогового тестирования.
Ответы на модуль 1 (МНОЖЕСТВА И ОТНОШЕНИЯ) по предмету дискретная математика.

2) Какое утверждение является верным? бинарное отношение R называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
3) Какое утверждение является неверным? конечное множество является равномощным любому своему собственному подмножеству.
4) Как называется замкнутый обход симметричного мультиграфа по всем вершинам по одному разу? гамилътоновым циклом.
5) Как называется бинарное отношение, рефлексивное, антисимметричное и транзитивное? квазипорядок.
6) Какое утверждение не является верным? элементы множества не могут сами являться множествами.
7) Что такое граф? вершины и дуги.

9) Что понимается под множеством? совокупность некоторых объектов.
10) Как называется множество непустых подмножеств множества, если каждый элемент данного множества принадлежит в точности одному из его подмножеств, каждое из которых не является пустым? разбиением множества.
11) Какое множество А называется подмножеством множества В? если все элементы множества А принадлежат В.
12) Какое множество называют счетным? любое множество, равномощное множеству всех натуральных чисел.
13) Как называется бинарное отношение, которое только рефлексивно и транзитивно? отношение предпорядка.
14) Какое множество называется универсальным или универсумом? множество, содержащее все элементы, находящиеся в рассмотрении.
15) Какое утверждение является неверным? в сетевом графике имеются циклы.
16) Как называется симметричный граф, если любые две его вершины соединены между собой ребром? полный граф.
17) Какой граф называется связным? если любые две вершины графа соединены хотя бы одним путем.
18) Как называются отличающиеся друг от друга хотя бы одним элементом выборки длины k, составленные из n-элементного множества? сочетания без повторений из n элементов по k.
19) Какое свойство счетных множеств является неверным? любое подмножество счетного множества бесконечно.
20) Какие множества А и В называются равными или совпадающими? если они состоят из одних и тех же элементов.
21) Что понимается под решением задачи оптимизации «в слабом смысле»? нахождение единственного произвольного элемента.
22) Что такое задача перечисления в комбинаторике? если необходимо выделить все элементы множества, удовлетворяющие заданным свойствам.
23) Как называется последовательность дуг графа, таких, что конец любой дуги кроме последней совпадает с началом следующей дуги? путем в графе.
24) Что называется рacкраской (вершин) графа G? такое задание цветов вершинам G, что если [а, b] ребро, то вершины а и b имеют различные цвета.
25) Как называется замкнутый обход мультиграфа по всем ребрам по одному разу? эйлеровым циклом.
Ответы на модуль 2 (АЛГЕБРА И ТОПОЛОГИЯ) по предмету дискретная математика.
1) Что представляет собой тривиальный фильтр множества X? семейство F подмножеств X, состоящее лишь из самого множества X.
2) Как называется полугруппа с единицей? моноид.
3) Какой фильтр будет мажорировать любой фильтр окрестностей точки , если X — топологическое пространство? тривиальный фильтр.
4) Как называется нейтральный элемент мультипликативного группоида? единица.
5) Как называется совокупность предикатных и функциональных символов с указанием их местности? сигнатура.
6) Как называется формула, представляющая собой объединение, в которое входят по одному разу все множества (со знаками дополнения или без дополнений) на данном универсуме? конституента нуля.
7) Что называется алгебраическими системами? множества, на которых кроме операций заданы отношения.

9) Какой фильтр фильтрует множество X вплоть до одноточечного множества, состоящего из одной данной точки? ультрафильтр.
10) Какое утверждение является неверным? каждое множество, за исключением универсального, может быть задано объединением конституент единицы.
11) В каком случае решетчатая топология является тривиальной? когда разбиение состоит только из одной части заданного множества.
12) Что такое полная система булевых функций? набор булевых функций, если любая булева функция выражается через них при помощи операции суперпозиции в конечном числе раз.
13) Какой класс булевых функций называется замкнутым? если всякая суперпозиция функций данного класса будет функцией из этого класса.
14) Как называется нейтральный элемент аддитивного группоида? нуль.
15) Какое утверждение является неверным? любая топология мажорирует дискретную топологию.
16) Как называется 0-местный функциональный символ? константа.
17) Какое утверждение верно? циклическая группа всегда абелева.
18) Что не является условием, выполнение которого говорит о том, что семейство τ задает топологию во множестве X? (X — произвольное множество 
19) Как называется кольцо, в котором все отличные от нуля элементы составляют группу по умножению? тело.
20) Как называется формула алгебры множеств, представляющая собой пересечение, в которое входят по одному разу все множества (со знаками дополнения или без дополнений) на данном универсуме? конституента единицы.
21) Какие элементы а и b частично упорядоченного множества с нулем 0 и единицей 1 называются дополнительными друг для друга? если их пересечение равно нулевому элементу 0, а объединение дает единичный элемент 1.
22) Какая сигнатура называется функциональной? не содержащая предикатных (функциональных) символов.
23) Что называется мощностью алгебраической системы? мощность носителя системы.
24) Что такое терм? функциональное выражение, составленное с помощью сигнатурных функциональных символов.
25) Сколько будет всего разных булевых функций одной переменной? четыре.
Ответы на модуль 3 (АЛГЕБРА ЛОГИКИ) по предмету дискретная математика.
1) Какое высказывание истинно? никакая переменная не может быть одновременно свободной и связанной.
2) Какая дизъюнктивная нормальная форма (ДНФ) называется совершенной? дизъюнкция некоторых конституент единицы, среди которых нет одинаковых.
3) Какая формула аксиоматической теории называется теоремой? формула, которая выводится только из аксиом, не используя никаких гипотез.
4) В каком случае формула 
5) Какие формулы называются равносильными в данной интерпретации I = 〈М, Ф〉? формулы f и g, если формулы выражают в данной интерпретации один и тот же предикат.
6) Что называется длиной формулы логики предикатов? общее число входящих в нее символов предикатов (атомарных формул), логических символов и символов кванторов.
7) Какая формула логики предикатов называется нормальной? приведенная формула, если она содержит все символы кванторов впереди или кванторов вовсе нет.

9) Какое высказывание истинно? любая булева функция, не являющаяся константой 0, представима в виде сокращенной ДНФ.
10) Что называется функцией алгебры логики (ФАЛ) от п переменных 


11) Что называется элементарным произведением? конъюнкт, в который любая переменная входит не более одного раза.
12) Что такое предикат? повествовательное предложение с параметрами.
13) Чем полностью характеризуются формулы алгебры логики семантически? таблицами истинности.
14) Какой дизъюнкт называется хорновским? дизъюнкт, у которого среди литер не более одной положительной.
15) Какие формулы называются равносильными на множестве М? формулы f и g, если они равносильны во всех интерпретациях, заданных на множестве М.
16) Какое утверждение является неверным? формула φ опровержима тогда и только тогда, когда она является тождественно истинной.
17) Как называется конъюнкция литер? конъюнктом.
18) Какое свойство алгоритма означает, что описываемый им процесс и сам алгоритм могут быть разбиты на отдельные элементарные этапы, возможность выполнения которых на ЭВМ у пользователя не вызывает сомнений? дискретность.
19) В каком случае говорят, что формула φ представляет функцию f? если булева функция f и формула φ имеют одну и ту же таблицу истинности.
20) Что называется дизъюнктивной нормальной формой (ДНФ)? дизъюнкция конъюнктов.
21) Какое свойство алгоритма означает, что он должен приводить к получению результата за конечное число шагов? результативность.
22) Что называется высказыванием? повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
23) Какое высказывание является неверным? проблема распознавания применимых машин Тьюринга алгоритмически разрешима.
24) Какое утверждение является неверным? в аксиоматической теории можно одновременно иметь два доказательства некоторой теоремы и ее отрицания.
25) Какое высказывание является ложным? тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению.
Ответы на модуль 4 (КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ) по предмету дискретная математика.
1) Как называется логическая операция, соответствующая союзу «тогда и только тогда, когда»? эквивалентностью.
2) Что называется конъюнкцией? бинарная логическая операция, соединяющая две двоичных переменных а и b, принадлежащих множеству {0, 1}, в такую переключательную функцию с, которая равна 1 (истинна) только тогда, когда равны 1 (истинны) обе переменных.
3) Что называют словом или цепочкой в алфавите V? произвольный кортеж из множества 
4) В каком случае код является исправляющим все ошибки? в случае, когда в передаваемом слове имеется не более k ошибок, тогда и только тогда, когда наименьшее расстояние между кодовыми словами 
5) Каждое правило какой грамматики имеет вид: в правой части правила может содержаться не более одного вхождения нетерминала? линейной грамматики.
6) В каком случае код является обнаруживающим? в случае, когда в передаваемом слове имеется не более чем k ошибок, тогда и только тогда, когда наименьшее расстояние между кодовыми словами 
7) Как называется зафиксированный порядок переменных, каждая из которых имеет свой вес? базой функции.

9) Что называется эквиваленцией? логическая операция, соединяющая две переменных в такую переключательную функцию, которая истинна тогда, когда обе образующих ее переменных одновременно истинны или одновременно ложны.
10) Какой такт в функционировании автоматов называют неустойчивым? если очередное изменение состояния автомата происходит только за счет изменения внутреннего состояния — элементов памяти.
11) Какое утверждение является верным? автоматы Мура менее быстродействующие, чем автоматы Мили.
12) Как называется логическая операция, соответствующая союзу «если, … то»? импликацией.
13) Каждое правило какой грамматики имеет вид: левая часть каждого правила вывода есть нетерминал, а правая — произвольная (может быть и пустая) цепочка в объединенном алфавите? контекстно-свободной грамматики.
14) Как называется логическая операция, соответствующая частице «не», словосочетанию «неверно, что»? инверсией.
15) Какой код называется групповым? если множество всех кодовых слов образует группу.
16) При каком способе переключательная функция 
17) При каком способе переключательная функция 
18) Что называется дизъюнкцией? бинарная логическая операция, соединяющая две переменные а и b в такую переключательную функцию c, которая равна 0 (ложна) только тогда, когда ложны обе переменные (равны 0).
19) Какое утверждение является верным? при задании автомата ориентированным графом (орграфом) его вершины сопоставляют с внутренними состояниями.
20) Как называются конечные автоматы, имеющие больше, чем одно внутреннее состояние? последовательностными конечными автоматами.
21) Как называют объединение всех степеней языка L? итерацией.
22) Как называется автомат, если из любого его состояния достижимо любое другое состояние? сильно связанным.
23) Для какого основного класса грамматик характерно следующее: на правила вывода не накладывается никаких дополнительных ограничений? для грамматики типа 0.
24) Какую подцепочку х цепочки у называют началом (или префиксом) цепочки у? если у = xz для некоторой непустой цепочки z.
25) Что называется импликацией? логическая операция, соединяющая две переменных а и b в такую переключательную функцию c, которая равна 0 (ложна) только тогда, когда а истинно, а b ложно.
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 1
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Деление математики на классическую и дискретную.
История дискретной математики
- Упрощение логических функций с помощью законов
алгебры логики
- Даны отрезки А = [-4; 5], B
= [2; 6], C = [5; 10]. Найдите следующее множество и
изобразите его кругами Эйлера:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 2
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Понятие множеств. Язык теории множеств
- Метод минимизации логических функции с помощью
карт Карно или диаграмм Вейча
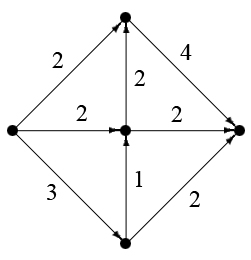
- Определите по
рисунку справа вид графа, степени его вершин. Имеет ли граф висячие
вершины?
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 3
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Изображение
множеств. Подмножества, универсальные множества, мощность множества
- Свойства сложения по модулю два (М2 или строгой
дизъюнкции)
- Проверьте, являются ли булевы функции F1 и F2
эквивалентными:
F1 = X →
(Y ≡ Z) и F2 = (X → Y) ≡ (X → Z)
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 4
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Способы задания множеств
- Многочлен Жегалкина, порядок его построения
- Проверьте, являются ли булевы функции F1
и F2 эквивалентными:
F1 = X ∙ (Y ≡ Z) и F2 = (XY)
≡ (XZ)
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 5
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Операции над множествами:
объединение множеств, пересечение множеств, разность множеств - Важнейшие замкнутые классы
- Определите по
рисунку слева вид графа и постройте таблицы инцидентности и смежности
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 6
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Универсальные множества.
Дополнение множества. Разбиения множества. Диаграммы Эйлера-Венна
- Упрощение логических функций с помощью законов
алгебры логики
- Постройте совершенную ДНФ по таблице истинности и
преобразуйте ее в полином Жегалкина:
|
X1 |
X2 |
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 7
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Определение графов и основные
понятия (вершины, ребра, степень вершины, виды вершин).
- Упрощение логических функций с помощью законов
алгебры логики
- Даны отрезки А = [-7; 3], B
= [1; 5], C = [4; 10]. Найдите следующие множества и
изобразите их кругами Эйлера:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 8
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Кортеж. Прямое произведение
множеств. Декартово произведение множеств
- Теорема о полноте системы логических: функций.
Критерий Поста-Яблонского
- По заданной функции постройте таблицу истинности,
приведите функцию к минимальной ДНФ:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 9
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Определение соответствий.
Обратное соответствие. Композиция соответствий
- Эйлеровы и Гамильтоновы графы
- Даны отрезки А = [-2; 4], B
= [2; 6], C = [5; 10]. Найдите следующие множества и
изобразите их кругами Эйлера:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 10
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Виды графов (полный, ориентированный, связный, с
висячими вершинами, изоморфный, циклический, нуль-граф)
- Метод математической индукции
- Выполните действия и определите
мощность полученного множества
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 11
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Логические конечные автоматы с
памятью
- Операции над графами
- Проверьте, являются ли булевы функции F1
и F2 эквивалентными:
F1 = X → (Y
Ú Z) и F2 = (X → Y) Ú (X → Z);
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 12
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Логические конечные автоматы без
памяти
- Деревья. Лес. Разрезы
- Выполните действия и определите
мощность полученного множества
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 13
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Построение совершенной нормальной формы
логической функции по таблице истинности или ее нормальной форме
- Правильный автомат (автомат
Мура). Упрощённый вид диаграммы для правильных автоматов
- Используя законы алгебры логики доказать
справедливость Закона склеивания относительно дизъюнкции и
конъюнкции:и
.
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 14
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Транспортные сети: основные
понятия и определения
- Понятие предиката. Область определения и область
истинности предиката
- Доказать с помощью таблиц истинности
справедливость закона де Моргана относительно операций конъюнкции и
дизъюнкции
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 15
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Применение алгоритмов на графах
в коммуникационных сетях (поиск кратчайшего пути).
- Операции над предикатами
- Проверьте, являются ли булевы функции F1 и F2
эквивалентными, еслии
.
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 16
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Булевы функции двух
переменных, их три категории
- Словарная функция автомата.
Финальная функция автомата
- Проверьте, являются ли булевы функции F1 и F2
эквивалентными, еслии
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 17
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Определение значения логических функций
- Формализация предложений с помощью логики
предикатов
3.
Постройте логическое выражение по заданной таблице истинности, приведите
его к минимальной ДНФ алгебраически:
|
X1 |
X2 |
X3 |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный техникум
(филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 18
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Кванторные операции над
предикатами
- Таблица автомата. Принцип работы
автомата. Диаграмма автомата
- Минимизируйте булеву функцию с помощью карт Карно или
диаграмм Вейча:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 19
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Составление таблиц истинности сложных функций
- Формализация предложений с
помощью логики предикатов
- Вычислите значение функции F(x1, x2, x3) при заданных значениях аргументов x1
= 0, x2
= 1, x3
= 1 и при x1
= 0, x2
= 0, x3
= 1: F(x1, x2, x3) =
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 20
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Понятие бинарного отношения;
примеры бинарных отношений
- Формулы алгебры
логики, позволяющие производить
тождественные преобразования логических выражений
3.
Минимизируйте булеву функцию с помощью карт Карно или диаграмм Вейча:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 21
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Сравнение логических функций и определение их
тождественности - Понятие предикатной формулы;
свободные и связанные переменные
3.
Постройте логическое выражение по заданной таблице истинности, приведите
его к минимальной ДНФ алгебраически:
|
X1 |
X2 |
X3 |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного бюджетного
образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 22
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Деление математики на классическую и дискретную.
История дискретной математики
- Формы представления логических функций
- Постройте совершенные ДНФ и соответствующие минимальные
формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте
соответствующий логический элемент.
|
X1 |
X2 |
X3 |
F |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 23
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Доказательство теорем алгебры логики
- Базовые множества для автомата:
входной алфавит, выходной алфавит, множество состояний
- По заданной функции постройте таблицу истинности,
приведите функцию к минимальной ДНФ:
F(x1,x2,x3) =
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 24
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Виды графов(полный,
ориентированный, связный, с висячими вершинами, изоморфный, циклический,
нуль-граф).
- Построение отрицаний к
предикатам, содержащим кванторные операции
3.
Докажите или опровергните:
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 25
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Диаграмма бинарного отношения.
Рефлексивные бинарные отношения
- Эйлеровы и Гамильтоновы графы
- Построить таблицу истинности для следующей
формулы: A &
(B ÚÞ
)
Преподаватель __________
Зам.директора по учебной
работе ____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 26
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Транспортные
сети: основные понятия и определения
- Изображение множеств. Подмножества, универсальные
множества, мощность множества
- Постройте совершенные ДНФ и соответствующие минимальные
формы для булевых функций, заданных таблично, с помощью карт Карно.
Постройте соответствующий логический элемент.
|
X1 |
X2 |
X3 |
F |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 27
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Операции над множествами:
объединение множеств, пересечение множеств, разность множеств
- Симметричные бинарные отношения.
Транзитивные бинарные отношения
- Построить таблицы истинности алгебраически для
следующей формулы: A Ú (B ÚÞ)
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 28
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и комплексы, 2 курс
- Отношение эквивалентности;
теорема о разбиении множества на классы эквивалентности
- Многочлен Жегалкина, порядок его построения
- Вычислите значение функции F(x1, x2, x3) при
заданных значениях аргументов x1
= 1, x2
= 0,
x3
= 1 и при x1 = 1, x2 = 0, x3 = 1:
F(x1,x2,x3) =
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 29
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Понятие множеств. Язык теории
множеств
- Операции над графами
- Вычислите значение функции F(x1, x2, x3) при
заданных значениях аргументов x1
= 0, x2
= 0,
x3
= 1 и при x1 = 0, x2 = 1, x3 = 1:
F(x1,x2,x3) =
Преподаватель __________
Зам.директора по учебной работе
____________
Ейский морской рыбопромышленный
техникум (филиал)
федерального государственного бюджетного
образовательного
учреждения высшего профессионального
образования
«Астраханский государственный технический университет»
Экзаменационный билет № 30
Дисциплина «Дискретная математика»
Специальность 230113 Компьютерные системы и
комплексы, 2 курс
- Кортеж.
Прямое произведение множеств. Декартово произведение множеств
- Метод математической индукции
- Упростите функцию, приведя ее к минимальной ДНФ: F(x1,x2,x3) =
Преподаватель __________
Зам.директора по учебной работе
____________
Главная /
Программирование /
Дискретная математика
Дискретная математика — ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Дискретная математика — одна из важнейших составляющих современной математики. С одной стороны, она включает фундаментальные основы математики — теорию множеств, математическую логику, теорию алгоритмов; с другой стороны, является основным математическим аппаратом информатики и вычислительной техники и потому служит базой для многочисленных приложений в экономике, технике, социальной сфере.
Каково число логических функций от 3 переменных?
Существуют ли простые графы
без петель с 5 вершинами
со следующим набором степеней:
(1)
(1,2,3,4,5)
(2)
(1,2,3,3,5)
(3)
(1,2,3,3,4)
(4)
(2,2,3,3,4)
Даны множества A = {a,b,d,e,f}, B = {b,c,e,g}, С = {a,d,f}.
Отметьте верное равенство:
(1)
С = A∩B
(2)
С = AB
(3)
С = A∪B
(4)
С = BA
Встретились 6 друзей, и каждый пожал руку каждому.
Сколько всего было рукопожатий?
(1)
6
(2)
12
(3)
15
(4)
30
Какие из множеств замкнуты относительно сложения?
(1)
множество натуральных чисел
(2)
множество нечетных чисел
(3)
множество квадратных корней из натуральных чисел
(4)
множество натуральных чисел, кратных 3
В таблице приведены три функции f1,
f2, f3
от переменных x, y, z:
x |
y |
z |
f1 |
f2 |
f3 |
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
Какие из этих функций содержат несущественные переменные?
Сколько ребер могут иметь простые графы без петель
с 5 вершинами?
(1)
одно ребро
(2)
5 ребер
(3)
10 ребер
(4)
25 ребер
Множество A содержит 5 элементов,
множество B содержит 8 элементов. Сколько элементов может содержать их пересечение?
(1)
8 элементов
(2)
6 элементов
(3)
5 элементов
(4)
3 элемента
Сколькими способами можно выбрать гласную и согласную буквы
из слова «схема»?
(1)
5
(2)
6
(3)
12
(4)
25
Какие из операций ассоциативны?
(1)
вычитание чисел
(2)
сложение чисел
(3)
разность множеств
Какие из функций ассоциативны?
(1)
импликация
(2)
конъюнкция
(3)
штрих Шеффера?
Какой радиус может быть у графа
с 5 вершинами?
В группе из 17 человек
английский язык изучают 10 человек,
французский язык изучают 6 человек
и оба языка изучают 2 человека.
Сколько человек в группе не изучает
ни английский, ни французский языки?
Какие из операций коммутативны?
(1)
вычитание чисел
(2)
умножение чисел
(3)
пересечение множеств
Какая из формул эквивалентна формуле
(¬x&y)∨(x&z)∨(¬x&z)?
(1)
(x∨¬z)&(y∨z)
(2)
(¬x∨z)&(y∨z)
(3)
(x∨z)&(y∨z)
Какое расстояние между двумя вершинами возможно графе с 5 вершинами?
Чему равна проекция множества A = {(1,2),(1,3),(2,3),(3,4)} на первую координату?
(1)
{1,2,3,4}
(2)
{1,2,3}
(3)
{2,3,4}
На вершину горы ведут пять дорог.
Сколькими способами турист может подняться на гору
и спуститься с нее?
(1)
5
(2)
10
(3)
25
(4)
100
Какие из операций над множествами ассоциативны?
(1)
объединение
(2)
пересечение
(3)
разность
Функция f задана таблицей:
x |
y |
z |
f |
|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Какой из полиномов Жегалкина ей соответствует?
(1)
xyz⊕xz⊕x⊕y⊕z
(2)
xyz⊕yz⊕x⊕z
(3)
xy⊕xz⊕y⊕z
(4)
xz⊕x⊕y⊕z
Какие из графов, приведенных на рисунке,
являются эйлеровыми?

(1)
первый граф
(2)
второй граф
(3)
третий граф
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(c,4),(e,3)}.
Какое из множеств является образом элемента b при этом соответствии?
(1)
{1,2,3,4}
(2)
{1,4}
(3)
{2,3}
Сколькими способами можно составить
трехцветный полосатый флаг, если имеется материал
пяти различных цветов?
(1)
5
(2)
20
(3)
60
(4)
125
Отметьте подмножества, которые в алгебре целых чисел со сложением
образуют подалгебру:
(1)
множество чисел, кратных 5
(2)
множество [0,1]
(3)
множество натуральных чисел
Какие из функций являются монотонными?
(1) конъюнкция
(2) импликация
(3) штрих Шеффера
Граф задан матрицей смежности:
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
Отметьте каким он является:
(1)
сильно связным
(2)
односторонне связным
(3)
слабо связным
(4)
несвязным
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(d,3)}.
Отметьте верное утверждение:
(1)
G всюду определено;
(2)
G функционально;
(3)
G сюръективно?
Сколько различных слов можно получить
перестановками букв в слове abcd?
(1)
4
(2)
12
(3)
24
(4)
256
Какие из множеств с указанной операцией над элементами образуют полугруппу?
(1)
четные числа с операцией сложения
(2)
целые числа с операцией вычитания
(3)
рациональные числа с операцией умножения
(4)
множество {-1,1} с операцией умножения
Какая из функций является линейной?
(1) эквивалентность
(2) стрелка Пирса
(3) конъюнкция
Отметьте графы, в которых возможна топологическая сортировка:
(1)
сильно связные
(2)
односторонне связным
(3)
слабо связные
(4)
несвязные
Какие из множеств являются счетными?
(1) множество натуральных чисел;
(2) множество рациональных чисел;
(3) множество действительных чисел;
(4)
множество [0,1]
Сколькими способами можно выбрать три различные краски из имеющихся пяти (порядок красоок важен)?
(1)
3
(2)
60
(3)
15
(4)
35
Какие из множеств с операцией сложения образуют группу?
(1)
целые числа, кратные 3
(2)
множество {-1,1}
(3)
неотрицательные целые числа
(4)
целые числа
Какие из перечисленных систем функций функционально полны в слабом смысле?
(1)
дизъюнкция и сложение по модулю 2
(2)
импликация
(3)
эквивалентность и сложение по модулю 2
(4)
конъюнкция и дизъюнкция
Какую длину может иметь максимальный путь
в ациклическом графе с n вершинами?
(1)
1
(2)
2
(3)
n-1
(4)
n
Между множествами A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(a,1),(c,3),(d,3),(d,4)}
и H = {(a,2),(b,1),(c,3),(d,3)}.
Какое соответствие функционально?
(1)
G и H
(2)
только G
(3)
только H
(4)
ни G, ни H
В палитре художника 5 различных красок.
Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане.
Затем берет следующую кисть, окунает ее в любую из красок и делает второе пятно по соседству.
Сколько различных комбинаций существует для трех пятен? Порядок пятен на ватмане не важен?
(1)
10
(2)
25
(3)
35
(4)
125
Какие из множеств с указанной операцией над элементами образуют группу?
(1)
множество {-1,1} с операцией умножения
(2)
рациональные числа с операцией умножения
(3)
неотрицательные целые числа с операцией сложения
(4)
четные числа с операцией сложения
В таблице приведены три функции f1,
f2, f3
от переменных x, y, z:
x |
y |
z |
f1 |
f2 |
f3 |
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Какие из этих функций функционально полны в слабом смысле?
Каким может быть ориентированное дерево?
(1)
сильно связным
(2)
односторонне связным
(3)
слабо связным
Функция f(x1,x2) имеет тип A2*B,
функция g(y1,y2) имеет тип CA*A.
Какой тип имеет функция f(x1,g(y1,y2))?
(1)
A2*B
(2)
CA*A
(3)
ACA*B
(4)
A2CA*B
Какими из следующих
свойств обладают биномиальные коэффициенты?
(1)
Cnn-k=Cnk
(2)

(3)
C2nn=(n!)2
Чему равен единичный элемент в группе целых чисел со сложением?
(1)
его не существует
(2)
0
(3)
1
Дано равенство ∀x∀yP(x,y) = ∃x∃yP(x,y).
Какие из утверждений верны?
(1)
Это равенство неверно при любых Р.
(2)
Это равенство верно при любых Р.
(3)
Это равенство при некоторых Р верно, а при некоторых других Р неверно.
В потоковой сети, приведенной на рисунке,
все пропускные способности равны 4:
Нарушены ли в ней правила распределения потоков?
(1)
Нет, все верно.
(2)
Да, нарушен закон Кирхгофа.
(3)
Да, нарушено ограничение на пропускную способность.
Между точками горизонтальной прямой задано отношение «левее»
(x левее y). Отметьте верное утверждение:
(1) отношение рефлексивно
(2) отношение антирефлексивно
(3) отношение симметрично
(4) отношение транзитивно
Слова длины 5 в алфавите {a,b,c,d}
перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0.
Какой номер будет иметь слово bcacd?
(1)
214
(2)
395
(3)
618
(4)
732
Какой элемент является образующей в группе целых чисел со сложением?
(1)
такого элемента не существует
(2)
0
(3)
1
Какая из формул исчисления предикатов выражает
тот факт, что в множестве М, в котором определен
частичный порядок, не существует максимального элемента?
(1)
∀x∃y(x∈M→((y∈M)&(x<y)))
(2)
∀x∃y((x∈M)&(y∈M)&(x<y))
(3)
∀x∃y((x∈M)∨((y∈M)&(x<y)))
Граф является двудольным, если он …
(1) имеет цикл с четным числом вершин
(2) имеет цикл с нечетным числом вершин
(3) ациклический граф
Объединение двух отношений частичного порядка будет отношением частичного порядка …
(1) всегда
(2) иногда (может быть, а может не быть)
(3) никогда
Чему равно число таблиц размером 23
с элементами из множества мощности 3?
(1)
120
(2)
216
(3)
729
(4)
801
Чему равна наименьшая верхняя грань для {c,e}?

Отметьте неверную формулу:
(1)
∀x∀yP(x,y) = ∀y∀xP(x,y)
(2)
∀x∃yP(x,y) = ∃y∀xP(x,y)
(3)
∀x(P(x)&Q(x)) = ∀xP(x)&∀xQ(x).
Степень Cn
матрицы смежности C
ориентированного графа G
содержит ненулевые элементы во всех
клетках главной диагонали если:
(1)
все вершины G имеют петли
(2)
некоторые вершины G имеют петли
(3)
граф G содержит циклы
(4)
граф G — сильно связный
На множестве A = {a,b,c,d} задано бинарное отношение
R = {(a,b),(a,c),(b,c),(c,d)}. Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
(1)
(d,a)
(2)
(a,d), (b,d)
(3)
никакие, так как R транзитивно;
(4)
(a,d)
Даны три множества: A = {a,b,c},
B = {-1,1}, C = {0,1}.
Каково число различных функций типа AB*C2?
(1)
24
(2)
64
(3)
46
(4)
10
Чему равна наибольшая нижняя грань для {b,d}?

Каково число логических функций от 4 переменных?
Существуют ли простые графы
без петель с 4 вершинами
со следующим набором степеней:
(1)
(1,2,3,4)
(2)
(1,2,3,3)
(3)
(1,2,2,3)
(4)
(1,1,2,3)
Сколько четных двузначных чисел можно составить из цифр 2,3,6,7,9 (каждую цифру в числе можно использовать только 1 раз)?
(1) 5
(2) 8
(3) 10
(4) 25
Какие из множеств замкнуты относительно умножения?
(1)
множество натуральных чисел
(2)
множество нечетных чисел
(3)
множество положительных чисел
(4)
множество отрицательных чисел
В таблице приведены три функции f1,
f2, f3
от переменных x, y, z:
x |
y |
z |
f1 |
f2 |
f3 |
|---|---|---|---|---|---|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
Какие из этих функций содержат несущественные переменные?
Сколько ребер могут иметь простые графы без петель
с 6 вершинами?
(1)
одно ребро
(2)
6 ребер
(3)
15 ребер
(4)
36 ребер
Множество A содержит 6 элементов,
множество B содержит 7 элементов. Сколько элементов может содержать их объединение?
(1)
9 элементов
(2)
7 элементов
(3)
6 элементов
(4)
4 элемента
Сколькими способами можно выбрать гласную и согласную буквы
из слова «здание»?
(1)
6
(2)
9
(3)
18
(4)
24
Какие из операций ассоциативны?
(1)
умножение чисел
(2)
объединение множеств
(3)
деление чисел
Какие из функций ассоциативны?
(1)
дизъюнкция
(2)
стрелка Пирса
(3)
сложение по модулю 2
Какой радиус может быть у графа
с 4 вершинами?
Множества A, B, C выражены через три других множества
D, E, F следующими равенствами
(знак пересечения опущен): A = D(E∪F), B = DE∪DF, C = (DE)∩(DF).
Отметьте верное равенство:
В группе из 15 человек
6 человек увлекаются театром,
8 человек увлекаются спортом
и 3 человека увлекаются и театром, и спортом.
Сколько человек в группе не увлекаются
ни театром, ни спортом?
Какие из операций коммутативны?
(1)
сложение чисел
(2)
пересечение множеств
(3)
разность множеств
Какая из формул эквивалентна формуле
(x&¬y)∨(y&z)∨(¬y&z)?
(1)
(x∨¬z)&(y∨z)
(2)
(x∨z)&(¬y∨z)
(3)
(¬x∨z)&(y∨z)
Какое расстояние между двумя вершинами возможно графе с 4 вершинами?
Чему равна проекция множества A = {(1,3),(2,3),(2,4),(3,1)} на вторую координату?
(1)
{1,2,3,4}
(2)
{1,2,2,1}
(3)
{1,3,4,1}
(4)
{3,3,4,1}
Надо послать 4 срочных письма.
Сколькими способами можно это сделать, если для передачи
писем можно послать трех курьеров и каждое письмо
можно дать любому из курьеров?
(1)
3
(2)
4
(3)
12
(4)
24
Какие из операций над множествами коммутативны?
(1)
объединение
(2)
пересечение
(3)
разность
Функция f задана таблицей:
x |
y |
z |
f |
|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Какой из полиномов Жегалкина ей соответствует?
(1)
xyz⊕xy⊕yz⊕z
(2)
xyz⊕yz⊕x⊕z
(3)
xy⊕yz⊕y⊕z
(4)
xz⊕x⊕y⊕1
Какие из графов, приведенных на рисунке,
являются эйлеровыми?

(1)
первый граф
(2)
второй граф
(3)
третий граф
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(a,3),(b,3),(c,1),(e,3),(e,4)}.
Какое из множеств является прообразом элемента 3 при этом соответствии?
(1)
{a,b,c,e}
(2)
{a,b,e}
(3)
{a,c}
В группе из 20
человек нужно выбрать старосту и профорга.
Сколькими способами это можно сделать?
(1)
20
(2)
40
(3)
380
(4)
400
Отметьте подмножества, которые в алгебре целых чисел с умножением
образуют подалгебру:
(1)
множество чисел, кратных 3
(2)
множество [0,1]
(3)
множество отрицательных чисел
Какие из функций являются монотонными?
(1)
отрицание
(2)
сложение по модулю 2
(3)
дизъюнкция
Отметьте каким является граф заданный матрицей смежности:
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
(1) сильно связным
(2) односторонне связным
(3) несвязным
(4) слабо связным
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(b,1),(c,1),(d,4)}.
Отметьте верные утверждения:
(1)
G всюду определено
(2)
G функционально
(3)
G обратимо
(4)
G взаимно однозначно
Сколько различных слов можно получить
перестановками букв в слове abcde?
(1)
5
(2)
20
(3)
120
(4)
55
Какие из множеств с указанной операцией над элементами образуют полугруппу?
(1)
неотрицательные целые числа с операцией сложения
(2)
нечетные числа с операцией сложения
(3)
положительные рациональные числа с операцией умножения
(4)
нечетные числа с операцией умножения
Какие из функций являются линейными?
(1)
сложение по модулю 2
(2)
штрих Шеффера
(3)
дизъюнкция
(4)
константа
Какие графы могут совпадать со своим
графом конденсации?
(1)
сильно связным;
(2)
односторонне связным;
(3)
слабо связным;
(4)
несвязным?
Какое из множеств является конечным?
(1) множество всех натуральных чисел;
(2) множество всех рациональных чисел;
(3) действительные числа отрезка [0,1]
(4) множество {1,2,3}
Сколькими способами из 10
спортсменов можно отобрать команду из 6 человек?
(1)
C106
(2)
60
(3)
A106
(4)
610
Какие из множеств с операцией сложения образуют группу?
(1)
нечетные числа
(2)
рациональные числа
(3)
множество [-1,1]
(4)
целые числа, имеющие остаток от деления на 4, равный 3
Какие из перечисленных систем функций функционально полны в слабом смысле?
(1)
дизъюнкция и отрицание
(2)
штрих Шеффера
(3)
эквивалентность и отрицание
(4)
конъюнкция и импликация
Дан ациклический граф с n вершинами.
Сколько в нем может быть вершин, которые не являются ни источниками, ни стоками?
(1) n
(2) n+1
(3) n2
(4) n-2
Между множествами A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(a,1),(b,1),(c,3),(d,4)}
и H = {(a,1),(c,1),(c,3),(d,4)}.
Какое соответствие функционально?
(1)
G и H
(2)
только G
(3)
только H
(4)
ни G, ни H
В кондитерском магазине продавались три сорта пироженных:
эклеры, наполеоны и слоеные. Сколькими способами можно купить
4 пироженных?
(1)
4
(2)
9
(3)
12
(4)
15
Какие из множеств с указанной операцией над элементами образуют группу?
(1)
степени двойки с целыми показателями с операцией умножения
(2)
рациональные числа с операцией сложения
(3)
положительные рациональные числа с операцией деления
(4)
нечетные числа с операцией сложения
В таблице приведены три функции f1,
f2, f3
от переменных x, y, z:
x |
y |
z |
f1 |
f2 |
f3 |
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Какие из этих функций функционально полны в слабом смысле?
Сколько центров может быть у дерева
с n вершинами?
(1)
1
(2)
2
(3)
n-1
(4)
n
Функция f(x1,x2) имеет тип AB→C,
функция g(y1,y2) имеет тип AC→A.
Какой тип имеет функция f(g(y1,y2),x2)?
(1)
AB→C
(2)
AC→A
(3)
ACB→C
(4)
ABAC→C
Какими из следующих свойств обладают биномиальные коэффициенты?
(1) Cnn-k=Cnk
(2) 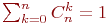
(3) Cn+1k=Cnk+Cnk-1
Чему равен единичный элемент в группе целых степеней двойки с умножением?
(1)
его не существует
(2)
1
(3)
2
Дано равенство ∀x∃yP(x,y) = ∃x∀yP(x,y).
Какие из утверждений верны?
(1)
Это равенство неверно при любых Р.
(2)
Это равенство верно при любых Р.
(3)
Это равенство при некоторых Р верно, а при некоторых других Р неверно.
В потоковой сети, приведенной на рисунке,
все пропускные способности равны 4:
Нарушены ли в ней правила распределения потоков?
(1)
Нет, все верно.
(2)
Да, нарушен закон Кирхгофа.
(3)
Да, нарушено ограничение на пропускную способность.
На множестве действительных чисел задано отношение |x-y|<5.
Отметьте верное утверждение:
(1) отношение рефлексивно
(2) отношение антирефлексивно
(3) отношение симметрично
(4) отношение транзитивно
Слова длины 5 в алфавите {a,b,c,d}
перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0.
Какой номер будет иметь слово abcad?
(1)
84
(2)
99
(3)
125
(4)
212
Какой элемент является образующей в группе целых степеней двойки с умножением?
(1)
такого элемента не существует
(2)
1
(3)
2
Какая из формул исчисления предикатов выражает
тот факт, что в множестве М, в котором определен
частичный порядок, не существует минимального элемента?
(1)
∀x∃y(x∈M→((y∈M)&(y<x)))
(2)
∀x∃y((x∈M)&(y∈M)&(y<x))
(3)
∀x∃y((x∈M)∨((y∈M)&(y<x)))
Во сколько цветов можно раскрасить цикл, содержащий
9 вершин?
(1)
в 2 цвета
(2)
в 3 цвета
(3)
в 4 цвета
Каким может быть дополнение к отношению эквивалентности?
(1) рефлексивным
(2) симметричным
(3) антисимметричным
Чему равно число таблиц размером 33
с элементами из множества мощности 2?
(1)
72
(2)
81
(3)
512
(4)
1024
Чему равна наименьшая верхняя грань для {c,g}?

Отметьте неверную формулу:
(1)
∀x(P(x)&Q(x)) = ∀xP(x)&∀xQ(x)
(2)
∃x(P(x)&Q(x)) = ∃xP(x)&∃xQ(x)
(3)
∃x∃yP(x,y) = ∃y∃xP(x,y).
Ориентированный граф G содержит циклы.
Какое из утверждений всегда верно?
(1)
степень Cn матрицы
смежности C ориентированного
графа G содержит ненулевые
элементы во всех клетках главной диагонали
(2)
степень Cn матрицы
смежности C ориентированного
графа G содержит ненулевые
элементы во некоторых клетках главной диагонали
(3)
сумма 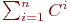
смежности C ориентированного
графа G содержит ненулевые
элементы в некоторых клетках главной диагонали
(4)
сумма 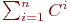
смежности C ориентированного
графа G содержит ненулевые
элементы во всех клетках главной диагонали
На множестве A = {a,b,c,d} задано бинарное отношение
R = {(a,d),(b,d),(d,c)}. Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
(1)
(c,d)
(2)
(a,c), (b,c)
(3)
никакие, так как R транзитивно;
(4)
(a,b), (b,a)
Даны три множества: A = {1,2,3},
B = {a,b}, C = {0,1}.
Каково число различных функций типа AB2→C?
(1)
24
(2)
144
(3)
212
(4)
512
Чему равна наибольшая нижняя грань для {e,g}?

Каково число логических функций от 5 переменных?
Существуют ли простые графы
без петель с 6 вершинами
со следующим набором степеней:
(1)
(1,2,3,4,5,6)
(2)
(1,2,3,4,5,5)
(3)
(1,2,3,4,4,5)
(4)
(1,3,3,3,3,5)
Даны множества A = {a,b,d,e}, B = {b,c,e,f,g}, С = {c,f,g}.
Отметьте верное равенство:
(1)
С = A∩B
(2)
С = AB
(3)
С = A∪B
(4)
С = BA
Сколько нечетных двузначных чисел можно составить из цифр 1,2,5,7,8 (цифры можно использовать только 1 раз)?
(1)
5
(2)
12
(3)
15
(4)
25
Какие из множеств замкнуты относительно сложения?
(1)
множество положительных чисел
(2)
множество отрицательных чисел
(3)
множество целых степеней двойки
(4)
множество четных чисел
В таблице приведены три функции f1,
f2, f3
от переменных x, y, z:
x |
y |
z |
f1 |
f2 |
f3 |
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Какие из этих функций содержат несущественные переменные?
Сколько ребер могут иметь простые графы без петель
с 4 вершинами?
(1)
одно ребро
(2)
4 ребер
(3)
6 ребер
(4)
16 ребер
Множество A содержит 5 элементов,
множество B содержит 8 элементов. Сколько элементов может содержать разность AB?
(1)
0 элементов
(2)
2 элемента
(3)
5 элементов
(4)
8 элементов
Сколькими способами можно выбрать гласную и согласную буквы
из слова «пехота»?
(1)
6
(2)
9
(3)
15
(4)
36
Какие из операций ассоциативны?
(1)
возведение в степень
(2)
пересечение множеств
(3)
объединение множеств
Какие из функций ассоциативны?
(1)
эквивалентность
(2)
импликация
(3)
сложение по модулю 2
Какой радиус может быть у графа
с 6 вершинами?
Множества A, B, C выражены через три других множества
D, E, F следующими равенствами
(знак пересечения опущен): A = D∪EF, B = ((DE)∪E)F, С = DF∪EF.
Отметьте верное равенство:
В группе из 20 человек
5 человек сдали экзамен по истории на «отлично»,
7 человек сдали экзамен по высшей математике на «отлично»
и 2 человека сдали экзамен по обоим предметам на «отлично».
Сколько человек в группе не сдали на «отлично»
ни экзамен по истории, ни экзамен по высшей математике?
(1)
2
(2)
6
(3)
10
(4)
14
Какие из операций коммутативны?
(1)
деление чисел
(2)
возведение в степень
(3)
объединение множеств
Какая из формул эквивалентна формуле
(x&y)∨(y&z)∨(¬y&z)?
(1)
(x∨¬z)&(y∨z)
(2)
(x∨z)&(y∨z)
(3)
(¬x∨z)&(y∨z)
Какое расстояние между двумя вершинами возможно графе с 6 вершинами?
Чему равна проекция множества A = {(1,4),(2,1),(2,3),(4,3)} на первую координату?
(1)
{1,2,3,4}
(2)
{1,2,4}
(3)
{1,3,4}
Трое студентов сдают экзамен.
Сколькими способами могут быть поставлены
им отметки, если известно, что никто
из них не получил неудовлетворительной
отметки?
(1)
3
(2)
9
(3)
27
(4)
81
Отметьте дистрибутивны слева множества:
(1)
объединение относительно пересечения
(2)
пересечение относительно разности
(3)
разность относительно объединения
Функция f задана таблицей:
x |
y |
z |
f |
|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Какой из полиномов Жегалкина ей соответствует?
(1)
xyz⊕xy⊕x⊕y⊕1
(2)
xyz⊕x⊕y⊕1
(3)
xy⊕x⊕y⊕z
(4)
xz⊕x⊕y⊕1
Какие из графов, приведенных на рисунке,
являются эйлеровыми?

(1)
первый граф
(2)
второй граф
(3)
третий граф
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(b,1),(c,3),(d,1),(d,4),(e,3)}.
Какое из множеств является образом элемента d при этом соответствии?
(1)
{1,2,3,4}
(2)
{1,2,3}
(3)
{1,4}
В некоторых видов спортивных
соревнований исходом является определение
участников, занявших первое, второе и третье
места. В соревновании участвует 10
человек. Сколько возможно различных исходов?
(1)
10
(2)
30
(3)
720
(4)
1000
Отметьте подмножества, которые в алгебре действительных чисел с умножением
образуют подалгебру:
(1)
множество целых степеней двойки
(2)
множество {0,1,2}
(3)
множество натуральных чисел
Какая из функций являются монотонной?
(1)
эквивалентность
(2)
стрелка Пирса
(3)
константа
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(c,1),(c,3),(d,3),(d,4)}.
Отметьте верное утверждение:
(1)
G всюду определено;
(2)
G функционально;
(3)
G сюръективно?
Сколько различных слов можно получить
перестановками букв в слове abc?
Какие из множеств с указанной операцией над элементами образуют полугруппу?
(1)
целые числа, кратные 7, с операцией сложения
(2)
положительные рациональные числа с операцией деления
(3)
степени двойки с целыми показателями с операцией умножения
(4)
целые числа с операцией сложения
Какие из функций являются линейными?
(1)
отрицание
(2)
константа
(3)
импликация
Каким может быть граф конденсации?
(1)
сильно связным
(2)
односторонне связным
(3)
слабо связным
(4)
несвязным
Какие из множеств имеют мощность континуума:
(1) множество натуральных чисел;
(2) множество рациональных чисел;
(3) множество действительных чисел;
(4) множество [0,1]
Сколько существует двухэлементных
подмножеств множества {a,b,c,d}?
(1)
4
(2)
6
(3)
12
(4)
16
Какие из множеств с операцией сложения образуют группу?
(1)
неотрицательные рациональные числа
(2)
целые степени двойки
(3)
целые числа, кратные 4
(4)
множество {0} (состоящее только из нуля)
Какие из перечисленных систем функций функционально полны в слабом смысле?
(1)
стрелка Пирса
(2)
импликация и отрицание
(3)
сложение по модулю 2 и отрицание
(4)
импликация и дизъюнкция
Отметьте возможные длины максимального пути в ациклическом графе с 6 вершинами и 5 ребрами:
Между множествами A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(b,1),(c,2),(d,2),(d,3)}
и H = {(a,2),(b,2),(c,4),(d,1)}.
Какое соответствие функционально?
(1)
G и H
(2)
только G
(3)
только H
(4)
ни G, ни H
В почтовом отделении имеются открытки 3 видов.
Сколькими способами можно купить набор из 5 открыток?
(1)
10
(2)
15
(3)
21
(4)
25
Какие из множеств с указанной операцией над элементами образуют группу?
(1)
целые числа с операцией вычитания
(2)
целые числа, кратные 3, с операцией сложения
(3)
рациональные числа, отличные от нуля, с операцией умножения
(4)
нечетные числа с операцией умножения
В таблице приведены три функции f1,
f2, f3
от переменных x, y, z:
x |
y |
z |
f1 |
f2 |
f3 |
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Какие из этих функций функционально полны в слабом смысле?
Сколько висячих вершин может быть у дерева
с n вершинами?
Функция f(x1,x2) имеет тип AC→B,
функция g(y1,y2) имеет тип AC→C.
Какой тип имеет функция f(x1,g(y1,y2))?
(1)
AC→B
(2)
AC→C
(3)
A2C→B
(4)
ACAC→C
Какими из следующих
свойств обладают биномиальные коэффициенты?
(1)
C2nn=Cn+1n
(2)
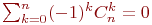
(3)
Cn+1k=Cnk+Cnk-1
Чему равен единичный элемент в группе {-1,1} с умножением?
(1)
его не существует
(2)
1
(3)
-1
Дано равенство ∀x∃yP(x,y) = ∃y∀xP(x,y).
Какие из утверждений верны?
(1)
Это равенство неверно при любых Р.
(2)
Это равенство верно при любых Р.
(3)
Это равенство при некоторых Р верно, а при некоторых других Р неверно.
В потоковой сети, приведенной на рисунке,
все пропускные способности равны 4:
Нарушены ли в ней правила распределения потоков?
(1)
Нет, все верно.
(2)
Да, нарушен закон Кирхгофа.
(3)
Да, нарушено ограничение на пропускную способность.
На множестве натуральных чисел задано отношение «x+y
делится на 2». Отметьте верное утверждение:
(1) отношение рефлексивно
(2) отношение антирефлексивно
(3) отношение симметрично
(4) отношение транзитивно
Слова длины 5 в алфавите {a,b,c,d}
перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0.
Какой номер будет иметь слово caabd?
(1)
625
(2)
519
(3)
812
(4)
907
Какой элемент является образующей в группе {-1,1} с умножением?
(1)
такого элемента не существует
(2)
1
(3)
-1
Какая из формул исчисления предикатов выражает
тот факт, что в множестве М, в котором определен
частичный порядок, существует максимальный элемент?
(1)
∃x∀y(((x∈M)&(y∈M)&(x<y))→(x=y))
(2)
∀x∃y(((x∈M)&(y∈M)&(x<y))→(x=y))
(3)
∃x∃y(((x∈M)&(y∈M)&(x<y))→(x=y))
Для любого k число путей
длины k, начинающихся с любой вершины
графа G, всегда одинаково, если
(1)
G — неориентированное дерево
(2)
G — неориентированный цикл
(3)
G — полный граф
Каким может быть дополнение к отношению строгого порядка?
(1) рефлексивным
(2) симметричным
(3) антисимметричным
Чему равно число таблиц размером 3x2
с элементами из множества мощности 3?
(1)
216
(2)
256
(3)
512
(4)
729
Чему равна наименьшая верхняя грань для {b,f}?

Отметьте неверную формулу:
(1)
∀x∀yP(x,y) = ∀y∀xP(x,y)
(2)
∀x(P(x)∨Q(x)) = ∀xP(x)∨∀xQ(x)
(3)
∃x(P(x)∨Q(x)) = ∃xP(x)∨∃xQ(x).
На множестве A = {a,b,c,d} задано бинарное отношение
R = {(a,b),(b,c),(b,d)}. Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
(1)
(a,c), (a,d)
(2)
(c,d), (d,c)
(3)
никакие, так как R транзитивно;
(4)
(b,a)
Даны два множества: A = {a,b,c},
B = {0,1}.
Каково число различных функций типа AB2→B2?
(1)
48
(2)
124
(3)
412
(4)
256
Чему равна наибольшая нижняя грань для {c,f}?

Ответы на экзамен — Дискретная математика — файл ex_discret.doc
приобрести
Ответы на экзамен — Дискретная математика
скачать (117.3 kb.)
Доступные файлы (1):
- Смотрите также:
- Чудинов К.М. (состав.) Дискретная математика (Документ)
- Галкина М.Ю. Дискретная математика (Документ)
- Гусева А.И., Тихомирова А.Н. Дискретная математика для информатиков и экономистов (Документ)
- Довгий П.С., Поляков В.И. Арифметические основы ЭВМ (Документ)
- Новиков Ф.А. Дискретная математика для программистов (Документ)
- Ответы по дискретной математике (Шпаргалка)
- Шпаргалки на гос.экзамен по экологии для студентов СФУ специальности 280201 (Документ)
- Эвнин А.Ю. Дискретная математика. Конспект лекций (Документ)
- Дискретная математика (Документ)
- Алексеев В.В. Элементы теории множеств и теории графов. Сборник задач и упражнений по курсу Дискретная математика (Документ)
- Эвнин А.Ю. Задачник по дискретной математике (Документ)
- Чудесенко. Учебник по высшей математике (Документ)
ex_discret.doc
Вопросы по курсу «Дискретная математика».
- Множества. Отношения. Функции
- Множества (конечные и бесконечные).
Понятие множества нельзя определить через более общие понятия, так как таких понятий в математике нет. Понятие множества является настолько общим, что для него невозможно дать формальное определение. Интуитивно, под множеством понимается совокупность различных объектов, объединенных по какому-то одному или нескольким признаков. Объекты, составляющие множество, называются элементами. Тот факт, что объект x принадлежит множеству A, передается записью xA ( читается — “элемент x принадлежит множеству A”).. Если x не является элементом A, то пишут x
A. Элементы множеств обычно обозначаются строчными латинскими буквами x, y, a, b, c ; множества часто обозначают прописными латинскими буквами A, B, C, X, Y.
Если множество содержит конечное число элементов, то говорят, что оно конечно, в противном случае множество называется бесконечным. Число элементов конечного множества A называется мощностью множества A и обозначается |A|. В дальнейшем мы будем различать общий (текущий) элемент x множества A, т.е. произвольный элемент, характеризующийся единственным свойством “принадлежать множеству A”, и конкретные элементы a, b, c каждый из которых отличен от других. Множество A, состоящее из элементов a,b,c,… записывается A={a,b,c,…}.
Подмножества.
Понятие подмножества возникает тогда, когда необходимо рассматривать некоторое множество не самостоятельно, а как часть другого, более широкого множества.
Множество B называется подмножеством множества A, если всякий элемент множества B является элементом множества A. Запись BA ( не исключает, что B=A).
Определённое ранее пустое множество по определению является подмножеством любого множества.
По определению пустое множество является конечным.
По определению множество является подмножеством самого себя, AA.
Таким образом, у каждого множества (кроме пустого) есть по крайней мере два подмножества — само множество и пустое.
Важным понятием является понятие подмножества. Понятие подмножества всегда применяется к паре множеств.
Определение
Говорят, что множество А является подмножеством множества В (пишут А В) тогда и только тогда, когда каждый элемент множества А является элементом множества В.
Теорема
Для того, чтобы множество А являлось подмножеством множества В, необходимо и достаточно, чтобы AB = Ш.
Множество всех подмножеств множества А обозначают 2A. Ясно, что Ш 2A и А
2A. Они называются несобственными подмножествами множества А. Остальные подмножества (если они есть) называются собственными.
Пример
Пусть А = {1,2,3}. Ясно, что 2A = {Ш, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.
Операции над множествами и их свойства.
Алгебраическими операциями называют такие, при выполнении которых результирующее множество либо пусто, либо состоит из элементов, из которых состоят и множества, подвергающиеся операциям.
Кардинальными операциями называют такие операции, при выполнении которых появляются новые элементы.
Основными алгебраическими операциями над множествами являются следующие:
— пересечение множеств,
— объединение множеств.
-разность множеств.
Пусть А и В — произвольные множества. Их пересечением называется множество
АВ={x| x
A и x
B}.
Объединением множеств А и В называется множество
АВ={x|x
A или x
B}.
Разностью множеств А и В называется множество АВ={x|xA, но x
B}.
Используя понятие универса, можно ввести еще две операции над множествами — дополнение и симметрическую разность множеств.
Дополнением множества А (до универса J) называется множество =JA, т.е.
={x| x
J, но x
A}.
Симметрической разностью множеств А и В называется множество
АВ=(AB)
(BA).
Если АВ=
, то говорят, что множества А и В не пересекаются.
Геометрическое изображение.
Определение
Дополнением ко множеству А относительно универсального множества I называется множество, обозначаемое Ā, определяемое
Свойства разности и дополнения:
Определение
Объединением множеств А и В называется множество, обозначаемое А В, определяемое
Свойства объединения множеств:
1.
2.
3.
4.
5.
6.
Определение
Пересечением множеств А и В называется множество, обозначаемое А В, определяемое
Свойства пересечения множеств:
1.
2.
3.
4.
5.
6.
Определение
Разностью множеств А и В называется множество, обозначаемое АВ, (А-В), определяемое
Свойства разности множеств:
1.ЕслитоАВ=А.
2.ЕслиАВ,тоАВ=.
3. А В = А (АВ).
Имеют место следующие равенства:
- AШ = A.
- ШA = Ш.
- AI = Ш.
- IA = Ā.
- AA = Ш.
Определение
Симметрической разностью множеств А и В называют множество, обозначаемое А?В (А―В), определяемое A?B ? (AB) (BA).
Имеет место равенство:
A?B = (A B)(A
B)
Имеют место следующие равенства:
- А?В = B?A – коммутативность.
- А?I = Ā.
А?Ш = A.
Способы задания множеств.
Способы задания множеств.
1. Перечислением своих элементов.
A={a,b,c,…}.
2. Через описание ограничительного свойства.
A={x| P(x)} — A множество таких элементов x, которые обладают свойством P(x).
В дальнейшем мы будем пользоваться общепринятыми обозначениями множеств:
N — множество натуральных чисел,
Z — множество целых чисел,
Q — множество рациональных чисел,
C — множество комплексных чисел,
R — множество действительных чисел,
— пустое множество.
Универсальное множество. (?)
Истинным, строгим или собственным подмножеством множества А называется такое его подмножество В, что ВА и В
А. Запись В
А, где
— знак строгого включения.
По отношению к множеству А — пустое множество и само множество А называется несобственным, нестрогим или не истинным подмножествами множества А.
Таким образом, мы имеем следующие свойства множеств:
1. АВ
А
В и А
В.
2. АВ
А
В или А=В.
3. АВ
А
В.
4. АВ
А
В.
5. АВ и В
С
А
С.
6. АВ и В
С
А
С.
7. АВ и В
С
А
С.
Первые четыре свойства следуют из введенных ранее определений.
Покажем выполнение остальных свойств.
Свойство 5.
Докажем его методом от противного.
Пусть АВ и В
С но А
С и А
С.
Тогда существует такой элемент аА, но а
С. Тогда, т.к. В
С, то а
В.
Получили противоречие: аА, а
В, но А
В.
Свойство 6.
Так как АВ и В
С, то по свойству 3 А
В и В
С и по свойству 5 А
С. Осталось показать, что А
С. Пусть это не так и А=С . Т.е. для любого элемента а, а
А
а
С. Так как В
С, то В
С и найдется элемент в,в
В. , но в
С. Так как А
В, то в
А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны.
Свойство 7.
Так как ВС, то по свойству 3 В
С и тогда по свойству 5 А
С. Осталось показать, что А
С. Действительно, так как В
С, то найдется элемент а, а
С, но а
В. Так как А
В, то а
А. Отсюда а
С, но а
А, т.е. А
С.
Если все рассматриваемые в ходе рассуждений множества являются подмножествами некоторого фиксированного множество J, то это множество называют универсальным ( для рассматриваемого набора множеств) множеством или универсом. Таким образом, универс — это такое множество, что любое рассматриваемое множество является его подмножеством.
Рассмотрим множество А={a,b,c}. Найдем все его различные подмножества. Это: пустое множество , три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества — само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или
.
Характеристическая функция множества.
Характеристической функцией ХA множества А называется одноместная функция, равная 0 на элементах множества А и 1 за пределами А. Характеристическая функция называется частичной, если она не определена за пределами А. Множество А называется примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна. Множество А называется частично рекурсивным, если его характеристическая функция частично рекурсивна.
Множество А называется рекурсивно перечислимым, если существует двухместная частично рекурсивная функция ѓ(a,x) такая, что уравнение ѓ(a,x) = 0 имеет решение тогда и только тогда, когда а О А.
Задачу кластеризации удобно формулировать использую характеристическую функцию. Характеристическая функция может принимать два значения: 0 — если элемент не принадлежит кластеру, и 1 — если элемент принадлежит кластеру. Используя характеристическую функцию, опишем кластеры следующей матрицей разбиения:
,
где k-ая строчка матрицы указывает на принадлежность объекта
к кластерам
.
Матрица должна обладать следующими свойствами:
; (12.4)
; (12.5)
Для оценки качества разбиения используется критерий разброса, показывающий сумму расстояний от объектов до центра своего кластера. Для евклидового пространства этот критерий записывается так [1]:
; (12.6)
где — к-й объект кластеризации;
— i-й кластер;
— центр i-го кластера.
Кластеризацию объектов можно сформулировать как следующую задачу оптимизации: найти матрицу
, минимизирующую значение критерия (12.6). Дискретный характер четкого разбиения приводит к трудностям нахождения оптимальной кластеризации из-за негладкости целевой функции.
Булеан.
Пусть А произвольное конечное n- элементное множество. Найдем мощность множества P(A), |P(А)|= , где S={0,1,…,n}.
Для определения величины |Р(А)| воспользуемся формулой бинома Ньютона.
, при условиях, что a=в=1.
Получаем, =|P(A)|.
Замечание.
Множество называется булеаном множества А.
- Декартово произведение.
Кардинальными операциями называются такие операции, при применении которых в результирующем множестве появляются новые элементы.
Примером кардинальных операция является прямое (декартово) произведение множеств.
Прямым произведением множеств А и В называется множество
АВ={(a,b)| a
A, b
B}, т.е. множество тех и только тех пар, первая компонента которых принадлежит множеству А, а вторая В.
Через — обозначают, соответственно, декартов квадрат и декартову n-ую степень множества А.
Отношения (рефлексивности, симметричности, асимметричности, антисимметричности, транзитивности, антитранзитивности) и их свойства.
Отношения эквивалентности.
- Функция — отображение.
Отношение f на AxB называется функцией из A в B , если
если это отображение является функцией и выполняется условие
, то говорят, что
-если , то функция
(f – образ множества A)
— множество значений
Биекция.
-отображение называется инъективным (инъекция), если из того, что
называется отображением “на”
-называется сюръективным, если для любых
-отображение f называется взаимооднозначным или биекцией, если это отображение является и инъективным и сюръективным
если для любого и
:
—
если A=B, то эти отображения называются перестановкой в множестве A.
Эквивалентность множеств.
Счетные множества.
Счетным множеством называется всякое множество, элементам которого можно поставить во взаимно однозначное соответствие множество натуральных чисел.
Отсюда, счетное множество — это бесконечное множество, элементы которого можно перенумеровать натуральными числами.
Примерами счетных множеств, кроме множества натуральных чисел, являются:
— множество целых чисел Z,
— множество всех четных положительных (отрицательных) чисел,
— множество натуральных степеней числа 2,
— множество рациональных чисел Q,
— множество алгебраических чисел и т.д.
Покажем, например, счетность множества алгебраических чисел.
Число а называется алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами.
Так как множество целых чисел счетно, то занумеруем их, например, следующим образом:
если целое число n неотрицательно,
то поставим ему в соответствие номер 2n+1, (1)
если целое число n отрицательное,
то поставим ему в соответствие номер 2|n|.
Каждому уравнению вида :
(2)
поставим в соответствие натуральное число:
, где 2,3,…,p — простые числа, а
— номер целого числа
(коэффициента уравнения (1)), полученного после приведенной нумерации (1).
Таким образом можно перенумеровать все уравнения типа (2). Так как каждое уравнение (2) имеет не более n различных корней, то тем самым доказывается счетность множества алгебраических чисел.
Свойства счетных множеств.
Свойство 1.
Всякое подмножество счетного множества конечно или счетно.
Действительно, если А — счетное множество, то его элементы можно перенумеровать. Пусть В — подмножество множества А. Тогда, если среди элементов множества В есть элемент с наибольшим номером, то множество В является конечным, в противном случае множество В будет счетным.
Свойство 2.
Объединение любого конечного или счетного числа счетных множеств, есть счетное множество.
Для доказательства этого свойства используется так называемая Канторовская диагональная процедура.
Свойство 3.
Всякое бесконечное множество содержит счетное подмножество.
Действительно, если А — бесконечное множество, то в нем есть хотя бы один элемент а. Внесем его в строящееся подмножество В, присвоив этому элементу номер 1. Так как А — бесконечное множество, то в нем после удаления элемента а, останутся элементы. Возьмем любой элемент, присвоим ему номер 2, удалим его из множества А и включим его в множество В, и т.д. Построенное таким образом множество В будет счетным.
Мощность множества. Несчетность множества действительных чисел. Мощность интервала (0; 1). Примеры.
- Элементы теории графов
- Понятие графа,
1.Множество точек (вершин, узлов) и множество линий (ребер, дуг), которые соединяют эти точки, называются графом.
2. Графом называется упорядоченная пара множества X (мн-во вершин) и мн-во его двухэлементных подмножеств.
псевдографа,
Если в графе допускаются кратные рёбра и петли, то он называется псевдографом.
мультиграфа,
Если в графе оказываются петли, то он называется мультиграфом.
орграфа.
1. Есть мн-во точек и мн-во линий, соед эти точки, которые образуют граф, если эти линии имеют стрелки (они упорядочены), то он называется орграфом.
2. Если пары в наборе ребер упорядочены, то граф называется ориентированным.
Способы задания графов.
Задается множество V (вершин) и набор элементов X (рёбер), которые состоят из пар (v,w), если пара имеет вид (v,v), то это петля.
Матрица смежности. Матрица инцидентности.
Графы Г и Г0 можно представить в аналитической форме либо матрицей смежности А(Г), либо матрицей инцидентности В(Г).

Граф и отношение.
??? возможно это то,что он задаётся отношением
Геометрическое изображение графа.
???Линии (ребра графа) и точки (вершины графа).
Плоский граф.
Граф называется плоским (планарным), если его можно уложить на плоскости так, чтобы его ребра негде не пересекались кроме вершин.
Топологическая реализация графа.
???в этой лекции идёт тема маршрута
- Полный граф.
Граф называется полным, если линии такого графа образуют полную цепь (она связывает все вершины графа без образования петель и контуров)
- Степень вершины графа, свойства.
Степенью вершины графа называется число рёбер, инцидентных данной вершине рёбер (степень вершины a равна 2).
- Число ребер полного графа.
???
- Теорема о сумме степеней всех вершин графа.
-в графе G порядка n сумма степеней всех его вершин есть частное число, равное
(E – число рёбер)
- Теорема о числе нечетных вершин графа.
Число нёчётных вершин любого графа четно. (вершина чётная, если её степень чётное число).
- Теорема о графе с вершинами степеней 0 и n — 1.
Во всяком графе порядка n (n?2?непонятный знак) не может быть одновременно вершин степени 0 и n-1.
- Маршрут,
2 определения 1-учебник, 2-тетрадь.
1.Введём понятие маршрута для графа G=(V,X) (и соответственно понятие пути для орграфа D=(V,X)). Последовательность
(где ), в которой чередуются вершины и рёбра (дуги) и для каждого
ребро (дуга) xj имеет вид
, называется маршрутом, соединяющим вершины
(путём из
в
), при этом
называется начальной, а
— конечной вершиной, а все остальные – внутренними.
2. Маршрутом, соединяющим вершины xi и xj называется такая последовательность рёбер, в которой каждые два соседних ребра инцидентны одной вершине, где начальная вершина xi и конечная xj.
-Простой маршрут – когда рёбра не пересекаются.
цепь,
Любой минимальный путь (маршрут) является простой цепью (в ней нет повторяющихся вершин).
замкнутый маршрут,
Когда в маршруте есть совпадающие вершины.
цикл,
Если в маршруте нет совпадающих рёбер, то он называется цикл.
Простой цикл – нет совпадающих вершин.
их длины.
???кол-во вершин (маршрут) или кол-во рёбер (цикл).
- Связность вершин, графа. Расстояние между вершинами графа.
- Изоморфизм графов.
- Дерево.
Дерево – связанный граф, не имеющий циклов (так как любые две его вершины соединены простым путём).
Корневое дерево.
Иногда выделяется вершина – корень дерева.
Корневое дерево — ???
Число ребер дерева с n вершинами.
- Взвешенный граф. Алгоритм построения покрывающего дерева (минимального, максимального).
Граф называется взвешенным, если его ребра ставятся в соответствие числа (упорядоченные наборы).
Алгоритм построения покрывающего дерева.
Алгоритм использует раскрашивание ребер графа в 2 цвета: ребро в зеленый, если оно включается в покрывающее дерево, иначе оно окрашивается в оранжевый. Для того чтобы ребро не окрашивалось в зеленый цвет, надо чтобы оно не образовывало цикла с ребрами, уже включенными в покрывающеее дерево. Для проверки этого из вершин ребер включенных в покрывающее дерево, образуют множество — букеты. Причем обе вершины, инцтдентные ребру, включенные в покрывающее дерево, входят в один букет, но в процессе построения покрывающего дерева может участвовать несколько букетов. Процесс построения покрывающего дерева заканчивается, когда все вершины графа включаются в один букет. Или это условие эквивалентно следущему: число окрашенных ребер должно быть на 1 меньше порядка графа.
Пусть граф G не содержитпетель G=(x,e).
1. Выбираем произвольно ребро, окрашивая его в зеленый цвет. А из его кольцевых вершин образуем букет.
2. Во множестве неокрашенных ребер выбираем любое ребро и переходим к рассмотрению остальных 4 случаев:
а). Но если такого ребра нет,то это значит , что граф не имеет покрывающего дерева и является не связным. Обе вершины выбранного графа принадлежат одному букету ребро, следовательно окрашиваем в оранжевый цвет и преходим на п. 2
б). Обе выбранные вершины не принадлежат ни одному букету, тогда ребро окрашиваем в зеленый цвет, а из его кольцеввых вершин образуем новый букет.
в). Одна из вершин выбранного ребра принадлежит одному букету, а другая кольцевая вершина не принадлежит ни одному букету. Тогда ребро окрашиваем в зеленый цвет, а вторую кольцевую вершину включаем в тот же букет.
| a | b | c | d | e | |
| a | — | 5 | 50 | 80 | 90 |
| b | 5 | — | 70 | 60 | 50 |
| c | 50 | 70 | — | 8 | 20 |
| d | 80 | 60 | 8 | — | 10 |
| e | 90 | 50 | 20 | 10 | — |
г). одна из вершин выбранного ребра принадлежит одному букету, а другая – другому, тогда ребро окрашивают в зеленый цвет, а букеты объединяем.
3. Если все вершины находятся в одном букете, или число окрашенных зеленым цветом ребер на 1 меньше порядка графа, то конец.
Ребра зеленого цвета определяют покрывающее дерево, иначе переходим к пункту 2.
Этот алгоритм обладает свойством: каждое ребро рассматривается не более одного раза, следовательно число шагов работы этого алгоритма не более числа ребер. Такие алгоритмы называют «жадными», «поедающими». Граф, имеющий покрывающее дерево — связный граф.
| Шаг | Ребро | Цвет | Букет1 | Букет2 |
| 1 | (c,e) | зеленый | c,e | |
| 2 | (b,a) | зеленый | b,d | |
| 3 | (a,b) | зеленый | b,d,a | |
| 4 | (a,d) | оранжевый | ||
| 5 | (b,c) | зеленый | c,b,e,d,a |
Пример построения покрывающего дерева:
— полный граф
Ребра: (a,b),(b,c),(c,d),(d,e),(a,e),(a,c),(a,d),(b,c),(b,d),(c,e).
В
| Шаг | Ребро | Цвет | Букет1 | Букет2 | Вес |
| 1 | (a,b) | зеленый | a,b | 5 | |
| 2 | (c,d) | зеленый | с,d | 8 | |
| 3 | (d,e) | зеленый | с,a,e | 10 | |
| 4 | (c,e) | оранжевый | |||
| 5 | (a,c) | зеленый | a,b,c,d,e | — | 50 |
Алгоритм:
1. Выбираем вершину хо, окрашиваем, приписываем ей значение ?(хо)=0, считаем, что у=хо
2. Для всех вершин графа G пересчитываем все величины d(x) по следущему правилу: d(x)=min{d(x); d(y)+f(x,y)}. Для всех полученных значений d(xi), где xi – неокрашенные, выбираем наименьшее, значит соответствующую вершину окрашиваем, присваиваем эту вершину переменной у. Окрашиваем ребро, входящее в эту вершину и составляющую min среди всех неокрашенных вершин.
3. Если у?xк(у нее совпадает с конечной), то переходим к пункту 2.
Если для всех неокрашенных вершин d(xi)=?, то делаем вывод, что в исходном графе отсутствует кратчайший путь от вершин x0 в xк. Этот алгоритм позволяет находить кратчайший путь из одной вершины в другую(если он существует). При этом весовая функция, определенная на множестве ребер должна быть положительна. Ребрам могут присваиваться только положительные числа.
Свойства алгоритма.
1. Если получился кратчайший путь из вершины x0 в неокрашенной вершине х, проходящей через вершину у, то кратчайший путь из у в х тоже будет кратчайшим.
2. Алгоритм представляет собой процедуру наращивания покрывающего дереву кратчайщих путей с корнем в вершине x0.
- 3. Получив кратчайший путь из x0 в xк, но остались неокрашенные вершины, то продолжая выполнять алгоритм, получим кратчайшие пути до всех неокрашенных вершин, следовательно этот алгоритм позволяет получать для исходного графа G покрывающее дерево кратчайших путей с корнем в исходной точке x0.
Вопросы по курсу «Дискретная математика»
Задачи с экзаменов по дискретной математикеКафедра дискретной математики7 семестр, 2005 г.Это задачи, собранные с экзаменов по дискретной математике в 2005–2006 году. Естественно, на полнотуданный список не претендует. За сбор задач и набор решений спасибо Сергею Гладких, Стасу Куприянову, ИреШитовой, Мите Копьёву, Юре Притыкину, Мише Левину и Пете Митричеву.Последняя компиляция: 14 мая 2006 г.Обновления документа — на сайте http://dmvn.mexmat.net.Об опечатках и неточностях пишите на dmvn@mccme.ru.Далее очень часто будет использоваться обозначение B := {0, 1}.Задача 1. Пусть f (x) : Bn −→ B — булева функция, такая чтоXf (x) = n2 .x∈{0,1}nДоказать, что L(f ) = On3log2 n.Решение. Для начала представляем нашу функцию в виде_f (x) =xσ1 1 .
. . xσnn ,(1)где дизъюнкция берется только по тем n2 наборам, на которых функция равна единице. Такоепредставление дает нам сложность порядка n3 , а мы хотим меньше.1◦ . Заметим, что, фактически, мы хотим реализовать n2 функций вида xσ1 1 . . . xσnn . Разобьем это множество функций на два: xi1 . . . xik и xj1 ∨ . .
. ∨ xjl , то есть каждая конъюнкцияразбивается на конъюнкцию «положительных» степеней и конъюнкцию отрицаний. Их потомеще нужно будет склеивать, но асимптотики нам это не испортит. Далее мы ограничиваемсяреализация 1-го множества — со вторым все аналогично.2◦ . Рассмотрим наше множество функций как матрицу n2 × n. Если xi входит в j-ю конъюнкцию, ставимна ij-е место 1, иначе 0. Итак, задача сведена к реализации такой вот матрицыn3за O log n операций. 3й нетривиальный шаг.
Разбиваем матрицу на блоки по ⌈log2 n⌉ строк.2И замечаем, что это — проверочные матрицы двоичного кода Хемминга! А их мы умеем реализовывать за ∼ n операций (подробнее см. записки семинаров А. В. Чашкина). А таких блоков2у нас как раз logn n . Умножаем и получаем то, что требовалось. 2Задача 2. Найти минимальное число элементов единичной задержки, необходимых дляреализации автомата без входов, генерирующего периодическую последовательность с периодом (10000111), и оценить сложность порождающей этот автомат СФЭ.Задача 3.
Построить проверочную матрицу троичного кода Хемминга, содержащую тристроки.Задача 4. Дано поле из m := pn элементов (α1 , . . . αm ). Найти суммуXαi1 αi2 αi3 .i1 <i2 <i31(2)Решение. Здесь написан просто-напросто (с точностью до знака) элементарный симметрический многочлен третьего порядка. А мы знаем, что все элементы поля удовлетворяют уравнению xm − x = 0.
По теореме Виета, все элементарные симметрические многочлены, кромеодного (σm ), равны нулю, значит, в частности, наша сумма тоже равна нулю. Задача 5. Найти функцию Эйлера ϕ(n) через формулу включений-исключений.∗ Задача 6. Дано регулярное событие A = 0 (1111)∗00(00)∗ . Построить автомат, распознающий это событие.Задача 7. Найти вес ограниченно-детерминированной функции, которая равна 1 тогда итолько тогда, когда x ∈ A, а A = {1((00)∗(1111)∗ )∗ }.Задача 8.
Дан автомат без входов. Найти минимальное число элементов единичной задержки и функциональных элементов в базисе всех двуместных булевых функций для реализации (1110)∗.Задача 9. A := {f ∈ P2 (n) : f (x) = f (x)}, x = (x1 , . . . , xn ) ∈ Bn . Найти max L(f ).f ∈AЗадача 10. Пусть m(n, d) — максимальная мощность двоичного кода длины n с кодовымрасстоянием d. Доказать неравенство m(n, d) 6 2m(n − 1, d).Решение.
Решается по индукции. Рассмотрим самый мощный код длины n, разобьём слована две группы: с последним битом 0 и с последним битом 1. В каждой группе слов не больше,чем m(n − 1, d). Задача 11. Пусть f : B∗ → B∗ — детерминированная функция, гдеt1, P x = 2047;if (x1 , . . . , xt ) =i=10, иначе.(3)Найти вес функции f , построить для неё диаграмму Мура и написать канонические уравнения.Решение. Построим дерево для нашей функции и рассмотрим вершину на уровне t. Еслизначение функции на входящем в неё ребре равно 0, то дальше будет либо нулевое поддерево,либо по единичной ветви мы придём в вершину со значением 1.
Из начала это произойдёт за2047 шагов, из вершины 1-го уровня — за 2046, . . . , из вершины 2046-го уровня — за 1 шаг,из вершины 2047-го уровня — за 0 шагов. Таким образом, всего получаем 2048 состояний плюснулевое дерево — всего 2049. Это и есть вес функции f .Канонические уравненияy(t) = F (x(t), q(t))q(t + 1) = G(x(t), q(t))q(1) = 0находятся из таблицы:2×0101…010101qF00001010… …2046 02046 12047 12047 02048 02048 0G0112…204620472047204820482048Задача 12.
Найти мощность 6-разрядного двоичного кода, если любой шар в B6 содержит1 или 2 элемента кода.Задача 13. Известно, что a1 = 2, a2 = 2, иan = −2an−2 + cosπn.2Найти an в явном виде.Задача 14. ПустьA=( nXi=1Найти асимптотику L(A).) nXai xi ai = 2 (mod 3) .i=1Задача 15.
Дан [n, k]-код. Найти максимальное n, при котором этот код исправляет однуошибку.Задача 16. Найти L {x ⊕ y, x ↓ y} .Задача 17. При каких r и q существует однозначное кодирование r-буквенного алфавитав q-буквенном, такое что для него в неравенстве Крафта – Макмиллана выполняется строгоеравенство?Задача 18. Сколько существует монотонных функций от n переменных, принимающихзначение 1 ровно на 7 наборах?nPЗадача 19. Пусть x = (x1 , x2 , . . . , xn ), где xi — булевы. Пусть |x| =2i−1 xi . Пусть A —1 √ множество булевых функций, таких что f (x) = f (y), если |x| ≡ |y| (mod 2 n ). Найти L(A)(оценить порядок).Ответ: Ответ:√2√ n.n√Решение.
Оценка снизу. Таких функций хотя бы 2 n−1 . С другой стороны, если применить лемму о количестве графов с p вершинами и q ребрами и оценить количество схем с неnболее, чем h элементами так же, как когда мы доказывали оценку снизу 2n , то получится какраз нужная оценка.√Оценка сверху. Если мы сможем находить остаток от |x| по модулю 2[ n] , то далее по теоре√ме Лупанова мы достроим схему из порядка 2[ n] , которая реализует нашу функцию. Отлично,осталось построить схему из полиномиального числа элементов, реализующую нахождение |x|3(mod a). Числа 2i (mod a) для i = 0, 1, . . . , n − 1 мы можем предвычислить в двоичном виде.Останется в таком случае решить следующую задачу: на входы схемы подаются числа нольили один. Тогда нужно сложить все из наших чисел 2i (mod a), для которых на i + 1 входеподали единицу.
То есть реально нужно построить схему, складывающую два двоичных числа.Ну, а так как ⊕ реализуется через конъюнкцию, дизъюнкцию и отрицание, то можно считатьего элементом. А из ⊕ уже можно с помощью стандартной техники сложения двоичных чисел на компьютере построить такую схему, складывая числа побитово, и имея дополнительныеэлементы для битов переполнения. Последняя компиляция: 14 мая 2006 г.Обновления документа — на сайте http://dmvn.mexmat.net.Об опечатках и неточностях пишите на dmvn@mccme.ru.4.
Демонстрационный вариант экзамена по дисциплине «Дискретная математика»
Инструкция для студентов
На выполнение письменной работы по математике дается 2 астрономических часа (120 минут).
Экзаменационная работа состоит из двух частей: основной и дополнительной.
При выполнении любого задания требуется предоставить ход решения и указать ответ.
Правильное выполнение задания оценивается баллами. Баллы, полученные за все задания, суммируются.
Критерии оценки выполнения работы:
|
Оценка |
Число баллов, необходимых для получения оценки |
|
«3» (удовлетворительно) |
9-13 |
|
«4» (хорошо) |
14-17 |
|
«5» (отлично) |
18-20 |
Основная часть
1. (1балл) Даны множества А={ 4,7,11}, B={1,4,5,7}, U={1,2,3,4,5,9,10,11}. Определите мощность множества 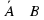
2. (1 балл) Изобразите с помощью кругов Эйлера множество 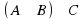
3. (1 балл) Вычислить
4. (1 балл) Найти 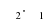


5. (1 балл) Составьте матрицу смежности, инцидентности для графа
6. (1 балл) Упростите формулу
7. (1 балл) Постройте таблицу истинности формулы 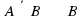
8. (1 балл) Запишите СДНФ и СКНФ для булевой функции, заданной вектором значений f=(11001010).
9. (1 балл) Запишите суждение в виде формулы логики предикатов: «Не всякое действительное число является рациональным».
10. (1 балл) Для автомата, заданного таблицей, постройте диаграмму Мура
|
α / q |
0 |
1 |
2 |
3 |
|
0 |
(1;1) |
(3;0) |
(2;0) |
(2;0) |
|
1 |
(1;2) |
(2;0) |
(3;0) |
(3;0) |
Дополнительная часть
11. (2 балла) Найдите центр, радиус, диаметр графа:
12. (2 балла) Дано множество 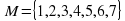
13. (2 балла) Докажите, что при любом натуральном n имеет место равенство
14. (2 балла) Исследуйте булеву функцию 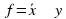
15. (2 балл) Составьте МДНФ для булевой функции f(000)=f(001)=f(100)=f(110)=1.