Экзамен по геометрии 7 класс билеты с ответами атанасян

Билет №1

1. Виды треугольников по длине сторон. Периметр треугольника.

Треугольники бывают:

Равнобедренный (равны две стороны), разносторонний (все стороны по величине разные),

равносторонний —все стороны равны Периметром треуг называется сумма длин его сторон)

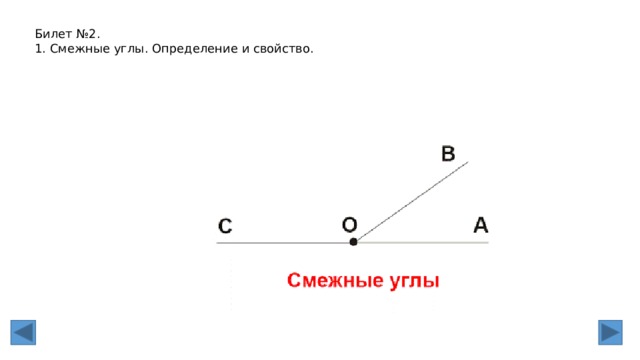
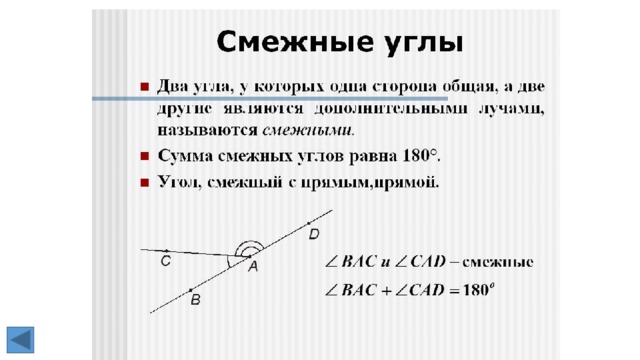
2. Смежные углы (определение). Теорема о сумме смежных углов.

Смежными называются два угла, у которых одна сторона общая, а две другие являются

дополнительными лучами (т.е. имеют общее начало и дополняют друг друга до прямой).

Сумма смежных углов равна 180°.

Дано: ∠АОВ и ∠ВОС смежные.

Доказать: ∠АОВ + ∠ВОС = 180°

Доказательство:

∠АОС = ∠АОВ + ∠ВОС по свойству измерения углов,

∠АОС = 180°, так как является развернутым, ⇒ ∠АОВ + ∠ВОС = 180°

3. Задача по теме «Признаки равенства треугольников».

Отрезки AC и BD пересекаются в точке О. AO=OC, BO=OD. При проведении отрезков AB

и CD образуются треугольники BAO и OCD. Докажите, что ∆ BAO=∆ OCD.

Билет №2

1. Отрезок (определение). Середина отрезка. Основное свойство расположение точек

на прямой.

Отрезок — это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и

конец, а значит можно измерить её длину.

Середина отрезка — это точка на заданном отрезке, находящаяся на равном расстоянии от

обоих его концов отрезка.

из трёх точек на прямой одна и только одна лежит между двумя другими.

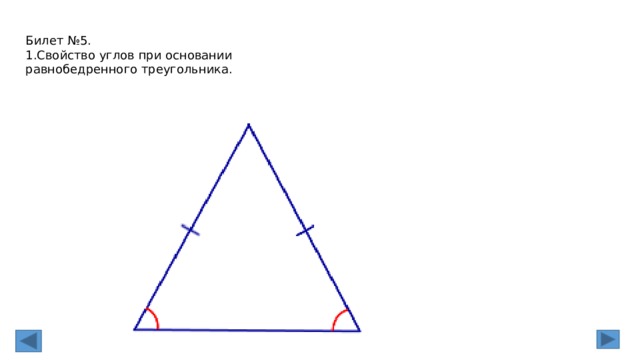
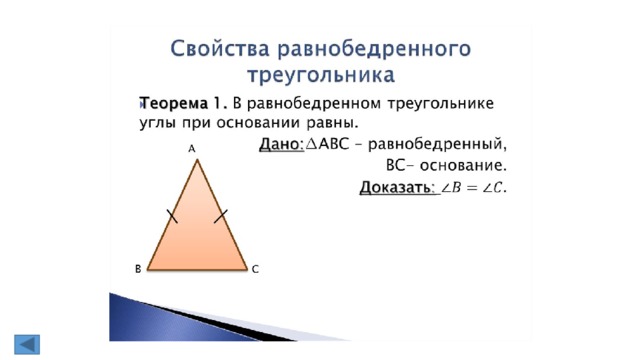
2. Свойства равнобедренного треугольника (доказательство одного из них).

Свойства равнобедренного треугольника:

1. В равнобедренном треугольнике углы при основании равны.

Доказательство:

пусть АВС — равнобедренный треуг с основанием АВ. Докажем, что у него А= В.

Тр САВ равен тр СВА по первому признаку равенства треугДействительно, СА=СВ,

СВ=СА, угол С= углу С.Из равенства треугольников следует, что угол А= углу В. Теорема

доказана.

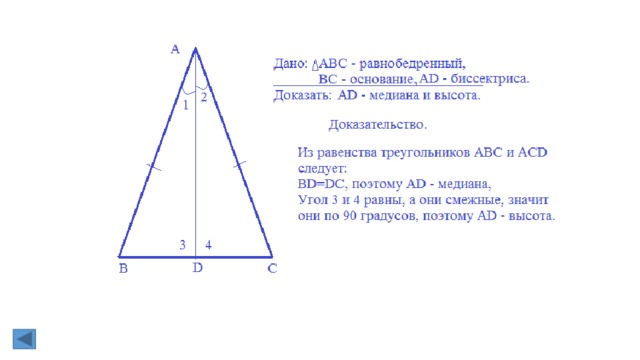
2 В равнобедренном треуг биссектриса , проведённая к основанию , является медианной и

высотой .

Доказательство:

Рассмотрим треугольники ACF и BCF (важно правильно их назвать!)

1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))

2) ∠ACF=∠BCF (так как CF — биссектриса по условию).

3) сторона CF — общая.

Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон и углов.

Таким образом, AF=BF, следовательно, CF — медиана.

∠AFC=∠BFC. А так как эти углы — смежные, значит, они прямые: ∠AFC=∠BFC=90º.

Значит, CF — высота.

Что и требовалось доказать.

3. Задача по теме «Окружность и ее элементы».

Найдите длину радиуса окружности, если длина диаметра равна 14,5 см.

Билет № 3

1. Основные геометрические фигуры на плоскости. Основное свойство

принадлежности точек и прямых.

Основными геометрическими фигурами на плоскости являются точка и прямая. Какова бы

ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не

принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

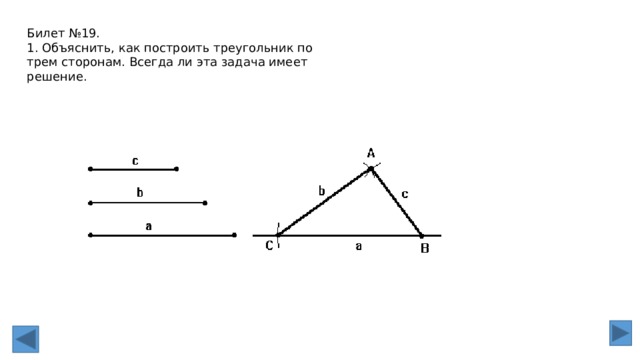
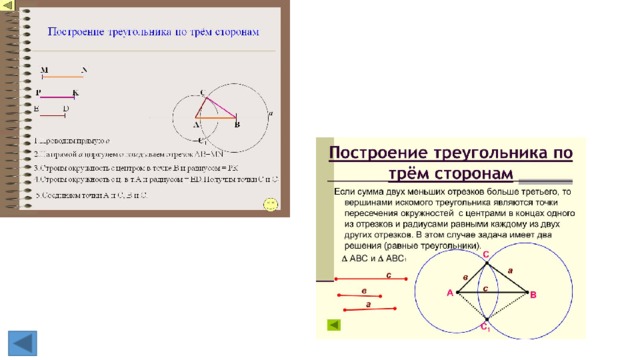
2. Построение треугольника по трём сторонам.

Даны три отрезка: a,b иc, равные сторонам искомого треугольника..

В этом случае перед началом построения необходимо убедиться, исполняется ли

неравенство треугольника (длина каждого отрезка меньше суммы длин двух остальных

отрезков), и эти отрезки могут быть сторонами треугольника.

Если да, то:,

1. Провести прямую.

2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и

отметить другой конец отрезка B.

3. Провести окружность с центром A и радиусом, равным отрезку b.

4. Провести окружность с центром B и радиусом, равным отрезку c.

5. Точка пересечения окружностей является третьей вершиной искомого треугольника.

3. Задача по теме «Вертикальные углы».

Один из вертикальных углов равен 45º. Найдите остальные углы.

Билет № 4

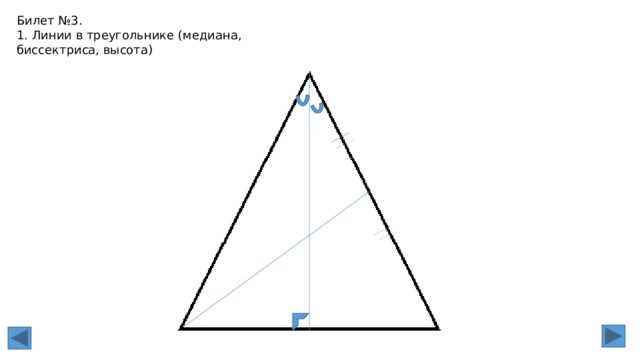
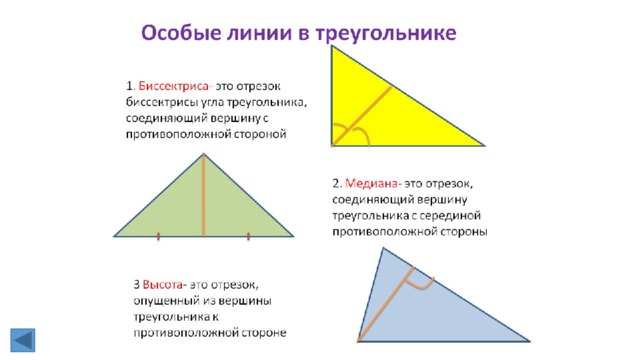
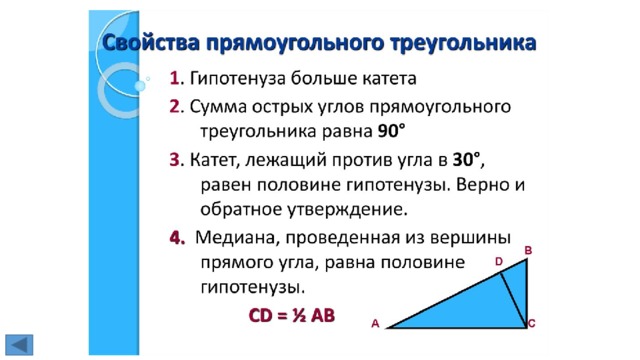
1. Высота, биссектриса, медиана треугольника (определения).

Медиана — это отрезок, соединяющий вершину треугольника с серединой

противоположной стороны.

Биссектриса — это отрезок, делящий угол треугольника на две равные части.

Высота треугольника — это перпендикуляр, опущенный из любой вершины

треугольника на противоположную сторону, или на ее продолжение.

2. Теорема о свойстве катета, лежащего против угла в 30º.

Так как сумма острых углов прямоугольного треугольника равна 90º, то∠B=90º-

∠A=90º—30º=60º.Построим треугольник ADC, равный треугольнику ABC.В нем

∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).Отсюда,

∠BAD=∠CAD+∠CAB=60º.Следовательно, в треугольнике ABD все углы

равны:∠BAD=∠D=∠B=60º.Значит, треугольник ABC — равносторонний, и все его

стороны равны: AB=AD=BD.BC=DC (по построению),

поэтому Что и требовалось доказать.

3. Задача по теме » Признаки параллельности прямых».

Один из внутренних накрест лежащих углов, образованных при пересечении двух

параллельных прямых третьей прямой, равен 50º. Найдите градусные меры

остальных углов.

Билет № 5

1. Взаимное расположение двух прямых. Основное свойство параллельных

прямых.

1)прямые пересекаются (т. е. имеют одну общую точку), 2) прямые параллельны и не

совпадают, 3) прямые совпадают( множ—во общих точек)

Через точку не лежащую на прямой, можно провести прямую параллельную данной, причем

только одну.

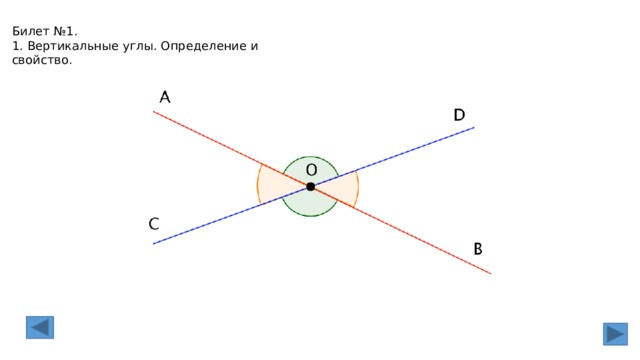
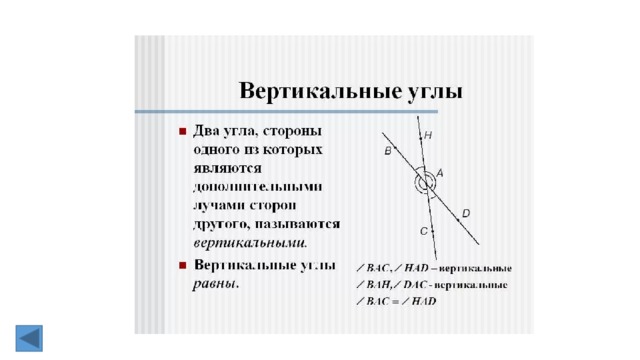
2. Вертикальные углы (определение). Свойства вертикальных углов.

Два угла называются вертикальными, если стороны одного угла являются продолжениями

сторон другого.

Вертикальные углы равны

Дано: – 1 и – 2 – вертикальные углы.

Доказать: – 1 = – 2.

Доказательство. – 3 является смежным и с – 1, и с – 2. Сумма смежных углов равна 180°,

поэтому – 1 + – 3 = 180о , – 2 + – 3 = 180о . Отсюда получаем, что – 1 = 180о –– 3, – 2 = 180о

– – 3. Пра— вые части равенств равны, значит, равны и левые. Следовательно, – 1 = – 2. Итак,

вертикальные углы равны

3. Задача по теме » Соотношения между сторонами и углами

треугольника».

В треугольнике ABC AB=4 см, AC=6 см,BC=5 см. Какой угол треугольника наименьший, а

какой наибольший?

Билет №6

1. Полуплоскость. Луч (определение). Основное свойство расположения точек

относительно прямой на плоскости.

Любая прямая на плоскости разделяет её на две части, которые называются

полуплоскостями. Полуплоскость – это часть плоскости, лежащая по одну сторону от любой

прямой на этой плоскости. Луч — это часть прямой, состоящая из всех точек этой прямой,

лежащих по одну сторону от одной её точки. Эта точка называется началом луча.

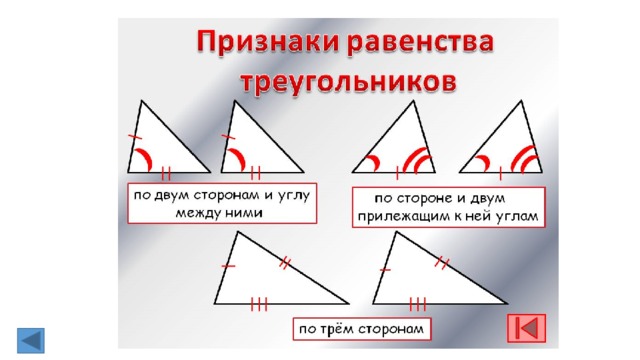
2. Первый признак равенства треугольников.

Доказать, что треугольник ABC равен треугольнику DEF.

Доказательство:

1. Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг

на друга, так чтобы вершина С совпадала с вершиной F.

2. При этом отрезки СА и СВ наложатся на отрезки FE и FD.

3. А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по

условию), то отрезок АВ также совпадёт со стороной ED.

4. Это в свою очередь даст совмещение вершин А и D, В и Е.

5. Следовательно, треугольники полностью совместятся, а значит, они равны.

Теорема доказана.

3. Задача по теме » Сумма углов треугольника».

В треугольнике ABC даны два угла:

=57º. Найдите третий угол.

Билет № 7

1. Угол (определение). Измерение углов. Основные свойства измерения углов.

У

́

гол — геометрическая фигура, образованная двумя лучами (сторонами угла),

выходящими из одной точки (которая называется вершиной угла).

За единицу измерения углов обычно принимается угол, составляющий одну сто

восьмидесятую часть развернутого угла. Считают, что величина этого угла равна одному

градусу, обозначают 1

о

.

Градусная величина угла показывает, сколько раз угол в один градус и его части

укладываются в этом угле. Прибор для измерения транспортир.

1)Каждый угол имеет определенную градусную меру большую нуля.

2)Развернутый угол равен 180 градусам.

3) Градусная мера угла равна сумме градусных мер углов,на которые он разбивается любым

лучом,проходящим между его сторонами.

2. Второй признак равенства треугольника.

(Второй признак равенства треугольников — по стороне и двум прилежащим к ней углам)

Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне

и прилежащим к ней углам другого треугольника то такие треугольники равны.

Дано:ΔABC, ΔA

1

B

1

C

1

, AB=A

1

B

1

, ∠A=∠A

1

, ∠B=∠B

1

.

Доказать: ΔABC= ΔA

1

B

1

C

1

Доказательство:

Так как AB=A

1

B

1

, то треугольник A

1

B

1

C

1

можно наложить на треугольник ABC так, чтобы

• сторона A

1

B

1

совместилась со стороной AB,

• точки C

1

и С лежали по одну сторону от прямой AB.

Поскольку ∠A=∠A

1

, сторона A

1

С

1

при этом наложится на луч AC.

Так как ∠B=∠B

1

, сторона B

1

C

1

наложится на сторону BC.

Точка С

1

принадлежит как стороне A

1

С

1

, так и стороне B

1

C

1

, поэтому С

1

лежит и на луче AC,

и на луче CB.

Лучи AC и CB пересекаются в точке C. Следовательно, точка С

1

совместится с точкой C.

Значит, сторона A

1

С

1

совместится со стороной AC, а сторона B

1

C

1

— со стороной BC.

Таким образом, при наложении треугольники ABC и A

1

B

1

C

1

полностью совместятся.

А это означает, что ΔABC= ΔA

1

B

1

C

1

(по определению).

Что и требовалось доказать.

3. Задача по теме » Высота, медиана и биссектриса треугольника».

Отрезок СЕ является медианой ACD. Известно, что AE=2,5 см, AC=3 см, CD=4 см.

Найдите периметр треугольника ACD.

Билет № 8

1. Треугольник (определение). Равные треугольники. Существование

треугольника, равному данному.

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной

прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника. Соединяющие вершины отрезки называются

сторонами треугольника. Треугольник обозначается указанием его вершин.

Треугольники называются равными, если у них соответствующие стороны равны и

соответствующие углы равны.

Каков бы ни был треугольник, существует треугольник, равный данному,

отложенный в треугольника, равного данному. заданном направлении, относительно

заданной полупрямой.

2. Третий признак равенства треугольника.

(Третий признак равенства треугольников — по трём сторонам)

Если три стороны одного треугольника соответственно равны трём сторонам другого

треугольника, то такие треугольники равны.

Дано:

ΔABC,

ΔA

1

B

1

C

1

,

AB=A

1

B

1

, AC=A

1

C

1

, BC=B

1

C

1

.

Доказать:

ΔABC= ΔA

1

B

1

C

1

Доказательство:

Приложим треугольник A

1

B

1

C

1

к треугольнику ABC так, чтобы

• вершина A

1

совместилась с вершиной A,

• вершина B

1

совместилась с вершиной B,

• точки C

1

и C лежали по разные стороны от прямой AB.

При этом возможны три случая взаимного расположения луча CC

1

и угла ACB.

I. Луч CC

1

проходит внутри угла ACB.

Проведём отрезок CC

1

.

По условию AC=A

1

C

1

и BC=B

1

C

1

, поэтомутреугольники ACC

1

и BCC

1

— равнобедренные с

основанием CC

1

.

По свойству равнобедренного треугольника, ∠ACC

1

=∠AC

1

C и ∠BCC

1

=∠BC

1

C.

Если к равным углам прибывать равные углы, то получим равные углы:

Таким образом, ∠ACB=∠AC

1

B.

Точки A

1

и A, B

1

и B совмещены, то есть ∠AC

1

B и ∠A

1

C

1

B

1

— один и тот же угол.

Для треугольников ABC и A

1

B

1

C

1

имеем:

AC=A

1

C

1

, BC=B

1

C

1

(по условию), ∠ACB=∠A

1

C

1

B

1

(по доказанному).

Следовательно, ΔABC= ΔA

1

B

1

C

1

(по 1 признаку равенства треугольников).

II. Луч CC

1

проходит внутри угла ACB.

Так как AC=A

1

C

1

и BC=B

1

C

1

, треугольники ACC

1

и BCC

1

— равнобедренные с основанием

CC

1

и ∠ACC

1

=∠AC

1

C и ∠BCC

1

=∠BC

1

C (как углы при основании).

Если из равных углов вычесть равные углы, то получим равные углы:

Таким образом, ∠ACB=∠AC

1

B и ΔABC= ΔA

1

B

1

C

1

(по 1 признаку равенства треугольников).

III. Луч CC

1

совпадает со стороной угла ACB.

По условию BC=B

1

C

1

, поэтому треугольник BCC

1

— равнобедренный с основанием CC

1

.

Отсюда ∠C

1

=∠C (как углы при основании) и ΔABC= ΔA

1

B

1

C

1

(по 1 признаку равенства

треугольников).

Что и требовалось доказать.

3. Задача по теме «Неравенства треугольника».

Существует ли треугольник со сторонами 7 см, 2 см и 10 см? Ответ обоснуйте.

Билет № 9

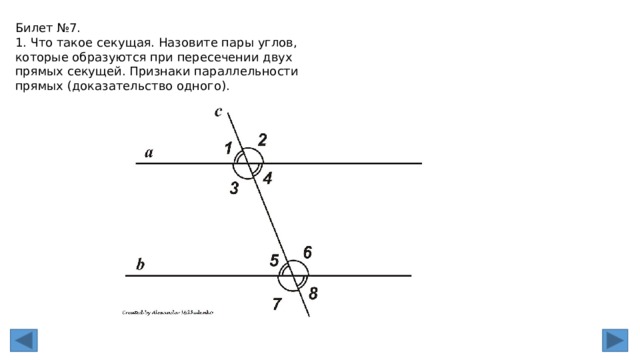
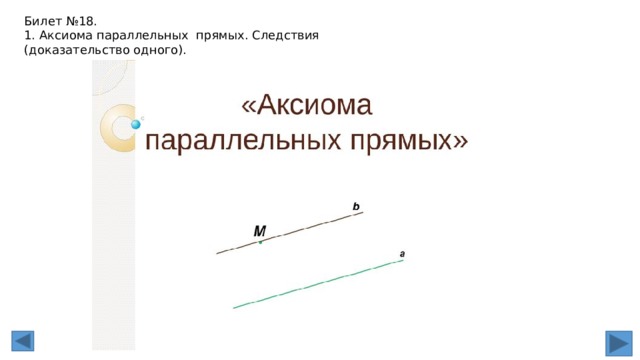
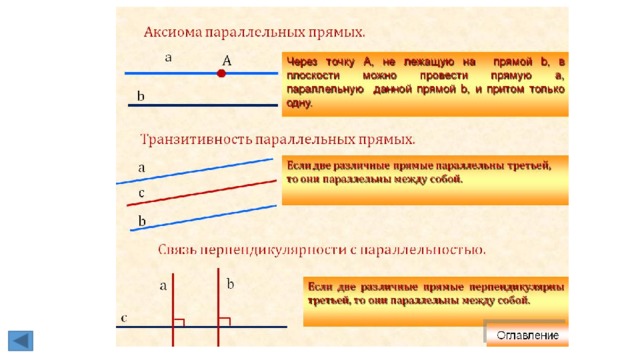
1. Углы, образованные при пересечении двух прямых секущей. Аксиома

параллельности прямых (без доказательства)

При пересечении прямых секущей образуются такие пары углов:

• Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними

односторонними углами.

• Углы, лежащие между прямыми и по разные стороны от секущей, называются

внутренними разносторонними углами.

• Углы, лежащие по одну сторону секущей, но один из них лежит между заданными

прямыми, а другой не лежит между ними, называются соответствующими.

Через любую точку плоскости, расположенную вне данной прямой, можно провести

единственную прямую, параллельную данной

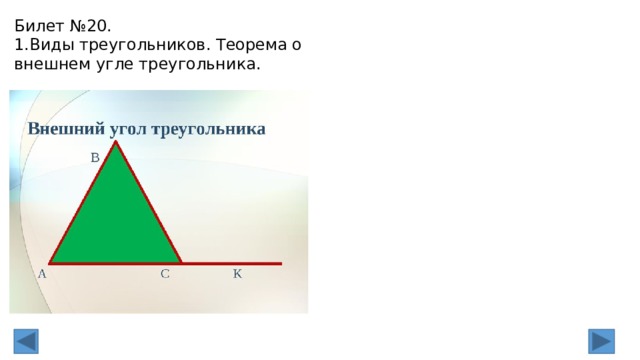
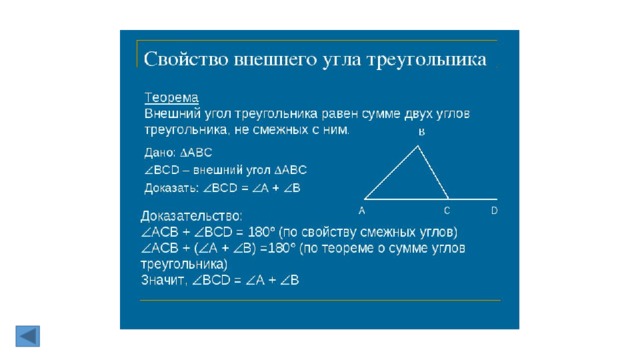
2. Внешний угол треугольника (определение). Теорема о внешнем угле

треугольника.

Внешним углом треугольника называется угол, смежный с каким—нибудь углом

этого треугольника.

Внешний угол треугольника равен сумме двух углов треугольника, не смежных

с ним

Доказательство.

Пусть ABC – данный треугольник. По теореме о сумме углов в треугольнике

∠ ABС + ∠ BCA + ∠ CAB = 180 º.

Отсюда следует

∠ ABС + ∠ CAB = 180 º — ∠ BCA = ∠ BCD

Теорема доказана.

3. Задача по теме «Признаки равенства прямоугольных треугольников».

У треугольников ABC и DEK:

, AC=DK, AB=DE. Докажите, что

.

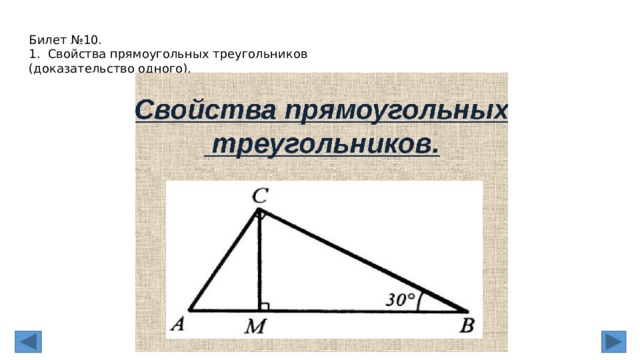
Билет № 10

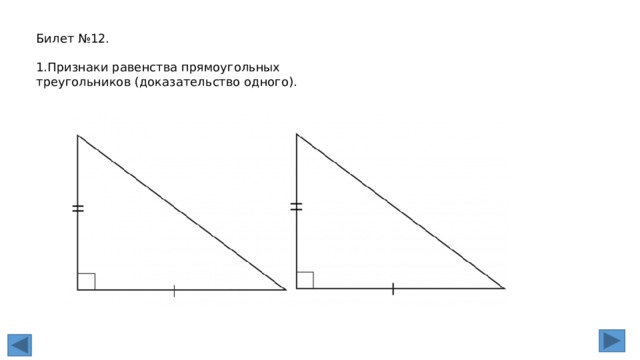
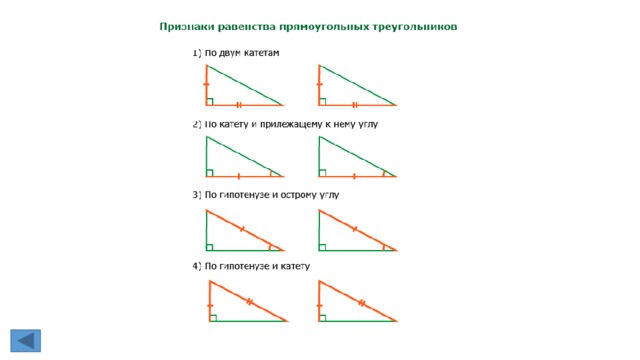
1. Прямоугольный треугольник. Признаки равенства прямоугольных

треугольников (без доказательства).

Прямоуго

́

льный треуго

́

льник — это треугольник, в котором один угол прямой (то

есть составляет 90 градусов)

Признак равенства прямоугольных треугольников по двум катетам

Если два катета одного прямоугольного треугольника соответственно равны двум

катетам другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и гипотенузе

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны

катету и гипотенузе другого прямоугольного треугольника, то такие треугольники

равны.

Признак равенства по гипотенузе и острому углу

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно

равны гипотенузе и острому углу другого прямоугольного треугольника, то такие

треугольники равны.

Признак равенства прямоугольных треугольников по катету и острому углу

Если катет и острый угол одного прямоугольного треугольника соответственно равны

катету и острому углу другого прямоугольного треугольника, то такие треугольники

равны.

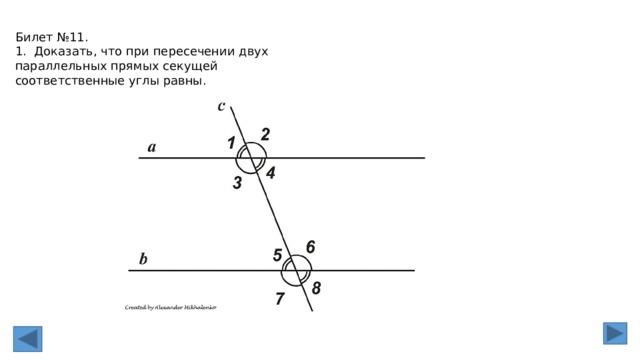
2. Параллельные прямые (определение). Признаки параллельности двух прямых

(доказательство одного из них).

Две прямые a и b на плоскости, которые не

пересекаются, называются параллельными и обозначаются a∥b.

Признак 1: Если при пересечении двух прямых секущей накрест лежащие углы

равны, то прямые параллельны.

Доказательство:

Через точку К — середину отрезка секущей — проведем перпендикуляр к прямой b —

КН, продлим его до пересечения с прямой а.

АК = КВ, так как К середина АВ,

углы при вершине К равны как вертикальные,

∠КВН = ∠КАН’ по условию, ⇒

ΔВКН = ΔАКН’ по стороне и двум прилежащим к ней углам.

Значит ∠АН’К = ∠ВНК = 90°.

Обе прямые а и b перпендикулярны третьей прямой НН‘, значит они параллельны.

Признак 2. Если при пересечении двух прямых секущей соответственные углы равны,

то прямые параллельны.

Доказательство:

∠1 = ∠2 по условию (соответственные углы)

∠3 = ∠1 как вертикальные, ⇒

∠2 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому

признаку.

Признак 3: Если при пересечении двух прямых секущей сумма односторонних углов

равна 180°, то прямые параллельны.

Доказательство:

∠1 + ∠2 = 180° по условию (односторонние углы),

∠2 + ∠3 = 180° так как эти углы смежные,

значит ∠1 = ∠3, а это накрест лежащие углы, значит прямые параллельны по

первому признаку.

3. Задача по теме » Угол. Измерение углов».

Известно, что

=90º. Луч OD делит угол AOB на два угла:

, если угол AOD в два раза меньше угла DOB.

Билет № 11

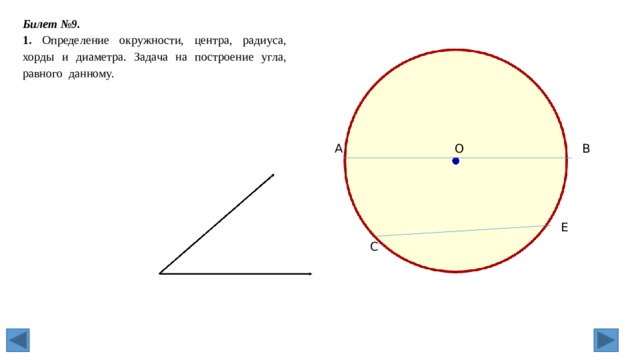
1.Окружность (определение). Радиус, хорда, диаметр окружности.

Окружность—это геометрическая фигура, состоящая из множества точек, находящихся

на одинаковом расстоянии от точки, называемой центром окружности.

Радиус— это отрезок, соединяющий центр окружности и любую точку окружности.

Диаметр—это отрезок, соединяющий две точки окружности и проходящий через центр.

Хорда— это отрезок, соединяющий две любые точки окружности.

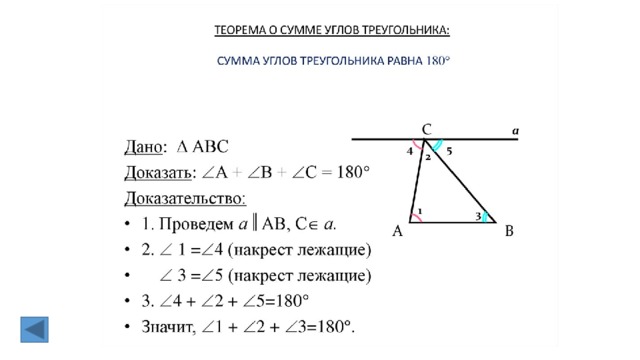
3. Треугольник (определение). Теорема о сумме углов треугольника.

Треугольником называется фигура, которая состоит из трех точек, не лежащих на

одной прямой, и трех отрезков, попарно соединяющих эти точки.

Сумма углов треугольника равна 180 градусам

Дано: ABC

Доказать: 1+ 2+ 3=180

o

Доказательство:

1) Проведём а BC, А а

2) 5= 1 – накрест лежащие углы при параллельных

прямых а и ВС и секущей АВ.

3) 3= 4 – накрест лежащие углы при

параллельных прямых а и ВС и секущей АС.

4) 5+ 2+ 4=180

o

(развёрнутый угол)

5) 1+ 2+ 3=180

o

Теорема доказана

4. Задача по теме «Свойство катета, лежащего против угла в 30º».

В треугольнике ABC

=60º, AB=3,7 см. Найдите длину отрезка BC.

Билет № 12

1. Высота, биссектриса, медиана треугольника (определения).

Медиана — это отрезок, соединяющий вершину треугольника с серединой

противоположной стороны.

Биссектриса — это отрезок, делящий угол треугольника на две равные части.

Высота треугольника — это перпендикуляр, опущенный из любой вершины треугольника

на противоположную сторону, или на ее продолжение.

2. Построение треугольника по трём сторонам.

Даны три отрезка, требуется построить из них треугольник.

Данная задача является задачей на построение, для решения которой требуется циркуль и

линейка.

При этом следует помнить, что не из каждых трех отрезков можно построить треугольник.

Как известно, любая сторона треугольника должна быть меньше суммы двух остальных.

Поэтому если один из данных отрезков длиннее, чем два других вместе взятые, то при

построении они просто уложатся на первом отрезке, и треугольника не получится.

Алгоритм построения треугольника по трем сторонам сводится к следующему:

1. Рисуется прямая.

2. На ней откладывается отрезок, равный одной из данных сторон. Это можно сделать

как циркулем, так и линейкой.

3. Строится окружность (или ее часть) радиусом, равным второму отрезку, и с центром в

одной из точек, отложенной на прямой.

4. Строится окружность (или ее часть) радиусом, равным третьему отрезку, и с центром

во второй из точек, отложенных на прямой.

5. К точке пересечения окружностей проводятся отрезки из точек на прямой. Если были

построены не маленькие части окружностей, то таких точек может оказаться две.

Отрезки надо проводить лишь к одной любой из них.

В результате получается треугольник, стороны которого равны данным отрезкам.

Действительно, ведь одна из его сторон была отмерена на прямой по одному из данных

отрезков, а две другие — радиусы, которые равны второму и третьему заданным отрезкам.

3. Задача по теме «Внешний угол треугольника».

В треугольнике ABC

=40º, внешний угол при вершине B равен 70º. Найдите

остальные внутренние углы треугольника.

Билет № 13

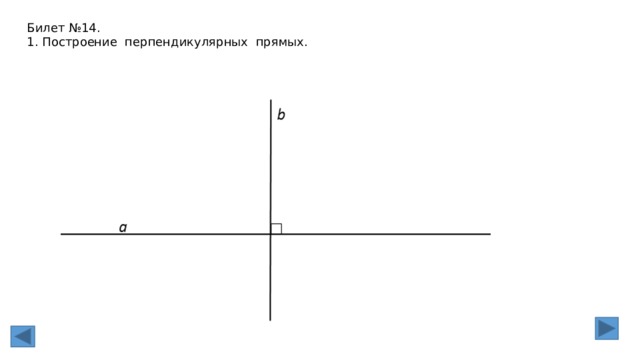
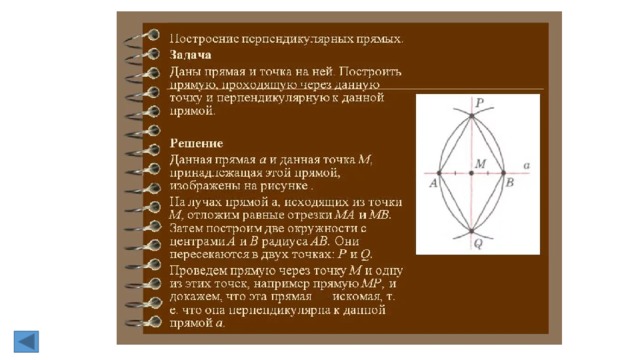
1. Перпендикулярные прямые (определение). Перпендикуляр к прямой.

Две прямые называются перпендикулярными, если они пересекаются под прямым

углом

. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если

прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

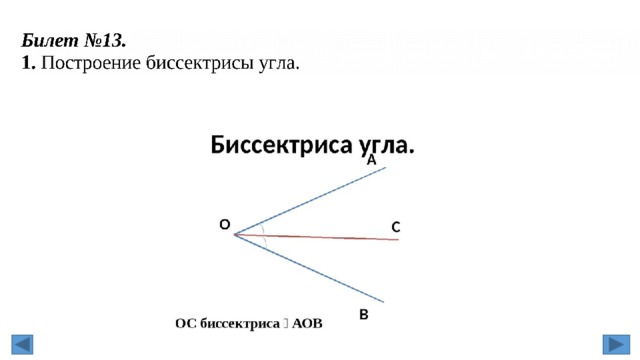
2. Построение биссектрисы угла.

Построить биссектрису данного угла.

Из вершины A данного угла как из

центра описываем окружность

произвольного радиуса r. Пусть B и С –

точки ее пересечения со сторонами угла.

Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их

пересечения отличная от A.

Проведем луч AD.

Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства

треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC.

3. Задача по теме «Свойства равнобедренного треугольника«.

В равнобедренном треугольнике ABC AE – высота, BC— основание. Известно, что BC=12,8

см. Найдите длину отрезка CE.

Билет № 14

1. Виды треугольников по величине углов.

Остроугольный треугольник — это треугольник, все углы

которого острые (то есть градусная мера каждого угла

меньше 90º).

Прямоугольный треугольник — это треугольник, у

которого один угол прямой (то есть имеет градусную меру

90º).

Тупоугольный треугольник — это треугольник, у

которого один угол — тупой (то есть имеет градусную

меру больше 90º).

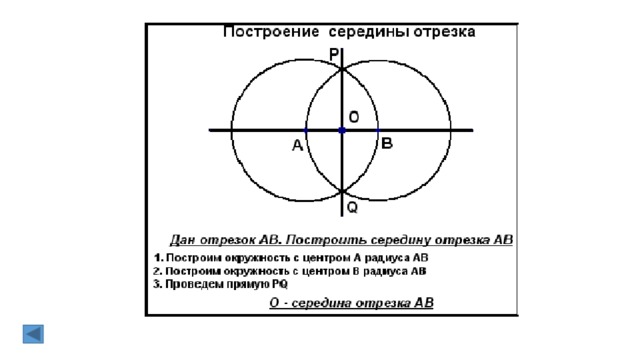
2. Деление отрезка пополам.

Пусть AB данный отрезок. Описываем окружность

радиусом AB с центром в точках A и B. Пусть эти

окружности пересекаются в точках С1 и С2.

Точки С1 и С2 лежат в разных полуплоскостях от

прямой AB. Проведем через точки С1 и С2 прямую.

Пусть она пересекает прямую AB в некоторой точке О.

Точка О – средина отрезка AB.

Док—во. Δ C1AC2 = Δ C1BC2 по третьему признаку

равенства треугольников (AC1 = BC1, AC2 = BC2, по

построению и С1С2 — общая). Поэтому ∠ AC1C2 = ∠

BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму

признаку равенства треугольников (∠ AC1C2 = ∠

BC1C2, AC1 = BC1 по построению, OC1 – общая).

Следовательно AO = OB и O – середина отрезка AB.

3. Задача по теме » Смежные углы».

Найдите смежные углы, если один из них в два раза больше другого.

Билет № 15

1. Расстояние от точки до прямой. Расстояние между параллельными прямыми.

Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной

точки на данную прямую.

Расстоянием между параллельными прямыми называется расстояние от какой—нибудь точки

одной прямой до другой прямой.

Поэтому, чтобы найти расстояние между параллельными прямыми, надо:

1) выбрать на одной из параллельных прямых точку;

2) опустить из выбранной точки к другой прямой перпендикуляр;

3) найти длину этого перпендикуляра.

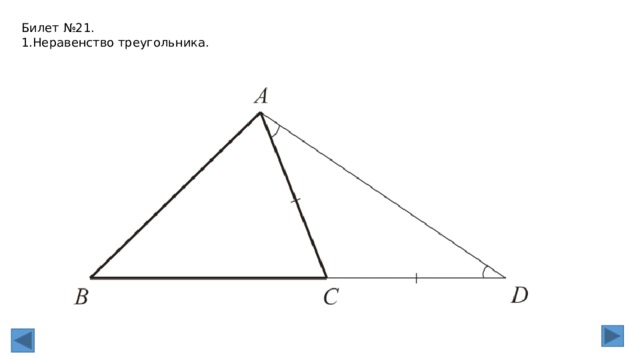
2. Неравенство треугольника.

Теорема.

Каждая сторона треугольника меньше суммы двух других сторон.

Доказательство.

Рассмотрим произвольный треугольник ABC и докажем, что AB<AC+СB. Отложим на

продолжении стороны AC отрезок СD, равный стороне СB.

В равнобедренном треугольнике BCD 1 = 2,

а в треугольнике ABD угол ABD > 1 и,

значит, угол ABD > 2. Так как в

треугольнике против большего угла лежит

большая сторона, то AB < AD. Но AD = AC

+ CD = AC + CB, поэтому AB < AC + CB.

Теорема доказана.

Следствие.

Для любых трех точек A, B и С, не лежащих на одной прямой, справедливы неравенства:

AB < AC + CB, AC < AB + BC, BC < BA + AC.

3. Задача по теме » Взаимное расположение окружностей».

Две окружности диаметром 4 и 8 см касаются внешним образом. Найдите расстояние между

центрами этих окружностей.

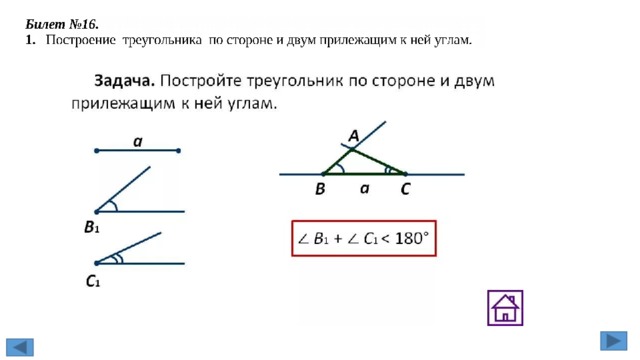
Билет № 16

1. Равносторонний треугольник. Свойства равностороннего треугольника

Треугольник называется равносторонним, если все его стороны равны.

Свойства

В равностороннем треугольнике все углы равны между собой и равны 60

0

:

В равностороннем треугольнике высоты, биссектрисы, медианы и пересекаются в

одной точке, которая называется центром равностороннего треугольника.

2. Теорема о соотношении между сторонами и углами треугольника.

Теорема

В треугольнике:

1) против большей стороны лежит больший угол;

1) против большего угла лежит большая сторона.

1) Дано: ∆ ABC, AC>AB.

Доказать: ∠B>∠C.

Доказательство:

Отложим на стороне AC отрезок AK: AK=AB.

Так как AC>AB, то точка K лежит между точками A и C. Следовательно,

∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.

Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.

Значит, у него углы при основании равны: ∠ABK=∠AKB.

Для треугольника BCK ∠AKB — внешний.

Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.

Имеем:

2) Дано: ∆ ABC,

∠B>∠C.

Доказать: AC>AB.

Доказательство:

(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда

либо AC=AB, либо AC<AB.Если AC=AB, то треугольник ABC — равнобедренный с

основанием BC и у него углы при основании равны: ∠B=∠C, что противоречит

условию.По доказанному в пункте 1), против большей стороны лежит больший угол.

Поэтому, если AC<AB, то ∠B<∠C. Снова пришли к противоречию.Значит,

выдвинутое нами предположение неверно. Следовательно, AC>AB.

Что и требовалось доказать.

3. Задача по теме «Смежные и вертикальные углы «.

Сумма данного угла и вертикального ему угла равна 60º. Найдите величину

вертикального и смежных с ним углов.

Билет № 17

1. Равносторонний треугольник. Свойства равностороннего треугольника.

Треугольник называется равносторонним, если все его стороны равны.

Свойства

В равностороннем треугольнике все углы равны между собой и равны 60

0

:

В равностороннем треугольнике высоты, биссектрисы, медианы и пересекаются в

одной точке, которая называется центром равностороннего треугольника.

3. Вертикальные углы (определение). Свойства вертикальных углов

Вертикальные углы — это пары углов с общей вершиной, которые образованы при

пересечении двух прямых так, что стороны одного угла являются продолжением

сторон другого

3. Задача по теме «Отрезок. Измерение отрезков «.

На отрезке OD, длина которого 24 см, отмечена точка A. Найдите длину отрезка AD, если

отрезок OA на 8 см длиннее отрезка AD.

Билет № 18

1. Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства

прямоугольного треугольника (без доказательства)

Треугольник называется прямоугольным, если один из его углов прямой. Стороны,

прилежащие к прямому углу, называются катетами прямоугольного треугольника, а

сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.

1. Сумма острых углов равна 90

2. Катет лежащий против угла 30 равен половине гипотенузы

3. Обратная теорема: Если катет равен половине гипотенузы, то угол, лежащий

против него равен 30

2. Построение угла, равному данному.

Отложить от данного луча угол, равный данному.

Решение. Данный угол с вершиной А и луч ОМ

Проведем произвольную окружность с центром в вершине О данного угла. Пусть В и С —

точки пересечения окружности со сторонами угла (рис а). Радиусом ОВ проведем

окружность с центром в точке О — начальной точке данного луча (рис. б). Точку

пересечения этой окружности с данным лучом обозначим С

1

. Опишем окружность с

центром С

1

и радиусом ВС. Точка В

1

пересечения двух окружностей лежит на стороне

искомого угла. Это следует из равенства Δ ОBC = Δ ОВ

1

С

1

(третий признак равенства

треугольников).

2. Задача по теме «Внутренние и внешние углы треугольника «.

Один из внешних углов прямоугольного треугольника равен 130º. Найдите острые

углы треугольника

Билет № 19

1. Отрезок (определение). Длина отрезка. Основное свойство измерения отрезков.

Отрезок — это часть прямой, которая ограничена двумя точками, т.е. она имеет начало

и конец, а значит можно измерить её длину

Расстоянием между двумя точками называется длина отрезка .

1.Каждый отрезок имеет определенную длину, большую нуля.

2.Длина отрезка равняется сумме длин частей, на которые он разбивается любой

своей внутренней точкой.

3.При этом, если точки A и B совпадают, будем считать, что расстояние между ними

равно нулю.

4.Два отрезка называются равными, если равны их длины.

2. Теорема о соотношении между сторонами и углами треугольника.

Теорема

В треугольнике:

1) против большей стороны лежит больший угол;

1) против большего угла лежит большая сторона.

1) Дано: ∆ ABC, AC>AB.

Доказать: ∠B>∠C.

Доказательство:

Отложим на стороне AC отрезок AK: AK=AB.

Так как AC>AB, то точка K лежит между точками A и C. Следовательно,

∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.

Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.

Значит, у него углы при основании равны: ∠ABK=∠AKB.

Для треугольника BCK ∠AKB — внешний.

Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.

Имеем:

2) Дано: ∆ ABC,

∠B>∠C.

Доказать: AC>AB.

Доказательство:

(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо

AC=AB, либо AC<AB.Если AC=AB, то треугольник ABC — равнобедренный с

основанием BC и у него углы при основании равны: ∠B=∠C, что противоречит

условию.По доказанному в пункте 1), против большей стороны лежит больший угол.

Поэтому, если AC<AB, то ∠B<∠C. Снова пришли к противоречию.Значит, выдвинутое

нами предположение неверно. Следовательно, AC>AB.

Что и требовалось доказать.

3. Задача по теме «Виды треугольников «.

Периметр равностороннего треугольника DEK равен 18 см. Найдите стороны

треугольника DEK .

Билет № 20

1. Угол (определение). Развернутый угол. Внутренняя и внешняя область угла.

Основное свойство откладывания углов.

Угол — это геометрическая фигура, состоящая из двух различных лучей, выходящих из

одной точки.

Лучи называются сторонами угла, а их общее начало — вершиной угла.

Развернутый угол — это угол, стороны которого лежат на одной прямой.Градусная мера

развёрнутого угла равна 180º.Каждая сторона развернутого угла дополняет другую сторону

до прямой, то есть стороны развёрнутого угла являются дополнительными лучами. Угол

разделяет плоскость на две части, каждая из которых также называется углом, то может

возникнуть неоднозначность в том, какой именно из углов рассматривается. Чтобы

наглядно показать, о каком именно угле идёт речь, на чертеже обычно делается какое—

нибудь специальное обозначение.

Тот из углов, который рассматривается, на чертеже обычно отмечают дугой,

проведённой от одной стороны угла до другой:

Часть плоскости, расположенная между

сторонами рассматриваемого угла

называется внутренней областью угла. Часть

плоскости не принадлежащая

рассматриваемому углу называется внешней

областью угла:

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной

градусной мерой, меньшей 180°,и только один.

3.Теорема о существовании и единственности перпендикуляра к прямой.

Теорема.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую

перпендикуляр, и только один.

Доказательство

Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через

какую—нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает

прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что

бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.

Значит отрезок AB ⊥ a.

Теперь докажем единственность перпендикуляра AB.

Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.

Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как

сумма всех углов в треугольнике 180 °. Теорема доказана.

3. Задача по теме «Сумма углов треугольника «.

Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.

Источник

Муниципальное общеобразовательное учреждение – средняя общеобразовательная школа №3

имени Л. Г. Венедиктовой города  Маркса Саратовской области

«Рассмотрено»

Руководитель МО

_____________.

Протокол № ___  от

«____»____________2017 г.

«Согласовано»

Заместитель директора школы по УВР

_____________

 «____»____________2017 г.

«Утверждено»

Директор школы

_______________  

Приказ №  ___    от

«____»____________2017 г.

Билеты по геометрии

для промежуточной аттестации

обучающихся 7б класса

по УМК Л.С. Атанасян и др.

Составила: Абросимова Галина Евгеньевна,

учитель высшей категории

2016 -2017 учебный год

Г. Маркс

Пояснительная записка

В структуре контрольных измерительных материалов (КИМов) государственной итоговой аттестации (ГИА) выделено три модуля «Алгебра», «Геометрия», «Реальная математика».

В целях лучшей подготовки к ГИА в 9 классе проводится промежуточная аттестация в форме устного экзамена по геометрии.

Экзамен позволяет решить следующие задачи:

1. Оценивание знаний и умений, сформированных впри изучении геометрии.

2. Развитие познавательного интереса.

3. Более глубокое понимание и осмысление обучающимися изученного материала.

4. Формирование целостного восприятия изученного материала.

Экзамен по геометрии позволяет оценить следующие знания и умения учащихся:

1. Владение основными понятиями и свойствами геометрических фигур:

  • знать основные геометрические понятия;
  • знать условные обозначения;
  • применять определения и свойства для решения различного рода задач;

2. Владение основными обще учебными умениями:

  • обобщать, анализировать делать выводы;
  • применять полученные знания для решения различных задач;
  • использовать инструменты для построения;
  • излагать решение последовательно, четко, связано, обоснованно;
  • правильно применять систему условных обозначений при ведении записей.

Билеты по геометрии составлены на основе требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте основного общего образования.

Для проведения экзамена по геометрии предлагаются 20 билетов, состоящих из трех вопросов.

Билеты по геометрии состоят из трех заданий:

— первое задание — теоретический вопрос, не требующий доказательств (формулировки определений и теорем, знание формул);

— второе задание — теоретический вопрос, предполагающий развернутый ответ (доказательство теорем, вывод формул, построений с обоснованием);

— третье задание — практический вопрос (задача базового уровня сложности  № 9, из открытого банка заданий для проведения ОГЭ).

Рекомендации по оцениванию. (в школе 10 бальная система оценивания)

Отметка «8 — 10» выставляется при условии верного ответа на теоретические вопросы и решении задачи или при ответе на теоретические вопросы и решении задачи, возможно с незначительными недочетами.

Отметка «5 — 7» выставляется при условии верного ответа на теоретические вопросы и решении задачи или при ответе на один теоретический вопрос и решении задачи.

Отметка «3 — 4» выставляется при условии верного ответа на 1- ый вопрос и решении задачи, возможно с некоторыми незначительными недочетами.

Отметка «2» выставляется при неполных ответах на теоретические вопросы, и если обучающимся не решена задача.

Отметка «1» выставляется во всех остальных случаях.

При ответе, обучающемуся могут быть заданы дополнительные вопросы членами экзаменационной комиссии, но они не должны выходить за рамки содержания билета, выбранного обучающимся.

БИЛЕТ № 1

  1. Луч  и угол (определение). Какой луч называется биссектрисой угла? Сделайте рисунок.
  2. Докажите, что если накрест лежащие углы равны, то прямые параллельны (1 признак параллельности прямых).
  3. В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=6324

БИЛЕТ № 2

  1. Основные геометрические фигуры на плоскости. Отрезок (определение). Сделайте рисунок.
  2. Докажите, что углы при основании равнобедренного треугольника равны (теорема о свойстве равнобедренного треугольника).
  3. Прямые m и n параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=6271

БИЛЕТ № 3

  1. Измерение и сравнение отрезков, середина отрезка. Длина отрезка. Сравнение отрезков.
  2. Докажите, что в равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой (свойство биссектрисы равнобедренного треугольника).
  3. В равностороннем треугольнике  ABC  медианы  BK  и  AM  пересекаются в точке O. Найдите https://oge.sdamgia.ru/formula/e2/e28bc48a8eca1a4795a9cb56307ef791p.png.

https://oge.sdamgia.ru/get_file?id=3421

БИЛЕТ № 4

  1. Измерение и сравнение углов. Свойства измерения углов.
  2. Докажите, что если соответственные углы при пересечении двух прямых секущей равны, то прямые параллельны (2 признак параллельности прямых).
  3. В равностороннем треугольнике ABC биссектрисы CN и AM  пересекаются в точке P. Найдите https://oge.sdamgia.ru/formula/d5/d51e74d2940d0653a0ea3266e861bbb9p.png.

https://oge.sdamgia.ru/get_file?id=3422

БИЛЕТ № 5

  1. Виды углов. Сделайте рисунок.
  2. Докажите, что если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны (3 признак параллельности прямых).
  3. Биссектрисы углов N и M треугольника  MNP  пересекаются в точке  A. Найдите  https://oge.sdamgia.ru/formula/eb/ebd5199deb66d437b090676f57880416p.png, если  https://oge.sdamgia.ru/formula/a7/a75a4aa09c273936a7619d6059d972abp.png, а  https://oge.sdamgia.ru/formula/9c/9cd746aa7045cbd142175d2748b87877p.png

https://oge.sdamgia.ru/get_file?id=3420

БИЛЕТ № 6

  1. Какие углы называются смежными? Чему равна сумма смежных углов? Могут ли быть смежными прямой и острый углы? Сделайте рисунок.
  2. Докажите, что в треугольнике:1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона (теорема о соотношения между сторонами и углами треугольника).
  3. Найдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 52°. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=6347

БИЛЕТ № 7

  1. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Сколько пар вертикальных углов образуется при пересечении двух прямых? Сделайте рисунок.
  2. Докажите, что если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
  3. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/4c/4c4084401e5eab6760efd01305c50c4bp.png, https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса. Найдите угол https://oge.sdamgia.ru/formula/f1/f1b68d66337a81cfa0d2076171cba2a8p.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10107

БИЛЕТ № 8

  1. Взаимное расположение двух прямых. Какие прямые называются перпендикулярными? Каким свойством обладают две прямые, перпендикулярные к третьей прямой? Сделайте рисунок.
  2. Докажите, чтосумма углов треугольника равна 1800 .
  3. На плоскости даны четыре прямые. Известно, что  https://oge.sdamgia.ru/formula/2c/2c2c5e270e7ce9606f217746070a4d1dp.png,  https://oge.sdamgia.ru/formula/89/8986ece5bc2863ecf157ba34835c806fp.png,  https://oge.sdamgia.ru/formula/c8/c8f6c9474f4b635b0e1996d866660420p.png. Найдите  https://oge.sdamgia.ru/formula/98/982e4655807b55adc5e9d7c40c5dfc3fp.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=2393

БИЛЕТ № 9  

  1. Определение треугольника и его элементов. Равные треугольники.
  2. Докажите, что при пересечении двух параллельных прямых секущей, накрест лежащие углы равны (свойство накрест лежащих углов).
  3. Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB.

Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=6269

БИЛЕТ № 10

  1. Сформулируйте признаки равенства треугольников. Сделайте рисунок.
  2. Докажите, что при пересечении двух параллельных прямых секущей соответственные углы равны (свойство соответственных углов).
  3. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=22

БИЛЕТ № 11

  1. Определение перпендикуляра к данной прямой.
  2. Какой угол называется внешним углом треугольника? Докажите, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним (теорема о внешнем угле треугольника).
  3. В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах.

БИЛЕТ № 12

  1. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Сделайте рисунок.
  2. Докажите, что при пересечении двух параллельных прямых секущей сумма односторонних углов равна 1800 (свойство односторонних углов).
  3. В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах

https://oge.sdamgia.ru/get_file?id=6267

БИЛЕТ № 13

  1. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Чем отличаются понятия «биссектриса угла» и «биссектриса треугольника»? Поясните с помощью рисунка.
  2. Докажите, что сумма двух острых углов прямоугольного треугольника равна 900  (свойство прямоугольного треугольника).
  3. Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10154

БИЛЕТ № 14

  1. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Сделайте рисунок.
  2. Докажите, что катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы (свойство прямоугольного треугольника)
  3. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 84 и BC = BM. Найдите AH.

https://oge.sdamgia.ru/get_file?id=6279

БИЛЕТ № 15

  1. Виды треугольников. Классификация по длине стороны и величине угла. Сделайте рисунок.
  2. Докажите, что катет прямоугольного треугольника равен половине гипотенузы, то угол,  лежащий против этого катета, равен 300 (свойство прямоугольного треугольника).
  3.  Углы, отмеченные на рисунке одной дугой, равны. Найдите угол  https://oge.sdamgia.ru/formula/7b/7b7f9dbfea05c83784f8b85149852f08p.png. Ответ дайте в градусах.https://oge.sdamgia.ru/get_file?id=2364

БИЛЕТ № 16

  1. Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности. Как связаны радиус и диаметр окружности? Сделайте рисунок.
  2. Докажите, что каждая сторона треугольника меньше суммы двух других сторон. Что такое неравенство треугольника?
  3. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/b8/b82337d7568aa6717a851c2934660202p.png, https://oge.sdamgia.ru/formula/50/5089fa881630360a9b3361469c1a0c5dp.png — медиана, https://oge.sdamgia.ru/formula/5a/5aba58a978e3d95c8212984fc9a99045p.png. Найдите https://oge.sdamgia.ru/formula/25/25ec916d56b8212e569dbf2e4e4b51d4p.png.

https://oge.sdamgia.ru/get_file?id=10233

БИЛЕТ № 17

  1. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
  2. Сформулируйте и докажите утверждение о признаке равенства прямоугольных треугольников по гипотенузе и острому углу.
  3. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/94/94623831cd335a1267dd5f75f120b4f5p.png, https://oge.sdamgia.ru/formula/85/85334f98f676301dc8188d112909c95ep.png. Найдите угол https://oge.sdamgia.ru/formula/16/16e3de8d26a12b8f6531361a84e8fa1cp.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10100

БИЛЕТ № 18

  1. Что такое секущая по отношению к двум прямым? Назовите пары углов, которые образуются при пересечении двух прямых секущей. Сделайте рисунок.
  2. Сформулируйте и докажите утверждение о признаке равенства прямоугольных треугольников по гипотенузе и катету.
  3. В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=6267

БИЛЕТ № 19

  1. Аксиома параллельных прямых. Следствия.
  2. Сформулируйте и докажите утверждение о признаке равенства прямоугольных треугольников по двум  катетам.
  3. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

 https://oge.sdamgia.ru/get_file?id=6432

БИЛЕТ № 20

  1. Что называется расстоянием от точки до прямой? Что называется расстоянием между параллельными прямыми? Объясните, какой отрезок называется наклонной, проведённый из данной точки к данной прямой.
  2. Сформулируйте и докажите утверждение о признаке равенства прямоугольных треугольников по катету и прилежащему острому углу.
  3. Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите периметр этого треугольника.https://oge.sdamgia.ru/get_file?id=8508

Приложение

Требования к уровню подготовки учащихся 7 класса  (из рабочей программы педагога)

           Должны знать:

определение точки, прямой, отрезка, луча, угла; единицы измерения отрезка, угла; определение вертикальных и смежных углов, их свойства; определение перпендикулярных прямых; определение треугольника, виды треугольников, признаки равенства треугольников, свойства равнобедренного треугольника, определение медианы, биссектрисы, высоты; определение параллельных прямых, их свойства и признаки; соотношение между сторонами и углами треугольника, теорему о сумме углов треугольника; определение прямоугольного треугольника, его свойства и признаки.

Должны уметь: обозначать точки, отрезки и прямые на рисунке, сравнивать отрезки и углы, с помощью транспортира проводить биссектрисуугла; изображать прямой, острый, тупой и развернутый углы; изображать треугольники и находить их периметр; строить биссектрису, высоту и медиану треугольника; доказывать признаки равенства треугольников; показывать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности двух прямых; доказывать теорему о сумме углов треугольника; знать, какой угол называется внешним углом треугольника; применять признаки прямоугольных треугольников к решению задач; строить треугольники по трем элементам.

        Должны владеть компетенциями:познавательной,коммуникативной, информационной и рефлексивной.

Способны решать следующие жизненно-практические задачи:самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем энциклопедий и справочником для нахождения информации, самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем.

Задачи из открытого банка ОГЭ включённые в билеты (задачи № 9)

Равнобедренные треугольники

1. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите https://oge.sdamgia.ru/formula/d5/d51e74d2940d0653a0ea3266e861bbb9p.png.https://oge.sdamgia.ru/get_file?id=3422

Решение.

В равностороннем треугольнике ABC все углы равны 60°. Биссектрисы CN и AM делят углы пополам, поэтому https://oge.sdamgia.ru/formula/0e/0e933c08088f95e7a54f86d0b90005bfp.png = https://oge.sdamgia.ru/formula/5f/5f940633549c56d92d67022e81b6c5d6p.png = https://oge.sdamgia.ru/formula/29/29083439b8b695e0ea2dce20a9986992p.png Сумма углов в треугольнике равна 180°, поэтому https://oge.sdamgia.ru/formula/52/52140e78810eed0a80463be8a557e2b8p.png Вертикальные углы равны, следовательно, https://oge.sdamgia.ru/formula/31/31c8cbb064df6d6040fad0c98ae4fddbp.png

Ответ: 120.

2. https://oge.sdamgia.ru/get_file?id=3421В равностороннем треугольнике  ABC  медианы  BK  и  AM  пересекаются в точке O. Найдите https://oge.sdamgia.ru/formula/e2/e28bc48a8eca1a4795a9cb56307ef791p.png.

Решение.

Медианы в равностороннем треугольнике являются биссектрисами и высотами, поэтому https://oge.sdamgia.ru/formula/05/05bf250b5bebb8092d4eca31f0f77454p.png. Треугольник AOK — прямоугольный, поэтому https://oge.sdamgia.ru/formula/3b/3b62ab4c6555c29d828fd87418896c1fp.png.

Ответ: 60.

3.https://oge.sdamgia.ru/get_file?id=22

В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.

Решение.

Углы ACB и BAC равны, т. к. находятся при основании равнобедренного треугольника; пусть один из них равен x. Поскольку сумма углов треугольника равна 180°, имеем: ∠ABC = 180° − x − x. Угол ACB смежен с углом 123°, значит, равен 180° − 123° = 57°. Следовательно, x = 57°, откуда ∠ABC = 180° − 2·57° = 66°.

Ответ: 66.

4.

В треугольнике ABC AC = BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.https://oge.sdamgia.ru/get_file?id=6265

Решение.

Сумма смежных углов равна 180°, откуда https://oge.sdamgia.ru/formula/58/583800b5528ab9cdb9b31a423d06e5abp.png Треугольник ABC — равнобедренный, поэтому https://oge.sdamgia.ru/formula/20/208b5dfe50bae698bae70a04458717bfp.png Сумма углов треугольника равна 180°, следовательно, https://oge.sdamgia.ru/formula/da/da1a6ab62d404c41fcfeee45e6895071p.png

Ответ: 112.

5.

 https://oge.sdamgia.ru/get_file?id=6269Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.

Решение.

Треугольник https://oge.sdamgia.ru/formula/72/72c5cc0e2586935d16539f31a2a4fec4p.png — равнобедренный, поэтому https://oge.sdamgia.ru/formula/c1/c148322516b83901973f2c3992df319dp.png Найдём угол https://oge.sdamgia.ru/formula/7b/7bcee9c87cc47aecda06f35ac072811bp.png https://oge.sdamgia.ru/formula/ed/edc7f5bdf38903fe927aad1da5ce2c9fp.png

Ответ: 9.

6.

 https://oge.sdamgia.ru/get_file?id=6432В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

Решение.

Сумма смежных углов равна 180°, поэтому https://oge.sdamgia.ru/formula/af/afcc6050a33107c3498b86a3c6626abfp.png В равнобедренном треугольнике углы при основании равны, следовательно, https://oge.sdamgia.ru/formula/08/08211fbbfd8670bfcd399867b72c4145p.png

Ответ: 57.

7.

 https://oge.sdamgia.ru/get_file?id=8508Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите периметр этого треугольника.

8.

В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/94/94623831cd335a1267dd5f75f120b4f5p.png, https://oge.sdamgia.ru/formula/85/85334f98f676301dc8188d112909c95ep.png. Найдите угол https://oge.sdamgia.ru/formula/16/16e3de8d26a12b8f6531361a84e8fa1cp.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10100

Решение.

Треугольник https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png — равнобедренный, следовательно, https://oge.sdamgia.ru/formula/d6/d6b1c5bb91e8f5d9b22f188a62a9209cp.png

Ответ: 36

9.

Треугольники общего вида

 https://oge.sdamgia.ru/get_file?id=6267В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.

Решение.

Пусть угол https://oge.sdamgia.ru/formula/60/6049a05f7a3b31a10d06a72bffce1bd3p.png равен https://oge.sdamgia.ru/formula/2a/2a6ccaea07db0dd364bbe96c2ca411ecp.png угол https://oge.sdamgia.ru/formula/79/79661ff25e39af70fc48d7785f587e85p.png равен https://oge.sdamgia.ru/formula/31/3126c4c47e931f82ea4124877142a1dcp.png Сумма углов в треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png равна 180°, откуда https://oge.sdamgia.ru/formula/16/16b1590f034d8126479837c248bb9269p.png Аналогично, из треугольника https://oge.sdamgia.ru/formula/56/56c0bc0e475820687969fbc9797b4361p.png https://oge.sdamgia.ru/formula/ca/cad74eb4f56463104c53516a8ced6e37p.png Получаем систему уравнений:

https://oge.sdamgia.ru/formula/d1/d16f3992edaab61e00267acae5c4b938p.png

Таким образом, угол https://oge.sdamgia.ru/formula/79/79661ff25e39af70fc48d7785f587e85p.png равен 62°.

Ответ: 62.

10.

 https://oge.sdamgia.ru/get_file?id=6279В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 84 и BC = BM. Найдите AH.

Решение.

Поскольку https://oge.sdamgia.ru/formula/50/5089fa881630360a9b3361469c1a0c5dp.png — медиана, https://oge.sdamgia.ru/formula/71/71b2f69bf86336ddc42af4784e6fd1e1p.png Рассмотрим треугольник https://oge.sdamgia.ru/formula/16/16678454a2e61ccd869e411ff902ebe1p.png https://oge.sdamgia.ru/formula/66/6624ec92126c308ef1d8be4594f030a1p.png следовательно, треугольник https://oge.sdamgia.ru/formula/39/396262ee936f3d3e26ff0e60bea6cae0p.png — равнобедренный, https://oge.sdamgia.ru/formula/1b/1baa5a77aeff33338948c1e0c4466462p.png — высота, следовательно, https://oge.sdamgia.ru/formula/1b/1baa5a77aeff33338948c1e0c4466462p.png — медиана, откуда https://oge.sdamgia.ru/formula/24/248a905555dd3c342cd4d265b2c81615p.png Найдём https://oge.sdamgia.ru/formula/df/df0ce8e1e66d48ab99aca1fea9834c46p.png https://oge.sdamgia.ru/formula/4e/4e4fd1796a84ef7846b8e895dd99b746p.png

Ответ: 63.

11.

https://oge.sdamgia.ru/get_file?id=6324В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах.

Решение.

Поскольку https://oge.sdamgia.ru/formula/50/5089fa881630360a9b3361469c1a0c5dp.png — медиана, https://oge.sdamgia.ru/formula/ec/ecaca69de6573f3f00dd3498973046dap.png Найдём https://oge.sdamgia.ru/formula/5e/5eaf73be718c358ea19bebfbe5e59929p.png https://oge.sdamgia.ru/formula/7a/7a97768db8938ceb575f271ea6ee64f9p.png Рассмотрим треугольники https://oge.sdamgia.ru/formula/cb/cb4eea774d166f98c6bc5fc878e7964ap.png и https://oge.sdamgia.ru/formula/6d/6da5eeff9e1aab2744ca5ee53c53e3d1p.png они прямоугольные, https://oge.sdamgia.ru/formula/00/002f27e5064e874ecf4f5def17d1b797p.png равно https://oge.sdamgia.ru/formula/37/373446b64759bf84bdce2442bcbd97f9p.png https://oge.sdamgia.ru/formula/1b/1baa5a77aeff33338948c1e0c4466462p.png — общая, следовательно, треугольники равны. Откуда https://oge.sdamgia.ru/formula/66/6624ec92126c308ef1d8be4594f030a1p.png то есть треугольник https://oge.sdamgia.ru/formula/e4/e40558450360f747f2ce0d9f9c74bf24p.png — равнобедренный, значит, https://oge.sdamgia.ru/formula/11/11497c2de058db8ccbfa53e6af8a010bp.png Углы https://oge.sdamgia.ru/formula/5d/5d307fe6f0078e0943f2175a8b1347fbp.png и https://oge.sdamgia.ru/formula/39/396262ee936f3d3e26ff0e60bea6cae0p.png — смежные, вместе составляют развёрнутый угол, поэтому https://oge.sdamgia.ru/formula/07/0783a63f4bab96fa659705990c006b93p.png

Ответ: 140.

12.

В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/b8/b82337d7568aa6717a851c2934660202p.png, https://oge.sdamgia.ru/formula/50/5089fa881630360a9b3361469c1a0c5dp.png — медиана, https://oge.sdamgia.ru/formula/5a/5aba58a978e3d95c8212984fc9a99045p.png. Найдите https://oge.sdamgia.ru/formula/25/25ec916d56b8212e569dbf2e4e4b51d4p.png.

https://oge.sdamgia.ru/get_file?id=10233

Решение.

Так как https://oge.sdamgia.ru/formula/50/5089fa881630360a9b3361469c1a0c5dp.png — медиана, следовательно https://oge.sdamgia.ru/formula/17/17ac8e3dc7ee97ef4073c3ebbea12c57p.png

Ответ: 27

13. В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах.

Решение.

Сумма углов треугольника равна 180°. Следовательно, https://oge.sdamgia.ru/formula/b7/b7d303045868f9293b6a972ed120c49ap.png

Ответ: 53

Углы

14. https://oge.sdamgia.ru/get_file?id=3420Биссектрисы углов N и M треугольника  MNP  пересекаются в точке  A. Найдите  https://oge.sdamgia.ru/formula/eb/ebd5199deb66d437b090676f57880416p.png, если  https://oge.sdamgia.ru/formula/a7/a75a4aa09c273936a7619d6059d972abp.png, а  https://oge.sdamgia.ru/formula/9c/9cd746aa7045cbd142175d2748b87877p.png

Решение.

По определению биссектрисы https://oge.sdamgia.ru/formula/c1/c1f6f91ef9d06baee483095c383f93fep.png и https://oge.sdamgia.ru/formula/98/983e9c3acd4e9826fc3c0f353430f63cp.png. В треугольнике NAM:

https://oge.sdamgia.ru/formula/a1/a15937ad89baaeea59e8dc175b1741fdp.png.

Ответ: 117.

15. Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10154

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен https://oge.sdamgia.ru/formula/12/12eb7aee42a80ca3cc1f997aa4141b15p.png

Ответ: 67

16. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол  https://oge.sdamgia.ru/formula/7b/7b7f9dbfea05c83784f8b85149852f08p.png. Ответ дайте в градусах.https://oge.sdamgia.ru/get_file?id=2364

Решение.

Углы 1 и 2 равны как вертикальные, поэтому https://oge.sdamgia.ru/formula/61/616bd9fa1c3ff38ea257085eacaad3dap.png

Ответ: 40.

17. https://oge.sdamgia.ru/get_file?id=2393На плоскости даны четыре прямые. Известно, что  https://oge.sdamgia.ru/formula/2c/2c2c5e270e7ce9606f217746070a4d1dp.png,  https://oge.sdamgia.ru/formula/89/8986ece5bc2863ecf157ba34835c806fp.png,  https://oge.sdamgia.ru/formula/c8/c8f6c9474f4b635b0e1996d866660420p.png. Найдите  https://oge.sdamgia.ru/formula/98/982e4655807b55adc5e9d7c40c5dfc3fp.png. Ответ дайте в градусах.

Решение.

Так как https://oge.sdamgia.ru/formula/32/326ed78701f2b5816bbe9788cc858f6bp.png и https://oge.sdamgia.ru/formula/1d/1d6093d2c231bf4605adf938f6139e0bp.png, односторонние и их сумма равна 180°, прямые, которые заключают эти углы, — параллельны. Найдем угол, смежный с углом 3: https://oge.sdamgia.ru/formula/f3/f3c22fed2ee3d3a87782de110cecc51dp.png Этот угол и угол 4 соответственные и равны так как прямые параллельны.

Таким образом, угол 4 = 125°.

Ответ: 125.

18. https://oge.sdamgia.ru/get_file?id=6271Прямые m и n параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.

Решение.

https://oge.sdamgia.ru/get_file?id=6272Введём обозначение как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 =  22°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 22° − 72° = 86°.

Ответ: 86.

19. https://oge.sdamgia.ru/get_file?id=6347Найдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 52°. Ответ дайте в градусах.

Решение.

Углы AOD и DOB — смежные, вместе составляют развёрнутый угол, следовательно, ∠AOD = 180° − ∠DOB = 180° − 52° = 128°. Поскольку OK — биссектриса угла AOD, ∠AOK = ∠DOK = ∠AOD/2 = 128°/2 = 64°.

Ответ: 64.

20. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/4c/4c4084401e5eab6760efd01305c50c4bp.png, https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса. Найдите угол https://oge.sdamgia.ru/formula/f1/f1b68d66337a81cfa0d2076171cba2a8p.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10107

Решение.

Поскольку https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса, https://oge.sdamgia.ru/formula/60/6016f9c58884e9cc8b731be498b92b2ep.png.

Ответ: 24

Дополнительные задачи при подготовке к экзамену

Треугольники общего вида

1. В треугольнике два угла равны 31° и 94°. Найдите его третий угол. Ответ дайте в градусах.

Решение.

Сумма углов треугольника равна 180°. Следовательно, https://oge.sdamgia.ru/formula/7e/7e6182955c75a2432b70bc6e9f5f2f62p.png

Ответ: 55

Углы

2. Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10292

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен https://oge.sdamgia.ru/formula/6f/6fa0aa7fab08797aa17ee7b45417ddd7p.png

Ответ: 69

3. Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10292

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен https://oge.sdamgia.ru/formula/9e/9e5b2757f563eec52aa6d573ef21ba0cp.png

Ответ: 27

4. Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10292

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен https://oge.sdamgia.ru/formula/16/168bcab27420bff5d42344477f01f0cdp.png

Ответ: 33

5. https://oge.sdamgia.ru/get_file?id=3405Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.

Решение.

Углы 1 и 2 равны как вертикальные, поэтому https://oge.sdamgia.ru/formula/bc/bc82a3d469c3c5f1cac67564afbe6506p.png

Ответ: 40.

.

6. https://oge.sdamgia.ru/get_file?id=6323Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.

Решение.

Углы AOD и DOB — смежные, вместе составляют развёрнутый угол, следовательно, ∠AOD = 180° − ∠DOB = 180° − 108° = 72°. Поскольку OK — биссектриса угла AOD, ∠AOK = ∠KOD = ∠AOD/2 = 72°/2 = 36°.

Ответ: 36.

7. https://oge.sdamgia.ru/get_file?id=6347Найдите величину угла AOK, если OK — биссектриса угла AOD, ∠DOB = 64°. Ответ дайте в градусах.

Решение.

Углы AOD и DOB — смежные, вместе составляют развёрнутый угол, следовательно, ∠AOD = 180° − ∠DOB = 180° − 64° = 116°. Поскольку OK — биссектриса угла AOD, ∠AOK = ∠DOK = ∠AOD/2 = 116°/2 = 58°.

Ответ: 58.

8. https://oge.sdamgia.ru/get_file?id=6350На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах.

Решение.

Поскольку MD — биссектриса, ∠DMB = ∠DMC = 60°. Углы AMС, CMD и DMB вместе составляют развёрнутый угол, откуда

∠AM С = 180° − ∠DMB − ∠DMC = 180° − 60° − 60° = 60°.

Ответ: 60.

9. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/69/69850c4bd686e8ba99b27c63601c76d4p.png, https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса. Найдите угол https://oge.sdamgia.ru/formula/f1/f1b68d66337a81cfa0d2076171cba2a8p.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10161

Решение.

Поскольку https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса, https://oge.sdamgia.ru/formula/e2/e25cf095a7fd6de5607729a388d8fd56p.png.

Ответ: 23

10. В треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в градусах.

Решение.

Сумма углов треугольника равна 180°. Следовательно, https://oge.sdamgia.ru/formula/7d/7d1715b1ea1634c21cac90e389a51c6dp.png

Ответ: 68

11. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/19/198e1ce6c748c4214f79385c81270459p.png, https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса. Найдите угол https://oge.sdamgia.ru/formula/f1/f1b68d66337a81cfa0d2076171cba2a8p.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10281

Решение.

Поскольку https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса, то https://oge.sdamgia.ru/formula/aa/aaac52f7a7c332ca62d99faaa0fd5f1cp.png. Таким образом, https://oge.sdamgia.ru/formula/d6/d6f54ed6d705771d579e052c92fb705cp.png

Ответ: 31

12. В треугольнике https://oge.sdamgia.ru/formula/90/902fbdd2b1df0c4f70b4a5d23525e932p.png известно, что https://oge.sdamgia.ru/formula/6e/6e1d38b46ee224bd5dadd6bb3ad00babp.png, https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса. Найдите угол https://oge.sdamgia.ru/formula/f1/f1b68d66337a81cfa0d2076171cba2a8p.png. Ответ дайте в градусах.

https://oge.sdamgia.ru/get_file?id=10281

Решение.

Поскольку https://oge.sdamgia.ru/formula/e1/e182ebbc166d73366e7986813a7fc5f1p.png — биссектриса, то https://oge.sdamgia.ru/formula/aa/aaac52f7a7c332ca62d99faaa0fd5f1cp.png. Таким образом, https://oge.sdamgia.ru/formula/7e/7eb3dcd168a9eb58d707d879cc5a66bdp.png

Ответ: 13

Дополнительные задачи на экзамене:

  1. В равнобедренном треугольнике DEK с основанием DK отрезок EF – биссектриса, DK=16 см, угол DEF равен 43º. Найти KF, угол DEK  и угол EFD.
  2. Треугольник МРК равнобедренный с основанием МК. Прямая n пересекает сторону РК в точке А и сторону МК – в точке В. Найти углы треугольника АВК, если угол Р равен 72º, угол М равен 54º и параллельна МР.
  3. В треугольнике АВС угол при вершине А равен 40º, а угол ВСЕ смежный с углом АСВ, равен 80º. Доказать, что биссектриса угла ВСЕ параллельна прямой АВ.
  4. Найти углы равнобедренного треугольника, если угол при основании в два раза больше угла, противолежащего основанию.
  5. Найти углы равнобедренного треугольника, если угол при основании в три раза меньше внешнего угла, смежного с ним.
  6. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. Найти углы этого треугольника, если угол ADB равен 120º.
  7. В прямоугольном  треугольнике АВС угол В равен 600, гипотенуза равна 12 см. Найдите катет АВ.
  8. В прямоугольном треугольнике АВС угол С прямой, угол В равен 450, АС=6. Найдите ВС.
  9. Найдите угол АВС, изображённый на рисунке

Абросимова Г.Е. Билеты по геометрии 7 класс по УМК АтанасянСтраница

Источник

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3»

_____________________________________________________________________________

БИЛЕТЫ ДЛЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ

ПО ГЕОМЕТРИИ В УСТНОЙ ФОРМЕ ДЛЯ 7 КЛАССОВ

Пояснительная записка

Билеты для промежуточной аттестации по геометрии в устной форме за курс 7 класса составлены на основе федерального государственного стандарта основного общего образования, примерной программы основного общего образования по математике (Примерная программа по учебным предметам «Математика 5 – 9 класс: проект» – М.: Просвещение, 2011 г), Требований к результатам освоения основной образовательной программы основного общего образования, установленных в Федеральном государственном образовательном стандарте основного общего образования. Экзаменационные билеты ориентирована на содержание учебника Геометрия: 7 – 9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2014.

Промежуточная аттестация обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:

личностные:

  • умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

  • критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

  • креативность мышления, инициативу, находчивость, активность при решении геометрических задач;

  • умение контролировать процесс и результат учебной математической деятельности;

  • способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

метапредметные:

регулятивные универсальные учебные действия:

  • умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

  • умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы;

  • умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;

  • понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

  • умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

  • умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

познавательные универсальные учебные действия:

  • умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;

  • формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);

  • формирование первоначальных представлений об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;

  • умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;

  • умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

  • умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

  • умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

  • умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

коммуникативные универсальные учебные действия:

  • умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;

  • умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов;

  • слушать партнера;

  • формулировать, аргументировать и отстаивать свое мнение;

предметные:

  • овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (геометрическая фигура, величина) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;

  • умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;

  • овладение навыками устных письменных, инструментальных вычислений;

  • овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;

  • усвоение систематических знаний о плоских фигурах и их свойствах, умение применять систематические знания о них для решения геометрических и практических задач;

  • умение измерять длины отрезков, величины углов;

  • умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочные материалы и технические средства.

Содержание заданий экзаменационных билетов разработано по основным темам курса геометрии для 7 класса. Содержание раздела «Начальные геометрические сведения» подразделяется на следующие темы: «Прямая и отрезок», «Точка, прямая, отрезок», «Луч и угол. Сравнение отрезков и углов», «Равенство геометрических фигур. Измерение отрезков и углов», «Длина отрезка. Градусная мера угла. Единицы измерения», «Виды углов. Вертикальные и смежные углы», «Биссектриса угла», «Перпендикулярные прямые». Раздел «Треугольники» имеет темы «Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Окружность. Дуга, хорда, радиус, диаметр. Построения с помощью циркуля и линейки. Основные задачи на построение: деление отрезка пополам; построение угла, равному данному; построение биссектрисы угла; построение перпендикулярных прямых. Раздел «Параллельные прямые» содержит темы «Параллельные и пересекающиеся прямые», «Теоремы о параллельности прямых», «Определение. Аксиомы и теоремы. Доказательство от противного. Теорема, обратная данной». Раздел «Соотношения между сторонами и углами треугольника» содержит темы «Сумма углов треугольника», «Внешние углы треугольника. Виды треугольников», «Теорема о соотношениях между сторонами и углами треугольника», «Неравенство треугольника», «Прямоугольные треугольники; свойства и признаки равенства прямоугольных треугольников», Расстояние от точки до прямой. Расстояние между параллельными прямыми», «Построения с помощью циркуля и линейки. Построение треугольника по трем элементам».

Комплект билетов по информатике имеет следующую структуру: каждый билет содержит две части — теоретическую и практическую. Теоретическая часть предполагает устный ответ учащихся с возможной демонстрацией необходимой для ответа иллюстративной части. Это может быть описание объектов изучения, их существенных признаков, свойств, связей между ними, т.е. раскрытие сущности изученного объекта. Практическая часть содержит задание, которое решает определённую геометрическую задачу.

Примерное время, отводимое на подготовку ученика к ответу – 15-20 минут.

Отметка «5» ставится, если ученик ответил на все теоретические вопросы и решил задачу.

Отметка «4» ставится, если ученик ответил:

— на все теоретические вопросы

— на первый теоретический вопрос и решил задачу.

Отметка «3» ставится, если ученик ответил:

— на первый теоретический вопрос;

— на второй теоретический вопрос и решил задачу;

— решил задачу.

В остальных случаях ставится отметка «2».

Экзаменационные билеты по геометрии с задачами. 7 класс.

Билет №1.

1. Точки. Прямые. Отрезки.

2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.

3. Задача на тему «Смежные углы».

Найдите величины смежных углов, если один из них в 5 раз больше другого.

Билет №2.

1. Виды треугольников.

2. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

Отрезки AC и BM пересекаются и точкой пересечения делятся пополам. Доказать, что треугольник ABC равен треугольнику CMA.

Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

3. Задача на тему «Окружность».

На окружности с центром О отмечены точки А и В так, что угол AOB прямой. Отрезок ВС — диаметр окружности. Докажите, что хорды AB и AC , равны.

Билет №4.

1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.

2. Доказать, что если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Внешний угол треугольника».

Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.

Билет №5.

1. Определение параллельных прямых, параллельные отрезки.

2. Сформулировать и доказать первый признак равенства треугольников.

3. Задача на тему «Треугольники».

В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.

Билет №6.

1. Луч Угол. Виды углов.

2. Свойство углов при основании равнобедренного треугольника.

3. Задача на тему «Свойства параллельности двух прямых».

Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы.

Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

2. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Отрезок АМ-биссектриса треугольника ABC. Через точку M проведена прямая, параллельная AC и пересекающая сторону AB в точке E. Доказать, что треугольник AME равнобедренный.

Билет №8.

1. Объясните, как построить треугольник по двум сторонам и углу между ними.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Второй признак равенства треугольников».

На биссектрисе угла А взята точка E, а на сторонах этого угла точки В и С такие, что угол AEC равен углу AEB. Доказать, что BE равно CE.

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Неравенство треугольника.

3. Задача на тему «Признаки параллельности двух прямых».

Отрезки AB и CM пересекаются в их общей середине. Доказать, что прямые AC и BM параллельны.

Билет №10.

1. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Соотношения между сторонами и углами треугольника».

Доказать, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.

Билет №11.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

3. Задача на тему «Смежные углы».

Найти смежные углы, если один из них на 45 больше другого.

Билет №12.

1. Смежные углы ( определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.

3. Задача на тему «Свойства равнобедренного треугольника».

Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.

Билет №13.

1. Вертикальные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.

3. Задача на тему «Признаки равенства треугольников».

Отрезки AB и CE пересекаются в их общей середине О. На отрезках AC и BE отмечены точки К и M так, что AK равно BM. Доказать, что OK равно OM.

Билет №14.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.

2. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.

3. Задача на тему «Свойства прямоугольных треугольников».

Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.

Билет №15.

1. Какая теорема называется обратной к данной теореме. Привести примеры.

2. Доказать, что если две прямые параллельны третьей, то они параллельны.

3. Задача на тему «Признаки параллельности двух прямых».

Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50. Найти эти углы.

Билет №16.

1. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

2. Свойство внешнего угла треугольника.

3. Задача на тему «Расстояние от точки до прямой».

Через середину отрезка проведена прямая. Доказать, что концы отрезка равноудалены от этой прямой.

Билет №17

1. Параллельные прямые. Расстояние между параллельными прямыми.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

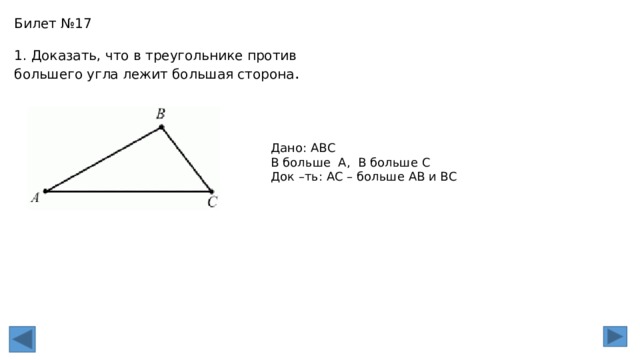
3. Задача на тему «Признаки параллельности двух прямых».

В треугольнике ABC угол А равен 40, а угол ВСЕ, смежный с углом ACB, равен 80.Доказать, что биссектриса угла ВСЕ параллельна прямой AB.

Билет №18.

1. Признаки равенства прямоугольных треугольников.

2. Доказать свойство вертикальных углов.

3. Задача на тему «Расстояние от точки до прямой».

В равнобедренном треугольнике ABC с основанием АС = 37 см, внешний угол при вершине В равен 60. Найти расстояние от вершины С до прямой AB.

Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника».

Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найти боковую сторону данного треугольника.

Билет №20.

1. Объясните, как построить биссектрису данного угла.

2. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

3. Задача на тему «Свойства прямоугольных треугольников».

В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120, АС + АВ = 18 см. Найти AC и AB.

Билет №21.

1. Объясните, как найти середину отрезка.

2. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

В треугольниках ABC и MKE отрезки СО и EH медианы, BC=KE, угол В равен углу К и угол С равен углу E. Доказать, что треугольник АСО равен треугольнику MEH.

Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42°

Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Свойства равнобедренного треугольника».

Найдите углы при основании MP равнобедренного треугольника МОР, если MK – его биссектриса и OKM = 96°.

Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Неравенство треугольника».

В равнобедренном треугольнике одна сторона равна 25см, а другая равна 10 см. Какая из них является основанием?

Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Вертикальные углы».

Прямые АВ и CD пересекаются в точке О. Угол АОС равен 580. Найдите угол ВОD.

Экзаменационные билеты по геометрии. 7 класс.

Билет №1.

1. Точки. Прямые. Отрезки.

2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.

3. Задача на тему «Смежные углы».

Билет №2.

1. Виды треугольников.

2. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

3. Задача на тему «Окружность».

Билет №4.

1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.

2. Доказать, что если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Внешний угол треугольника».

Билет №5.

1. Определение параллельных прямых, параллельные отрезки.

2. Сформулировать и доказать первый признак равенства треугольников.

3. Задача на тему «Треугольники».

Билет №6.

1. Луч Угол. Виды углов.

2. Свойство углов при основании равнобедренного треугольника.

3. Задача на тему «Свойства параллельности двух прямых».

Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

2. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

3. Задача на тему «Признаки параллельности двух прямых». .

Билет №8.

1. Объясните, как построить треугольник по двум сторонам и углу между ними.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Второй признак равенства треугольников».

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Неравенство треугольника.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №10.

1. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Соотношения между сторонами и углами треугольника».

Билет №11.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

3. Задача на тему «Смежные углы».

Билет №12.

1. Смежные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.

3. Задача на тему «Свойства равнобедренного треугольника».

Билет №13.

1. Вертикальные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.

3. Задача на тему «Признаки равенства треугольников».

Билет №14.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.

2. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.

3. Задача на тему «Свойства прямоугольных треугольников».

Билет №15.

1. Какая теорема называется обратной к данной теореме. Привести примеры.

2. Доказать, что если две прямые параллельны третьей, то они параллельны.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №16.

1. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

2. Свойство внешнего угла треугольника.

3. Задача на тему «Расстояние от точки до прямой».

Билет №17

1. Параллельные прямые. Расстояние между параллельными прямыми.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №18.

1. Признаки равенства прямоугольных треугольников.

2. Доказать свойство вертикальных углов.

3. Задача на тему «Расстояние от точки до прямой».

Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника».

Билет №20.

1. Объясните, как построить биссектрису данного угла.

2. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

3. Задача на тему «Свойства прямоугольных треугольников».

Билет №21.

1. Объясните, как найти середину отрезка.

2. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

В треугольниках ABC и MKE отрезки СО и EH медианы, BC=KE, угол В равен углу К и угол С равен углу E. Доказать, что треугольник АСО равен треугольнику MEH.

Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Свойства равнобедренного треугольника».

Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Неравенство треугольника».

Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Вертикальные углы».

Источник

Утверждаю:____________ Гераскин А.А. Согласовано:_________Козина Т.И.

Директор МБОУ СОШ №11 Зам. Директора

Подготовила : Куракина С.М._________ 2016год

Билеты по геометрии 7 класс

Билет 1

1. Определение равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника(доказать)..

2. Определение биссектрисы угла. Построение биссектрисы угла.

3. Найдите величины смежных углов, если один из них в 5 раз больше другого.

4. Докажите равенство отрезков соединяющих середину основания равнобедренного треугольника с серединами боковых сторон.

________________________________________________________________________________________________________

Билет 2

1. Определение смежных углов. Свойства смежных углов. (доказать).

2. Определение треугольника. Построение треугольника по трем сторонам.

3. Отрезки MN и DK пересекаются в их общей середине В. Докажите равенство треугольников MDB и NKB.

4. Треугольники ABC и BAD равны. Точки C и D лежат по разные стороны от прямой AB. Докажите, что прямые AC и BD параллельны

________________________________________________________________________________________________________

Билет 3

1. Определение вертикальных углов. Свойство вертикальных углов(доказать)..

2. Определение перпендикулярных прямых. Построение прямой, проходящей через точку, не лежащую на данной прямой и перпендикулярную к данной прямой.

3. Найдите периметр равнобедренного треугольника ADC с основанием AD, если AD = 7 см, DC = 8 см.

4. Докажите, что в треугольнике медиана не меньше высоты, проведённой из той же вершины.

_______________________________________________________________________________________________________

Билет 4

1. Определение равных треугольников. Первый признак равенства треугольников (доказательство).

2. Определение отрезка. Деление отрезка пополам.

3. Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126° .

4. Отрезки А В и СМ пересекаются в точке О. Луч ОК является биссектрисой угла MOB. Найдите угол МОК, если угол АОМ равен 86° .

______________________________________________________________________________________________________

Билет 5

1. Определение медианы треугольника. Свойство медианы равнобедренного треугольника. (доказательство).

2. Определение угла. Построение угла, равного данному.

3. Точки М, N, R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR. Рассмотреть все случаи.

4. Найдите углы при основании MP равнобедренного треугольника МОР, если МК — его

биссектриса и угол OKM = 96°.

________________________________________________________________________________________________________

Билет 6

1. Определение параллельных прямых. Признаки параллельности прямых (доказательство одного из признаков по выбору учащегося).

2. Определение треугольника. Построение треугольника по стороне и прилежащим к ней двум углам.

3. Угол, противолежащий основанию равнобедренного треугольника, равен 50° . Найдите величину внешнего угла при основании.

4. В треугольнике МОК угол O равен 76°, а угол М в 3 раза меньше внешнего угла при вершине К Найдите неизвестные углы треугольника.

______________________________________________________________________________________________________

Билет 7

1. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. (Доказательство одной из теорем по выбору учащегося.)

2. Определение треугольника. Построение треугольника по двум сторонам и углу между ними.

3. Найдите углы треугольника, на которые высота разбивает равносторонний треугольник.

4 В треугольнике АВС проведены биссектрисы АК и СМ, которые пересекаются в точке О. Найдите угол АВС, если угол АОС равен 110°.

________________________________________________________________________________________________________

Билет 8

1. Определение треугольника. Теорема о сумме углов треугольника. (доказать).

2. Определение окружности, центра, радиуса, хорды и диаметра.

3. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .

4. Треугольник МСВ — равносторонний, ВК и MP — его медианы, пересекающиеся в точке О. Докажите равенство треугольников ВОР и МОК.

_______________________________________________________________________________________________________

Билет 9

1 Определение внешнего угла. Свойство внешнего угла. Доказательство.

2. Построить прямоугольный треугольник АВС по двум катетам

3. Найдите сторону равнобедренного треугольника, если две другие его стороны равны: а) 8см и 2см, б) 5см и 3см

4. На сторонах АВ и ВС треугольника АВС взяты точки D и E соответственно. Из этих точек опущены перпендикуляры DK и EP к прямой АС, DK = EP, угол ADK равен углу PEC. Докажите, что АВ = ВС.

______________________________________________________________________________________________________

Билет 10

1. Определение прямоугольного треугольника. Свойства прямоугольного треугольника. Доказательство свойства катета, лежащего напротив угла в 30°

2. Определение высоты треугольника. Свойство высоты равнобедренного треугольника

3. Найдите смежные углы, если один из них на 55° больше другого.

4. В треугольниках АВС и А1В1С1 АВ = А1В1, АС = А1С1, угол А равен углу А1, точки D и D1 лежат соответственно на сторонах АС и А1С1, угол DBC равен углу D1B1C1. Докажите, что треугольник BDC равен треугольнику B1 D1C1.

________________________________________________________________________________________________________

Билет 11

1. Соотношение между сторонами и углами в треугольнике. Доказательство прямой и обратной теоремы.

2. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

3. Равные отрезки AB и CD пересекаются в точке О, так что АО = СО. Докажите равенство углов АВС и ADС

4. На сторонах О отмечены точки А и В так, что ОА = ОВ. Через эти точки проведены прямые, перпендикулярные к сторонам угла и пересекающиеся в точке С. Докажите, что луч ОС – биссектриса О

____________________________________________________________________________________________________

Билет 12

1. Равнобедренный треугольник. Признак равнобедренного треугольника (доказать)..

2 Какая теорема называется обратной к данной теореме. Привести примеры.

3. Найдите длину отрезка AM и градусную меру угла АВК, если ВМ-медиана, а ВК -биссектриса треугольника ABC и известно, что АС =1 см, угол ABC равен 84°

4. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.

_____________________________________________________________________________________________________

Билет 13

1.Неравество треугольника .Доказательство теоремы.

2.Метод доказательства от противного.

3 Луч SО является биссектрисой угла S .На сторонах угла отложены равные отрезки SM и SN . Докажите равенство треугольников SMO и SNO.

4 Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15см. Найдите гипотенузу и меньший катет.

______________________________________________________________________________________________________

Билет 14

.1. Расстояние между параллельными прямыми. Теорема о свойстве параллельных прямых (доказать).

2. Определение треугольника. Виды треугольников в зависимости от углов и сторон.

3. . В равнобедренном треугольнике АВС с основанием АС медиана BD равна половине стороны АС. Найдите углы треугольника АВС

4. Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.

________________________________________________________________________________________________________

Билет 15

1 Определение равных треугольников. 2-й признак равенства треугольников (доказать).

2..Аксиома параллельных прямых. Следствия из аксиомы параллельных прямых .

3. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126°

4. В треугольнике АВС А = С, а высота AD делит сторону ВС пополам. Найдите АС, если BD = 7,8см.

___________________________________________________________________________________________________

Билет 16

1. Признаки равенства прямоугольных треугольников (доказательство признака по гипотенузе и катету)

2. Линии в треугольнике ( медиана, биссектриса, высота).Показать на рисунке.

3 Внутренние односторонние углы, образованные при пересечении двух параллельных прямых секущей, относятся как 2 : 3. Чему равны эти углы?.

4 . В равнобедренном треугольнике ABC с основанием АС=37см, внешний угол при вершине В равен 60 градусам. Найти расстояние от вершины С до прямой AB.

___________________________________________________________________________________________________

Билет 17

1.Определение равных треугольников. 3-й признак равенства треугольников (доказать).

2.Луч Угол. Виды углов .

3. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210°. Найти эти углы.

4. В прямоугольном треугольнике ABC с прямым углом С внешний Угол при вершине А равен 120°, АС+АВ=18см. Найти AC и AB

Источник

Билеты по геометрии. 7 класс.

Билеты по геометрии.

7 класс.

Выбери билет. 1 2 3 4 5 6 7 14 13 12 11 10 9 8 15 16 17 18 19 20 21 Конец!!!

Выбери билет.

1

2

3

4

5

6

7

14

13

12

11

10

9

8

15

16

17

18

19

20

21

Конец!!!

  Билет №9. 1. Определение окружности, центра, радиуса, хорды и диаметра. Задача на построение угла, равного данному. А В О Е С

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра. Задача на построение угла, равного данному.

А

В

О

Е

С

Билет №3. 1. Линии в треугольнике (медиана, биссектриса, высота)

Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота)

Билет №17 1. Доказать, что в треугольнике против большего угла лежит большая сторона . Дано: АВС В больше А, В больше С Док –ть: АС – больше АВ и ВС

Билет №17

1. Доказать, что в треугольнике против большего угла лежит большая сторона .

Дано: АВС

В больше А, В больше С

Док –ть: АС – больше АВ и ВС

Билет №20. 1.Виды треугольников. Теорема о внешнем угле треугольника.

Билет №20.

1.Виды треугольников. Теорема о внешнем угле треугольника.

Билет №6. 1.Свойство биссектрисы равнобедренного треугольника.

Билет №6.

1.Свойство биссектрисы равнобедренного треугольника.

Билет №7. 1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей. Признаки параллельности прямых (доказательство одного).

Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей. Признаки параллельности прямых (доказательство одного).

Билет №15. 1.Построение середины отрезка.

Билет №15.

1.Построение середины отрезка.

Билет №1. 1. Вертикальные углы. Определение и свойство.

Билет №1.

1. Вертикальные углы. Определение и свойство.

Билет №11. 1. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

Билет №11.

1. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

Билет №4. 1.Признаки равенства треугольников(доказательство одного).

Билет №4.

1.Признаки равенства треугольников(доказательство одного).

Билет №8. 1. Теорема о сумме углов треугольника.

Билет №8.

1. Теорема о сумме углов треугольника.

Билет №19. 1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

Билет №2. 1. Смежные углы. Определение и свойство.

Билет №2.

1. Смежные углы. Определение и свойство.

Билет №5. 1.Свойство углов при основании равнобедренного треугольника.

Билет №5.

1.Свойство углов при основании равнобедренного треугольника.

Билет №12. 1.Признаки равенства прямоугольных треугольников (доказательство одного).

Билет №12.

1.Признаки равенства прямоугольных треугольников (доказательство одного).

Билет №18. 1. Аксиома параллельных прямых. Следствия (доказательство одного).

Билет №18.

1. Аксиома параллельных прямых. Следствия (доказательство одного).

Билет №10. 1. Свойства прямоугольных треугольников (доказательство одного).

Билет №10.

1. Свойства прямоугольных треугольников (доказательство одного).

Билет №21. 1.Неравенство треугольника.

Билет №21.

1.Неравенство треугольника.

Билет №14. 1. Построение перпендикулярных прямых.

Билет №14.

1. Построение перпендикулярных прямых.

Источник

Геометрия 7 Контрольные работы Атанасян — контрольные работы по геометрии в 7 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта) В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Атанасян 7. Поурочные планы
  Самостоятельные работы

Уровень 1 — самый легкий, уровень 2 — средний, уровень 3 — самый сложный.

ГЛАВА I. НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ

К-1. Контрольная работа по геометрии с ответами «Основные свойства простейших геометрических фигур. Смежные и вертикальные углы» (урок 10):

К-1 Уровень 1 + Ответы
  К-1 Уровень 2 + Решения
  К-1 Уровень 3 + Решения

ГЛАВА II. ТРЕУГОЛЬНИКИ

К-2. Контрольная работа по геометрии с ответами «Треугольники» (урок 28):

К-2 Уровень 1 + Ответы
  К-2 Уровень 2 + Решения
  К-2 Уровень 3 + Решения

ГЛАВА III. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

К-3. Контрольная работа по геометрии с ответами «Параллельные прямые» (урок 41):

К-3 Уровень 1 + Ответы
  К-3 Уровень 2 + Решения
  К-3 Уровень 3 + Решения

ГЛАВА IV. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

К-4. Контрольная работа по геометрии с ответами «Сумма углов треугольника. Соотношения между сторонами и углами треугольника» (урок 49):

К-4 Уровень 1 + Решения
  К-4 Уровень 2 + Решения
  К-4 Уровень 3 + Решения

К-5. Контрольная работа по геометрии с ответами «Прямоугольный треугольник. Построение треугольника по трем элементам» (урок 61):

К-5 Уровень 1 + Решения
  К-5 Уровень 2 + Ответы
  К-5 Уровень 3 + Ответы

ПОВТОРЕНИЕ за курс 7 класса

К-6 «Итоговая контрольная работа» за курс 7 класса (с ответами).

К-6 Уровень 1 + Ответы
  К-6 Уровень 2 + Решения
  К-6 Уровень 3 + Решения

ПОЯСНЕНИЯ

По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

Атанасян 7. Поурочные планы
  Самостоятельные работы

Смотрите также: ВСЕ КОНТРОЛЬНЫЕ РАБОТЫ в 7 классе

Вы смотрели: Геометрия 7 Контрольные работы Атанасян — контрольные работы по геометрии в 7 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Контрольные работы по геометрии от других авторов и УМК:

УМК МЕРЗЛЯК: Дидактические материалы 7 класс (5 контрольных работ по 2 варианта)

УМК АТАНАСЯН: Мельникова. Контрольные работы в 7 классе

УМК АТАНАСЯН: Геометрия 7 класс УЧЕБНИК (задачи из учебника с ответами)

УМК ПОГОРЕЛОВ: Гусев. Дидактические материалы по геометрии 7 класс

УМК БУТУЗОВ (МГУ — школе): Геометрия. Дидактические материалы. 7 класс

К любому УМК: Глазкова, КИМ: контрольные работы. 7 класс

Источник

Билет 1

  1. Определение равнобедренного треугольника.
    Свойство углов при основании равнобедренного
    треугольника.
  2. Определение биссектрисы угла. Построение
    биссектрисы угла.
  3. Найдите величины смежных углов, если один из них
    в 5 раз больше другого.

Билет 2

  1. Определение смежных углов. Свойство смежных
    углов.
  2. Определение треугольника. Построение
    треугольника по трем сторонам.
  3. Отрезки MN и DK пересекаются в их общей
    середине B. Докажите равенство треугольников MDB
    и NKB.

Билет 3

  1. Определение вертикальных углов. Свойство
    вертикальных углов.
  2. Определение перпендикулярных прямых.
    Построение прямой, проходящей через точку, не
    лежащую на данной прямой и перпендикулярную к
    данной прямой.
  3. Найдите периметр равнобедренного треугольника ADC
    с основанием AD, если AD = 7 см, DC = 8 см.

Билет 4

  1. Определение равных треугольников. Признаки
    равенства треугольников (доказательство одного
    из признаков по выбору учащегося).
  2. Определение отрезка. Деление отрезка пополам.
  3. Найдите неразвернутые углы, образованные при
    пересечении двух прямых, если сумма двух из них
    равна 126° .

Билет 5

  1. Определение медианы треугольника. Свойство
    медианы равнобедренного треугольника.
  2. Определение угла. Построение угла, равного
    данному.
  3. Точки М, N и R лежат на одной
    прямой, MN = 11 см, RN = 20 см. Найдите
    расстояние MR.

Билет 6

  1. Определение параллельных прямых. Признаки
    параллельности прямых (доказательство одного из
    признаков по выбору учащегося).
  2. Определение треугольника. Построение
    треугольника по стороне и двум углам.
  3. Угол, противолежащий основанию равнобедренного
    треугольника, равен 50° . Найдите величину
    внешнего угла при основании.

Билет 7

  1. Аксиома параллельных. Теоремы об углах,
    образованных двумя параллельными прямыми и
    секущей. (Доказательство одной из теорем по
    выбору учащегося.)
  2. Определение треугольника. Построение
    треугольника по двум сторонам и углу между ними.
  3. Найдите углы треугольника, на которые высота
    разбивает равносторонний треугольник.

Билет 8

  1. Определение треугольника. Теорема о сумме углов
    треугольника.
  2. Построение равнобедренного треугольника по
    боковой стороне и высоте, проведенной к
    основанию.
  3. Найдите все углы, образованные при пересечении
    двух параллельных прямых секущей, если один из
    них равен 42° .

Билет 9

  1. Определение внешнего угла. Свойство внешнего
    угла.
  2. Определение медианы треугольника. Построение
    медианы треугольника.
  3. Найдите все углы, образованные при пересечении
    двух параллельных прямых секущей, если один из
    них 126° .

Билет 10

  1. Определение прямоугольного треугольника.
    Свойство катета, лежащего напротив угла в 30° .
  2. Определение высоты треугольника. Построение
    высоты.
  3. Найдите смежные углы, если один из них на 55°
    больше другого.

Билет 11

  1. Соотношение между сторонами и углами в
    треугольнике.
  2. Построение прямой, проходящей через данную
    точку и параллельную данной прямой.
  3. Луч SR является биссектрисой угла S, а
    отрезки SM и SN равны. Докажите равенство
    треугольников SMO и SNO.

Билет 12

  1. Равнобедренный треугольник. Признак
    равнобедренного треугольника.
  2. Определение перпендикулярных прямых.
    Построение прямой, проходящей через точку,
    лежащую на данной прямой, перпендикулярно к
    данной прямой.
  3. Найдите длину отрезка AM и градусную меру
    угла ABK, если BM – медиана, а BK –
    биссектриса треугольника ABC и известно, что AC
    = 17 см, угол ABC равен 84° .

Задачи 4 к экзаменационным билетам по
геометрии. 7 класс

(Данные задачи ученик получает на
экзамене)

Билет 1

Докажите равенство отрезков, соединяющих
середину основания равнобедренного
треугольника с серединами боковых сторон.

Билет 2

Известно, что OAM = OAK и MBS = KBS.Докажите,
что AK = AM, BM = BK.

Билет 3

Прямая а пересекает стороны угла A.
Докажите ,что 1 = 2, если известно, что 5 = 6.

Билет 4

Отрезки AB и CM пересекаются в точке O.
Луч OK является биссектрисой угла MOB.
Найдите угол MOK, если угол AOM равен 86° .

Билет 5

Прямая а пересекает стороны угла А.
Докажите,что 1 = 2, если известно, что 3 = 4.

Билет 6

Найдите углы при основании MP
равнобедренного треугольника МОР, если MK
– его биссектриса и OKM =
96°.

Билет 7

В треугольнике MOK O =
76°, а угол M в 3 раза меньше внешнего угла при
вершине K. Найдите неизвестные углы
треугольника.

Билет 8

Отрезки AB и CM параллельны и равны.
Докажите, что AM = BC.

Билет 9

Докажите, что AB = CM.

Билет 10

Треугольник MCB – равносторонний, BK и MP
– его медианы, пересекающиеся в точке O.
Докажите равенство треугольников BOP и MOK.

Билет 11

Прямая, пересекающая основание
равнобедренного треугольника, параллельна одной
из боковых сторон. Докажите, что она отсекает
равнобедренный треугольник.

Билет 12

В треугольниках BCK и B1C1K1CM
и С1M1 – биссектрисы, CM = C1M1,
углы BCK и B1C1K1 равны, углы
CMK и C1M1K1 тоже равны.
Докажите равенство треугольников BCK и B1C1K1.

Литература

  1. Учебник “Геометрия 7–9”, авт.: Л.С. Атанасян, В.Ф.
    Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина.
  2. Книга для учителя “Изучение геометрии в 7, 8, 9
    классах”, Л.С. Атанасян и др.
Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Экзамен по геометрии 7 класс билеты ответы 2021
  • Экзамен по вождению на квадроцикле видео
  • Экзамен по геологии тест
  • Экзамен по географии рассказ
  • Экзамен по вождению мопеда

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии