Гидрогазодинамика
Укажите
номер правильного ответа
1. Давление
характеризует напряженное состояние
жидкости, вызванное действием
сжимающих усилий;
2.Давление
в жидкости изменяется за счет
объемных (массовых)
сил;
3. Закон
распределения абсолютного давления в
жидкости, находящейся в неподвижном
закрытом сосуде с р0рат
определяется выражением
р = р0+gh;
4. Эпюра избыточного
давления на вертикальную стенку
закрытого резервуара с р0рат
представляет собой
трапецию.
5. Эпюра избыточного
давления на дно закрытого резервуара
с р0 >
рат – это
прямоугольник;
6. Закрытый
резервуар с вакуумметрическим давлением
рвак = 0,2 ´
105 Па заполнен водой. На
глубине h = 3 м от
свободной поверхности подключен
пружинный манометр. Определите абсолютное
давление в точке подключения манометра.
0,1 х 105Па;
7. Сила давления
жидкости на вертикальную стенку
резервуара определяется по давлению
в центре тяжести
стенки.
8. Два вертикальных
резервуара (квадратный со стороной а
= 0,6 м и цилиндрический диаметром d
= 0,6 м) заполнены жидкостью на одинаковую
высоту. Каково соотношение сил давления
жидкости на боковые стенки этих
резервуаров?
силы давления в
рассматриваемых резервуарах одинаковы.
9.В жидкости,
находящейся в закрытом сосуде, при
абсолютном давлении на свободной
поверхности р0 <
рат
избыточное давление
возможно при определенной глубине.
10. Высота воды
в открытом пьезометре, присоединенном
к резервуару равна 1 м. Найдите величину
избыточного давления в точке подключения.
104Па;
11. Вакуумметрическое
давление – это …
разность атмосферного
и абсолютного давления;
12. Укажите пределы
изменения вакуума
от 0 до рат;
13. Избыточное
давление – это
превышение
абсолютного давления над атмосферным
давлением;
14. В формуле
рабс = р0 +
rgh
при р0 = рат величина
rgh
характеризует
избыточное давление
столба жидкости высотой h;
15. Величина
избыточного давления равна 5 кПа. Найдите
пьезометрическую высоту , соответствующую
этому давлению
0,5 м;
16. Движение
жидкости называют неустановившемся,
когда
-изменяется во
времени местная скорость в данной точке
пространства, занятого движущейся
жидкостью;
17. Линия
тока и траектория частицы жидкости
совпадают
при
установившемся движении;
18.Найдите
гидравлический радиус для
напорного
движения жидкости
в трубе квадратного сечения;
(размер 0,1х 0,1м)
0,025
м;
19.Укажите
соотношение между
скоростями
жидкости в двух различных
сечениях по длине плавно изменяющегося
движения
u1
=u2(d2/d1)2;
20.Понятие
«напор» характеризует
энергетическое
состояние жидкости.
21.Напорная
и пьезометрическая линии представляют
собой расходящиеся линии в трубопроводе
сужающемся;
22.Пьезометрическая
линия имеет уклон вверх вдоль потока
в трубопроводе
расширяющемся;
23.Найдите
гидравлический уклон при движении
жидкости в цилиндрическом трубопроводе
длиной 10 м. Показания пьезометров в
начальном и конечном сечениях равны
соответственно 1,1 и 1,0 м
0,01;
24. Пьезометрический
напор в живом сечении потока равен (при
значении полного напора 1,05 м и средней
скорости 1 м/с)
-
1,0 м;
25. Определить
режим течения жидкости в трубопроводе
диаметром 0,032 м при скорости 1 м/с и
кинематической вязкости 0,01 см2/с
турбулентный;
26.Распределение
скоростей по сечению потока более
равномерное
при турбулентном
режиме.
27.Наиболее
существенно влияет на потери напора
по длине при ламинарном режиме
диаметр трубопровода;
28.С увеличением
диаметра трубопровода потери напора
по длине потока
уменьшаются;
29.Влияние
скорости на потери напора по длине
более существенно
при турбулентном
режиме;
30.Укажите
параметр, наиболее существенно влияющий
на потери напора по длине при турбулентном
режиме
диаметр трубопровода;
31.Коэффициент
гидравлического трения при турбулентном
режиме определяется с учетом
вида жидкости,
диаметра и состояния поверхности
трубы, скорости;
32.Для заданных
диаметра трубы и свойств жидкости
влияние шероховатости стенок на
коэффициент гидравлического трения
сильнее сказывается
при высоких
скоростях движения.
33.Понятие
«гидравлический уклон» связано
с уклоном напорной
линии;
34.При
ламинарном режиме коэффициент
гидравлического трения зависит
от режима движения
жидкости;
35. При расчете
коротких трубопроводов учитывают
местные потери
и потери по длине потока.
36.Имеется
параллельное соединение труб (d1
< d2, l1 = l2).
Потери напора
одинаковые.
37.Расчет
разветвленного тупикового трубопровода
выполняется с учетом
баланса расходов
в узловых точках;
38.При
известном напоре в начальной точке
разветвленного (сложного) трубопровода
диаметры труб на участках определяются
с учетом
расхода жидкости
и потерь напора на участках;
39.При
неизвестном напоре в начальной точке
разветвленного (сложного) трубопровода
диаметры труб на участках определяются
с учетом
расхода жидкости
и скорости движения.
40.Наиболее
существенно влияет на пропускную
способность отверстия (насадка) в стенке
резервуара
диаметр отверстия;
41.При
увеличении напора в 4 раза расход
жидкости через отверстие в стенке
резервуара возрастает (при d=const)
в 2 раза;
42.Скорость
звука является характеристикой
сжимаемости
жидкости (газа);
43.Закон
сохранения массы для потока сжимаемого
газа (жидкости) записывается в виде
;
44.Закон
сохранения энергии для совершенного
газа в энергетически изолированной
системе имеет вид
;
45.Параметры
торможения газа соответствуют
нулевой скорости.
46.Параметры
торможения газа остаются постоянными
по длине потока
для изоэнтропического
процесса.
47.С увеличением
скорости газа
уменьшается
давление pи плотностьρ, отношениеp/ρ.
48.Максимальная
скорость газа достигается при
температуре,
равной нулю;
49.С увеличением
скорости установившегося адиабатического
течения температура идеального
совершенного газа
уменьшается;
50.Для
критического режима течения газа
характерно соотношение
M=
1.
51. Местная
скорость звука для данного газа зависит
от
температуры;
52.Скорость
звука с увеличением скорости газа
уменьшается;
53. Коэффициент
скорости определяется по формуле
λ =
u/aкр.
54. Скорость
течения газа u
и скорость звука а связаны
соотношением
u
=aM.
55. При сверхзвуковом
течении газа с увеличением сечения
потока
давление уменьшается
, а скорость увеличивается.
56. Сверхзвуковое
течение на выходе сопла Лаваля получим,
когда
поток на входе
сверхзвуковой, в критическом сечении
скорость газа uравна
скорости звукаа.
57. В сопле Лаваля
расчетный режим течения реализуется
при
p2=pвн.
58. Скачки
уплотнения могут возникать
при переходе
сверхзвукового течения в дозвуковое;
59. Для сверхзвукового
потока после скачка уплотнения имеем
М < 1.
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ ТЕПЛОТЕХНИКИ
Укажите
номер правильного ответа
1. Уравнение для
расчета теплоты в изохорном процессе
имеет вид
;
2. Связь между
параметрами для изохорного процесса
определяется выражением
;
3. Связь
между параметрами изобарного процесса
определяется выражением
;
4. Процессы
дизельного двигателя в координатных
осях T—S
представлены на рисунке
3)
5. Цикл Ренкина
в координатных осях P
— V представлен
на рисунке
1
6. Уравнение
для расчета термического КПД двигателя
внутреннего сгорания с подводом теплоты
при P = const
и v = const
имеет вид
;
7. Уравнение
для расчета термического КПД двигателя
внутреннего сгорания с подводом теплоты
при v = const
имеет вид
;
8. Уравнение
для расчета КПД цикла Ренкина имеет
вид
.
9. Цикл
Отто в координатных осях T
— S представлен
на рисунке
2
10. Уравнение
для расчета КПД цикла Карно имеет вид
;
11. Процесс
расширения газа, в котором совершается
наибольшая работа, показан на графике
а;
12. Цикл Карно в
координатных осях T
– S представлен
на рисунке
13. Связь между
параметрами изотермического процесса
определяется выражением
;
14. Процесс,
имеющий минимальный теплообмен, показан
на графике
а;
15. Изотермический
процесс показан на графике
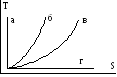
г.
16. Процессам, в
которых подводится теплота, соответствует
график
а;
17. При нагревании
газа больше изменится энтропия в
процессе
дросселирования.
18. Уравнение
работы для изотермического процесса
имеет вид
;
19. Уравнение для
изменения энтропии в изохорном процессе
имеет вид
;
20.
Уравнение для изменения энтропии в
адиабатном процессе
;
21. Адиабатный
процесс показан на графике
а;
22. Закону Ньютона
– Рихмана соответствует уравнение
;
23. Уравнение
теплопередачи имеет вид
;
24. Закону
теплопроводности (Фурье) соответствует
уравнение
25. Показатель
адиабаты К определяется выражением
;
26. Передача
теплоты от одной среды другой через
стенку называется
теплопередачей.
27. В абсорбционных
холодильных установках в качестве
хладона используется
бинарная смесь.
28. Сухой насыщенный
водяной пар имеет степень сухости
;
29. Процесс
парообразования проходит при
и
.
30. Критерий
Нуссельта характеризует
интенсивность
теплоотдачи;
31. Критерий
Рейнольдса характеризует
режим вынужденного
движения;
32. Критерий
Грасгофа характеризует
подъемную
силу при естественной конвекции.
33. Критерий
Прандля характеризует
физические
свойства подвижной среды;
34. Горючими
элементами твердого и жидкого топлива
являются
;
35. При расчете
тепловых потерь через пол площадь пола
разделяют на зоны шириной
2,0 м;
36. При дросселировании
идеального газа остается постоянным
энтальпия;
37. Минимальная
работа в компрессоре затрачивается,
если сжатие
изотермическое;
38. Основные
тепловые потери через ограждение
определяются по формуле
;
39. Тепловые
потери на отопление здания по укрупненным
показателям определяются по формуле
;
40. Значение
удельной отопительной характеристики
здания qот
зависит от
объема и
назначения здания;
41. Наиболее
совершенными являются ледники
с боковым
расположением льда.
42. В животноводческом
помещении необходимый воздухообмен
(м3/час), исходя из допустимого
содержания водяных паров, вычисляется
по формуле
;
43. В животноводческом
помещении необходимый воздухообмен
(м3/час), исходя из допустимой
концентрации СО2, вычисляется
по формуле
;
44. В животноводческом
помещении необходимый воздухообмен
(м3/час) по избыточной
теплоте рассчитывают по формуле
;
45. Математическое
выражение первого закона термодинамики
для изолированных систем имеет вид
.
46. Уравнение
первого закона термодинамики через
энтальпию имеет вид
;
47. Уравнение
политропного процесса имеет вид
.
48. Закон Стефана
— Больцмана при лучистом теплообмене
имеет вид
;
49. В вакууме
процесс переноса теплоты осуществляется
тепловым
излучением;
50. Наибольшее
значение теплопроводности имеют
чистые металлы.
51. В котельных
установках деаэрация воды производится
для удаления
растворенных газов;
52. В котельных
установках катионитовые фильтры
предназначены
для умягчения
воды;
53. Значение
показателя адиабаты зависит от
числа атомности
газа;
54. Холодильный
коэффициент обратимого цикла Карно
определяется по формуле
;
55. Температура
кипения воды зависит от
давления;
56. Основным
горючим элементом твердого и жидкого
топлива является
углерод;
57. Расход теплоты
на технологические нужды определяется
по формуле
;
58. Для сгорания
1 кг водорода требуется кислорода
8 кг;
59. Критерий
Нуссельта характеризует
интенсивность
теплоотдачи;
60. Минимальная
работа в компрессоре затрачивается,
если сжатие
изотермическое;
УСТАНОВИТЕ
СООТВЕТСТВИЕ
61. Установите
соответствие между законом
и его математическим выражением
|
Закон |
Математическое |
|
1) |
|
|
2) |
|
62. Установите
соответствие между процессом
и показателем политропы n
|
Процесс |
Показатель |
|
1) |
n |
|
2) |
n |
|
3) |
n |
63. Установите
соответствие между
парокомпрессионным агрегатом холодильной
машины и видом процесса
|
Парокомпрессионный холодильной |
Вид |
|
1) |
адиабатное |
|
2) |
изобарно-изотермическая |
|
3) |
адиабатное |
|
4) испаритель |
изобарно-изотермическое |
64. Установите
соответствие между видом
теплообмена и законом
|
Вид |
Показатель |
|
1) |
г) |
|
2) |
б) закон Ньютона |
УСТАНОВИТЕ
ПРАВИЛЬНУЮ ПОСЛЕДОВАТЕЛЬНОСТЬ
65. Последовательность
определения термического КПД идеальных
циклов ДВС:
1 установление
характеристик цикла;
3 определение
количества подведенной и отведенной
теплоты;
4 определение КПД
цикла;
2 определение
температуры рабочего тела в характерных
точках цикла.
66. Порядок
определения теплового потока Ф
при свободной конвекции:
2 по критериальной
зависимости рассчитывается критерий
Нуссельта Nu;
3 рассчитывается
коэффициент теплоотдачи α;
1 рассчитывается
критерий Грасгофа Gr;
4 определяется
тепловой поток Ф.
ДОПОЛНИТЕ
67. Теплообменник,
в котором теплоносители разделены
стенкой, называется рекуперативный
68. Процесс,
происходящий при постоянной температуре,
называетсяизотермическим
69. Процесс
парообразования проходит при постоянном
давлении и постоянной температуре
70. Основным
горючим элементом твердого и жидкого
топлива является углерод
НЕТРАДИЦИОННЫЕ
И ВОЗОБНОВЛЯЕМЫЕ
ИСТОЧНИКИ
ЭНЕРГИИ
Укажите номер
правильного ответа
1. Характерной
особенностью энергосистем на
возобновляемых источниках энергии
является:
незначительное
влияние на окружающую среду в небольших
установках;
2. Характерной
особенностью энергосистем на
возобновляемых источниках энергии
является:
рассеянная энергия
с плотностью сотни Вт/м2;
3. К электростанциям,
использующим возобновляемые источники
энергии, относятся:
приливные,
волновые, солнечные;
4. Плоские
коллекторы используют энергию солнечного
излучения
прямую и
рассеянную;
-
Концентраторы
используют энергию солнечного излучения
только прямую;
-
Фотобатареи
используют энергию солнечного излучения
прямую и рассеянную.
7. Фотобатареи
преимущественно используют спектр
солнечного излучения
видимый.
8.
Система, использующая солнечную энергию
для частичного или полного
покрытия отопительной нагрузки
потребителя без применения
солнечных коллекторов и специального
оборудования, когда приемниками
и аккумуляторами солнечной энергии
являются конструктивные
элементы здания или сооружения
называется:
пассивная
система солнечного отопления;
9.
Система, использующая солнечную энергию
для нагрева теплоносителя
в солнечных коллекторах с целью
частичного или полного покрытия
отопительной нагрузки данного потребителя
называется:
активная
система солнечного отопления;
10. Не требуется
устройство слежения за солнцем в
солнечной установке, называемой
плоский
коллектор.
11. Начальный
вращающий момент, развиваемый
ветроколесом, при прочих равных условиях
больше у ветроколеса
многолопастного.
12. Отношение
энергии, воспринимаемой ветроколесом,
к полной энергии, которой обладает
воздушный поток называется:
коэффициент
использования энергии ветра;
13. В ветроустановках
с вертикальной осью используется
следующая система ориентации ветроколеса
на ветер
нет необходимости
ориентации.
14. Для получения
механической энергии чаще находят
применение ветроколёса
многолопастные.
15. Мощность
ветроколеса в большей степени зависит
от:
скорости ветра;
16. При одинаковом
диаметре и скорости ветра частота
вращения больше для ветроколеса с
горизонтальной осью
однолопастного;
17. В системе
автоматического регулирования частоты
вращения ветроколеса в качестве
исходного сигнала используется:
скорость ветрового
потока;
18. Мощность
ветроэнергетической установки
определяется:
диаметром рабочего
колеса, скоростью ветра, плотностью
воздуха;
19. В состав
ветроэлектрической установки входят:
ветродвигатель,
редуктор, генератор электрической
энергии;
20. Мощность
проектируемой ГЭС рассчитывается по
параметрам:
напор, расход;
21. Из перечисленных
гидротурбин является активной:
гидротурбина
Пельтона (ковшовая);
22. Мощность
водотока при напоре Н = 5м и расходе Q
= 0,5 м3/с будет равна:
25 кВт;
23. Работа приливной
электростанции невозможна в случае,
если
уровень воды в
море равен уровню в бассейне.
24. Прямое
осознанное или косвенное и неосознанное
воздействие человека и результатов
его деятельности, вызывающее изменение
природной среды и естественных ландшафтов
называется:
антропогенное
воздействие на природу;
25. Прямое
преобразование солнечной энергии в
электрическую называется:
фотоэлектрическое;
26. К основным
элементам солнечной тепловой
электростанции не относится:
солнечная
батарея.
27. Ток солнечной
батареи можно увеличить:
путем
параллельного включения солнечных
элементов;
28. Напряжение
солнечной батареи можно увеличить:
путем
последовательного включения солнечных
элементов;
29. К факторам
неблагоприятного воздействия
ветроэнергетики на окружающую среду
не относятся:
изменение теплового
баланса, затенение больших территорий;
30. Республика
Башкортостан относится к территориям
со среднегодовой скоростью ветра:
3,5…6
м/с;
31. Сводные
сведения об энергетических
ресурсах ветра, составленные в виде
таблиц, диаграмм, графиков и карт для
определённой территории называются:
ветровой
кадастр;
32. Ветроэлектростанции,
возводимые на небольшом удалении от
берега, называются:
прибрежные;
33. Небольшое
многолопастное ветроколесо, служащее
для автоматической ориентации основного
колеса ветродвигателя относительно
воздушного потока называется:
виндроза.
34.
Зависимость выходной мощности
ветроагрегата от скорости ветра
незаторможенного потока называется:
энергетическая
характеристика;
35. Отношение
величины механической энергии,
развиваемой ветроколесом, и полной
энергии ветра, проходящей через ометаемую
площадь ветроколеса называется:
коэффициент
использования энергии ветра;
36. На рисунке
представлено изображение
ротора Дарье;
37. Глубинное
тепло земли относится к следующему
виду энергии:
геотермальная.
38. В комбинированных
системах геотермальное тепло используется
для
подогрева
питательной воды на тепловых
электростанциях;
39. Месторождения
пароводяных смесей РФ, перспективных
для освоения, расположены главным
образом:
на Камчатке,
Курильских островах, о. Сахалин.
40. Наиболее
интенсивными являются приливы,
возникающие под влиянием притяжения:
Луны;
41. Отношение
фактической (планируемой) выработки к
экономически целесообразной (возможной)
называется:
коэффициент
выработки за счет вторичных энергетических
ресурсов;
42. Для утилизации
тепла уходящих дымовых газов котельных
применяется:
экономайзер;
43. Шлаки,
образующиеся при переработке твердых
бытовых отходов, могут успешно
использоваться:
для производства
строительных материалов;
44. Продуктом
высокоскоростного пиролиза не является:
бензин;
45. Наиболее
эффективным способом использования
водорода является применение его в
виде: 5…10%-ной добавки к бензину;
УКАЖИТЕ НОМЕРА
ДВУХ ПРАВИЛЬНЫХ ОТВЕТОВ
46. Основные
преимущества возобновляемых источников
энергии:
неисчерпаемость;
экологическая
чистота;
47. Основные
направления использования солнечной
энергии:
получение
тепловой энергии;
преобразование
ее в электрическую энергию;
48. Приливная
энергия характеризуется
неизменностью
ее среднемесячного потенциала в сезонном
и многолетних циклах;
прерывистостью
в течение суток;
49. В целлюлозно-бумажной
промышленности горючими вторичными
энергетическими ресурсами являются:
сульфитный
и сульфатный щелоки;
кора и древесные
отходы;
50. Биогазовая
установка предназначена для выработки
горючего газа;
высококачественного
удобрения;
УКАЖИТЕ НОМЕРА
ТРЕХ ПРАВИЛЬНЫХ ОТВЕТОВ
51. Основные
виды ГЭС, это: гидроэлектрические;
приливные;
гидроаккумулирующие;
52. По виду
энергии вторичные энергетические
ресурсы разделяются на следующие
группы: топливные (горючие);
тепловые;
ресурсы с
избыточным давлением.
53. К основным
направлениям производства энергетического
топлива из отходов лесопереработки
относятся: гидролиз с получением
спиртов;
получение
синтетической нефти;
пиролиз
с получением пиролитического топлива
и газа.
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично


Подборка по базе: тест 3 четверть куб. 9 кл. 22-23 г. вопросы и ответы .doc, давлетов вопросы.docx, Тестовые вопросы к разделу 3_ просмотр попыткимуз — C строгое со, Тестовые вопросы к разделу 3_ просмотр попытки — 1ВерноБаллов 1,, Тестовые вопросы к разделу 4_ просмотр попытки.pdf, Тест с ответами по теме _Актуальные вопросы сестринского дела в , Тестовые вопросы к разделу 2_ Выполнение работ по должности служ, ТЕОРЕТИЧЕСКИЙ МИНИМУМ ПО КУРСУ МЕХАНИКИ И МОЛЕКУЛЯРНОЙ ФИЗИКИ ДЛ, Контрольная работа по курсу КС 2 второй курс-2.pdf, Основы использования и конфигурирования 1С Предприятие Вопросы.o
Экзаменационные вопросы по курсу «Гидрогазодинамика»
- Основные определения гидростатики (поверхностные и массовые силы, гидростатическое давление).
Поверхностные силы (силы, пропорциональные поверхности, на которую они действуют) – силы воздействия окружающей жидкости на рассматриваемый объём.
Массовые силы (силы, пропорциональные массе жидкости) – силы, действие которых обусловлено внешним силовым полем (например, полем силы тяжести, электрическим, магнитным и т.д.).
Гидростатическое давление – это давление, производимое на жидкость силой тяжести.
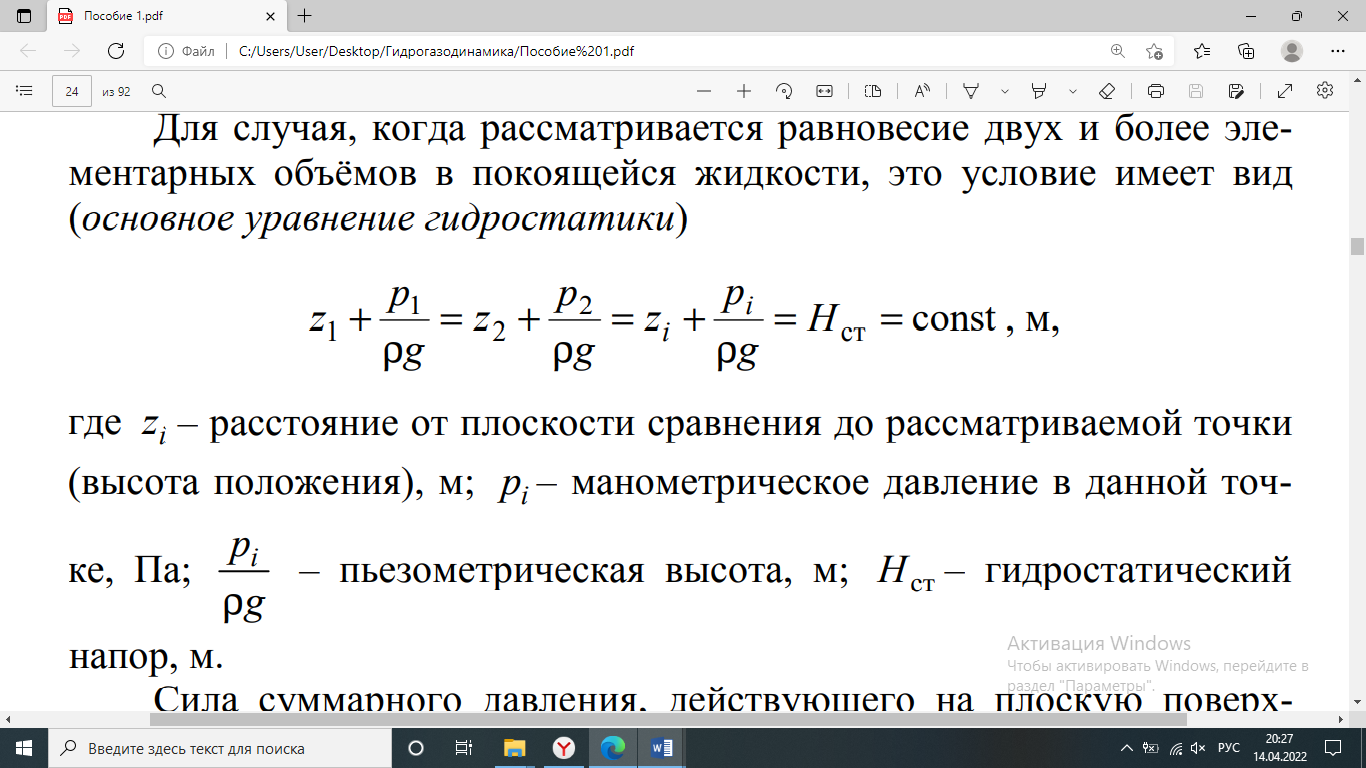
- Основное уравнение гидростатики. Закон Паскаля.
- Силы, действующие в покоящейся жидкости на плоские стенки. Сила суммарного давления жидкости на плоские поверхности.
Силы, действующие в жидкости, делятся на массовые, объёмные и поверхностные
Массовые силы (силы, пропорциональные массе жидкости) – силы, действие которых обусловлено внешним силовым полем (например, полем силы тяжести, электрическим, магнитным и т.д.)
Объёмные силы (силы, пропорциональные объёму жидкости). Массовые и объёмные силы имеют одинаковое значение, если во всех точках исследуемого объёма среды её плотность не изменяется
Поверхностные силы (силы, пропорциональные поверхности, на которую они действуют) – силы воздействия окружающей жидкости на рассматриваемый объём. К поверхностным силам относятся силы давления и вязкости.
- Сила суммарного давления жидкости на цилиндрические поверхности (центр давления, полная сила давления, объем тела давления).

Объем тела давления находят геометрически. При необходимости сложное тело давления можно разбить на элементарные и просуммировать их объемы.
- Закон Архимеда и его приложения. Водоизмещение.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения.
- Методы и приемы изучения механики жидкости и газа.
Жидкость и газы представляют собой системы материальных точек (молекул, атомов). Состояние вещества является функцией давления и температуры.
- В твёрдых телах кинетическая энергия движения молекул (атомов) недостаточна для выхода атомов из узлов кристаллической решётки, поэтому твёрдые тела сохраняют форму и объём.
- В жидкостях кинетическая энергия молекул достаточна для выхода из узлов решётки и поэтому определённая часть молекул хаотически перемещается по всему объёму, но их энергия недостаточна для выхода за пределы жидкости, поэтому жидкости сохраняют объём, но не сохраняют форму, а принимают форму сосуда.
- В газе энергия молекул достаточна для преодоления связей между молекулами, поэтому газы не сохраняют ни формы, ни объёма. Газ в беспредельном пространстве расширяется до бесконечности.
- Молекулярная структура и особенности жидкого и газообразного состояний; силы притяжения и отталкивания.
В жидком состоянии вещество сохраняет объём, но не сохраняет форму. Это означает, что жидкость может занимать только часть объёма сосуда, но также может свободно перетекать по всей поверхности сосуда. Жидкое состояние обычно считают промежуточным между твёрдым телом и газом. Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембран
Газообразное состояние характерно тем, что оно не сохраняет ни форму, ни объём. Газ заполняет всё доступное пространство и проникает в любые его закоулки. Это состояние, свойственное веществам с малой плотностью. Переход из жидкого в газообразное состояние называют испарением, а противоположный ему переход из газообразного состояния в жидкое — конденсацией.
Силы притяжения Эти силы являются самыми значимыми для взаимодействия между частицами вещества. По своей природе они являются электростатическими.
Силы отталкивания начинают действовать, когда межмолекулярное расстояние сокращается до предельно возможного минимума. При таком сближении начинают соприкасаться внешние уровни электронов двух атомов. Как следует из принципа Паули, являющегося одним из базовых положений квантовой механики, заполненные электронные оболочки не могут проникать одна внутрь другой. Величина таких сил в значительной степени зависит от особенностей строения молекулы определенного вещества.
- Основные уравнения кинетической теории газов.
Основное уравнение кинетической теории газов утверждает, что между давлением в газе p и средней кинетической энергией молекулы K существует простая связь: p 2/3 n K , где n – концентрация молекул.
- Основные физические свойства жидкостей. Определение жидкостей; плотность жидкостей; удельный вес; сжимаемость и температурные расширения жидкостей.
К основным физическим свойствам жидкости, которые рассматриваются в гидродинамике, относятся плотность, удельный вес, удельный объем, температурное расширение, сжимаемость и вязкость
Плотность — это отношение массы вещества к его объему:
р = m/V
Удельный вес — это отношение веса жидкости к занимаемому объему:
у = mg/V = pg.
Сжимаемость — свойство жидкости изменять объем при изменении давления
Температурное расширение — свойство жидкости изменять свой объем при изменении температуры. С ростом температуры объем жидкости увеличивается и наоборот. Различные жидкости при увеличении температуры на одну и ту же величину увеличиваются в объеме по разному.
- Пластичные жидкости. Ньютоновские жидкости.
| Пластичные жидкости в статических условиях ведут себя как твердые материалы, но при воздействии на них определенной силой они начинают течь. Минимальное усилие, которое необходимо приложить к системе, чтобы она начала течь называется предельным напряжением сдвига (f’). | |
|
|
| Томатный кетчуп является ярким примером пластичных жидкостей: пока бутылку с продуктом не потрясти или ударить по ней, кетчуп течь не будет. После преодоления критического напряжения сдвига пластичные жидкости могут вести себ я как ньютоновские, псевдопластичные или дилатантные. |
Жидкости, для которых вязкость не зависит от скорости деформации, называются ньютоновскими. Характерными ньютоновскими жидкостями являются вода и маловязкие моторные топлива.
Поведение ньютоновских жидкостей отлично видно на графиках зависимости напряжения сдвига (А) или вязкости (В) от скорости сдвига.
На практике это означает, что вязкость жидкости при данной температуре остается постоянной и не зависит от модели вискозиметра, шпинделя или скорости сдвига. Стандарты вязкости Brookfield являются также ньютоновскими жидкостями и подходять для всех моделей вискозиметров Brookfield.
Для неньютоновских жидкостей вязкость изменяется при изменении скорости сдвига. Для этих жидкостей модель вискозиметра, шпиндель и скорость сдвига влияют на конечный результат; для неньютоновских жидкостей измереяется, так называемая, «кажущаяся вязкость». Точности и воспроизводимости результатов для таких жидкостей можно достичь только при воспроизведении всех параметров измерений (модели вискозиметра, шпинделя, температуры и т.д.).
- Гипотеза сплошности среды. Длина свободного пробега молекул.
Гипотеза сплошности: тело называется сплошным, если в любом бесконечно малом объеме содержится бесконечное количество материальных точек.
Длина свободного пробега молекулы — это среднее расстояние {displaystyle lambda }, которое пролетает частица за время между двумя последовательными столкновениями
- Закон Ньютона. Динамическая вязкость. Кинематическая вязкость. Гипотеза Ньютона о вязкостном трении. Вязкость в условных градусах Энглера.
Первый закон Ньютона: закон инерции
Определение
Если на тело не действуют внешние силы, то покоящееся тело будет оставаться в покое, а движущееся тело останется в равномерном движении по прямой.
Второй закон Ньютона: основной закон динамики
Определение
Существует связь между силой (F), которая действует на тело (массы m), и ускорением (a). Тело приобретает ускорение из-за действующей на него силы.
Третий закон Ньютона: закон равенства действия и противодействия
Определение
На каждое действие существует равное и противоположное противодействие/реакция.
Динамическая вязкость
Динамическая вязкость определяет величину сопротивления текучести жидкости при перемещении ее слоя площадью 1 см2 на расстояние в 1 см со скоростью 1 см/сек. В СИ (Международной системе единиц) данный показатель измеряется в Па•с (паскаль•секунда). В системе же СГС единицей измерения вязкости является пуаз (в честь Ж. Пуазейля, французского физика).
Чем выше вязкость жидкости, тем, соответственно, больше время ее истечения. Например, чем дольше по времени краска, нефть, смола, мед или любая другая жидкая среда будет вытекать через воронку, тем больше будет вязкость данного вещества.
С точки зрения физики динамическая вязкость обозначает потерю давления за единицу времени (поэтому в системе СИ этот параметр и измеряется в Па•с). У жидкостей данный параметр снижается при росте температуры (то есть когда среда нагревается, она течет легче) и повышается при увеличении давления.
Кинематическая вязкость
Кинетическая вязкость — это соотношение коэффициента динамической вязкости жидкости к ее плотности. В системе СИ эта величина выражается в м2/с, а в системе СГС — в стоксах (Ст).
Кинетическая вязкость у жидкостей демонстрирует, насколько легко способно течь данное вещество. В практическом применении это связано с тем, насколько продукт густой. На данный показатель температура влияет несколько меньше, нежели на абсолютную вязкость, ведь тепло также уменьшает и плотность (при нагревании молекулы смещаются дальше друг от друга).
Условная вязкость (ВУ) — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма жидкости через вертикальную трубку определённого диаметра. Условная вязкость измеряется в градусах Энглера, и определяется отношением времени истечения 200 см3 испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 см3 дистиллированной воды из того же прибора при +20 градусах Цельсия.
- Поверхностное натяжение жидкостей, формула Лапласа. Поверхностное натяжение в капиллярных трубках.
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
- Свойства напряжений поверхностных сил.
1 св-во: напряжения поверхностных сил, действующих по произвольной площадке в данной точки жи/ти, зависят от девяти скалярных величин: 3 нормальных напряжений (Рхх , Руу, Рzz ) и 6 касательных (τху, τ xz, τyz, τyx, τzx, τzy). 2 св-во: если в жи/ти отсутствуют касательные напряжения, то нормальные напряжения в данной точке не зависят от ориентации площадки. 3 св-во: капельная жи/ть способна воспринимать произвольные сжимающие усилия (отрицательное нормальное напряжение) без разрыва сплошности. Однако жи/ть практически терпит разрыв при растяжении, то есть в ней могут провялятся лишь нормальные сжимающиеся усилия
- Основные понятия о движении жидкости (живое сечение, смоченный периметр, расход, скорость, гидравлический радиус. Установившееся и неустановившееся движение).
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения..
Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками
Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.
Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω
Гидравлический радиус потока R — отношение живого сечения к смоченному периметру
Установившееся – это такое движение, при котором его характеристики в лю-бой точке потока остаются неизменными во времени, средняя скорость υ, давление в любом сечении р, форма струи не меняются во времени.
Неустановившееся движение — это такое движение, когда скорость и давление в каждой точке изменяются с течением времени, т. е. являются функция-ми координат и времени.
- Идеальная жидкость. Общая интегральная форма уравнений количества движения и момент количества движения.
Идеа́льная жи́дкость — в гидродинамике — воображаемая жидкость (сжимаемая или несжимаемая), в которой отсутствует вязкость. Из-за отсутствия вязкости в ней нет касательных напряжений между двумя соседними слоями жидкости[1].
Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.
При решении некоторых задач МЖГ используется уравнение количества движения. Важнейшей особенностью этого уравнения является то, что для определения действующих сил не нужно знать существа процессов, происходящих внутри выделенного участка потока жидкости, нужно знать только параметры жидкости на границах участка. В механике твердого тела известна теорема об изменении количества движения. Она гласит: элементарное изменение количества движения некоторой массы m по какому-либо направлени. равно элементарному импульсу равнодействующей сил, приложенных к этой массе в том же направлении, т.е. d(mñ) = F dt,
Уравнение момента количества движения не является новым независимым уравнением гидрогазодинамики. Оно представляет новую форму уравнения движения, членами которого являются не силы и не количество движения, а моменты сил и моменты количества движения. Это уравнение широко используется при исследовании вращательного движения жидкости, является основным в теории турбомашин.
Уравнение момента количества движения для жидкого объема так же, как и для твердого тела, устанавливает, что момент равнодействующей внешних сил относительно произвольной оси равен полной производной по времени от суммарного момента количества движения относительно той же оси, т. е.
| r | r | d | r r | |||
| ∑F × r | = | (∑mc × r ), | (4.6) | |||
| dt | ||||||
где r – радиусы векторы внешних сил и элементарных масс, имеющих скорости c ; mc × r – момент количества движения элементарной массы т.
- Реальная жидкость. Интегральная форма количества движения и момента количества движения.
Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).
- Уравнение неразрывности течения (уравнение постоянства расхода).

- Ламинарное и турбулентное течение жидкости. Критерий Рейнольдса.
Ламинарное (слоистое) течение – это такое течение, при котором слои жидкости текут, не перемешиваясь, скользя друг относительно друга. Ламинарное течение является стационарным, т.е. скорость течения в каждой точке пространства остается постоянной.
Турбулентное (вихревое) течение – это такое течение, при котором скорости частиц жидкости в каждой точке беспорядочно меняются. Турбулентное течение — это хаотическое, крайне нерегулярное, неупорядоченное течение жидкости.
- Ламинарное течение жидкости в круглой трубе с прямой осью.
- Турбулентное течение, гипотеза связи пульсационных составляющих со средней скоростью потока.
- Установившееся и неустановившееся движение жидкости.
Установившееся – это такое движение, при котором его характеристики в лю-бой точке потока остаются неизменными во времени, средняя скорость υ, давление в любом сечении р, форма струи не меняются во времени.
Неустановившееся движение — это такое движение, когда скорость и давление в каждой точке изменяются с течением времени, т. е. являются функция-ми координат и времени.
- Линии тока и траектории.
Линией тока называется линия, касательная к каждой точке которой совпадает по направлению с вектором скорости в данный момент времени.
Семейство линий тока дает картину течения в данный момент времени, можно сказать, моментальный снимок направлений скоростей потока.
Через каждую точку пространства может проходить множество траекторий частиц, они могут пересекаться и пересекать сами себя.
Линии тока не пересекаются ни сами с собой, ни с другими линиями тока, так как вектор скорости в одной точке пространства не может иметь два разных значения в данный момент времени. Исключение составляют лишь особые точки, в которых скорость V = 0 (критические точки или точки торможения) или V = ∞ (исток, сток)
Необходимо четко представлять разницу между линией тока и траекторией движения частицы. Если траектория отражает изменение положения частицы с течением времени, то линия тока указывает направление скоростей разных частиц в один и тот же момент времени. И только при установившемся движении линия тока совпадает с траекторией частицы. В этом случае траектории всех частиц, проходящих через какую-либо точку пространства, будут одинаковыми, следовательно, в каждый момент времени все частицы, которые лежат на траектории, будут образовывать и линию тока. В случае неустановившегося движения линии тока и траектория частицы не совпадают.
- Трубка тока (поверхность тока).
Трубка тока – простой и наглядный кинематический образ. Разбив весь поток на достаточно узкие трубки тока, можно, пользуясь основным свойством трубки – непроницаемостью ее боковой поверхности, изучать бесконечно малые перемещения выделенного объема жидкости. Между двумя произвольными линиями тока количество протекающей жидкости постоянно, поскольку вектор скорости лежит в касательной плоскости к поверхности трубки тока. То же самое можно сказать и о трубке тока: расход жидкости через любое сечение трубки тока одинаков.
Поверхность тока – поверхность, построенная для фиксированного момента времени, в каждой точке которой вектор скорости лежит в касательной плоскости. Если выделить в движущейся жидкости некоторый бесконечно малый замкнутый контур, через каждую точку которого можно провести линию тока, то совокупность всех линий тока образует замкнутую поверхность – трубку тока (рис. 2.2). Жидкость, движущуюся внутри трубки тока, называют элементарной струйкой.
- Уравнение Д. Бернулли для движения идеальной жидкости.
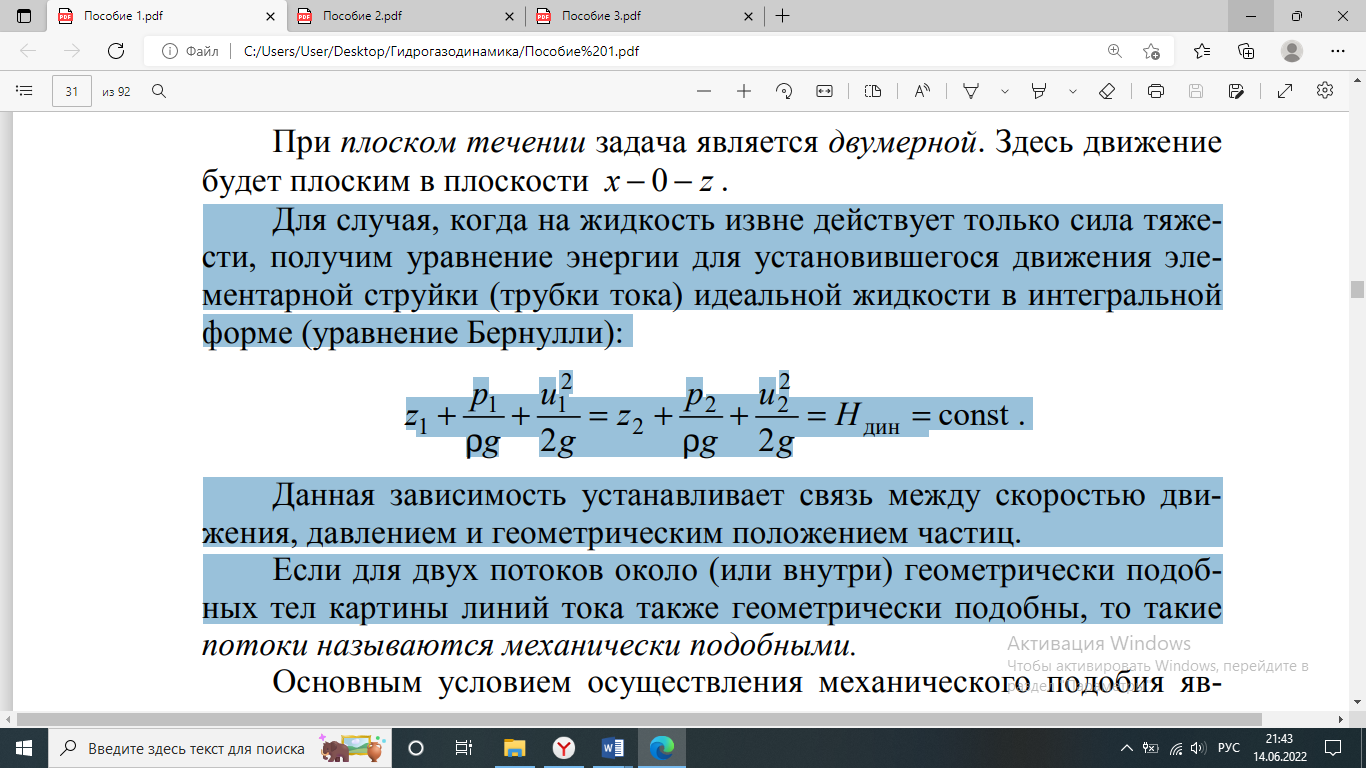
- Уравнение Д. Бернулли для движения реальной жидкости. Физический и геометрический смысл уравнения Д. Бернулли.
- Одномерные потоки жидкости и газа.
- Модели турбулентных течений. Уравнения Рейнольдса для турбулентных потоков.
- Уравнения Навье-Стокса.
- Измерение скорости потока в открытом канале и закрытых трубопроводах. Трубка Пиго- Прандтля.
Поток в открытом канале описывает случаи, когда верхняя поверхность текущей жидкости открыта для воздуха; поперечное сечение потока определяется только формой канала на нижней стороне и изменяется в зависимости от глубины жидкости в канале. Методы, подходящие для фиксированного поперечного сечения потока в трубе, не полезны в открытых каналах. Измерение расхода в водных путях является важным приложением для измерения расхода в открытых каналах; такие установки известны как измерители потока.
Level to flow[править/ править код]
Уровень воды измеряется в специально отведенной точке за водосливом или в лотке с использованием различных вспомогательных устройств (барботеры, ультразвуковые, поплавковые и дифференциальные давления являются распространенными методами). Эта глубина преобразуется в скорость потока в соответствии с теоретической формулой вида{displaystyle Q=KH^{X}}, где {displaystyle Q}— скорость потока, {displaystyle K}— постоянная, {displaystyle H}— уровень воды, и {displaystyle X} показатель степени, который изменяется в зависимости от используемого устройства; или он преобразуется в соответствии с эмпирически полученными точками данных уровня / расхода («кривая расхода»). Затем скорость потока может быть интегрирована с течением времени в объемный расход. Устройства от уровня до расхода обычно используются для измерения расхода поверхностных вод (родников, ручьев и рек), промышленных сбросов и сточных вод. Из них водосливы используются на потоках с низким содержанием твердых частиц (обычно поверхностных вод), в то время как желоба используются на потоках с низким или высоким содержанием твердых частиц.[17]
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Трубка Пито — Прандтля — прибор для измерения скорости течения жидкости или газа, основанный на одновременном измерении полного и статического давлений в какой либо точке потока
- Измерение расхода потока в каналах произвольных сечений с помощью водомера Вентури.

- Гидравлические сопротивления. Потери напора на трение по длине трубопровода. Формула Дарси-Вейсбаха.
Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:
Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.
Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.
- Основные понятия и определения пограничного слоя.
Пограничным слоем называется область течения, где силы вязкости соизмеримы с силами инерции. Различают пристенный пограничный слой (ПС) – слой жидкости, непосредственно прилегающий к твёрдой поверхности, и свободный ПС – аэродинамический след за обтекаемым телом, в котором силы вязкости существенны. Внешний поток – область течения, где можно пренебречь силами вязкости и считать жидкость идеальной. Уравнения, описывающие движение жидкости во внешнем потоке, более простые, чем уравнения Навье – Стокса, уравнения Эйлера.
- Ламинарный пограничный слой на пластине.
- Критическое число Рейнольдса. Отрыв пограничного слоя.
Отрыв пограничного слоя (англ. Boundarylayerseparation) — явление отсоединения слоя вязкого потока жидкости (газа) от обтекаемой им поверхности.
Точка отсоединения пограничного слоя называется точкой отрыва. В области между отсоединившимся пограничным слоем и обтекаемой поверхностью развивается возвратно-вихревое (не обязательно вязкое) течение.
- Уравнение пограничного слоя в интегральной форме.
- Переход ламинарного пограничного слоя в турбулентный.
- Турбулентный пограничный слой на пластине.
- Распределение скоростей по сечению потока. Особенности движения жидкости в началь ном участке трубы.
При ламинарном движении жидкости в цилиндрической трубе распределение скоростей по сечению имеет вид параболы и схематически изображается телескопическим (рис.): у стенок трубы скорости равны нулю, а при удалении плавно возрастают и достигают максимального значения на оси трубы.
- Местные потери напора в трубах. Гидравлический удар.
Местные потери напора — это потери, обусловленные местными гидравлическими сопротивлениями, то есть такими элементами трубопроводов, в которых вследствие изменения поперечных размеров или конфигурации происходит деформация потока.
Гидравлический удар – это резкое повышение давления в трубопроводах и каналах с движущейся жидкостью при внезапном изменении скорости потока. Это сложный динамический волновой процесс образования упругих деформаций жидкости и их распространения по длине трубопровода.
Гидравлический удар создает ударную волну в виде распространяющегося в жидкости фронта резкого, почти мгновенного изменения ее параметров — давления и скорости. С явлением гидравлического удара приходится сталкиваться при быстром срабатывании задвижек, когда резкое прекращение тока жидкости вызывает в трубопроводе волну повышенного давления, что зачастую приводит к разрыву стенок.
- Потери напора при внезапном (резком) изменении сечения трубопровода.
- Расчет длинных трубопроводов при квадратичном законе сопротивления.
- П
отери напора при постепенном изменении сечения трубопровода.
- Потери напора при повороте трубы.

- Местные потери в трубах при малых числах Рейнольдса. Взаимное влияние местных со противлений.

- Кавитация в местных сопротивлениях.

- Простые трубопроводы. Методика расчета.
Трубопровод называют простым, если жидкость транспортируется по нему от питателя к приемнику без ответвлений потока, но может иметь различные диаметры и включать местные сопротивления.
Имеем простой трубопровод с постоянным диаметром , который работает под напором
.
Рис. 41 Схема расчета прямого трубопровода (случай первый)
Для сечений 1 — 1 и 2 — 2 напишем уравнение Бернулли:
.
Так как
, давление
, тогда уравнение примет вид:
(119)
Так как мы имеем гидравлически длинный трубопровод, то пренебрегая местным сопротивлением, получим
(120)
где и
.
- Сложные трубопроводы. Методика расчета.
Трубопроводы, содержащие последовательные, параллельные соединения и разветвления простых трубопроводов называются сложными.
Гидравлический расчет трубопроводов производят по методикам:
1) удельных гидравлических сопротивлений;
2) удельных потерь напора на трение;
3) приведенного коэффициента местного сопротивления на трение;
4) приведения местных сопротивлений к линейным.
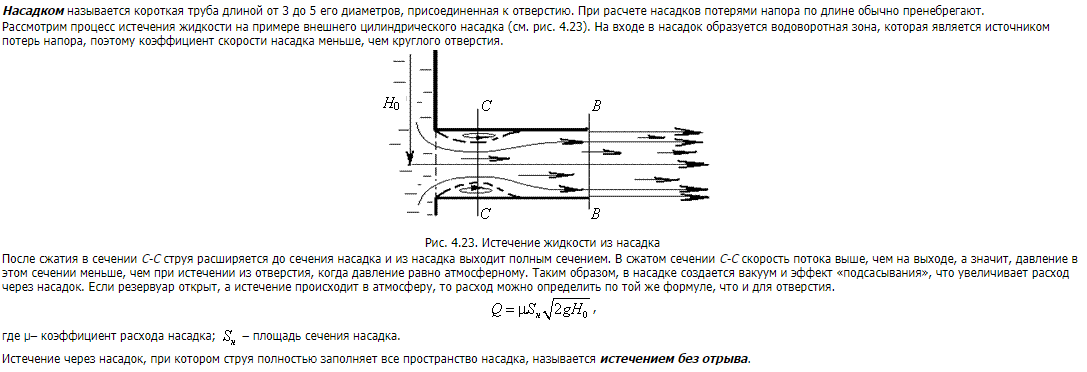
- Истечение жидкостей через отверстия и насадки.
Истечение жидкости через отверстие может происходить при постоянном и переменном напоре. Если истечение жидкости через отверстие происходит в атмосферу или другую газовую среду, то такое отверстие называется незатопленным. Если же истечение идет под уровень, а не в атмосферу – затопленным.
При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи. Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.
При истечении жидкости, через отверстие в тонкой стенке на некотором расстоянии от стенки (l = do), происходит сжатие струи. Площадь живого сечения струи будет меньше площади отверстия. Это объясняется тем, что частицы жидкости при входе в отверстие имеют скорости различных направлений.
С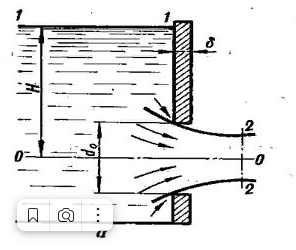
- Определяющие параметры газовых потоков. Скорость звука.
Параметры газового потока ( скорость, давление, температура) по окружности газового тракта всегда имеют некоторую неравномерность. Такой же след оставляют разделительные стойки на входе в компрессор. Температура газа обычно имеет несколько пиков, соответствующих числу камер сгорания. К неравномерности параметров газового потока приводит также несимметричность входа в компрессор, наличие окон для отбора или перепуска воздуха, стойки на выходе из турбины, ограниченные размеры испытательного бокса и другие конструктивные особенности установки.
Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).
Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.
Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.
- Сопло Лаваля для получения сверхзвуковых скоростей.
- Прямые скачки уплотнения.
- Косые скачки уплотнения.
- Тепловые и конденсационные скачки в потоке.
- Основы расчетов двухкомпонентных и двухфазных течений, фазовое равновесие в потоке.
Шпоры — Основы гидрогазодинамики — файл n1.rtf
приобрести
Шпоры — Основы гидрогазодинамики
скачать (6288.1 kb.)
Доступные файлы (1):
n1.rtf
Экзаменационные вопросы по курсу «Гидрогазодинамика»
1. Силы, действующие в жидкости
2. Методы изучения движения жидкости
3. Траектория, линия тока, трубка тока, струя
4. Градиент, дивергенция, циркуляция, вихрь
5. Основная теорема кинематики (первая теорема Гельмгольца)
6. Тензор скоростей деформации
7. Уравнение сплошности
8. Нормальное и касательное напряжение, действующие в движущейся жидкости
9. Уравнение движения сплошной среды в напряжениях
10. Напряжения, действующие в идеальной жидкости
11. Уравнение движения идеальной жидкости (Эйлера)
12. Уравнение движения идеальной жидкости (Эйлера) в форме Громека
13. Теорема Бернулли
14. Основные понятия и определения потенциальных течений
15. Комплексный потенциал, комплексная скорость
16. Частные случаи плоских потенциальных течений
17. Безциркуляционное обтекание круглого цилиндра
18. Обобщенный закон Ньютона
19. Уравнения движения вязкой несжимаемой жидкости (Навье-Стокса)
20. Подобие гидродинамических явлений
21. Критериальные уравнения. Критерии и числа подобия
22. Моделирование ГГД явлений
23. Ламинарное и турбулентное движение
24. Пограничный слой и его характерные толщины
25. Переход ламинарного ПС в турбулентный
1. Силы, действующие в жидкости
В жидкостях могут существовать только распределенные силы: массовые (объемные) и поверхностные.
1) Массовые силы действуют на каждую точку выделенного объема ? и пропорциональны массе частиц. Например, сила тяжести, центробежное ускорение, сила электростатического напряжения, сила Кориолиса и т.д.
Массовые силы характеризуются вектором плотности массовых сил:
,
который представляет собой предел отношения главного вектора массовых сил к массе частицы при стремлении массы к нулю.
В проекциях на координатные оси он может быть записан:
X, Y, Z – проекции на координатные оси.
2) Поверхностные силы характеризуются напряжениями:
— это предел отношения главного вектора поверхностной силы, приложенного к и величине этой площадки при стремлении ее к нулю. Величина напряжения зависит от выбора направления площадки.
— нормальное напряжение
— касательное напряжение
2. Методы изучения движения жидкости
Существует два метода изучения движения жидкости: метод Эйлера и метод Лагранжа.
1. Метод Лагранжа: выделяется частица в движущейся жидкости и исследуется ее траектория в зависимости от координат и времени.


a, b, c – это постоянные, которые определяют положение точки в начальный момент времени.
2. Метод Эйлера: задается метод распределения скорости в потоке в зависимости от координат и времени:

x, y, z –переменные Эйлера.
Чтобы определить скорости в какой-либо точке надо задать ее координаты. Поле ускорений потока можно получить если продифференцировать систему (3):
Получили систему, описывающую поле ускорений.
Локальные ускорения, показывающие как изменяется скорость в какой-либо точке потока с течением времени ().
Конвективные ускорения (все остальное в правой части), связанные с перемещением точки или среды (т.е. с конвекцией). Течение может быть стационарным или нестационарным (изменяется во времени). Для стационарных задач локальные ускорения равны нулю. Самые простые течения стационарные, плоские и одномерные. Для стационарной и плоской задачи исследуется течение только по двум координатам. Еслирассматривается одномерная стационарная задача, тогда:
3. Траектория, линия тока, трубка тока, струя
Траектория – это линия, изображающая путь пройденный частицей за определенный промежуток времени.
Линия тока – это мгновенная векторная линия, в каждой точке которой в данный момент времени касательная по направлению совпадает с вектором скорости.
В стационарных задачах линии тока и траектории совпадают, т.к. нормальная составляющая скорости к линии тока равна нулю, жидкость через линию тока не перетекает. В плоских течениях количество жидкости между двумя линиями тока в любых сечениях будет одинаково. Если линии тока приближаются, то скорость потока увеличивается, и наоборот. Через каждую точку в потоке можно провести только одну линию тока, исключение составляют особые точки: критические точки. А и В – это критические точки. Поверхность непроницаемого тела – поверхность тока, а линии тока, расположенные на поверхности называется нулевыми линиями тока.
Если в жидкости провести замкнутый контур и через каждую точку провести линию тока, получим поверхность тока. Жидкость внутри поверхности называется трубкой тока. Через поверхность тока жидкость не перетекает, следовательно через каждое сечение трубки тока проходит одно и то же количество жидкости. Если через каждую точку контура провести траекторию, то часть жидкости, которая ограничена поверхностью траектории называется струей. Струя совпадает с трубкой тока в стационарном течении.
4. Градиент, дивергенция, циркуляция, вихрь
1. Градиент.
Рассмотрим действие векторного оператора Гамильтона на скалярную функцию ?. Скалярная величина – это параметр, которому нельзя придать направление.
Градиент скалярной функции – это вектор направленный по нормали к линии постоянного значения в сторону возрастания функции и модуль его равен частной производной от функции по направлению указанной нормали.
2. Дивергенция.
Рассмотрим скалярное умножение векторного оператора и двух величин скорости:
Дивергенция является скалярной величиной, показывает расхождение вектора скорости, определяет закон относительного изменения объема. Например, если течение стационарное и жидкость несжимаемая, то при в жидкости отсутствуют источники или стоки. При
имеется источник, при
имеется сток. Уравнение
часто используется для замыкания системы уравнений движения несжимаемой жидкости и является уравнением сплошности.
3. Циркуляция.
Характеризует интенсивность вращательного движения жидкости.
Вычисляется, например, по контуру АВ:
— элемент контура АВ
4. Вихрь вектора скорости.
Рассмотрим векторное произведение оператора на вектор скорости:
Рассмотрим вращение точки вокруг оси, проходящей через начало координат с угловой скоростью .
Если в жидкости , это указывает на наличие вращающихся объемов, вихрей жидкости. Интерес представляют течения для которых
, такие течения называются безвихревыми или потенциальными,. Т.к. в этом случает существует потенциал вектора скорости ?, который связан с составляющими вектора скорости следующими соотношениями:
;
;
;
5. Основная теорема кинематики (первая теорема Гельмгольца)
Из теоретической механики известно, что скорость движения любой точки твердого тела складывается из поступательного вместе с некоторым полюсом и вращательного движения вокруг оси, проходящей через этот полюс: . Для жидкой частицы основная теорема кинематики гласит, что скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и деформационного. Квазитвердое состоит из поступательного вращательного:
. Для доказательства рассмотрим движение точки М с координатами x, y, z, которая находится в окрестности точки М0 (x0, y0, z0) и составляющая для точки М0 скорости (u0, ?0, w0), тогда раскладывая функцию скорости в ряд Тейлора и сохраняя компоненты первого порядка малости, составляющие скорости для точки М можно записать:

Преобразуем первое уравнение. Для этого разноименные части представим следующим образом:
;

— первая теорема Гельмгольца квазитвердое движение деформационное движение
6. Тензор скоростей деформации
Компоненты , входящие в скорость деформации, могут быть представлены в виде матрицы, которая называется тензором скоростей деформации:
— диагональные компоненты.
Тензор симметричен относительно главной диагонали
Рассмотрим диагональные компоненты. В жидкости выделим отрезок АВ длиной dx (отрезок на оси х). Рассмотрим перемещение отрезка вдоль оси х. Скорости в точках А и В не равны. Через время dt отрезок займет положение . Произошла линейная деформация отрезка АВ на величину:
Если разделим линейную деформацию на длину отрезка:
скорость линейной деформации – скорость растяжения или сжатия линейного отрезка расположенного на оси х в направлении оси х. Аналогично:
скорости относительных линейных деформаций вдоль соответствующих осей. Сумма диагональных компонент определяет дивергенцию вектора скорости, т.е.
закон относительного изменения объема.
Рассмотрим перемещение отрезка АВ расположенного на оси х и длиной dx в направлении оси dy).
Ввиду малости угла
угловая деформация линейного отрезка в направлении оси у.
скорость угловой деформации или скорость скашивания в направлении оси у. Если отрезок расположить на оси у, то — скорость скашивания в направлении оси х.
— средняя скорость угловой деформации в плоскости ху.
Таким образом недиагональные компоненты характеризуют скорости скашивания или угловых деформаций в соответствующих плоскостях.
7. Уравнение сплошности
Уравнение сплошности – это уравнение закона сохранения массы:
Выделим в жидкости элементарный объем с плотностью ?.
Следовательно:
Второй член полученного уравнения выражает закон относительного изменения объема,. Т.е. дивергенцию.
Плотность в общем случае зависит от координат и времени:
Поэтому:
уравнение сплошности (неразрывности).
Если течение стационарное, то уравнение упрощается:
Если жидкость несжимаемая, т.е. , то
8. Нормальное и касательное напряжение, действующие в движущейся жидкости
Закон сохранения количества движения для неизолированной системы может быть записан в виде:
где — главный вектор количества движения системы
— главный вектор внешних сил, действующих на систему
В жидкости выделим элементарный тетраэдр с гранями ,
,
,
. Индекс показывает перпендикулярно какой оси расположены грани,
— наклонная грань. К граням приложены соответствующие напряжения
,
,
,
(не перпендикулярные граням). Масса тетраэдра
. На тетраэдр действуют массовые и поверхностные силы. Массовые характеризуются вектором плотности
, поверхностные – напряжениями.
— скорость центра инерции тетраэдра
— третий порядок малости
— второй порядок малости
Членами третьего порядка малости пренебрегаем.
и т.д.
пх
Получим связь напряжений, действующих на грани выделенного тетраэдра:
В проекциях на координатные оси это уравнение может быть переписано:
В записанной системе называются нормальными напряжениями, а
и т.д. называются касательными напряжениями. Все напряжения могут быть записаны в матричной форме в виде симметричного тензора напряжений:
Первый индекс определяет ось, относительно которой расположена грань, второй – ось на которую проецируется напряжение.
9. Уравнение движения сплошной среды в напряжениях
Рассмотрим элементарный параллелепипед с ребрами . Объем его
. На него действуют массовые и поверхностные силы определяемые главным вектором внешних сил
. К параллелепипеду применим закон сохранения количества движения:
Для определения главного вектора поверхностных сил рассмотрим все силы, дающие проекцию на ось х. Для граней перпендикулярных х проекцию дают только силы, создаваемые нормальными напряжениями. Поэтому равнодействующая этих сил равна:
Аналогично для граней перпендикулярных z получим равнодействующую равную:
Равнодействующая поверхностных сил в проекции на ось х равна:
Тогда закон сохранения количества движения в проекции на х можно записать:
Полученная система называется системой уравнений движения сплошной среды в напряжениях. В левой части стоит полная производная от скоростей, которые могут быть расписаны через локальные и конвективные составляющие ускорения. При определенных условиях левая часть значительно упрощается (стационарное, двухмерное или одномерное течение).

систему можно записать в виде одного уравнения в векторной форме записи:
10. Напряжения, действующие в идеальной жидкости
В идеальной жидкости отсутствуют силы трения, следовательно касательные напряжения равны нулю. Применительно к элементарному тетраэдру проекция напряжения, приложенного к произвольной наклонной грани на ось х равна:
С другой стороны:
Аналогично для проекций на у:
и
Таким образом в идеальной жидкости величина нормального напряжения в любой точке не зависит от направления площадки к которой напряжение приложено. В идеальной жидкости величина нормального напряжения в точке называется гидродинамическим давлением в этой точке. Модель идеальной жидкости упростила постановку и решение многих задач, в которых влиянием сил трения можно пренебречь.
Знак «минус» ставится, т.к. жидкость оказывает давление на выделенный объем в направлении противоположном внешней нормали.
11. Уравнение движения идеальной жидкости (Эйлера)
Для вывода воспользуемся уравнениями движения в напряжениях:

Справедлива, как для сжимаемой, так и для несжимаемой жидкости. Если жидкость сжимаемая, то необходимо ввести функцию координаты от времени:
Если жидкость несжимаемая, то
12. Уравнение движения идеальной жидкости (Эйлера) в форме Громека
Все преобразования выполним на первом уравнении:
Отсюда:

— система уравнений движения для и.ж. в форме Громека
Рассмотрим далее движение, предполагая, что массовая сила имеет потенциал и течение баротропное.
Первое предположение утверждает, что у массовых сил имеется потенциал, связанный соотношениями с массовыми силами:
;
;
,
U — потенциал массовых сил.
Второе: баротропным считается течение, у которого ? считается только функцией давления.
Например, баротропными течением является:
- ?=const – газ или жидкость несжимаемы
- движение среды изотермическое —
- движение среды адиабатное —
Условие баротропности предполагает, что существует некоторая функция Р, зависящая от давления, которая определяется выражением:
Функция Р связана с р и ? соотношениями:
;
;
.
Подставим в систему уравнений Громека потенциал массовых сил и функцию Р:

— система уравнений Эйлера в форме Громека
Достоинство системы заключается в том, что отдельно выделен ротор, который при определенных условиях может быть равен нулю и система значительно упрощается. Последний член равен нулю, если: 1) — статическая задача; 2)
— течение безвихревое или потенциальное.
Сумма, стоящая во второй компоненте, имеет определенный физический смысл. В векторной форме система может быть записана в виде одного уравнения:
13. Теорема Бернулли
Рассмотрим стационарное баротропное течение под действием массовых сил, т.е. можно записать:
умножим уравнение скалярно на вектор скорости, тогда последний член равен нулю, т.к. идет скалярное перемножение перпендикулярных векторов.
— единичный вектор в направлении вектора скорости. Вектор скорости направлен по касательной к линии тока или к траектории, т.к. течение стационарное, следовательно:
— производная по направлению.
выражение отражает теорему Бернулли: при стационарном баротропном течении идеальной жидкости под действием потенциальных массовых сил сумма кинетической энергии единицы объема, функции давления приведенного к единице массы потенциала массовых сил сохраняет постоянное значение вдоль любой линии тока.
Если бы скалярно умножили исходное уравнение на вектор угловой скорости, то получили бы аналогичный результат вдоль вихревой линии.
Если течение потенциальное, то и сразу же получается:
и
во всем потоке, т.е. трехчлен Бернулли сохраняет постоянное значение во всей области потенциального потока.
Рассмотрим потенциальное течение несжимаемой жидкости под действием сил тяжести. Т.к. жидкость несжимаема то :
У сил тяжести потенциал равен: , z – координата.
(1),
— удельный вес
Все эти составляющие имеют размерность давления и называются напорами: — скоростной или динамический напор; р – пьезометрический напор;
— геометрический напор; ро – полный напор
При стационарном течении идеальной несжимаемой жидкости полный напор, равный сумме , сохраняет постоянное значение вдоль любой линии тока, а при потенциальном течении во всей области потока.
В задачах, в которых можно пренебречь влиянием геометрического напора, уравнение Бернулли упрощается и приобретает вид:
Уравнение (1) разделим на , тогда:
все компоненты измеряются в метрах и называются высотами: — скоростная высота,
— пьезометрическая высота, z – нивелирная высота, Н – гидравлическая высота. При стационарном движении идеальной несжимаемой жидкости высота
сохраняет постоянное значение вдоль любой линии тока (или вихревой линии), а при потенциальном течении во всем токе.
14. Основные понятия и определения потенциальных течений
Потенциальные течения – это течения, у которых во всем потоке, следовательно существует функция ?, называемая потенциалом, зависит ?(х,у,z,t) и связана с составляющими U соотношениями:
то есть
Записанные соотношения могут быть записаны и для любой другой функции, которая отличается от ? на константу: . Таким образом, уравнение потенциала определяется с точностью до константы. Геометрическое место точек с одинаковым значением ? образуют эквипотенциальные поверхности, уравнения которых:
. Так как
, следовательно вектор U расположен по перпендикулярам в любой точке эквипотенциальной поверхности. Так как вектор U касателен к линии тока, то линии тока перпендикулярны эквипотенциальной поверхности.
Рассмотрим стационарное плоское течение, то есть , тогда
и
.
Уравнение сплошности имеет вид:
Таким образом, потенциал U удовлетворяет уравнению Лапласа, следовательно является гармонической функцией.
Введем в рассмотрение функцию ?, связанную с составляющими U уравнениями:
и
Функция ? удовлетворяет уравнению сплошности, т.к.
? – функция тока, она также определяется с точностью до постоянной.
Уравнение называется уравнением линии тока.
В плоских течениях эквипотенциальные поверхности дают проекции на плоскость (х,у) в виде линии, поэтому часто в задачах рассматриваются эквипотенциальные линии которые перпендикулярны линии тока.
В потенциальном потоке , в плоском течении
функция тока ? гармоническая
Сравнение потенциала ? и ? позволяет записать:
—
условие Коши-Римана.
15. Комплексный потенциал, комплексная скорость
Из теории комплексной переменной известно, что если две функции ? и ?, зависящие от х и у, удовлетворяют условиям Коши-Римана, то комплексная величина будет не просто зависеть, а являться функцией от комплексной переменной
, то есть существует некоторая функция
, действительной частью которой является ?, а мнимой ?.
.
Функция имеет большое значение при изучении плоских потенциальных течений и называется комплексным потенциалом или характеристической функцией течения.
Так как является аналитической функцией от
, то ее производная не зависит от направления дифференцирования, а зависит только от положения точки в пространстве, то есть
по условию Коши-Римана:
Если вектор U разложить в комплексной плоскости годографа U, то .
Производная от комплексного потенциала дает зеркальное изображение комплексной U относительно действительной оси. Обозначим ее как
.
В теории комплексной переменной числа и
называют сопряженными, назовем
как сопряженную U. Таким образом, производная от комплексного потенциала определяет
.
Таким образом, если изменяется какое-то плоское потенциальное течение, то для него можно подобрать уравнение комплексного потенциала, проанализировать его и просчитать составляющие U в любой точке. С другой стороны для любого потенциала можно определить вид течения.
Экзаменационные вопросы по курсу «Гидрогазодинамика»
Всего 43 файла:
Расширенный поиск
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Книга, 2 курс, 4 семестр, *.pdf
Гидрогазодинамика, Учебное пособие, Г.П. Дикий, О.Н. Остряков (1989) МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Книга, 2 курс, 4 семестр, *.pdf халява проверен
Учебное пособие Авторы: Г.П. Дикий, О.Н. Остряков
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 2 курс, 4 семестр, *.pdf
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.pdf
МЭИ, ИДДО, Гидрогазодинамика, Лекции, 4 курс, *.pdf
Лекция 1. Энергетические системы (2019) МЭИ, ИДДО, Гидрогазодинамика, Лекции, 4 курс, *.pdf халява проверен
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.rar
5 типарь мой (2017) МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.rar халява проверен
Типовой №5, лектор Дмитриев С.С.
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Экзамен, 3 курс, 5 семестр, *.zip
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.rar
3 типовой ггд в MathCad (2017) МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.rar проверен
Лектор Дмитриев
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.pdf
Mathcad — типовой 2б.pdf (2017) МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 3 курс, 5 семестр, *.pdf халява проверен
типовой расчет 2б (по соплам) 19 варианта
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Контрольная, 2 курс, 4 семестр, *.zip
Задачи из контрольной (2016) МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Контрольная, 2 курс, 4 семестр, *.zip не проверен
Задачи Нитусова из контрольной
МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
5 лаба. Ипээф (2016) МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar не проверен
Фото рукописной лабы.
МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
7 лаба. ИПЭЭФ (2016) МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar не проверен
Фото рукописной лабы.
МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
16 Лаба.ИПЭЭф (2016) МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar не проверен
МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
3 лаба.ИПЭЭф (2016) МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar не проверен
Фото рукописной лабы.
МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
2 лаба.ИПЭЭф (2016) МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar не проверен
Фото рукописной лабы.
МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
1 лаба.ИПЭЭф (2016) МЭИ, ИЭВТ (ИПЭЭф), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar не проверен
Фото рукописной лабы.
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Методичка, 2 курс, 4 семестр, *.jpg
Стр. 16 из методички по гидрогазодинамике (1970) МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Методичка, 2 курс, 4 семестр, *.jpg халява не проверен
Отфотканные задачи по Гидрогазодинамике (условия)
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.rar
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, 2 курс, 4 семестр, *.zip
Некоторые домашние задачи для дистанта, ИТАЭ, Нитусов, 2013 МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, 2 курс, 4 семестр, *.zip не проверен
Последние задачи для дистанционного решения. Когда Нитусыч их задавал, рыб на них не было, мб кому пригодится
Задача 1
Вода течет по длинной круглой горизонтальной трубе диаметром d = = 200 мм. Определить падение давления, отнесенное к единице длины трубы ΔP/l при массовом расходе m=130 кг
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.zip
Лабораторные работы по ГГД МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Лабораторная, 2 курс, 4 семестр, *.zip не проверен
Все лабораторные работы в mcd
МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 2 курс, 4 семестр, *.zip
Четвертый(?) типовой расчет по ГГД МЭИ, ИТАЭ (ИТТФ, ТЭФ), Гидрогазодинамика, Типовой расчет, 2 курс, 4 семестр, *.zip не проверен
Дистанционное обучение






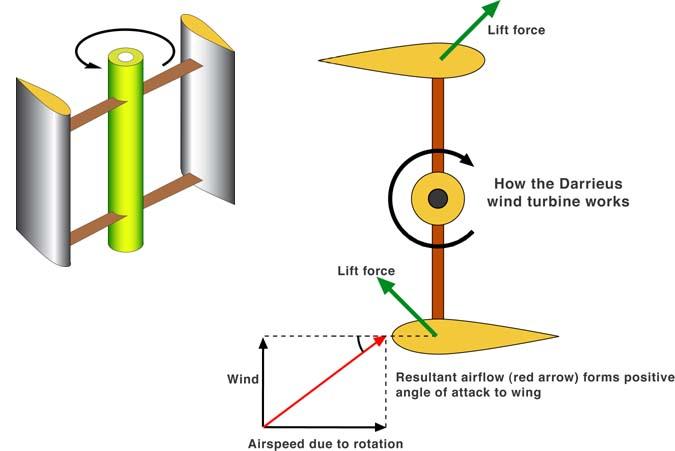
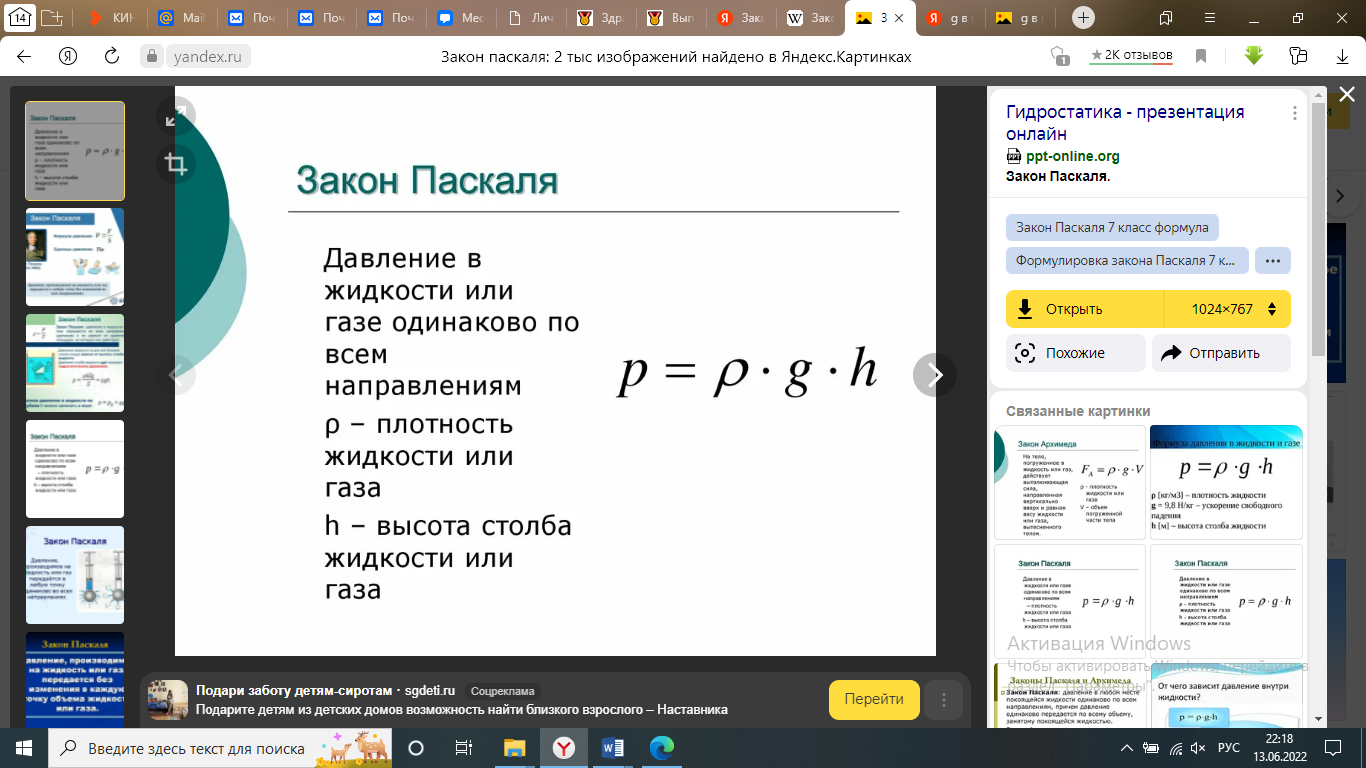



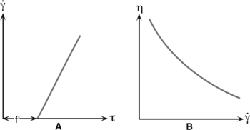

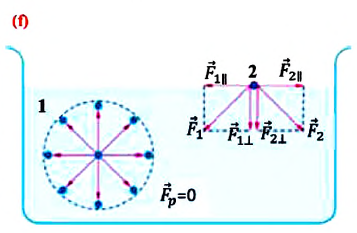



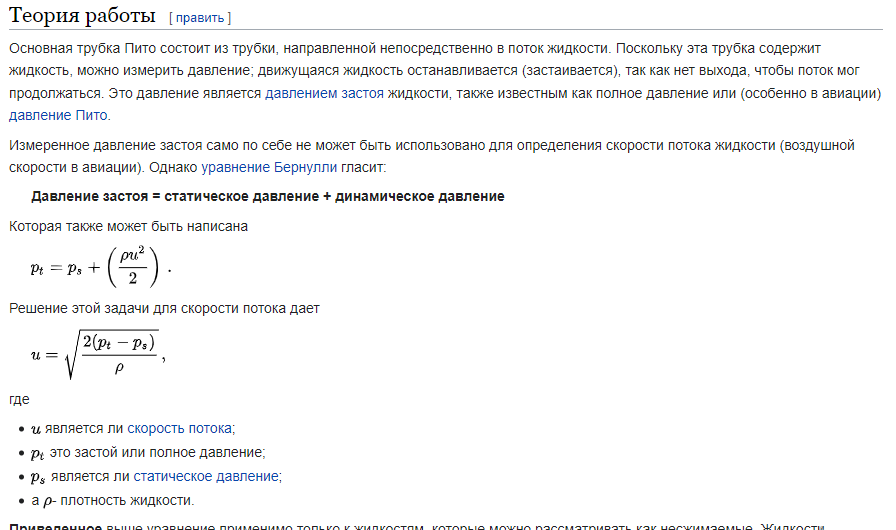
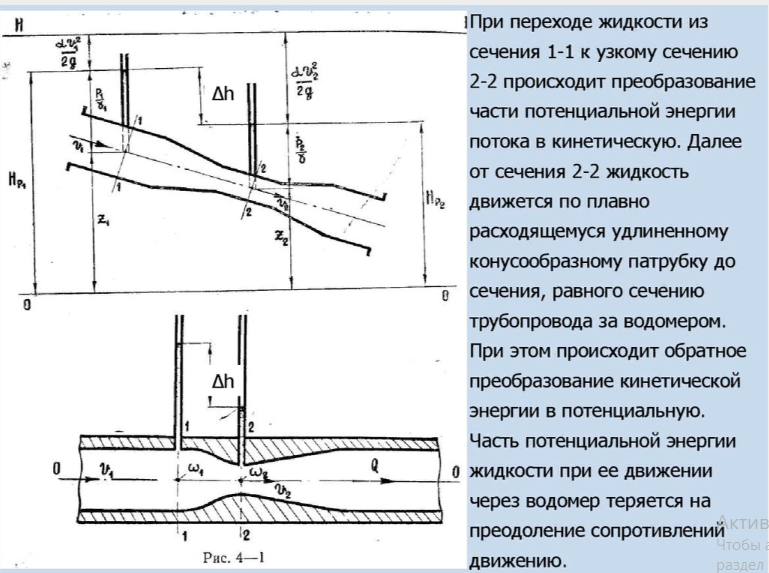





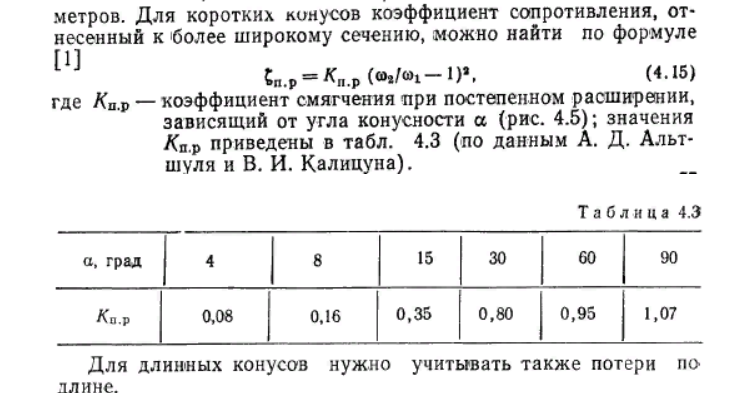 отери напора при постепенном изменении сечения трубопровода.
отери напора при постепенном изменении сечения трубопровода.