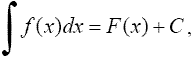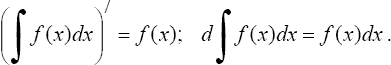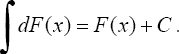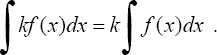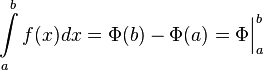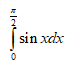Экзамен по интегралам

Первообразная
и неопределенный интеграл. Основные
свойства неопределенного интеграла.

Первообразная
и неопределенный интеграл

Первообразной
функцией для функции f(x) называется
такая функция F(х), производная которой
равна данной функции

F'(x)
= f(x).

Обозначение

где
F'(x) = f(x). Функция f(x) называется
подынтегральной функцией, а выражение
f(x)dx — подынтегральным выражением.
2.
Свойства неопределенного интеграла

1.
Производная неопределенного интеграла
равна подынтегральной функции;
дифференциал от неопределенного
интеграла равен подынтегральному
выражению, т.е.

2.
Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой
функции и произвольной постоянной, т.е.

3.
Постоянный множитель можно вынести из
под знака интеграла, т.е. если k = const ≠
0, то

4
. Неопределенный интеграл от алгебраической
суммы двух функций равен алгебраической
сумме интегралов от этих функций в
отдельности.
2.
Таблица основных интегралов.

3.
Основные методы интегрирования. Примеры.

Наиболее
важными методами интегрирования
являются:
1)
метод непосредственного интегрирования
(метод разложения),

Пример.
2)
метод подстановки (метод введения новой
переменной),

Пример.
3)
метод интегрирования по частям.

Пример.
Найти неопределенный интеграл ∫xe^-2xdx

Воспользуемся
методом интегрирование по частям.
Положим u=x, dv=e^-2xdx.
Тогда du=dx, v=∫xe^-2xdx=-e^-2x+C
Следовательно
по формуле имеем:
∫xe^-2xdx=x(-e^-2x)-∫-^-2dx=-e^-2x—e^-2x+C

4.
Определенный интеграл. Площадь
криволинейной трапеции. Формула
Ньютона-Лейбница.

Определённый
интеграл — аддитивный монотонный нормированный функционал,
заданный на множестве пар, первая
компонента которых
есть интегрируемаяфункция или функционал,
а вторая — область в множестве задания
этой функции (функционала)

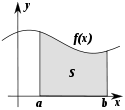
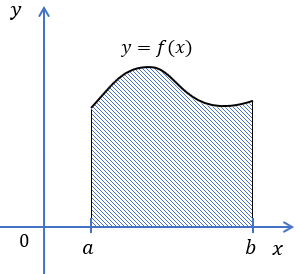
Определённый
интеграл 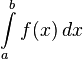численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми и и
графиком функции .

Если непрерывна
на отрезке и —
её любая первообразная на этом отрезке,
то имеет место равенство

5.
Основные свойства определенного
интеграла. Формулы замены переменной
и интегрирования по частям в определенном
интеграле.

Сво-во
:

Если
функция интегрируема
по Риману на ,
то она ограничена на нем

Формула
интегрирования по частям в определенном
интеграле выводится так же, как и для
неопределенного интеграла, и имеет
вид

6.
Несобственные интегралы.

Определённый
интеграл называется несобственным,
если выполняется, по крайней мере, одно
из следующих условий:

Предел a
или b (или оба предела) являются
бесконечными;
Функция
f(x) имеет одну или несколько точек
разрыва внутри отрезка [a, b]

7.
Двойной интеграл.

В
математическом анализе кратным или
многократным интегралом называют
множество интегралов, взятых от
переменных. Например: Замечание: кратный
интеграл − это определённый интеграл,
при его вычислении всегда получается
число

8.
Обыкновенные дифференциальные уравнения
(ОДУ). Основные определения. Задача Коши
для уравнений первого и второго порядков.

Обыкнове́нные
дифференциа́льные уравне́ния (ОДУ) —
это дифференциальное
уравнение вида

где —
неизвестная функция ,
зависящая от независимой переменной ,
штрих означает дифференцирование по .
Число
называется порядком дифференциального
уравнения(1)

Задача
Коши
(задача с начальным условием).
Пусть функция f(x, y) определена
в области D,
точка .
Требуется найти решение уравнения

;

(8)

удовлетворяющее
начальному условию

y(x₀)
= y₀;

(9)

(начальное
условие
(9) часто
записывают
в
форме ).
Теорема
Коши
(существования
и
решения
задачи
Коши).
Если
в
области D функция f(x, y) непрерывна
и
имеет
непрерывную
частную
производную ,
то
для
любой
точки в
окрестности
точки x₀ существует
единственное
решение
задачи
((8),(9)).
Мы
примем
эту
теорему
без
доказательства.
На
самом
деле
для
существования
решения
в
окрестности
точки x₀ достаточно
только
непрерывности
функции f(x, y);
условие
непрерывности обеспечивает
единственность
этого
решения. 6
9.
Основные виды ОДУ первого порядка.
Методы решения.
Уравнения
с разделяющимися переменными
Дифференциальное
уравнение называется уравнением
с разделяющимися (отделяющимися)
переменными,
если его правая часть представима в
виде .
Тогда, в случае ,
общим решением уравнения является .
Дифференциальное
уравнение  называется однородным,
если  —
однородная функция нулевой степени.
Функция  называется
однородной степени ,
если для любого  выполняется
равенство .
Замена приводит
при однородное
уравнение к уравнению с разделяющимися
переменными:
Подставив
в исходное уравнение, получаем:
,
что
является уравнением с разделяющимися
переменными.
Квазиоднородные
уравнения
Дифференциальное
уравнение называется квазиоднородным,
если для любого выполняется
соотношение .
Данное
уравнение решается заменой :
В
силу квазиоднородности, положив ,
получаем:
,
что,
очевидно, является однородным уравнением.
Линейные
уравнения[править | править
исходный текст]
Основная
статья: Линейное
дифференциальное уравнение
Дифференциальное
уравнение называется линейным и
может быть решено двумя методами:
методом интегрирующего множителя или
методом вариации постоянной.
Метод
интегрирующего множителя[править | править
исходный текст]
Пусть
задана функция —
интегрирующий множитель, в виде:
Умножим
обе части исходного уравнения на ,
получим:
Легко
заметить, что левая часть является
производной функции по .
Поэтому уравнение можно переписать:
Проинтегрируем:
Таким
образом, решение линейного уравнения
будет:
Метод
вариации постоянной (метод
Лагранжа)[править | править
исходный текст]
Основная
статья: Метод
Лагранжа (дифференциальные уравнения)
Рассмотрим
однородное уравнение .
Очевидно, это уравнение с разделяющимися
переменными, его решение:
Решения
исходного уравнения будем искать в
виде:
Подставив
полученное решение в исходное уравнение:
,
получаем:
,
где —
произвольная константа.
Таким
образом, решение исходного уравнения
можно получить путем подстановки в
решение однородного уравнения:
10.
ОДУ высших порядков допускающие
понижение порядка. Методы решения.
Если
дифференциальное уравнение
F(x, y, y ‘,…, y⁽ⁿ⁾ )
= 0
содержит
производную неизвестной функции y = y(x)
порядка n выше
первого, то его называют уравнением n-го
порядка и относят к уравнениям
высших порядков.
Такое
уравнение в нормальной форме имеет вид
y⁽ⁿ⁾ = f (x, y, y ‘,
…, y⁽ⁿ^—

1) ).
Пусть D область
определения функции f (x, y, y ‘,
…, y⁽ⁿ^—

1) ),
D из Rⁿ^+

1 . Функция
y
= y(x)
называется решением уравнения n–го
порядка на отрезке [a; b]
, если:
−
при
всех x ∈
[a; b]
точка (x, y(x), y ‘(x)
,…, y⁽ⁿ⁻¹⁾ )
принадлежит области D;
− y
= y(x)
дифференцируема n раз
на [a; b]
и при всех x ∈
[a; b]
выполняется тождество y⁽ⁿ⁾(x)
≡ f (x, y(x), y ‘(x),
…, y⁽ⁿ^—

1) (x)
).
График
решения y
= y(x)
называется интегральной
кривой уравнения.
Для
того, чтобы найти вполне определенную
интегральную кривую, нужно задать
дополнительные условия. Для уравнения n –го
порядка таких условий должно быть n.
Начальной
задачей или задачей
Коши для
уравнения n–го
порядка
y⁽ⁿ⁾ = f (x, y, y ‘,
…, y⁽ⁿ^—

1) )
называется
задача отыскания решения y
= y(x),
удовлетворяющего начальным условиям
y(x₀)
= y₀, y ‘(x₀)
= y₁₀, …, y⁽ⁿ^—

1) (x₀)
= y₍_n_—

1)0 .
Здесь
(x₀, y₀, y₁₀, …, y₍_n_—

1)0 )
фиксированная точка области D.
Любое
фиксированное решение y =
φ(x)
— решение некоторой задачи Коши —
называется частным
решением уравнения
.
Общим
решением уравнения n –го
порядка называется функция y =
φ(x,C₁,…, C_n)
, зависящая от n произвольных
постоянных C₁,…, C_n и
удовлетворяющая следующим требованиям:
−
при
любых допустимых значениях
постоянных C₁,…, C_n функция y =
φ(x,C₁,…, C_n)
является решением уравнения на [a;b]
;
−
какова
бы ни была начальная точка
(x₀, y₀, y₁₀, …, y₍_n_—

1)0 )
∈ D ,
существуют такие значения постоянных
значения C₁^*,…, C_n^* такие,
что функция y =
φ(x,C₁^*,…, C_n^*)
удовлетворяет начальным условиям
φ(x₀,C₁^*,…, C_n^*)
= y₀, φ
‘(x₀,C₁^*,…, C_n^*)
= y₁₀, …, φ⁽ⁿ^—

1)(x₀,C₁^*,… , C_n^*)
= y₍_n_—

1)0 .
Равенство
Φ(x,C₁,…,
C_n) =
0 называется общим
интегралом уравнения n –го
порядка в области D ,
если оно неявно определяет общее решение
уравнения .
Если
в результате каких–либо преобразований
порядок n уравнения F(x, y, y ‘,…, y⁽ⁿ⁾ )
= 0 может
быть понижен, то говорят, что
уравнениедопускает
понижение порядка.
К
уравнениям, допускающим понижение
порядка, относятся в частности, уравнения,
не содержащие искомой функции и ее
производных до некоторого порядка, ,
т.е. уравнения вида
Заменой z(x)
= y⁽^k⁾(x)
такое уравнение сводится к уравнению
(n−k)–го порядка:
Если z = z(x,C₁,…,C_n-k)
решение этого уравнения, то общее
решение уравнения n–го
порядка может быть вычислено по формуле
Простейшее
уравнение, допускающее понижение
порядка — уравнение вида y⁽ⁿ⁾ = f (x),
его общее решение имеет вид

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Площади фигур, ограниченных графиками функций

02.02.2022
1279
0

Образовательный тест по теме «Площади фигур, ограниченных графиками функций» позволяет выполнить проверку знаний учащихся по темам «Определенный интеграл», «Геометрический смысл определенного интеграла».
В тесте требуется сопоставить изображение фигуры, ограниченной графиками функции, и определенный интеграл, описывающий её.
Тест одновариантный, состоит из 10 заданий.

Источник

Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!

Список вопросов теста

Вопрос 1

Как называют операцию нахождения первообразной для данной функции?

Вопрос 2

Какая из формул является формулой Ньютона — Лейбница?

Вопрос 3

Как называют фигуру, изображённую на рисунке?

Вопрос 4

Вычислите данный интеграл.

Вопрос 5

Вычислите данный интеграл.

Вопрос 6

Вычислите данный интеграл.

Варианты ответов

-0,5
1
-1
0

Вопрос 7

Вычислите данный интеграл.

Варианты ответов

1
cos 3a
a
0

Вопрос 8

Вычислите данный интеграл.

Вопрос 9

Вычислите данный интеграл.

Вопрос 10

Сопоставьте интегралы и их значения.

Варианты ответов

Источник

Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.

Отлично

Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.

Отлично

Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.

Отлично

Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.

Отлично

Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.

Хорошо

Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.

Отлично

Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.

Отлично

Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.

Отлично

Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.

Хорошо

Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.

Отлично

Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.

Отлично

Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.

Отлично

Источник

Алгоритм решения интегралов

Неопределённым интегралом функции называется множество всех первообразных этой функции.

Первообразной функции называется такая функция, производная которой равна исходной функции, т.е., если – первообразная функции , то:

Операция интегрирования является операцией обратной операции дифференцирования.

Определённым интегралом функции на отрезке называется разность первообразных функции, вычисленных на концах этого отрезка.

Определённый интеграл вычисляется при помощи формулы Ньютона-Лейбница:

Для нахождения интегралов функций, используются свойства интегралов, а также таблица интегралов.

Таблица основных интегралов

Таблица основных интегралов, – постоянная величина

$[int x^{n}dx = frac{x^{n + 1}}{n + 1} + C, (n = const, n neq -1)]$

$[int frac{dx}{x^{n}} = -frac{1}{n - 1}cdotfrac{1}{x^{n-1}} + C, (n = const, n neq -1)]$

$[int frac{dx}{sqrt{x}} = 2sqrt{x} + C]$

$[int frac{dx}{x} = ln{|x|} + C]$

$[int a^{x}dx = frac{a^{x}}{ln a} + C, (a > 0, a neq 1)]$

$[int e^{x}dx = e^{x} + C]$

$[int frac{dx}{cos^{2}x} = tg{x} + C]$

$[int frac{dx}{sin^{2}x} = - ctg{x} + C]$

$[int frac{dx}{1 + x^{2}} = arctg{x} + C]$

$[int frac{dx}{sqrt{1 - x^{2}}} = arcsin{x} + C]$

$[int frac{dx}{1 - x^{2}} = frac{1}{2}cdotlnleft | frac{1 + x}{1 - x} right | + C]$

$[int frac{dx}{sqrt{x^{2} pm a^{2}}} = ln | x + sqrt{x^{2} pm a^{2}} | + C]$

$[int frac{dx}{ ch^{2}x} = th{x} + C]$

$[int frac{dx}{ sh^{2}x} = - cth{x} + C]$

Примеры решений интегралов

Задача

Вычислить интеграл:

Решение

По таблице интегралов находим:

$[int xdx = frac{x^{2}}{d2} + C]$

Ответ

$[int xdx = frac{x^{2}}{d2} + C]$

Задача

Вычислить интеграл:

Решение

По таблице интегралов находим:

$[int sqrt{x}dx = int x^{frac{1}{2}}dx = frac{x^{frac{3}{2}}}{frac{3}{2}} = frac{2}{3}xsqrt{x} + C]$

Ответ

$[int sqrt{x}dx = frac{2}{3}xsqrt{x} + C]$

Задача

Вычислить интеграл:

$[int frac{dx}{sqrt{x}}]$

Решение

По таблице интегралов находим:

$[int frac{dx}{sqrt{x}} = 2sqrt{x} + C]$

Ответ

$[int frac{dx}{sqrt{x}} = 2sqrt{x} + C]$

Задача

Вычислить интеграл:

$[int 7x^{5}dx]$

Решение

Вынося постоянный множитель 7 за знак интеграла, по таблице интегралов находим:

$[int 7x^{5}dx = 7int x^{5}dx = 7cdotfrac{x^{6}}{6} + C]$

Ответ

$[int 7x^{5}dx = 7cdotfrac{x^{6}}{6} + C]$

Задача

Вычислить интеграл:

$[int (x^{3} + 5x)dx]$

Решение

Интеграл суммы равен сумме интегралов, поэтому:

$[int (x^{3} + 5x)dx = int (x^{3})dx + int (5x)dx = frac{x^{4}}{4} + 5cdotfrac{x^{2}}{2} + C = frac{x^{4} + 10x^{2}}{4} + C]$

Ответ

$[int (x^{3} + 5x)dx = frac{x^{4} + 10x^{2}}{4} + C]$

Задача

Вычислить интеграл:

$[int (x^{4} - x^{2} + 4)dx]$

Решение

Интеграл суммы равен сумме интегралов, поэтому:

$[int (x^{4} - x^{2} + 4)dx = int (x^{4})dx - int (x^{2})dx + int (4)dx = frac{x^{5}}{5} - frac{x^{3}}{3} + 4x + C]$

Ответ

$[int (x^{4} - x^{2} + 4)dx = frac{x^{5}}{5} - frac{x^{3}}{3} + 4x + C]$

Задача

Вычислить интеграл:

Решение

Преобразуя подынтегральную функцию к виду степенной, находим её интеграл по таблице интегралов:

$[int sqrt[n]{x}dx = int {x}^{frac{1}{n}}dx = frac{x^{frac{n + 1}{n}}}{frac{n + 1}{n}} + C = frac{ncdot x^{frac{n + 1}{n}}}{n + 1} + C = frac{n}{n + 1}xsqrt[n]{x} + C]$

Ответ

$[int sqrt[n]{x}dx = frac{n}{n + 1}xsqrt[n]{x} + C]$

Задача

Вычислить интеграл:

$[int sqrt[n]{x^{m}}dx]$

Решение

Преобразуя подынтегральную функцию к виду степенной, находим её интеграл по таблице интегралов:

$[int sqrt[n]{x}dx = int {x}^{frac{m}{n}}dx = frac{x^{frac{m + n}{n}}}{frac{m + n}{n}} + C = frac{ncdot x^{frac{m + n}{n}}}{m + n} + C = frac{n}{m + n}xsqrt[n]{x^{m}} + C]$

Ответ

$[int sqrt[n]{x}dx = frac{n}{m + n}xsqrt[n]{x^{m}} + C]$

Задача

Вычислить интеграл:

$[int (frac{3}{x^{5}} - frac{2}{x^{4}} + frac{1}{x^{3}})dx]$

Решение

Интеграл суммы равен сумме интегралов, поэтому:

$[int (frac{3}{x^{5}} - frac{2}{x^{4}} + frac{1}{x^{3}})dx = int (frac{3}{x^{5}})dx - int (frac{2}{x^{4}})dx + int (frac{1}{x^{3}})dx]$

Далее найдём каждый интеграл суммы:

$[int (frac{3}{x^{5}})dx = 3frac{x^{-4}}{-4} + C = -frac{3}{4}cdotfrac{1}{x^{4}} + C]$

$[int (frac{2}{x^{4}})dx = 2frac{x^{-3}}{-3} + + C = - frac{2}{3}cdotfrac{1}{x^{3}} + C]$

$[int (frac{1}{x^{3}})dx = frac{x^{-2}}{-2} + C = - frac{1}{2}cdotfrac{1}{x^{2}} + C]$

Ответ

$[int (frac{3}{x^{5}} - frac{2}{x^{4}} + frac{1}{x^{3}})dx = -frac{3}{4}cdotfrac{1}{x^{4}} + frac{2}{3}cdotfrac{1}{x^{3}} - frac{1}{2}cdotfrac{1}{x^{2}} + C]$

Задача

Вычислить интеграл:

Решение

Интеграл суммы равен сумме интегралов, поэтому:

Далее, применяя таблицу интегралов, находим интегралы функций синус и косинус:

Ответ

Источник

ИНТЕГРАЛ.

Вариант 1.

1. Какой из
интегралов нельзя вычислять с помощью формулы Ньютона-Лейбница:

а) ; б) ; в) ;
г) ?

2. Вычислите интеграл .

а) 5,5; б) 11;
в) -5,5; г) другой ответ.

3. Вычислите интеграл .

а) ; б) ; в) 0; г)
другой ответ.

4. Вычислите интеграл .

а) ; б) 2; в);
г) другой ответ.

5. Вычислите интеграл, пользуясь его геометрической
интерпретацией, .

а) 4,5;
б) 2,25; в) 9;
г) другой ответ.

6. Найдите площадь фигуры, ограниченной
линиями y=2x, y=0, x=1 и x=3.

а) 8; б)
4; в) 6; г) другой ответ.

7. Найдите площадь фигуры, ограниченной
графиком функции y=x²—x и осью абсцисс.

а) ; б) ; в) ; г) другой ответ.

8. Найдите площадь фигуры, ограниченной
линиями y=2x—x² и y=x.

а) ; б) 1; в) ; г) другой ответ.

9. При каком значении а верно равенство
?

а) -1; б)
1; в) -2; г) другой ответ.

10. Найдите объем фигуры, полученной вращением
криволинейной трапеции, ограниченной линиями y=x², x=0 и x=1, y=0 вокруг оси абсцисс.

а) ; б) ; в) ; г) другой ответ.

Вариант 2.

1. Какой из
интегралов нельзя вычислять с помощью формулы Ньютона-Лейбница:

а) ; б) ; в) ;
г) ?

2. Вычислите интеграл .

а) —; б) ; в) 2; г)
другой ответ.

3. Вычислите интеграл .

а) ; б) ; в) 0; г)
другой ответ.

4. Вычислите интеграл .

а) ; б) ; в);
г) другой ответ.

5. Вычислите интеграл, пользуясь его
геометрической интерпретацией, .

а) 2; б) 3; в)
4; г) другой ответ.

6. Найдите площадь фигуры, ограниченной
линиями y=-4x, y=0, x=-1 и x=0.

а) 2; б) 4; в)
6; г) другой ответ.

7. Найдите площадь фигуры, ограниченной
графиком функции y=4x²-1 и осью абсцисс.

а) ; б) ; в) ; г) другой ответ.

8. Найдите площадь фигуры, ограниченной
линиями y=6-x,y= и y=0.

а) ; б) ; в) ;
г) другой ответ.

9. При каком значении а верно равенство
?

а) -1; б)
1; в) -0,5; г) другой ответ.

10. Найдите объем фигуры, полученной вращением
криволинейной трапеции, ограниченной линиями y=0,5x, x=2
и x=1, y=0 вокруг оси абсцисс.

а) ; б) ; в) ; г) другой ответ.

Вариант 3.

1. Какой из
интегралов нельзя вычислять с помощью формулы Ньютона-Лейбница:

а) ; б) ; в) ;
г) ?

2. Вычислите интеграл .

а) —; б) ; в) 0,5; г)
другой ответ.

3. Вычислите интеграл .

а) ; б) ; в) 0; г)
другой ответ.

4. Вычислите интеграл .

а) ; б) ; в); г) другой ответ.

5. Вычислите интеграл, пользуясь его
геометрической интерпретацией, .

а) 2; б) ; в) ; г) другой ответ.

6. Найдите площадь фигуры, ограниченной
линиями y=6x, y=0, x=1 и x=2.

а) 3; б) 9;
в) 6; г) другой ответ.

7. Найдите площадь фигуры, ограниченной
графиком функции y=3x²-6x и осью абсцисс.

а) ; б) ; в) ; г) другой ответ.

8. Найдите площадь фигуры, ограниченной
линиями y=x³, y=.

а) ; б) ; в) ;
г) другой ответ.

9. При каком значении а верно равенство
?

а) 0; б)
1; в) -1; г) другой ответ.

а) ; б) ; в) ; г) другой ответ.

Вариант 4.

1. Какой из
интегралов нельзя вычислять с помощью формулы Ньютона-Лейбница:

а) ; б) ; в) ; г)
?

2. Вычислите интеграл .

а) —; б) ; в) -5; г) другой ответ.

3. Вычислите интеграл .

а) ; б) ; в) 0; г)
другой ответ.

4. Вычислите интеграл .

а) ; б) ; в);
г) другой ответ.

5. Вычислите интеграл, пользуясь его
геометрической интерпретацией, .

а) 2; б) ; в) ; г) другой ответ.

6. Найдите площадь фигуры, ограниченной
линиями y=-4x, y=0, x=1 и x=4.

а) 15,5; б) 21;
в) 31; г) другой ответ.

7. Найдите площадь фигуры, ограниченной
графиком функции y=-x²-2x и осью абсцисс.

а) ; б) ; в) ; г) другой ответ.

8. Найдите площадь фигуры, ограниченной
линиями y=x², x=y².

а) ; б) ; в) ; г) другой ответ.

9. При каком значении а верно равенство
?

а) 0; б) -2;
в) 2; г) другой ответ.

10. Найдите объем фигуры, полученной вращением
криволинейной трапеции, ограниченной линиями y=x, x=1
и x=3, y=0 вокруг оси абсцисс.

а) ; б) ; в) ;
г) другой ответ.

ИНТЕГРАЛ

№	1	2	3	4	5	6	7	8	9	10
В-1	б	в	в	в	а	а	а	а	а	б
В-2	а	б	б	б	в	а	в	в	в	а
В-3	б	в	в	в	б	б	б	а	а	б
В-4	а	а	б	б	в	г	б	а	в	в

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На рисунке изображён график функции y  =  F(x)  — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x)  — одна из первообразных функции f(x).

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1.

На рисунке изображён график некоторой функции y = f(x). Функция   — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл

Пройти тестирование по этим заданиям

Источник

Линейные
уравнения[править | править
исходный текст]

Метод
интегрирующего множителя[править | править
исходный текст]

Метод
вариации постоянной (метод
Лагранжа)[править | править
исходный текст]

Площади фигур, ограниченных графиками функций

Список вопросов теста

Вопрос 1

Вопрос 2

Вопрос 3

Вопрос 4

Вопрос 5

Вопрос 6

Варианты ответов

Вопрос 7

Варианты ответов

Вопрос 8

Вопрос 9

Вопрос 10

Варианты ответов

Алгоритм решения интегралов

Примеры решений интегралов

Новое и интересное на сайте:

Линейные уравнения[править | править исходный текст]

Метод интегрирующего множителя[править | править исходный текст]

Метод вариации постоянной (метод Лагранжа)[править | править исходный текст]

Площади фигур, ограниченных графиками функций

Список вопросов теста

Вопрос 1

Вопрос 2

Вопрос 3

Вопрос 4

Вопрос 5

Вопрос 6

Варианты ответов

Вопрос 7

Варианты ответов

Вопрос 8

Вопрос 9

Вопрос 10

Варианты ответов

Алгоритм решения интегралов

Примеры решений интегралов

Новое и интересное на сайте:

Линейные
уравнения[править | править
исходный текст]

Метод
интегрирующего множителя[править | править
исходный текст]

Метод
вариации постоянной (метод
Лагранжа)[править | править
исходный текст]