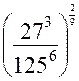Экзамен по математике 11 класс в техникуме

Государственное бюджетное профессиональное

образовательное учреждение Республики Мордовия

«Рузаевский техникум железнодорожного и городского транспорта

имени А.П. Байкузова»

Контрольные работы

Преподавателя  Лазаревой Л.Н.

на 2020-2021 учебный год

Предмет   Математика

Курс I     Группа 15

Специальность 23.02.07 «Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей»

Контрольные работы составлены в соответствии с образовательной программой по специальности 23.02.07 «Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей»

Преподаватель   Лазарева Л.Н.  ___________________

Рассмотрен на заседании цикловой комиссии общеобразовательных дисциплин

Протокол № ______       от «______»___________2020 г.

Председатель цикловой комиссии   Качкалова С.С.. ___________________

Контрольная работа № 1. «Действительные числа»                  Вариант № 1

1. Вычислите:
2. Представьте выражение в виде степени положительного числа х:
3. Упростите выражение:  
4. Упростите выражение:
5. Решите уравнение:
6. Упростите выражение: , где а < 0
7. Найдите значение выражения при m = 5:      
8. Решите систему уравнений:  Найдите у – х, где (х;у) – решение системы.

Контрольная работа № 1. «Действительные числа»                  Вариант № 2

1. Вычислите:  
2. Представьте выражение в виде степени положительного числа х:
3. Упростите выражение:  
4. Упростите выражение:
5. Решите уравнение:  
6. Упростите выражение:  
7. Найдите значение выражения при а = 16, в = 9   
8. Решите систему уравнений: . Найдите у – х, если (х;у) – решение системы.

Контрольная работа № 2. «Степенная функция»                  Вариант № 1

1. Найти область определения функции  
2. Изобразить эскиз графика функции и перечислить её основные свойства. Пользуясь свойствами этой функции: 1)сравнить с единицей  2)сравнить
3. Решить уравнения:
4. Установить, равносильны ли уравнения: ;
5. Найти функцию, обратную данной ; найти её область определения и множество значений.

_______________________________________________________________________________________

Контрольная работа № 2. «Степенная функция»                  Вариант № 2

1. Найти область определения функции
2. Изобразить эскиз графика функции и перечислить её основные свойства. Пользуясь свойствами этой функции: 1)сравнить с единицей 2)сравнить
3. Решить уравнения:
4. Установить, равносильны ли уравнения
5. Найти функцию, обратную данной  ; найти её область определения и множество значений.

Контрольная работа № 3 « Параллельность прямых и плоскостей» Вариант № 1

1. В тетраэдре DABC дано < ADB = 54°, < BDC = 72°, < CDA = 90°, DA = 20 см, BD = 18 см, DC = 21см. Найдите: а) длину ребра BC; б) площадь боковой грани BCD.
2. Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 90 см. Найдите каждое ребро параллелепипеда, если известно, что AB/BC = 2/3, BC/BB1 = 3/4.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью ABC1.  Докажите, что построенное сечение является параллелограммом.

_______________________________________________________________________________________

Контрольная работа № 3 « Параллельность прямых и плоскостей» Вариант № 2

1. В тетраэдре DABC дано < ADB = 54°, < BDC = 72°, < CDA = 90°, DA = 20 см, BD = 18 см, DC = 21см. Найдите: а) длину ребра AB; б) площадь боковой грани ABD.
2. Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 84 см. Найдите каждое ребро параллелепипеда, если известно, что AB/BC = 1/2, BC/BB1 = 2/3.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью ACC1. Докажите, что построенное сечение является параллелограммом.

Контрольная работа № 4 « Перпендикулярность прямых и плоскостей» Вариант № 1

1. Через вершину С прямоугольного треугольника  проведена прямая , перпендикулярная к плоскости этого треугольника. Найдите расстояния  и , если катеты треугольника равны 4см и см.
2. Найдите диагональ прямоугольного параллелепипеда , если его измерения равны
3. Изобразите куб  и постройте его сечение плоскостью, проходящей через ребро  и перпендикулярной плоскости
4. Прямая PQ параллельна плоскости . Через точки P и Q проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость в точках  и  соответсввенно. Докажите, что

_______________________________________________________________________________________

Контрольная работа № 4 « Перпендикулярность прямых и плоскостей» Вариант № 2

1. Через вершину С прямоугольного треугольника  проведена прямая , перпендикулярная к плоскости этого треугольника. Найдите расстояния  и , если катеты треугольника равны 3см и см.
2. Найдите диагональ прямоугольного параллелепипеда , если его измерения равны
3. Изобразите куб  и постройте его сечение плоскостью, проходящей через ребро  и перпендикулярной плоскости
4. Прямая PQ параллельна плоскости . Через точки P и Q проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость в точках  и  соответственно. Докажите, что

_______________________________________________________________________________________

Контрольная работа № 4 « Перпендикулярность прямых и плоскостей» Вариант № 3

1. Через вершину С прямоугольного треугольника  проведена прямая , перпендикулярная к плоскости этого треугольника. Найдите расстояния  и , если катеты треугольника равны 8см и см.
2. Найдите диагональ прямоугольного параллелепипеда , если его измерения равны
3. Изобразите куб  и постройте его сечение плоскостью, проходящей через ребро  и перпендикулярной плоскости
4. Прямая PQ параллельна плоскости . Через точки P и Q проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость в точках  и  соответственно. Докажите, что

_______________________________________________________________________________________

Контрольная работа № 4 « Перпендикулярность прямых и плоскостей» Вариант № 4

1. Через вершину С прямоугольного треугольника  проведена прямая , перпендикулярная к плоскости этого треугольника. Найдите расстояния  и , если катеты треугольника равны 6см и см.
2. Найдите диагональ прямоугольного параллелепипеда , если его измерения равны
3. Изобразите куб  и постройте его сечение плоскостью, проходящей через ребро  и перпендикулярной плоскости
4. Прямая PQ параллельна плоскости . Через точки P и Q проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость в точках  и  соответственно. Докажите, что

Контрольная работа № 5 « Показательная функция»                                   Вариант № 1

1. Вычислите: (10-5·1002)-1
2. Схематически изобразите график функции y=2x, перечислите ее свойства. Сравните выражения 2–11 и 2–12.
3. Сравните числа (1/3)10 и (1/3)11
4. Решите уравнение (1/5)2-3x = 25
5. Решите уравнение
6. Найдите область определения функции: у =
7. Решите уравнение:

_______________________________________________________________________________________

Контрольная работа № 5 « Показательная функция»                                        Вариант № 2

1. Вычислите: (10-7·1004)-1
2. Схематически изобразите график функции y=(1/2)x, перечислите ее свойства. Сравните выражения (1/2)7 и (1/2)9.
3. Сравните числа (0,7)-12 и (0,7)-11
4. Решите уравнение (0,1)2x-3 = 100
5. Решите уравнение
6. Найдите область определения функции: у =
7. Решите уравнение:

_______________________________________________________________________________________

Контрольная работа № 5 « Показательная функция»                                          Вариант № 3

Вычислите: (10-5·1003)-1

1. Схематически изобразите график функции y=2x, перечислите ее свойства. Сравните выражения 2–15 и 2–14.
2. Сравните числа (1/7)8 и (1/7)10
3. Решите уравнение (1/2)0,5x+1 = 8
4. Решите уравнение
5. Найдите область определения функции: у =
6. Решите уравнение:

Контрольная работа № 5 « Показательная функция»                                          Вариант № 4

1. Вычислите: (10-5·1003)-1
2. Схематически изобразите график функции y=(1/2)x, перечислите ее свойства. Сравните выражения (1/2)8 и (1/2)11.
3. Сравните числа (0,6)-11 и (0,6)-13
4. Решите уравнение (1/3)2,5x-2 = 27
5. Решите уравнение
6. Найдите область определения функции: у =
7. Решите уравнение:

_______________________________________________________________________________________

Контрольная работа № 5 « Показательная функция»                                          Вариант № 5

1. Вычислите: (10-7·1003)-1
2. Схематически изобразите график функции y=2x, перечислите ее свойства. Сравните выражения 216 и 218.
3. Сравните числа (1/4)-6 и (1/4)-7
4. Решите уравнение (1/7)1-3x = 49
5. Решите уравнение
6. Найдите область определения функции: у =
7. Решите уравнение:

_______________________________________________________________________________________

Контрольная работа № 5 « Показательная функция»                                      Вариант  № 6

1. Вычислите: (10-9·1004)-1
2. Схематически изобразите график функции y=(1/2)x, перечислите ее свойства и сравните выражения (1/2)-5 и (1/2)-7
3. Сравните числа (1/8)10 и (1/8)11
4. Решите уравнение (1/6)4-3x = 36
5. Решите уравнение
6. Найдите область определения функции: у =
7. Решите уравнение:

Контрольная работа № 6 « Логарифмическая функция»                     Вариант № 1

1. Вычислить  1) log 13 169; 2) log 5 625; 3) log 1/2 32; 4) log 9 27 5) log 25 125 6) log 15 225; 7) log 4 256 ; log..1/5 125; 9) log 16 64
2. Найдите значение выражения  
3. Решить уравнение
4. Найдите область определения функции
5. Найдите значение выражения log3(9b), если log3b = 5.
6. Решите неравенство log2( 1 – 0,3)4.
7. Укажите наименьшее целое число из области определения функции
8. Найдите произведение корней уравнения .
9. Найдите значение выражения
10. Вычислить по таблицам или с помощью микрокалькулятора  log 1,2 2

_______________________________________________________________________________________

Контрольная работа № 6 « Логарифмическая функция»                     Вариант № 2

1. Вычислить 1) log 15 225; 2) log 4 256; 3) log..1/5 125; 4) log 16 64 5) log 13 169; 6) log 5 625; 7) log 1/2 32; log 25 125 9) log 16 64
2. Найдите значение выражения
3. Решить уравнение .
4. Найдите область определения функции y = log0,1(0,01 –)
5. Найти значения выражения , если .
6. Решите неравенство  
7. Найдите наименьшее значение функции
8. Найдите наибольшее целое решение неравенства
9. Найдите значение выражения
10. Вычислить по таблицам или с помощью микрокалькулятора  log 1,3 2

Контрольная работа № 7 «Многогранники»                               Вариант № 1

В правильной треугольной призме сторона основания равна 10 см и высота равна 15 см. Вычислить площадь боковой и полной поверхностей призмы

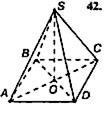
Стороны основания правильной четырехугольной пирамиды равны 30, боковые рёбра равны 39. Найдите площадь поверхности этой пирамиды.

Контрольная работа № 7 «Многогранники»                               Вариант № 2

В правильной четырехугольной призме сторона основания равна 12 дм и высота равна 8 дм. Вычислить площадь боковой и полной поверхностей призмы

Стороны основания правильной четырехугольной пирамиды равны 10, боковые рёбра равны 13. Найдите площадь поверхности этой пирамиды.

Контрольная работа № 7 «Многогранники»                               Вариант № 3

В правильной шестиугольной призме сторона основания равна 23 см и высота равна 5 дм. Вычислить площадь боковой и полной поверхностей призмы

Стороны основания правильной четырехугольной пирамиды равны 30, боковые рёбра равны 39. Найдите площадь поверхности этой пирамиды.

Контрольная работа № 7 «Многогранники»                               Вариант № 4

В правильной пятиугольной призме сторона основания равна 40 см и высота равна 10 см. Вычислить площадь боковой и полной поверхностей призмы

Стороны основания правильной четырехугольной пирамиды равны 10, боковые рёбра равны 13. Найдите площадь поверхности этой пирамиды.

Контрольная работа № 8 «Тригонометрические формулы»               Вариант №1

Вариант 1.

1. Найдите значение выражения:
2. Сравните с нулём выражения: sin 1200, cos 1950, ctg 3590.
3. Вычислите:
4. Упростите выражение:
5. Упростите выражение: sinα * cos α * ctg α – 1
6. Упростите выражение:
7. Вычислите: 2sin 150 * cos 150
8. Вычислите: cos
9. Представив 1050 как 600 + 450, вычислите sin 1050.
10. Дано: sin α = – где . Найдите tg 2α 

_______________________________________________________________________________________

Контрольная работа № 8 «Тригонометрические формулы»               Вариант №2

1. Найдите значение выражения:
2. Сравните с нулём выражения: sin 1870, cos 2150, tg 800.
3. Вычислите:
4. Упростите выражение:
5. Упростите выражение: 
6. Упростите выражение:
7. Вычислите:
8. Вычислите: cos1500
9. Представив 150 как 450 – 300, вычислите cos 150.
10. Дано: cos α = – где . Найдите ctg 2α 

Контрольная работа № 9 «Тригонометрические уравнения»               Вариант №1

1. Вычислите arcsin () + 2arctg(-1)
2. Вычислите arcсos () + 2arcctg()
3. Решите уравнение: sin x —=0
4. Решите уравнение: cos 2x=1
5. Укажите уравнение, которому соответствует решение: :
6. Решите уравнение: 6sin2 x + sin x – 1 = 0
7. Решите уравнение: 2sin2 x —sin 2x =0

_______________________________________________________________________________________

Контрольная работа № 9 «Тригонометрические уравнения»               Вариант №2

1. Вычислите: arcsin () + 0,5arctg (- )
2. Вычислите: arcсos () + arcctg ()
3. Решите уравнение: sin x +=0
4. Решите уравнение: ctg (x+)=
5. Укажите уравнение, которому соответствует решение: :
6. Решите уравнение: cos2 x — 4sin x + 3 = 0
7. Решите уравнение: sin2 x -3sin x cos x =0

Контрольная работа № 10    «Векторы в пространстве»     Вариант № 1

1. Даны точки А(8; — 3; — 1) и В(6; -1; -4). Найдите длину вектора АВ
2. Даны точки А(6; — 3; 2); В(6; -1; 4); С(6; — 3; 2) и D(2; -7; 3). Вычислите косинус угла между прямыми АВ и СD.
3. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки А(6; — 3; 2); В(3; -1; 4) и С(3; — 3; 2).
4. Изобразите куб  и вычислите косинус угла между прямыми ВВ1 и ВА1.

_______________________________________________________________________________________

Контрольная работа № 10    «Векторы в пространстве»     Вариант № 2

1. Даны точки А(4; — 3; — 2) и В(3; -1; — 5). Найдите длину вектора АВ.
2. Даны точки А(2; — 3; 1); В(6; -1; 4); С(5; — 3; 2) и D(3; -7; 3). Вычислите косинус угла между прямыми АВ и СD.
3. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки А(7; — 3; 2); В(4; -1; 4) и С(4; — 3; 2).
4. Изобразите куб  и вычислите косинус угла между прямыми АА1 и ВА1

_______________________________________________________________________________________

Контрольная работа № 10    «Векторы в пространстве»     Вариант № 3

1. Даны точки А(7; — 4; — 2) и В(5; -1; — 5). Найдите длину вектора АВ.
2. Даны точки А(7; — 3; 4); В(6; -1; 2); С(2; — 1; 1) и D(4; -7; 6). Вычислите косинус угла между прямыми АВ и СD.
3. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки А(8; — 3; 2); В(5; -1; 4) и С(6; — 3; 2).
4. Изобразите куб  и вычислите косинус угла между прямыми АВ1 и СА1

_______________________________________________________________________________________

Контрольная работа № 10    «Векторы в пространстве»     Вариант № 4

1. Даны точки А(5; — 3; 2) и В(3; -1; 8). Найдите длину вектора АВ.
2. Даны точки А(4; — 2; 2); В(6; -1; 4); С(4; — 3; 2) и D(5; -7; 3). Вычислите косинус угла между прямыми АВ и СD.
3. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки А(9; — 3; 2); В(6; -1; 4) и С(5; — 3; 2).
4. Изобразите куб  и вычислите косинус угла между прямыми СС1 и DА1

_______________________________________________________________________________________

Контрольная работа № 10    «Векторы в пространстве»     Вариант № 5

1. Даны точки А(4; — 3; -6) и В(1; -1; -2). Найдите длину вектора АВ.
2. Даны точки А(5; — 1; 2); В(6; -2; 4); С(1; — 3; 2) и D(4; -7; 3). Вычислите косинус угла между прямыми АВ и СD.
3. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки А(5; — 3; 2); В(2; -1; 4) и С(4; — 3; 2).
4. Изобразите куб  и вычислите косинус угла между прямыми DD1 и CА1.

_______________________________________________________________________________________

Контрольная работа № 10    «Векторы в пространстве»     Вариант № 6

1. Даны точки А(3; — 3; — 6) и В(1; -1; -4). Найдите длину вектора АВ.
2. Даны точки А(3; — 7; 2); В(6; -4; 4); С(3; — 3; 2) и D(1; -7; 3). Вычислите косинус угла между прямыми АВ и СD.
3. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки А(4; — 3; 2); В(1; -1; 4) и С(3; — 3; 2).
4. Изобразите куб  и вычислите косинус угла между прямыми ВВ1 и CА1.

Контрольная работа № 11 « Метод координат в пространстве» Вариант № 1

1.Какой угол образуют единичные векторы а и b , если известно, что векторы а + 2 b и 5 а — 4 b взаимно перпендикулярны?

2.В кубе  длина ребра равна 1, М – центр грани ДД1С1 С. Используя метод координат, найдите: 1) Угол между прямыми АМ и В1Д; 2)расстояние между серединами отрезков АМ и В1Д.

3. Даны две точки: А, лежащая на оси ординат, и В(1; 0; 1). Прямая АВ составляет с плоскостью Охz угол в 300. Найдите координаты точки А.

4.Найдите координаты вектора а, коллинеарного вектору b {6; 8; -7,5} и образующего тупой угол с координатным вектором j , если | а | = 50.

_______________________________________________________________________________________

Контрольная работа № 11 « Метод координат в пространстве» Вариант № 2

1. Даны точки А( — 1; 2; 1), В(3; 0; 1), С(2; -1; 0) и Д(2; 1; 2). Найдите:

1) угол между векторами АВ и СД;

2)расстояние между серединами отрезков АВ и СД.

2.Основанием прямой призмы АВСА!В!С! служит равнобедренный треугольник АВС, <АСВ = 1200, АС = СВ = ВВ1. Используя векторы, найдите угол между прямыми АВ и СВ1.

3.Даны две точки: А, лежащая в плоскости Оху, и В(1; 1; 1), причём абсцисса точки А равна её ординате. Прямая АВ составляет с плоскостью Оzу угол в 300. Найдите координаты точки А.

4.Даны векторы а {7; 0; 0} и b {0; 0; 3;}. Найдите множество точек М, для каждой из которых выполняются условия ОМ * а = 0 и ОМ * b = 0, где О – начало координат.

Контрольная работа № 12  «Тригонометрические функции»     Вариант № 1

Найти область определения и множество значений функции  

Выяснить, является функция  чётной или нечётной

Найти все корни уравнения , принадлежащие отрезку

Сравнить выражения   и  

Изобразить схематически график функции  ;  на  

Найти наибольшее и наименьшее значения функции

Построить график функции . При каких значениях х функция возрастает?

_______________________________________________________________________________________

Контрольная работа № 12  «Тригонометрические функции»     Вариант № 2

Найти область определения и множество значений функции  

Выяснить, является функция  чётной или нечётной

Найти все корни уравнения , принадлежащие отрезку

Сравнить выражения   и  

Изобразить схематически график функции   на  

Найти наибольшее и наименьшее значения функции

Построить график функции  . При каких значениях  х  функция  убывает?

Контрольная работа № 1 « Производная и ее геометрический смысл»    Вариант 1

1. Найдите производную функции

2. Найдите значение производной функции  в точке

4. Найдите значение углового коэффициента касательной, проведенной к графику функции  в точке с абсциссой  

5. Найдите , если sin 

6. Напишите уравнение касательной к графику функции  в точке с абсциссой  

7. Найдите скорость и ускорение точки в момент времени c., если она движется прямолинейно по закону  (координата  измеряется метрах).

8. Определите точку максимума функции

9. Найдите наибольшее и наименьшее значение функции  на промежутке  

10. Найдите производную функции

_______________________________________________________________________________________

Контрольная работа № 1 « Производная и ее геометрический смысл»    Вариант 2

1. Найдите производную функции  

2. Найдите значение производной функции  в точке

3. Для какой функции найдена производная sin 

4. Найдите значение углового коэффициента касательной, проведенной к графику функции  в точке с абсциссой

5. Найдите , если .

6. Напишите уравнение касательной к графику функции  в точке с абсциссой .

7. Найдите скорость и ускорение точки в момент времени cек., если она движется прямолинейно по закону  (координата  измеряется в метрах).

8. Определите минимум функции

9. Укажите наибольшее и наименьшее значение функции  на данном промежутке .

10. Вычислите производную функции, если

Контрольная работа № 2 «Применение производной к исследованию функции» Вариант 1

1) Найти стационарные точки функций

а)

б)

в)

2) Найти интервалы возрастания и убывания функции  

3) Найти экстремумы функций

а)

б)

4) Построить график  на [-1; 2]

5) Найти наименьшее и наибольшее значения функции  на [0; 1,5]

6) Среди прямоугольников, сумма длин двух сторон у которых равна 20, найти прямоугольник наибольшей площади.

_______________________________________________________________________________________

Контрольная работа № 2 «Применение производной к исследованию функции» Вариант 2

1) Найти стационарные точки функций

а)

б)

в)

2) Найти интервалы возрастания и убывания функции

3) Найти экстремумы функций

а)

б)

4) Построить график  на [-1; 2]

5) Найти наименьшее и наибольшее значения  на [-1; 1,5]

6) Найти ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.

Контрольная работа № 2 «Применение производной к исследованию функции» Вариант 3

1) Найти стационарные точки функций

а)

б)

в)

2) Найти интервалы возрастания и убывания функции  

3) Найти экстремумы функций

а)

б)

4) Построить график  на [-2; 2]

5) Найти наименьшее и наибольшее значения функции  на [0,5; 1,5]

6) Среди прямоугольников, сумма длин двух сторон у которых равна 40, найти прямоугольник наибольшей площади.

_______________________________________________________________________________________

Контрольная работа № 2 «Применение производной к исследованию функции» Вариант 4

1) Найти стационарные точки функций

а)

б)

в)

2) Найти интервалы возрастания и убывания функции

3) Найти экстремумы функций

а)

б)

4) Построить график  на [-2; 2]

5) Найти наименьшее и наибольшее значения  на [-1; 1,5]

6) Найти ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 20.

Контрольная работа № 3 «Цилиндр, конус и шар»                      Вариант № 1

1. Найдите площадь поверхности конуса, высота которого равна 12 см, а радиус основания 9 см.

2. Развертка боковой поверхности цилиндра является квадратом, диагональ которого 10 см. Найдите площадь боковой поверхности цилиндра.

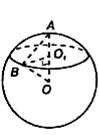
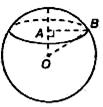
3. Запишите уравнение сферы с центром в точке A (-2; -9; 1), проходящей через точку N (6; -8; -7).

4. Докажите, что уравнение x2 – x + y2 – 2y + z2 + 3z = 12,5 является уравнением сферы и найдите центр и радиус этой сферы.

_______________________________________________________________________________________

Контрольная работа № 3 «Цилиндр, конус и шар»                      Вариант № 2

1. Найдите площадь поверхности конуса, высота которого равна 24 см, а радиус основания 10 см.
2. Развертка боковой поверхности цилиндра является квадратом, диагональ которого 10 см. Найдите площадь боковой поверхности цилиндра.
3. Запишите уравнение сферы с центром в точке A (-3; -5; 4), проходящей через точку N (2; -2; -7).
4. Докажите, что уравнение x2 – x + y2 – 4y + z2 + 3z = 29,5 является уравнением сферы и найдите центр и радиус этой сферы.

_______________________________________________________________________________________

Контрольная работа № 3 «Цилиндр, конус и шар»                      Вариант № 3

1. Найдите площадь поверхности конуса, высота которого равна 20 см, а радиус основания 15 см.
2. Развертка боковой поверхности цилиндра является квадратом, диагональ которого 20 см. Найдите площадь боковой поверхности цилиндра.
3. Запишите уравнение сферы с центром в точке A (-4; -2; 2), проходящей через точку N (1; -8; -3).
4. Докажите, что уравнение x2 – 3x + y2 – y + z2 + 2z = 21,5 является уравнением сферы и найдите центр и радиус этой сферы.

_______________________________________________________________________________________

Контрольная работа № 3 «Цилиндр, конус и шар»                      Вариант № 4

1. Найдите площадь поверхности конуса, высота которого равна 15 см, а радиус основания 8 см.
2. Развертка боковой поверхности цилиндра является квадратом, диагональ которого 10 см. Найдите площадь боковой поверхности цилиндра.
3. Запишите уравнение сферы с центром в точке A (-3; -2; 4), проходящей через точку N (4; -7; -2).
4. Докажите, что уравнение x2 + 3x + y2 – y + z2 + 4z = 12,5 является уравнением сферы и найдите центр и радиус этой сферы.

_______________________________________________________________________________________

Контрольная работа № 3 «Цилиндр, конус и шар»                      Вариант № 5

1. Найдите площадь поверхности конуса, высота которого равна 16 см, а радиус основания 12 см.

2. Развертка боковой поверхности цилиндра является квадратом, диагональ которого 15 см. Найдите площадь боковой поверхности цилиндра.

3. Запишите уравнение сферы с центром в точке A (-3; -1; 6), проходящей через точку N (4; -6; -1).

4. Докажите, что уравнение x2 + 2x + y2 – 3y + z2 + z = 2,5 является уравнением сферы и найдите центр и радиус этой сферы.

_______________________________________________________________________________________

Контрольная работа № 3 «Цилиндр, конус и шар»                      Вариант № 6

1. Найдите площадь поверхности конуса, высота которого равна 24 см, а радиус основания 7 см.

2. Развертка боковой поверхности цилиндра является квадратом, диагональ которого 10 см. Найдите площадь боковой поверхности цилиндра.

3. Запишите уравнение сферы с центром в точке A (-3; -4; 4), проходящей через точку N (2; -1; -2).

4. Докажите, что уравнение x2 – 4x + y2 – 3y + z2 + z = 9,5 является уравнением сферы и найдите центр и радиус этой сферы.

Контрольная работа № 4 «Интеграл»                                               Вариант №1

1. Определите функцию f(x), для которой F(x) = x2 – sin2x – 1 является первообразной:
2. Найдите первообразные для функций а)  б)  в)  г)
3. Для функции f(x) = х2 найдите первообразную F, проходящую через точку A(-1;2)
4. Точка движется по прямой так, что её скорость в момент времени t равна V (t) = t + t2. Найдите путь, пройденный точкой за время от 1 до 3 сек, если скорость измеряется в м /сек.
5. Вычислите определенные интегралы  а)   б)   в)  
6. Найдите площадь криволинейной трапеции, ограниченной линиями у = – х2 + 9 и у = 0
7. Найдите площадь фигуры, ограниченной линиями у =  и у = х
8. Вычислите площадь фигуры, ограниченной графиком функции у = 2 – х2, касательной к этому графику в его точке с абсциссой х = — 1 и прямой х = 0

_______________________________________________________________________________________

Контрольная работа № 4 «Интеграл»                                      Вариант №2

1. Определите функцию f(x), для которой F(x) = – cos — x3 + 4 является первообразной:
2. Найдите первообразные для функций а)  б)  в)  г)
3. Для функции f(x) = 2x — 2 найдите первообразную F, график которой проходит через точку А(2;1)
4. Точка движется по прямой так, что её скорость в момент времени t равна V (t) =3 + 0,2 t. Найдите путь, пройденный точкой за время от 1 до 7 сек., если скорость измеряется в м /сек
5. Вычислите определенные интегралы  а)   б)    в)
6. Найдите площадь криволинейной трапеции, ограниченной линиями у = 2х2, у = 0, х = 2
7. Найдите площадь фигуры, ограниченной линиями у = 5 – х2 , у = 1
8. Вычислите площадь фигуры, ограниченной графиком функции у = – х2 + 3, касательной к этому графику в его точке с абсциссой х = 1 и прямой х = 0.

Контрольная работа № 4 «Интеграл»                                               Вариант №3

1. Определите функцию f(x), для которой F(x) = x2 – sin2x – 1 является первообразной:
2. Найдите первообразные для функций    а) f(x)=10x2-2x   б) f(x)=8x3-x+4  в) f(x)=9√x  f (x) = 4х3 + cos x
3. Для функции f(x) = х2 найдите первообразную F, принимающую заданное значение в заданной точке F (- 1) = 2
4. Точка движется по прямой так, что её скорость в момент времени t равна V (t) = t + t2. Найдите путь, пройденный точкой за время от 1 до 3 сек, если скорость измеряется в м /сек.
5. Вычислите определенные интегралы  а)   б)    в)
6. Найдите площадь криволинейной трапеции, ограниченной линиями у = – х2 + 3 и у = 0
7. Найдите площадь фигуры, ограниченной линиями у =  и у = х
8. Вычислите площадь фигуры, ограниченной графиком функции у = 2 – х2, касательной к этому графику в его точке с абсциссой х = — 1 и прямой х = 0

_______________________________________________________________________________________

Контрольная работа № 4 «Интеграл»                                      Вариант №4

1. Определите функцию f(x) , для которой F(x) = – cos — x3 + 4 является первообразной:
2. Найдите первообразные для функций  а)  б)  в)  г) 
3. Для функции f(x) = 2x — 2 найдите первообразную F, график которой проходит через точку А(2;1)
4. Точка движется по прямой так, что её скорость в момент времени t равна V (t) =3 + 0,2 t. Найдите путь, пройденный точкой за время от 1 до 7 сек., если скорость измеряется в м /сек
5. Вычислите определенные интегралы  а)   б)    в)
6. Найдите площадь криволинейной трапеции, ограниченной линиями у = 2х2, у = 0, х = 2
7. Найдите площадь фигуры, ограниченной линиями у = 5 – х2 , у = 1
8. Вычислите площадь фигуры, ограниченной графиком функции у = – х2 + 3, касательной к этому графику в его точке с абсциссой х = 1 и прямой х = 0.

Контрольная работа № 5 «Объемы тел»                   Вариант №1

1. Докажите, что уравнение x2 – x + y2 – 2y + z2 + 3z = 12,5 является уравнением сферы и найдите центр и радиус этой сферы.
2. Найдите радиус цилиндра, если его объем равен 1199,9 π см 3, а высота равна 7,1 см.
3. Найдите объем пирамиды с высотой 5√3 см, основанием которой служит равносторонний треугольник со стороной 14 см.
4. Найдите радиус и площадь поверхности сферы, если объем шара, ограниченного этой сферой, равен 288π см 3
5. В правильной треугольной пирамиде боковые грани наклонены к основанию под углом . Расстояние от центра основания до боковой грани равно . Найдите объём пирамиды.
6. Цилиндр описан около шара. Объем цилиндра равен 18. Найдите объем шара.
7. В правильной четырёхугольной пирамиде  сторона основания равна 6, боковое ребро 5. Найдите: 1)площадь боковой поверхности пирамиды; 2)объём пирамиды; 3)угол наклона боковой грани к плоскости основания.

_______________________________________________________________________________________

Контрольная работа № 5 «Объемы тел»                   Вариант №2

1. Докажите, что уравнение x2 – x + y2 – 4y + z2 + 3z = 29,5 является уравнением сферы и найдите центр и радиус этой сферы.
2. Найдите радиус цилиндра, если его объем равен 1016,4 π см 3, а высота равна 8,4 см.
3. Найдите объем пирамиды с высотой 7√3 см, основанием которой служит равносторонний треугольник со стороной 12см.
4. Найдите радиус и площадь поверхности сферы, если объем шара, ограниченного этой сферой, равен 166⅓π см3.
5. Сторона основания правильной шестиугольной пирамиды равна 5, а угол между боковой гранью и основанием равен .Найдите объём пирамиды.
6. Цилиндр описан около шара. Объем цилиндра равен 15. Найдите объем шара.
7. В правильной треугольной пирамиде  сторона основания равна , боковое ребро равно 5. Найдите: 1)площадь боковой поверхности пирамиды; 2)объём пирамиды; 3)угол между боковым ребром и плоскостью основания.

_______________________________________________________________________________________

Контрольная работа № 5 «Объемы тел»                   Вариант №3

1. Докажите, что уравнение x2 – 3x + y2 – y + z2 + 2z = 21,5 является уравнением сферы и найдите центр и радиус этой сферы.
2. Найдите радиус цилиндра, если его объем равен 1339,2 π см 3, а высота равна 9,3 см.
3. Найдите объем пирамиды с высотой 4√3 см, основанием которой служит равносторонний треугольник со стороной 16 см.
4. Найдите радиус и площадь поверхности сферы, если объем шара, ограниченного этой сферой, равен 85⅓π см3.
5. В правильной треугольной пирамиде боковые грани наклонены к основанию под углом . Расстояние от центра основания до боковой грани равно . Найдите объём пирамиды.
6. Цилиндр описан около шара. Объем цилиндра равен 12. Найдите объем шара.
7. В правильной четырёхугольной пирамиде  сторона основания равна 6, боковое ребро 5. Найдите: 1)площадь боковой поверхности пирамиды; 2)объём пирамиды; 3)угол наклона боковой грани к плоскости основания.

Контрольная работа № 5 «Объемы тел»                   Вариант №4

1. Докажите, что уравнение x2 + 3x + y2 – y + z2 + 4z = 12,5 является уравнением сферы и найдите центр и радиус этой сферы.
2. Найдите радиус цилиндра, если егообъем равен 1575 π см 3, а высота равна 7 см.
3. Найдите объем пирамиды с высотой 17 см, основанием которой служит прямоугольный треугольник с катетами 12 см и 7 см.
4. Найдите радиус и объем шара, если площадь поверхности сферы, ограничивающей этот шар, равна 324π см3.
5. Сторона основания правильной шестиугольной пирамиды равна 10, а угол между боковой гранью и основанием равен .Найдите объём пирамиды.
6. Цилиндр описан около шара. Объем цилиндра равен 18. Найдите объем шара.
7. В правильной треугольной пирамиде  сторона основания равна , боковое ребро равно 5. Найдите: 1)площадь боковой поверхности пирамиды; 2)объём пирамиды; 3)угол между боковым ребром и плоскостью основания.

_______________________________________________________________________________________

Контрольная работа № 5 «Объемы тел»                   Вариант №5

1. Докажите, что уравнение x2 + 2x + y2 – 3y + z2 + z = 2,5 является уравнением сферы и найдите центр и радиус этой сферы.
2. Найдите радиус цилиндра, если его объем равен 1734π см3, а высота равна 6 см.
3. Найдите объем пирамиды с высотой 18 см, основанием которой служит прямоугольный треугольник с катетами 14 см и 5 см.
4. Найдите радиус и объем шара, если площадь поверхности сферы, ограничивающей этот шар, равна 256π см3.
5. В правильной треугольной пирамиде боковые грани наклонены к основанию под углом . Расстояние от центра основания до боковой грани равно . Найдите объём пирамиды.
6. Цилиндр описан около шара. Объем цилиндра равен 15. Найдите объем шара.
7. В правильной четырёхугольной пирамиде  сторона основания равна 6, боковое ребро 5. Найдите: 1)площадь боковой поверхности пирамиды; 2)объём пирамиды; 3)угол наклона боковой грани к плоскости основания.

_______________________________________________________________________________________

Контрольная работа № 5 «Объемы тел»                   Вариант №6

1. Докажите, что уравнение x2 – 4x + y2 – 3y + z2 + z = 9,5 является уравнением сферы и найдите центр и радиус этой сферы.
2. Найдите радиус цилиндра, если его объем равен 2048 π см 3, а высота равна 8 см.
3. Найдите объем пирамиды с высотой 19 см, основанием которой служит прямоугольный треугольник с катетами 16 см и 3 см.
4. Найдите радиус и объем шара, если площадь поверхности сферы, ограничивающей этот шар, равна 196π см3.
5. Сторона основания правильной шестиугольной пирамиды равна 8, а угол между боковой гранью и основанием равен .Найдите объём пирамиды.
6. Цилиндр описан около шара. Объем цилиндра равен 12. Найдите объем шара.
7. В правильной треугольной пирамиде  сторона основания равна , боковое ребро равно 5. Найдите: 1)площадь боковой поверхности пирамиды; 2)объём пирамиды; 3)угол между боковым ребром и плоскостью основания.

Контрольная работа № 6 «Элементы комбинаторики»                 Вариант № 1

1. Сколькими способами можно обозначить вершины восьмиугольника буквами C, D, M, N, U, V, T, Q?
2. Сколькими способами можно расставить на полке 10 книг, из которых три книги являются трехтомником?
3. В группе 25 человек. Сколькими способами можно составить хоккейную команду из шести человек для выступления на соревнованиях?
4. В группе преподается 11 предметов. Сколькими способами можно составить расписание на учебный день из шести уроков, при условии, что уроки не повторяются?
5. Сколько различных трехзначных чисел можно составить из цифр 1; 2; 3; 4?
6. Сколько двузначных чисел можно составить из пяти цифр: 2; 3; 5; 7; 8? Сколько среди них чисел, кратных 3?
7. Сколько анаграмм можно составить из слова «барабан»?
8. На уроке рисования первокласснику надо раскрасить прямоугольник, треугольник и круг в один из четырех цветов (желтый, синий, красный или зеленый) так, чтобы все три фигуры были разных цветов. а) Сколько существует способов раскрашивания этих трех фигур? б) Сколько среди них способов раскрашивания, в которых круг будет зеленым?

___________________________________________________________________________________

Контрольная работа № 6 «Элементы комбинаторики»                Вариант № 2

1. Сколькими способами можно обозначить вершины шестиугольника буквами C, D, A, B, E, F?
2. Сколькими способами можно расставить на полке 8 книг, из которых две книги являются двухтомником?
3. В группе 22 человека. Сколькими способами можно составить команду КВН из семи человек для выступления на конкурсе?
4. В группе преподается 10 предметов. Сколькими способами можно составить расписание на учебный день из шести уроков, при условии, что уроки не повторяются?
5. Сколько различных четырехзначных чисел можно составить из цифр 1; 2; 3?
6. Сколько трехзначных чисел можно составить из четырех цифр: 1; 4; 5; 8? Сколько среди них чисел, кратных 5?
7. Сколько анаграмм можно составить из слова «колокол»?
8. Ученик на уроке труда вырезает из цветной бумаги звезду, квадрат и круг. У него имеется пять листов бумаги разных цветов (желтый, зеленый, красный, синий и фиолетовый). Ученик хочет вырезать все три фигуры разного цвета, но при этом звезда должна быть непременно красной или синей. а) Сколько существует способов вырезания фигур заданным образом? б) Сколько среди них способов, в которых круг будет фиолетовым?

Контрольная работа № 7 «Элементы теории вероятностей»           Вариант № 1

1. В мешке лежат 5 черных, 4 белых и 6 красных одинаковых по форме шаров. Не глядя, вынимают один шар. Какова вероятность того, что шар окажется красным? Какова вероятность того, что шар окажется черным или белым? Какова вероятность того, что шар окажется синим?
2. Из 22 лотерейных билетов три являются выигрышными. Какова вероятность того, что оба билета окажутся выигрышными? Какова вероятность того, что выигрышным окажется ровно один билет?
3. В ящике находятся 90 электроламп, четыре из которых испорчены. Какова вероятность того, что три взятые наугад лампы исправны?
4. Стрелок попадает в мишень при выстреле с вероятностью 0,9. Какова вероятность того, что в серии из трех выстрелов стрелок попал ровно один раз? Ровно два раза? Хотя бы два раза?
5. В коробке «Ассорти» лежат 30 одинаковых по виду шоколадных конфет, из которых 18 штук со сливочной начинкой и 12 штук — с ореховой. Выбираются наугад две конфеты. Какова вероятность того, что обе конфеты окажутся с ореховой начинкой?
6. Ученику надо выучить к зачету 34 вопроса. Он выучил 22 вопроса. На зачете он вытягивает два билета из 34, по одному вопросу в каждом. Какова вероятность того, что ответ хотя бы на один вопрос он знает?
7. Выпускники девятого класса выбрали для продолжения образования следующие профили обучения: 7 человек — юридический, 12 человек — экономический, 6 человек — математический и 10 человек — гуманитарный. Какова вероятность того, что случайно встреченный выпускник этого класса выбрал математический профиль обучения?

___________________________________________________________________________________

Контрольная работа № 7 «Элементы теории вероятностей»           Вариант № 2

1. В мешке лежат 6 черных, 7 белых и 3 красных одинаковых по форме шаров. Не глядя, вынимают один шар. Какова вероятность того, что шар окажется черным? Какова вероятность того, что шар окажется красным или белым? Какова вероятность того, что шар окажется черным, белым или красным?
2. Из 18 лотерейных билетов четыре являются выигрышными. Какова вероятность того, что ни один из четырех билетов не является выигрышным? Какова вероятность того, что выигрышным окажется ровно один билет?
3. В ящике находятся 80 электроламп, четыре из которых испорчены. Какова вероятность того, что три взятые наугад лампы исправны?
4. Стрелок попадает в мишень при выстреле с вероятностью 0,8. Какова вероятность того, что в серии из трех выстрелов стрелок попал ровно один раз? Ровно два раза? Хотя бы два раза?
5. В коробке «Ассорти» лежат 27 одинаковых по виду шоколадных конфет, из которых 15 штук со сливочной начинкой и 12 штук — с ореховой. Выбираются наугад две конфеты. Какова вероятность того, что обе конфеты окажутся с ореховой начинкой?
6. Ученику надо выучить к зачету 32 вопроса. Он выучил 24 вопроса. На зачете он вытягивает два билета из 32, по одному вопросу в каждом. Какова вероятность того, что ответ хотя бы на один вопрос он знает?
7. Выпускники девятого класса выбрали для продолжения образования следующие профили обучения: 7 человек — юридический, 12 человек — экономический, 6 человек — математический и 10 человек — гуманитарный. Какова вероятность того, что случайно встреченный выпускник этого класса выбрал гуманитарный профиль обучения?

Контрольная работа №8   «Элементы математической статистики» Вариант № 1

1. По статистике ежедневных продаж в одном из супермаркетов чеки со скидкой составляют 15%. В течение дня супермаркет посетило 2055 человек. Сколько человек приблизительно получили скидку?
2. Вероятность того, что семена огурцов взойдут, равна 0,84. Сколько семян приблизительно было взято для проращивания, если взошло 140 семян?
3. На соревновании по фигурному катанию фигурист за произвольную программу получил следующие баллы: 4,8; 4,6; 4,1; 4,6; 4,5; 4,3; 4,6; 4,5; 4,5; 4,3. а) Составьте таблицу распределения данных. б) Найдите объем выборки, кратность и частоту каждой варианты.
4. На детской метеостанции ученик производил замеры температуры воздуха в течение 15 дней мая в одно и то же время и получил следующий ряд значений (в °C): 12,4; 12,4; 12,8; 14,1; 15; 15; 14,8; 14,1; 13,9; 13,5; 15; 15; 14,8; 14,1; 12,4. а) Составьте таблицу распределения данных и распределения частот. б) Найдите размах, моду и среднее значение данного ряда чисел.

___________________________________________________________________________________

Контрольная работа № 8  «Элементы математической статистики» Вариант № 2

1. Во время распродажи цена на оргтехнику была снижена в среднем на 30%, при этом цена на принтеры была снижена на 12% от среднего снижения цен на всю оргтехнику. Какова была цена принтера во время распродажи, если до распродажи он стоил 5400 рублей?
2. Вероятность брака при использовании современных высокоточных технологий равна 0,0015. Сколько качественных изделий выпускает предприятие, если число бракованных изделий за исследуемый период было равно 2?
3. На соревновании по фигурному катанию фигурист за произвольную программу получил следующие баллы: 5,9; 5,9; 5,7; 6,0; 5,8; 5,9; 5,8; 5,7; 5,8; 5,9. а) Составьте таблицу распределения данных. б) Найдите объем выборки, кратность и частоту каждой варианты.
4. На экзамене учащиеся класса получили следующие результаты по 100-балльной шкале: 36, 38, 45, 48, 48, 49, 52, 53, 55, 53, 48, 63, 67, 69, 67, 72, 72, 69, 53, 55, 69, 72, 70, 53, 67. а) Постройте графики распределения данных и распределения частот. б) Найдите размах, моду и среднее значение данного ряда чисел.

Программа

итогового экзамена по математике

Раменское,

2013 г.

Пояснительная записка

Программа итогового экзамена по математике предназначена для студентов СПО.

Тест является основной формой проверки знаний за курс математики.

Объем теста – 20 заданий.

Продолжительность проведения экзамена – 5 часов.

Программа итогового экзамена по математике

Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем, согласно стандарта.

1. Тригонометрия:

Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.

1. Производная:

Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.

1. Первообразная:

Основное свойство первообразной. Правила нахождения первообразных.

1. Понятие степени:

Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.

5. Показательная и логарифмическая функции:

Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.

6. Стереометрия:

Многогранники. Тела вращения.

Критерии оценки контрольной работы

1 задание:

Степень с рациональным показателем – 1 балл

2 задание:

Степень с рациональным показателем – 1 балл

3 задание:

Свойства логарифмической функции – 1 балл

4 задание:

Основные тригонометрические формулы – 2 балла

5 задание:

Основные тригонометрические формулы–2 балла

6 задание:

Решение тригонометрических уравнений– 1 балл

7 задание:

Решение иррациональных уравнений – 2 балла

8 задание:

Решение показательных уравнений – 2 балла

9 задание:

Метод интервалов — Решение иррациональных уравнений – 1 балл

10 задание:

Свойства тригонометрических функций – 1 балл

11 задание:

Вычисление производных — 1 балл

12 задание:

Нахождение первообразной функции – 1 балл

13 задание:

Решение логарифмических уравнений – 1 балл

14 задание:

Нахождение максимального и минимального значений функции – 2 балла

15 задание:

Свойства тел в стереометрии – 1 балл

16 задание:

Площадь криволинейной трапеции – 3 балла

17 задание:

Построение графика логарифмической функции – 3 балла

18 задание:

Решение показательных неравенств — 3 балла

19 задание:

Многогранники — 3 балла

20 задание:

Тела вращения — 3 балла

Рекомендации для проверки (проведения) экзаменационного теста.

Тест состоит из 20 заданий.

Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и отметьте соответствующую ячейку в таблицу ответов.

Максимальный балл за тест – 35.

0 – 14 баллов — «2» («неудовлетворительно»)

15 – 19 баллов — «3» («удовлетворительно»)

21 – 29 баллов — «4» («хорошо»)

30 – 35 баллов — «5» («отлично» )

Ответы

Вариант 1

Вариант 2

Вариант 3

Бланк ответов

экзаменационного теста

по математике

Ф.И.О.___________________________________________________

Группа № ________________________

Специальность ____________________

___ вариант.

Вариант 1

1. Вычислите 29 – 15.

1. 2) 43 3) 73 4) 101.

1. Упростите выражение .

1. 5 2) 1 3) 10 4) 0.

3) Упростите выражение – 2.

1) 2) 1 3) 8 4) 20.

4) Найдите значение , если = -0,8 и .

1) -0,6 2) 0,6 3) 0,2 4) 0,36

5) Упростите выражение 7cos²α – 5 + 7sin²α.

1) 1 + cos²α 2) 2 3) -12 4) 12.

6) Решите уравнение = 1.

1)2n, n 2) 3) +2n, n 4) n, n

7) Укажите промежуток, которому принадлежит корень уравнения = -х.

1) 2) (35;37) 3) (-2; 4) .

Укажите промежуток, которому принадлежит корень уравнения = 8.

1) [-4;0) 2) [0;1) 3) [-∞;-4) 4) [4;6).

9) Решите неравенство ≤0.

1) (-∞;-2) [) 2) [-2;) ( 1;+∞) 3) (-∞;-2) 4) (-∞;-5) (-2;.

10) Найдите множество значений функции у =– 2.

1) [3;1] 2) (-∞;+∞) 3) [-1;1] 4) [-3;-1].

11) Найдите производную функции f(x) = .

1) -4 2) -8 3) 8 4) .

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1.

1) х² + х⁴ – х 2) 2х² + 4х⁴ 3) 2 + 12х² 4) х²+х⁴.

13) Решите равнение + = .

1) 0 2) 4 3) 9 4) 15.

14) Найдите точки максимума функции у = х³ – 3х² .

1) 0 2) 2 3) -2 4) 3.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1.

1) 5 2) 10 3) 3 4) 31.

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2.

1) 8 2) 2 3) 5 4) 6.

17) Укажите область определения функции у =.

1) (-∞;0)(2;+∞) 2) (-2;+∞) 3) (2;+∞) 4) (0;2).

18) Найдите наибольшее целое решение неравенства – 1 0.

1) 0 2) -1 3) 1 4) 2.

19) Площади двух граней прямоугольного параллелепипеда равны 56дм² и 192дм², а длина их общего ребра 8дм. Найдите объем параллелепипеда.

1) 840 2) 1029 3) 1344 4) 1210.

20) Образующая конуса равна 12см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 384 2) 192 3) 24 4) 648.

Вариант 2

1. Вычислите 7 — 3∙.

1. 2) 8 3) -5 4) -17.

1. Упростите выражение .

1) 1,2 2) 5 3) 4) .

3) Упростите выражение + — .

1) 2 +2 2) 7 3) 3 — 6 4) 2.

4) Найдите значение, если = и 0.

1) — 2) 3) 4) .

5) Упростите выражение -3sin²α — 6 – 3cos²α.

1) 1 2) 2cosα 3) cosα + 4) -9 .

6) Укажите промежуток, которому принадлежит корень уравнения = -х.

1) 2) (-;-10) 3) 4) .

7) Решите уравнение = 1.

1) n, n 2) 3) +2n, n 4) n,n.

Укажите промежуток, которому принадлежит корень уравнения = 125.

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).

9) Решите неравенство ≤ 0.

1) (-2;) 2) [-2;2) (;+∞) 3) (-∞;3) 4) (-∞;-2) (].

10) Найдите множество значений функции у = + 4.

1) [3;5] 2) (-∞;+∞) 3) [-1;1] 4) [-5;-3].

11) Найдите производную функции f(x) = .

1) 3 2) 3) -3 4) —.

12) Укажите первообразную функции f(x) = 3х² + 2х -4.

1) х³+ х² — 4х 2) 6х + 2 3) х³+ х² 4) х²+ х – 4х.

13) Решите равнение + =

1) 0 2) 11 3) 3 4) 12.

14) Найдите точку минимума функции у = х² — 1.

1) -1 2) 1 3) -2 4) 0.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6.

1) 55 2) 7 3) 49 4) 11.

16) Вычислите площадь фигуры (S), ограниченной линиями у = х³ + 1, у = 0, х = 0, х = 2.

1) 8 2) 5 3) 6 4) 4.

17) Укажите область определения функции у =.

1) (-∞;0)(4;+∞) 2) (-4;+∞) 3) (4;+∞) 4) (0;4).

18) Найдите наименьшее целое решение неравенства – 1 0.

1) 0 2) 1 3) -1 4) 2.

19) Площади двух граней прямоугольного параллелепипеда равны 35см² и 42см², а длина их общего ребра 7см. Найдите объем параллелепипеда.

1) 840 2) 10290 3) 770 4) 210.

20) Образующая конуса равна 24см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 3840 2) 1092 3) 5184 4) 648.

Вариант 3

1) Вычислите 2∙ – 0,9⁰

1)10,9 2) 11 3) 9,1 4) 9.

2) Упростите выражение

1. 2) 2 3) 0,7 4) 36.

3) Упростите выражение — +

1) -1 + 2) -2 3) 0 4) .

4) Найдите значение , если = — и

1) 2) 3) 4)

5) Упростите выражение -4sin²α +5 – 4cos²α

1) 1 2) 1 + 8sin²α 3) 1 + 8cos²α 4) 9.

6) Укажите промежуток, которому принадлежит корень уравнения = -х

1) 2) (-∞;-2) 3) 4) .

7) Решите уравнение = -1

1) 2)0 3) +2n, n 4) n, n

Укажите промежуток, которому принадлежит корень уравнения = 16

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).

9) Решите неравенство ≥0

1) (-∞;-8] (; 2) 2) [-8;) ( 2;+∞) 3) (-∞; 2) 4) (-∞;-8) (2; +∞.

10) Найдите множество значений функции у = – 1

1) [-1;1] 2) (-∞;+∞) 3) [-2;0] 4) [0;2].

11) Найдите производную функции f(x) =

1) -18 2) 6 3) 18 4) .

12) Укажите первообразную функции f(x) = 5х⁴ – 2х + 1

1) 5х⁵ – 2х² + 1 2) 20х³ – х 3) х⁴ – 2х + х 4) х⁵ – х² + х.

13) Решите равнение + =

1) 15 2) 5 3) 4 4) 10.

14) Найдите точку максимума функции у = 4х – х⁴

1) 4 2) 2 3) -4 4) 0.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7

1) 19 2) 11 3) 121 4) 36.

16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х³, у = 0, х = 0, х = 1.

1) 1 2) 3) 4) 1.

17) Укажите область определения функции у =.

1) (-3;+∞) 2) (-∞;0)(3;+∞) 3) (3;+∞) 4) (0;3).

18) Найдите наибольшее целое решение неравенства – 1 0.

1) 1 2) -1 3) 2 4) 0.

19) Площади двух граней прямоугольного параллелепипеда равны 20см² и 45см², а длина их общего ребра 5см. Найдите объем параллелепипеда.

1) 240 2) 120 3) 180 4) 4500.

20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 3804 2) 2192 3) 2187 4) 6408.

ВАРИАНТЫ ВЫПУСКНЫХ ЭКЗАМЕНОВ ЗА КУРС СРЕДНЕЙ ШКОЛЫ
с 1967 до 2008 года

В 1967 был проведён эксперимент, а с 1968 года устные выпускные экзамены по алгебре и началам анализа во всех советских школах стали письменными. С 1967 до начала 70-х годов экзамен состоял из четырёх, затем пяти, а с 1990 года — шести неизвестных заранее задач, составляемых министерством образования. С 2002 по 2008 год этот способ проверки знаний использовался только для учащихся математических и физико-математических классов. Для тех, кто занимался по базовой или гуманитарной программе, в 2001 году был вновь был проведен эксперимент, а с 2002 года проводился экзамен по открытым текстам: вариант состоял из 10 заданий, взятых из заранее опубликованного задачника. Продолжительность экзаменов составляла 5 астрономических часов.

Ниже мы приводим задания выпускных экзаменов по математике, проводившихся в России с 1967 до 2008 год включительно, пока эта форма экзамена не уступила место единому новой, в формате ЕГЭ и ГВЭ. Для базовых, физико-математических и математических классов ежегодно составлялось несколько экзаменационных работ по нескольким часовым поясам, каждая в двух равноценных вариантах. Обозначение 1991-Э1-2 означает второй вариант первой работы 1991 года. Варианты углубленной программы до 1977 года и те, у которых стоит метка «ищем», мы найти не смогли. Если они у вас есть — присылайте.

С 2009 по 2015 год выпускные экзамены из школ были объединены со вступительными экзаменами в вузы и проводились в формате Единого государственного экзамена. С 2016 года ЕГЭ по математике стал проводиться в двух форматах: к прежнему (профильному) экзамену, объединяющему в себе выпускной и вступительный экзамен, добавился экзамен другой структуры и сложности, называвшийся ЕГЭ по базовой математике.

В 2020 году ЕГЭ по базовой математике был отменен (школьники могли выпуститься из школы, не сдавая экзаменов), а в 2021 году экзаменом для выпускников школ, не планирующих поступать в университеты, был ГВЭ — государственный выпускной экзамен. ЕГЭ профильного уровня по-прежнему сочетает в себе функции впускного экзамена из школ и вступительного экзамены в вузы.

Варианты ЕГЭ-профиль, ЕГЭ-база и различные варианты ГВЭ представлены на сайте Решу ЕГЭ.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет №1

1.       
Корни
натуральной степени из числа и их свойства.

2.       
Перпендикуляр
и наклонная.

3.       
Событие,
вероятность события.

4.           
Примеры:

1)
Решить уравнения

2)Найти
предел

5.                
 Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№2

1.    
Степени
с рациональными показателями, их свойства.

2.    
Параллелепипед.
Куб.

3.    
Понятие
о пределе последовательности.

4.    
Примеры:

1)Упростите выражение

cos²x-6+sin²x

2) Найти производную

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№3

1.    
Логарифми
его свойства

2.     Двугранный угол.

3.     Понятие о
производной функции, её геометрический смысл.

4.     Примеры:

1) Найти значение производной функции

f¹(x)
при x=0—1

2) Найти предел

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№4

1.     Радианная
мера угла

2.     Раскрытие
неопределенностей 0/0  и  ∞/∞.

3.     Цилиндр.

4.     Примеры:

1)Вычислите

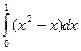
2) Упростите выражение   

cos⁴x—sin⁴x

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№5

1.       
Основные
тригонометрические тождества

2.       
Геометрические преобразования пространства:
параллельный перенос

3.       
Понятие о производной функции

4.       
Примеры

1)Необходимо
выбрать в подарок 4 из 10 имеющихся  книг. Сколькими способами можно это
сделать?

2)
Найти значение производной функции

f¹(x) при x=1

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№6

1.     Геометрический
смысл производной функции

2.     Геометрические
преобразования пространства: симметрия относительно плоскости

3.     Шар и сфера, их
сечения.

4.     Примеры:

1)  
Из 30 участников собрание надо
выбрать председателя и секретаря. Сколькими способами это можно сделать?

2)    Найти
производную

f(x)=xcosx

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№7

1.     Физический смысл
производной функции

2.    
Арксинус, арккосинус, арктангенс
числа

3.    
Формулы
объема куба, прямоугольного параллелепипеда

4.    
Примеры:

1)  Сколько шестизначных чисел (без повторения цифр) можно
составить из цифр 0, 3, 5, 6, 7, 8?

2)  Решите уравнения

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№8

1.    
Функции.Область
определения и множество значений; график функции.

2.     Производные суммы,
разности, произведения, частного.

3.    
Формулы
объема цилиндра

4.     Примеры:

1)   
Сколькими способами 8 человек
могут встать в очередь в театральную кассу?

2)  Вычислить:1)
;  2)

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№9

1.     Исследование
функции по схеме.

2.     Производные
основных элементарных функций.

3.     Формулы
объема куба.

4.     Примеры:

1)     
Вычислить

           2)          3) 

2)    Решить
уравнения

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№10

1.     Действия над
векторами в пространстве

2.     Производные
основных элементарных функций.

3.     Параллелепипед.
Куб.

4.     Примеры:

1)     
Упростить:

(sin²x+tx²xsin²x)ctgx

2)   
Найти
значение выражения

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№11

1.     Перпендикуляр и
наклонная.

2.     Понятие о пределе последовательности.

3.    
Логарифми
его свойства.

4.    
Примеры

1)Вычислите

 5^-4 *
5⁶;                3)   7¹⁰ : 7¹²;                  
5)  (3^-4)^-1;

2)Написать
уравнение касательной к графику  функции в точке с абсциссой x₀

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№12

1.     Корни
натуральной степени из числа и их свойства

2.     Производные суммы,
разности, произведения, частного.

3.     Аксиомы
стереометрии

4.     Примеры:

1)      Вычислите

  4⁴ *4^-3;            
65^-3 : 65^-3;                (8²)^-2
* 8³

2)    В группе 30 студентов. Необходимо выбрать старосту,
заместителя старосты и профорга. Сколько существует способов это сделать?

5. 
Задача :

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№13

1.     Пирамида.
Правильная пирамида.

2.     Показательная
функция, свойства и график.

3.    
Арксинус, арккосинус, арктангенс
числа

4.    
Примеры:

1)   
Вычислить:

  81* 3^-4;                
2)  9^-6 * 9⁵;                      3)   (3^-1)⁵
*27²; 

2)   
Порядок выступления 7 участников конкурса
определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

5.    
Задача

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№14

1.     Шар
и сфера, их сечения

2.     Основные
понятия комбинаторики

3.     Действия над
векторами в пространстве

4.     Примеры

1)   
Вычислить:

 6⁰
: 6^-3   5)   9^-2 :  3^-6;                               6) 
125^-4 : 25^-5

2)     Вычислите

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№15

1.    
Формулы
объема цилиндра

2.    
Степени
с рациональными показателями, их свойства.

3.     Основные
тригонометрические тождества

4.     Примеры:

1)   
Решите уравнение    

sin²x = cosx—
cos²x

2)    
Найти производную

f ¹(x) при x=0 —1

5.     Задача

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№16

1.     Формулы
объема цилиндра, конуса

2.     Исследование
функции по схеме.

3.     Раскрытие
неопределенностей 0/0 

4.     Примеры:

1)   
Вычислите

2)    В шахматном турнире участвуют 16 человек. Сколько
партий должно быть сыграно в турнире, если между любыми двумя участниками
должна быть сыграна одна партия?

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№17

1.     Формулы
объема шара

2.     Раскрытие
неопределенностей ∞/∞.

3.     Параллельный
перенос

4.     Примеры:

1)    Решите
графически 

2) На борту самолёта 12 мест рядом с
запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные
места неудобны для пассажира высокого роста. Пассажир В. высокого роста.
Найдите вероятность того, что на регистрации при случайном выбореместа пассажиру
В. достанется удобное место, если всего в самолёте 300 мест

5.    Задача:

МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ
КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№18

1.    
Формулы
объема куба, прямоугольного параллелепипеда

2.     Радианная мера
угла.

3.    
Логарифмическая
функция, свойства и график

4.    
Примеры:

1)   
Вычислите

2)    
 

Из множества натуральных чисел от 10 до 19 наудачу
выбирают        одно число. Какова вероятность того, что оно делится на 3?

5.     Задача

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№19

1.    
Формулы
объема призмы

2.    
Физический
смысл производной

3.    
Событие,
вероятность события

4.    
Примеры:

1) Напишите
первые пять членов последовательности.

а_n=2ⁿ+1/2ⁿ

2)Решите
уравнение

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№20

1.    
Формулы
объема пирамиды, усеченной пирамиды 

2.    
Геометрический
смысл производной

3.     Степенная
функция,  свойства и график.

4.     Примеры:

1)    Решить уравнения

2)   В
сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос
по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
достанетсявопрос
по ботанике.

5.    Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№21

1.     Площади
поверхностей тел вращения.

2.     Понятие о
производной функции

3.     Функции.Область
определения и множество значений; график функции

4.     Примеры:

1)    Решите уравнения

2)   В
сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос
по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
не достанетсявопроса по неравенствам.

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№22

1.    
Векторы
в пространстве.

2.     Основные
тригонометрические тождества.

3.    
Раскрытие
неопределенностей 0/0.

4.    
Примеры:

1)   
Решить
уравнение

3(x-2)-5=4-(5x-1)

2)   
Исследуйте
функцию и постройте график

f(x)=3x^-1

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№23

1.     Площади
поверхностей тел вращения.

2.     Логарифми его
свойства

3.     Радианная мера
угла.

4.     Примеры:

1)  Решить уравнения

.

2)Исследуйте
функцию и постройте график

f(x)=x²+2

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№24

1.     Конус. Усеченный
конус. 

2.    
Корни
натуральной степени из числа и их свойства.      

3.    
Арксинус, арккосинус, арктангенс
числа

4.    
Примеры:

1)    Вычислите

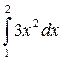
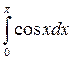
2)   
Первести из градусной меры в радианную

 45⁰,60⁰,36⁰

5.
Задача