Переводной экзамен по математике
6 класс
Вариант 0601
Общее время работы – 90 минут
Характеристика работы:
Всего в работе 15 заданий – базового уровня.
Работа состоит из тем: «Делители и кратные», «Дроби», «Отношения и пропорции», «Нахождение дроби от числа», «Углы», «Решение уравнений», «Координатная плоскость».
Советы и указания по выполнению работы:
Начать советуем с заданий, которые вызывают у Вас меньше затруднений, затем переходит к другим. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы.
Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Ответы на вопросы 6, 7, 8, 9 записывать в виде последовательности букв, без запятых и пробелов.
Оценивание работы:
Задания с 1 по 5 оцениваются по 1 баллу.
Задания с 6 по 9 оцениваются по 2 балла.
Задания с 10 по 15 оцениваются по 3 балла.
Баллы, полученные за верно выполненные задания, суммируются.
Для успешной сдачи переводной работы необходимо набрать не менее 16 баллов.
Часть А
|
Ответы на задания с 1 по 9 впишите в БЛАНК №1 |
-
Какие числа являются делителями числа 57?
-
1, 3, 6, 19 и 57;
-
1, 3, 19 и 57;
-
3, 9 19 и 57;
-
1, 2 и 57.
-
Вычислите:
-
;
-
;
-
-
4.
-
Найдите неизвестный член пропорции
-
х =
;
-
х = 2;
-
х = 3;
-
х = 0,2.
-
Найдите х, если |x| = 3,1.
-
– 3,1 и 3,1;
-
3,1;
-
– 3,1;
-
0.
-
Вычислите:
-
Сопоставьте понятие с верным определением:
|
1) |
Правильная дробь – это … |
А) |
дробь, в которой числитель больше или равен знаменателю |
|
2) |
Сокращение дроби – это … |
Б) |
дробь, в которой числитель меньше знаменателя |
|
3) |
Неправильная дробь – это… |
В) |
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель |
|
4) |
Дополнительный множитель – это… |
Г) |
Деление числителя и знаменателя на одно и то же число |
-
Сопоставьте формулу с верным названием:
|
1) |
(a + b) ∙ c = ac + bc |
А) |
свойство единицы |
|
2) |
a + (– a) = 0 |
Б) |
распределительное свойство |
|
3) |
a ∙ 1 = a |
В) |
переместительное свойство |
|
4) |
a + b = b + a |
Г) |
свойство противоположных чисел |
-
Сопоставьте понятие с верным определением:
|
1) |
Луч – это … |
А) |
линия, имеющая начало и конец |
|
2) |
Прямая – это … |
Б) |
линия, имеющая начало и не имеющая конца |
|
3) |
Отрезок – это… |
В) |
геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами |
|
4) |
Ломанная – это … |
Г) |
линия, не имеющая ни конца, ни начала |
-
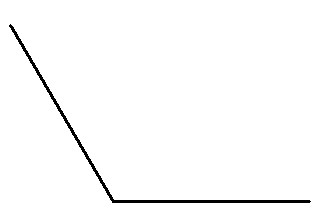
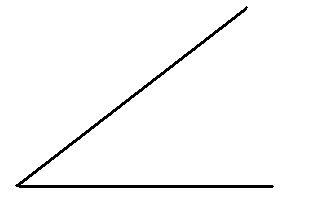
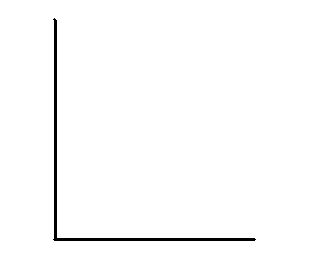
Сопоставьте угол с верным названием:
|
1) |
|
А) |
прямой |
|
2) |
|
Б) |
тупой |
|
3) |
|
В) |
острый |
Часть Б
|
Ответы с ПОЛНЫМ решением на задания с 10 по 15 впишите в БЛАНК №2 |
-
Найдите значение выражения
-
Решите уравнение: 8х = – 62,4 + 5х
-
Решите уравнение: (0,6 + 2х)(7х – 2,8) = 0
-
Ученик прочитал 45% всей книги, после чего ему осталось прочитать еще 165 страниц. Сколько страниц в этой книге?
-
Найдите длину окружности, если ее диаметр 15 см.
-
Отметьте на координатной плоскости точки А(–4; 0), В (2; 6), С (–4; 3), D (4; –1). Проведите луч АВ и отрезок СD. Найдите координаты точки пересечения луча АВ и отрезка CD.(За единичный отрезок принимать 1 клетку)
Переводной экзамен по математике
6 класс
Вариант 0602
Общее время работы – 90 минут
Характеристика работы:
Всего в работе 15 заданий – базового уровня.
Работа состоит из тем: «Делители и кратные», «Дроби», «Отношения и пропорции», «Нахождение дроби от числа», «Углы», «Решение уравнений», «Координатная плоскость».
Советы и указания по выполнению работы:
Начать советуем с заданий, которые вызывают у Вас меньше затруднений, затем переходит к другим. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы.
Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Ответы на вопросы 6, 7, 8, 9 записывать в виде последовательности букв, без запятых и пробелов.
Оценивание работы:
Задания с 1 по 5 оцениваются по 1 баллу.
Задания с 6 по 9 оцениваются по 2 балла.
Задания с 10 по 15 оцениваются по 3 балла.
Баллы, полученные за верно выполненные задания, суммируются.
Для успешной сдачи переводной работы необходимо набрать не менее 16 баллов.
Часть А
|
Ответы на задания с 1 по 9 впишите в БЛАНК №1 |
-
Какие числа являются делителями числа 51?
1) 1, 2 и 51;
-
1, , 17 и 51;
-
1, 3, 9 и 17;
-
1, 3, 9, 17 и 51.
-
Вычислите:
-
;
-
;
-
-
6
.
-
Найдите неизвестный член пропорции
-
х = 12,6;
-
х = 1,26;
-
х = 3;
-
х = 0,3.
-
Найдите y, если |y| = 7,2.
-
0;
-
7,2;
-
– 7,2;
-
7,2 и – 7,2.
-
Вычислите:
.
-
Сопоставьте понятие с верным определением:
|
1) |
Коэффициент – это … |
А) |
равенство с одной или несколькими неизвестными величинами. |
|
2) |
Уравнение – это… |
Б) |
такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство. |
|
3) |
Подобные слагаемые – это… |
В) |
числовой множитель при буквенном выражении |
|
4) |
Корень уравнения – это… |
Г) |
Слагаемые, имеющие одинаковую буквенную часть |
-
Сопоставьте понятие с верным определением:
|
1) |
(a – b) ∙ c = ac – bc |
А) |
свойство взаимно обратных чисел |
|
2) |
(a + b) + c = a + (b + c) |
Б) |
свойство нуля |
|
3) |
a ∙ |
В) |
сочетательное свойство |
|
4) |
a ∙ 0 = 0 |
Г) |
распределительное свойство |
-
Сопоставьте понятие с верным определением:
|
1) |
Ломанная – это … |
А) |
линия, имеющая начало и не имеющая конца |
|
2) |
Отрезок – это… |
Б) |
геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами |
|
3) |
Луч – это … |
В) |
линия, не имеющая ни конца, ни начала |
|
4) |
Прямая – это … |
Г) |
линия, имеющая начало и конец |
-
Сопоставьте угол с верным названием:
|
1) |
|
А) |
прямой |
|
2) |
|
Б) |
тупой |
|
3) |
|
В) |
острый |
Часть Б
|
Ответы с ПОЛНЫМ решением на задания с 10 по 15 впишите в БЛАНК №2 |
-
Найдите значение выражения
-
Решите уравнение: 7х = – 95,4 – 2х
-
Решите уравнение: (0,8 – 4x)(5х + 5,5) = 0
-
До обеда рабочий выполнил 65% всего задания, после чего ему осталось изготовить еще 105 деталей. Сколько деталей должен изготовить рабочий по заданию?
-
Найдите площадь круга, радиус которого 6 см.
-
На координатной плоскости проведите прямую MN через точки M (
4;
2) и N (5; 4) и отрезок KD, соединяющий точки K(–9;4) и D (–6; –8). Найдите координаты точки пересечения отрезка KD и прямой MN. (За единичный отрезок принимать 1 клетку)
М-6 ит тестир 1 вариант
А1 Определите количество делителей числа 45
- 4 2) 5 3) 7 4) 6
А2. Наибольший общий делитель чисел 125 и 150 равен
1) 75 2) 25 3) 5 4) 10
А3 Вычислите:2

2)
3) 3
4)
А4 Вычислите: 3
- 1
2)
3) 1
4) 1
А5 Найдите неизвестный член пропорции 9 : Х = 45 : 15
- 5 2) 6 3)
4) 4
А6 Какие из чисел являются противоположными?
- 0 и 2 2) 3 и
3) 5 и —
4) 19 и — 19
А7 .Вычислите: 
- – 19 2) 18 3) 67 4) -67
А8. Найдите корни уравнения | Х | = 15,8
- 15,8 2) 15,8 и – 15,8 3) – 15,8 4) нет корней
В1. Вычислите: 45 + 16 – (- 15) – 16 +44 -15
В2 Решите уравнение: 4х + 5 = 2х — 8
С1. Найдите координаты точки пересечения прямых АВ и СК, если А(-2 ; 2),
В( 2 ; -1,5), С(-5 ; 0 ), К( 2 ; 3).
М-6 ит тестир 2 вариант
А1 Определите количество делителей числа 48
1)4 2) 10 3) 7 4) 6
А2. Наибольший общий делитель чисел 120 и 150 равен
1) 75 2) 25 3) 5 4) 30
А3 Вычислите:4

1)


А4 Вычислите: 3
1)1


А5 Найдите неизвестный член пропорции 32 : Х = 40 : 5
- 5 2) 6 3)
4) 4
А6 Какие из чисел являются противоположными?
- 12 и -12 2) 3 и
3) 5 и —
4) 19 и 1,9
А7 .Вычислите: 
- 61 2) 18 3) 13 4) -61
А8. Найдите корни уравнения | Х | = 24,1
- 24,1 2)- 24,1 3) – 24,1 и 24,1 4) нет корней
В1. Вычислите: 35 + 18 – (- 15) – 18 +36 -15
В2 Решите уравнение: 7х + 5 = 5х — 15
С1. Найдите координаты точки пересечения прямых АВ и СК, если А(-5 ; -1),
В( 3; 3), С(-4 ; 2,5 ), К( 3 ; -1).
Тесты по математике для 6 класса
Данная работа является итоговой формой диагностики знаний учащихся при завершении учебного года.
Работа представлена в двух вариантах, она состоит из заданий, отвечающих базовому минимуму и более высоким требованиям.
В заданиях с А1 по А8 имеются 4 варианта ответа, из которых только один верный. Учащимся необходимо выбрать номер верного ответа.
В заданиях В1 и В2 нужно записать только ответ. Решение задания С1 необходимо аккуратно и разборчиво записать на листе.
Время выполнения 45 минут.
Критерии оценивания работы:
5-6 заданий базового уровня – «3»,
7-8 заданий – «4»,
9-11 заданий – «5».
Если ученик выполнил верно любые 5 заданий из части А и одно и части В, то выставляется оценка «4».
Ответы к тестам:
|
№ п/п |
ответ |
|
А1 |
2 |
|
А2 |
4 |
|
А3 |
4 |
|
А4 |
2 |
|
А5 |
4 |
|
А6 |
1 |
|
А7 |
1 |
|
А8 |
3 |
|
В1 |
61 |
|
В2 |
-10 |
|
С1 |
(-1; 1 ) |
1 вариант 2 вариант
|
№ п/п |
ответ |
|
А1 |
4 |
|
А2 |
2 |
|
А3 |
4 |
|
А4 |
1 |
|
А5 |
3 |
|
А6 |
4 |
|
А7 |
3 |
|
А8 |
2 |
|
В1 |
89 |
|
В2 |
— 6,5 |
|
С1 |
( -1,5; 1,5 ) |
В период с 15 марта по 21 мая 2021 года состоялись всероссийские проверочные работы по математике в 6 классах.
После проведения ВПР в школах стали доступны реальные варианты и критерии оценки.
Для каждой школы варианты формировались индивидуально из банка заданий ВПР.
→ рабочие тетради ВПР для 6 класса
ВПР 2021 по математике для 6 класса с ответами
| Комплект заданий ВПР 1 | |
| Вариант 1 | Скачать ответы |
| Вариант 2 | Скачать ответы |
| Комплект заданий ВПР 2 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект заданий ВПР 3 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект заданий ВПР 4 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект заданий ВПР 5 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект заданий ВПР 6 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект заданий ВПР 7 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект заданий ВПР 8 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект заданий ВПР 9 | |
| variant 1 | otvet |
| variant 2 | otvet |
| Комплект заданий ВПР 10 | |
| variant 1 | otvet |
| variant 2 | otvet |
На выполнение работы по математике даётся 60 минут. Работа содержит 13 заданий.
Типы заданий, сценарии выполнения заданий ВПР 2021по математике 5 класс
В заданиях 1–2 проверяется владение понятиями отрицательные числа, обыкновенная дробь.
В задании 3 проверяется умение находить часть числа и число по его
части.
В задании 4 проверяется владение понятием десятичная дробь.
Заданием 5 проверяется умение оценивать размеры реальных объектов окружающего мира.
В задании 6 проверяется умение извлекать информацию, представленную в таблицах, на диаграммах.
В задании 7 проверяется умение оперировать понятием модуль числа.
В задании 8 проверяется умение сравнивать обыкновенные дроби, десятичные дроби и смешанные числа.
В задании 9 проверяется умение находить значение арифметического выражения с обыкновенными дробями и смешанными числами.
Задание 10 направлено на проверку умения решать несложные логические задачи, а также на проверку умения находить пересечение, объединение, подмножество в простейших ситуациях.
В задании 11 проверяются умения решать текстовые задачи на проценты, задачи практического содержания.
Задание 12 направлено на проверку умения применять геометрические представления при решении практических задач, а также на проверку навыков геометрических построений.
Задание 13 является заданием повышенного уровня сложности и направлено на проверку логического мышления, умения проводить математические рассуждения.
Успешное выполнение обучающимися заданий 12 и 13 в совокупности
с высокими результатами по остальным заданиям говорит о
целесообразности построения для них индивидуальных образовательных
траекторий в целях развития их математических способностей.
Связанные страницы:
Переводной экзамен по математике 6 класс в тестовой форме
Экзаменационная работа по структуре и содержанию приближена к новой форме итоговой аттестации в 9 классе.
Экзаменационная работа составлена в 2-х вариантах. К экзаменационной работе прилагается бланк для заполнения ответов 1 части. Бланк заполняется черной гелевой ручкой печатными буквами. Для объективности выставления оценки бланк разделен на 2 части. В 1-ой части есть ФИО ученика и код ученика. Во 2-ой части, которая отдается проверяющему учителю — только код ученика.
Содержание переводного экзаменационного материала соответствует «Обязательному минимуму содержания основного общего образования по математике».
Работа состоит из двух частей.
Часть I направлена на проверку достижения уровня базовой подготовки. Она содержит задания, предусматривающие три формы ответа:
- задания с выбором ответа из четырех предложенных;
- задания с кратким ответом;
- задания на соотнесения.
С помощью этих заданий проверяется знание и понимание важных элементов содержания, владение основными алгоритмами, умение применить знания к решению математических задач, на сводящихся к прямому применению алгоритма, а так же применение знаний в простейших практических ситуациях. При выполнении заданий первой части учащиеся должны продемонстрировать определенную системность знаний и широту представлений, умение переходить с одного математического языка на другой, узнавать стандартные задачи в разнообразных формулировках.
Часть II состоит из трех заданий с развернутым ответом и направлена на дифференцированную проверку повышенного уровня владения материалом. Все задания этой части носят комплексный характер. Они позволяют проверить владение формально-оперативным алгебраическим аппаратом, способность к интеграции знаний из различных тем школьного курса, владение исследовательскими навыками, а так же умение найти и применить нестандартные приемы рассуждений. При выполнении второй части работы учащиеся должны продемонстрировать умение математически грамотно записать решение, приводя при этом необходимые пояснения и обоснования. Задания второй части расположены по нарастанию сложности – от относительно простой задачи до достаточно сложной, требующей свободного владения материалом курса и высокого уровня математического развития.
На проведение экзамена отводится 90 минут.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Бланк для 6 класса»
Заполнять гелевой или капиллярной ручкой ЧЕРНЫМИ чернилами ЗАГЛАВНЫМИ ПЕЧАТНЫМИ БУКВАМИ
|
Фамилия |
|
||||||||||||||||||||||||||||||||
|
Имя |
|
||||||||||||||||||||||||||||||||
|
Отчество |
|
||||||||||||||||||||||||||||||||
|
Предмет |
|
Дата |
|
Код участника |
|
———————————————————————————————————————
|
Номер варианта |
Номер аудитории |
Код участника |
Класс |
Подпись участника тестирования |
||||||||||||||||
|
|
|
|
|
О
Ответы на задания части 1 Замена ошибочных ответов на задания части 1
|
А |
Б |
В |
Г |
А |
Б |
В |
Г |
|||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||
|
5 |
||||||||||||||||||||||||||||||
|
6 |
||||||||||||||||||||||||||||||
|
7 |
||||||||||||||||||||||||||||||
|
8 |
||||||||||||||||||||||||||||||
|
9 |
||||||||||||||||||||||||||||||
|
10 |
||||||||||||||||||||||||||||||
|
11 |
|
Номер варианта |
Номер аудитории |
Код участника |
Класс |
Подпись участника тестирования |
||||||||||||||||
|
|
|
|
|
Просмотр содержимого документа
«М-6 вариант 2»
М – 6 Переводной экзамен по математике
Вариант 2
Часть I
-
Укажите верное утверждение
А) 55 кратно 11 Б) 77 кратно 9
В) 47 кратно 2 Г) 565 кратно 25
2. Сколько делителей у числа 18?
А) три Б) пять В) шесть Г) другой ответ
3. Вычислите:
А) 0,3 Б) – 3 В) 3 Г) – 0,3
4. Найдите значение выражения:
А) 2,1 Б) – 2,1 В) – 13,44 Г) 13,44
5. Скорость течения реки км в час. Какое расстояние пройдет плот за ч?
Ответ:_________________________
6. Соедините стрелками взаимно обратные числа.
1) 2)
3)
4)
А) 2,4 Б) 1,2 В) Г)
7. Найдите площадь круга, радиус которого равен 7 см.
Ответ:_________________________
8. Найдите неизвестный член пропорции:
А) 12,6 Б) 1,26 В) 3 Г) 0,3
9. Раскройте скобки и упростите выражение – 3(2x – y) – 2x.
А) Б)
В)
Г)
10. Решите уравнение – 0,28х + 0,8 = – 1,3
Ответ:_________________________
11. В двух цехах фабрики работают 480 человек. Число людей, работающих во втором цехе, составляет 35% от числа людей работающих на фабрике. Сколько человек работает в первом цехе?
А) 1680 Б) 16,8 В) 168 Г) 312.
Часть II
1. Упростите выражение: 8p + 9n – 2p – 16n –35 и найдите его значение, если p = 4, n = .
2. Найдите значение выражения
3. Решите уравнение:
4. Периметр треугольника равен 34,8 см. Длина первой стороны составляет 72% от длины второй стороны, а длина третьей стороны составляет длины первой стороны. Найдите длину каждой стороны треугольника.
М – 6 Переводной экзамен по математике
Вариант 1
Часть I
-
Укажите верное утверждение
А) 3 делитель 412 Б) 4 делитель 514
В) 9 делитель 517 Г) 25 делитель 875
2. Какое из данных чисел кратно 5?
А) 699995 Б) 55358 В) 457409 Г) 6510152
3. Вычислите:
А) 1,252 Б) – 1,252 В) 12,52 Г) – 12,52
4. Найдите значение выражения: .
А) – 1,68 Б) – 8,68 В) 8,68 Г) 1,68
5. Турист проходит в среднем км в час. Какое расстояние он пройдет за
ч?
Ответ:_________________________
6. Соедините стрелками взаимно обратные числа.
1) 2)
3)
4)
А) Б)
В) 3,4 Г) 0,3
7. Найдите площадь круга, диаметр которого равен 16 см.
Ответ:_________________________
8. Найдите неизвестный член пропорции:
А) 1,8 Б) 2 В) 3 Г) 0,2
9. Раскройте скобки и упростите выражение 5(8а ─ b) +3b.
А) 40a ─2b Б) 40a+2b В) 40a+ 8b Г) 40a─8b.
10. Решите уравнение 6,8х – 3 = – 4,7
Ответ:_________________________
11. Роман состоит из двух глав и занимает в книге 340 страниц. Число страниц первой главы составляет 45% от числа страниц романа. Сколько страниц во второй главе?
А) 1530 Б) 187 В) 153 Г) 15,3.
Часть II
1. Упростите выражение: 5s + 8z – 7s – 17z +15 и найдите его значение, если s = 4, z = .
2. Найдите значение выражения
3. Решите уравнение:
4. Периметр треугольника равен 46,4 см. Длина первой стороны составляет 96% от длины второй стороны, а длина третьей стороны составляет длины первой стороны. Найдите длину каждой стороны треугольника.
Ключ к ответам:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
1 вар |
Г |
А |
В |
Б |
10 |
1-Б 2-Г 3-В 4-А |
64π=200,96 |
Г |
А |
-0,25 |
Б |
|
2 вар |
А |
В |
А |
В |
8 |
1-В 2-Г 3-А 4-Б |
49π=153,86 |
А |
А |
7,5 |
Г |
Просмотр содержимого документа
«Пояснительная записка экзамена 6 класса»
1. Бессонова Жанна Петровна
2. МОУ «ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 78», г.Саратов
3. учитель математики, информатики и ИКТ.
Переводной экзамен по математике 6 класс в тестовой форме
Экзаменационная работа по структуре и содержанию приближена к новой форме итоговой аттестации в 9 классе.
Экзаменационная работа составлена в 2-х вариантах. К экзаменационной работе прилагается бланк для заполнения ответов 1 части. Бланк заполняется черной гелевой ручкой печатными буквами. Для объективности выставления оценки бланк разделен на 2 части. В 1-ой части есть ФИО ученика и код ученика. Во 2-ой части, которая отдается проверяющему учителю — только код ученика.
Содержание переводного экзаменационного материала соответствует «Обязательному минимуму содержания основного общего образования по математике».
Работа состоит из двух частей.
Часть I направлена на проверку достижения уровня базовой подготовки. Она содержит задания, предусматривающие три формы ответа:
-
задания с выбором ответа из четырех предложенных;
-
задания с кратким ответом;
-
задания на соотнесения.
С помощью этих заданий проверяется знание и понимание важных элементов содержания, владение основными алгоритмами, умение применить знания к решению математических задач, на сводящихся к прямому применению алгоритма, а так же применение знаний в простейших практических ситуациях. При выполнении заданий первой части учащиеся должны продемонстрировать определенную системность знаний и широту представлений, умение переходить с одного математического языка на другой, узнавать стандартные задачи в разнообразных формулировках.
Часть II состоит из трех заданий с развернутым ответом и направлена на дифференцированную проверку повышенного уровня владения материалом. Все задания этой части носят комплексный характер. Они позволяют проверить владение формально-оперативным алгебраическим аппаратом, способность к интеграции знаний из различных тем школьного курса, владение исследовательскими навыками, а так же умение найти и применить нестандартные приемы рассуждений. При выполнении второй части работы учащиеся должны продемонстрировать умение математически грамотно записать решение, приводя при этом необходимые пояснения и обоснования. Задания второй части расположены по нарастанию сложности – от относительно простой задачи до достаточно сложной, требующей свободного владения материалом курса и высокого уровня математического развития.
На проведение экзамена отводится 90 минут.
Учащимся в начале экзамена выдаются тексты первой и второй частей работы, которые выполняются последовательно и бланк 1 части, куда учащиеся отмечают выбранные варианты ответа.
Условия проведения экзамена и проверки работ
Ответы первой части работы записываются в бланк в специально отведенное для этого место. Все необходимые вычисления, преобразования производятся в черновике. Черновики не проверяются и не учитываются при выставлении отметки.
Задания второй части также выполняются на бланках в отведенное для этого место с записью хода решения. Формулировки заданий не переписываются, рисунки не перечерчиваются.
Дополнительные материалы и оборудование
Справочная литература, калькуляторы, мобильные телефоны на экзамене не используются.
Для оценивания результатов выполнения работ учащимися применяются два количественных показателя: традиционная отметка и рейтинг (от 0 до 19 баллов).
Рейтинг формируется путем подсчета общего количества баллов, полученных учащимися за выполнение первой и второй частей работы. За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Во второй части работы за каждое задание начисляется 2 балла, которые зачисляются в рейтинговую оценку ученика при верном выполнении этого задания.
Критерии оценивания
|
Отметка |
Количество баллов |
|
«3» |
8-11 |
|
«4» |
12-15 |
|
«5» |
16-19 |
Экзамен по математике в 6 классе
Данный материал предназначен для проведения итоговой аттестации по
математике за курс 6 класса. Составлен на основе государственного
стандарта основного общего образования 2010 года, авторской программы
Муравина Г.К. и Муравиной О.В., и учебника «Математика. 6 класс» авт.
Г.К. Муравин, О.В.Муравина.-Дрофа, 2013г. Москва.
Инструкция по выполнению работы
Работа состоит из двух частей и содержит 16 заданий.
Часть I содержит 12 заданий базового уровня: 6 заданий с выбором
верного ответа и 6 заданий с кратким ответом. Задания части I считаются
выполненными, если учащийся указал букву верного ответа (в заданиях 1-6),
дал верный ответ в виде числа или величины (в заданиях 7-12).
Часть II содержит 4 заданий с развернутым ответом, соответствующих
уровню возможностей и доступных учащимся, хорошо успевающим по
математике. При их выполнении надо записать полное решение и ответ.
Дополнительные материалы и оборудование: справочная литература,
калькуляторы, мобильные телефоны на экзамене не используются.
Разрешается использовать таблицу простых чисел.
Время выполнения экзаменационной работы— 90 минут.
Для оценивания результатов выполнения работы применяются
отметки «2», «3», «4», или «5», которые соответствуют определенному
количеству баллов, которые необходимо набрать при выполнении заданий.
За каждое верно выполненное задание базового уровня (части I) начисляется
1 балл. Задания II части: 13 и 14 оцениваются в 2 балла; 15—16 задания по 3
балла за каждое. В заданиях 11 и 12 допускается оценивание в 0,5 балла.
Итого 22 балла за успешное выполнение всех 16 заданий.
Схема формирования общего балла
Критерии оценивания заданий Части 2
№ 13
Критерии оценки выполнения задания
Ход решения верный, получен верный ответ.
Ход решения верный, но допущена одна вычислительная ошибка, в
результате которой возможен неверный ответ.
Другие случаи, не соответствующие указанным критериям.
Критерии оценки выполнения задания
Ход решения верный, получен верный ответ.
Ход решения верный, но допущена одна вычислительная ошибка, в
результате которой возможен неверный ответ, в задании не записан
ответ.
Другие случаи, не соответствующие указанным критериям.
Комментарий. Наличие правильного ответа при отсутствии решения
оценивается в 0 баллов.
№15
Критерии оценки выполнения задания
Ход решения верный. Задача верно решена по действиям или с
помощью составленного выражения.
Ход решения верный, решение завершено, но имеется одна
непринципиальная ошибка, не влияющая на правильность хода
решения. В результате этой ошибки возможен неверный ответ.
Большая часть задачи выполнена, но решение не доведено до
конца
Другие случаи, не соответствующие указанным критериям.
Критерии оценки выполнения задания
Ход решения задачи верный.
Ход решения верный, решение завершено, но имеется одна
непринципиальная ошибка, не влияющая на правильность хода
решения. В результате этой ошибки возможен неверный ответ.
Большая часть задачи выполнена, но решение не доведено до
конца.
Другие случаи, не соответствующие указанным критериям.
Экзаменационная работа по математике за курс 6 класса
Ученика(цы) 6Б класса ____________________________________
Вариант 1
Часть 1
В заданиях 1 – 6 выбрать верный ответ из числа предложенных.
1. Какая из записей является разложением на множители числа 36?
А. 2 3 6 Б. 30 + 6 В. 40 – 1 4 Г. 72 : 2
2. В пропорции
неизвестный член равен
А. 4,5. Б.
. Г. 4,8.
3. Принтер печатает одну страницу за 6 с. Сколько страниц можно распечатать на этом
принтере за t мин?
А. 6t с. Б. 10t с. В. 0,1t с. Г.
с.
4. Что больше: 26% учащихся школы или
учащихся этой школы?
А. 26% учащихся Б.
учащихся В. Эти числа равны Г. Данных для ответа
недостаточно
5. Какой из указанных цифр нужно заменить *, чтобы число 781* делилось и на 3, и на 5?
А. 0. Б. 2. В. 3. Г. 5.
6. За n одинаковых тетрадей и m одинаковых блокнотов заплатили c р. Тетрадь стоит a р.
Сколько стоят m блокнотов?
А. c – am Б. c – an В. c – (n + m) Г. c : (n + m)
В заданиях 7 – 12 записать только ответ.
7. Почтовый конверт стоит 13 руб. 40 коп. Какое наибольшее число конвертов можно
купить на 170 рублей?
Ответ:_____________________________
8. Решите уравнение
Ответ:_____________________________
9. Найдите значение выражения
Ответ:_____________________________
10. На клетчатой бумаге с клетками размером 1 см 1 см изображён треугольник
(см. рисунок). Найдите его площадь в квадратных сантиметрах.
Ответ:____________________________
11. Содержание соли в растворе составляет 16%.
А. Сколько килограммов соли содержится в 75 кг раствора?
Б. Сколько килограммов такого раствора можно приготовить из 8,8 кг соли?
А. Ответ: ___________________________
Б. Ответ:_____________________________
12. А. На участке дороги бетонные плиты длиной 6 м заменяют новыми длиной 8 м.
Сколько нужно новых плит для замены 240 старых?
Б. Для изготовления 10 деталей требуется
кг металла. Сколько металла пойдёт на
изготовление 12 таких деталей?
А. Ответ: ___________________________
Б. Ответ:________________________
В заданиях 13 – 16 записать решение и ответ.
Часть 2
13. 2 балла. Сократите дробь
.
14. 2 балла. Решите уравнение
.
15. 3 балла. Из двух городов навстречу друг другу одновременно вышли два
поезда, причем скорость одного из них 93,75 км/ч, а скорость другого на 12,3 км/ч
меньше. Через какое время после начала движения поезда встретятся, если расстояние
между городами 438 км?
16. 3 балла. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик
со средней скоростью 35км/ч, через пункт С едет автобус со средней скоростью 30км/ч.
Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со
средней скоростью 40км/ч. На рисунке показана схема дорог и расстояние между
пунктами по дорогам. Все три автомобиля одновременно выехали из А. Какой автомобиль
добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
Экзаменационная работа по математике за курс 6 класса
Ученика(цы) 6Б класса ____________________________________
Вариант 2
Часть 1
В заданиях 1 – 6 выбрать верный ответ из числа предложенных.
1. Какая из записей является разложением на множители числа 42?
А. 2 3 7 Б. 36 + 6 В. 49 – 1 7 Г. 84 : 2
2. В пропорции
неизвестный член равен
А.
. Г. 0,15.
3. Принтер печатает одну страницу за 4 с. Сколько страниц можно распечатать на этом
принтере за t мин?
А.
с. В. 4t с. Г. 15t с.
4. Что больше: 25% учащихся школы или
учащихся этой школы?
А. 25% учащихся Б.
учащихся В. Эти числа равны Г. Данных для ответа
недостаточно
5. Какой из указанных цифр нужно заменить *, чтобы число 537* делилось и на 2,
и на 3?
А. 5. Б. 6. В. 7. Г. 8.
6. За n одинаковых коробок конфет заплатили на c рублей больше, чем за m одинаковых
пачек печенья. Коробка конфет стоит a рублей. Сколько стоят m пачек печенья?
А. c – am Б. an – c В. c – (n + m) Г. c : (n + m)
В заданиях 7 – 12 записать только ответ.
7. Сырок стоит 6 рублей 60 копеек. Какое наибольшее число сырков можно купить на 80
рублей?
Ответ:_____________________________
8. Решите уравнение
Ответ:_____________________________
9. Найдите значение выражения
Ответ:_____________________________
10. На клетчатой бумаге с клетками размером 1 см 1 см изображён треугольник
(см. рисунок). Найдите его площадь в квадратных сантиметрах.
Ответ:_____________________________
11. Содержание соли в растворе составляет 16%.
А. Сколько килограммов соли содержится в 75 кг раствора?
Б. Сколько килограммов такого раствора можно приготовить из 8,8 кг соли?
А. Ответ: ___________________________
Б. Ответ:_____________________________
12. А. На участке дороги бетонные плиты длиной 6 м заменяют новыми длиной 8 м.
Сколько нужно новых плит для замены 240 старых?
Б. Для изготовления 10 деталей требуется
кг металла. Сколько металла пойдёт на
изготовление 12 таких деталей?
А. Ответ: ___________________________
Б. Ответ:__________________________
В заданиях 13 – 16 записать решение и ответ.
Часть 2
13. 2 балла. Сократите дробь
.
14. 2 балла. Решите уравнение:
;
15. 3 балла. Из деревень A и B, расстояние между которыми 26 км, одновременно
навстречу друг другу выехали два велосипедиста. В момент встречи преодоленные ими
расстояния относились соответственно как
. Какое расстояние проехал до встречи
велосипедист из деревни A?
16. 3 балла. Из пункта A в пункт D ведут три дороги. Через пункт B едет грузовик
со средней скоростью 32 км/ч, через пункт C едет автобус со средней скоростью 44 км/ч.
Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со
средней скоростью 48 км/ч. На рисунке показана схема дорог и расстояние между
пунктами по дорогам. Все три автомобиля одновременно выехали из A. Какой автомобиль
добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
Экзаменационная работа по математике за курс 6 класса
Ученика(цы) 6Б класса ____________________________________
Вариант 3
Часть 1
В заданиях 1 – 6 выбрать верный ответ из числа предложенных.
1. Какая из записей является разложением на множители числа 48?
А. 40+8 Б. 2*2*2*2*3 В. 49 – 1 Г. 96 : 2
2. В пропорции
неизвестный член равен
А.
. Г. 0,15.
3. Принтер печатает одну страницу за 5 с. Сколько страниц можно распечатать на этом
принтере за t мин?
А.
с. Б.
с. В. 5t с. Г. 15t с.
4. Что больше: 20% учащихся школы или
учащихся этой школы?
А. 20% учащихся Б.
учащихся В. Эти числа равны Г. Данных для ответа
недостаточно
5. Какой из указанных цифр нужно заменить *, чтобы число 537* делилось и на 2,
и на 5?
А. 5. Б. 0. В. 3. Г. 8.
6. За n одинаковых коробок конфет заплатили на c рублей больше, чем за m одинаковых
пачек печенья. Коробка конфет стоит a рублей. Сколько стоят m пачек печенья?
А. c – am Б. an – c В. c – (n + m) Г. c : (n + m)
В заданиях 7 – 12 записать только ответ.
7. Сырок стоит 6 рублей 60 копеек. Какое наибольшее число сырков можно купить на 90
рублей?
Ответ:_____________________________
8. Решите уравнение
Ответ:_____________________________
9. Найдите значение выражения
Ответ:_____________________________
10. На клетчатой бумаге с клетками размером 1 см 1 см изображён треугольник
(см. рисунок). Найдите его площадь в квадратных сантиметрах.
Ответ:_____________________________
11. Содержание соли в растворе составляет 14%.
А. Сколько килограммов соли содержится в 75 кг раствора?
Б. Сколько килограммов такого раствора можно приготовить из 9,8 кг соли?
А. Ответ: ___________________________
Б. Ответ:_____________________________
12. А. На участке дороги бетонные плиты длиной 4 м заменяют новыми длиной 6 м.
Сколько нужно новых плит для замены 240 старых?
Б. Для изготовления 7 деталей требуется
кг металла. Сколько металла пойдёт на
изготовление 12 таких деталей?
А. Ответ: ___________________________
Б. Ответ:__________________________
В заданиях 13 – 16 записать решение и ответ.
Часть 2
13. 2 балла. Сократите дробь
.
.
14. 2 балла. Решите уравнение
.
15. 3 балла. Из деревень A и B, расстояние между которыми 26 км, одновременно
навстречу друг другу выехали два велосипедиста. В момент встречи преодоленные ими
расстояния относились соответственно как
. Какое расстояние проехал до встречи
велосипедист из деревни A?
16. 3 балла. Из пункта A в пункт D ведут три дороги. Через пункт B едет грузовик
со средней скоростью 32 км/ч, через пункт C едет автобус со средней скоростью 44 км/ч.
Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со
средней скоростью 48 км/ч. На рисунке показана схема дорог и расстояние между
пунктами по дорогам. Все три автомобиля одновременно выехали из A. Какой автомобиль
добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
Экзаменационная работа по математике за курс 6 класса
Ученика(цы) 6Б класса ____________________________________
Вариант 4
Часть 1
В заданиях 1 – 6 выбрать верный ответ из числа предложенных.
1. Какая из записей является разложением на множители числа 24?
А. 2 2 6 Б. 30 + 6 В. 40 – 1 4 Г. 72 : 2
2. В пропорции
неизвестный член равен
А. 4,5. Б.
. Г. 4,8.
3. Принтер печатает одну страницу за 9 с. Сколько страниц можно распечатать на этом
принтере за t мин?
А. 9t с. Б. 10t с. В. 0,1t с. Г.
с.
4. Что больше: 33% учащихся школы или
учащихся этой школы?
А. 33% учащихся Б.
учащихся В. Эти числа равны Г. Данных для ответа
недостаточно
5. Какой из указанных цифр нужно заменить *, чтобы число 781* делилось и на 3, и на 2?
А. 0. Б. 2. В. 3. Г. 5.
6. За n одинаковых тетрадей и m одинаковых блокнотов заплатили c р. Тетрадь стоит a р.
Сколько стоят m блокнотов?
А. c – am Б. c – an В. c – (n + m) Г. c : (n + m)
В заданиях 7 – 12 записать только ответ.
7. Почтовый конверт стоит 11 руб. 20 коп. Какое наибольшее число конвертов можно
купить на 150 рублей?
Ответ:_____________________________
8. Решите уравнение
Ответ:_____________________________
9. Найдите значение выражения
Ответ:_____________________________
10. На клетчатой бумаге с клетками размером 1 см 1 см изображён треугольник
(см. рисунок). Найдите его площадь в квадратных сантиметрах.
Ответ:____________________________
11. Содержание соли в растворе составляет 12%.
А. Сколько килограммов соли содержится в 75 кг раствора?
Б. Сколько килограммов такого раствора можно приготовить из 8,4 кг соли?
А. Ответ: ___________________________
Б. Ответ:_____________________________
12. А. На участке дороги бетонные плиты длиной 6 м заменяют новыми длиной 3 м.
Сколько нужно новых плит для замены 240 старых?
Б. Для изготовления 10 деталей требуется
кг металла. Сколько металла пойдёт на
изготовление 16 таких деталей?
А. Ответ: ___________________________
Б. Ответ:________________________
В заданиях 13 – 16 записать решение и ответ.
Часть 2
13. 2 балла. Сократите дробь
.
14. 2 балла. Решите уравнение
15. 3 балла. Из двух городов навстречу друг другу одновременно вышли два
поезда, причем скорость одного из них 93,75 км/ч, а скорость другого на 12,3 км/ч
меньше. Через какое время после начала движения поезда встретятся, если расстояние
между городами 438 км?
16. 3 балла. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик
со средней скоростью 35км/ч, через пункт С едет автобус со средней скоростью 30км/ч.
Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со
средней скоростью 40км/ч. На рисунке показана схема дорог и расстояние между
пунктами по дорогам. Все три автомобиля одновременно выехали из А. Какой автомобиль
добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
ВПР 2021 по математике 6 класс реальные варианты с ответами всероссийской проверочной работы для проведения с 15 марта по 21 мая 2021 года. P.S дату проведения ВПР школа выбирает самостоятельно.
Реальные варианты ВПР 2021 по математике 6 класс с ответами:
-
Вариант №1 ВПР 2021 по математике 6 класс с ответами
-
Вариант №2 ВПР 2021 по математике 6 класс с ответами
-
Вариант №3 ВПР 2021 по математике 6 класс с ответами
-
Вариант №4 ВПР 2021 по математике 6 класс с ответами
-
Вариант №5 ВПР 2021 по математике 6 класс с ответами
-
Вариант №6 ВПР 2021 по математике 6 класс с ответами
-
Вариант №7 ВПР 2021 по математике 6 класс с ответами
-
Вариант №8 ВПР 2021 по математике 6 класс с ответами
-
Вариант №9 ВПР 2021 по математике 6 класс с ответами
-
Вариант №10 ВПР 2021 по математике 6 класс с ответами
-
Вариант №11 ВПР 2021 по математике 6 класс с ответами
-
Вариант №12 ВПР 2021 по математике 6 класс с ответами
-
Вариант №13 ВПР 2021 по математике 6 класс с ответами
-
Вариант №14 ВПР 2021 по математике 6 класс с ответами
-
Вариант №15 ВПР 2021 по математике 6 класс с ответами
-
Вариант №16 ВПР 2021 по математике 6 класс с ответами
-
Вариант №17 ВПР 2021 по математике 6 класс с ответами
-
Вариант №18 ВПР 2021 по математике 6 класс с ответами
-
Вариант №19 ВПР 2021 по математике 6 класс с ответами
-
Вариант №20 ВПР 2021 по математике 6 класс с ответами
На выполнение работы по математике даётся 60 минут. Работа содержит 13 заданий. В заданиях, после которых есть поле со словом «Ответ», запишите ответ в указанном месте. В задании 12 нужно сделать чертёж или рисунок.
В заданиях, после которых есть поле со словами «Решение» и «Ответ», запишите решение и ответ в указанном месте. Если Вы хотите изменить ответ, зачеркните его и запишите рядом новый.
Интересные задания с вариантов:
1)Задумали число. От этого числа отняли 213 и получили число, которое на 55 меньше половины задуманного числа. Найдите задуманное число.
2)На рисунке изображены здание и стоящее рядом дерево. Высота здания равна 19 м. Какова примерная высота дерева? Ответ дайте в метрах.
3)На диаграмме показана средняя дневная температура в каждом месяце в городе Эдмонтон. На вертикальной оси указана температура в градусах Цельсия, на горизонтальной — месяцы.
4)Даны числа: 5,67; 0,56; 5,31; 0,06 и 3,52. Три из них отмечены на координатной прямой точками P, Q и R.
5)В коробке с ёлочными игрушками лежит 18 ёлочных шаров: 7 красных, 6 зелёных и 5 синих. Наугад из коробки достают несколько шаров. Выберите верные утверждения и запишите в ответе их номера. 1) Если достать 14 шаров, то среди них обязательно будут шары трёх разных цветов. 2) Если достать 7 шаров, то среди них обязательно будут 2 шара разного цвета. 3) Если достать 3 шара, то они обязательно будут трёх разных цветов. 4) Если достать 12 шаров, то среди них обязательно будет шар красного цвета.
6)В июле весы стоили 2700 рублей. В августе они подешевели на 12%, а в сентябре подешевели ещё на 25%. Сколько рублей стали стоить весы в октябре? Запишите решение и ответ.
7)Задумали двузначное число, которое делится на 15. Когда к этому числу справа приписали его последнюю цифру, получилось трёхзначное число, которое даёт остаток 3 при делении на 9. Какое число задумали? Запишите решение и ответ.
8)К задуманному числу прибавили седьмую часть этого же числа, и получилось 336. Найдите задуманное число.
9)На рисунке изображены здание и стоящее рядом дерево. Высота дерева равна 10 м. Какова примерная высота здания? Ответ дайте в метрах.
10)В классе учится 20 человек, из них 13 человек посещают исторический кружок, а 10 — химический. Выберите утверждения, которые верны при указанных условиях. 1) Каждый учащийся этого класса посещает оба кружка. 2) Найдутся хотя бы двое учащихся этого класса, кто посещает оба кружка. 3) Каждый, кто посещает исторический кружок, обязательно посещает и химический кружок. 4) Меньше 11 человек посещают и исторический кружок, и химический кружок. В ответе запишите номера выбранных утверждений.
11)Аня и Катя купили подарок своему другу Коле на день рождения. Подарок стоил 320 рублей. При покупке Катя заплатила 15% этой суммы, остальное заплатила Аня. На следующий день Катя отдала Ане 45 рублей. Сколько ещё рублей Катя должна отдать Ане, чтобы их затраты на подарок были равными?
12)Света загадала число. Она сказала: «Если моё число разделить на 11, то остаток будет в 2 раза меньше, чем частное». Какое число загадала Света, если известно, что загаданное число больше 170, но меньше 200?
13)Задумали число. Это число на 96 больше девятой части задуманного числа. Найдите задуманное число.
14)На рисунке изображены дерево и растущий рядом куст. Высота куста равна 1,6 м. Какова примерная высота дерева? Ответ дайте в метрах.
15)На координатной прямой точками K, M, N, P и Q отмечены числа. Известно, что среди отмеченных есть числа 2,81; 3,72 и 2,4.
16)Во время диспансеризации в школе измерили рост учащихся. Оказалось, что рост каждого одиннадцатиклассника больше 165 см и меньше 190 см. Выберите верные утверждения и запишите в ответе их номера. 1) В этой школе обязательно найдётся одиннадцатиклассник ростом ровно 195 см. 2) Разница в росте между любыми двумя одиннадцатиклассниками этой школы или меньше, или равна 25 см. 3) Рост любого одиннадцатиклассника в этой школе меньше 190 см. 4) В этой школе обязательно найдётся одиннадцатиклассник ростом ровно 160 см
17)Сумма трёх чисел равна 160. Первое число составляет 14% этой суммы. Второе число в четыре раза больше первого. Найдите третье число.
18)В погребе хранилось несколько головок сыра. Ночью пришли мышки и съели 10 головок сыра, причём все съели поровну. Следующей ночью пришли не все мышки, а только 11, и доели оставшийся сыр, но каждая мышка съела в два раза меньше сыра, чем накануне. Сколько головок сыра хранилось в погребе?
19)Задумали число. От этого числа отняли 108 и получили число, которое на 24 меньше трети задуманного числа. Найдите задуманное число.
20)На рисунке изображены скамейка и двухъярусная кровать. Высота скамейки 50 см. Какова примерная высота двухъярусной кровати? Ответ дайте в сантиметрах.
21)Перед футбольным турниром измерили рост игроков футбольной команды. Оказалось, что рост каждого из футболистов этой команды больше 170 см и меньше 190 см. Выберите утверждения, которые верны при указанных условиях. 1) В этой футбольной команде обязательно есть игрок, рост которого равен 170 см. 2) Разница в росте любых двух игроков этой футбольной команды составляет более 10 см. 3) Рост любого футболиста этой команды меньше 190 см. 4) В этой футбольной команде нет игроков с ростом 169 см.
22)Первое число составляет 85% второго числа, а третье — 20% второго числа. Найдите первое число, если известно, что оно больше третьего на 26.
23)В шести ящиках лежат красные, синие и белые шары. Число синих шаров в каждом ящике равно общему числу белых шаров во всех остальных ящиках. А число белых шаров в каждом ящике равно общему числу красных шаров во всех остальных ящиках. Сколько всего шаров лежит в ящиках, если известно, что их количество нечётно, больше 50 и меньше 100?
24)Задумали число. От этого числа отняли 243 и получили число, которое на 51 меньше половины задуманного числа. Найдите задуманное число.
25)На рисунке изображены дерево и растущий рядом куст. Высота куста равна 1,2 м. Какова примерная высота дерева? Ответ дайте в метрах.
26)На координатной прямой точками K, M, N, P и Q отмечены числа. Известно, что среди отмеченных есть числа 3,4; 5,71 и 5,22.
27)Даша и Маша купили подарок своему другу Толе на день рождения. Подарок стоил 350 рублей. При покупке Маша заплатила 16% этой суммы, остальное заплатила Даша. На следующий день Маша отдала Даше 60 рублей. Сколько ещё рублей Маша должна отдать Даше, чтобы их затраты на подарок были равными?
28)Сумма очков на противоположных гранях обычного игрального кубика равна 7. Например, если на грани 1 очко, то на противоположной грани 6 очков, если на грани 2 очка, то на противоположной 5 очков. На рисунке 1 изображён игральный кубик. На рисунке 2 изображён этот же кубик. Напишите на рисунке 2 число очков на грани, которая отмечена знаком вопроса.
29)Катя загадала четырёхзначное число. Из загаданного числа она вычла сумму его цифр, у полученной разности зачеркнула одну цифру и получила число 235. Какую цифру зачеркнула Катя?
30)Половина задуманного числа на 70 больше седьмой части самого задуманного числа. Найдите задуманное число.
31)Про три числа известно, что первое число составляет 70% второго числа, а третье — 35% второго числа. Найдите второе число, если известно, что первое число больше третьего на 14. Запишите решение и ответ.
32)Ира загадала число. Она сказала: «Если моё число разделить на 15, то остаток будет в 2 раза меньше, чем частное». Какое число загадала Ира, если известно, что загаданное число больше 170, но меньше 200?
33)К задуманному числу прибавили шестую часть этого же числа, и получилось 252. Найдите задуманное число.
34)Юра обедает в столовой. На обед он взял суп, плов и чай. Плов стоил 60% всей суммы, уплаченной за обед, суп — 30%. Чай стоил 25 рублей. Сколько рублей заплатил Юра за обед?
35)Задумали двузначное число. Когда это число умножили на произведение его цифр, получилось 1995. Какое число задумали?
36)Задумали число. Из 140 вычли половину задуманного числа, в результате осталась пятая часть задуманного числа. Найдите задуманное число.
37)На рисунке изображены комод и стоящая на нём ваза с цветами. Высота вазы вместе с цветами равна 50 см. Какова примерная высота комода? Ответ дайте в сантиметрах.
38)Задумали число. Из 156 вычли четверть задуманного числа и получили восьмую часть задуманного числа. Найдите задуманное число.
39)На рисунке изображены щука и окунь. Длина окуня 20 см. Какова примерная длина щуки? Ответ дайте в сантиметрах.
40)Даша и Маша купили подарок своему другу Толе на день рождения. Подарок стоил 350 рублей. При покупке Маша заплатила 16% этой суммы, остальное заплатила Даша. На следующий день Маша отдала Даше 60 рублей. Сколько ещё рублей Маша должна отдать Даше, чтобы их затраты на подарок были равными?
41)Ксюша загадала число. Она сказала: «Если моё число разделить на 11, то остаток будет в 2 раза меньше, чем частное». Какое число загадала Ксюша, если известно, что загаданное число больше 140, но меньше 170?
42)Задуманное число на 84 больше, чем треть самого задуманного числа. Найдите задуманное число.
43)Сумма трёх чисел равна 175. Первое число составляет 64% этой суммы. Второе число в четыре раза меньше первого. Найдите разность между наибольшим и наименьшим числами.
44)Саша и Костя по очереди вычёркивают по одной цифре из числа 568439, пока не останется трёхзначное число. Саша начинает, и его задача — сделать это трёхзначное число как можно меньше. А Костя хочет, чтобы трёхзначное число было как можно больше. Может ли Саша получить число меньшее 565, как бы ни действовал Костя?
45)Задумали число. Это число на 153 больше четверти задуманного числа. Найдите задуманное число.
46)В коробке с ёлочными игрушками лежит 11 ёлочных шаров: 5 красных, 4 зелёных и 2 синих. Наугад из коробки достают несколько шаров. Выберите верные утверждения и запишите в ответе их номера. 1) Если достать 8 шаров, то среди них обязательно будет шар красного цвета. 2) Если достать 3 шара, то они обязательно будут трёх разных цветов. 3) Если достать 5 шаров, то среди них обязательно будут 2 шара разного цвета. 4) Если достать 10 шаров, то среди них обязательно будут шары трёх разных цветов.
47)Сумма трёх чисел равна 170. Первое число составляет 15% этой суммы. Второе число в пять раз больше первого. Найдите третье число.
48)Задумали число. Из 195 вычли удвоенное задуманное число и получили шестую часть задуманного числа. Найдите задуманное число.
49)Сумма трёх чисел равна 250. Первое число составляет 72% этой суммы. Второе число в четыре раза меньше первого. Найдите разность между наибольшим и наименьшим числами.
50)Вика загадала число. Она сказала: «Если моё число разделить на 13, то остаток будет в 2 раза меньше, чем частное». Какое число загадала Вика, если известно, что загаданное число больше 170, но меньше 200?
51)Задумали число. От этого числа отняли 187, полученный результат умножили на 6 и получили треть задуманного числа. Найдите задуманное число
52)Петя в компьютерном магазине купил товары на сумму 1400 рублей. На покупку клавиатуры было израсходовано 50% этой суммы, а на покупку мыши — 35% всей суммы. Сколько рублей стоили остальные товары, купленные Петей?
53)В восьми ящиках лежат красные, синие и белые шары. Число синих шаров в каждом ящике равно общему числу белых шаров во всех остальных ящиках. А число белых шаров в каждом ящике равно общему числу красных шаров во всех остальных ящиках. Сколько всего шаров лежит в ящиках, если известно, что их количество чётно и меньше 130?
54)Задумали число. К этому числу прибавили шестую часть задуманного числа и получили 378. Найдите задуманное число.
55)Игорь обедает в столовой. На обед он взял гороховый суп, плов и чай. Плов стоил 52% всей суммы, уплаченной за обед, гороховый суп — 38%. Чай стоил 27 рублей. Сколько рублей заплатил Игорь за обед?
56)В мешке находится 29 белых перчаток и 31 чёрная перчатка. Перчатки достают из мешка парами. Если достали пару перчаток одного цвета, то в мешок кладут чёрную перчатку. Если достали пару перчаток разного цвета, то в мешок кладут белую перчатку. Какого цвета окажется перчатка, которая останется в мешке последней?
57)Задумали число. Половина этого числа на 76 больше шестой части задуманного числа. Найдите задуманное число.
58)В январе весы стоили 2500 рублей. В феврале они подешевели на 5%, а в марте подешевели
ещё на 20%. Сколько рублей стали стоить весы в апреле?
59)В трёх ящиках лежат красные, синие и белые шары. Число синих шаров в каждом ящике равно общему числу белых шаров во всех остальных ящиках. А число белых шаров в каждом ящике равно общему числу красных шаров во всех остальных ящиках. Сколько всего шаров лежит в ящиках, если известно, что их количество нечётно, больше 10 и меньше 30?
60)Контрольную работу писало 30 учеников. За выполнение контрольной работы выставляется одна из отметок: «5», «4», «3» или «2». Отметку «4» получили 30% учеников, писавших контрольную, а тех, кто получил «2» или «3», было на 6 человек меньше, чем тех, кто получил «4». Сколько учеников получили отметку «5»?
61)Задумано двузначное число, которое делится на 8. К нему справа приписали это же число ещё раз. Оказалось, что получившееся четырёхзначное число делится на 11. Какое число задумано?
62)В пяти ящиках лежат красные, синие и белые шары. Число синих шаров в каждом ящике равно общему числу белых шаров во всех остальных ящиках. А число белых шаров в каждом ящике равно общему числу красных шаров во всех остальных ящиках. Сколько всего шаров лежит в ящиках, если известно, что их количество чётно, больше 100 и меньше 130?
63)Вася обедает в столовой. На обед он взял борщ, плов и компот. Плов стоил 55% всей суммы, уплаченной за обед, борщ — 30%. Компот стоил 30 рублей. Сколько рублей заплатил Вася за обед?
64)Задумали число. От этого числа отняли 313 и получили число, которое на 71 меньше половины задуманного числа. Найдите задуманное число
65)За первый час велосипедист проехал три седьмых всего пути, а за второй — оставшиеся 28 км. Сколько всего километров велосипедист проехал за два часа?
66)Ваня обедает в столовой. На обед он взял борщ, пюре с котлетой и чай. Пюре с котлетой стоило 64% всей суммы, уплаченной за обед, борщ — 21%. Чай стоил 24 рубля. Сколько рублей заплатил Ваня за обед?
67)На рисунке изображены принтер и три лотка для бумаг. Высота всех трёх лотков вместе 20 см. Какова примерная высота принтера? Ответ дайте в сантиметрах.
68)Игорь обедает в столовой. На обед он взял гороховый суп, плов и чай. Плов стоил 52% всей суммы, уплаченной за обед, гороховый суп — 38%. Чай стоил 27 рублей. Сколько рублей заплатил Игорь за обед?
69)Задумали двузначное число. Когда это число умножили на произведение его цифр, получилось 3400. Какое число задумали?
70)Хоккейные коньки стоили 4500 руб. Сначала цену снизили на 20%, а потом эту сниженную цену повысили на 20%. Сколько стали стоить коньки после повышения цены? Запишите решение и ответ.
71)Велосипед стоил 7500 руб. Сначала цену снизили на 15%, а потом эту сниженную цену повысили на 15%. Сколько стал стоить велосипед после повышения цены? Запишите решение и ответ.
72)Лодка стоила 24000 руб. Сначала цену повысили на 12%, затем эту повышенную цену повысили еще на 12%. Сколько стала стоить лодка после второго повышения цены? Запишите решение и ответ.
73)Цены на яблоки сначала выросли на 60%, а затем понизились на 20%. Сколько изначально стоили яблоки, если после понижения цен они стали стоить 128 руб? Запишите решение и ответ.
74)Цены на крабов сначала понизились на 20%, а затем повысились на 25%. Сколько изначально стоили крабы, если после повышения цен они стоили 150 руб.? Запишите решение и ответ.
75)Евграфий взял у приятеля взаймы 20000 руб. в декабре. Каждый месяц, начиная с января, он выплачивает 20% от оставшейся суммы долга. Сколько денег он заплатит приятелю в феврале?
76)Кира взяла у подруги взаймы 35000 руб. в мае. Каждый месяц, начиная с июня, она выплачивает 35% от оставшейся суммы долга. Сколько денег она заплатит подруге в июле?
77)В мае билеты на самолет до Амстердама стоили 17000 руб. В июне цены выросли на 20%, а в июле понизилась и стали 15300 руб. На сколько процентов понизились цены в июле?
78)Феанор прошел в первый день своего пути 20% от запланированного маршрута, во второй день он прошел 24% от оставшегося маршрута. Определите, сколько всего запланировал пройти Феанор, если во второй день он прошел 24 км?
79)Финголфин отправился в поход протяженностью 600 лиг. В первый день он прошел 25% от запланированного пути, а во второй день он прошел 20% от оставшегося расстояния. Сколько лиг прошел Финголфин во второй день?
80)На начало понедельника на складе было 120 холодильников. В конце рабочего дня на складе осталось 75% от первоначального количества холодильников. Определите, сколько процентов от первоначального количества холодильников, оказалось на складе после того, как туда завезли еще 60 единиц товара.
81)На конец воскресенья в магазине было 220 шкафов. В понедельник было продано 40 шкафов. Определите, сколько стало шкафов в магазине, если во вторник их количество пополнилось в размере 40% от оставшихся после продажи в понедельних 40 шкафов.
82)Мотоцикл стоил 56000 руб. Сначала цену повысили на 24%, а затем еще на 30%. Определите, сколько стал стоить мотоцикл после второго повышения цены.
83)Цена на лопату резко повысилась на 15%, после чего понизилась на 20%. Определите, сколько стоила лопата изначально, если после всех изменений она стала стоить 92 руб?
84)Ванадий собрался в поход на лыжах. В первый день он прошел 25% пути, а во второй день — на 10% больше, чем в первый. Определите, сколько осталось пройти Ванадию, если он запланировал всего пройти 540 км?
85)Петр собрался в путешествие на велосипеде. В первый день он проехал 20% от всего пути, а во второй — на 15% меньше, чем в первый день. Определите, сколько осталось проехать Петру, если длина его маршрута составляет 720 км.
86)Бригада рабочих за первый день сделала 25% от запланированного количества деталей, а во второй день — 40% от оставшегося количества. Определите, сколько деталей запланировала сделать бригада рабочих, если во второй день они сделали 120 деталей.
87)Цена на носки выросла сначала на 24%, а затем еще на 16%. Определите разность между конечной и первоначальной ценой, если изначально цена составляла 200 руб.
88)Цена на вальтрап сначала понизилась на 25%, после чего понизилась еще на 20%. Найдите разность между первоначальной и конечной ценой, если после всех превращений вальтрап стал стоить 12000 руб.
89)Яхта «Гайда» прошла в первую неделю 28% от запланированного пути, а во вторую — на 16% меньше, чем в первую. Определите, сколько км прошла яхта за первые 2 недели, если всего длина маршрута составляет 6400 км.
90)Тарас взял в долг у приятеля в сентябре. Каждый месяц, начиная с октября, он выплачивает 25% от оставшейся суммы. Определите, какую сумму взял в долг у своего приятеля Тарас, если он заплатил в ноябре 3000 руб.
91)Кондратий дал в долг своему другу некоторую сумму денег в марте. Начиная с апреля, друг выплачиваете ему 20% от оставшейся суммы долга каждый месяц. Определите, сколько одолжил другу Кондратий, если в мае он получил 5400 руб.
92)Фома, выполняя свою домашнюю работу, тратит на выполнение задания по математике 60% времени, 20% от оставшегося времени у него уходит на задание по литературе. Определите, сколько всего времени уходит у Фомы на выполнение домашнего задания, если на выполнение задания по литературе у него уходит 40 минут. Ответ укажите в минутах.
93)Толя, выполняя физические упражнения, тратит на выполнение приседаний 25% времени, 40% от оставшегося времени уходят на бег. Определите, сколько времени уходит у Толи на выполнение физических упражнений, если на бег он тратит 120 минут. Ответ дайте в минутах.
94)На доске написано число. Олег играет в арифметическую игру: он может либо стереть последнюю цифру написанного числа, либо прибавить к написанному числу число 2018 и записать полученный результат, стерев предыдущее число. Может ли Олег, действуя таким образом, в конце концов получить число 1? Если да, покажите как; если нет, объясните почему.
95)Друзья Алеша, Боря и Витя учатся в одном классе. Один из них ездит домой от школы на автобусе, другой — на трамвае, а третий — на троллейбусе. Однажды после уроков Алёша пошёл проводить своего друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!» Кто на чем ездит домой?
96)На одном заводе работают три друга: слесарь, токарь и сварщик. Их фамилии: Борисов, Иванов и Семёнов. У слесаря нет ни братьев, ни сестёр, он самый младший из друзей. Семёнов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика.
97)В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода, причём вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей?
98)На даче поселились пятеро мальчиков: Андрюша, Боря, Володя, Гена и Дима. Все были разного возраста: одному был 1 год, другому — 2 года, остальным 3, 4 и 5 лет. Володя был самым маленьким, Диме было столько лет, сколько Андрюше и Гене вместе. Сколько лет Боре? Возраст кого еще из мальчиков можно определить?
99)Племя людоедов поймало Робинзона Крузо. Вождь сказал: «Мы рады бы отпустить тебя, но по нашему закону ты должен сказать какое-нибудь утверждение. Если оно окажется истинным, мы съедим тебя. Если оно окажется ложным, тебя съест наш ручной лев.» Что сказать Робинзону, чтобы людоеды его отпустили?
100)В Стране Чудес проводилось следствие по делу об украденной муке. На суде Мартовский Заяц заявил, что муку украл Болванщик. В свою очередь Болванщик и Соня дали показания, которые по каким-то причинам не были записаны. В ходе судебного заседания выяснилось, что муку украл лишь один из трёх подсудимых и что только он дал правдивые показания. Кто украл муку?
101)На суде каждый из троих подсудимых обвинял одного из двух других. Оказалось, что первый был единственным, кто говорил правду. Если бы каждый стал обвинять другого из них (но не себя), то второй был бы единственным, кто сказал правду. Кто виновен?
102)Как, имея лишь два сосуда ёмкостью 5 и 7 л, налить из крана 6 л воды?
103)В первый сосуд входит 9 л, во второй — 5 л, а в третий — 3 л. Первый сосуд наполнен водой, а остальные два пусты. Как с помощью этих сосудов отмерить 1 л воды? Как отмерить 4 л воды?
104)В бочке находится не менее 13 вёдер бензина. Как отлить из неё 8 вёдер с помощью 9-вeдёрной и 5-вeдёрной бочек?
105)12-вeдёрная бочка наполнена керосином. Как разлить его на две равные части, пользуясь пятивeдёрной и восьмиведёpной бочками?
106)Как взвесить груз на чашечных весах с гирями, если гири правильные, а весы неправильные?
107)Есть четыре камня, разной массы. За какое наименьшее число взвешиваний на весах без гирь можно найти самый тяжёлый и лёгкий камни?
108)Докажите что, среди любых n плюс 1 натуральных чисел найдутся хотя бы два числа, которые при делении на n дают одинаковые остатки.
109)На чудо-яблоне растут бананы и ананасы. За один раз разрешается сорвать два плода. Если сорвать два банана или два ананаса, то вырастет ещё один ананас, а если сорвать банан и ананас, то вырастет банан. В итоге остался один плод. Какой это плод, если неизвестно, сколько бананов и ананасов росло вначале?
110)Иван-царевич имеет два волшебных меча, один из которых может отрубить Змею Горынычу 21 голову, а второй — 4 головы, но тогда у Змея Горыныча отрастает 2020 голов. (Однако если, например, у Змея Горыныча осталось лишь 3 головы, то рубить их ни тем, ни другим мечом нельзя.) Может ли Иван отрубить Змею Горынычу все головы, если в самом начале у него было 100 голов?
111)За один ход число, написанное на доске, разрешается либо заменить на удвоенное, либо стереть у него последнюю цифру. Вначале на доске написано число 456. Можно ли из него получить число 14?
112)Двое играют в следующую игру. Имеется три кучки камней: в первой — 10, во второй — 15, в третьей — 20. За ход разрешается разбить любую кучку на две меньшие; проигрывает тот, кто не сможет сделать ход. Кто выиграет?
113)Двое по очереди ломают шоколадку 6 х 8. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре, тот, кто делает первый ход, или второй?
114)На доске написаны 10 единиц и 10 двоек. За ход можно стереть две любые цифры и, если они были одинаковыми, написать 2, а если разными — 1. Если последняя оставшаяся на доске цифра — 1, то выиграл первый игрок, если 2 — то второй. Кто при правильной игре выиграет?
115)Коля и Петя купили одинаковые беговые лыжи. Сколько стоит одна пара лыж, если Петя уплатил стоимость лыж трёхрублёвыми купюрами, Коля — пятирублёвыми, а всего они дали в кассу меньше 10 купюр?
116)Чтобы узнать, является ли число 1601 простым, его стали последовательно делить на 2, 3, 5 и т. д. На каком простом числе можно прекратить испытания?
117)Найти наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.
118)Тренер купил несколько мячей, скакалок, обручей и заплатил за все покупки 1540 рублей. Скакалка стоит 330 рублей, обруч — 220 рублей, мяч — 90 рублей. Сколько мячей, скакалок и обручей купил тренер? Ответ поясните.
119)Задумали двузначное число. Когда это число умножили на произведение его цифр, получили 744. Какое число задумали. Напишите свое решение.
120)Саша и Костя по очереди вычеркивают по одной цифре из числа 456127, пока не останется трехзначное число. Саша начинает, и его задача — сделать трехзначное число как можно меньше. а Костя хочет, чтобы трехзначное число было как можно больше. Может ли Саша получить число меньше 445, как бы не действовал Костя? Напишите свое решение.
Смотрите также на нашем сайте ВПР:
ВПР 2021 ответы и задания всероссийские проверочные работы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Весной 2021 года в проходят ВПР по математике в 6 классах в обязательном порядке для всех школ страны.
Варианты всероссийской проверочной работы формируются для каждой школы индивидуально из банка заданий ВПР.
→ новая демоверсия 2022 года
Варианты ВПР по математике для 6 класса 2021 с ответами
| Комплект заданий 1 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект заданий 2 | |
| Вариант 1 | Ответы + критерии |
| Вариант 2 | Ответы + критерии |
| Комплект заданий 3 | |
| Вариант 1 | Скачать ответы |
| Вариант 2 | Скачать ответы |
| Комплект заданий 4 | |
| Вариант 1 | Скачать ответы |
| Вариант 2 | Скачать ответы |
| Комплект заданий 5 | |
| Вариант 1 | Скачать ответы |
| Вариант 2 | Скачать ответы |
| Комплект заданий 6 | |
| variant 1 | Скачать ответы |
| variant 2 | Скачать ответы |
| Комплект заданий 7 | |
| variant 1 | otvet+kriterii |
| variant 2 | otvet+kriterii |
| Комплект заданий 8 | |
| variant 1 | otvet+kriterii |
| variant 2 | otvet+kriterii |
| Комплект заданий 9 | |
| variant 1 | kriterii |
| variant 2 | kriterii |
| Комплект заданий 10 | |
| variant 1 | kriterii |
| variant 2 | kriterii |
Подходы к отбору содержания, разработке структуры проверочной работы
Всероссийские проверочные работы основаны на системно-деятельностном, компетентностном и уровневом подходах.
В рамках ВПР наряду с предметными результатами обучения учеников основной школы оцениваются также метапредметные результаты, в том числе уровень сформированности универсальных учебных действий (УУД) и овладения межпредметными понятиями.
Предусмотрена оценка сформированности следующих УУД.
Личностные действия: личностное, профессиональное, жизненное самоопределение.
Регулятивные действия: планирование, контроль и коррекция, саморегуляция.
Общеучебные универсальные учебные действия: поиск и выделение необходимой информации; структурирование знаний; осознанное и произвольное построение речевого высказывания в письменной форме; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; моделирование, преобразование модели.
Логические универсальные действия: анализ объектов в целях выделения признаков; синтез, в том числе выведение следствий; установление причинно-следственных связей; построение логической цепи рассуждений; доказательство.
Коммуникативные действия: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Связанные страницы:

 ;
; ;
;
 ;
;
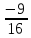
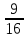
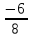
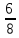
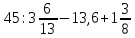
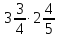
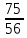 ;
;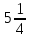 ;
;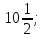
 .
.
 .
.
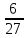
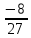
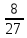
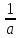
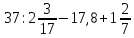
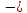 4;
4; 











