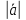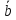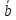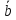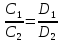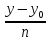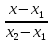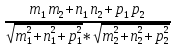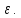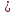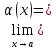Экзамен по математике бнту

1.
Матрица

Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.

Числовая
матрица
– все элементы матрицы числа.

Квадратная
матрица
– m=n.

Операции
над матрицами

Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).

Произведение
– каждый элемент матрицы умножается
на число (с).

2
Транспонирование

Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.

Умножение
матриц

Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).

При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c₁₁=a₁₁b₁₁+a₁₂b₂₁+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)

3.
Определители
2 и 3 порядков

Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.

Для
2-го порядка Δ вычисляется по формуле:
a₁₁a₂₂-a₁₂a₂₁
(крест накрест).

Для
3-го порядка по правилу треугольников.

Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.

4.Определитель
n-го порядка

Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.

Миноры
и алгебраические дополнения

Минор
матрицы А соответствующей элементу
A_ij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. A_ij=(-1)­^i+jM_ij
называется алгебраическим дополнением
к элементу a_ij.

Разложение
определителя

Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = a_i1A_i1+
a_i2A_i2+…+
a_inA_in

5.
Обратная
матрица. Теорема о существовании
обратной матрицы

Обратная
матрица существует только для квадратных
матриц.

Если
обратная матрица существует, то она
единственна.

Матрица
А^-1
обратная
А,
если выполняется условие: А^-1А=А
А^-1=Е
(единичная матрица).

Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).

Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(А^с).

Вычисление
обратной матрицы: 1) Находим Δ0,
2) Вычислем алгебр. доп., 3) Строим А^с
и
вычисляем:

А^-1=*
А^с
, 4) Делаем проверку А^-1А=Е

6.
Ранг
матрицы

Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор M_k0
(k
— какой-то порядок минора) и все M_k+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).

Элементарные
преобразования

1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.

Теорема
о базисном миноре

Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.

7.
СЛАУ
(система линейных алгебраических
уравнений)

Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b₁,
b_2,
b₃)
– столбец свободных членов. (x₁,
x_2,
x₃)
– решение системы, если при подстановке
их в систему получаются верные равенства.

Решение
систем по формулам Крамера

Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.

8.
СЛАУ
(система линейных алгебраических
уравнений)

Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b₁,
b_2,
b₃)
– столбец свободных членов. (x₁,
x_2,
x₃)
– решение системы, если при подстановке
их в систему получаются верные равенства.

Матричный
метод

Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А^-1=*
А^с.
Затем находим переменные (x,
y,
z)
и делаем проверку.

9.
Решение
произвольных СЛАУ

Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу
.

Теорема
Кренекера-Капелли

Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу
.

Если:
1) r_A==n,
то система имеет единственное решение.
n
– последний член элемента (a_1n)

2)
r_A=,
то система имеет бесконечное кол-во
решений.

10.
Векторы
в пространстве

Вектор
– это направленный отрезок.

– свободный;

– имеющий точку приложения. Длина
вектора – модуль.

Линейные
операции над векторами

1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов

и

явл.
,
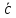
начало которого совпадает с началом 1
вектора (),
а конец — с концом 2 вектора.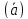

2)
вычитание (.
Разностью

и

явл.
,
конец которого совпадает с концом
,
а начало — с концом
.

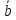
3)
умножение на число (Условия: 1) существует
;
2)

и

направлены одинаково если с0.

11.
Координаты
вектора в пространстве.

3
вектора ()
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.
=a_x+a_y+a_z

=
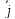
(x₂—x₁,
y₂—y₁,
z₂—z₁).

=
– длина
вектора

Направляющие
косинусы вектора

a_x
= Пр_Ox
=
*cosα; a_y
= Пр_Oy
=

cosβ;
a_z
= Пр_Oz
=

cosγ;
cosα=

Проекции
вектора на ось

образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.

12.
Скалярное
произведение 2 векторов

Это
число, равное произведению длин этих
векторов на cos
угла между ними.
*
=
*cosφ

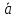
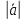
Свойство:
1)
*
=
*

2)
(*)
=
**)

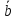
3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.

4)
*=0,
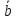
если
вектора

и

явл. Ортогональными (
⊥
).

13.
Векторное
произведение 2 векторов

Векторным
произведением 2 векторов

и

явл.
,
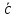
который удовлетворяет условиям: 1)

⊥
,
;

2)
,
,

– правая тройка векторов. 3)

=
*sinφ
(модуль произв. 2 векторов – площадь
параллелограмма)

Свойство:

1)
=
—

2)

=
+

3)
=
0 если


//

14.
Смешанное
произведение 3 векторов

Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.

**
= ()

—
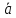
объём параллелепипеда.

Свойство:

1)
От перемены мест множителей произведение
не меняется.

=

=

2)
Если умножить на число, то оно умножается
с одним из членов произведения.

3)
(α-
β)(
= α(+
β (

15.
Базис
в пространстве

Компланарные
векторы лежат в одной плоскости.

3
любых некомпланарных вектора образуют
базис в пространстве.

Разложение
вектора по базису

Любой
вектор можно разложить по базису таким
способом: допустим B
(,)
– базис, а (α,
β, γ)
координаты определённого вектора,
например
.
Тогда разложение

по базису имеет вид:
=
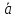
α+
β+
γ

16.
Прямая
на плоскости

Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор

= (𝐴,
𝐵)
является вектором нормали к прямой 𝑙.
Произвольная точка плоскости 𝑀(𝑥,
𝑦)
принадлежит прямой 𝑙
тогда и только тогда, когда

⊥
,
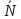
т.е. скалярное произведение этих векторов
*
=
0

Её
уравнения

1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали 𝐴(𝑥–𝑥₀)+𝐵(𝑦−𝑦₀)=0

2)
Общее уравнение прямой: 𝐴𝑥
+ 𝐵𝑦
+ 𝐶
= 0

17.
Различные
уравнения плоскости

а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0

б)
Уравнение проходящее через точку
M₀(x₀,y₀,z₀)
и ⊥
вектору нормали
(A,B,C):
A(x—x₀)
+ B(y—y₀)
+C(z—z₀)=0

в)
Уравнение плоскости, проходящей через
3 заданные точки.

г)
Уравнение плоскости в отрезках:

18.
Угол
между плоскостями

Допустим,
мы имеем 2 уравнения плоскости (α: A₁x
+ B₁y
+ C₁z
+ D₁
= 0
и β: A₂x
+ B₂y
+ C₂z
+ D₂
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos=
(отношение произведения
₁*₂
к произведению модулей векторов
нормали).

Взаимное
расположение плоскостей

Две
плоскости в пространстве либо
параллельны, либо пересекаются.

α₁//α₂
– коллинеарные ⇒
==
– условие
параллельности.

α₁⊥α₂
⇒
⊥
⇒
*=0.
=0
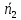
– условие
⊥.

19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве

1)
Параметрическое уравнение: x=x₀+mt,
y=y₀+nt,
z=z₀+pt

(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M₀(x₀,
y₀,
z₀)
∈l.

2)
Каноническое уравнение:

=

=

3)
Уравнение прямой проходящей через 2
точки:

=

=

4)
Общее уравнение прямой в пространстве:

20.
Угол
между прямыми и их взаимное расположение

Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы
₁
и
₂.
Тогда угол между 2 прямыми

можно найти по формуле: cos=

Условие
//-ти:
₁
//₂
⇒

==

Условие
⊥—ти:

Расстояние
от точки до прямой в пространстве

У
нас есть уравнение прямой

=

=
,
её направляющий вектор

(m,n,p)
и точка не принадлежащая этой прямой
M(x₁,y₁,z₁).
Расстояние от точки до прямой определяется
по формуле:

21.
Угол
между прямой и плоскостью.

Допустим,
у нас есть каноническое уравнение
прямой

=

=

и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=

22.
Взаимное
расположение прямой и плоскости

Условие
//-ти:
Am+Bn+Cp
= 0

Условие
⊥—ти:

Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.

23.
Эллипс

Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.

Вывод
канонического уравнения

+

= 1

Геометрические
свойства

1)
Эллипс является кривой 2-го порядка.

2)
Является ограниченной фигурой.

3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.

4)
a – большая ось; b
– малая ось; Вершины: А₁(а,0);
А₂(-а,0);
В₁(0,
b);
В₂(0,
—b);

5)

=

– эксцентриситет эллипса; 0
1.

6)
Прямые
x
=

– директриса эллипса. При

=1 ⇒
а=с; а=b
– уравнение окружности.
+=

24.
Гипербола

Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.

Вывод
канонического уравнения

—

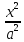
= 1

Геометрические
свойства

1)
Является кривой 2-го порядка.

2)
Является неограниченной кривой.

3)
Является симметричной фигурой.

4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;

5)

=

– эксцентриситет эллипса;

1.

6)
x
=

– директриса.
1

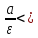
7)
y
=
x
– асимптоты

25.
Парабола

Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)

Вывод
канонического уравнения

p-
(параметр) расстояние от F
до L.
F(;0)
– фокус параболы. x=.
Уравнение: y²=2px

Геометрические
свойства

1)
Является кривой 2-го порядка.

2)
Симметричная фигура, ось симметрии –
Ox.

3)
Неограниченная фигура

4)

= 1
– эксцентриситет

26.
Числовая
последовательность

Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xⁿ
– числовая последовательность.

Предел

Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.

Теорема
о сходимости

Если
xⁿ
имеет
предел, то он единственный. xⁿ
наз.
ограниченной, если существует n
и все члены удовлетворяют
M,
nN

27.
Предел
функции

Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)

Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного

существует положительная дельта,
зависящая от

Теорема
о существовании предела функции

Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.

28.
Односторонние
пределы функции

Левый
и правый пределы называют односторонними
пределами.

1)
Число b
называется правым пределом функции
при x→a
справа если для всех
0
существует дельта от
,
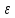
такой что 0следовательно
модуль f(x)-b
,
следовательно x

2)
Число b
называется левым пределом функции при
x→a
слева если для всех
0
существует дельта от
,
такой что —b
следовательно модуль f(x)-b
,
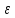
следовательно x

Теорема
о существовании предела функции

Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.

29.
Бесконечно-малые
и их свойства.

Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.

При
x→a
lim

=
предел не существует.

Основные
свойства

1°  
Сумма конечного числа б.м функций
является функцией б.м.

3°  
Произведение двух б.м функций есть
функция б.м.

4°  
Произведение б.м функции на константу
является б.м функцией.

5°  
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.

6°  
Функция ,
обратная
к б.м функции α(x)

0,
есть функция бесконечно большая. Верно
и обратное.

30.
Бесконечно-большие
функции.

Бесконечно
большая функция
– это функция, предел которой
стремится к
.

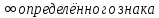
Теорема
о связи бесконечно-большой и
бесконечно-малой функции

Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию
.
Тогда для любого числа 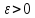 существует
такое число дельта
,
что для всех x,
удовлетворяющих неравенству
 ,
выполняется неравенство ,
т.е.
 .
А из этого следует, что функция  —
бесконечно большая.

Работа добавлена на сайт samzan.net: 2016-03-13

Вопросы к экзамену по высшей математике (БНТУ, АТФ, 1 курс)

1.  Матрицы и действия над ними (Основные определения, линейные операции над матрицами, умножение матриц, многочлены от матриц, транспонирование матрицы).
2.  Определитель матрицы и их свойства.
3.  Разложение определителя по элементам ряда.
4.   Матрица обратная к данной.
5.  Миноры и алгебраические дополнения.
6.  Ранг матрицы.
7.  Метод окаймляющих миноров для вычисления ранга матрицы.
8.  Системы линейных уравнений (матричная запись системы линейных уравнений, эквивалентные системы уравнений).
9.  Решение невырожденных линейных систем. Формула Крамера.
10.  Теорема Кронекера-Капелли.
11.  Решение произвольных линейных систем.
12.  Системы однородных линейных уравнений. Фундаментальная система решений.
13.  Метод Гаусса.
14.  Линейное пространство.
15.  Понятие линейного пространства.
16.  Линейная зависимость и независимость векторов.
17.  Размерность и базис пространства.
18.  Координаты вектора.
19.  Матрица системы векторов.
20.  Матрица перехода от одного базиса к другому.
21.  Евклидово пространство.
22.  Ортонормированный базис.
23.  Скалярное произведение векторов.  
24.  Векторное произведение векторов.  
25.  Смешанное произведение векторов.  

Прямая и плоскость в пространстве

1.  Общее уравнение плоскости в пространстве.
2.  Уравнение плоскости проходящей через заданную точку.
3.  Уравнение плоскости проходящей через три заданных точки.
4.  Угол между плоскостями
5.  Взаимное расположение двух плоскостей.
6.  Расстояние от точки до плоскости.
7.  Прямая как пересечение двух плоскостей.
8.  Параметрическое, каноническое уравнение прямой.
9.  Пересечение прямой и плоскости.
10.  Угол между прямой и плоскостью.
11.  Угол между прямыми.
12.  Взаимное расположение двух прямых.
13.  Расстояние от точки до прямой.

Поверхности второго порядка

1.  Кривые второго порядка (эллипс, гипербола, парабола, круг).
2.  Эллипсоид.
3.  Гиперболоид (однополостный, двуполостный).
4.  Параболоиды (эллиптический, гиперболический).
5.  Некоторые уравнения поверхности (цилиндрическая поверхность).

Множество вещественных чисел. Комплексные числа. Числовые поверхности

1.  Действительные числа.
2.  Комплексные числа.
3.  Точная верхняя и нижняя граница.
4.  Предел последовательности.
5.  Монотонные последовательности (теорема).
6.  Число e.

Предел функции

1.  Понятие функции и ее предела по Коши и Гейне.
2.  Определение правого и левого предела функции.
3.  Свойства функции имеющее предел при x→a (теорема об ограниченности функций имеющей предел).
4.  Определение бесконечно малых, бесконечно больших функций и их свойства.
5.  Основные теоремы о пределах.
6.  Сравнение бесконечно малых функций. Эквиваленты бесконечно малых.
7.  Первый замечательный предел и его следствия.
8.  Второй замечательный предел (доказательство и его интерпретация).

Непрерывные функции. Производные.

1.  Определение непрерывной функции в точке и на сегменте (a;b).
2.  Теорема об ограниченности функций на отрезке.
3.  Теорема Больцано-Коши об обращении функции в нуль.
4.  Теорема о существовании функции обратной данной.
5.  Точки разрыва функции и их классификация.

Дифференциальные исчисления функции обратные одной переменной

1.  Понятие производной.
2.  Производная слева и справа.
3.  Геометрический смысл производной.
4.  Механический смысл производной.
5.  Понятие дифференцируемости функции.

Дифференцируемость и непрерывность (теорема о необходимых и достаточных условиях дифференцируемости функции, доказательства).

1.  Теорема о взаимосвязи дифференцируемости и непрерывности функции в точке.
2.  Произведение суммы, произведения, частного функции (доказательство).
3.  Производная сложной функции (теорема, доказательство).
4.  Вычисление производной xα sin(x), cos(x), logax, ax.
5.  Производная неявной функции.
6.  Производная функции заданной параметрически.
7.  Гиперболические функции.
8.  Дифференциал функции (связь дифференциала функции с производной).
9.  Правило вычисления дифференциала.
10.  Производные высших порядков.
11.  Дифференциал высших порядков.

Основные теоремы дифференциального исчисления

1.  Определение монотонно возрастающей и монотонно убывающей функции. Max, min функции.
2.  Теорема об необходимых условиях возрастания или убывания функции.
3.  Теорема об необходимых условиях существования экстремума функции.
4.  Теорема о достаточном существовании экстремума.
5.  Теорема Ролля о корнях производной.
6.  Теорема Лагранжа о конечных приращений.
7.  Теорема Коши об отношении приращения двух функций.
8.  Правило Лопиталя.
9.  Формула Тейлора.
10.  Теорема о возможном представлении формулы в ряд Тейлора.
11.  Оценка остаточного члена ряда Тейлора в формуле Маклорена.
12.  Разложение по формуле Маклорена некоторых функций ex, sin(x), cos(x), ln(1+x).

Исследование функции

1.  Признаки монотонности функции:
2.  Теорема об необходимом условии неубывания, невозрастания функции.
3.  Теорема о достаточном условии возрастания функции.
4.  Схема исследования дифференцируемой функции на max и min с помощью первой производной.
5.  Исследование функции на экстремум с помощью второй производной (теорема, доказательства).
6.  Схема исследования функции не наименьшее и наибольшее значение функции на отрезке.
7.  Выпуклость и вогнутость, точки перегиба (теорема о достаточном условии существования точки перегиба функции).
8.  Асимптоты функции. Вертикаль и наклонная.
9.  Уравнение касательной и нормали.

Частичный предварительный просмотр текста

РЕАЛЬНЫЕ ЭКЗАМЕНАЦИОННЫЕ ВАРИАНТЫ 2011−2022 ГОДОВ
ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2022

Централизованное тестирование по математике 2022 года с решениями. Вариант 1.

Централизованное тестирование по математике 2022 года с решениями. Вариант 2.

Централизованное тестирование по математике 2022 года с решениями. Вариант 9.

Централизованное тестирование по математике 2022 года с решениями. Вариант 10.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2021

Централизованное тестирование по математике 2021 года с решениями. Вариант 1.

Централизованное тестирование по математике 2021 года с решениями. Вариант 2.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2020

Централизованное тестирование по математике 2020 года с решениями. Вариант 1.

Централизованное тестирование по математике 2020 года с решениями. Вариант 2.

Централизованное тестирование по математике 2020 года с решениями. Вариант 9.

Централизованное тестирование по математике 2020 года с решениями. Вариант 10.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2019

Централизованное тестирование по математике 2019 года с решениями. Вариант 1.

Централизованное тестирование по математике 2019 года с решениями. Вариант 2.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2018

Централизованное тестирование по математике 2018 года с решениями. Вариант 1.

Централизованное тестирование по математике 2018 года с решениями. Вариант 2.

Централизованное тестирование по математике 2018 года с решениями. Вариант 3.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2017

Демонстрационная версия ЦТ по математике 2016−2017 учебного года с решениями.

Централизованное тестирование по математике 2017 года с решениями. Вариант 1.

Централизованное тестирование по математике 2017 года с решениями. Вариант 2.

Централизованное тестирование по математике 2017 года с решениями. Вариант 3.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2016

Централизованное тестирование по математике 2016 года с решениями. Вариант 1.

Централизованное тестирование по математике 2016 года с решениями. Вариант 2.

Централизованное тестирование по математике 2016 года с решениями. Вариант 3.

Централизованное тестирование по математике 2016 года с решениями. Вариант 4.

Централизованное тестирование по математике 2016 года с решениями. Вариант 5.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2015

Централизованное тестирование по математике 2015 года с решениями. Вариант 1.

Централизованное тестирование по математике 2015 года с решениями. Вариант 2.

Централизованное тестирование по математике 2015 года с решениями. Вариант 3.

Централизованное тестирование по математике 2015 года с решениями. Вариант 4.

Централизованное тестирование по математике 2015 года с решениями. Вариант 5.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2014

Централизованное тестирование по математике 2014 года с решениями. Вариант 1.

Централизованное тестирование по математике 2014 года с решениями. Вариант 2.

Централизованное тестирование по математике 2014 года с решениями. Вариант 3.

Централизованное тестирование по математике 2014 года с решениями. Вариант 4.

Централизованное тестирование по математике 2014 года с решениями. Вариант 5.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2013

Централизованное тестирование по математике 2013 года с решениями. Вариант 1.

Централизованное тестирование по математике 2013 года с решениями. Вариант 2.

Централизованное тестирование по математике 2013 года с решениями. Вариант 3.

Централизованное тестирование по математике 2013 года с решениями. Вариант 4.

Централизованное тестирование по математике 2013 года с решениями. Вариант 5.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2012

Централизованное тестирование по математике 2012 года с решениями. Вариант 1.

Централизованное тестирование по математике 2012 года с решениями. Вариант 2.

Централизованное тестирование по математике 2012 года с решениями. Вариант 3.

Централизованное тестирование по математике 2012 года с решениями. Вариант 4.

Централизованное тестирование по математике 2012 года с решениями. Вариант 5.

ЭКЗАМЕНАЦИОННЫЕ РАБОТЫ ЦТ 2011

Централизованное тестирование по математике 2011 года с решениями. Вариант 1.

Централизованное тестирование по математике 2011 года с решениями. Вариант 2.

Централизованное тестирование по математике 2011 года с решениями. Вариант 3.

Централизованное тестирование по математике 2011 года с решениями. Вариант 4.

Централизованное тестирование по математике 2011 года с решениями. Вариант 5.