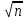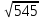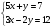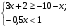Экзамен по математике для поступления в техникум

Тесты 1 вариант

1) В течении июля цены на картофель дважды увеличивались на 10 % . Цены на картофель в течении июля увеличились:

а) на 19 % в) на 21% с) на 20 д) на 25% е) на 18 %

2) В магазин привезли 14 т капусты, 30 % всей капусты продали. Сколько капусты осталось?

а) 9,8 т в) 10,2 т с) 4,2 т д) 8,3 т е) 5 т

3) Первый член геометрической прогрессии b₁ = 4, а знаменатель q =3. Найдите сумму первых пяти членов прогрессии.

а) 160 в) 484 с) 324 д) 380 е) 424

4) Разложите многочлен на множители: 15 ах + 20 ау

а) 5а (3х+4у) в) 5 (3ах+4ау) с) 5 (3х+4у) д) 5а (3х-4у) е) 5 (3ах-4ау)

5) Четырехугольник АВСD является ромбом, у которого сторона АВ равна 17 см, диагональ ВD равна 30 см. Найдите длину диагонали АС.

а) 8 см в) 16 см с) 17 см д) 14 см е) 20 см

6) Найдите tg х, если cos х= — 0,6 и х- угол третьей четверти.

а) 1/4 в) -3/4 с) -4/3 д) 4/3 е) -1

7) Найдите площадь треугольника, если ВС = 7 см, АС= 14 см. Угол С равен 30 градусов.

а) 31 см² в) 28,3 см² с) 40,1 см² д) 24,5 см² е) 12,5 см²

Средняя линия трапеции равна 7 см. Одно из её оснований больше другого на 4 см. Найдите основания трапеции.

а) 10 см и 4 см в) 8 см и 6 см с) 5 см и 9 см д) 11 см и 3 см е) 2 см и 12 см

9) Большая сторона параллелограмма равна 5 см. Найдите вторую сторону параллелограмма, если периметр равен 18 см.

а) 12 в) 4 с) 7,5 д) 3 е) 5,5

10) Решите неравенство: х² -8х +12

а) (- ∞; 2) в) (-2; 6) с) (- ∞; -2) д) (6; ∞) е) (2; 6)

11) Из 0,3 т свежих яблок получается 57 кг сушеных. Сколько сушеных яблок получится из 4,5 т свежих?

а) 855 в) 85,5 с) 8,55 д) 38 е) 3,8

12) На сколько процентов изменилась величина, если она увеличилась в 2 раза?

а) на 50 % в) на 100 % с) на 150 % д) на 200 % е) на 25 %

13) Вычислите 2,929 * 8,356 + 2,929 * 1,646.

а) 29,29 в) 2,929 с) 0,2929 д) 2929 е) 292,9

14) Решите уравнение 2,9х + 7,4 = х+ 1,7

а) -3 в) 3 с) -0,3 д) 0,3 е) -0,03

15) Автомобиль на 56,8 км пути затратил 4,26 л бензина. Сколько литров бензина потребуется ему, чтобы проехать 160 км?

а) 6 л в) 11,59 л с) 12 л д) 12,4 л е) 12,12л

16) Для 3 лошадей на 60 дней запасли 900 кг сена. Сколько сена надо запасти для 5 лошадей на 120 дней?

а) 30 000 кг в) 3 т с) 3 000 кг д) 30 т е) 0,3 т

17) В течении января цена на яблоки выросла на 30 %, а в течении февраля- на 20 %. На сколько процентов поднялась цена за 2 месяца?

а) на 56 % в) на 55 % с) на 54 % д) на 58 % е) на 60 %.

18) Найдите наименьшее целое х, удовлетворяющее неравенству -4х

а) 5 в) 4 с) 3 д) -4 е) -3

19) Решите неравенство: 30+ 5х

а) (-1; 1) в) (-1; ∞ ) с) (- ∞; -1) д) (-1; ∞) е) (-∞; -1)

20) С помощью числа π составьте выражение в радианах для дуги 30⁰ .

а) π/6 в) π/3 с) нельзя составить д) 5π/ 6 е) 2π/3

21) Угол 24⁰ выразите в радианах.

а) π/15 в) 2π/15 с) 3π/15 д) 4π/15 е) π/3

22) Найдите Х₈ , если Х_n = —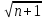

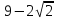
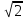
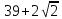
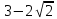
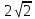
а) в) 2 -3 с) д) е) — 9.

23) Найдите 5-й член арифметической прогрессии: 19; 15; 11; …

а) -1 в) -3 с) 0 д) 1 е) 3

24) Определите радиус описанной около прямоугольного треугольника окружности, если катет равный 10 см. лежит против угла 45 градусов.

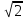
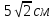
а) 20 см в) 10 см с) 10 см д) е) 5 см.

25) Определите длину вектора АВ. Если известны координаты точек А (-5; 4) и В (3; -2).

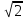
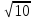
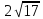
а) 2 в) 2 с) 10 д) е) 12

Тесты 2 вариант.

1) Найдите сумму первых двадцати членов арифметической прогрессии: 2; 5; ….

а) -590 в) 610 с) 640 д) 625 е) -610

2) В течении сентября цены на картофель дважды уменьшились на 10 %. Цены на картофель в течение сентября снизились

а) на 19 % в) на 21 % с) на 20 % д) на 15 % е) другой ответ

3) Сторона ромба равна 17 см, а одна из диагоналей 16 см. Найдите вторую диагональ.

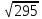
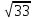
а) 15 см в) 30 см с) д) е)

4) В равнобокой трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60 градусов. Найдите меньшее основание.

а) 1,5 м в) 1,3 м с) 1,7 м д) 1,8 м е) 2 м.

5) Учитель проверил 18 тетрадей, что составляет 2/5 всех тетрадей. Сколько всего тетрадей?

а) 40 в) 24 с) 45 д) 38 е) 30

6) Углы, образованные стороной ромба с его диагоналями относятся как 5:4. Определить углы ромба (в градусах).

а) 70 и 110 в) 60 и 120 с) 50 и 130 д) 80 и 100 е) 40 и 140

7) Один из углов, получившихся при пересечении двух прямых, равен 110 градусов. Чему равны остальные углы (в градусах)?

а) 100 и 80 в) 110 и 70 с) 120 и 60 д) 90 и 90 е) 130 и 50

В саду 9 фруктовых деревьев, что составляет 45 % всех деревьев. Сколько всего в саду деревьев?

а) 50 в) 28 с) 46 д) 20 е) 15

9) Решите уравнение: 2х + 5 = 2 (х+1) + 11

а) 4,5 в) 4 с) -4,5 д) нет решений е) – 2.

10) MNPQ – прямоугольник, NP = 5 cм, MP = 12 см, О- точка пересечения диагоналей. Найдите периметр треугольника NОP.

а) 16 см в) 23 см с) 17 см д) 7 см е) 29 см

11) Один из корней квадратного уравнения равен 2. Найдите второй корень уравнения

х² + 17х -38 =0.

а) 19 в) -19 с) 15 д) -15 е) 16

12) Один из смежных углов в 5 раз меньше другого. Найдите разность между этими углами.

а) 120⁰ в) 110⁰ с) 100⁰ д) 90⁰ е) 80⁰

13) Сколько человек было в кино, если 1 % всех зрителей составляет 7 человек.

а) 300 в) 700 с) 400 д) 500 е) 600

14) После увеличения цены на товара на 50 %, она стала равна 12 000 тенге. Первоначальная цена товара составляла:

а) 6 000 в) 4 000 с) 8 000 д) 10 000 е) 9 000

15) Упростите выражение: С+С+2+С-19

а) С+ 21 в) С³ -17 с) С-17 д) 3С-17 е) 3С+21

16) Основания трапеции 7 см и 15 см, а высота- 8 см. Найдите площадь трапеции.

а) 176 см² в) 840 см² с) 88 см² д) 16 см² е) 60 см²

17) Упростите выражение: 14,7а (-5b)0,4.

а) 39аb в) -39аb с) -28,4аb д) -29,4аb е) 29,4аb

18) Найдите среднее арифметическое чисел: 5,9; 6,4; 5,7.

а) 6,3 в) 6 с) 6,1 д) 5,8 е) 6,2.

19) Решите неравенство: (х+5) (3-х) ˂ 0

a) (-5; 3) в) (- ∞; -3) U(5; +∞) с) (-3; 5) д) (- ∞; -5) U(3; +∞) е) (-3; 5]

20) Выполните действия: 728:1 +1(272- 0:272).

а) 728 в) 729 с) 990 д) 900 е) 1000

21) Упростите: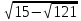

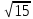
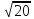
а) 2 в) -11 с) -2; 2 д) е) -2

22) Решите уравнение: 3х² -5х+2 = 0

а) -1; -2/3 в) -2/3; 2/3 с) 1; -2/3 д) 2/3; 1 е) 0; -1

23) Упростите выражение: 2cos² х- 1+ sin² х.

а) cos² х в) 2(1- sin² х) с) 3 cos² х д) sin² х е) -2sin² х.

24) Решите уравнение: 23- 4(3х +8) = 1-17х

а) -0,4 в) 25 с) -2,5 д) 2 е) 0,4

25) Под дождевой трубой поставили бочку вместимостью 180 л. Вода с крыши стекает в бочку через трубу по 8 л за одну минуту. Но в то же время через щель в бочке вытекает за одну минуту 3 л воды. Через сколько минут наполнится бочка?

а) 38 мин в) 36 мин с) 32 мини д) 30 мин е) 34 мин

Код ответов:

1 вариант

1В 2А 3В 4А 5В 6Д 7Д 8С 9В 10Е 11А 12В 13А 14А 15С 16С 17А 18А 19Е 20А 21В 22Д 23Е 24Д 25С

2 вариант

1В 2А 3В 4С 5С 6Д 7В 8Д 9Д 10С 11В 12А 13В 14С 15Д 16С 17Д 18В 19Д 20Е 21А 22Д 23А 24Д 25В

Мы занимаемся обработкой ваших ответов

Тесты по математике.

1- вариант.

1. Решите уравнение: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

2. Решите неравенство: x²-3x-100

A) x6; B) -2xC) xx5; D) нет решений; E) 0x

3.Решите систему уравнений :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

4. Упростите выражение 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

5. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+2; D) 2х²+5х-3. E) 2х²+5х-2

6. Решите уравнение: 2хּּּ (5+3х) – хּּ (6х – 2 ) = 2 х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

7. Решением системы уравнений:

является пара чисел

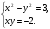
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2) E) (-1;-3).

8. Упростите выражение: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

9. Найдите произведение корней уравнения: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

10. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

11. Стороны треугольника не превосходят соот­ветственно 0,7м; 1,2м; 1,8м. Оцените периметр Р (м) данного треугольника.

A) РР 3,7 C) Р =3,7 D)Р 3,7 E) P -3,7

12. Какие из чисел -2,5, 1,4, 1 и 2,5 являются решением неравенства: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 1,4

13. Округлите до сотых: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

14. Решите систему неравенств:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) не имеет решения.

15. Вычислите: .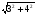

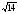
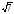
A) 7; B) ; C) 5; D) . E)3;

16. Найдите значение выражения — 4х² – 2х + 5 при х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

17. Представьте 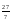в виде смешанного числа:

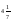
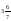
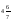
A) ; B); C) ; D) свой ответ. E)3

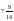
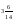
18. Значение выражения — равно:

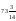
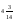
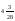
A) ; B); C); D) свой ответ. E)4

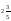
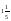
19. Турист проехал на автобусе часа, потом на попутной машине часа. Сколько часов турист был в пути?

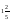
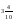
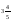
A) ; B); C); D) свой ответ. E)4

20.Из точек А(0,4) и В(0,6) лежит левее на координатном (числовом) луче:

A) А; B) В; C) нет ответа; D) свой ответ. E) AB

21.Между числами 2,3 и 3,1 заключено натуральное число:

A) 2,4; C) 2;

B) 3; D) свой ответ. E)4

22. При увеличении числа 2495,189 на 56,82 получим:

A) 8177,189; C) 2551,271;

B) 2552,009; D) свой ответ.

23. Вычислите .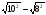

A) 2; B)6; C) 4; D). E)-4

24. Внесите множитель под знак корня .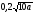

A) ; B); C); D). E)

25.Вынесите множитель из-под знака корня .

A) 3; B) 9; C) 3; D). E) 2

2- вариант.

1. Вычислите: .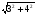

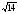
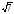
A) 7; B) ; C) 5; D) . E)3;

2. Найдите значение выражения — 4х² – 2х + 5 при х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

3. Представьте 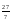в виде смешанного числа:

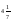
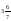
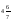
A) ; B); C) ; D) свой ответ. E)3

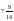
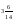
4. Значение выражения — равно:

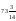
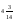
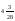
A) ; B); C); D) свой ответ. E)4

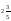
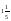
5. Турист проехал на автобусе часа, потом на попутной машине часа. Сколько часов турист был в пути?

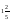
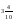
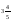
A) ; B); C); D) свой ответ. E)4

6.Из точек А(0,4) и В(0,6) лежит левее на координатном (числовом) луче:

A) А; B) В; C) не знаю; D) свой ответ. E) AB

7.Между числами 2,3 и 3,1 заключено натуральное число:

A) 2,4; C) 2;

B) 3; D) свой ответ. E)4

8. При увеличении числа 2495,189 на 56,82 получим:

A) 8177,189; C) 2551,271;

B) 2552,009; D) свой ответ. E) нет ответа

9. Вычислите .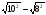

A) 2; B)6; C) 4; D). E)-4

10. Внесите множитель под знак корня .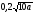

A) ; B); C); D). E)

11.Вынесите множитель из-под знака корня .

A) 3; B) 9; C) 3; D). E) 2

12. Решите уравнение: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13. Решите неравенство: x²-3x-100

A) x6; B) -2xC) xx5; D) нет решений; E) 0x

14.Решите систему уравнений :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Упростите выражение 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Решите уравнение: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Решением системы уравнений:

является пара чисел

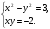
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Упростите выражение: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Найдите произведение корней уравнения: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

22. Стороны треугольника не превосходят соот­ветственно 0,7м; 1,2м; 1,8м. Оцените периметр Р (м) данного треугольника.

A) РР 3,7 C) Р =3,7 D)Р 3,7 E) P -3,7

23. Какие из чисел -2,5, 1,4, 1 и 2,5 являются решением неравенства: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 1,4

24. Округлите до сотых: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

25. Решите систему неравенств:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) не имеет решения.

3- вариант.

1. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

2. Стороны треугольника не превосходят соот­ветственно 0,7м; 1,2м; 1,8м. Оцените периметр Р (м) данного треугольника.

A) РР 3,7 C) Р =3,7 D)Р 3,7 E) P -3,7

3. Какие из чисел -2,5, 1, 4, 1 и 2,5 являются решением неравенства: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 1,4

4. Округлите до сотых: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

5. Решите систему неравенств:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) не имеет решения.

6. Вычислите: .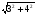

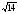
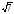
A) 7; B) ; C) 5; D) . E)3;

7. Найдите значение выражения — 4х² – 2х + 5 при х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

8. Представьте 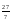в виде смешанного числа:

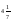
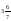
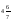
A) ; B); C) ; D) свой ответ. E)3

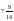
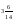
9. Значение выражения — равно:

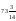
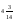
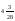
A) ; B); C); D) свой ответ. E)4

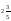
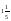
10. Турист проехал на автобусе часа, потом на попутной машине часа. Сколько часов турист был в пути?

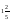
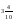
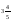
A) ; B); C); D) свой ответ. E)4

11.Из точек А(0,4) и В(0,6) лежит левее на координатном (числовом) луче:

A) А; B) В; C) не знаю; D) свой ответ. E) AB

12. Решите уравнение: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13. Решите неравенство: x²-3x-100

A) x6; B) -2xC) xx5; D) нет решений; E) 0x

14.Решите систему уравнений :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Упростите выражение 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Решите уравнение: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Решением системы уравнений:

является пара чисел

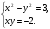
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Упростите выражение: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Найдите произведение корней уравнения: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21.Между числами 2,3 и 3,1 заключено натуральное число:

A) 2,4; C) 2;

B) 3; D) свой ответ. E)4

22. При увеличении числа 2495,189 на 56,82 получим:

A) 8177,189; C) 2551,271;

B) 2552,009; D) свой ответ. E) нет ответа

23. Вычислите .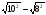

A) 2; B)6; C) 4; D). E)-4

24. Внесите множитель под знак корня .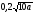

A) ; B); C); D). E)

25.Вынесите множитель из-под знака корня .

A) 3; B) 9; C) 3; D). E) 2

1- нұсқа.

1. Теңдеуді шеш: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

2. Теңсіздікті шеш: x²-3x-100

A) x6; B) -2xC) xx5; D) жауабы жоқ; E) 0x

3.Теңдеулер жүйесін шеш :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

4. Ықшамда: 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

5. Көпмүшенің бөлінуі: (6х³+19х²+19х+6) : (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

6. Теңдеуді шеш: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

7. Теңдеулер жүйесін шеш:

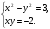
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

8. Ықшамда: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

9.Түбірлердің көбейтіндісін тап: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

10. Көпмүшенің бөлінуі: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

11. Үшбұрыштың қабырғалары: 0,7м; 1,2м; 1,8м. Периметрін тап Р (м) .

A) РР 3,7 C) Р 3,7 D)Р 3,7 E) P -3,7

12. Қай сандар -2,5, -1, 1 и 2,5 теңсіздіктің шешімі болады: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5 E) 3

13. Жүздікке дейін дөнгелет: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

14. Теңдеулер жүйесін шеш:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) шешімі жоқ.

15.Есепте: .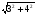

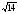
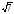
A) 7; B) ; C) 5; D) . E)3;

16. Есептін мәнін тап: — 4х² – 2х + 5 х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

17. Аралас бөлшекке айналдыр :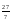

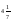
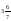
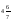
A) ; B); C) ; D) өз жауабын; E)3

18. Есепте — :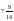

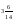
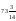
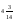
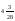
A) ; B); C); D) өз жауабы; E)4

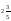
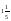
19. Жолаушы автобуспен сағат және көлікпен сағат жүрді. Барлығы қанша сағат жолда болды?

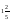
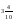
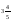
A) ; B); C); D) өз жауабы E)4

20.Қай нүкте А(0,4) және В(0,6) координатаның сол жағында орналасқан:

A) А; B) В; C) жауабы жоқ; D) өз жауабы E) AB

21.Екі санның арасында 2,3 және 3,1 қандай натурал сан орналасқан:

A) 2,4; C) 2;

B) 3; D) өз жауабы E)4

22. 2495,189 және 56,82 қосындысы неге тең :

A) 8177,189; C) 2551,271;

B) 2552,009; D) өз жауабы E) жауабы жоқ

23. Есепте:.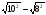

A) 2; B)6; C) 4; D). E)-4

24. Санды түбірдің ішіне еңгіз: .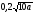

A) ; B); C); D). E)

25.Ықшамда: .

A) 3; B) 9; C) 3; D). E) 2

2- нұсқа.

1. Есепте: .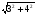

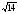
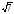
A) 7; B) ; C) 5; D) . E)3;

2. Есепте: — 4х² – 2х + 5 егер х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

3. Аралас бөлшекке айналдыр :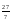

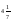
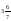
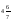
A) ; B); C) ; D) өз жауабын E)3

4. Есепте: —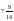

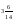
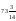
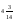
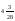
A) ; B); C); D) өз жауабын E)4

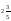
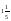
5. Жолаушы автобуспен сағат және көлікпен сағат жүрді. Барлығы қанша сағат жолда болды?

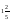
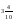
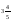
A) ; B); C); D) өз жауабын E)4

6. Қай нүкте А(0,4) және В(0,6) координатаның сол жағында орналасқан:

A) А; B) В; C)жауабы жоқ; D) өз жауабын E) AB

7. Екі санның арасында 2,3 және 3,1 қандай натурал сан орналасқан:

A) 2,4; C) 2;

B) 3; D) өз жауабын E)4

8. 2495,189 және 56,82 қосындысы неге тең:

A) 8177,189; C) 2551,271;

B) 2552,009; D) өз жауабын E) жауабы жоқ

9. Есепте:.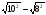

A) 2; B)6; C) 4; D). E)-4

10. Санды түбірдің ішіне еңгіз .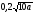

A) ; B); C); D) E)

11. Ықшамда .

A) 3; B) 9; C) 3; D) E) 2

12. Теңдеуді шеш: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13. Теңсіздікті шеш: x²-3x-100

A) x6; B) -2xC) xx5; D) жауабы жоқ ; E) 0x

14. Теңдеулер жүйесін шеш: :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Ықшамда: 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Көпмүшенің бөлінуі: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Теңдеуді шеш: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Теңдеулер жүйесін шеш:

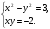
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Ықшамда: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Түбірлердің көбейтіндісін тап: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21. Көпмүшенің бөлінуі: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

22. Үшбұрыштың қабырғалары: 0,7м; 1,2м; 1,8м. Периметрін тап Р (м) .

A) РB) Р 3,7 C) Р 3,7 D)Р 3,7 E) P -3,7

23. Қай сандар -2,5, -1, 1 и 2,5 теңсіздіктің шешімі болады: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 3

24. Жүздікке дейін дөнгелет 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

25. Теңдеулер жүйесін шеш:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) жауабы жоқ

3- нұсқа.

1. Көпмүшенің бөлінуі: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

2. Үшбұрыштың қабырғалары: 0,7м; 1,2м; 1,8м. Периметрін тап Р (м) .

A) РB) Р 3,7 C) Р 3,7 D)Р 3,7 E) P -3,7

3. Қай сандар -2,5, -1, 1 и 2,5 теңсіздіктің шешімі болады: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 3

4. Жүздікке дейін дөнгелет 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

5. Теңдеулер жүйесін шеш:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) жауабы жоқ.

6. Есепте: .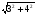

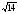
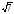
A) 7; B) ; C) 5; D) . E)3;

7. Есепте: — 4х² – 2х + 5 егер х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

8. Аралас бөлшекке айналдыр :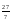

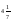
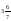
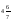
A) ; B); C) ; D) өз жауабын E)3

9. Есепте: —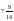

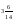
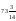
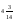
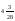
A) ; B); C); D) өз жауабын E)4

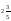
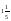
10. Жолаушы автобуспен сағат және көлікпен сағат жүрді. Барлығы қанша сағат жолда болды?

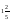
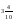
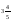
A) ; B); C); D) өз жауабын E)4

11. Қай нүкте А(0,4) және В(0,6) координатаның сол жағында орналасқан:

A) А; B) В; C) жауабы жоқ; D) өз жауабын E) AB

12. Теңдеуді шеш: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13.Теңсіздікті шеш: x²-3x-100

A) x6; B) -2xC) xx5; D) жауабы жоқ E) 0x

14. Теңдеулер жүйесін шеш:

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Ықшамда: 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Көпмүшенің бөлінуі: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Теңдеуді шеш: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Теңдеулер жүйесін шеш:

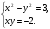
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Ықшамда: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Түбірлердің көбейтіндісін тап: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21. Екі санның арасында 2,3 және 3,1 қандай натурал сан орналасқан:

A) 2,4; C) 2;

B) 3; D) өз жауабын E)4

22. 2495,189 және 56,82 қосындысы неге тең::

A) 8177,189; C) 2551,271;

B) 2552,009; D) өз жауабын

23. Есепте: .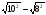

A) 2; B)6; C) 4; D). E)-4

24. Санды түбірдің ішіне еңгіз: .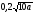

A) ; B); C); D). E)

25. Ықшамда: .

A) 3; B) 9; C) 3; D). E) 2

Ответы.

Государственное бюджетное образовательное учреждение

среднего профессионального образования

«Раменский политехнический техникум» МО

Программа

вступительного экзамена по математике

для поступающих

в ГБОУ СПО «Раменский политехнический техникум» МО

на базе основного общего образования

Раменское,

2012 г.

 Пояснительная записка

Программа вступительного  экзамена по математике предназначена для абитуриентов ГБОУ СПО «Раменский политехнический техникум» МО, поступающих на дневную форму обучения на базе основного общего образования и не имеющих результатов ГИА.

Тест является основной формой проверки знаний абитуриента за курс основной школы.

Объем теста – 15 заданий.

Продолжительность проведения экзамена – 5 часов.

 Программа вступительного экзамена по математике

    Для успешной подготовки к вступительному экзамену по математике в 2012 году поступающим в ГБОУ СПО «Раменский политехнический техникум» МО следует обратить особое внимание на повторение тем, согласно стандарта.

1. Алгебраические выражения:

Формулы сокращенного умножения. Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями. Степени.

1. Измерения, приближения, оценки:

Проценты. Нахождение отношения в процентах. Пропорция. Пропорциональная и обратно пропорциональная зависимость.

1. Уравнения и неравенства.

Уравнения с одной переменной. Корень уравнения. Квадратные уравнения. Решение рациональных уравнений. Система уравнений, решение систем. Неравенства с одной переменной.

1. Планиметрия:

Длина отрезка. Периметр фигуры. Равнобедренный треугольник. Прямоугольный треугольник. Теорема Пифагора.

5. Тригонометрия:

Основные тригонометрические формулы. Знаки тригонометрических функций в разных координатных четвертях.

 Критерии оценки контрольной работы

1 задание:

Вычисление длины отрезка – 3 балла

2 задание:

Сумма углов треугольника. Пропорция – 9 баллов

3 задание:

Свойство сторон равнобедренного треугольника, его периметр – 6 баллов

4 задание:

Свойство углов равнобедренного треугольника – 6 баллов

5 задание:

Теорема Пифагора – 5 баллов

6 задание:

Периметр прямоугольника – 3 балла

7 задание:

Формулы сокращенного умножения, сокращение дробей – 7 баллов

8 задание:

Свойства степени – 5 баллов

9 задание:

Решение линейного уравнения с одной неизвестной – 6 баллов

10 задание:

Решение неполного квадратного уравнения – 7 баллов

11 задание:

Решение полного квадратного уравнения – 7 баллов

12 задание:

Решение линейного неравенства с одной переменной – 7 баллов

13 задание:

Решение квадратного неравенства – 10 баллов

14 задание:

Формула тригонометрической единицы, знаки тригонометрических функций – 10 баллов

15 задание:

Решение системы линейных неравенств с одной переменной – 9 баллов

Рекомендации для проверки (проведения) экзаменационного теста.

Тест состоит из 15 заданий:

Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и поставьте соответствующую цифру в таблицу ответов.

Максимальный балл за тест – 100.

Граница оценок будет зависеть от того сколько баллов наберут поступающие на вступительном экзамене.

Бланк ответов вступительного теста

по математике

Ф.И.О.___________________________________________________

___ вариант.

1 вариант

1. Точка С принадлежит отрезку АВ. Найдите длину отрезка АВ, если АС=10см, СВ=8см.

1. 6см     2) 18см     3) 2см     4) 10см

2) Найдите углы треугольника, если они пропорциональны числам 2; 3 и 7.

      1)300;450;1050      2)150;600;1050      3)200;300;700          4)700;700;400

3) Периметр равнобедренного треугольника 35см. Его основание больше боковой                                    стороны в 1,5 раза. Найдите длину основания треугольника.

      1) 15см     2) 3,5см    3) 10см      4) 30см

4) Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами равен 800 .

      1) 1000         2) 800         3) 400         4) 500

5) У прямоугольного треугольника гипотенуза равна 5см, а один из катетов – 3см. Найдите длину второго катета.

      1) 16см      2) 9см      3) 4см        4) 25см

6) Стороны прямоугольника равны 7см и 3см. Найдите его периметр.

      1) 21см      2) 10см      3) 20см      4) 4см

7) Упростите выражение

      1)           2)         3)           4)

8) Представьте в виде степени выражение

      1)        2)            3)            4)

9) Решите уравнение  4х — 5,5 = 5х — 3(2х — 1,5)

      1) 3,5         2) 2               3) 0,8           4) 0,9

10) Решите уравнение  25 — 100 = 0

         1)        2) 0,5          3)         4)

11) Решите уравнение   х(х + 2) = 3

         1) -3;1      2) -1;3         3)          4) 1;3

12) Решите неравенство    3(3х – 1)  2(5х – 7)

1. )    2) (11;+  3) 4) (-11;+)

13) Решите неравенство  х2 – 2х  3

        2) (-1;3)          3);1)          4) (-

14) Найдите cos,если sin = — и 18002700

1)  2)3) —4)

15) Решите систему неравенств

2 вариант

1. Точка А принадлежит отрезку КС. Найдите длину отрезка АС, если КС=20см, КА=7см.

1)27см     2) 14см     3) 13см     4) 23см

1. Найдите углы треугольника, если они пропорциональны числам 6; 8 и 16.

      1)360;480;960      2)300;400;1100      3)300;400;800          4)600;300;900

3) Периметр равнобедренного треугольника 49 м. Его основание больше боковой                                    стороны на 1м. Найдите длину основания треугольника.

      1) 16м     2) 17м    3) 40м      4) 15м

4) Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании равен 400 .

      1) 1000         2) 400         3) 600         4) 1400

5) У прямоугольного треугольника катеты равны 3см и 4см. Найдите длину гипотенузы этого треугольника.

      1) 5см      2) 7см      3) 25см        4) 16см

6) Стороны прямоугольника равны 6см и 8см. Найдите его периметр.

      1) 14см      2) 28см      3) 48см      4) 2см

7) Упростите выражение

1.           2)         3)          4)

 Представьте в виде степени выражение

      1)        2)            3)            4)

9) Решите уравнение  4 – 5(3х + 2,5) = 3х + 9,5

      1) 1          2) 1,5               3)            4) -1

10) Решите уравнение  4 — 36 = 0

         1)        2)           3)         4) 3

11) Решите уравнение   х(х + 3) = 4

         1) -1;4      2) -4;1         3) 1;4         4) 1

12) Решите неравенство    5(х + 4)  2(4х – 5)

     2)      3)    4) (-;

13) Решите неравенство  х2 + х  6

          1)        2)           3) (-3 ; 2)          4)

14) Найдите sin,если cos = и  27000

1)  — 2)3)  4)

15) Решите систему неравенств  

Ответы

1 вариант

2 вариант