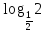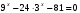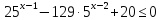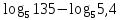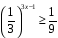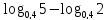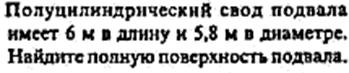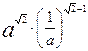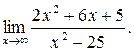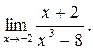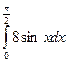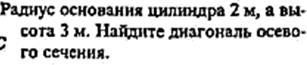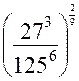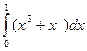Комитет общего и профессионального образования
Ленинградской области
ГБПОУ ЛО «Волховский колледж транспортного
строительства»
УТВЕРЖДАЮ
УТВЕРЖДАЮ
Заместитель директора
Заместитель
директора
по учебной работе
по учебной работе
__________ . «___»___________ 2017
г. «____»
_____________20___ г.
Экзаменационный материал
Дисциплина МАТЕМАТИКА
Группы 106, 111, 130 специальности 08.02.01,
08.02.05, 38.02.03
Преподаватель Петрова Людмила Львовна
Рассмотрено на заседании
цикловой Рассмотрено на заседании цикловой
комиссии .
комиссии . .
.
.
Протокол № от « »
2017г Протокол № ___ от «__» ______201 г
Председатель цикловой
комиссии Председатель цикловой комиссии
___________ _____________
г.
Волхов 2017
ВВЕДЕНИЕ
Экзамен по математике проводится письменно за
счет времени, выделяемого ФГОС СПО на промежуточную аттестацию, с
использованием экзаменационных материалов в виде набора контрольных заданий,
требующих краткого ответа и/или полного решения. На выполнение письменной
экзаменационной работы по математике дается 3 астрономических часа (180 минут).
Письменная
экзаменационная работа по математике составляется из 2-х частей: обязательной и
дополнительной. В обязательную часть включены задания минимально обязательного
уровня, в дополнительную часть — более сложные.
В обязательную часть работы включаются
задания базового уровня по всем основным разделам требований ФГОС — геометрия
(планиметрия и стереометрия), алгебра, начала математического анализа, теория
вероятностей, комбинаторика и статистика.
При выполнении заданий
обязательной
части обучающиеся должны продемонстрировать базовую математическую
компетентность. Задания этой группы проверяют базовые вычислительные и
логические умения и навыки, умение анализировать информацию, представленную в
графиках и таблицах, использовать простейшие вероятностные и статистические
модели, умение ориентироваться в простейших геометрических конструкциях,
владение основными алгоритмами, знание и понимание ключевых элементов
содержания (математических понятий, их свойств, приемов решения задач и пр.),
умение пользоваться математической записью, а также применять математические
знания в простейших практических ситуациях.
Обязательная часть содержит 15 заданий.
Дополнительная
часть направлена на проверку владения материалом на повышенном уровне и
умение решать математические задачи, не сводящиеся к прямому применению алгоритма.
Эта часть содержит 5 заданий повышенного уровня сложности из различных разделов
курса математики.
При выполнении
всех заданий дополнительной части обучающимся требуется представить описание
хода решения задачи и полученный ответ.
За правильное
выполнение любого задания из обязательной части обучающийся получает
один балл.
При выполнении задания из обязательной части,
где необходимо привести краткое решение, за неполное решение задания
(вычислительная ошибка, описка) выставляется 0,5 балла.
Если обучающийся
приводит неверное решение, неверный ответ или не приводит никакого ответа, он
получает 0 баллов.
За каждое задание дополнительной
части максимально можно получить 3 балла.
Максимальное
количество баллов за весь экзамен — 30 баллов.
За выполнение любого
задания из дополнительной части используются следующие
критерии оценки заданий:
|
Содержание критерия |
Баллы |
|
Приведено верное обоснованное решение, приведен правильный ответ |
3 |
|
Приведено верное решение, но допущена вычислительная |
2 |
|
Решение начато |
1 |
|
Неверное решение, |
0 |
Баллы, полученные за
все выполненные задания, суммируются.
Шкала перевода баллов
в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения |
|
«3» (удовлетворительно) |
15- 20 |
|
«4» (хорошо) |
21- 25 |
|
«5» (отлично) |
26 — 30 |
Тематика заданий
1 вопрос – задача на составление математической
модели;
2 вопрос – вычисление степенных выражений;
3 вопрос – решение иррациональных уравнений;
4 вопрос – решение систем уравнений;
5 вопрос – применение свойств логарифмов;
6-9 вопросы – определение свойств функции по
графику;
10 вопрос – нахождение значений
тригонометрических функций;
11 вопрос – определение нулей функции;
12 вопрос – производная или интеграл
элементарных функций;
13 вопрос – нахождение элементов
многогранников;
14 вопрос – тригонометрические уравнения;
15 вопрос – область определения функции;
16 вопрос – задача из раздела «Комбинаторика и
теория вероятностей»;
17 вопрос – показательное или логарифмическое
уравнение;
18 вопрос – нахождение объёмов или площадей
геометрических фигур;
19 вопрос – показательное или логарифмическое
неравенство;
20 вопрос– исследование функции с помощью
производной.
Примерный вариант
экзаменационной работы по математике за 1 курс
Обязательная часть
При выполнении заданий 1-5 запишите ход решения и полученный ответ.
1)
(1
балл) Стоимость одной поздравительной открытки 20 рублей. Сколько
открыток можно будет купить на 700 рублей во время распродажи, если скидка
составляет 35%?
2)
(1
балл) Вычислите значение выражения 
3)
(1
балл) Решите уравнение .
4)
(1
балл) Решите систему уравнений
5)

балл) Найдите значение выражения .
При выполнении заданий 6-9,
используя график функции
(см. рис. ниже) определите и запишите полученный ответ.
6)
(1
балл) Четность, нечетность функции.
7)
(1
балл) Нули функции.

(1
балл) Множество значений функции.
9)
(1
балл) При каких значениях
При выполнении заданий 10-15
укажите ход решения и запишите полученный ответ.
10)
(1
балл) Найдите значение , если известно,
что и
четверти.
11)
(1
балл) Найдите нули функции .
12)
(1
балл) Найти производную функции
13) (1 балл) В прямоугольном параллелепипеде известно,
что и
,
. Найдите длину
ребра .
14) (1 балл) (1 балл) Решите уравнение .
15) (1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-22
запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Сколькими
способами можно выбрать 5 человек на 5 различных должностей из 12 кандидатов
на эти должности?
17) (3 балла)
Найдите корень уравнения 
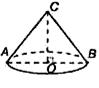
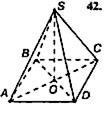
18) (3 балла) В правильной четырехугольной пирамиде точка
—
центр основания, вершина,
,
. Найдите боковое ребро
.
19) (3 балла) Решите неравенство .
20) (3 балла) Найдите наибольшее значение функции y =– 2x2 – 8х -12
на отрезке [–1; 7]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
10 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Налог на доходы составляет 13% от заработной платы. После удержания
налога на доходы Лариса Петровна получила 10440 рублей. Сколько рублей
составляет заработная плата Ларисы Петровны?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Наименьшее и наибольшее значения функции.

балл) Множество значений функции.
9) (1
балл) При каких значениях
При
выполнении заданий 10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1
балл) Найдите нули функции .
12) (1
балл) Найти производную функции
13) (1 балл) В правильной
четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
14)
(1 балл) Решите уравнение sin 2x = 1.
15) (1 балл) Найдите область определения
функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Из 12
полицейских необходимо составить наряд из 5 человек. Сколькими способами это
можно сделать?
17) (3 балла)
Найдите корни уравнения .
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 15см,
высота пирамиды равна 12см. Найти объём и площадь полной поверхности пирамиды.
19)
(3
балла) Решите неравенство .
20) (3 балла) Найдите
наименьшее значение функции y = x2 – 12x + 12 на отрезке [-1 ; 3 ]
Преподаватель Петрова Л.Л.
Комитет общего и профессионального образования
Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
9 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Флакон шампуня стоит 80 рублей. Какое наибольшее количество флаконов
можно купить на 500 рублей во время распродажи, когда скидка составляет 25%?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) На основании основного логарифмического тождества найдите
значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Наименьший положительный период функции.

балл) Множество значений функции.
9) (1
балл) Наименьшее и наибольшее значения функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1 балл) Найдите
нули функции
12) (1
балл) Найти производную функции
13) (1
балл) В прямоугольном параллелепипеде известно, что
,
,
.
Найдите длину ребра .
14) (1
балл) Решите уравнение cos x = –
.
15) (1
балл) Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Сколько 3-значных чисел можно составить из множества цифр
1,2,3,4,5,6,7,8,9 а) без повторений; б) с повторениями?
17) (3 балла) Найдите корни уравнения .
18)
(3 балла) Сторона основания правильной четырехугольной пирамиды равна 12см,
высота пирамиды равна 8см. Найти площадь полной поверхности пирамиды.
19)
(3 балла) Решите неравенство.
20) (3 балла) Найти
интервалы возрастания и убывания функции y = x4 – 32x2
– 75
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
8 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Билет на автобус стоит 15 рублей. Какое наибольшее число билетов можно
будет купить на 100 рублей после повышения цены билета на 20%?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Множество значений функции.

балл) Нули функции.
9) (1
балл) Четность, нечетность функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1
балл) Найдите нули функции
12) (1
балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
14) (1 балл)
Решите уравнение cos3 x = –1.
15)
(1 балл) Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Участники жеребьевки тянут из ящика
жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого
наудачу извлеченного жетона не содержит цифры 7.
17) (3 балла) Найдите корни уравнения .
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 10см,
высота пирамиды равна 8см. Найти объём и площадь полной поверхности пирамиды.
19)
(3 балла) Решите неравенство.
20) (3 балла) Найдите экстремумы функции y(x) = 2x3 – 3x2 – 12x + 5
выяснить их род.
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
7 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Из 75 девятиклассников школы 15 человека приняли участие в городских
спортивных соревнованиях. Сколько процентов девятиклассников не принимали
участия в этих соревнованиях?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции 
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Четность, нечетность функции.

балл) Монотонность функции.
9) (1
балл) Нули функции.

При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1 балл) Найдите нули
функции
12) (1
балл) Найти производную функции
13) (1
балл) В прямоугольном
параллелепипеде известно, что
,
,
.
Найдите длину ребра .
14) (1 балл)
Решите уравнение sin x = .
15) (1 балл)
Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Из 100 билетов выигрышными
являются 15. Какова вероятность того, что среди 6-ти билетов, взятых на удачу,
будет два выигрышных?
17) (3 балла) Найдите корни уравнения
.
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 5 м,
высота пирамиды равна 4 м. Найти объём и площадь полной поверхности пирамиды.
19 (3
балла) Решите неравенство
20 (3 балла) Найдите
наибольшее значение функции y =– 2x2 – 8х -12 на отрезке [–2; 6]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
6 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Дневная норма потребления витамина C
составляет 60 мг. Один мандарин в среднем содержит 35 мг витамина С. Сколько
примерно процентов дневной нормы витамина С получил человек, съевший один
мандарин?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение.
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Множество значений функции.
7) (1
балл) Четность, нечетность функции.

балл) Промежутки возрастания функции.
9) (1
балл) Нули функции.

При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр
основания, вершина,
,
. Найдите боковое ребро
14) (1 балл) Решите уравнение
cos 2x = 0
15)(1
балл) Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) В магазин поступило 25 телевизоров,
4 среди которых имеют скрытые дефекты. Наудачу отбираются 2 телевизора для
проверки. Какова вероятность того, что оба они не имеют дефектов?
17) (3 балла) Найдите корни
уравнения .
18) (3 балла) Апофема
правильной четырехугольной пирамиды равна 15см, высота пирамиды равна 12см.
Найти объем пирамиды и площадь ее полной поверхности.
19) (3 балла) Решите неравенство 
20) (3 балла) Найти
интервалы возрастания и убывания функций y = x4 – 2x2
+ 64.
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
5 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения
и полученный ответ.
1) (1
балл) Стоимость проезда в пригородном электропоезде составляет 198 рублей.
Школьникам предоставляется скидка 50 процентов. Сколько рублей стоит проезд
группы из 4 взрослых и 12 школьников?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Множество значений функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13)
(1 балл) В прямоугольном параллелепипеде известно, что
,
,
. Найдите длину
ребра .
14) (1 балл) Решите
уравнение sin 3x = –1.
15) (1 балл) Найдите
область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход обоснование решения и полученный ответ.
16) (3 балла) В
партии деталей 25 изделий высшего сорта, 35 изделий первого сорта и 5 нестандартных.
Деталь, выбранную наудачу, проверяют на соответствие стандарту. Найти
вероятность того, что она окажется нестандартной.
17) (3 балла) Найдите корни уравнения
.
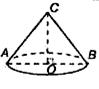
18) (3 балла) Высота конуса равна 9
см., радиус основания 4 см. Найти объем конуса и площадь его полной
поверхности.
19) (3 балла)
Решите неравенство .
20) (3 балла) Найти экстремумы функции y(x) = 2x4 – 4x2 + 20, выяснить их род.
Преподаватель
Петрова Л.Л.
Комитет общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
4 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения
и полученный ответ.
1) (1
балл) Тетрадь стоит 20 рублей. Сколько тетрадей можно купить на 200 рублей
после повышения цены на 25%?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Наименьший положительный период функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13)
(1 балл) В
прямоугольном параллелепипеде известно, что
,
,
. Найдите длину ребра
.
14) (1 балл) Решите
уравнение sin x = – .
15) (1 балл)
Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-18 запишите ход, обоснование решения и
полученный ответ.
16) (3 балла) Из 40 полицейских необходимо составить наряд из 8
человек. Сколькими способами это можно сделать?
17) (3 балла) Найдите корень уравнения .
18)
(3 балла) Стороны основания
правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите
площадь боковой поверхности этой пирамиды.
19)
(3 балла) Решите неравенство – 1
0.
.
20) (3 балла) Найдите
наибольшее значение функции y =– x2 + 4х + 8 на отрезке [ 3; 5]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
3 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) После повышения цены на 20% тетрадь стоит 30 рублей. Сколько стоила
тетрадь до повышения цены?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Множество значений функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
14)
(1 балл) Решите уравнение cos x = .
15)
(1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-20 запишите ход, обоснование решения и
полученный ответ.
16)(3 балла) Сколькими способами можно выбрать 6 человек
на 6 различных должностей из 10 кандидатов на эти должности?
17) (3 балла) Найдите корень уравнения .
18)
(3 балла) Стороны основания
правильной четырехугольной пирамиды равны 8, боковые ребра равны 5. Найдите
площадь поверхности этой пирамиды.
19)
(3 балла) Решите неравенство – 1
0.
20)(3 балла) Найти
интервалы возрастания и убывания функций
y =– x4 + 32x2 + 12.
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
2 Вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Коробка конфет стоит 60 рублей. Какое наибольшее количество коробок
можно купить на 400 рублей вовремя распродажи, когда скидки составляет 20%
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения 

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Значения переменной х, при .
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13)
(1 балл) В
прямоугольном параллелепипеде известно, что
,
,
. Найдите длину ребра
.
14) (1 балл)
Решите уравнение sin 2x = -1.
15) (1 балл) Найдите область
определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) В магазин поступило
26 телевизоров, 4 среди которых имеют скрытые дефекты. Наудачу
отбираются 2 телевизора для проверки. Какова вероятность того, что оба они не
имеют дефектов?
17) (3 балла) Найдите корень
уравнения .
18) (3 балла) Найти объем прямоугольного
параллелепипеда, диагональ которого равна 13см, а длина сторон основания равны
3см и 4см.
19)
(3 балла) Решите неравенство –
1 0.
20) (3 балла) Найдите
наибольшее значение функции y =– 2x2 – 8х – 12 на отрезке [–1; 7]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
1 Вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Стоимость проезда в электричке составляет 240 рублей. После нового года
ожидается повышение стоимости на 15%. Сколько будет стоить проезд после нового
года?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение.
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Нули функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Множество значений функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите значение , если известно, что
и
четверти.
11)
(1 балл) Найдите
нули функции
12)
(1 балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
14) (1 балл)
Решите уравнение sin 2x = 0.
15)(1 балл) Найдите
область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) В партии деталей 80 изделий высшего
сорта, 90 изделий первого сорта и 7 нестандартных. Деталь, выбранную
наудачу, проверяют на соответствие стандарту. Найти вероятность того, что она
окажется нестандартной.
17) (3 балла) Найдите корень
уравнения .
18) (3 балла) Стороны основания правильной
четырёхугольной пирамиды равны 6, боковые рёбра равны 5. Найдите площадь
поверхности этой пирамиды.
19)
(3 балла) Решите неравенство ≤16.
20) (3 балла) Найти
экстремумы функции y(x) = 3x4 + 4x3
– 12x2
+ 17, выяснить их род.
Преподаватель
Петрова Л.Л.
Инструкция для обучающихся по выполнению
экзаменационной работы
На выполнение
письменной экзаменационной работы по математике дается
3 астрономических часа
(180 минут).
Экзаменационная работа
состоит из 2-х частей: обязательной и дополнительной.
Обязательная часть содержат задания минимально
обязательного уровня, а дополнительная часть — более сложные задания.
При выполнении
большинства заданий обязательной части требуется представить ход решения и
указать полученный ответ. Только в нескольких заданиях достаточно представить
ответ. За правильное выполнение любого задания из обязательной части Вы
получаете один балл. Если Вы приводите неверное решение, неверный ответ или не
приводите никакого ответа, получаете 0 баллов за задание.
При выполнении любого задания дополнительной
части необходимо подробно описать ход решения и дать ответ.
Правильное выполнение заданий дополнительной
части оценивается
3 баллами.
Баллы, полученные за
все выполненные задания, суммируются. Постарайтесь правильно выполнить как можно
больше заданий и набрать как можно больше баллов.
Перед началом работы
внимательно ознакомьтесь со шкалой перевода баллов в отметки и обратите
внимание, что начинать работу следует с заданий обязательной части.
|
Отметка |
Число баллов, необходимое для получения |
|
«3» (удов.) |
9-15 |
|
«4» (хорошо) |
16-21 |
|
«5» (отлично) |
Более 21 |
Желаем успехов!
Преподаватель
Петрова Л.Л.
ЭКЗАМЕННАЦИОННЫЕ ЗАДАНИЯ
ПО МАТЕМАТИКЕ
Разработала: Донцова Валентина Викторовна
преподаватель ГАПОУ МО «КТК»
Пояснительная записка
Программа экзамена по математике за 1 семестр 1курса.
Экзамен в письменной форме из 10 заданий.
Продолжительность проведения экзамена – 5 часов.
Программа итогового экзамена по математике
Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем:
Тригонометрия:
Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.
Понятие степени:
Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.
3. Показательная функция:
Показательная функция. Свойства функций.
4. Стереометрия:
Многогранники.
Критерии оценки экзаменационной работы
|
Оценка «5» |
Оценка «4» |
Оценка «3» |
Оценка «2» |
|
90-100% (9-10 заданий) |
70-89% (7-8 заданий) |
50-69% (5-7 заданий) |
меньше 50% (меньше 5 заданий) |
Вариант 1
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 2
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 3
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 4
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 5
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 6
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 7
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 8
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 9
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 10
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 11
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 12
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 13
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 14
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 15
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 16
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 17
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 18
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 19
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 20
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Программа
итогового экзамена по математике
Раменское,
2013 г.
Пояснительная записка
Программа итогового экзамена по математике предназначена для студентов СПО.
Тест является основной формой проверки знаний за курс математики.
Объем теста – 20 заданий.
Продолжительность проведения экзамена – 5 часов.
Программа итогового экзамена по математике
Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем, согласно стандарта.
-
Тригонометрия:
Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.
-
Производная:
Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.
-
Первообразная:
Основное свойство первообразной. Правила нахождения первообразных.
-
Понятие степени:
Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.
5. Показательная и логарифмическая функции:
Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.
6. Стереометрия:
Многогранники. Тела вращения.
Критерии оценки контрольной работы
1 задание:
Степень с рациональным показателем – 1 балл
2 задание:
Степень с рациональным показателем – 1 балл
3 задание:
Свойства логарифмической функции – 1 балл
4 задание:
Основные тригонометрические формулы – 2 балла
5 задание:
Основные тригонометрические формулы–2 балла
6 задание:
Решение тригонометрических уравнений– 1 балл
7 задание:
Решение иррациональных уравнений – 2 балла
8 задание:
Решение показательных уравнений – 2 балла
9 задание:
Метод интервалов — Решение иррациональных уравнений – 1 балл
10 задание:
Свойства тригонометрических функций – 1 балл
11 задание:
Вычисление производных — 1 балл
12 задание:
Нахождение первообразной функции – 1 балл
13 задание:
Решение логарифмических уравнений – 1 балл
14 задание:
Нахождение максимального и минимального значений функции – 2 балла
15 задание:
Свойства тел в стереометрии – 1 балл
16 задание:
Площадь криволинейной трапеции – 3 балла
17 задание:
Построение графика логарифмической функции – 3 балла
18 задание:
Решение показательных неравенств — 3 балла
19 задание:
Многогранники — 3 балла
20 задание:
Тела вращения — 3 балла
Рекомендации для проверки (проведения) экзаменационного теста.
Тест состоит из 20 заданий.
Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и отметьте соответствующую ячейку в таблицу ответов.
Максимальный балл за тест – 35.
0 – 14 баллов — «2» («неудовлетворительно»)
15 – 19 баллов — «3» («удовлетворительно»)
21 – 29 баллов — «4» («хорошо»)
30 – 35 баллов — «5» («отлично» )
Ответы
Вариант 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
||||||||||||||||||
|
4 |
|
|
|
|
Вариант 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|||||||||||||
|
4 |
|
|
|
|
|
Вариант 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
Бланк ответов
экзаменационного теста
по математике
Ф.И.О.___________________________________________________
Группа № ________________________
Специальность ____________________
___ вариант.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
||||||||||||||||||||
|
2 |
||||||||||||||||||||
|
3 |
||||||||||||||||||||
|
4 |
Вариант 1
-
Вычислите 29
– 15.
-
2) 43 3) 73 4) 101.
-
Упростите выражение
.
-
5 2) 1 3) 10 4) 0.
3) Упростите выражение – 2
.
1) 2) 1 3) 8
4) 20.
4) Найдите значение , если
= -0,8 и
.
1) -0,6 2) 0,6 3) 0,2 4) 0,36
5) Упростите выражение 7cos2α – 5 + 7sin2α.
1) 1 + cos2α 2) 2 3) -12 4) 12.
6) Решите уравнение = 1.
1)2n, n
2)
3)
+2
n, n
4)
n, n
7) Укажите промежуток, которому принадлежит корень уравнения = -х.
1) 2) (35;37) 3) (-2;
4)
.

1) [-4;0) 2) [0;1) 3) [-∞;-4) 4) [4;6).
9) Решите неравенство ≤0.
1) (-∞;-2) [
) 2) [-2;
)
( 1;+∞) 3) (-∞;-2) 4) (-∞;-5)
(-2;
.
10) Найдите множество значений функции у =– 2.
1) [3;1] 2) (-∞;+∞) 3) [-1;1] 4) [-3;-1].
11) Найдите производную функции f(x) = .
1) -4 2) -8
3) 8
4)
.
12) Укажите первообразную функции f(x) = 2х + 4х3 – 1.
1) х2 + х4 – х 2) 2х2 + 4х4 3) 2 + 12х2 4) х2+х4.
13) Решите равнение +
=
.
1) 0 2) 4 3) 9 4) 15.
14) Найдите точки максимума функции у = х3 – 3х2 .
1) 0 2) 2 3) -2 4) 3.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1.
1) 5 2) 10 3) 3 4) 31.
16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х2, у = 0, х = 0, х = 2.
1) 8 2) 2 3) 5
4) 6
.
17) Укажите область определения функции у =.
1) (-∞;0)(2;+∞) 2) (-2;+∞) 3) (2;+∞) 4) (0;2).
18) Найдите наибольшее целое решение неравенства – 1
0.
1) 0 2) -1 3) 1 4) 2.
19) Площади двух граней прямоугольного параллелепипеда равны 56дм2 и 192дм2, а длина их общего ребра 8дм. Найдите объем параллелепипеда.
1) 840 2) 1029 3) 1344 4) 1210.
20) Образующая конуса равна 12см и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 384 2) 192 3) 24 4) 648.
Вариант 2
-
Вычислите 7 — 3∙
.
-
2) 8 3) -5 4) -17.
-
Упростите выражение
.
1) 1,2 2) 5 3) 4)
.
3) Упростите выражение +
—
.
1) 2 +2 2) 7 3) 3 — 6
4) 2.
4) Найдите значение, если
=
и 0
.
1) — 2)
3)
4)
.
5) Упростите выражение -3sin2α — 6 – 3cos2α.
1) 1 2) 2cosα 3) cosα + 4) -9 .
6) Укажите промежуток, которому принадлежит корень уравнения = -х.
1) 2) (-
;-10) 3)
4)
.
7) Решите уравнение = 1.
1) n, n
2)
3)
+2
n, n
4)
n,n
.

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).
9) Решите неравенство ≤ 0.
1) (-2;) 2) [-2;2)
(
;+∞) 3) (-∞;3) 4) (-∞;-2)
(
].
10) Найдите множество значений функции у = + 4.
1) [3;5] 2) (-∞;+∞) 3) [-1;1] 4) [-5;-3].
11) Найдите производную функции f(x) = .
1) 3 2)
3) -3
4) —
.
12) Укажите первообразную функции f(x) = 3х2 + 2х -4.
1) х3+ х2 — 4х 2) 6х + 2 3) х3+ х2 4) х2+ х – 4х.
13) Решите равнение +
=
1) 0 2) 11 3) 3 4) 12.
14) Найдите точку минимума функции у = х2 — 1.
1) -1 2) 1 3) -2 4) 0.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6.
1) 55 2) 7 3) 49 4) 11.
16) Вычислите площадь фигуры (S), ограниченной линиями у = х3 + 1, у = 0, х = 0, х = 2.
1) 8 2) 5 3) 6 4) 4.
17) Укажите область определения функции у =.
1) (-∞;0)(4;+∞) 2) (-4;+∞) 3) (4;+∞) 4) (0;4).
18) Найдите наименьшее целое решение неравенства – 1
0.
1) 0 2) 1 3) -1 4) 2.
19) Площади двух граней прямоугольного параллелепипеда равны 35см2 и 42см2, а длина их общего ребра 7см. Найдите объем параллелепипеда.
1) 840 2) 10290 3) 770 4) 210.
20) Образующая конуса равна 24см и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 3840 2) 1092 3) 5184 4) 648.
Вариант 3
1) Вычислите 2∙ – 0,90
1)10,9 2) 11 3) 9,1 4) 9.
2) Упростите выражение
-
2) 2 3) 0,7 4) 36.
3) Упростите выражение —
+
1) -1 + 2) -2 3) 0 4)
.
4) Найдите значение , если
= —
и
1) 2)
3)
4)
5) Упростите выражение -4sin2α +5 – 4cos2α
1) 1 2) 1 + 8sin2α 3) 1 + 8cos2α 4) 9.
6) Укажите промежуток, которому принадлежит корень уравнения = -х
1) 2) (-∞;-2) 3)
4)
.
7) Решите уравнение = -1
1) 2)0 3)
+2
n, n
4)
n, n

= 16
1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).
9) Решите неравенство ≥0
1) (-∞;-8] (
; 2) 2) [-8;
)
( 2;+∞) 3) (-∞; 2) 4) (-∞;-8)
(2; +∞

10) Найдите множество значений функции у = – 1
1) [-1;1] 2) (-∞;+∞) 3) [-2;0] 4) [0;2].
11) Найдите производную функции f(x) =
1) -18 2) 6
3) 18
4)
.
12) Укажите первообразную функции f(x) = 5х4 – 2х + 1
1) 5х5 – 2х2 + 1 2) 20х3 – х 3) х4 – 2х + х 4) х5 – х2 + х.
13) Решите равнение +
=
1) 15 2) 5 3) 4 4) 10.
14) Найдите точку максимума функции у = 4х – х4
1) 4 2) 2 3) -4 4) 0.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7
1) 19 2) 11 3) 121 4) 36.
16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х3, у = 0, х = 0, х = 1.
1) 1 2) 3)
4) 1
.
17) Укажите область определения функции у =.
1) (-3;+∞) 2) (-∞;0)(3;+∞) 3) (3;+∞) 4) (0;3).
18) Найдите наибольшее целое решение неравенства – 1
0.
1) 1 2) -1 3) 2 4) 0.
19) Площади двух граней прямоугольного параллелепипеда равны 20см2 и 45см2, а длина их общего ребра 5см. Найдите объем параллелепипеда.
1) 240 2) 120 3) 180 4) 4500.
20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 3804 2) 2192 3) 2187 4) 6408.
10-12. Чтение графика функции
Используя график функции у = f(x) (см. рис. ниже), определите и запишите ответ
10.1. Промежутки возрастания и убывания функции.
11.1. При каких значениях x
12.1. Наибольшее и наименьшее значения функции.
10.2. Промежутки возрастания и убывания функции.
11.2. Наибольшее и наименьшее значения функции.
12.2. При каких значениях x
10.3. Промежутки, на которых
11.3. Точки экстремума функции.
12.3. Наибольшее и наименьшее значения функции.
10.4. Нули функции.
11.4. Промежутки возрастания и убывания функции.
12.4. Наибольшее и наименьшее значения функции.
10.5. При каких значениях x функция y не имеет производной.
11.5. При каких значениях x выполняется
12.5. Наибольшее и наименьшее значения функции.
10.6. При каких значениях x выполняется
11.6. Промежутки возрастания и убывания функции.
12.6. При каких значениях x выполняется
10.7. При каких значениях x выполняется
11.7. Промежутки возрастания и убывания функции.
12.7. При каких значениях x выполняется
10.8. Область определения функции.
11.8. При каких значениях x выполняется
12.8. При каких значениях x выполняется
10.9. Область определения функции.
11.9. При каких значениях x выполняется
12.9. При каких значениях x выполняется
10.10. Область определения функции.
11.10. При каких значениях x выполняется 
12.10. Промежутки возрастания и убывания функции.
10.11. Область определения функции.
11.11. При каких значениях x выполняется
12.11. Промежутки возрастания и убывания функции.
10.12. Область определения функции.
11.12. При каких значениях x выполняется
12.12. Промежутки возрастания и убывания функции
.
10.13. Область определения функции.
11.13. При каких значениях x выполняется
12.13. При каких значениях x выполняется
10.14. При каких значениях x выполняется
11.14. При каких значениях x выполняется
12.14. Наибольшее и наименьшее значения функции.
10.15. Область определения функции.
11.15. При каких значениях x выполняется 
12.15. При каких значениях x выполняется
10.16. При каких значениях x выполняется
11.16. Промежутки возрастания и убывания функции.
12.16. Наибольшее и наименьшее значения функции.
10.17. При каких значениях x выполняется
11.17. Точки экстремума функции.
12.17. Промежутки возрастания и убывания функции.
10.18. При каких значениях x выполняется
11.18. Промежутки возрастания и убывания функции.
12.18. Наибольшее и наименьшее значения функции.
10.19. Область определения функции.
11.19. При каких значениях x выполняется
12.19. Точки экстремума функции.
10.20. При каких значениях x выполняется
11.20. При каких значениях x выполняется
12.20. Наибольшее и наименьшее значения функции.
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №1
-
Вычислите значение выражения
-
Решите уравнение
-
Вычислите значение выражения
-
Решите уравнение:
-
Решите уравнение
-
Вычислите
+
-
Найти угол между векторами
-
В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
-
. Решите уравнение
-
Решите неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №2
1. Вычислите значение выражения
2. Решите уравнение
3.Вычислите значение выражения: lg100-lg10+lg1
4. Решить уравнение
5.Решите уравнение
6. Вычислить
7. Даны координаты точек А(3;-2;1), В(5;1;-4),С(2;0;1),Д(5;-1;3). Найти угол между векторами АВ и СД.
8. На соревнованиях по лёгкой атлетике наш техникум представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?
9.Решить уравнение:5x+1+5x + 5x-1
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №3
1. Вычислите значение выражения: 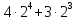
2. Решите уравнение : =11.
3.Вычислите значение выражения
4.Решите уравнения:
5. Вычислить:
6. Решить уравнение:
7.Найти скалярное произведение векторов:
8. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?
9.Решить уравнение: 7x -7x-1 = 6
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №4
1. Вычислите значение выражения.
2. Решите уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 0,5x+7*0,51-2x = 2
7.Найти скалярное произведение векторов:
8. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?
9.Решить уравнение: 3x+2 +3x = 10
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 5
1. Вычислите значение выражения. 2*53+3*52
2. Решите уравнение = 7
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7. Вычислите длину вектора:
8. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
9.Решить уравнение: 4x – 2x+1 = 48
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 6
1. Вычислите значение выражения. + log
8+ log
2
2. Решите уравнение =4.
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить: log8+ log
2
6. Решить уравнение: 112Х+5=1
7. Вычислите длину векторов:
8. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?.
9.Решить уравнение: 32x – 2*32x-1 – 2*32x-2 = 1
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 7
1. Вычислите значение выражения:
2. Решите уравнение =0
3. Вычислите значение выражения.
4.Решите уравнение
5 Найти ,
.
6. Решить уравнение: 17Х+2=Х
7. Вычислите длину вектора
8. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
9.Решить уравнение:2x + 2x-3 = 18
10. Решить неравенство:
.
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 8
1. Вычислите значение выражения:
2.
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 11х-10=121
7. Вычислите длину вектора
8. Из города А в город В ведут две дороги, из города В в С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
9.Решить уравнение: 3x +4*3x+1 = 13
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 9
1. Вычислите значение выражения:
2. Решите уравнение =0
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 11х-10=121
7 Найти скалярное произведение а ( 4; — 7; — 3) в ( 3; -2; 1)
8. Сколько двузначных чисел можно составить из чисел 1,2,3,4?
9.Решить уравнение: 5x+1 +3*5x-1 -6*5x +10 = 0
10. Решить неравенство:42x -5*4x + 4
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 10
1. Вычислите значение выражения:
2. Решить уравнение =
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 2х+1=64
7 Найти угол между векторами, а = 6i + 4k в =2 i -12 k
8. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
9.Решить уравнение: 2x+3— 2x+1 = 12
10. Решить неравенство:2x+2x+2≤ 20
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 11
1. Вычислите значение выражения:
2. Решить уравнение
= 5
3. Вычислите значение выражения.
—
4.Решите уравнение
5. Вычислить: 27log32
6. Решить уравнение: 4х+1=8
7 Найти скалярное произведение векторов а ( 4; — 7; — 3), в ( 3; -2; 1)
8. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
9.Решить уравнение: 2x+1 +2x-1 +2x =28
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 12
1. Вычислите значение выражения: 27log32+
2. Решить уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить: log8+ log
2
6. Решить уравнение: 4х+1=8
7 Найти скалярное произведение векторов а ( 4; — 7; — 3), в ( 3; -2; 1)
8. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
9.Решить уравнение: 3x-1 -3x +3x+1 = 63
10. Решить неравенство:
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 13
1. Вычислите значение выражения:
2. Решить уравнение
8
3. Вычислите значение выражения. 27log32
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = 3i + 4k , в =5 i+ 12 k
8. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?
9.Решить уравнение: 23x+2 -23x-2 = 30
10. Решить неравенство: 16x 0,125
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 14
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 2х+1=64
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 Сколькими способами можно разложить 7 разных монет в три кармана?
9.Решить уравнение: 2*4x =64
10. Решить неравенство 2x -2x-415
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 15
1. Вычислите значение выражения: при
.
2. Решить уравнение: 7
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить: log8+ log
2
6. Решить уравнение: 17х-16=1
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 Семь девушек водят хоровод. Сколькими различны ми способами они могут встать в круг?
9.Решить уравнение: 64x -8x -56 = 0
10. Решить неравенство: .
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 16
1. Найдите значение выражения при
.
2. Решить уравнение: 7
3. Вычислите значение выражения. log327-lg0,01+log0,6 0,36+log71.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение: 4x-1 =1
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
9.Решить уравнение: 16x -17*4x +16=0
10. Решить неравенство: 1002х+1
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 17
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения. log
8+ log
2
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
10. Решить неравенство: .
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 18
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = 4i + j -2k в = 3i + 4j -2k
8 Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими
способами он может сформировать команду, если 2 определенных мальчика
должны войти в команду?
9.Решить уравнение: 3x+9x-1 – 810 = 0
10. Решить неравенство: 7x-2 49
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 19
1. Вычислите значение выражения:
2. Решить уравнение
3. Вычислите значение выражения. log5250 – log52
4.Решите уравнение
5. Вычислить:
6. Решить уравнение:
7 Найти угол между векторами: а = -2i + 5j + 2k в = 7i + 6j -2k
8 В шахматном турнире принимали участие 15 шахматистов, причем
каждый из них сыграл только одну партию с каждым из остальных.
Сколько всего партий было сыграно в этом турнире?
9.Решить уравнение: 9x -3x – 6 = 0
10. Решить неравенство: 3x-2 9
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 20
1. Вычислите значение выражения: 60,5 3 0,5(0,25) 0,25 .
2. Решить уравнение = 5.
3. Вычислите значение выражения.
4.Решите уравнение
5. Вычислить
6. Решить уравнение:
7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k
8 Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
9.Решить уравнение: 52x -5x – 600 = 0
10. Решить неравенство log5 (4х+1) -1.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ зам. директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет №1
1.
Корни
натуральной степени из числа и их свойства.
2.
Перпендикуляр
и наклонная.
3.
Событие,
вероятность события.
4.
Примеры:
1)
Решить уравнения
2)Найти
предел
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________Гаджиева |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№2
1.
Степени
с рациональными показателями, их свойства.
2.
Параллелепипед.
Куб.
3.
Понятие
о пределе последовательности.
4.
Примеры:
1)Упростите выражение
cos2x-6+sin2x
2) Найти производную
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№3
1.
Логарифми
его свойства
2. Двугранный угол.
3. Понятие о
производной функции, её геометрический смысл.
4. Примеры:
1) Найти значение производной функции
f1(x)
при x=0—1
2) Найти предел
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№4
1. Радианная
мера угла
2. Раскрытие
неопределенностей 0/0 и ∞/∞.
3. Цилиндр.
4. Примеры:
1)Вычислите
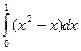
2) Упростите выражение
cos4x—sin4x
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№5
1.
Основные
тригонометрические тождества
2.
Геометрические преобразования пространства:
параллельный перенос
3.
Понятие о производной функции
4.
Примеры
1)Необходимо
выбрать в подарок 4 из 10 имеющихся книг. Сколькими способами можно это
сделать?
2)
Найти значение производной функции
f1(x) при x=1
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол№4 Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№6
1. Геометрический
смысл производной функции
2. Геометрические
преобразования пространства: симметрия относительно плоскости
3. Шар и сфера, их
сечения.
4. Примеры:
1)
Из 30 участников собрание надо
выбрать председателя и секретаря. Сколькими способами это можно сделать?
2) Найти
производную
f(x)=xcosx
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№7
1. Физический смысл
производной функции
2.
Арксинус, арккосинус, арктангенс
числа
3.
Формулы
объема куба, прямоугольного параллелепипеда
4.
Примеры:
1) Сколько шестизначных чисел (без повторения цифр) можно
составить из цифр 0, 3, 5, 6, 7, 8?
2) Решите уравнения
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№8
1.
Функции.Область
определения и множество значений; график функции.
2. Производные суммы,
разности, произведения, частного.
3.
Формулы
объема цилиндра
4. Примеры:
1)
Сколькими способами 8 человек
могут встать в очередь в театральную кассу?
2) Вычислить:1)
; 2)
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№9
1. Исследование
функции по схеме.
2. Производные
основных элементарных функций.
3. Формулы
объема куба.
4. Примеры:
1)
Вычислить
2)
3)
2) Решить
уравнения
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№10
1. Действия над
векторами в пространстве
2. Производные
основных элементарных функций.
3. Параллелепипед.
Куб.
4. Примеры:
1)
Упростить:
(sin2x+tx2xsin2x)ctgx
2)
Найти
значение выражения
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№11
1. Перпендикуляр и
наклонная.
2. Понятие о пределе последовательности.
3.
Логарифми
его свойства.
4.
Примеры
1)Вычислите
5-4 *
56; 3) 710 : 712;
5) (3-4)-1;
2)Написать
уравнение касательной к графику функции в точке с абсциссой x0
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№12
1. Корни
натуральной степени из числа и их свойства
2. Производные суммы,
разности, произведения, частного.
3. Аксиомы
стереометрии
4. Примеры:
1) Вычислите
44 *4-3;
65-3 : 65-3; (82)-2
* 83
2) В группе 30 студентов. Необходимо выбрать старосту,
заместителя старосты и профорга. Сколько существует способов это сделать?
5.
Задача :
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№13
1. Пирамида.
Правильная пирамида.
2. Показательная
функция, свойства и график.
3.
Арксинус, арккосинус, арктангенс
числа
4.
Примеры:
1)
Вычислить:
81* 3-4;
2) 9-6 * 95; 3) (3-1)5
*272;
2)
Порядок выступления 7 участников конкурса
определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
5.
Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№14
1. Шар
и сфера, их сечения
2. Основные
понятия комбинаторики
3. Действия над
векторами в пространстве
4. Примеры
1)
Вычислить:
60
: 6-3 5) 9-2 : 3-6; 6)
125-4 : 25-5
2) Вычислите
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№15
1.
Формулы
объема цилиндра
2.
Степени
с рациональными показателями, их свойства.
3. Основные
тригонометрические тождества
4. Примеры:
1)
Решите уравнение
sin2x = cosx—
cos2x
2)
Найти производную
f 1(x) при x=0 —1
5. Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№16
1. Формулы
объема цилиндра, конуса
2. Исследование
функции по схеме.
3. Раскрытие
неопределенностей 0/0
4. Примеры:
1)
Вычислите
2) В шахматном турнире участвуют 16 человек. Сколько
партий должно быть сыграно в турнире, если между любыми двумя участниками
должна быть сыграна одна партия?
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№17
1. Формулы
объема шара
2. Раскрытие
неопределенностей ∞/∞.
3. Параллельный
перенос
4. Примеры:
1) Решите
графически
2) На борту самолёта 12 мест рядом с
запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные
места неудобны для пассажира высокого роста. Пассажир В. высокого роста.
Найдите вероятность того, что на регистрации при случайном выбореместа пассажиру
В. достанется удобное место, если всего в самолёте 300 мест
5. Задача:
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ
КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных протокол ______________ |
УТВЕРЖДАЮ зам. _______________ |
Дисциплина«Математика»
Билет
№18
1.
Формулы
объема куба, прямоугольного параллелепипеда
2. Радианная мера
угла.
3.
Логарифмическая
функция, свойства и график
4.
Примеры:
1)
Вычислите
2)
Из множества натуральных чисел от 10 до 19 наудачу
выбирают одно число. Какова вероятность того, что оно делится на 3?
5. Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№19
1.
Формулы
объема призмы
2.
Физический
смысл производной
3.
Событие,
вероятность события
4.
Примеры:
1) Напишите
первые пять членов последовательности.
аn=2n+1/2n
2)Решите
уравнение
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№20
1.
Формулы
объема пирамиды, усеченной пирамиды
2.
Геометрический
смысл производной
3. Степенная
функция, свойства и график.
4. Примеры:
1) Решить уравнения
2) В
сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос
по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
достанетсявопрос
по ботанике.
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019г. |
Дисциплина«Математика»
Билет
№21
1. Площади
поверхностей тел вращения.
2. Понятие о
производной функции
3. Функции.Область
определения и множество значений; график функции
4. Примеры:
1) Решите уравнения
2) В
сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос
по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
не достанетсявопроса по неравенствам.
5. Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№22
1.
Векторы
в пространстве.
2. Основные
тригонометрические тождества.
3.
Раскрытие
неопределенностей 0/0.
4.
Примеры:
1)
Решить
уравнение
3(x-2)-5=4-(5x-1)
2)
Исследуйте
функцию и постройте график
f(x)=3x-1
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№23
1. Площади
поверхностей тел вращения.
2. Логарифми его
свойства
3. Радианная мера
угла.
4. Примеры:
1) Решить уравнения
.
2)Исследуйте
функцию и постройте график
f(x)=x2+2
5.
Задача:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
|
ОДОБРЕНО предметной общегуманитарных общеобразовательных Протокол Председатель П(Ц)К _____________ |
УТВЕРЖДАЮ заместитель директора по учебной работе __________ Квиралашвили Н.У 8 апреля 2019 г. |
Дисциплина«Математика»
Билет
№24
1. Конус. Усеченный
конус.
2.
Корни
натуральной степени из числа и их свойства.
3.
Арксинус, арккосинус, арктангенс
числа
4.
Примеры:
1) Вычислите
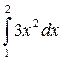
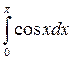
2)
Первести из градусной меры в радианную
450,600,360
5.
Задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин протокол №4 от 8 апреля 2019 г
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5














































































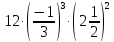
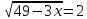
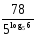
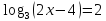
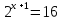
 +
+