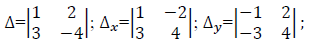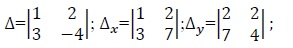Экзамен по математике заочное отделение

Каждый хочет, чтобы правда была на его стороне, но не каждый хочет быть на стороне правды.

  • Каталог тестов
  • Отправить отзыв
  • Вход в систему
  • Главная
  • /
  • Каталог тестов
  • /
  • Общеобразовательные
  • /
  • Математика и статистика

Вступительный тест по математике

Предлагаемый Вашему вниманию тест «Вступительный тест по математике» создан на основе одноименной базы знаний, состоящей из 80 вопросов.

В данном тесте будет задано 30 вопросов. Для успешного прохождения теста необходимо правильно ответить на 27 вопросов.

После ответа на каждый вопрос сразу будет отображаться правильный ответ, поэтому в этом режиме сделанный ответ исправить будет нельзя.

идет загрузка вопросов теста, пожалуйста подождите…

Просьба от разработчиков поделиться ссылкой. Спасибо!

Хотите встроить тест «Вступительный тест по математике» в свой сайт?

Или провести тестирование?

Индекс

Список вопросов базы знаний

Copyright testserver.pro 2013-2021

Источник

Вопросы и задачи к экзамену по математике для студентов заочного отделения

Специальность: 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта

Вопросы

  1. Определение производной. Нахождение производной с помощью определения.

  2. Физический смысл производной. Геометрический смысл производной.

  3. Правила нахождения производных. Производная суммы, разности и произведения, частного двух функций. Производная сложной функции.

  4. Таблица производных функций.

  5. Вторая производная функции, ее физический и геометрический смыслы.

  6. Уравнение касательной. Приближенное вычисление значения функции в точке. Примеры.

  7. Признаки возрастания и убывания функции. Пример.

  8. Признаки выпуклости функции, точки перегиба. Пример

  9. Определение критических точек и экстремумов функции. Признаки максимума и минимума функции.

  10. Исследование функции с помощью производной.

  11. Нахождение наибольшего и наименьшего значений функции.

  12. Решение задач из механики и физики с использованием производной

  13. Основные понятия множеств, способы задания и операции над множествами.

  14. Задания множеств, изображение множеств, выполнение операций над множествами.

  15. Диаграммы Эйлера- Венна.

  16. Основные тождества алгебры множеств

  17. События и их классификация. Способ сбора и группировки статистических сведений.

  18. Вычисление вероятности событий. Закон распределения дискретной случайной величины. Статистическая обработка данных.

  19. Способ сбора и группировки статистических сведений. Оценка неизвестной вероятности событий. Проверка статистических гипотез. Эмпирическая функция распределения.

  20. Численное интегрирование. Формула прямоугольников, трапеций. Оценка погрешности.

  21. Численное дифференцирование. Оценка погрешности в нахождении производной.

  22. Вычисление определенных интегралов.

  23. Решение задач на вычисление интегралов, площади криволинейной трапеции, длины дуги и объема тел вращения.

Задачи

  1. Найдите интегралы

  1. dx;

  2. (2x3+3x2-36x+15)dx;

  3. ;

  1. 2 Сделайте чертёж и вычислите площадь фигуры, ограниченной данными линиями:

  1. y=x3-1, y=0, x=0.

  2. y=x2-3x-4 и осью Ох.

  2. 3 Сделайте чертёж и вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной данными линиями:

  1. y=x3, y=0, x=0, x=2.

  2. xy=1, x=2, x=3, y=0.

  1. Скорость прямолинейного движения тела задана уравнением V(t)=9t2-20t (V- в м/с). Вычислите его путь, пройденный за четвертую секунду.

  2. Вычислите работу, которую нужно совершить при растяжении пружины на 8 см., если сила 3 Н растягивает пружину на 1 см.

  3. Даны следующие числовые множества: А={1,3,5,7,9,11}, B={2,5,6,11,12}, C={1,2,3,5,9,12}. Найти множества, которые будут получены в результате выполнения следующих операций:

  1. а) (АС)В; б) (АС)В) в) АBC; г) В(АС);

  1. Найти объединение, пересечение, разность и симметрическую разность множеств А и В, если

  1. а) А={1, 2, 3, 4, 5}, В={2, 4, 6, 8, 10}; б) А={а, б, в, г, д, е}, В={а, в, д, к, и};

  2. 8 Вычислить определённый интеграл по формуле прямоугольников

  3. 9 Вычислить определённый интеграл по формуле трапеций

  5. 10 Два стрелка стреляют в цель. Вероятность поражения цели при одном выстреле первым стрелком равна 0,8, вторым стрелком – 0,9. Найти вероятность того, что а) оба стрелка попадут в цель; б) хотя бы один стрелок попадёт в цель; в) только один стрелок попадёт в цель; г) оба стрелка промахнутся.

  7. 11. Дискретная случайная величина Х может принимать только два значения: х1 и х2, причём х12. Известны вероятность р1=0,1 возможного значения х1, математическое ожидание М(Х)=3,9 и дисперсия D(X)=0,99. Найти оставшиеся величины, если это возможно.

  8. 12. По сведениям автоинспекции, количество дорожных происшествий на улицах города в сентябре было таким: 8 6 9 7 8 11 9 8 7 11 5 6 7 8 7 10 9 8 12 7 8 8 6 9 11 10 9 9 8 7. Найти статистическое распределение выборки. Найти выборочную среднюю, дисперсию, среднее квадратическое отклонение.

Источник

Avatar

04.12.2020.
Тест. Математика, Прочее

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного
использования.
Администрация сайта не
проверяет возможные ошибки,
которые могут встретиться в тестах.

Линейная алгебра, Комплексные числа. Дифференциальное исчисление. Интегральное исчисление. Теория вероятностей

Список вопросов теста

Вопрос 1

Установите соответствие между неопределенными интегралами и соответствующей совокупностью первообразных:

1.

(int x^ndx)

2.

(intfrac{dx}{cos^2x})

3.

(intsin xdx)

4.

(intcos xdx)

Варианты ответов

  • (frac{x^{n+1}}{n+1}+C, left(left(nne-1right)right))

  • tgx+C, x(nefrac{pi}{2}+pi n, nin Z)

  • -cosx+C

  • sinx+C

Вопрос 2

Выберите правильный ответ. Найти интеграл (intfrac{dx}{x^3})

Варианты ответов

  • -3x-4 +C

  • (frac{x^2}{2}+C)

  • (-frac{^1}{2x^2}+C)

  • (frac{1}{2x^2}+C)

Вопрос 3

Выберите правильные ответы. К методам интегрирования относятся:

Варианты ответов
  • метод подстановки
  • метод интегрирования по частям
  • метод математической индукции
  • метод параллельных прямых

Вопрос 4

Выберите правильный ответ. Формула Ньютона-Лейбница имеет вид:

Варианты ответов

  • (int_{_a}^{^{^b}} fleft(xright)dx=Fleft(bright)-Fleft(aright))

  • (int_{_a}^{^{^b}} fleft(xright)dx=fleft(bright)-fleft(aright))

  • (int_{_a}^{^{^b}} fleft(xright)dx=Fleft(aright)-Fleft(bright))

  • (int_{_a}^{^b}fleft(xright)dx=fleft(aright)-fleft(bright))

Вопрос 5

Выберите правильный ответ. Геометрический смысл определенного интеграла заключается в следующем:

Варианты ответов
  • определенный интеграл равен площади криволинейной трапеции, ограниченной подынтегральной функцией, прямыми х=а и х=b и осью Ох
  • определенный интеграл равен периметру криволинейной трапеции, ограниченной подынтегральной функцией, прямыми х=а и х=b и осью Ох
  • определенный интеграл равен периметру прямоугольника, ограниченного прямыми х=а и х=b.
  • определенный интеграл равен площади прямоугольника, ограниченного прямыми х=а и х=b.

Вопрос 6

Выберите правильный ответ. Найдите площадь фигуры, ограниченной прямыми y=5x, x=2  и осью Ох

Варианты ответов
  • 2
  • 10
  • -14
  • -36

Вопрос 7

Установите соответствие между определенными интегралами и соответствующими значениями:

1.

(int_{_1}^{^{^2}}frac{dx}{x})

2.

(int_{_1}^{^2}left(x^2+xright)dx)

3.

(int_{_0}^{^1}3dx)

4.

(int_{_0}^{^1}2xdx)

Варианты ответов
  • ln2

  • (frac{23}{6})()

  • 3()

  • 1

Вопрос 8

Выберите правильный ответ. Число а в определенном интеграле(int_a^{^b}fleft(xright)dx) называется:

Варианты ответов
  • подынтегральной функцией
  • Нижний предел интегрирования
  • Верхний предел интегрирования
  • дифференциал функции

Вопрос 9

Решением дифференциального уравнения (y^/=y) является функция:

Варианты ответов

  • (y=Ce^x)

  • ()y=x+C

  • y=lnx+C

  • y=(frac{x}{C})

Вопрос 10

Порядком дифференциального уравнения называется

Варианты ответов
  • показатель степени неизвестной функции
  • порядок старшей производной, входящей в него
  • показатель степени независимой переменной
  • порядок производной независимой переменной и неизвестной функции.

Вопрос 11

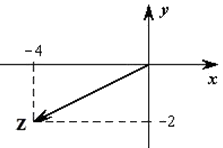
Чему равен модуль комплексного числа z=-3-4i?

Вопрос 12

Алгебраическая форма комплексного числа z, изображенного на рисунке, имеет вид 

Варианты ответов
  • z=4-2i
  • z=-4+2i
  • z=-4-2i
  • z=2-4i

Вопрос 13

Установите соответствие между комплекным числом z и комплексно-сопряженным к нему

1.

1-i

2.

2-2i

3.

-3-4i

4.

-4+6i

Варианты ответов
  • 1+i
  • 2+2i
  • -3+4i
  • -4-6i

Вопрос 14

Если матрица (A=binom{2 -1}{3 -2}), то матрица 4А имеет вид

Варианты ответов

  • (binom{2 -4}{3 -8})

  • (binom{8 -4}{3 -2})

  • (binom{8 -4}{12 -8})

  • (binom{8 -1}{12 -2})

Вопрос 15

Если матрицы (А=binom{2 3}{-1 0}) и В=(binom{5 0}{1 2}), то матрица А+В имеет вид

Варианты ответов

  • (binom{4 5}{7 8})

  • (binom{5 0}{9 10})

  • (binom{5 6}{-1 2})

  • (binom{7 3}{0 2})

Вопрос 16

Выберите правильный ответ. Приумножении матрицы А на матрицу В должно соблюдаться условие:

Варианты ответов
  • число строк матрицы А равно числу строк матрицы В
  • число строк матрицы А равно числу столбцов матрицы В
  • число столбцов матрицы А равно число строк матрицы В
  • Верный ответ отсутствует

Вопрос 17

Найдите определитель матрицы  (binom{ 3 4}{-1 5})

Вопрос 18

Для матрицы (А=binom{2 -4}{3 -1}) укажите сумму элементов, расположенных на побочной диагонали

Вопрос 19

При решении  систем линейных уравнений используются методы:

Варианты ответов
  • Крамера
  • математической индукции
  • Гаусса
  • прогрессии

Вопрос 20

Если матрица системы n уравнений квадратная и ее определитель не равен нулю, то система:

Варианты ответов
  • не имеет решений
  • имеет единственное решение
  • имеет ровно n решений
  • верный ответ отсутствует

Вопрос 21

При решении системы по правилу Крамера используют формулы:

Варианты ответов

  • (х_i=triangle-triangle_i)

  • (х_i=trianglecdottriangle_i)

  • (х_i=frac{triangle_i}{triangle})

  • верный ответ отсутствует

Вопрос 22

Решение системы 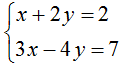 по правилу Крамера имеет вид

Варианты ответов

Вопрос 23

Установите соответствие …

1.

Число размещений из n элементов по m 

2.

Число перестановок

3.

Число сочетаний из n по m

Варианты ответов

  • (frac{n!}{left(n-mright)!})

  • n!

  • (frac{n!}{m!left(n-mright)!})

Вопрос 24

Два события А и В называются…, если появление одного из них меняет вероятность появления другого

Варианты ответов
  • зависимыми
  • противоположными
  • независимыми
  • совместными

Вопрос 25

Для вычисления вероятности суммы двух несовместных событий применяют формулу

Варианты ответов
  • Р(А+В)=Р(А)+Р(В)
  • Р(А+В)=Р(А)+Р(В)+Р(АВ)
  • Р(А+В)=Р(А)+Р(В)-Р(АВ)
  • нет правильного ответа

Вопрос 26

Дискретная случайная величина задана законом распределения вероятностей . Математическое ожидание М(Х) ревно…

Вопрос 27

Дискретная случайная величина Х задана законом распределения вероятностей . Если математическое ожидание равно М(Х)=5,6, то значение х2 равно…

Вопрос 28

Установите соответствие между функциями и их производными

1.

y=xn

2.

y=cosx

3.

y=lnx

4.

y=sinx

Варианты ответов

  • y/=nxn-1

  • y/=-sinx

  • y/=(frac{1}{x})

  • y/=cosx

Вопрос 29

Найдите угловой коэффициент касательной к графику функции y=x2+2x-4  в точке х0=-1

Вопрос 30

Производная функции (y=frac{ln x}{x}) равна

Варианты ответов

  • (frac{1+ln x}{x^2})

  • (frac{1}{x})

  • (frac{1+ln x}{x})

  • (frac{1-ln x}{x^2})

Вопрос 31

Установите соотвествие между функциями и их производными

1.

y=x2+3x-5

2.

y=x3+6x-10

3.

y=-x5+3x2-5x

4.

y=-x2-3x4-5x3

Варианты ответов

  • 2x+3

  • 3x2+6

  • -5x4+6x-5

  • -2x-12x3-15x2

Вопрос 32

Установите соответствие между правилами дифференцирования

1.

x/

2.

(left(u+vright)^{^/})

3.

(left(uvright)^/)

4.

(left(frac{u}{v}right)^/)

Варианты ответов
  • 1

  • u/+v/

  • u/v+uv/

  • (frac{u^/v-uv^/}{v^2})

Вопрос 33

Выберите правльные ответы. Асимптоты для графиков функций бывают:

Варианты ответов
  • Вертикальные
  • Горизонтальные
  • Наклонные
  • Параболические

Вопрос 34

Выберите правильные ответы. Экстремумами функции называются:

Варианты ответов
  • максимум функции
  • минимум функции
  • нули функции
  • любые точки функции

Вопрос 35

Выберите правильный ответ. Точка х0 называется точкой максимума функции, если производная в ней равна нулю и:

Варианты ответов
  • меняет свой знак с «-» на «+»
  • меняет свой знак с «+» на «-«
  • не меняет свой знак
  • правильного ответа нет

Вопрос 36

Выберите правильный ответ. Точка х0 называется точкой минимума функции функции, если производная в ней равна нулю и:

Варианты ответов
  • меняет свой знак с «-» на «+»
  • меняет свой знак с «+» на «-«
  • не меняет свой знак
  • правильного ответа нет

Вопрос 37

Найдите интеграл (int_{_{-1}}^{^1}4х^3dx)

Вопрос 38

Выберите правильный ответ. Выражение dx в определенном интеграле (int_{_а}^{^в}fleft(xright)dx) называется :

Варианты ответов
  • подынтегральной функцией
  • нижний предел интегрирования
  • верхний предел интегрирования
  • дифференциал функции

Вопрос 39

С помощью каких методов  численного интегрирования можно вычислить определенный интрал?

Варианты ответов
  • формула Симпсона
  • формула прямоугольников
  • формула трапеций
  • теорема Виета
  • Бином Ньютона
  • Треугольник Паскаля

Вопрос 40

Какие задачи не относятся к задачам численного дифференцирования?

Варианты ответов
  • Вычисление производной функции, заданной таблично
  • Нахождении производной от аналитической функции, непосредственное дифференцирование которой по каким-либо причинам затруднено
  • Вычисление приближенного значения функции
  • Нахождение площади криволинейной трапеции
  • численном решении обыкновенных дифференциальных уравнений

Источник
Пройдите тест, узнайте свой уровень и посмотрите правильные ответы!

Вычислите: 4,3-(-5,9).

Найдите разность 21 и 35.

Вычислите: 1,7-5,9.

Вычислите: -1,2-3,3.

Найдите корни уравнения |x|=12,4.

Вычислите: |-23|+(-13).

Найдите: |-6,8|.

Какое из чисел расположено на координатной прямой левее остальных?

Мы занимаемся обработкой ваших ответов

Источник
Вступительные испытания в ВУЗ по математике. Примеры с ответами

Высшее Учебное Заведение. Россия. ВИ. ЕГЭ. 2019, 2020, 2021, 2022 год

Если вы в этом году решили поступить в ВУЗ на очное обучение или заочное отделение, тогда вам придется сдавать Вступительные испытания ВИ. Если вы не сдавали ЕГЭ в школе, тогда вам пригодится эта информация для поступления в ВУЗ

На этой страницу вы можете бесплатно скачать тесты, задания и примеры вступительных экзаменов в ВУЗ, а так же подробное решение и ответы на задания.

Вступительные испытания в ВУЗ по математике. Примеры с ответами

Процедура проведения вступительного испытания

1. Вступительное испытание проводится в соответствии с действующими Правилами приема в бакалавриат и специалитет и Положением о порядке проведения вступительных испытаний МФТИ.

2. Вступительное испытание по математике проводится с совмещением письменной и устной форм.

3. Вступительное испытание состоит из четырех частей.

4. Первые три части вступительного испытания – решение задач с численным ответом. Длительность каждой части – 45 минут.

5. Первая часть вступительного испытания вступительного испытания, проводимого с использованием дистанционных технологий, проверяется программно-аппаратным способом.

6. Допуск ко второй письменной части и последующим частям вступительного испытания проводится по результатам проверки первой письменной части. Недопущенным ко второй и последующим частям вступительного испытания выставляется балл на основании проверки первой части вступительного испытания.

7. Четвертая часть вступительного испытания – устный опрос по задачам и программе вступительного испытания. Длительность устной части – до 30 минут.

Программа вступительного испытания

1. Натуральные числа. Делимость. Простые и составные числа. Признаки делимости. Наибольший общий делитель и наименьшее общее кратное.

2. Целые, рациональные, действительные числа и операции с ними.

3. Преобразование арифметических и алгебраических выражений. Формулы сокращённого умножения.

4. Числовые неравенства и их свойства.

5. Функция. Область определения и множество значений. График функции. Чётность, нечётность, периодичность функций. Линейная, квадратичная, степенная, дробно-рациональная функции и их свойства.

6. Линейные уравнения. Квадратные уравнения. Рациональные уравнения. Уравнения с модулем. Уравнения высших степеней. Разложение многочленов на множители.

7. Линейные неравенства. Квадратные неравенства. Рациональные неравенства. Неравенства с модулем.

8. Корень из числа и его свойства. Арифметический корень. Иррациональные уравнения. Иррациональные неравенства.

9. Арифметическая и геометрическая прогрессии и их свойства.

10. Комбинаторика. Правила суммы и произведения. Перестановки, размещения, сочетания.

11. Задачи на составление уравнений (задачи на движение, на проценты, на совместную работу, на смеси и пр.).

12. Тригонометрические формулы. Тригонометрические и обратные тригонометрические функции и их свойства. Преобразование тригонометрических выражений. Тригонометрические уравнения и неравенства.

13. Свойства степеней. Логарифмы и их свойства. Показательная и логарифмическая функции и их свойства. Показательные и логарифмические уравнения и неравенства.

14. Производная. Исследование функций с помощью производных.

15. Задачи с параметром.

16. Системы уравнений и неравенств.

17. Множества точек на координатной плоскости.

18. Планиметрия:

— смежные и вертикальные углы,

— признаки и свойства равнобедренного треугольника, признаки равенства треугольников,

— теоремы о параллельных прямых, сумма углов треугольника, сумма углов выпуклого многоугольника,

— геометрические места точек (множество внутренних точек угла, равноудалённых от его сторон, множество точек, равноудалённых от концов отрезка),

— медианы, биссектрисы, высоты треугольника и их свойства,

— подобие треугольников, теорема Фалеса, теорема о пропорциональных отрезках,

— четырёхугольники; параллелограмм, прямоугольник, ромб, квадрат, трапеция и их свойства,

— пропорциональные отрезки в прямоугольном треугольнике, теорема Пифагора,

— площадь и её свойства,

— формулы площади треугольника, параллелограмма, трапеции,

— точки пересечения высот, медиан, биссектрис, серединных перпендикуляров треугольника,

— теоремы синусов, косинусов и Менелая для треугольника,

— окружность и её свойства,

— касательная к окружности и её свойства,

— теоремы о пропорциональных отрезках в окружности,

— теоремы об углах, связанных с окружностью (вписанный угол, центральный угол, угол между касательной и хордой),

— окружность, описанная около треугольника; окружность, вписанная в треугольник,

— окружность, описанная около четырёхугольника; окружность, вписанная в четырёхугольник,

— правильные многоугольники и их свойства,

— длина окружности, площадь круга и его частей,

— векторы, скалярное произведение векторов,

— метод координат на плоскости.

19. Стереометрия. Параллельность прямых и плоскостей, перпендикулярность прямых и плоскостей. Объём фигуры; площадь поверхности фигуры. Куб, параллелепипед, призма, пирамида, шар, цилиндр, конус и их свойства. Векторы и координаты в пространстве. Сечения многогранников. Углы и расстояния в пространстве.

.

Источник

Сычева Жанна Петровна

На данной странице размещены материалы для студентов заочного отделения, обучающихся по специальностям:

23.02.03. Техническое обслуживание и ремонт автомобильного транспорта

19.02.10. Технология продукции общественного питания

38.02.05. Товароведение и экспертиза качества потребительских товаров

Скачать:

Предварительный просмотр:

Приложение 2.1  к ППССЗ  по профессии

23.02.03. Техническое обслуживание и ремонт автомобильного транспорта

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

ЕН.01 МАТЕМАТИКА

Заводоуковск,

2015

Рабочая программа учебной дисциплины «Математика» разработана на основе Федерального государственного  образовательного стандарта (далее – ФГОС), утвержденного Приказом Министерства образования и науки Российской Федерации по специальности среднего профессионального образования 23.02.03. Техническое обслуживание и ремонт автомобильного транспорта (пр.№184 от 17.03.10г.), входящей в состав укрупнённой группы профессии по направлению 23.00.00. Техника и технологии наземного транспорта.

Организация-разработчик:

Государственное автономное образовательное учреждение среднего профессионального образования Тюменской области «Заводоуковский агропромышленный техникум»

Разработчики:

Сычева Жанна Петровна, преподаватель высшей квалификационной категории

Хребтова Светлана Агафоновна, Заслуженный учитель РФ, преподаватель высшей квалификационной категории

СОДЕРЖАНИЕ

стр.
  1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

4
  1. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

5
  1. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

8
  1. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

9

1. ПАСПОРТ  ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

ЕН.01 МАТЕМАТИКА

1.1. Область применения программы

Программа учебной  дисциплины является частью  программы подготовки специалистов среднего звена среднего профессионального образования  по специальности 23.02.03. Техническое обслуживание и ремонт автомобильного транспорта (пр.№184 от 17.03.10г.), входящей в состав укрупнённой группы профессий по направлению 23.00.00. Техника и технологии наземного транспорта.

1.2. Место дисциплины в структуре основной профессиональной образовательной программы: математический и общий естественнонаучный цикл.

1.3. Цели и задачи дисциплины – требования к результатам освоения дисциплины:

В результате освоения дисциплины студент должен уметь:

  • решать обыкновенные дифференциальные уравнения;

В результате освоения дисциплины студент должен знать/понимать:

  • основные понятия и методы математического анализа, дискретной математики, теории вероятностей и математической статистики;
  • основные численные методы решения прикладных задач.

1.4. Рекомендуемое количество часов на освоение программы дисциплины:

максимальной учебной нагрузки студента 60 часов, в том числе:

обязательной аудиторной учебной нагрузки студента 14 часов;

самостоятельной работы студента 46 часов.

2. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

2.1. Объем учебной дисциплины и виды учебной работы

Вид учебной работы

Объем часов

Максимальная учебная нагрузка (всего)

60

Обязательная аудиторная учебная нагрузка (всего)

14

в том числе:

     практические занятия

12

Самостоятельная работа студента (всего)

46

в том числе:

практические занятия

     промежуточная аттестация: домашняя контрольная работа.

22

6

Итоговая аттестация: экзамен.

2.2. Тематический план и содержание учебной дисциплины ЕН.01 МАТЕМАТИКА

Наименование разделов и тем

Содержание учебного материала, лабораторные и практические работы,

самостоятельная работа студентов

Объем часов

Уровень освоения

1

2

3

4

Введение

Содержание учебного материала

1

1

2

Роль и место знаний по дисциплине в процессе освоения основной профессиональной образовательной программы по специальности.

Содержание дисциплины и ее задачи.

1

1

Тема 1.

Множества.

Операции над множествами

Содержание учебного материала

1

1

2

3

Множества. Элементы множеств.

Виды множеств.

Операции над множествами: объединение, пересечение, разность, дополнение.

2

2

2

Тема 2.

Дифференциальное исчисление

Содержание учебного материала

14

1

2

Предел функции.

Производная функции.

1

(изучается аудиторно)

2

3

4

Производная функции.

Дифференциал функции.

3

2

2

2

Практические занятия:

1

2

Вычисление пределов функции.

Вычисление производных функций.

2

2

(изучается аудиторно)

2

2

3

Решение прикладных задач.

4

2

Тема 3.

Интегральное исчисление

Содержание учебного материала

12

1

2

Метод замены переменной в неопределенном интеграле.

Интегрирование по частям.

1

(изучается аудиторно)

2

2

3

Определенный интеграл. Формула Ньютона – Лейбница. Геометрические приложения определенного интеграла.

3

2

1

2

3

4

Практические занятия:

1

2

Нахождение интегралов методом замены и интегрирования по частям.

Вычисление определенного интеграла.

2

2

(изучается аудиторно)

2

2

3

Решение прикладных задач.

4

2

Тема 4.

Дифференциальные уравнения

Содержание учебного материала

12

1

2

3

4

Обыкновенные дифференциальные уравнения.

Частное и общее решение.

Уравнения с разделяющимися переменными.

Однородные уравнения 1 – го и 2 – го порядка.

2

2

2

2

Практические занятия:

1

Решение дифференциальных уравнений с разделяющимися переменными.

4

(изучается аудиторно)

2

2

Решение линейных дифференциальных уравнений.

6

2

Тема 5.

Основные понятия теории вероятностей

Содержание учебного материала

10

1

2

3

Вероятность события. Свойства вероятности.

Теоремы сложения и умножения вероятностей.

Дискретная случайная величина. Числовые характеристики ДСВ.

2

2

2

Практические занятия:

— Нахождение вероятностей.

— Нахождение числовых характеристик ДСВ.

4

4

2

2

Тема 6.

Элементы математической статистики

Содержание учебного материала

4

1

2

3

4

Основные понятия математической статистики

Эмпирическая функция распределения

Полигон и гистограмма

Числовые характеристики выборки

2

2

2

2

Домашняя контрольная работа

6

Всего:

60

3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ

3.1. Требования к минимальному материально-техническому обеспечению

Реализация программы дисциплины требует наличия учебного кабинета математики.

Оборудование учебного кабинета: чертежные инструменты

Технические средства обучения: рабочее место студента, рабочее место преподавателя, персональный компьютер, мультимедийный проектор, интерактивная доска, электронные учебники, презентации, интернет

3.2. Информационное обеспечение обучения

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основные источники:

  1. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учебник: Допущено Минобразования России. – ИЦ Академия, 2013
  2. Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике: учеб. Пособие: Рекомендовано ФГУ «ФИРО». – ИЦ Академия, 2013.
  3. Григорьев С.Г., Иволгина С.В. Математика: учебник: Рекомендовано ФГУ «ФИРО»/ Под. Ред. В.А. Гусева. – ИЦ Академия, 2013.

Дополнительные источники:

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 2007
  2. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнения и задачах / в 2-х томах. – М.: Высшая школа, 2007
  3. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник: Допущено Минобразования России. – М.: Высшая школа, 2009.
  4. Щипачев В. С. Задачник по высшей математике. – М.: Высшая школа, 2008
  5. Щипачев В. С. Основы высшей математики. – М.: Высшая школа. 2008

Электронные ресурсы:

  1. http://mathem.h1.ru/ — Математика On- Line. Коллекция формул по математике, геометрии, высшей математике, справочной информации по математическим дисциплинам и математические статьи.
  2. http://www.math.ru  — Коллекция книг, видео-лекций, подборка занимательных математических фактов, различные по уровню и тематике задачи, истории из жизни математиков. Информация об олимпиадах, научных школах по математике.
  3. http://eqworld.ipmnet.ru/indexr.htm — Мир математических уравнений.

4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ

Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий и лабораторных работ, тестирования, а также выполнения студентами индивидуальных заданий, проектов, исследований.

Результаты обучения

(освоенные умения, усвоенные знания)

Формы и методы контроля и оценки результатов обучения

1

2

Умеет решать обыкновенные дифференциальные уравнения

Практическое задание

Знает основные понятия и методы математического анализа, дискретной математики, теории вероятностей и математической статистики

Тест  

Знает основные численные методы решения прикладных задач

Тест

Результаты

(освоенные общие компетенции)

Основные показатели результатов подготовки

Формы и методы контроля

1

2

3

OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес

объясняет место дисциплины в формировании профессиональной компетенций

Тестирование

ОК 2.1. Планирование деятельности

разбивает поставленную цель на задачи, подбирая из числа известных технологии (элементы технологий), позволяющие решить каждую из задач

Тестирование

ОК 2.3.

Определение методов решения профессиональных задач

выбирает способ (технологию) решения задачи в соответствии с заданными условиями и имеющимися ресурсами

Оценка выполнения ПЗ

ОК 3.2. Текущий контроль и коррекция деятельности

предлагает способ коррекции деятельности на основе результатов текущего контроля

Оценка выполнения ПЗ

ОК 3.3. Оценка результатов деятельности

оценивает результаты деятельности по заданным показателям

Оценка выполнения ПЗ

ОК 4.1. Поиск информации

формулирует вопросы, нацеленные на получение недостающей информации

Оценка выполнения ПЗ

ОК 4.2. Извлечение и первичная обработка информации

извлекает информацию по двум и более основаниям из одного или нескольких источников и систематизирует ее в самостоятельно определенной в соответствии с задачей информационного поиска структуре

Оценка выполнения ПЗ

ОК 4.3. Обработка информации

задает критерии для сравнительного анализа информации в соответствии с поставленной задачей деятельности

делает вывод о применимости общей закономерности в конкретных условиях

Оценка выполнения ПЗ

1

2

3

ОК 5. Владеть информационной культурой, анализировать и оценивать информацию с использованием информационнокоммуникационных технологии

выполняет поиск информации с использованием ИКТ, анализирует информацию, систематизирует её  

Оценка выполнения ПЗ

ОК 6.1.

Работа в команде (группе)

принимает и фиксирует решение по всем вопросам для группового обсуждения

Оценка выполнения ПЗ

ОК 6.2.

Эффективное общение: монолог

использует средства наглядности или невербальные средства коммуникации

Оценка выполнения ПЗ

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий

отвечает за работу членов команды, за результат выполненных заданий

Оценка выполнения ПЗ

ОК 8.1. Оценка собственного продвижения

анализирует формулирует запрос на внутренние ресурсы (знания, умения, навыки, способы деятельности, ценности, установки, свойства психики) для решения профессиональной задачи

Тестирование

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности

владеет навыками самообразования, умеет работать с источниками информации

Оценка выполнения ПЗ

ОК 10. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей)

умеет осуществлять расчеты

Тестирование

ПК 1.1. Организовывать и проводить работы по техническому обслуживанию и ремонту автотранспорта

умеет осуществлять расчеты

Тестирование

1

2

3

ПК 1.2. Осуществлять технический контроль при хранении, эксплуатации, техническом обслуживании и ремонте автотранспортных средств

умеет осуществлять расчеты

Тестирование

ПК 1.3. Разрабатывать технологические процессы ремонта узлов и деталей

умеет осуществлять расчеты

Тестирование

ПК 2.2. Контролировать и оценивать качество работы исполнителей работ

умеет осуществлять расчеты

Тестирование

Предварительный просмотр:

Приложение 2.1  к ППССЗ  по профессии

38.02.05. Товароведение и экспертиза качества потребительских товаров

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

ЕН.01 МАТЕМАТИКА

Заводоуковск,

2015

Рабочая программа учебной дисциплины «Математика» разработана на основе Федерального государственного  образовательного стандарта (далее – ФГОС), утвержденного Приказом Министерства образования и науки Российской Федерации по специальности среднего профессионального образования 38.02.05. Товароведение и экспертиза качества потребительских товаров (пр.№679 от 22.06.10г.), входящей в состав укрупнённой группы профессий по направлению 38.00.00. Экономика и управление.

Организация-разработчик:

Государственное автономное образовательное учреждение среднего профессионального образования Тюменской области «Заводоуковский агропромышленный техникум»

Разработчики:

Сычева Жанна Петровна, преподаватель высшей квалификационной категории

Хребтова Светлана Агафоновна, Заслуженный учитель РФ, преподаватель высшей квалификационной категории

СОДЕРЖАНИЕ

стр.
  1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

4
  1. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

5
  1. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

8
  1. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

9

1. ПАСПОРТ  ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

ЕН.01 МАТЕМАТИКА

1.1. Область применения программы

Программа учебной  дисциплины является частью  программы подготовки специалистов среднего звена среднего профессионального образования  по специальности 38.02.05. Товароведение и экспертиза качества потребительских товаров (пр.№679 от 22.06.10г.), входящей в состав укрупнённой группы профессий по направлению 38.00.00. Экономика и управление.

1.2. Место дисциплины в структуре основной профессиональной образовательной программы: программа относится к математическому и общему естественнонаучному циклу.

1.3. Цели и задачи дисциплины – требования к результатам освоения дисциплины:

В результате освоения дисциплины студент должен уметь:

  • решать прикладные задачи в области профессиональной деятельности;

В результате освоения дисциплины студент должен знать/понимать:

  • значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы;
  • основные математические методы решения прикладных задач в области профессиональной деятельности;
  • основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
  • основы интегрального и дифференциального исчисления.

1.4. Рекомендуемое количество часов на освоение программы дисциплины:

максимальной учебной нагрузки студента 60 часов, в том числе:

обязательной аудиторной учебной нагрузки студента 10 часов;

самостоятельной работы студента 50 часов.

2. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

2.1. Объем учебной дисциплины и виды учебной работы

Вид учебной работы

Объем часов

Максимальная учебная нагрузка (всего)

60

Обязательная аудиторная учебная нагрузка (всего)

10

в том числе:

     практические занятия

6

Самостоятельная работа студента (всего)

50

в том числе:

практические занятия

     промежуточная аттестация: домашняя контрольная работа.

28

6

Итоговая аттестация: экзамен.

2.2. Тематический план и содержание учебной дисциплины ЕН.01 МАТЕМАТИКА

Наименование разделов и тем

Содержание учебного материала, лабораторные и практические работы,

самостоятельная работа студентов

Объем часов

Уровень освоения

1

2

3

4

Введение

Содержание учебного материала

1

1

2

Роль и место знаний по дисциплине в процессе освоения основной профессиональной образовательной программы по специальности.

Содержание дисциплины и ее задачи.

1

1

Тема 1.

Множества.

Операции над множествами

Содержание учебного материала

1

1

2

3

Множества. Элементы множеств.

Виды множеств.

Операции над множествами: объединение, пересечение, разность, дополнение.

2

2

2

Тема 2.

Матрицы.

Операции над матрицами

Содержание учебного материала

16

1

2

3

Матрица. Виды матриц: прямоугольная, квадратная, матрица – строка, матрица – столбец, одноэлементная,  диагональная, единичная, нулевая.

Действия с матрицами: умножение матрицы на число, сложение матриц, вычитание матриц, умножение матриц, транспонирование матриц.

Определители 2-го и 3-го порядка.

1

(изучается аудиторно)

2

2

2

4

Системы линейных уравнений.

3

2

Практические занятия:

1

Решение систем линейных уравнений методом Крамера.

2

(изучается аудиторно)

2

2

3

Решение систем линейных уравнений матричным методом.

Решение систем линейных уравнений методом Гаусса.

6

4

2

2

Тема 3.

Дифференциальное исчисление

Содержание учебного материала

12

1

2

Предел функции.

Производная сложной функции.

1

(изучается аудиторно)

2

2

3

Дифференциал функции.

3

2

1

2

3

4

Практические занятия:

1

Вычисление производных.

1

(изучается аудиторно)

2

2

Вычисление производных. Решение прикладных задач.

7

2

Тема 4.

Интегральное исчисление

Содержание учебного материала

10

1

2

Метод замены переменной в неопределенном интеграле.

Интегрирование по частям.

1

(изучается аудиторно)

2

2

3

Определенный интеграл. Формула Ньютона – Лейбница.

1

2

Практические занятия:

1

Нахождение интегралов методом замены и интегрирования по частям.

1

(изучается аудиторно)

2

2

3

Вычисление определенного интеграла.

Решение прикладных задач.

3

4

2

2

Тема 5.

Комплексные числа

Содержание учебного материала

4

1

Комплексные числа: действительная и мнимая части комплексного числа, мнимая единица, сопряженные комплексные числа.  

1

(изучается аудиторно)

2

2

3

Тригонометрическая форма комплексного числа.

Действия с комплексными числами.

1

2

2

Практические занятия:

1

Действия с комплексными числами.

2

(изучается аудиторно)

2

Тема 6.

Основные понятия теории вероятностей

Содержание учебного материала

8

1

2

3

Вероятность события. Свойства вероятности.

Теоремы сложения и умножения вероятностей.

Дискретная случайная величина. Характеристики ДВС.

2

Практические занятия:

1

Вычисление вероятностей.

4

2

1

2

3

4

Тема 7.

Элементы математической статистики

Содержание учебного материала

2

1

2

3

Основные понятия математической статистики.

Эмпирическая функция распределения. Полигон и гистограмма.

Числовые характеристики выборки.

2

2

2

Домашняя контрольная работа

6

Всего:

60

3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ

3.1. Требования к минимальному материально-техническому обеспечению

Реализация программы дисциплины требует наличия учебного кабинета математики.

Оборудование учебного кабинета: чертежные инструменты

Технические средства обучения: рабочее место студента, рабочее место преподавателя, персональный компьютер, мультимедийный проектор, интерактивная доска, электронные учебники, презентации, интернет

3.2. Информационное обеспечение обучения

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основные источники:

  1. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учебник: Допущено Минобразования России. – ИЦ Академия, 2013
  2. Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике: учеб. Пособие: Рекомендовано ФГУ «ФИРО». – ИЦ Академия, 2013.
  3. Григорьев С.Г., Иволгина С.В. Математика: учебник: Рекомендовано ФГУ «ФИРО»/ Под. Ред. В.А. Гусева. – ИЦ Академия, 2013.

Дополнительные источники:

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 2007
  2. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнения и задачах / в 2-х томах. – М.: Высшая школа, 2007
  3. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник: Допущено Минобразования России. – М.: Высшая школа, 2009.
  4. Щипачев В. С. Задачник по высшей математике. – М.: Высшая школа, 2008
  5. Щипачев В. С. Основы высшей математики. – М.: Высшая школа. 2008

Электронные ресурсы:

  1. http://mathem.h1.ru/ — Математика On- Line. Коллекция формул по математике, геометрии, высшей математике, справочной информации по математическим дисциплинам и математические статьи.
  2. http://www.math.ru  — Коллекция книг, видео-лекций, подборка занимательных математических фактов, различные по уровню и тематике задачи, истории из жизни математиков. Информация об олимпиадах, научных школах по математике.
  3. http://eqworld.ipmnet.ru/indexr.htm — Мир математических уравнений

4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ

Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий и лабораторных работ, тестирования, а также выполнения студентами индивидуальных заданий, проектов, исследований.

Результаты обучения

(освоенные умения, усвоенные знания)

Формы и методы контроля и оценки результатов обучения

1

2

Умеет решать прикладные задачи в области профессиональной деятельности

Практическое задание

Знает значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы

Тест  

Знает основные математические методы решения прикладных задач в области профессиональной деятельности

Тест

Знает основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики

Тест

Знает основы интегрального и дифференциального исчисления

Тест

Результаты

(освоенные общие компетенции)

Основные показатели результатов подготовки

Формы и методы контроля

1

2

3

OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес

объясняет место дисциплины в формировании профессиональной компетенций

Тестирование

ОК 2.1. Планирование деятельности

разбивает поставленную цель на задачи, подбирая из числа известных технологии (элементы технологий), позволяющие решить каждую из задач

Тестирование

ОК 2.3.

Определение методов решения профессиональных задач

выбирает способ (технологию) решения задачи в соответствии с заданными условиями и имеющимися ресурсами

Оценка выполнения ПЗ

ОК 3.2. Текущий контроль и коррекция деятельности

предлагает способ коррекции деятельности на основе результатов текущего контроля

Оценка выполнения ПЗ

ОК 3.3. Оценка результатов деятельности

оценивает результаты деятельности по заданным показателям

Оценка выполнения ПЗ

ОК 4.1. Поиск информации

формулирует вопросы, нацеленные на получение недостающей информации

Оценка выполнения ПЗ

ОК 4.2. Извлечение и первичная обработка информации

извлекает информацию по двум и более основаниям из одного или нескольких источников и систематизирует ее в самостоятельно определенной в соответствии с задачей информационного поиска структуре

Оценка выполнения ПЗ

ОК 4.3. Обработка информации

задает критерии для сравнительного анализа информации в соответствии с поставленной задачей деятельности

делает вывод о применимости общей закономерности в конкретных условиях

Оценка выполнения ПЗ

1

2

3

ОК 5. Владеть информационной культурой, анализировать и оценивать информацию с использованием информационнокоммуникационных технологи

выполняет поиск информации с использованием ИКТ, анализирует информацию, систематизирует её  

Оценка выполнения ПЗ

ОК 8.1. Оценка собственного продвижения

анализирует формулирует запрос на внутренние ресурсы (знания, умения, навыки, способы деятельности, ценности, установки, свойства психики) для решения профессиональной задачи

Тестирование

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности

владеет навыками самообразования, умеет работать с источниками информации

Оценка выполнения ПЗ

ОК 10. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей)

умеет осуществлять расчеты

Тестирование

ПК 1.1. Выявлять потребность в товарах

выполняет расчеты движения товара на рынке

Тестирование

ПК 3.1. Участвовать в планировании основных показателей деятельности организации

выполняет расчеты показателей деятельности организации

Тестирование

Предварительный просмотр:

Приложение 2.1  к ППССЗ  по профессии

19.02.10. Технология продукции общественного питания

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

ЕН.01 МАТЕМАТИКА

Заводоуковск,

2015

Рабочая программа учебной дисциплины «Математика» разработана на основе Федерального государственного  образовательного стандарта (далее – ФГОС), утвержденного Приказом Министерства образования и науки Российской Федерации по специальности среднего профессионального образования 19.02.10. Технология продукции общественного питания (пр.№675 от 22.06.10г.),  входящих в  состав укрупненной группы профессий  по направлению 19.00.00. Промышленная экология и биотехнология.

Организация-разработчик:

Государственное автономное образовательное учреждение среднего профессионального образования Тюменской области «Заводоуковский агропромышленный техникум»

Разработчики:

Сычева Жанна Петровна, преподаватель высшей квалификационной категории

Хребтова Светлана Агафоновна, Заслуженный учитель РФ, преподаватель высшей квалификационной категории

СОДЕРЖАНИЕ

стр.
  1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

4
  1. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

5
  1. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

8
  1. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

9

1. ПАСПОРТ  ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

ЕН.01 МАТЕМАТИКА

1.1. Область применения программы

Программа учебной  дисциплины является частью  программы подготовки специалистов среднего звена среднего профессионального образования  по специальности 19.02.10. Технология продукции общественного питания (пр.№675 от 22.06.10г.),  входящих в  состав укрупненной группы профессий  по направлению 19.00.00. Промышленная экология и биотехнология.

1.2. Место дисциплины в структуре основной профессиональной образовательной программы: программа относится к математическому и общему естественнонаучному циклу.

1.3. Цели и задачи дисциплины – требования к результатам освоения дисциплины:

В результате освоения дисциплины студент должен уметь:

  • решать прикладные задачи в области профессиональной деятельности;
  • применять простые математические модели систем и процессов в сфере профессиональной деятельности;

В результате освоения дисциплины студент должен знать/понимать:

  • значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы;
  • основные понятия и методы математического анализа, теории вероятностей и математической статистики;
  • основы математические методы решения прикладных задач в области профессиональной деятельности.

1.4. Рекомендуемое количество часов на освоение программы дисциплины:

максимальной учебной нагрузки студента 60 часов, в том числе:

обязательной аудиторной учебной нагрузки студента 10 часов;

самостоятельной работы студента 50 часов.

2. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

2.1. Объем учебной дисциплины и виды учебной работы

Вид учебной работы

Объем часов

Максимальная учебная нагрузка (всего)

60

Обязательная аудиторная учебная нагрузка (всего)

10

в том числе:

     практические занятия

6

Самостоятельная работа студента (всего)

50

в том числе:

практические занятия

промежуточная аттестация: домашняя контрольная работа.

27

6

Итоговая аттестация: экзамен.

2.2. Тематический план и содержание учебной дисциплины ЕН.01 МАТЕМАТИКА

Наименование разделов и тем

Содержание учебного материала, лабораторные и практические работы,

самостоятельная работа студентов

Объем часов

Уровень освоения

1

2

3

4

Введение

Содержание учебного материала

2

1

2

Роль и место знаний по дисциплине в процессе освоения основной профессиональной образовательной программы по специальности.

Содержание дисциплины и ее задачи.

1

1

Тема 1.

Дифференциальное исчисление

Содержание учебного материала

18

1

2

Предел функции.

Производная сложной функции.

1

(изучается аудиторно)

2

2

3

Дифференциал функции.

5

2

Практические занятия:

1

2

3

Нахождение пределов функции.

Вычисление производных.

Решение прикладных задач.

2

4

6

2

2

2

Тема 2.

Интегральное исчисление

Содержание учебного материала

16

1

2

Метод замены переменной в неопределенном интеграле.

Интегрирование по частям.

1

(изучается аудиторно)

2

2

3

Определенный интеграл. Формула Ньютона – Лейбница. Геометрические приложения определенного интеграла.

5

2

2

2

Практические занятия:

1

Нахождение интегралов методом замены и методом интегрирования по частям.

2

(изучается аудиторно)

2

2

3

4

Вычисление определенного интеграла.

Решение прикладных задач.

4

4

2

2

1

2

3

4

Тема 3.

Основные понятия теории вероятностей

Содержание учебного материала

12

1

2

Вероятность события. Свойства вероятности.

Характеристики случайных величин.

1

(изучается аудиторно)

2

2

3

4

Дискретная случайная величина. Числовые характеристики ДСВ.

Непрерывная случайная величина. Числовые характеристики НСВ.

3

2

2

Практические занятия:

1

Нахождение вероятностей.

2

(изучается аудиторно)

2

2

Нахождение числовых характеристик ДСВ, НСВ.

6

2

Тема 4.

Элементы математической статистики

Содержание учебного материала

2

1

2

3

4

Основные понятия математической статистики.

Эмпирическая функция распределения.

Полигон и гистограмма.

Числовые характеристики выборки.

2

2

2

2

Тема 5.

Прикладные задачи

Содержание учебного материала

4

1

Решение транспортных задач.

1

(изучается аудиторно)

Практические занятия:

1

Решение прикладных задач.

2

(изучается аудиторно)

2

2

Решение транспортных задач.

1

2

Домашняя контрольная работа

6

2

Всего:

60

3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ

3.1. Требования к минимальному материально-техническому обеспечению

Реализация программы дисциплины требует наличия учебного кабинета математики.

Оборудование учебного кабинета: чертежные инструменты

Технические средства обучения: рабочее место студента, рабочее место преподавателя, персональный компьютер, мультимедийный проектор, интерактивная доска, электронные учебники, презентации, интернет

3.2. Информационное обеспечение обучения

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы

Основные источники:

  1. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учебник: Допущено Минобразования России. – ИЦ Академия, 2013
  2. Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике: учеб. Пособие: Рекомендовано ФГУ «ФИРО». – ИЦ Академия, 2013.
  3. Григорьев С.Г., Иволгина С.В. Математика: учебник: Рекомендовано ФГУ «ФИРО»/ Под. Ред. В.А. Гусева. – ИЦ Академия, 2013.

Дополнительные источники:

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 2007
  2. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнения и задачах / в 2-х томах. – М.: Высшая школа, 2007
  3. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник: Допущено Минобразования России. – М.: Высшая школа, 2009.
  4. Щипачев В. С. Задачник по высшей математике. – М.: Высшая школа, 2008
  5. Щипачев В. С. Основы высшей математики. – М.: Высшая школа. 2008

Электронные ресурсы:

  1. http://mathem.h1.ru/ — Математика On- Line. Коллекция формул по математике, геометрии, высшей математике, справочной информации по математическим дисциплинам и математические статьи.
  2. http://www.math.ru  — Коллекция книг, видео-лекций, подборка занимательных математических фактов, различные по уровню и тематике задачи, истории из жизни математиков. Информация об олимпиадах, научных школах по математике.
  3. http://eqworld.ipmnet.ru/indexr.htm — Мир математических уравнений

4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ

Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий и лабораторных работ, тестирования, а также выполнения студентами индивидуальных заданий, проектов, исследований.

Результаты обучения

(освоенные умения, усвоенные знания)

Формы и методы контроля и оценки результатов обучения

1

2

Умеет решать прикладные задачи в области профессиональной деятельности

Практическое задание

Умеет применять простые математические модели систем и процессов в сфере профессиональной деятельности

Практическое задание

Знает значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы

Тест

Знает основные понятия и методы математического анализа, теории вероятностей и математической статистики

Тест

Знает основы математические методы решения прикладных задач в области профессиональной деятельности

Тест

Результаты

(освоенные общие компетенции)

Основные показатели результатов подготовки

Формы и методы контроля

1

2

3

OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес

объясняет место дисциплины в формировании профессиональной компетенций

Тестирование

ОК 2.1. Планирование деятельности

разбивает поставленную цель на задачи, подбирая из числа известных технологии (элементы технологий), позволяющие решить каждую из задач

Тестирование

ОК 2.3.

Определение методов решения профессиональных задач

выбирает способ (технологию) решения задачи в соответствии с заданными условиями и имеющимися ресурсами

Оценка выполнения ПЗ

ОК 3.2. Текущий контроль и коррекция деятельности

предлагает способ коррекции деятельности на основе результатов текущего контроля

Оценка выполнения ПЗ

ОК 3.3. Оценка результатов деятельности

оценивает результаты деятельности по заданным показателям

Оценка выполнения ПЗ

ОК 4.1. Поиск информации

формулирует вопросы, нацеленные на получение недостающей информации

Оценка выполнения ПЗ

ОК 4.2. Извлечение и первичная обработка информации

извлекает информацию по двум и более основаниям из одного или нескольких источников и систематизирует ее в самостоятельно определенной в соответствии с задачей информационного поиска структуре

Оценка выполнения ПЗ

ОК 4.3. Обработка информации

задает критерии для сравнительного анализа информации в соответствии с поставленной задачей деятельности

делает вывод о применимости общей закономерности в конкретных условиях

Оценка выполнения ПЗ

1

2

3

ОК 5. Владеть информационной культурой, анализировать и оценивать информацию с использованием информационнокоммуникационных технологи

выполняет поиск информации с использованием ИКТ, анализирует информацию, систематизирует её  

Оценка выполнения ПЗ

ОК 6.1.

Работа в команде (группе)

принимает и фиксирует решение по всем вопросам для группового обсуждения

Оценка выполнения ПЗ

ОК 6.2.

Эффективное общение: монолог

использует средства наглядности или невербальные средства коммуникации

Оценка выполнения ПЗ

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий

отвечает за работу членов команды, за результат выполненных заданий

Оценка выполнения ПЗ

ОК 8.1. Оценка собственного продвижения

анализирует формулирует запрос на внутренние ресурсы (знания, умения, навыки, способы деятельности, ценности, установки, свойства психики) для решения профессиональной задачи

Тестирование

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности

владеет навыками самообразования, умеет работать с источниками информации

Оценка выполнения ПЗ

ОК 10. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей)

умеет осуществлять расчеты

Тестирование

ПК 1.1. Организовывать подготовку мяса и приготовление полуфабрикатов для сложной кулинарной продукции

умеет осуществлять расчеты

Тестирование

1

2

3

ПК 1.2. Организовывать подготовку рыбы и приготовление полуфабрикатов для сложной кулинарной продукции

умеет осуществлять расчеты

Тестирование

ПК 1.3. Организовывать подготовку домашней птицы для приготовления сложной кулинарной продукции

умеет осуществлять расчеты

Тестирование

ПК 2.1. Организовывать и проводить приготовление канапе, легких и сложных холодных закусок

умеет осуществлять расчеты

Тестирование

ПК 2.2. Организовывать и проводить приготовление сложных холодных блюд из рыбы, мяса и сельскохозяйственной (домашней) птицы

умеет осуществлять расчеты

Тестирование

ПК 2.3. Организовывать и проводить приготовление сложных холодных соусов

умеет осуществлять расчеты

Тестирование

ПК 3.1. Организовывать и проводить приготовление сложных супов

умеет осуществлять расчеты

Тестирование

ПК 3.2. Организовывать и проводить приготовление сложных горячих соусов

умеет осуществлять расчеты

Тестирование

ПК 3.3. Организовывать и проводить приготовление сложных блюд из овощей, грибов и сыра

умеет осуществлять расчеты

Тестирование

ПК 3.4. Организовывать и проводить приготовление сложных блюд из рыбы, мяса и сельскохозяйственной (домашней) птицы

умеет осуществлять расчеты

Тестирование

ПК 4.1. Организовывать и проводить приготовление сдобных хлебобулочных изделий и праздничного хлеба

умеет осуществлять расчеты

Тестирование

1

2

3

ПК 4.2. Организовывать и проводить приготовление сложных мучных кондитерских изделий и праздничных тортов

умеет осуществлять расчеты

Тестирование

ПК 4.3. Организовывать и проводить приготовление мелкоштучных кондитерских изделий.

умеет осуществлять расчеты

Тестирование

ПК 4.4. Организовывать и проводить приготовление сложных отделочных полуфабрикатов, использовать их в оформлении

умеет осуществлять расчеты

Тестирование

ПК 5.1. Организовывать и проводить приготовление сложных холодных десертов

умеет осуществлять расчеты

Тестирование

ПК 5.2. Организовывать и проводить приготовление сложных горячих десертов

умеет осуществлять расчеты

Тестирование

ПК 6.1. Участвовать в планировании основных показателей производства

умеет осуществлять расчеты

Тестирование

ПК 6.2. Планировать выполнение работ исполнителями

умеет осуществлять расчеты

Тестирование

ПК 6.3. Организовывать работу трудового коллектива

умеет осуществлять расчеты

Тестирование

ПК 6.4. Контролировать ход и оценивать результаты выполнения работ исполнителями

умеет осуществлять расчеты

Тестирование

ПК 6.5. Вести утвержденную учетно-отчетную документацию

умеет осуществлять расчеты

Тестирование

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

ЕН.01 МАТЕМАТИКА

Содержание курса, методические указания и задания контрольной работы

для студентов заочной формы обучения

по программе подготовки специалистов среднего звена

 23.02.03. Техническое обслуживание и ремонт автомобильного транспорта

2015 г.

РАССМОТРЕН

предметно-цикловой комиссией

Председатель _________Ж П. Сычева

Протокол №___«___»________2015 г.

Разработчик:

Сычева Ж.П., преподаватель высшей квалификационной категории

Для изучения курса «Математика» в помощь студенту предлагается учебно-методические материалы в 4 частях:

  1. Введение в математический анализ. Производная и ее приложения.
  2. Интегральное исчисление.
  3. Дифференциальные уравнения.
  4. Основы теории вероятностей и математической статистики.

Учебно-методические материалы содержат перечень тем, перечень рекомендованной литературы, варианты контрольного задания, обязательного для выполнения студентом. Приведен образец выполнения контрольной работы.

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ КУРСА

4

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

7

ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

8

КОНТРОЛЬНЫЕ ЗАДАНИЯ

11

ПРИЛОЖЕНИЕ 1

18

СОДЕРЖАНИЕ КУРСА

Часть 1. Введение в математический анализ. Производная и ее приложения

  1. Предел и непрерывность функции.
  2. Неопределенности.
  3. Производная. Определение. Свойства и формулы.
  4. Дифференциал функции.
  5. Производные высших порядков.
  6. Приложения дифференциального исчисления.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 2. Интегральное исчисление

  1. Первообразная. Неопределенный интеграл. Определение первообразной. Неопределенный интеграл. Определение первообразной, неопределенного интеграла, обозначение неопределенного интеграла.
  2. Таблица основных интегралов.
  3. Основные свойства неопределенного интеграла: интеграл от суммы двух функций, от произведения функции на постоянную, от производной и дифференциала.
  4. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
  5. Задача о вычислении площади криволинейной трапеции.
  6. Определенный интеграл. Определение интегральной суммы и определенного интеграла. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.
  7. Основные свойства определенного интеграла.
  8. Методы вычисления определенного интеграла: заменой переменной, по частям.
  9. Вычисление площади определенным интегралом.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 3. Дифференциальные уравнения

  1. Основные понятия и определения.
  2. Дифференциальное уравнение первого порядка, его общее решение.
  3. Основные типы дифференциального уравнения первого порядка (ДУ–I) и способы их решения: уравнения с разделяющимися переменными, однородные ДУ–I, линейные ДУ–I. Примеры решения ДУ–I.
  4. Дифференциальные уравнения второго порядка (ДУ–II).
  5. Линейные однородные и линейные неоднородные ДУ–II.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 4. Основы теории вероятностей и математической статистики

  1. Вероятность события. Свойства вероятности.
  2. Теоремы сложения и умножения вероятностей.
  3. Дискретная случайная величина. Числовые характеристики ДСВ.
  4. Основные понятия математической статистики
  5. Эмпирическая функция распределения
  6. Полигон и гистограмма
  7. Числовые характеристики выборки

Перечень рекомендуемой литературы

  1. Венцель Е. С., Овчаров Л. А. Теория вероятностей. – М.: Высшая школа, 2002
  2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002
  3. Гмурман В. Е. Теория вероятностей и математическая статистика, Учеб. пособие для  вузов. – М.: Высшая школа, 2003
  4. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  5. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник: Допущено Минобразования России. – М.: Высшая школа, 2009.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Студенты заочной формы обучения выполняют одну контрольную работу.

  1. Контрольная работа выполняется в отдельной тетради с нумерацией страниц и соблюдением полей для замечаний рецензентов. Текст рукописный (подчерк разборчивый).  Либо печатный вариант на листах формата А4, шрифтом Times New Roman, 14 пт., межстрочный интервал 1,5, поля: верхнее – 2 см, нижнее – 2 см, левое – 2 см, правое – 2 см, выравнивание текста – по ширине, красная строка – 1,25. Титульный лист оформляется в соответствии с приложением 1.
  2. При выполнении  контрольной работы, прежде всего, надо переписать условие задачи, дать подробное решение.
  3. Выполненная работа направляется на проверку и рецензирование. При положительной рецензии студент допускается к собеседованию, в ходе которого проверяются его знания и умения по решенным заданиям. В случае отрицательной рецензии контрольная работа возвращается студенту для доработки. При повторном представлении работы на проверку прилагается и первоначальный вариант с рецензией.
  4. Собеседование по контрольной работе проводится во время экзаменационной сессии в предусмотренное расписанием время. Студент может прийти на собеседование к преподавателю и в другое время в течение межсессионного периода в часы индивидуальных консультаций преподавателя.
  5. Студент должен выполнить контрольные задания по варианту, номер которого совпадает с последней цифрой его учебного номера.

Вариант

Номер практического задания

1

1, 11, 21, 31, 41

2

2, 12, 22, 32, 42

3

3, 13, 23, 33, 43

4

4, 14, 24, 34, 44

5

5, 15, 25, 35, 45

6

6, 16, 26, 36, 46

7

7, 17, 27, 37, 47

8

8, 18, 28, 38, 48

9

9, 19, 29, 39, 49

10

10, 20, 30, 40, 50

ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

  1. Вычислите пределы:

а)

б)

  1. Найдите производные:

а)

б)

в)  ,                

  1. Вычислите интегралы:

а)

б)  

в)

  1. Решите уравнения:

а)

 — общее решение дифференциального уравнения

Если , при , то  ⇒ 

— частное решение дифференциального уравнения

б)

в)

замена переменных: 

                          (1)

  1. Решите задачи:

а) Студент выучил 40 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,0

3,1

2,6

0,5

0,3

0,2

Решение:

Математическое ожидание:

Дисперсия: 

Среднее квадратическое отклонение:

КОНТРОЛЬНЫЕ ЗАДАНИЯ

  1. Вычислите пределы:

1.

а)

б)

2.

а)

б)

3.

а)

б)

4.

а)

б)

5.

а)

б)

6.

а)

б)

7.

а)

б)

8.

а)

б)

9.

а)

б)

10.

а)

б)
  1. Найдите производные:

11.

а)

б)              

в) дана функция   ,  найти  

12.

а)

б)

в)  дана функция,,  найти

13.

а)  

б)

 в) дана функция   , найти  

14.

а)        

б)

 в) дана функция   ,  найти  

15.

а)              

б)

в)  дана функция    ,найти  

16.

а)

б)

 в) дана функция  ,  найти  

17.

а)

б)

в)  дана функция   , найти

18.

а)

б)

в) дана функция   , найти

19.

а)

б)

в) дана функция   , найти

20.

а)

б)

в) дана функция   , найти

  1. Вычислите интегралы:

21.

а)

б)

в)

22.

а)

б)

в)

23.

а)

б)

в)

24.

а)

б)

в)

25.

а)

б)

в)

26.

а)

б)

в)

27.

а)

б)

в)

28.

а)

б)

в)

29.

а)

б)

в)

30.

а)

б)

в)

  1. Решите уравнения:

31.

а) , если  при

б)

в)

32.

а) , если  при

б)

в)

33.

а) , если  при

б)

в)

34.

а) , если  при

б)

в)

35.

а) , если  при

б)

в)

36.

а) , если  при

б)

в)

37.

а) , если  при

б)

в)

38.

а) , если  при

б)

в)

39.

а) , если  при

б)

в)

40.

а) , если  при

б)

в)

  1. Решите задачи:

41.

а) На стеллаже библиотеки в случайном порядке расставлено 8 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы один из взятых  учебников окажется в переплете.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,2

0,3

0,5

42.

а) В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найдите вероятность того, что среди отобранных студентов пять отличников.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,3

1,1

3,6

0,2

0,3

0,5

43.

а) В партии 100 одинаковых по внешнему виду изделий смешаны 40 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,0

5,5

1,6

0,2

0,3

0,5

44.

а) В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника окажутся в переплете.  

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,1

0,4

0,5

45.

а) В группе 16 студентов, среди которых 6 отличников. По списку наудачу отобраны 6 студентов. Найдите вероятность того, что среди отобранных студентов три отличника.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,3

3,1

7,5

0,3

0,3

0,4

46.

а) Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,5

5,1

6,6

0,2

0,3

0,5

47.

а) Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит хотя бы на один вопрос.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,4

0,4

0,2

48.

а) В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника без переплета.  

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,5

3,2

8,0

0,2

0,3

0,5

49.

а) В партии 80 одинаковых по внешнему виду изделий смешаны 20 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

5,8

5,1

7,4

0,3

0,5

0,2

50.

а) Студент выучил 30 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,3

4,5

6,7

0,3

0,1

0,6

ПРИЛОЖЕНИЕ 1

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

ЗАОЧНОЕ ОТДЕЛЕНИЕ

Регистрационный №_____

Дата регистрации «__» _________ 2015г.

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

Выполнил:

Антонова Е.А.

группа АТХз-01-15

Проверил:

Сычева Ж.П.

2015 г.

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

ЕН.01 МАТЕМАТИКА

Содержание курса, методические указания и задания контрольной работы

для студентов заочной формы обучения

по программе подготовки специалистов среднего звена

 38.02.05. Товароведение и экспертиза качества потребительских товаров

2015 г.

РАССМОТРЕН

предметно-цикловой комиссией

Председатель _________Ж П. Сычева

Протокол №___«___»________2015 г.

Разработчик:

Сычева Ж.П., преподаватель высшей квалификационной категории

Для изучения курса «Математика» в помощь студенту предлагается учебно-методические материалы в 5 частях:

  1. Элементы линейной алгебры.
  2. Введение в математический анализ. Производная и ее приложения.
  3. Интегральное исчисление.
  4. Комплексные числа.
  5. Основы теории вероятностей и математической статистики.

Учебно-методические материалы содержат перечень тем, перечень рекомендованной литературы, варианты контрольного задания, обязательного для выполнения студентом. Приведен образец выполнения контрольной работы.

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ КУРСА

4

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

7

ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

8

КОНТРОЛЬНЫЕ ЗАДАНИЯ

12

ПРИЛОЖЕНИЕ 1

20

СОДЕРЖАНИЕ КУРСА

Часть 1. Элементы линейной алгебры

  1. Матрицы. Виды матриц.
  2. Операции над матрицами.
  3. Определители: виды, приемы вычисления
  4. Обратная матрица.
  5. Системы линейных уравнений.
  6. Методы решения систем линейных уравнений: метод Крамера, матричный метод, Метод Гаусса.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 2. Введение в математический анализ. Производная и ее приложения

  1. Предел и непрерывность функции.
  2. Неопределенности.
  3. Производная. Определение. Свойства и формулы.
  4. Дифференциал функции.
  5. Производные высших порядков.
  6. Приложения дифференциального исчисления.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 3. Интегральное исчисление

  1. Первообразная. Неопределенный интеграл. Определение первообразной. Неопределенный интеграл. Определение первообразной, неопределенного интеграла, обозначение неопределенного интеграла.
  2. Таблица основных интегралов.
  3. Основные свойства неопределенного интеграла: интеграл от суммы двух функций, от произведения функции на постоянную, от производной и дифференциала.
  4. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
  5. Задача о вычислении площади криволинейной трапеции.
  6. Определенный интеграл. Определение интегральной суммы и определенного интеграла. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.
  7. Основные свойства определенного интеграла.
  8. Методы вычисления определенного интеграла: заменой переменной, по частям.
  9. Вычисление площади определенным интегралом.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 4. Комплексные числа

  1. Понятие комплексного числа. Представление комплексного числа на плоскости.
  2. Модуль комплексного числа.
  3. Операции над комплексными числами. Сложение комплексных чисел.
  4. Операции над комплексными числами. Вычитание комплексных чисел.
  5. Операции над комплексными числами. Умножение комплексных чисел.
  6. Комплексно-сопряженные числа.
  7. Операции над комплексными числами. Деление комплексных чисел.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 5. Основы теории вероятностей и математической статистики

  1. Вероятность события. Свойства вероятности.
  2. Теоремы сложения и умножения вероятностей.
  3. Дискретная случайная величина. Числовые характеристики ДСВ.
  4. Основные понятия математической статистики
  5. Эмпирическая функция распределения
  6. Полигон и гистограмма
  7. Числовые характеристики выборки

Перечень рекомендуемой литературы

  1. Венцель Е. С., Овчаров Л. А. Теория вероятностей. – М.: Высшая школа, 2002
  2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002
  3. Гмурман В. Е. Теория вероятностей и математическая статистика, Учеб. пособие для  вузов. – М.: Высшая школа, 2003
  4. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  5. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник: Допущено Минобразования России. – М.: Высшая школа, 2009.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Студенты заочной формы обучения выполняют одну контрольную работу.

  1. Контрольная работа выполняется в отдельной тетради с нумерацией страниц и соблюдением полей для замечаний рецензентов. Текст рукописный (подчерк разборчивый).  Либо печатный вариант на листах формата А4, шрифтом Times New Roman, 14 пт., межстрочный интервал 1,5, поля: верхнее – 2 см, нижнее – 2 см, левое – 2 см, правое – 2 см, выравнивание текста – по ширине, красная строка – 1,25. Титульный лист оформляется в соответствии с приложением 1.
  2. При выполнении  контрольной работы, прежде всего, надо переписать условие задачи, дать подробное решение.
  3. Выполненная работа направляется на проверку и рецензирование. При положительной рецензии студент допускается к собеседованию, в ходе которого проверяются его знания и умения по решенным заданиям. В случае отрицательной рецензии контрольная работа возвращается студенту для доработки. При повторном представлении работы на проверку прилагается и первоначальный вариант с рецензией.
  4. Собеседование по контрольной работе проводится во время экзаменационной сессии в предусмотренное расписанием время. Студент может прийти на собеседование к преподавателю и в другое время в течение межсессионного периода в часы индивидуальных консультаций преподавателя.
  5. Студент должен выполнить контрольные задания по варианту, номер которого совпадает с последней цифрой его учебного номера.

Вариант

Номер практического задания

1

1, 11, 21, 31, 41, 51

2

2, 12, 22, 32, 42, 52

3

3, 13, 23, 33, 43, 53

4

4, 14, 24, 34, 44, 54

5

5, 15, 25, 35, 45, 55

6

6, 16, 26, 36, 46, 56

7

7, 17, 27, 37, 47, 57

8

8, 18, 28, 38, 48, 58

9

9, 19, 29, 39, 49, 59

10

10, 20, 30, 40, 50, 60

ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

  1. Решите систему уравнений методом Крамера, методом Гаусса, матричным методом:

Метод Крамера:

Проверка:        

Метод Гаусса:

 ⇒  ⇒  ⇒  ⇒ .

Матричный метод:

                

Т.к. |А|= –11≠0, то система крамеровская и для невырожденной матрицы А можно найти обратную.

Ответ: .

  1. Вычислите пределы:

а)

б)

  1. Найдите производные:

а)

б)

в)  ,                

  1. Вычислите интегралы:

а)

б)  

в)

  1. Выполните действия с комплексными числами:

Найдите .

  1. Решите задачи:

а) Студент выучил 40 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,0

3,1

2,6

0,5

0,3

0,2

Решение:

Математическое ожидание:

Дисперсия: 

Среднее квадратическое отклонение:

КОНТРОЛЬНЫЕ ЗАДАНИЯ

  1. Решите систему уравнений методом Крамера, методом Гаусса, матричным методом:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

  1. Вычислите пределы:

11.

а)

б)

12.

а)

б)

13.

а)

б)

14.

а)

б)

15.

а)

б)

16.

а)

б)

17.

а)

б)

18.

а)

б)

19.

а)

б)

20.

а)

б)
  1. Найдите производные:

21.

а)

б)              

в) дана функция   ,  найти  

22.

а)

б)

в)  дана функция,,  найти

23.

а)  

б)

 в) дана функция   , найти  

24.

а)        

б)

 в) дана функция   ,  найти  

25.

а)              

б)

в)  дана функция    ,найти  

26.

а)

б)

 в) дана функция  ,  найти  

27.

а)

б)

в)  дана функция   , найти

28.

а)

б)

в) дана функция   , найти

29.

а)

б)

в) дана функция   , найти

30.

а)

б)

в) дана функция   , найти

  1. Вычислите интегралы:

31.

а)

б)

в)

32.

а)

б)

в)

33.

а)

б)

в)

34.

а)

б)

в)

35.

а)

б)

в)

36.

а)

б)

в)

37.

а)

б)

в)

38.

а)

б)

в)

39.

а)

б)

в)

40.

а)

б)

в)

  1. Выполните действия с комплексными числами:

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

  1. Решите задачи:

51.

а) На стеллаже библиотеки в случайном порядке расставлено 8 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы один из взятых  учебников окажется в переплете.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,2

0,3

0,5

52.

а) В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найдите вероятность того, что среди отобранных студентов пять отличников.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,3

1,1

3,6

0,2

0,3

0,5

53.

а) В партии 100 одинаковых по внешнему виду изделий смешаны 40 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,0

5,5

1,6

0,2

0,3

0,5

54.

а) В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника окажутся в переплете.  

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,1

0,4

0,5

55.

а) В группе 16 студентов, среди которых 6 отличников. По списку наудачу отобраны 6 студентов. Найдите вероятность того, что среди отобранных студентов три отличника.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,3

3,1

7,5

0,3

0,3

0,4

56.

а) Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,5

5,1

6,6

0,2

0,3

0,5

57.

а) Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит хотя бы на один вопрос.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,4

0,4

0,2

58.

а) В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника без переплета.  

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,5

3,2

8,0

0,2

0,3

0,5

59.

а) В партии 80 одинаковых по внешнему виду изделий смешаны 20 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

5,8

5,1

7,4

0,3

0,5

0,2

60.

а) Студент выучил 30 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,3

4,5

6,7

0,3

0,1

0,6

ПРИЛОЖЕНИЕ 1

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

ЗАОЧНОЕ ОТДЕЛЕНИЕ

Регистрационный №_____

Дата регистрации «__» _________ 2015г.

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

Выполнил:

Антонова Е.А.

группа Тз-01-15

Проверил:

Сычева Ж.П.

2015 г.

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

ЕН.01 МАТЕМАТИКА

Содержание курса, методические указания и задания контрольной работы

для студентов заочной формы обучения

по программе подготовки специалистов среднего звена

19.02.10. Технология продукции общественного питания

2015 г.

РАССМОТРЕН

предметно-цикловой комиссией

Председатель _________Ж П. Сычева

Протокол №___«___»________2015 г.

Разработчик:

Сычева Ж.П., преподаватель высшей квалификационной категории

Для изучения курса «Математика» в помощь студенту предлагается учебно-методические материалы в 4 частях:

  1. Введение в математический анализ. Производная и ее приложения.
  2. Интегральное исчисление.
  3. Основы теории вероятностей и математической статистики.
  4. Транспортные задачи.

Учебно-методические материалы содержат перечень тем, перечень рекомендованной литературы, варианты контрольного задания, обязательного для выполнения студентом. Приведен образец выполнения контрольной работы.

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ КУРСА

4

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

7

ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

8

КОНТРОЛЬНЫЕ ЗАДАНИЯ

11

ПРИЛОЖЕНИЕ 1

20

СОДЕРЖАНИЕ КУРСА

Часть 1. Введение в математический анализ. Производная и ее приложения

  1. Предел и непрерывность функции.
  2. Неопределенности.
  3. Производная. Определение. Свойства и формулы.
  4. Дифференциал функции.
  5. Производные высших порядков.
  6. Приложения дифференциального исчисления.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 2. Интегральное исчисление

  1. Первообразная. Неопределенный интеграл. Определение первообразной. Неопределенный интеграл. Определение первообразной, неопределенного интеграла, обозначение неопределенного интеграла.
  2. Таблица основных интегралов.
  3. Основные свойства неопределенного интеграла: интеграл от суммы двух функций, от произведения функции на постоянную, от производной и дифференциала.
  4. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
  5. Задача о вычислении площади криволинейной трапеции.
  6. Определенный интеграл. Определение интегральной суммы и определенного интеграла. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.
  7. Основные свойства определенного интеграла.
  8. Методы вычисления определенного интеграла: заменой переменной, по частям.
  9. Вычисление площади определенным интегралом.

Перечень рекомендуемой литературы

  1. Богомолов Н. В. Практические занятия по математике. Учеб. Пособие. – М.: Высшая школа, 1997
  2. Виноградова И. А., Олехник С. Н., Садовничий В. А.Задачи и упражнения по математическому анализу. В 2 книгах. Учебное пособие / Под ред. В. А. Садовничего – 2-е изд., перераб. – М.: Высшая школа. 2000
  3. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  4. Запорожец Г. И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966.
  5. Ильин В. А. Основы математического анализа / В. А. Ильин, Э. Г. Позняк. – М.: Наука, 1982.
  6. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970.
  7. Щипачев В. С. Задачник по высшей математике. – М.: 1998
  8. Щипачев В. С. Основы высшей математики. – М.: 1998

Часть 3. Основы теории вероятностей и математической статистики

  1. Вероятность события. Свойства вероятности.
  2. Теоремы сложения и умножения вероятностей.
  3. Дискретная случайная величина. Числовые характеристики ДСВ.
  4. Основные понятия математической статистики
  5. Эмпирическая функция распределения
  6. Полигон и гистограмма
  7. Числовые характеристики выборки

Перечень рекомендуемой литературы

  1. Венцель Е. С., Овчаров Л. А. Теория вероятностей. – М.: Высшая школа, 2002
  2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002
  3. Гмурман В. Е. Теория вероятностей и математическая статистика, Учеб. пособие для  вузов. – М.: Высшая школа, 2003
  4. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002
  5. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник: Допущено Минобразования России. – М.: Высшая школа, 2009.

Часть 4. Транспортные задачи

  1. Вероятность события. Свойства вероятности.
  2. Теоремы сложения и умножения вероятностей.
  3. Дискретная случайная величина. Числовые характеристики ДСВ.
  4. Основные понятия математической статистики
  5. Эмпирическая функция распределения
  6. Полигон и гистограмма
  7. Числовые характеристики выборки

Перечень рекомендуемой литературы

  1. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика  в упражнениях и задачах. В 2-х частях. – М.: высшая школа, 2002.
  2. Е. Г. Гольштейн, Д. Б. Юдин «Задачи линейного программирования транспортного типа», Москва, 1993.
  3. И. Л. Акулич, В. Ф. Стрельчонок «Математические методы и компьютерные технологии решения оптимизационных задач», Рига, 2000.
  4. Канатников А.Н., Крищенко А.П. Линейная алгебра. М.: Изд-во МГТУ им. Н.Э.
    Баумана, 2002.
  5. Схрейвер А. Теория линейного и целочисленного программирования. В 2-х т. М.: Мир, 1991.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Студенты заочной формы обучения выполняют одну контрольную работу.

  1. Контрольная работа выполняется в отдельной тетради с нумерацией страниц и соблюдением полей для замечаний рецензентов. Текст рукописный (подчерк разборчивый).  Либо печатный вариант на листах формата А4, шрифтом Times New Roman, 14 пт., межстрочный интервал 1,5, поля: верхнее – 2 см, нижнее – 2 см, левое – 2 см, правое – 2 см, выравнивание текста – по ширине, красная строка – 1,25. Титульный лист оформляется в соответствии с приложением 1.
  2. При выполнении  контрольной работы, прежде всего, надо переписать условие задачи, дать подробное решение.
  3. Выполненная работа направляется на проверку и рецензирование. При положительной рецензии студент допускается к собеседованию, в ходе которого проверяются его знания и умения по решенным заданиям. В случае отрицательной рецензии контрольная работа возвращается студенту для доработки. При повторном представлении работы на проверку прилагается и первоначальный вариант с рецензией.
  4. Собеседование по контрольной работе проводится во время экзаменационной сессии в предусмотренное расписанием время. Студент может прийти на собеседование к преподавателю и в другое время в течение межсессионного периода в часы индивидуальных консультаций преподавателя.
  5. Студент должен выполнить контрольные задания по варианту, номер которого совпадает с последней цифрой его учебного номера.

Вариант

Номер практического задания

1

1, 11, 21, 31, 41

2

2, 12, 22, 32, 42

3

3, 13, 23, 33, 43

4

4, 14, 24, 34, 44

5

5, 15, 25, 35, 45

6

6, 16, 26, 36, 46

7

7, 17, 27, 37, 47

8

8, 18, 28, 38, 48

9

9, 19, 29, 39, 49

10

10, 20, 30, 40, 50

ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

  1. Вычислите пределы:

а)

б)

  1. Найдите производные:

а)

б)

в)  ,                

  1. Вычислите интегралы:

а)

б)  

в)

  1. Решите задачи:

а) Студент выучил 40 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,0

3,1

2,6

0,5

0,3

0,2

Решение:

Математическое ожидание:

Дисперсия: 

Среднее квадратическое отклонение:

  1. Решите транспортную задачу, исходные данные которой приведены в таблице:

100

100

200

300

200

1

2

3

3

200

7

3

6

4

300

5

1

6

4

                

Находим начальное опорное решение:

100

100

200

300

200

1

100

2

0

3

100

3

—

200

7

—

3

—

6

0

4

200

300

5

—

1

100

6

100

4

100

Полученное начальное опорное решение

 

имеет  базисных переменных.

Вычислим значение целевой функции:

Проверим решение на оптимальность

Найдем потенциалы для занятых клеток:

Вычисляем оценки для не занятых клеток:

Начальное опорное решение является оптимальным, так как .

КОНТРОЛЬНЫЕ ЗАДАНИЯ

  1. Вычислите пределы:

1.

а)

б)

2.

а)

б)

3.

а)

б)

4.

а)

б)

5.

а)

б)

6.

а)

б)

7.

а)

б)

8.

а)

б)

9.

а)

б)

10.

а)

б)
  1. Найдите производные:

11.

а)

б)              

в) дана функция   ,  найти  

12.

а)

б)

в)  дана функция,,  найти

13.

а)  

б)

 в) дана функция   , найти  

14.

а)        

б)

 в) дана функция   ,  найти  

15.

а)              

б)

в)  дана функция    ,найти  

16.

а)

б)

 в) дана функция  ,  найти  

17.

а)

б)

в)  дана функция   , найти

18.

а)

б)

в) дана функция   , найти

19.

а)

б)

в) дана функция   , найти

20.

а)

б)

в) дана функция   , найти

  1. Вычислите интегралы:

21.

а)

б)

в)

22.

а)

б)

в)

23.

а)

б)

в)

24.

а)

б)

в)

25.

а)

б)

в)

26.

а)

б)

в)

27.

а)

б)

в)

28.

а)

б)

в)

29.

а)

б)

в)

30.

а)

б)

в)

  1. Решите задачи:

31.

а) На стеллаже библиотеки в случайном порядке расставлено 8 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы один из взятых  учебников окажется в переплете.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,2

0,3

0,5

32.

а) В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найдите вероятность того, что среди отобранных студентов пять отличников.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,3

1,1

3,6

0,2

0,3

0,5

33.

а) В партии 100 одинаковых по внешнему виду изделий смешаны 40 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,0

5,5

1,6

0,2

0,3

0,5

34.

а) В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника окажутся в переплете.  

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,1

0,4

0,5

35.

а) В группе 16 студентов, среди которых 6 отличников. По списку наудачу отобраны 6 студентов. Найдите вероятность того, что среди отобранных студентов три отличника.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,3

3,1

7,5

0,3

0,3

0,4

36.

а) Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,5

5,1

6,6

0,2

0,3

0,5

37.

а) Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит хотя бы на один вопрос.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,4

0,4

0,2

38.

а) В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника без переплета.  

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,5

3,2

8,0

0,2

0,3

0,5

39.

а) В партии 80 одинаковых по внешнему виду изделий смешаны 20 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

5,8

5,1

7,4

0,3

0,5

0,2

40.

а) Студент выучил 30 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

б) Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,3

4,5

6,7

0,3

0,1

0,6
  1. Решите транспортную задачу, исходные данные которой приведены в таблице:

41.

200

100

200

300

300

1

8

3

3

200

7

3

6

4

300

5

1

3

4

42.

50

100

200

150

100

1

2

3

3

150

7

3

6

4

250

5

1

6

4

43.

100

100

200

300

200

1

2

3

5

200

7

3

8

4

300

5

1

6

3

44.

100

300

200

300

200

1

2

3

3

300

8

3

7

4

400

5

1

6

4

45.

100

100

200

300

200

1

2

3

8

200

7

3

6

5

300

9

1

6

4

46.

100

100

200

300

100

2

2

3

3

200

11

3

7

4

400

8

1

6

4

47.

50

100

50

200

100

1

2

3

3

200

7

3

6

4

100

5

1

6

4

48.

100

100

200

300

200

1

2

3

3

200

7

3

6

4

300

5

1

6

4

49.

100

200

300

300

200

1

2

3

3

400

9

3

8

4

300

5

1

6

4

50.

100

100

200

300

200

1

2

3

3

200

7

3

9

4

300

6

1

7

4

ПРИЛОЖЕНИЕ 1

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

ЗАОЧНОЕ ОТДЕЛЕНИЕ

Регистрационный №_____

Дата регистрации «__» _________ 2015г.

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

Выполнил:

Антонова Е.А.

группа ОПз-01-15

Проверил:

Сычева Ж.П.

2015 г.

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

РАССМОТРЕНО

УТВЕРЖДАЮ

на заседании предметно-цикловой комиссии

Председатель ПЦК__________ Ж.П. Сычева              

Протокол №___ от «___» ___________2015г.

Заведующая заочным отделением

______ Т.В. Симонова

«___»_________2015г.

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ

ПО ДИСЦИПЛИНЕ ЕН.01 МАТЕМАТИКА

для студентов заочной формы обучения

по программе подготовки специалистов среднего звена

 23.02.03. Техническое обслуживание и ремонт автомобильного транспорта

Теоретические вопросы

  1. Предел и непрерывность функции. Неопределенности.
  2. Производная. Правила дифференцирования.
  3. Дифференциал функции.
  4. Производные высших порядков.
  5. Приложения дифференциального исчисления.
  6. Первообразная. Неопределенный интеграл.
  7. Правила интегрирования.
  8. Таблица основных интегралов.
  9. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
  10. Задача о вычислении площади криволинейной трапеции.
  11. Определенный интеграл. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.
  12. Основные свойства определенного интеграла.
  13. Методы вычисления определенного интеграла: заменой переменной, по частям.
  14. Вычисление площади определенным интегралом.
  15. Дифференциальное уравнение первого порядка, его общее решение.
  16. Основные типы дифференциального уравнения первого порядка (ДУ–I) и способы их решения.
  17. Дифференциальные уравнения второго порядка (ДУ–II).
  18. Линейные однородные и линейные неоднородные ДУ–II.
  19. Вероятность события. Свойства вероятности.
  20. Теоремы сложения и умножения вероятностей.
  21. Дискретная случайная величина. Числовые характеристики ДСВ.
  22. Основные понятия математической статистики.
  23. Эмпирическая функция распределения.
  24. Полигон и гистограмма.
  25. Числовые характеристики выборки.

Практические задания

  1. Вычислить предел .
  2. Вычислить предел .
  3. Вычислить предел .
  4. Вычислить предел .
  5. Вычислить предел .
  6. Вычислить предел .
  7. Вычислить предел .
  8. Найти производную функции.
  9. Найти производную функции .
  10. Найти производную функции .
  11. Найти производную функции .
  12. Найти производную функции .
  13. Найти производную функции .
  14. Найти производную функции .
  15. Найти производную функции .
  16. Найти производную функции .
  17. Найти интеграл .
  18. Найти интеграл .
  19. Найти интеграл .
  20. Найти интеграл .
  21. Найти интеграл .
  22. Найти интеграл .
  23. Найти интеграл .
  24. Найти интеграл .
  25. Найти интеграл .
  26. Решить уравнение .
  27. Решить уравнение .
  28. Решить уравнение .
  29. Решить уравнение .
  30. Решить уравнение .
  31. Решить уравнение .
  32. Решить уравнение .
  33. Решить уравнение .
  34. Решить уравнение .
  35. Решить уравнение .
  36. Решить задачу:

На стеллаже библиотеки в случайном порядке расставлено 8 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы один из взятых  учебников окажется в переплете.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,2

0,3

0,5
  1. Решить задачу:

В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника окажутся в переплете.  

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,3

1,1

3,6

0,2

0,3

0,5
  1. Решить задачу:

В группе 16 студентов, среди которых 6 отличников. По списку наудачу отобраны 6 студентов. Найдите вероятность того, что среди отобранных студентов три отличника.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,0

5,5

1,6

0,2

0,3

0,5
  1. Решить задачу:

Студент выучил 20 вопросов из 25. Найдите вероятность того, что он ответит хотя бы на один вопрос.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,1

0,4

0,5
  1. Решить задачу:

В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника без переплета.  

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,3

3,1

7,5

0,3

0,3

0,4
  1. Решить задачу:

В партии 80 одинаковых по внешнему виду изделий смешаны 20 изделий 1 сорта и 60 изделий второго сорта. Найдите вероятность того, что взятые наудачу два изделия окажутся одного сорта.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

2,5

5,1

6,6

0,2

0,3

0,5
  1. Решить задачу:

Студент выучил 30 вопросов из 50. Найдите вероятность того, что он ответит на три предложенных ему вопроса.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,4

0,4

0,2
  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

1,5

3,2

8,0

0,2

0,3

0,5

Преподаватель                                                                        Ж.П. Сычева

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

РАССМОТРЕНО

УТВЕРЖДАЮ

на заседании предметно-цикловой комиссии

Председатель ПЦК__________ Ж.П. Сычева              

Протокол №___ от «___» ___________2015г.

Заведующая заочным отделением

______ Т.В. Симонова

«___»_________2015г.

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ

ПО ДИСЦИПЛИНЕ ЕН.01 МАТЕМАТИКА

для студентов заочной формы обучения

по программе подготовки специалистов среднего звена

19.02.10. Технология продукции общественного питания

Теоретические вопросы

  1. Предел и непрерывность функции. Неопределенности.
  2. Производная. Правила дифференцирования.
  3. Приложения дифференциального исчисления.
  4. Первообразная. Неопределенный интеграл.
  5. Правила интегрирования. Таблица основных интегралов.
  6. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
  7. Определенный интеграл. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.
  8. Методы вычисления определенного интеграла: заменой переменной, по частям.
  9. Вычисление площади определенным интегралом.
  10. Вероятность события. Свойства вероятности.
  11. Теоремы сложения и умножения вероятностей.
  12. Дискретная случайная величина. Числовые характеристики ДСВ.
  13. Эмпирическая функция распределения. Полигон и гистограмма.
  14. Числовые характеристики выборки.
  15. Математическая модель транспортной задачи. Опорное решение транспортной задачи.
  16. Методы построения опорного решения транспортной задачи.

Практические задания

  1. Вычислить предел .
  2. Вычислить предел .
  3. Вычислить предел .
  4. Вычислить предел .
  5. Вычислить предел .
  6. Вычислить предел .
  7. Вычислить предел .
  8. Найти производную функции.
  9. Найти производную функции .
  10. Найти производную функции .
  11. Найти производную функции .
  12. Найти производную функции .
  13. Найти производную функции .
  14. Найти производную функции .
  15. Найти производную функции .
  16. Найти производную функции .
  17. Найти интеграл .
  18. Найти интеграл .
  19. Найти интеграл .
  20. Найти интеграл .
  21. Найти интеграл .
  22. Найти интеграл .
  23. Найти интеграл .
  24. Найти интеграл .
  25. Решить задачу:

На стеллаже библиотеки в случайном порядке расставлено 8 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы один из взятых  учебников окажется в переплете.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,2

0,3

0,5
  1. Решить задачу:

В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника окажутся в переплете.  

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,3

1,1

3,6

0,2

0,3

0,5
  1. Решить транспортную задачу методом минимальной стоимости:

50

100

50

200

100

1

2

3

3

200

7

3

6

4

100

5

1

6

4
  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,0

5,5

1,6

0,2

0,3

0,5
  1. Решить задачу методом северо-западного угла:

100

100

200

300

200

1

2

3

8

200

7

3

6

5

300

9

1

6

4
  1. Решить задачу методом северо-западного угла:

100

100

200

300

100

2

2

3

3

200

11

3

7

4

400

8

1

6

4

Преподаватель                                                                        Ж.П. Сычева

Предварительный просмотр:

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ТЮМЕНСКОЙ ОБЛАСТИ

«ЗАВОДОУКОВСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»

РАССМОТРЕНО

УТВЕРЖДАЮ

на заседании предметно-цикловой комиссии

Председатель ПЦК__________ Ж.П. Сычева              

Протокол №___ от «___» ___________2015г.

Заведующая заочным отделением

______ Т.В. Симонова

«___»_________2015г.

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ

ПО ДИСЦИПЛИНЕ ЕН.01 МАТЕМАТИКА

для студентов заочной формы обучения

по программе подготовки специалистов среднего звена

38.02.05. Товароведение и экспертиза качества потребительских товаров

Теоретические вопросы

  1. Матрицы. Виды матриц. Операции над матрицами.
  2. Определители: виды, приемы вычисления
  3. Обратная матрица.
  4. Методы решения систем линейных уравнений: метод Крамера, матричный метод, Метод Гаусса.
  5. Предел и непрерывность функции. Неопределенности.
  6. Производная. Правила дифференцирования.
  7. Приложения дифференциального исчисления.
  8. Первообразная. Неопределенный интеграл.
  9. Правила интегрирования. Таблица основных интегралов.
  10. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
  11. Определенный интеграл. Геометрический смысл. Формула Ньютона-Лейбница для вычисления определенного интеграла.
  12. Методы вычисления определенного интеграла: заменой переменной, по частям.
  13. Вычисление площади определенным интегралом.
  14. Вероятность события. Свойства вероятности.
  15. Теоремы сложения и умножения вероятностей.
  16. Дискретная случайная величина. Числовые характеристики ДСВ.
  17. Эмпирическая функция распределения. Полигон и гистограмма.
  18. Числовые характеристики выборки.
  19. Понятие комплексного числа. Модуль комплексного числа.
  20. Операции с комплексными числами.

Практические задания

  1. Вычислить предел .
  2. Вычислить предел .
  3. Вычислить предел .
  4. Вычислить предел .
  5. Вычислить предел .
  6. Вычислить предел .
  7. Вычислить предел .
  8. Найти производную функции.
  9. Найти производную функции .
  10. Найти производную функции .
  11. Найти производную функции .
  12. Найти производную функции .
  13. Найти производную функции .
  14. Найти производную функции .
  15. Найти производную функции .
  16. Найти производную функции .
  17. Найти интеграл .
  18. Найти интеграл .
  19. Найти интеграл .
  20. Найти интеграл .
  21. Найти интеграл .
  22. Найти интеграл .
  23. Найти интеграл .
  24. Найти интеграл .
  25. Решить задачу:

На стеллаже библиотеки в случайном порядке расставлено 8 учебников, причем 3 из них в переплете. Библиотекарь берет наудачу три учебника. Найдите вероятность того, что хотя бы один из взятых  учебников окажется в переплете.

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,3

5,1

10,6

0,2

0,3

0,5
  1. Решить задачу:

В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найдите вероятность того, что оба учебника окажутся в переплете.  

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

3,3

1,1

3,6

0,2

0,3

0,5
  1. Решить систему линейных уравнений методом Крамера:

  1. Решить задачу:

Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения.

4,0

5,5

1,6

0,2

0,3

0,5
  1. Решить систему линейных уравнений методом Крамера:

  1. Решить систему линейных уравнений методом Крамера:

  1. Решить систему линейных уравнений методом Крамера:

  1. Решить систему линейных уравнений методом Крамера:

  1. Выполните действия с комплексными числами:
  2. Выполните действия с комплексными числами:
  3. Выполните действия с комплексными числами:
  4. Выполните действия с комплексными числами:
  5. Выполните действия с комплексными числами:
  6. Выполните действия с комплексными числами:

Преподаватель                                                                        Ж.П. Сычева

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Экзамен по математике за 9 класс для детей с овз
  • Экзамен по математике для студентов 1 курса колледжа
  • Экзамен по математике для поступления в физмат класс 8 класс
  • Экзамен по математике для поступления в университет
  • Экзамен по математике для поступления в техникум

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии