Вопросы к зачетам и экзаменам
Уважаемые студенты!
В соответствии с программой курса высшей математики в первом семестре для вас подготовлены 5 контрольных работ «Проверь себя» (с ответами).
Выполнение этих работ будет хорошей подготовкой к текущим и экзаменационному тестам по высшей математике. (скачать )
В соответствии с программой курса высшей математики во втором семестре для вас подготовлены 3 контрольные работы по интегральному исчислению, рядам и дифференциальным уравнениям «Проверь себя» (с ответами). Выполнение этих работ будет хорошей подготовкой к текущим и экзаменационному тестам по высшей математике. (скачать)
Примеры вопросов к зачету и экзамену по математике,информатике (скачать )
nike air max 1 metallic silver
Уважаемые студенты!
В соответствии с программой курса высшей математики в первом семестре для вас подготовлены 5 контрольных работ «Проверь себя» (с ответами).
Выполнение этих работ будет хорошей подготовкой к текущим и экзаменационному тестам по высшей математике. (скачать )
В соответствии с программой курса высшей математики во втором семестре для вас подготовлены 3 контрольные работы по интегральному исчислению, рядам и дифференциальным уравнениям «Проверь себя» (с ответами). Выполнение этих работ будет хорошей подготовкой к текущим и экзаменационному тестам по высшей математике. (скачать)
Тренировочные тесты для подготовки к экзамену, по семестрам:
1 семестр (скачать — 114 Кб);
2 семестр (скачать — 65 Кб);
3 семестр:
Для студентов 2 курса (3 семестр) факультета ЭТ, изучающих теорию функций комплексного переменного (ТФКП) и операционное исчисление (ОИ) (скачать — 53 Кб);
Для студентов факультета НТ, ИТ, АИТ, изучающих теорию функций комплексного переменного (ТФКП), операционное исчисление (ОИ) и теорию вероятностей (ТВ) (скачать — 66 Кб);
Для студентов факультета ИТ, АИТ, изучающих теорию функций комплексного переменного (ТФКП), операционное исчисление (ОИ) и теорию поля (ТП) (скачать — 81 Кб);
Для студентов факультета ТЭ, изучающих теорию функций комплексного переменного (ТФКП), операционное исчисление (ОИ), теорию поля (ТП) и уравнения математической физики (УМФ) (скачать — 86 Кб);
Для студентов факультета ХТ, ПП, ЭТ,ИТ изучающих теорию вероятностей (ТВ) и математическую статистику (МС) (скачать — 16 Кб);
Для студентов факультета ИЭ, изучающих теорию вероятностей (ТВ) (скачать — 16 Кб);
4 семестр:
Для студентов 2 курса (4 семестр) факультетов ТЭ, ЭТ, АИТ изучающих теорию вероятностей (ТВ) и математическую статистику (МС) (скачать — 33 Кб);
Для студентов факультетов ИТ, АИТ изучающих уравнения математической физики (УМФ), теорию вероятностей (ТВ) и математическую статистику (МС) (скачать — 50 Кб).
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.2015200 Кб193.jpg
☆
#08.06.2015176 Кб194.jpg
☆
#08.06.2015151 Кб195.jpg
☆
#08.06.2015169 Кб196.jpg
☆
#08.06.2015137 Кб207.jpg
☆
#08.06.2015196 Кб198.jpg
☆
#08.06.2015145 Кб209.jpg
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20152 Ф151AFU
☆
#
☆
#
☆
#
☆
#08.06.2015266 Кб41А0-Насос буровой ВО.cdw
☆
#08.06.2015258 Кб32А1-Насос буровой ВО.cdw
☆
#08.06.2015338 Кб36А1-Насос СБ.cdw
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20150 ФАЗЭ +2 учебника
☆
#
☆
#08.06.20151 Мб20ГП_1.cdr
☆
#08.06.20152 Мб11ГП_10.cdr
☆
#08.06.2015592 Кб11ГП_11.cdr
☆
#08.06.2015426 Кб11ГП_12.cdr
☆
#08.06.2015995 Кб15ГП_13-15.cdr
☆
#08.06.2015626 Кб13ГП_16-18.cdr
☆
#08.06.2015718 Кб10ГП_19-21.cdr
☆
#08.06.2015529 Кб11ГП_2.cdr
☆
#08.06.2015469 Кб11ГП_22.cdr
☆
#08.06.2015497 Кб14ГП_23.cdr
☆
#08.06.20156 Мб11ГП_24-27.cdr
☆
#08.06.20152 Мб12ГП_3.cdr
☆
#08.06.20152 Мб11ГП_4.cdr
☆
#08.06.20152 Мб49ГП_5.cdr
☆
#08.06.20152 Мб11ГП_6.cdr
☆
#08.06.20152 Мб11ГП_7.cdr
☆
#08.06.20152 Мб11ГП_8.cdr
☆
#08.06.20152 Мб13ГП_9.cdr
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20157 Ф48ДУ
☆
#
☆
#08.06.201510 Ф47Ряды
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.201518 Кб28При токе 4070.wmf
☆
#08.06.201522 Кб28При токе 8000.wmf
☆
#08.06.201549 Кб29отчет.odt
☆
#08.06.201589 Кб28Расчет мощности.xmcd
☆
#08.06.2015624 б28Расчет нагрева масла.dhe
☆
#08.06.20158 Кб28Расчет нагрева масла.mod
☆
#
☆
#08.06.20155 Кб28Расчет нагрева масла.res
☆
#
☆
#08.06.201534 Кб28lab2.mdl
☆
#08.06.201518 Кб28ras.xmcd
☆
#08.06.201527 Кб28zad.mdl
☆
#08.06.201545 Кб29отчет..odt
☆
#
☆
#08.06.201590 Кб28Скляров, Марущак, Куликов.ms10
☆
#08.06.201590 Кб28Скляров, Марущак, Куликов.ms10 (Security copy)
☆
#08.06.201527 Кб28Скляров, Марущак, Куликов.xmcd
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.201528 Кб30Работа 1.xmcd
☆
#08.06.20153 Кб30Скляров.Марущак-раб.1.mrj
☆
#08.06.20153 Кб30Скляров.Марущак-раб.1.mr~
☆
#
☆
#08.06.201557 Кб28Работа 2.xmcd
☆
#08.06.2015204 Кб28Скляров.Марущак. Куликов-раб.2.mrj
☆
#08.06.2015204 Кб28Скляров.Марущак. Куликов-раб.2.mrj (Security copy)
☆
#
☆
#08.06.2015162 Кб30Работа 3.xmcd
☆
#08.06.20150 Фработа №4
☆
#
☆
#08.06.201560 Кб28Работа 5.xmcd
☆
#
☆
#08.06.201564 Кб29Куликов, Скляров, Марущак.Работа 6.ms10
☆
#08.06.201510 Кб29Скляров.Марущак. Куликов-раб.6 отчет.mrj (Security copy).ods
☆
#
☆
#08.06.201560 Кб28Куликов, Скляров, Марущак.Работа 7.ms10
☆
#08.06.201560 Кб28Куликов, Скляров, Марущак.Работа 7.ms10 (Security copy)
☆
#08.06.20158 Кб30Скляров.Марущак. Куликов-раб.7 отчет.mrj (Security copy).ods
☆
#
☆
#08.06.201515 Кб29Расчет кабеля.xmcd
☆
#08.06.2015192 б28Расчет нагрева масла.dhe
☆
#08.06.20158 Кб28Расчет нагрева масла.mod
☆
#
☆
#08.06.20155 Кб28Расчет нагрева масла.res
☆
#08.06.2015218 б28Скляров.Марущак. Куликов-раб.Емкостного соротивление.dcf
☆
#08.06.201552 б28Скляров.Марущак. Куликов-раб.Емкостного соротивление.dec
☆
#08.06.2015226 б28Скляров.Марущак. Куликов-раб.Емкостного соротивление.des
☆
#
☆
#08.06.20152 Кб28Скляров.Марущак. Куликов-раб.Емкостного соротивление.res
☆
#08.06.2015372 б28Скляров.Марущак. Куликов-раб.Расчет кабеля..dhe
☆
#08.06.20155 Кб28Скляров.Марущак. Куликов-раб.Расчет кабеля..mod
☆
#
☆
#08.06.20153 Кб28Скляров.Марущак. Куликов-раб.Расчет кабеля..res
☆
#08.06.201538 Кб29Куликов, Скляров, Марущяк.ms10
☆
#08.06.201565 Кб29СК, МА.xls
☆
#
☆
#
☆
#
☆
#
☆
#08.06.201557 Кб28Схема 03.04.12.ms10
☆
#08.06.20151 Мб28Схема05.03.12.ms10
☆
#08.06.2015184 б28ЭТ-4.dht
☆
#08.06.2015992 б28ЭТ-4.mod
☆
#
☆
#08.06.2015320 б28ЭТ-4.res
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20150 ФПо темам
☆
#
☆
#
☆
#
☆
#08.06.201513 Мб1515_dataAB 2.12.10.dbv
☆
#08.06.201513 Мб15dataCD_10.12.10.dbv
☆
#
☆
#08.06.201510 Мб15dataAB_09.dbv
☆
#08.06.201510 Мб15dataCD_09.dbv
☆
#
☆
#08.06.20159 Мб15dataAB.dbv
☆
#08.06.20159 Мб15dataCD.dbv
☆
#08.06.2015971 б16avtoex.exe.lnk
☆
#08.06.20159 Кб15AVTOEX.GID
☆
#08.06.2015144 Кб15AVTOEX.HLP
☆
#08.06.201510 Мб16dataAB-02-10.dbv
☆
#08.06.201513 Мб19dataCD_10.12.10.dbv
☆
#
☆
#
☆
#
☆
#08.06.20150 Фковка и штамповка четыре тома
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.201589 Кб15Лаб1.m3d
☆
#08.06.2015117 Кб6Лаб2.m3d
☆
#08.06.2015140 Кб10сечение конуса.m3d
☆
#08.06.2015101 Кб6сфера.m3d
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20157 Ф45ООП
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20153 Ф103ОС
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20155 Мб2LIST1,3.CATDrawing
☆
#
☆
#08.06.20155 Мб4LIST1,3_Лист_1.dwg
☆
#08.06.20153 Мб2LIST1,3_Лист_1.frw
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20150 ФРЗА ЭЭС
☆
#
☆
#08.06.20154 Ф12СПО
☆
#
☆
#
☆
#08.06.201521 Ф4V4
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.201515 Кб4inf_kc.rtf
☆
#08.06.201516 Кб4inf_ktc.rtf
☆
#08.06.201516 Кб4inf_zh.rtf
☆
#
☆
#08.06.201543 б2AUTORUN.INF
☆
#
☆
#08.06.201520 Кб2DICT.HLP
☆
#08.06.2015229 Кб2MICRO.HLP
☆
#08.06.20151 Кб2READ_ME.TXT
☆
#08.06.2015145 Кб2SHEM.HLP
☆
#
☆
#
☆
#08.06.20152 Ф20хос
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#28.03.201614 Мб30*Лопатин В.В. Русский орфографический словарь.pdf
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
1
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#07.06.2015191 Кб76-10.doc
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.201525 Мб16Д. Кирьянов — Mathcad 13.pdf
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#07.06.201518 Мб272Н и ПС Лекции НАСОСЫ и НПС 14-17.doc
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
1
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20152 Мб82Процессы и аппараты нефтегазо- переработки.docx
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.20152 Мб32С. В. АДЕЛЬСОИ процессы и аппраты.docx
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
1
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#08.06.2015238 Кб37шпоры сапр тп.docx
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
☆
#
Комплексный сборник тестов с ответами по Высшей математике
Кривые второго порядка
Правильный ответ подчёркнут.
1. Кривой II порядка является
— эллипс, не вырожденный в окружность
— гипербола
— парабола
— окружность
2. Кривой II порядка является
— эллипс, не вырожденный в окружность
— гипербола
— парабола
— окружность
3. Кривой II порядка является
— эллипс, не вырожденный в окружность
— гипербола
— парабола
— окружность
4. Кривой II порядка является
— эллипс, не вырожденный в окружность
— гипербола
— парабола
— окружность
Прямые и плоскости в пространстве
Правильный ответ выделен и подчёркнут.
1. Уравнением плоскости, проходящей через точку и перпендикулярной прямой
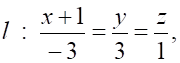
а. б.
в.
2. Общее уравнение плоскости, содержащей точку и параллельной плоскости
, имеет вид
а.
б.
в.
г.
3. Плоскость перпендикулярна плоскости
а.
б.
в.
г. £
4. Прямая, проходящая через точки и
, перпендикулярна плоскости
а.
б.
в.
г.
5. Даны три прямых на плоскости: ,
и
Верным является утверждение
а. и
перпендикулярны
б. и
перпендикулярны
в. и
перпендикулярны
г. перпендикулярных прямых нет
6. Уравнением плоскости, проходящей через точку и перпендикулярной прямой
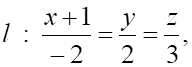
а.
б.
в.
г.
тест 7. Общее уравнение плоскости, содержащей точку и параллельной плоскости
, имеет вид
а.
б.
в.
г.
8. Плоскость перпендикулярна плоскости
а.
б.
в.
г.
Прямые на плоскости
Правильный ответ выделен и подчёркнут.
1. Прямая, проходящая через точку и параллельная прямой
имеет вид
а.
б.
в.
г.
2. Уравнением прямой, содержащей точку и параллельной прямой
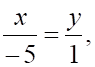
а.
б.
в.
г.
3. Общее уравнение прямой, содержащей точки и
имеет вид
а.
б.
£
£
Треугольник на плоскости
Правильный ответ выделен и подчёркнут.
1. Длина стороны в треугольнике
с вершинами
,
,
равна
а. б.
в.
г.
2. Длина медианы в треугольнике
с вершинами
,
,
равна
а. б.
в.
г.
3. Угол в треугольнике с вершинами
,
и
а. прямой б. тупой в. острый
4. В треугольнике , где
,
,
, угол при вершине
равен
а. б.
в.
г.
5. В треугольнике , где
,
,
, угол
а. прямой б. тупой в. острый
Линейная алгебра. Алгебра матриц. Обратная матрица. Определители
Правильный ответ выделен и подчёркнут.
1тест. Обратной к матрице 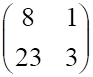
а. б.
в.
г.
2. Определитель матрицы 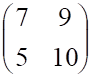
а. б.
в.
г.
3. Определитель матрицы 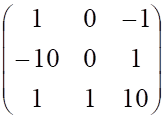
а. б.
в.
г.
4. Определитель матрицы 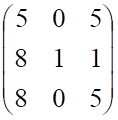
а. б.
в.
г.
5. Определитель матрицы 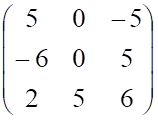
а. б.
в.
г.
6. Уравнение для нахождения собственных значений матрицы имеет вид
а.
б.
в.
г. £
Сумма и произведение матриц
Правильный ответ выделен и подчёркнут.
1. Выражение эквивалентно
а. б.
в.
г.
2. Выражение эквивалентно
а. б.
в.
г.
3. Произведение матриц 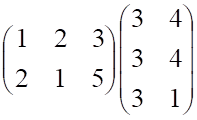
а. б.
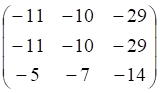
г.
4. Заданы матрицы 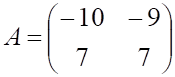
. Произведение
равно
а. б.
в.
г.
5. Заданы матрицы 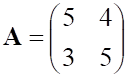
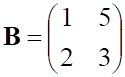
равно
а. б.
в.
г.
6. Заданы матрицы 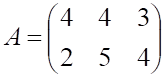
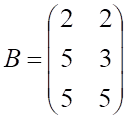
равна
а. б.
в.
г.
тест №7. Транспонированной к матрице 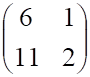
а. б.
в.
г.
Векторная алгебра
Правильный ответ выделен и подчёркнут.
1. Заданы векторы и
. Выражение
равно
а. б.
в.
г.
2. Заданы векторы и
. Длина вектора
равна
а. б.
в.
г.
3. Из векторов ,
и
, ортогональными являются
а. и
б. и
в. и
г. и
,
и
Комплексные числа
Правильный ответ выделен и подчёркнут.
1. Сумма если
,
, равна
а. б.
в.
г.
2. Произведение если
,
, равно
а. б.
в.
г.
Системы линейных уравнений
Правильный ответ выделен и подчёркнут.
1. Система линейных уравнений 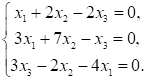
а. одно нулевое решение
б. бесконечно много решений
в. одно ненулевое решение
г. нет решений
2. Частным решением системы линейных уравнений 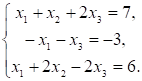
а. б.
в.
г.
3. Система линейных уравнений 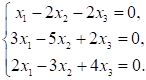
а. одно решение£ два решения
б. бесконечно много решений
в. нет решений
4. Матричное уравнение с невырожденной квадратной матрицей А имеет решение
а. б.
в.
г.
5. Матричное уравнение с невырожденной квадратной матрицей А имеет решение
а. б.
в.
г.
Математический анализ. Дифференциальное исчисление
Правильный ответ выделен и подчёркнут.
1 — тест. Производная функции равна
а.
б.
в.
г.
2. Производная функции равна
а.
б.
в.
г.
3. Производная функции 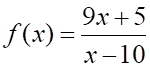
а. б.
в.
г.
4. Частной производной для функции
является
а. б.
в.
г.
5. Производная функции равна
а. б.
в.
г.
6. Градиент функции равен
а.
б.
в.
г.
7. Смешанная производная для функции
равна
а. б.
в.
г.
8. Достаточным условием выпуклости функции на интервале
является
а. на
б. на
в. на
г. на
9. Достаточным условием убывания функции на интервале
является
а. на
б. на
в. на
г. на
10. Точкой локального экстремума функции является
а. б.
в.
г.
11. Градиент функции равен
а.
б.
в.
г.
Дифференциальные уравнения
Правильный ответ выделен и подчёркнут.
тест — 1. Общим решением дифференциального уравнения является
а.
б.
в.
г.
Интегральное исчисление
Правильный ответ выделен и подчёркнут.
1. Определенный интеграл 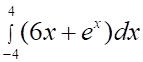
а. б.
в.
г.
2. Несобственный интеграл равен
а. б.
в.
г.
3. Несобственный интеграл 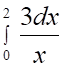
а. б.
в.
г.
4. Определенный интеграл 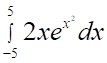
а. б.
в.
г.
5. Несобственный интеграл 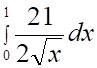
а. б.
в.
Последовательности
Правильный ответ выделен и подчёркнут.
1. Примером неограниченной последовательности является последовательность
а. б.
в.
г.
2. Примером сходящейся последовательности является последовательность
а. б.
в.
г.
3. Примером ограниченной последовательности является последовательность
а. б.
в.
г.
4. Примером бесконечно малой последовательности является последовательность
а. б.
в.
г.
5. Примером бесконечно большой последовательности является последовательность
а. б.
в.
г.
6. Примером ограниченной последовательности является последовательность
а. б.
в.
г.
7. Примером бесконечно малой последовательности является последовательность
а. б.
в.
г.
8. Примером бесконечно большой последовательности является последовательность
а. б.
в.
г.
9_тест. Примером ограниченной последовательности является последовательность
а. б.
в.
г.
Предел функции
Правильный ответ выделен и подчёркнут.
1. Предел 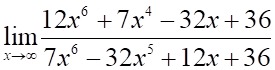
а. б.
в.
г.
2. Предел 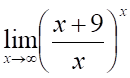
а. б.
в.
г.
3. Предел равен
а. б.
в.
г.
Ряды
Правильный ответ выделен и подчёркнут.
1. Радиус сходимости ряда 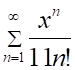
а. б.
в.
г.
2. Радиус сходимости ряда 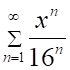
а. б.
в.
г.
3. Радиус сходимости ряда 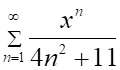
а. б.
в.
г.
Теория вероятностей
Правильный ответ выделен и подчёркнут.
1. Распределение дискретной случайной величины задано таблицей
Математическое ожидание равно
а. б.
в.
г.
2. Распределение дискретной случайной величины задано таблицей
Математическое ожидание равно
а. б.
в.
г.
3. Распределение дискретной случайной величины задано таблицей
Дисперсия равна
а. б.
в.
г.
тест_4. Распределение дискретной случайной величины задано таблицей
Дисперсия равна
а. б.
в.
г.
Классическая вероятность
Правильный ответ выделен и подчёркнут.
1. Вероятность, что кубик упадет на грань « «, при условии, что выпадет нечетная грань, равна
а. б.
в.
г.
2. В урне находится красных и
черных шаров. Вероятность на удачу достать два красных шара равна
а. б.
в.
г.
3. Вероятность попадания в цель при одном выстреле равна Вероятность того, что из двух выстрелов попали оба раза, равна
а. б.
в.
г.
4. Урна содержит белых и
черных шаров. Вероятность наудачу достать первым белый шар, а вторым черный, равна
а. б.
в.
г.
5. Количество способов, которыми можно выбрать экзаменационных билетa из
, равно
а. б.
в.
г.
Бакалавриат/Специалитет
Прием на обучение по программам
бакалавриата и программам специалитета
СамГТУ на базе среднего общего образования
осуществляется по результатам ЕГЭ
(п.18. Правил приема в СамГТУ).
Отдельные категории поступающих на
обучение по программам бакалавриата и
программам специалитета могут сдавать
общеобразовательные вступительные
испытания, проводимые СамГТУ самостоятельно
(п.19. Правил приема в СамГТУ).
Перечень вступительных испытаний на
каждое направление подготовки
(специальность) установлен Правилами
приема в СамГТУ (Приложение №1 Правил
приема в СамГТУ).
Результаты ЕГЭ текущего года и прошлых
лет загружаются в информационную систему
СамГТУ автоматически из федеральной
информационной системы (ФИС ГИА и
Приема).
В личном кабинете абитуриента в разделе
Вступительные испытания после подачи
документов и заявления и их проверки
модераторами отражается:
-
перечень вступительных испытаний по
общеобразовательным предметам и
дополнительным вступительным испытаниям
творческой и профессиональной
направленности для поступления на
выбранные в заявлении направления
подготовки (специальности); -
результаты
ЕГЭ (при наличии) по каждому
общеобразовательному предмету; -
персональное
расписание вступительных испытаний,
проводимых СамГТУ самостоятельно по
каждому общеобразовательному предмету
(при наличии) с указанием даты и времени,
формы проведения вступительного
испытания (очно, дистанционно), информация
о проведении консультаций; -
персональное
расписание дополнительных вступительных
испытаний творческой и профессиональной
направленности (при наличии) с указанием
даты и времени, формы проведения
вступительного испытания (очно,
дистанционно), информация о проведении
консультаций; -
результаты
указанных выше вступительных испытаний.
В случае, если вступительное испытание
проводится очно, то дополнительно
указывается место проведения с указанием
адреса.
В случае, если вступительное испытание
проводится дистанционно, то перед
экзаменом будет размещена ссылка на
ресурс в системе дистанционного обучения
СамГТУ. При проведении вступительного
испытания осуществляется обязательная
идентификация личности поступающего.
Также может быть использована система
прокторинга. При проведении видеоконференций
используется сервис ZOOM.
Для прохождения вступительного испытания
в системе дистанционного обучения
СамГТУ рекомендуется использовать
персональный компьютер/ноутбук с
установленной вебкамерой и микрофоном,
планшет с диагональю экрана не менее
10”. Для сдачи экзамена крайне нежелательно
использование смартфонов.
Со всеми особенностями проведения
вступительных испытаний как в очной,
так и в дистанционной форме, поступающих
ознакамливают во время консультаций,
которые обычно проходят накануне
экзамена в формате видеоконференции.
Информация о проведении консультаций
также размещается в персональном
расписании.
Если предусмотрено проведение
вступительного испытания в разные дни,
в разделе Вступительные испытания
возможна запись на вступительное
испытание на определенную дату и время.
Количество мест для записи на конкретную
дату ограничено.
Дополнительное вступительное испытание
творческой и профильной направленности
и вступительное испытание по одному
общеобразовательному предмету можно
сдать только один раз.
Ознакомиться с перечнем, формой
проведения, с особенностями проведения
для лиц с ограниченными возможностями,
программами, расписанием, результатами
вступительных испытаний можно на сайте
СамГТУ в разделе Поступающим/Вступительные
испытания.
 |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «Самарский государственный Технический университет» |
К а ф е д р а «Высшая математика и
прикладная информатика»
^
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Учебно-методическое пособие
по специальным разделам высшей математики
Самара 2008
УДК 519.21
Теория вероятностей и математическая статистика. Учебно-метод. пособ. по спец. главам высш. матем./ Самар. гос. техн. ун-т. Сост. В.Н. Гревцева, Л.В. Лиманова, Л.А. Муратова. Самара, 2008. 22 с.
Представлены задачи и их решения из следующих разделов курса высшей математики: теория вероятностей и математическая статистика. Пособие содержит тренировочные задания.
Предназначено для студентов всех специальностей СамГТУ.
Ил. . Библиогр.: 9 назв.
Печатается по решению редакционно-издательского совета СамГТУ
Пособие состоит из двух разделов: теории вероятностей и математической статистики. В каждом разделе даны подробные решения типовых задач, условия задач определяются программой курса высшей математики для IV семестра СамГТУ.
Раздел «Теория вероятностей» представлен задачами по темам: алгебра событий, классическое определение вероятности, формула полной вероятности, формула Бейеса, дискретная случайная величина и ее распределения, непрерывная случайная величина и ее распределения, предельные теоремы.
В разделе «Математическая статистика» рассматриваются задачи по темам: метод моментов для точечной оценки параметров распределения, определение доверительного интервала, проверка гипотезы о виде распределения, элементы теории корреляции.
Пособие содержит тренировочный тест (стр.16) с типовыми задачами по указанным темам.
Используемые для решения формулы обозначены в круглых скобках и приведены в конце пособия.
Основное назначение пособия – помочь студенту при изучении данного материала и подготовке к экзамену по высшей математике.
^
Задача 1. Прибор содержит 3 элемента с вероятностями отказа 0,1;0,4 и 0,2. Найти вероятности отказа а) одного элемента; б) двух или трех элементов; в) хотя бы одного элемента.
Решение. Обозначим — cобытие, означающее отказ
— го элемента,
— отказ одного элемента,
— отказ двух или трех элементов,
— отказ хотя бы одного элемента. Тогда для случая а) запишем
,
где — событие, означающее безотказную работу элемента
. Слагаемые этой суммы – несовместные события. Поэтому, согласно формуле
для несовместных событий,
Сомножители в последнем выражении – независимые события, значит, в соответствии с формулой
для независимых событий
.
Поскольку (формула
), получаем
.
В случае б) имеем .
Как и в случае а) справедливы следующие соотношения:
.
В случае в) искомое событие , причем слагаемые – совместные события, и для вычисления вероятности нужно использовать формулу
для произвольных событий, но можно решить задачу проще, используя противоположное событие
и формулу
.
Так как означает отказ одного или двух или трех элементов, то
— событие, дополняющее
до полной группы – означает безотказную работу всех трех элементов.
Поскольку и события
,
,
независимы, получаем
.
Задача 2. В урне 10 белых и 5 черных шаров. Из урны извлекают два шара. Найти вероятность того, что шары а) белые; б) одного цвета; в) разного цвета.
Решение. Пусть событие означает извлечение белого шара,
— извлечение черного шара и пусть индекс есть номер извлечения.
Тогда в случае а) искомое событие имеет вид (первый шар – белый и второй шар – белый). Поскольку
и
зависимы, используем формулу вероятности произведения
для произвольных событий:
.
находим согласно классическому определению вероятности
:
,
где — общее число случаев,
— число случаев, благоприятных событию
. Так как среди 15 шаров 10 белых, получаем
.
есть условная вероятность события
(второй шар – белый) при условии, что
(первый шар – белый) произошло. Но если первым взят белый шар, то среди 14 оставшихся шаров белых – 9, поэтому
.
Получаем: .
В случае б) искомое событие есть ( оба шара белые или оба шара черные), причем слагаемые несовместны, а сомножители зависимы. Тогда вероятность согласно формулам
,
равна:
.
В случае в) будем находить вероятность события ( первый шар белый, второй — черный или наоборот, первый – черный, а второй – белый).
Получим в соответствии с формулами ,
.
Задача 3. Среди 14 билетов 4 выигрышных. Найти вероятность того, что из 6 купленных билетов ровно 2 выигрышных.
Решение. Можно использовать способ решения, рассмотренный в задаче 2 (искомое событие запишется в виде суммы 15 слагаемых). Поступим иначе и решим задачу с помощью классического определения вероятности события (формула (4)):
,
где — общее число случаев,
— число случаев, благоприятных событию
.
Из 14 билетов 6 штук можно выбрать способами. Здесь
— число сочетаний из 14 элементов по 6 элементов. Значит,
. Два выигрышных билета могут быть выбраны из 4 билетов
способами. Остальные (4 билета) должны быть невыигрышными, их можно выбрать из 10 невыигрышных
способами.
Так как на один способ выбора двух выигрышных билетов приходится способов выбора невыигрышных билетов, то на
способов выбора двух выигрышных билетов приходится
способов выбора невыигрышных билетов.
Итак, . Тогда

Число сочетаний из элементов по
элементов находим по формуле
:
.
При этом получим: 
Задача 4. В первой урне 20 шаров, среди них 3 белых, во второй урне 15 шаров и среди них 2 белых. Из первой урны взяли шар и переложили во вторую. Какова вероятность, что шар, взятый после этого из второй урны, белый?
Решение. Пусть событие — извлечение белого шара из второй урны. Возможны две гипотезы:
— из первой урны взяли белый шар,
— из первой урны взяли шар другого цвета.
По формуле полной вероятности вероятность события с учетом двух гипотез равна
:
.
Вероятности гипотез составляют,
.
Найдем условные вероятности. Если из первой урны взяли белый шар и переложили во вторую, то во второй урне стало 16 шаров, среди которых 3 белых. Поэтому . Если же из первой урны взяли шар другого цвета и переложили во вторую, то во второй урне стало 16 шаров, но число белых шаров (их 2) не изменилось и, значит,
.
Подставив полученные значения в формулу полной вероятности, найдем :
.
Задача 5. Один завод производит в 3 раза меньше приборов, чем второй. Вероятность безотказной работы прибора первого завода – 0,9, второго – 0,7. случайным образом выбранный прибор отказал. Какова вероятность, что он сделан на втором заводе?
Решение. Обозначим — событие, состоящее в том, что выбранный прибор отказал. Возможны две гипотезы:
— прибор сделан на первом заводе,
— на втором.
Задача решается по формуле Бейеса, так как событие – прибор отказал – произошло. Запишем формулу Бейеса для случая двух гипотез:

Найдем вероятности гипотез и
до опыта. На один прибор первого завода приходится 3 прибора второго завода, значит доля первого завода
, второго
.
Найдем условные вероятности. Вероятность отказа прибора при условии, что он изготовлен на первом заводе, равна . Если же прибор сделан на втором заводе, то вероятность отказа
.
Осталось найти вероятность гипотезы после опыта ( то есть при условии, что
произошло):

Задача 6. Дискретная случайная величина Х задана законом распределения.
-
X 2 P
0,3
Найти , если
.
Решение. Так как , то
. Математическое ожидание и дисперсия для дискретных случайных величин определяются по формулам (8). То есть
, тогда
, откуда
.
Далее .
Задача 7. Дискретная случайная величина задана законом распределения
-
X -1 4 P
Найти ,
, если
.
Решение. Используя формулу для математического ожидания дискретной случайной величины, согласно которой
, имеем
. Кроме того,
. Решая получившуюся систему уравнений

,
.
Задача 8. Найти дисперсию случайной величины Х — числа появлений события А в 10 независимых испытаниях, если вероятности появления события в каждом испытании одинаковы, а .
Решение. Испытания независимы, а вероятности одинаковы, значит, случайная величина распределена по биномиальному закону (9); для него ,
.
Так как ,
, то
. Кроме того
. Тогда
Задача 9. Найти вероятность того, что при 8 подбрасываниях монеты герб появится ровно 3 раза.
Решение. Это биноминальное распределение, так как вероятность появления герба при каждом подбрасывании постоянна (равна 0,5). Тогда вероятность появления события в
испытаниях ровно
раз можно найти по формуле
:
,
где — число сочетаний из
элементов по
элементов (формула
),
.
Так как ,
, получим
.
Задача 10. Устройство содержит 2000 одинаковых элементов с вероятностью отказа для каждого за время , равной 0,001. Найти вероятность того, что за время
откажут а) меньше трех элементов; б) не меньше одного элемента.
Решение. Это биномиальное распределение, но поскольку число элементов велико, а вероятность отказа каждого мала, можно применить формулу Пуассона :
,
.
Так как ,
, то
.
а) Искомая величина есть
.
б) Используя вероятность противоположного события, получим
.
Задача 11. Непрерывная случайная величина задана функцией

.
Решение. Найдем сначала плотность распределения (формула (11)):

Применяя формулы (14), (15) и (17), получим
;
;
.
Задача 12. Непрерывная случайная величина задана плотностью распределения

.
Решение. Согласно формуле (12) имеем.
Отсюда найдем константу А: ,
,
.
Применяя формулу (13):
,
получим .
Задача 13. Непрерывная случайная величина распределена по показательному закону с плотностью
Найти ,
,
.
Решение. Задачу можно решать с помощью формул (13) — (15), но проще воспользоваться формулами для показательного распределения (18):
Тогда
Задача 14. Непрерывная случайная величина X распределена равномерно на отрезке. Найти
,
,
.
Решение. Равномерное распределение подчиняется формулам (19):
;
.
Найдем плотность распределения:

Тогда согласно (13)
,
поэтому
Задача 15. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами и
. Деталь считается годной, если ее диаметр не менее 1,9 см и не более 4 см. Определить процент брака.
Решение. Если случайная величина распределена по нормальному закону, то вероятность попадания её на интервал определяется формулой
:
,
где — математическое ожидание,
— среднее квадратическое отклонение,
— функция Лапласа
, значения которой находят по таблице приложений
.
Подставляя в эту формулу заданные значения, получаем (с учетом нечетности функции ):
.
Тогда процент годных деталей равен 81,85; соответственно брак составит 18,15%.
Задача 16. Случайные ошибки взвешивания распределены нормально с параметрами и
. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине
.
Решение. Для нормального распределения вероятность того, что абсолютная величина отклонения случайной величины от математического ожидания
меньше положительного числа
, задается формулой
:
,
где — функция Лапласа
. С учетом исходных данных получаем
.
Задача 17. Непрерывная случайная величина распределена нормально с ,
. Найти интервал, в котором согласно правилу «трех сигм» попадает случайная величина с вероятностью 0,9973.
Решение. Правило «трех сигм» представлено формулой (23)
.
Так как то
откуда
.
Решая последнее неравенство, получаем
,
откуда .
Задача 18. Вероятность поражения мишени при одном выстреле 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена 88 раз.
Решение. Для решения этой задачи можно воспользоваться локальной теоремой Лапласа (24):
,
где 
находят по табл. приложений [1]).
По условию,
,
,
. Тогда
.
Задача 19. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,5. Найти вероятность того, что событие появится от 60 до 80 раз.
Решение. Задача решается с помощью интегральной теоремы Лапласа (25)
,
где — функция Лапласа (21).
Здесь Тогда
.
Задача 20. Игральную кость бросают 125 раз. Найти вероятность того, что относительная частота появления шестерок отклонится от его вероятности не более чем на 0,1.
Решение. Воспользуемся формулой (26)
,
где — функция Лапласа (21). Так как
,
(вероятность выпадения шестерки при бросании игральной кости),
,
, то
.
^
Задача 21. Методом моментов по выборке
-
X 3 4 5 n
70 20 10
найти точечную оценку параметра , предполагая, что теоретическое распределение является показательным:
Решение. Согласно методу моментов нужно приравнять начальный теоретический момент первого порядка (математическое ожидание ) к начальному эмпирическому моменту первого порядка (выборочному среднему
):
.
По формулам (18) для показательного распределения имеем: . Выборочное среднее находим по формуле
:
,
где — варианта выборки,
— частота
,
— объем выборки.
Получаем .
Приравнивая моменты, находим :
=>
.
Задача 22. Найти доверительный интервал для оценки математического ожидания нормального распределения при доверительной вероятности (надежности), равной , если выборочное среднее
, среднее квадратическое отклонение
, а объем выборки
.
Решение. Доверительный интервал для математического ожидания при нормальном распределении равен :
,
где — выборочное среднее,
— среднее квадратическое отклонение,
— объем выборки,
,
— затабулированная функция Лапласа
.
Так как , из соотношения
получаем
и с помощью таблиц находим
. Тогда
и
.
Задача 23. По выборке из 24 вариант выдвинута гипотеза о нормальном распределении генеральной совокупности. Используя критерий Пирсона при уровне значимости среди заданных значений
= {34, 35, 36, 37, 38} указать: а) наибольшее, для которого нет оснований отвергать гипотезу; б) наименьшее, начиная с которого гипотеза должна быть отвергнута.
Решение. Найдем число степеней свободы с помощью формулы
:
,
где — число групп выборки (вариант),
— число параметров распределения.
Так как нормальное распределение имеет 2 параметра ( и
), получаем
.
По таблице критических точек распределения
, по заданному уровню значимости
и числу степеней свободы
определяем критическую точку
.
В случае а) для значений , равных 34 и 35, нет оснований отвергать гипотезу о нормальном распределении, так как
. А наибольшее среди этих значений
.
В случае б) для значений 36, 37, 38 гипотезу отвергают, так как . Наименьшее среди них
.
Задача 24. По данным корреляционной таблицы найти выборочный корреляционный момент (ковариацию):
-
X Y
-1 0 1 2 2 20 10 0 30 3 0 10 20 10
Решение. Выборочный корреляционный момент определяется равенством
:
.
Здесь ,
— варианты (наблюдавшиеся значения) признаков
и
,
— частота пары вариант
,
— объем выборки,
,
— выборочные средние.
Найдем выборочные средние с помощью соотношения :
,
,
где ,
— частоты вариант
и
.
Так как , получаем
,
.
Тогда
Задача 25. Найти выборочное уравнение прямой линии регрессии:
а) на
, б)
на
, если известны: выборочные средние
,
, выборочные дисперсии
,
, выборочный коэффициент корреляции
.
Решение. а) Выборочное уравнение прямой линии регрессии на
имеет вид
,
где ,
.
Поскольку ,
, получаем уравнение
, или
.
б) Согласно выборочному уравнению прямой линии регрессии на
:
.
Поэтому получаем
, или
.
^
| № |
Задания |
Варианты ответов |
||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1. | Студент знает 10 из 30 вопросов программы. Найти вероятность того, что он знает 3 вопроса из 3-х ему предложенных. | |||||
| 2. | Один завод производит в два раза больше приборов, чем другой. Вероятность безотказной работы прибора первого завода – 0,8; второго – 0,9. Случайно взятый прибор отказал. Какова вероятность, что он сделан на 2-м заводе? | |||||
| 3. | Дискретная случайная величина X задана рядом распределения |
0,42 | 0,24 | 0,2 | 0,22 | 0,44 |
| 4а. | Найти вероятность того, что при 10 подбрасываниях монеты герб появится ровно 5 раз. | |||||
| 4б. | Устройство состоит из 1000 элементов с вероятностью отказа для каждого за время ^ , равной 0,002. Найти вероятность того, что за время Т откажет хотя бы 1 элемент. | е-2 | 1-е-1 | 1-е | е-1 | 1-е-2 |
| 5. | Непрерывная случайная величина X задана функцией распределения:  . Найти среднее квадратическое отклонение . Найти среднее квадратическое отклонение |
|||||
| 6а. | Непрерывная случайная величина Х распределена равномерно на отрезке [-2;6]. Найти М(Х) и D(X). | 4 и |
2 и |
2 и |
||
| 6б. | Непрерывная случайная величина распределена по показательному закону с плотностью  . Найти М(Х) и D(X). . Найти М(Х) и D(X). |
|||||
| 6в. | Непрерывная случайная величина X распределена по нормальному закону с М(X)=1, D(X)=4. Найти Р |
0,0606 | 0,202 | 0,0305 | 0,0484 | 0,0822 |
| 7а. | Вероятность появления события в каждом из 100 независимых испытаниях постоянна и равна 0,5. Найти вероятность того, что событие появится ровно 55 раз. | 0,0484 | 0,0212 | 0,084 | 0,0242 | 0,0606 |
| 7б. | Вероятность поражения мишени при одном выстреле 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена не более 84 раз. | 0,8413 | 0,1587 | 0,3413 | 0,2672 | 0,6418 |
| 8а. | Найти доверительный интервал для оценки математического ожидания нормального распределения при доверительной вероятности (надежности), равной |
(0,38;1,62) | (-1,16;3,16) | (-0,08;2,08) | (0,34;1,66) | (0,26;1,74) |
| 8б. | Методом моментов по выборке
найти точечную оценку параметра |
0,6 | 2,3 | 1,8 | 1,2 | 0,4 |
| 8в. | Указать наименьшее из заданных значений |
25 | 39 | 30 | 36 | 33 |
| 9. | Найти выборочное уравнение прямой линии регрессии X на Y, если известны выборочные средние А) Г) |
А | Б | В | Г | Д |
| 10. | По данным корреляционной таблицы найти выборочный корреляционный момент (ковариацию) |
0,43 | 0,72 | 0,57 | 0,29 | 0,41 |
^
-
№ задачи 1 2 3 4а 4б 5 6а 6б 6в 7а 7б 8а 8б 8в 9 10 № ответа 4 1 5 4 5 3 3 3 1 1 1 5 5 4 2 3
^
для произвольных A и B;
(1)
для произвольных
;
если A и В несовместны
для произвольных A и B;
если A и В независимы (2)
(3)
(4)
(5)
(6)

Числовые характеристики дискретных случайных величин
(8)
Биномиальное распределение
(9)
Распределение Пуассона
(10)
Непрерывные случайные величины:
(11)
(12)
(13)
(14)
(15)
(16)
(17)
Показательное распределение

;
; (18)
, если
Равномерное распределение

;
(19)
Нормальное распределение

;
;
(20)

(22)
(23)
, где

(25)
(26)
, где
(27)
Доверительный интервал для математического ожидания:
(28)
, или
(29)
(30)
(31)
(32)
^
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.:Высш.шк.,2004.
- Вентцель Е.С. Теория вероятностей. М.:ACADEMIA,2003.
- Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высш.шк., 2004.
- Данко П.Е. Высшая математика в упражнениях и задачах: В 2 ч. / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. М. : ОНИКС 21 век; Мир и Образование. Ч.2.-2003.
- Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. М.: Высшая школа. 1982.
- Математика – 8 для студентов вузов. Учебное пособие / В.А. Кузнецов, Ю.П. Самарин; СамГТУ, Самара, 2001.
- Математика – 9 для студентов вузов. Учебное пособие / В.А. Кузнецов Ю.П. Самарин; СамГТУ, Самара, 2002.
- Севастьянов Б.А., Чистяков В.П. Сборник задач по теории вероятностей. М.: Наука. 1980.
- Чистяков В.П. Курс теории вероятностей. М.: Наука. 1998.
ОГЛАВЛЕНИЕ
- Теория вероятностей. ………………………. ………….……….4
- Математическая статистика………………………………..……13
- Тренировочный тест………………………………………..……16
- Список формул….………………………………………….…….18
- Библиографический список………………….………………….21
Теория вероятностей и математическая статистика.
Составители: ГРЕВЦЕВА Валентина Николаевна,
Лиманова Лариса Владимировна, МУРАТОВА Лидия Александровна
Редактор Н. В. Б е г а н о в а
Технический редактор Г. Н. Ш а н ь к о в а
Подписано в печать 10.05.08.
Формат 60х84. 1/16. Бум. типогр.№2.
Печать офсетная.
Усл. п. л. 1,39. Усл. кр.-отт. 1,39. Уч.-изд. л. 1,25.
Тираж 100 экз. С-22.
Государственное образовательное учреждение высшего профессионального образования «Самарский государственный технический университет»
443100, г. Самара, ул. Молодогвардейская, 244, Главный корпус
| Дата | 02.10.2011 |
| Размер | 277,8 Kb. |
| Тип | Учебно-методическое пособие, Образовательные материалы |