Всего: 211 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: Яндекс: Тренировочная работа ЕГЭ по математике. Вариант 1.
Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1х1.
Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1х1.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 19.03.2019. Вариант 2
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Всего: 211 1–20 | 21–40 | 41–60 | 61–80 …
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
ФОРМУЛА ПИКА
Площадь искомой фигуры можно найти по формуле:
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:
Отметим узлы:
1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма:
Отметим узлы:
M = 18 (обозначены красным)
N = 20 (обозначены синим)
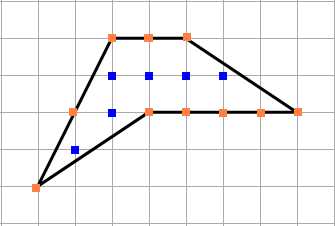
Найдём площадь трапеции:
Отметим узлы:
M = 24 (обозначены красным)
N = 25 (обозначены синим)
Найдём площадь многоугольника:
Отметим узлы:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:
Отметим узлы:
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ«.
Найдём площадь фигуры:
Опишем около неё прямоугольник:
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.
Итого клеток: ( 1 + 2 + 39 = 42).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями – посчитайте площади двумя способами
Ну и напоследок фигуры с “дырками”. Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).
А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика
( S = frac{22}{2} + 3 -1 = 13.)
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
Что получилось?
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).
И тогда
( displaystyle {{S}_{полн. пов. }}=3{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})
Вспомним теперь, что
( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma ).
У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle {{S}_{Delta ASB}}).
Пользуясь основной формулой площади и теоремой Пифагора, находим
( displaystyle {{S}_{Delta ASB}} = frac{1}{2}asqrt{b^2-frac{a^2}{4}})
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle S={{a}^{2}}sqrt{3}).
13
Фев 2014
Категория: Планиметрия
Площади фигур, нарисованных на клетчатой бумаге
2014-02-13
2014-02-13

Клетку считаем размером 1×1 ед.
Попробуйте решить сами предложенные задачи!
Могу сказать следующее – ответ будет выражаться целым числом 
Надо сказать, что кто знаком с такого рода задачками, обычно выдает ответ в считанные секунды… Другие же озадачиваются зачастую тем, а что же делать с площадью круга?.. Куда ж спрятать …
Итак, ищем площадь «ракеты».
Задача 1.
Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными 1.
Решение: + показать
Следующая задача предлагалась А. Лариным в одном из Тренировочных вариантов.
Задача 2.
Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными 1.
Решение: + показать
Ну уж если вы справились с «кувшином», то и с «плачущим сердцем» разберетесь также легко, уверена!
Задача 3.
Найдите суммарную площадь фигур, изображенных на рисунке, считая стороны квадратных клеток равными 1.
Решение: + показать
Ну а вам я, желаю, конечно, чтоб ваше сердце только б пело, радостно пело!
Автор: egeMax |
комментариев 6
1 способ:
Площадь фигур по формулам.
|
S= Рис2
|
2 способ: Площадь фигуры как сумма площадей её
частей
Задача 1. Найдём площадь фигуры АВСD (см.рис.4). Если клетки размером 1х1см.

фигуру АВСD на части (1, 2, 3 и 4).
По
свойству площадей:
S
= S1
+ S2
+ S3
+ S4
=
= (1∙4):2 + (1∙3):2 + 1∙1
+ (1∙2):2 =
= 2
+ 1,5 + 1 + 1 = 5,5 см²
Ответ:
5,5 см²
Рис.4
3 способ: Площадь фигуры как часть
площади прямоугольника
Конечно, есть ещё способы
нахождения фигур на клеточной бумаге. Например, можно просто считать количество
целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки,
но это довольно долго и трудно, особенно если фигура сложной формы.
Задача 2. Найдём площадь фигуры АВСD (см.рис.5). Если клетки размером 1х1см.
Опишем
около фигуры АВСD прямоугольник.
Из
площади прямоугольника (в данном случае это квадрат) вычтем площади полученных
простых фигур (1, 2, 3 и 4):

= Sпр – S1 – S2 – S3 – S4 =
= 4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 –
(3∙1):2 = 16 –
1,5 – 1,5 – 1,5 – 1,5 = 10 см²
Ответ: 10 см²
Рис.5
4 способ :Формула Пика
Есть такие фигуры на клеточной бумаге, для которых эти формулы применить очень
трудно, да и эта работа занимает много времени. А на экзамене по математике в
9-м и в 11-м классе каждая минута дорога! Площади многоугольников, вершины
которых расположены в узлах решетки, можно вычислять очень быстро.Есть
интересная формула, которая связывает их площадь с количеством узлов, лежащих
внутри и на границе данного многоугольника. Эта замечательная и простая формула
называется формулой Пика. Знакомство с формулой Пика особенно актуально
накануне сдачи ЕГЭ и ОГЭ. С помощью этой формулы можно без проблем решать
большой класс задач, предлагаемых на экзаменах,—это задачи на нахождение
площади многоугольника, изображённого на клетчатой бумаге. Маленькая формула
Пика заменит целый комплект формул, необходимых для решения таких задач.
Формула Пика будет работать «одна за всех…»!

Пусть В –
число узлов решетки, расположенных строго внутри многоугольника,
Г
– число узлов решетки, расположенных на его границе, включая вершины,
S
— его площадь. Тогда справедлива формула Пика: S
= В + – 1.
Эта формула не является секретной. Об этой формуле обычно рассказывается
применительно к нахождению площади треугольника. Автор этой формулы австрийский
математик Георг Пик (приложение 1). [8]
Формула Пика
верна для всех рассмотренных выше примеров. Теперь мы знаем, что если
многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для
него верна формула Пика.
Рассмотрим
применение формулы Пика на примерах:
Задача 3.
Найдем
площадь треугольника (см.рис.7. Отметим узлы (пересечение линий) на границе треугольника
и внутри треугольника:
В = 34
(обозначены синим), Г = 15 (обозначены оранжевым).
Рис.7
S= 34 +
15/2 – 1 = 40,5 ед²
Ответ:
40,5
Понятно, что находить
площадь трапеции, параллелограмма, треугольника проще и быстрее по
соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у
которого пять и более углов эта формула работает хорошо. [9]
Задача 4. Найдем площадь пятиугольника

внутри пятиугольника:
В = 43 (обозначены синим),
Г = 14 (обозначены оранжевым).
S=
43 + 14/2 – 1 = 49 ед²
Ответ: 49
Рис.8
Кто
же такой Георг Александер Пик?
Австрийский математик Георг Александер Пик
родился 10 августа 1859 году в Вене. Его отец, будучи руководителем частного
института, предпочел до 11 лет обучать мальчика на дому, а потом отдал его
сразу в четвертый класс гимназии, которую он окончил в 1875 году.
В 16 лет Георг поступил в Венский
университет. В 20 лет получил право преподавать физику и математику.
Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик
получил место экстраординарного профессора математики, затем в 1892г. стал
ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким
университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна
профессором в университет. Пик и физик Антон Лампа были главными инициаторами
этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии
сдружился, в 1911г. возглавил кафедру теоретической
физики в Немецком университете в Праге. Круг математических интересов Пика был
чрезвычайно широк. [8]
Среди всего многообразия достижений
австрийского математика выделяется формула для вычисления площадей
многоугольников с вершинами в узлах клетки открытая им в 1899 году. Она стала
широко известна только в 1969 году, после того, как Гуго Штейнгауз включил ее в
свою знаменитую книгу «Математический калейдоскоп». В Германии эта теорема
включена в школьные учебники.
После выхода в 1927 году
на пенсию Пик вернулся в свой родной город Вену. Однако после аншлюса
(присоединение) 12 марта 1938 года Австрии с Германией ему снова пришлось
перебраться в Прагу. В сентябре 1938 года фашистская Германия вторглась на территорию
Чехословакии. Г.А. Пик был брошен в концентрационный лагерь в Терзинштадте, где
и умер две недели спустя.
Задачи
с практическим содержанием
Поможет
нам формула Пика и для решения геометрических задач с практическим содержанием,
когда объект изображен на клетчатой бумаге в масштабе. [4]
Задача 5.
Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой
1 × 1см в масштабе 1 см – 200 м (рис. 9).

площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S
= В + – 1
В
= 8, Г = 7.
S
= 8 + 7/2 – 1 = 10,5 см²
Т.к.
1 см² — 200² м², то
Sмассива
= 40000 · 10,5 = 420 000 м²
Рис. 9 Ответ:
420

Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 ×
1см в масштабе 1 см – 100 м (рис. 10).
Рис.10
Найдём
S
площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S
= В + – 1. В = 7, Г = 4.
S
= 7 + 4/2 – 1 = 8 см², т.к. 1 см² — 100² м², то
Sполя
= 10000 · 8 = 80 000
м²
Ответ:
80 000 м²
Из
всех задач по геометрии у нас вызывают интерес задачи на решётках. И это не
случайно. Такие задачи в учебниках по геометрии не встречаются, а на экзаменах
и в олимпиадных заданиях они есть. Вот такие задачки надо научиться решать.
Существует достаточное количество способов нахождения площадей фигур на
клетчатой бумаге.
Мы
рассмотрели основные из них. Задачи, поставленные в самом начале нашей работой,
выполнили. Все предложенные способы, нахождения площадей плоских фигур, на
клетчатой бумаге нам очень интересны, но самым результативным оказался способ
решения по формуле Пика.
Формула
Пика — это настоящий клад для тех ребят, которые не могут выучить все формулы
для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как
разбить фигуру на части или выполнить дополнительное построение. С другой
стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге
умеет находить с помощью вышеперечисленных приёмов, а формула Пика нужна, чтобы
решить задачу ещё и этим способом , тем самым проверить правильность своего
предыдущего решения, сверив полученные ответы.
Анализ
решений показал, что применение формулы Пика даёт возможность решать задачи на
нахождение площади многоугольника, изображённого на клетчатой бумаге очень
быстро и легко. Это позволяет экономить время на экзамене Эта работа была нам
интересна, и мы надеемся, что результаты наших исследований, помогут учащимся
при сдаче экзамена по математике.
Приложение 1

16 апреля 1880 года под руководством Лео Кёнигсберга Пик защитил докторскую
диссертацию «О классе абелевых интегралов». В 1881 году он получил место
ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо
было пройти хабилитацию. Для этого он написал работу «Об
интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882
году, вскоре после разделения Пражского университета на чешский (Карлов
университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком
университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская
деятельность в
Немецком университете в Праге в 1888 г. Пик получил место экстраординарного
профессора математики, затем в 1892г. стал ординарным профессором. В
1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги
для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и
физик Антон Лампа были главными инициаторами этого
назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии
сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком
университете в Праге. Круг математических интересов Пика был чрезвычайно широк.
В частности, им написаны работы в области функционального анализа и дифференциальный геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений
и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика,
интерполяция Пика — Неванлинны, лемма Шварца-Пика. Широкую известность получила
открытая им в 1899 году теорема Пика для расчёта площади
многоугольника. В Германии эта теорема включена в школьные учебники. [8]
Приложение 2
Исследование
площадей многоугольников, изображенных на клетчатой бумаге.
Найдите
площадь окрашенной фигуры, изображенной на чертеже. Размер каждой клетки равен
1см * 1см. Ответ дайте в квадратных сантиметрах.
Задача 1.

Г=10, В=27.
Решение: S=27+10:2-1=31(кв.
ед.)
Ответ:
31 кв.ед.
Задача 2.
Дано:
Г=3, В=0.
Решение: S=0+3:2-1=1 (кв. ед)
Ответ: 1 кв. ед.
Задача 3.

Г=4, В=0.
Решение: S=0+4:2-1=1 (кв.ед.)
Ответ: 1 кв.ед.
Задача 4.

Дано:
Г=6, В=3.
Решение: S=3+6:2-1=5 (кв.ед.)
Ответ: 5 кв.ед.
Задача 5.
Дано:

Решение: S=16+6:2-1=17(кв.ед.)
Ответ: 17 кв.ед.
Задача 6: Найти площадь «ракеты».
Дано:
Г=20, В=25.
Решение: S=25+20:2-1=34 (кв.ед.)
Ответ: 34 кв.ед.
Задача 7: Найти
площадь кувшина.
Дано:
Г=6, В=14.
Решение: S=14+6:2-1=16 (кв.ед.)
Ответ: 16 кв.ед.
Задача 8: Найти площадь «плачущего сердца».

Г=10, В=4.
Решение: S=4+10:2-1=8 (кв.ед.)
Ответ: 8 кв.ед.
Задача 9.
Дано:
Г-9, В=11.
Решение: S= 11+9:2-1=14,5 (кв.ед.)
Ответ: 14,5
кв.ед.
Задача 10.
Дано:
Г=26, В=32.
Решение: S=32+26:2-1=44 (кв.ед.)
Ответ: 44 кв.ед.
Задача 11.
Дано:
Г=16, В=27.
Решение: S=27+16:2-1=34 (кв.ед.)
Ответ: 34 кв.ед.
Приложение 3 Задача
1.
Найдём площадь фигуры АВСD (см.рис.6). Если клетки
размером 1х1см.

Из площади прямоугольника вычтем площади полученных простых
фигур (1, 2, 3 и 4):
S
= Sпр – S1 – S2 – S3 – S4 =
=
3∙6 – (4∙1):2 – (2∙2):2 – (4∙1):2 – (2∙2):2 =
= 18 – 2 – 2 – 2 – 2 =
10 см²
Рис.6
Ответ:
10 см²
Задача 2. Найдём
площадь фигуры АВСD (см.рис.1). Если клетки размером 1х1см.

на части (1 и 2).
По
свойству площадей:
S
= S1
+ S2
=
=
(2∙3):2 + 3∙2 =
= 3
+ 6 = 9 см²
Ответ:
9 см²
Рис.1
Задача 3. Найдём площадь фигуры АВСD (см.рис.5). Если клетки размером 1х1см.

Из площади прямоугольника (в
данном случае это квадрат) вычтем площади полученных простых фигур (1, 2 и 3):
S
= Sпр – S1 – S2 – S3 =
=
4∙4 – (4∙4):2 – (2∙1):2 – (2∙1):2 = 16 – 8 – 1 – 1 =
=
6 см²
Рис.5
Ответ: 6 см²
Приложение 4
1.
Найдите
площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
2.
Найдите
площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
3.
Найдите
площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
4.
Найдите
площадь четырехугольника ABCD, считая стороны квадратных клеток равными
1.
5. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
6. Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными 1.
7. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
8. 
9.
Найдите площадь
параллелограмма ABCD, считая стороны квадратных клеток равными
1.
10.
Найдите площадь
треугольника ABC, считая стороны квадратных клеток равными 1.
11.
Найдите площадь
трапеции ABCD, считая стороны квадратных клеток равными 1.
12.
Найдите площадь
четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Как найти площадь геометрической фигуры по клеточкам?
Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь.
Площадь фигуры по клеточкам
Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.
Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.
Узел — это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.
Площадь фигуры по клеточкам находится по формуле:
N — количество узлов, которые находятся внутри фигуры.
M — количество узлов, которые находятся на границах (на вершинах и сторонах).
Примеры нахождения площади по клеточкам
1) Найдём площадь треугольника. Будем считать, что одна клетка — это 1 см.
Отметим внутренние узлы и узлы, которые находятся на границах.
N = 7 (внутренние).
M = 8 (узлы на границах).
Площадь треугольника S = 7 + 8/2 — 1 = 10 см².
2) Найдём площадь трапеции по клеточкам, одна клетка — это 1 см. Отметим все узлы и подсчитаем их количество.
N = 11 (внутренние).
M = 12 (узлы на границах).
Площадь трапеции S = 11 + 12/2 — 1 = 16 см².
3) Найдём площадь произвольного многоугольника. Одна клетка — это 1 см.
Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.
N = 6 (внутренние узлы).
M = 8 (узлы на границах).
Площадь многоугольника S = 6 + 10/2 — 1 = 10 см².
www.bolshoyvopros.ru
Вычисление площадей фигур, изображенных на клетчатой бумаге
При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.
Возможны следующие случаи.
1. Фигура представляет собой треугольник, параллелограмм, трапецию:
1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;
2) подставить найденные величины в формулу площади.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.
Рис. 1. Треугольник
Решение. Подсчитываем клеточки и находим: . По формуле получаем: .
2 Фигура представляет собой многоугольник
Если фигура представляет собой многоугольник то возможно использовать следующие методы.
Метод разбиения:
1) разбить многоугольник на треугольники, прямоугольники;
2) вычислить площади полученных фигур;
3) найти сумму всех площадей полученных фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.
Рис. 2. Многоугольник
Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.
Рис. 3. Многоугольник. Метод разбиения
Площади треугольников равны: , , , площадь прямоугольника — . Складывая площади всех фигур получим:
Метод дополнительного построения
1) достроить фигуру до прямоугольника
2) найти площади полученных дополнительных фигур и площадь самого прямоугольника
3) из площади прямоугольника вычесть площади всех «лишних» фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.
Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.
Рис. 4. Многоугольник. Метод дополнения
Площадь большого прямоугольника равна , прямоугольника, расположенного внутри — , площади «лишних» треугольников — , , тогда площадь искомой фигуры .
При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.
Формула Пика
Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.
Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Например, для многоугольника, изображенного на рисунке 5.
Рис. 5. Узлы в формуле Пика
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.
Рис. 6. Многоугольник. Формула Пика
Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:
Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.
1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.
Рис. 7. Условие задачи 1
2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).
Рис. 8. Условие задачи 2
3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.
Рис. 9. Условие задачи 3
4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.
Рис. 10. Условие задачи 4
5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии. Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.
Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.
Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Литература:
- Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
- Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
- Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.
yun.moluch.ru
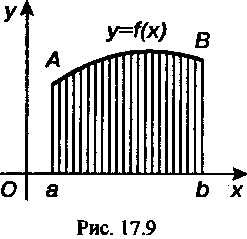
Площадь криволинейной трапеции, ограниченной сверху графиком функции, слева и справа — прямымиСоответственно,
Снизу — осью(рис. 17.9), вычисляется по формуле
(17.26)
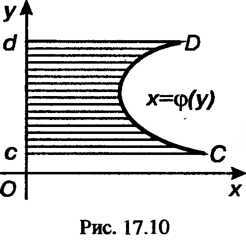
Площадь криволинейно трапеции(рис. 17.10), ограниченной справа
Графиком функции, сверху и снизу — соответственно прямыми
, слева — осью, определяется формулой
(17.27)
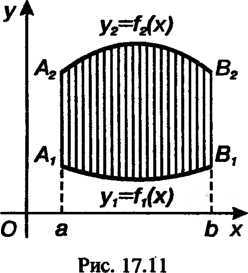
Площадь криволинейной фигуры, ограниченной сверху графиком
Функции, снизу — графиком функции, слева и справа —
Прямыми(рис. 17.11), вычисляется по формуле
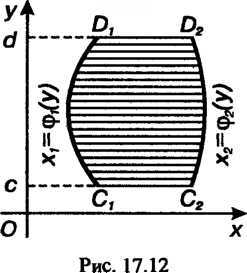
Площадь фигурыОграниченной слева и справа соответственно гра
Фиками функций, снизу и сверху — прямыми
(рис. 17.12), определяется формулой
(17.29)
Если линия, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениямиГде
То
(17.30)
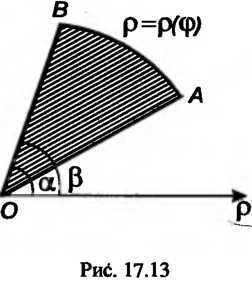
Площадь сектора(рис. 17.13), ограниченного дугой линии, заданной уравнением в полярных координатах, и двумя полярными радиусами
И, соответствующими значениям, определяется формулой
Пример 17.13. Найти площадь фигуры, ограниченной линиейИ осью
Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (рис. 17.14). Решая систему уравнений
Получаем
Следовательно,
По формуле (17.26) находим
Пример 17.14. Найти площадь фигуры, ограниченной линиейИ осью
Данная фигура представляет собой криволинейную трапецию, прилежащую к оси(см. рис. 17.15). Найдем точки пересечения линии с осью, для чего решим систему уравнений. Из этой системы получаем
; это означает, что в формуле (17.27), которой здесь необходимо пользоваться, нужно положить
Следовательно,
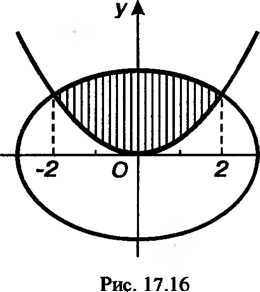
Пр имер 17.5, Вычислить площадь фигуры, ограниченной линиями
Данная фигура ограничена сверху дугой эллипсаСнизу — дугой пара
Болы(рис. 17.16).
Площадь вычислим по формуле (17.28).
Решая систему уравнений находим- абсциссы точек пе
Ресечения заданных линий; следовательно,
’ Каждое из уравнений разрешаем
Относительно
(В формуле (17.28) через обозначена функция, график которой ограничивает фигуру сверху.)
Таким образом, искомая площадь
Для вычисления первого интеграла применим подстановку, тогда
Поскольку
Пример 17.16. Вычислить площадь области, ограниченной эллипсом
В силу симметрии эллипса относительно координатных осей достаточно вычислить площадь части области, лежащей в первой четверти, и результат умножить на 4. Заметим, что в этом случаеМеняется от 0 доПоэтомуБудет меняться отДо 0. По формуле (17.30) находим
Замечание. В частном случае, когда, получаем-
Площадь круга радиуса
Пример 17.17. Вычислить площадь области, ограниченной лемнискатой
Принимая во внимание симметрию линии относительно ее оси (см. п. 2.10), по формуле (17.31) получаем
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Расчет площади комнаты: способы, формулы, примеры
Процедура проведения ремонта в помещении требует обязательного расчета площади стен, потолка и пола. Так как во время покупки строительных материалов эти значения помогают не ошибиться в их количестве. О способах и примерах расчета площади помещения поговорим далее.
Оглавление:
- Причины для проведения расчета площади комнаты
- Площадь комнаты: проведение расчета площади пола
- Определение площади прямоугольной комнаты и потолка
- Какова площадь комнаты в которой имеются ниши и выступы
- Как определить площадь комнаты с неровными стенами
- Как высчитать площадь комнаты, в которой имеется многоуровневый потолок
- Определение общей площади комнаты
- Определение минимальной площади комнаты
- Оптимальная площадь комнаты
Причины для проведения расчета площади комнаты
Существует большое количество причин, по которым определяется площадь стен, потолка или пола в помещении. В некоторых случаях, необходимы данные об общей площади комнаты. Предлагаем ознакомиться с наиболее часто встречающимися причинами определения площади комнаты или отдельных ее частей:
- если планируются работы по установке подвесных потолков, то необходимо определить общую площадь потолка, для определения количества материалов, используемых при проведении работ;
- при установке натяжных потолков, также нужно вычислить общую площадь потолка, чтобы предварительно спланировать материальные средства;
- для покраски или отделки потолка также следует знать его площадь, практически все лакокрасочные изделия и грунтовки имеют в технических характеристиках показатель расхода на один квадратный метр;
- отделка стен гипсокартоном требует вычисления общей площади стен, для покупки нужного количества материала;
- при найме строителей, например, для отделки пола плиткой, каждый метр квадратный имеет определенную стоимость, которая считается в конце выполнения работ;
- при продаже дома или при его оформлении, такой параметр как жилая площадь, площадь кухни и других комнат также является особо важным.
Площадь комнаты: проведение расчета площади пола
Для определения площади пола существуют разные причины: ремонт и покупка материалов для его отделки, проведение теплоизоляции, вычисление полезной площади и т.д.
Проще всего определить площадь помещения квадратной или прямоугольной формы. В таком случае, понадобится значение длины и ширины пола, которые умножаются друг на друга. Данный вариант не требует освобождения помещения от шкафов и прочей мебели. Достаточно просто измерить расстояние. Однако, при наличии камина в комнате, следует его площадь вычесть из общего полученного результата.
В принципе, все предметы, которые находятся на полу постоянно и не имеют возможности в перемещении, например, встраиваемые шкафы, вычисляются из общей площади пола.
Более сложным представляется расчет площади пола в помещении, которое имеет неправильную форму. Стандартные комнаты, конечно имеют форму прямоугольника или квадрата, хотя существуют помещения с разного рода нишами, углублениями, арками, выступами и т.д. Такой вариант подсчета площади пола более сложный, так как требует вычисления площади фигур, входящих в состав помещения по отдельности.
Для вычисления общей площади следует разбить пространство на несколько правильных фигур, в виде прямоугольников, трапеций, квадратов и т.д. Например, если помещение имеет г-образную форму, то достаточно его разделить на два прямоугольника, вычислить площадь каждого из них и суммировать полученные результаты.
Если помещение имеет г-образную форму, однако она проходит не под прямым углом, то кроме двух прямоугольников в нем еще присутствует треугольное пространство, площадь которого также вычисляется. Для вычисления площади треугольника достаточно один катет умножить на другой.
При наличии полукруглых фрагментов в виде цилиндрических или сегментных частиц, расчеты усложняются. Для расчета площади пола в такой комнате требуется также разделить пространство на несколько частей, площадь которых вычисляется по отдельности.
Бывают варианты помещений, которые имеют разные уровни пола, то есть возвышенности или уклоны. Таким образом, помещение разделяется на несколько зон. Например, в кухне выделяется столовая и рабочая части. То же самой и бывает с потолком, например, многоуровневым. Для вычисления площади пола с уступами или возвышенностями, следует опять же разделить пространство на части в виде прямоугольников или квадратов, а те самые выступы, измерить линейкой и вычислить их площадь. Таким способом получится провести расчет общей площади помещения.
Учтите, что в таком случае предпочтительно использовать рулетку, которая устанавливается вблизи основания. Кроме того, потребуется карандаш и тетрадь, для записывания всех значений. В итоге, покупка краски и определение количества отделочного материала для пола выполнится быстро.
Не выполняйте замеры по стене, так как она может быть кривой и приведет к возникновению неточности в процессе определения площади пола. Особой сложностью отличаются работы по определения площади пола, на котором имеются уступы в виде полукруга или волны. Данная ситуация предполагает измерение каждой из дуг, нахождение радиусов и раздробление площади на несколько геометрических фигур. С помощью определения площади для каждой из них вычисляется общая формула асимметричного сегмента.
Определение площади прямоугольной комнаты и потолка
Прямоугольное помещение является наиболее типичным и часто встречающимся вариантом. Для расчета площади достаточно длину помещения умножить на его ширину. Например, если длина комнаты составляет 3,40 м, а ее ширина 5,20 м, то для определения площади потолка достаточно 3,40х5,20, в итоге получится 17, 68 метров квадратных площади. Для расчета периметра потолка используется другая формула, которая подразумевает сумму удвоенных его длины и ширины. То есть, периметр потолка ровняется 2х3,40+2х5,20=17,2 м.
Поэтому, в процессе закупки профилей, потребуется 17,2 метра материала. Однако, рекомендуется, даже при проведении точнейших расчетов, покупать материал с запасом в 10-15 процентов, для компенсации различного рода механических повреждений и стыков.
Какова площадь комнаты в которой имеются ниши и выступы
Для определения площади такого помещения следует изрядно потрудиться и выполнить такие действия:
1. Сделайте проект комнаты с учетом всех конструктивных особенностей.
2. Измерьте и обозначьте значения высоты и длины по всем ровным стенам.
3. С помощью линейки и угольника разделите пространство на несколько зон, в виде правильных фигур.
4. Каждую из сторон фигуры следует измерить и обозначить в проекте.
5. Согласно формуле для расчета площади фигуры определите значения каждой из них и суммируйте полученные результаты.
Как определить площадь комнаты с неровными стенами
При наличии помещения, в котором стены имеют вид многогранников или непрямых непропорциональных фигур, расчеты проводить гораздо сложнее. Измерить периметр в таком помещении достаточно просто. Следует использовать рулетку и пройти с ней по всей комнате, измеряя каждый из участков по отдельности.
Площадь комнаты определяется путем проведения зарисовок и проектирования помещения. После того как эскиз готов, разбиваем пространство таким образом, чтобы получить максимальное количество пропорциональных фигур в виде квадрата, треугольника или прямоугольника.
Для того, чтобы определить площадь сегмента, который имеет форму прямоугольника с одинаковыми ребрами, достаточно измерить величину катетов, которые умножаются между собой и разделяются пополам. То есть, для определения площади треугольного сегмента с катетами 0,5 и 0,9 м следует провести такие расчеты:
0,5х0,9/2= 0,225 метра квадратных.
Как высчитать площадь комнаты, в которой имеется многоуровневый потолок
Потолок, на котором имеются уступы рассчитать сложнее, однако вполне реально. Существуют многоярусные потолки, которые имеют форму прямых линий их расчет проводить легко, но бывают такие конструкции, которые требуют особой внимательности, так как они состоят из дуго- или волнообразных фрагментов для расчета которых требуется приложить особые усилия.
Рассчитывать каждый из участков слишком долго и затратно, тем более, что в итоге получится не всегда правильный результат. Ведь, дуги, сконструированные на потолке могут быть произвольными.
Проще всего определить площадь комнаты по общей площади пола. Для этого, следует выполнить ряд действий:
1. Измерьте все прямые участки стен.
Предпочтительно проводить замеры поближе к потолку, так как длина стены сверху и снизу помещения может отличаться.
2. Определите площадь пола по ранее указанным способам.
3. На каждом из вертикальных участков измерьте их высоту и длину и умножьте эти показатели.
4. Прибавьте их к общему значению площади пола.
Определение общей площади комнаты
Для того, чтобы ответить на вопрос как узнать площадь комнаты в квадратных метрах, предлагаем ознакомиться с инструкцией, которая поможет выполнить эту задачу:
1. Позаботьтесь об очищении пространства возле стен.
Стены комнаты должны быть в свободном доступе. Таким образом, повысится правильность и точность измерения. При возможности лучше освободить помещение целиком, так как в проведении определенных расчетов потребуется измерять и центральные участки.
2. Определите в помещении участки, имеющие правильную форму.
Если помещение имеет вид прямоугольника, то в делении оно не нуждается. В противном случае, комната разделяется на фигуры в виде квадратов, полукругов, трапеций, треугольников или прямоугольников.
3. Сделайте эскиз помещения, так работать станет легче.
Измерение площади комнаты нужно выполнять по эскизу, на котором отмечаются все замеры. Совет: При отсутствии бумаги и при необходимости проведения срочного замера, используйте клейкую ленту, которая крепится на каждую стену.
4. Длина и ширина комнаты, площадь.
Каждая стена должна быть измерена по ширине и длине желательно дважды. Для того, чтобы не измерять всю стену целиком, ее нужно разбить на несколько фрагментов, а в итоге, полученные результаты суммировать.
Для того, чтобы убедиться в правильности проведения расчета, при наличии свободного времени, замеры проводятся дважды.
5. Определите площадь каждого из участков:
- площадь прямоугольника ровняется умножению его длины на ширину;
- площадь квадрата, это одна из его сторон в квадрате;
- площадь треугольника — высота и сторона, умножаются между собой и полученное значение разделяется на два;
- площадь круга число Пи умножается на радиус в квадрате.
6. Площади ранее определенных участков складываются между собой.
Определение минимальной площади комнаты
1. Участки в виде прямоугольника.
С помощью рулетки измеряется длина и ширина участка, они умножаются между собой. Данные чаще всего округляют до сантиметров.
2. Треугольник.
Площадь данного участка определяется путем умножения одной стороны треугольника на его высоту, то есть линию, опущенную с вершины треугольника, которая разделяет его на две равных части. Полученное значение удваивается.
3. Окружность или полуокружность.
Определение радиуса. Данное значение переводится в квадрат, умножается на число Пи. При наличии полукруга, значение разделяется на два.
Кроме того, в интернете существуют специальные онлайн калькуляторы, позволяющие провести все расчеты быстро и качественно. Для работы с ними достаточно выбрать форму участка комнаты, измерить его с помощью рулетки и ввести данные. Программа сама проведет все необходимые расчеты и определит площадь.
Оптимальная площадь комнаты
Каждая комната имеет свой размер, и во время планировки дома, этот фактор учитывается в соответствии с их назначением. Минимальное значение площади обычной жилой комнаты составляет восемь метров квадратных.
Площадь общей комнаты или гостиной должна составлять от 13 до 23 метров квадратных. Спальня должна располагаться в углу дома, и быть не проходным помещением.
Минимальная высота жилого помещения — 240 см. Не рекомендуется обустраивать комнаты с высотой более 300 см, так как они совсем непрактичны, для их обогрева в зимнее время потребуется большое количество материальных вложений.
Каждая комната должна отличаться наличием естественного освещения. Минимум 30 % всех стен должны приходиться на окна. Учтите, что предпочтительнее устанавливать окна на южной стороне, так как зимой, на северной стороне, они будут провоцировать большие теплопотери.
Если жилая площадь дома или квартиры составляет от 15 до 55 метров квадратных, то минимальная площадь кухни должны быть 6 метров квадратных. При планировке кухни в зданиях с жилой площадью более 55 квадратных метров, кухня должна занимать минимум пятую часть всего дома.
Если кухня занимает более 10 квадратных метров, возможен вариант ее использования в качестве столовой или комнаты для приема гостей. Минимальная ширина прихожей составляет 140 см, в ней также должно присутствовать естественное освещение.
Для детской комнаты достаточно площади в 10-15 метров квадратных. Самыми маленькими должны быть ванная и туалет. Их площадь ровняется 4-8 квадратным метрам.
strport.ru
Площадь сложных фигур — Памятки по математике — Памятки ученикам
Площадь всей фигуры равна сумме площадей её частей.
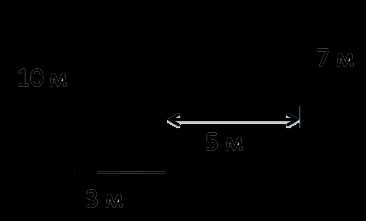
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
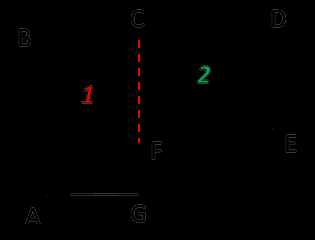
SEFKL = 10 • 3 = 30 м2
SCDEF = FC • CD
SCDEF = 7 • 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD.
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB • BC
SABCD = 5 • 4 = 20 см2
S ABC = SABCD : 2
S ABC = 20 : 2 = 10 см2
S ABC = S ACD = 10 см2.
www.mamapapa-arh.ru
Как найти площадь фигуры по клеточкам 4 класс впр по математике
Задание 5.1 № 868
На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.
Найди площадь этой фигуры. Ответ дай в кв. см.
В ответе писать единицы измерения не нужно.
Задание 5.2 № 869
На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.
Нарисуй по клеточкам прямоугольник, площадь которого равна площади изображённой фигуры.
Должно быть зачтено любое решение, удовлетворяющее условию.
Источник: ВПР по математике 4 класс 2018 год. Вариант 1., ВПР по математике 4 класс 2019 год. Вариант 17.
Перенесем выделенный коричневым треугольник снизу фигуры наверх в обведенное пунктиром место. При этом площадь фигуры не изменится, а фигура превратится в прямоугольник длиной 5 и шириной 4. Площадь этого прямоугольника равна
Источник: ВПР по математике 4 класс 2018 год. Вариант 1., ВПР по математике 4 класс 2019 год. Вариант 17.
Задание 5.1 № 868
Задание 5.2 № 869
Источник ВПР по математике 4 класс 2018 год.
Math4-vpr. sdamgia. ru
24.07.2018 3:00:29
2018-07-24 03:00:29
Источники:
Https://math4-vpr. sdamgia. ru/problem? id=868
Решу ВПР по математике 4 класс — начальные классы, презентации » /> » /> .keyword { color: red; } Как найти площадь фигуры по клеточкам 4 класс впр по математике
Решу ВПР по математике 4 класс
Решу ВПР по математике 4 класс
На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.
Найди площадь этой фигуры.
Ответ дай в квадратных сантиметрах
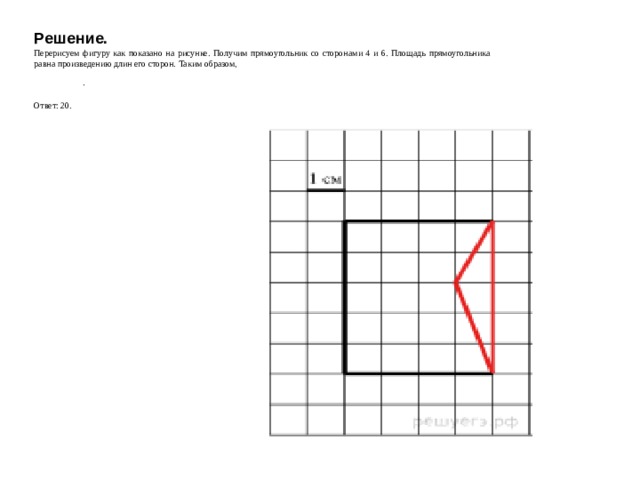
Задание 5.2 № 2689
Нарисуй по клеточкам прямоугольник, площадь которого равна площади изображённой фигуры.
Перерисуем фигуру как показано на рисунке. Получим прямоугольник со сторонами 4 и 6. Площадь прямоугольника равна произведению длин его сторон. Таким образом,
Задание 5.1 № 1274
На клетчатом поле со стороной квадратной клетки 1 см изображена фигура.
Задание 5.2 № 1275
На клетчатом поле со стороной квадратной клетки 1 см изображена фигура.
Изобрази на рисунке выше по клеткам квадрат с периметром 16 см так, чтобы он целиком поместился в данной фигуре (не вылезал за границы).
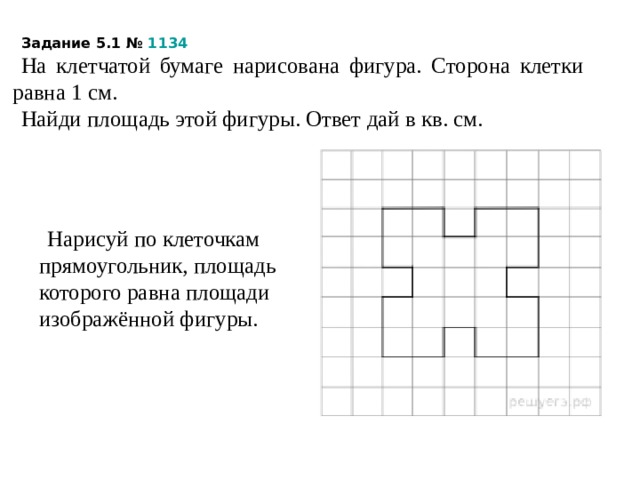
Задание 5.1 № 1134
На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.
Найди площадь этой фигуры. Ответ дай в кв. см.
Нарисуй по клеточкам прямоугольник, площадь которого равна площади изображённой фигуры.
Площадь фигуры равна количеству клеточек, которые в нее входят. Таких клеточек 21.
Следовательно, площадь фигуры равна 21 см 2 .
Задание 5.1 № 1064
На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.
Найди периметр этой фигуры. Ответ дай в сантиметрах.
Задание 5.2 № 1065
На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.
Нарисуй по клеточкам квадрат, периметр которого равен периметру этой фигуры.
Задание 5.1 № 994
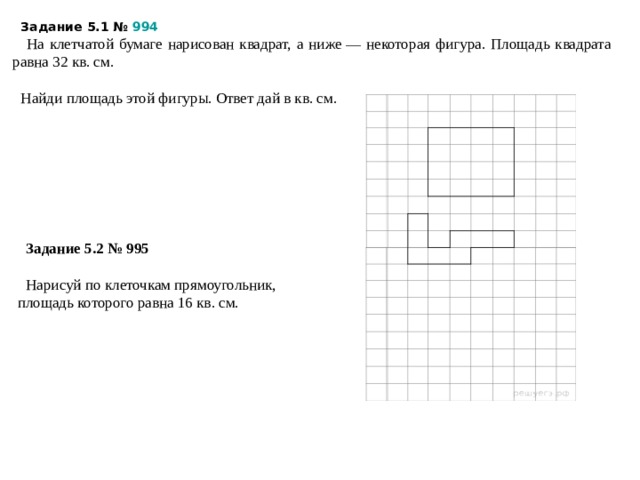
На клетчатой бумаге нарисован квадрат, а ниже — некоторая фигура. Площадь квадрата равна 32 кв. см.
Найди площадь этой фигуры. Ответ дай в кв. см.
Задание 5.2 № 995
Нарисуй по клеточкам прямоугольник, площадь которого равна 16 кв. см.
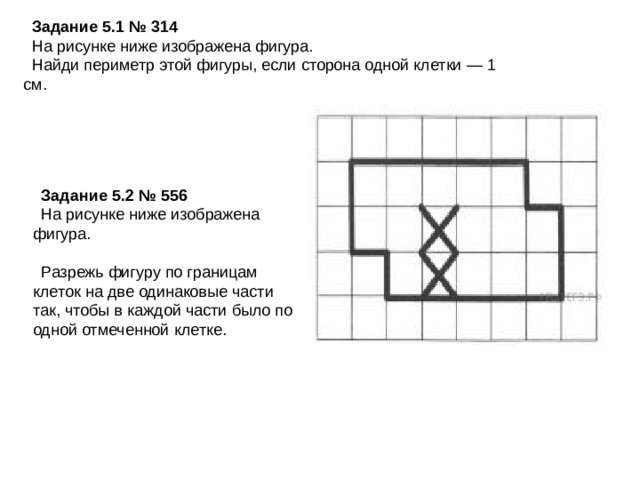
Задание 5.1 № 314
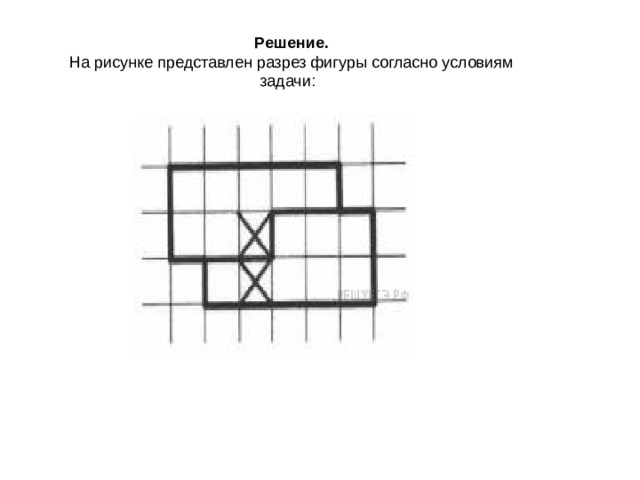
Задание 5.2 № 556
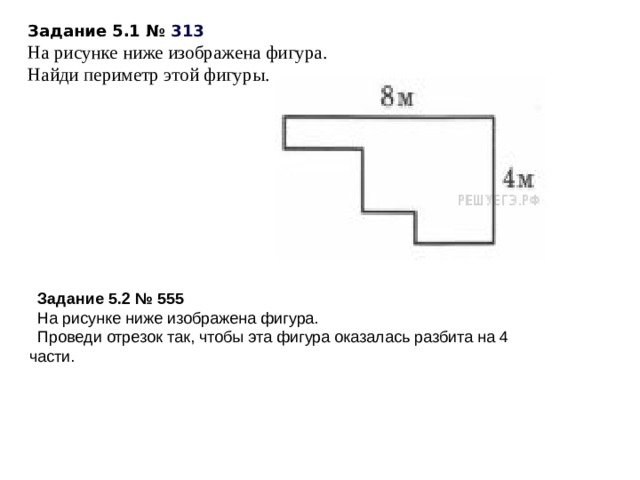
Задание 5.1 № 313
На рисунке ниже изображена фигура.
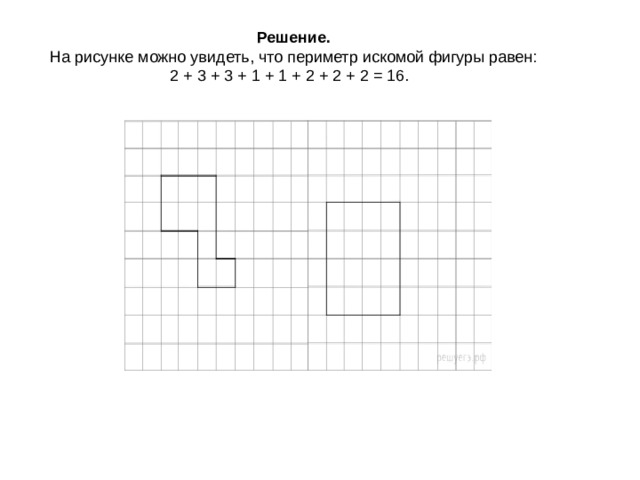
Найди периметр этой фигуры.
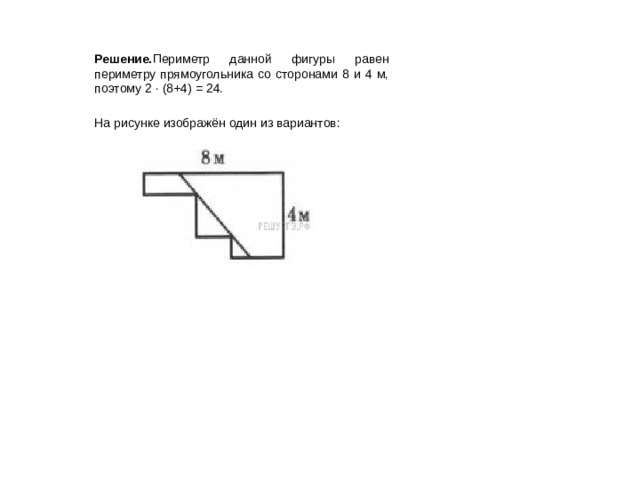
Задание 5.2 № 555
Решение. Периметр данной фигуры равен периметру прямоугольника со сторонами 8 и 4 м, поэтому 2 · (8+4) = 24.
Нарисуй по клеточкам квадрат, периметр которого равен периметру этой фигуры.
Kopilkaurokov. ru
07.02.2020 0:54:54
2020-02-07 00:54:54
Источники:
Https://kopilkaurokov. ru/nachalniyeKlassi/presentacii/reshu_vpr_po_matematike_4_klass
ВПР по математике 4 класс. » /> » /> .keyword { color: red; } Как найти площадь фигуры по клеточкам 4 класс впр по математике
ВПР по математике 4 класс
ВПР по математике 4 класс.
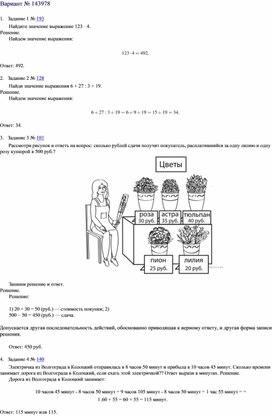
Рассмотри рисунок и ответь на вопрос: сколько рублей сдачи получит покупатель, расплатившийся за одну лилию и одну розу купюрой в 500 руб.?
Запиши решение и ответ.
1) 20 + 30 = 50 (руб.) — стоимость покупки; 2) 500 − 50 = 450 (руб.) — сдача.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу, и другая форма записи решения.
4. Задание 4 № 140
Электричка из Волгограда в Колоцкий отправилась в 8 часов 50 минут и прибыла в 10 часов 45 минут. Сколько времени занимает дорога из Волгограда в Колоцкий, если ехать этой электричкой?? Ответ вырази в минутах. Решение.
Дорога из Волгограда в Колоцкий занимает:
10 часов 45 минут — 8 часов 50 минут = 9 часов 105 минут — 8 часов 50 минут = 1 час 55 минут = = 1 60 + 55 = 60 + 55 = 115 минут.
Ответ: 115 минут или 115.
5. Задание 5.1 № 938
На клетчатой бумаге нарисован квадрат, а ниже — некоторая фигура. Площадь квадрата равна 32 кв. см.
Найди площадь этой фигуры. Ответ дай в кв. см. В ответе писать единицы измерения не нужно.
Заметим, что площадь одной клетки равняется 32 : 4 : 4 = 2 кв. см. Площадь фигуры равняется количеству входящих в неё клеток, умноженному на 2. Таким образом, площадь фигуры равняется 8 · 2 = 16.
6. Задание 5.2 № 995
На клетчатой бумаге нарисован квадрат, а ниже — некоторая фигура. Площадь квадрата равна 32 кв. см.
Нарисуй по клеточкам прямоугольник, площадь которого равна 16 кв. см.
Заметим, что площадь одной клетки равняется 32 : 4 : 4 = 2 кв. см.
Должно быть зачтено любое решение, удовлетворяющее условию.
7. Задание 6.1 № 333
В таблице приведены данные о численности населения трёх городов России в разные годы (в тыс. человек). Используя эти данные, ответь на вопросы. В ответ впишите число — год.
В каком году численность населения Казани была наибольшей?
Из таблицы видно, что численность населения Казани была наибольшей в 2010 году.
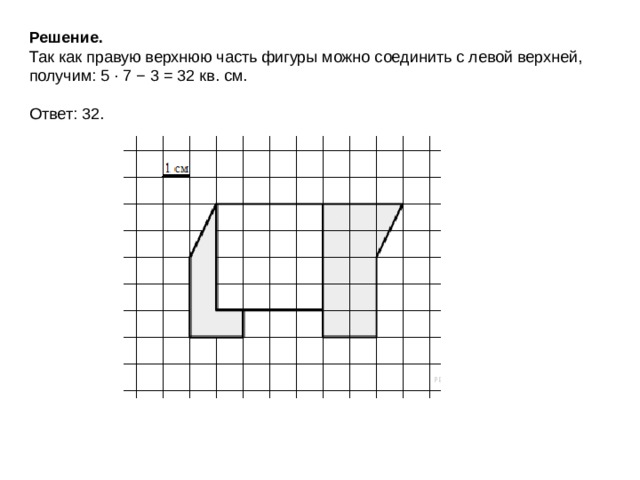
8. Задание 6.2 № 606
В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в двух городах России (по данным на конец 2013 года).
Мука пшеничная (1 кг)
Гречневая крупа (1 кг)
Сливочное масло (1 кг)
Филе куриное (1 кг)
В каком из городов и на сколько рублей окажется дороже следующий набор продуктов: 4 кг муки, 1 кг сливочного масла, 2 кг куриного филе?
Посчитаем соответствующий набор в каждом из городов:
Таким образом, в городе Краснодар дороже на 1061 — 1060 = 1 рубль.
Ответ: Краснодар 1.
9. Задание 7 № 99
Найди значение выражения (455 + 235) · 14 − 45.
Найдем значение выражения:
10. Задание 8 № 38
3 кг варенья разложили в банки по 400 г и в банки по 200 г. Банок по 400 г оказалось 4. Сколько потребовалось банок по 200 г?
Запиши решение и ответ.
В четырёх банках по 400 г содержится: 4 · 400 = 1600 г варенья.
Всего варенья 3 кг или 3000 г.
Значит, в банках по 200 г содержится: 3000 − 1600 = 1400 г варенья. Для хранения такого количества требуется: 1400 : 200 = 7 банок.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу.
11. Задание 9.1 № 393
Рассмотри рисунок и установи закономерность.
Сколько признаков меняется при переходе от одной фигуры к другой?
В каждой фигуре есть внутренняя часть (крестик, треугольник и круг), есть боковая часть (одна линия, две линии, три линии) и поворот самой фигуры. Следовательно, 3 признака.
12. Задание 9.2 № 1057
Вера, Игорь и Миша ловили окуней. Игорь поймал больше окуней, чем Вера. Вместе Игорь и Вера поймали столько же окуней, сколько поймал Миша. Меньше двух окуней не поймал никто из них, а все вместе они поймали 12 окуней.
Сколько окуней поймал Игорь?
Заметим, что Миша поймал столько же окуней, сколько Игорь и Вера вместе. Значит, Миша поймал половину окуней, а вторую половину поймали Игорь и Вера. Следовательно, Миша поймал 6 окуней. Тогда, поскольку никто из них не поймал меньше 2 окуней, и Игорь поймал окуней больше, чем Вера, Игорь поймал 4 окуня, а Вера 2 окуня.
13. Задание 10 № 1178
Модель цепи питания для степи можно представить в виде схемы. Например, на схеме ниже представлена схема питания из трёх звеньев.
Прочитай текст и изобрази пищевую цепь, включающее всех перечисленных в тексте животных и растений. Впиши в прямоугольники на схеме названия животных и растений.
Цепь питания — ряд взаимоотношений между группами организмов (растений, животных, грибов и микроорганизмов), при котором происходит перенос вещества и энергии путем поедания одних особей другими. Цепь питания в степи может быть довольно разнообразна. Она, как правило, начинается со степных растений и злаков. Ими питаются мыши и кузнечики.
Далее идут различные хищники, например — змеи, которые питаются мышами и кузнечиками. Кузнечиками также питается дрофа. В пищевой цепи могут принимать участие как один, так и несколько хищников, поедающих друг друга. Например, в степи коршуны питаются змеями, а дрофами питаются волки.
Схема для заполнения
Заполним схему, использую информацию из текста.
14. Задание 11 № 48
Из трёх кубиков сложили постройку. Если посмотреть на неё в направлении по стрелке, то будет видна фигура, состоящая из трёх квадратов (рис. 1). Из 27 таких же кубиков сложили куб (рис. 2). Затем с этого куба сняли несколько кубиков (рис. 3). Какая фигура будет видна, если смотреть на получившуюся постройку в направлении по стрелке?
Изобрази эту фигуру на клетчатом поле. Один кубик следует изображать одной клеткой.
Рисунок будет выглядеть следующим образом:
15. Задание 12 № 115
Дедушка с бабушкой, отправившись в лес за грибами, взяли с собой внука Артёма и внучку Настю. Все вместе они собрали 89 грибов. При этом бабушка вместе с Настей собрали не меньше, чем 45 грибов, а больше всех грибов собрал дедушка. Какое наибольшее число грибов мог собрать Артём? Решение.
Так как бабушка вместе с Настей собрали не меньше 45 грибов, тo кто-то из них двоих собрал больше 22 грибов (если бы и Настя и бабушка собрали не больше, чем по 22 гриба, то вдвоём они собрали бы не больше 44 грибов).
То есть либо Настя собрала не меньше, чем 23 гриба, либо бабушка собрала не меньше, чем 23 гриба. А поскольку дедушка собрал больше всех грибов, то дедушка собрал не меньше, чем 24 гриба. Отсюда следует, что бабушка, Настя и дедушка вместе собрали не меньше, чем 45 + 24 = 69 грибов. Поэтому на долю Артёма остаётся не больше, чем 89 − 69 = 20 собранных грибов.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу.
Znanio. ru
10.02.2019 8:20:47
2019-02-10 08:20:47
Источники:
Https://znanio. ru/media/vpr-po-matematike-4-klass-2516551

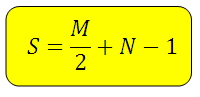



























 рис
рис