в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 589 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь параллелограмма, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, вершины которого имеют координаты (1; 7), (8; 2), (8; 4), (1; 9).
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, вершины которого имеют координаты (1;7), (5;3), (5;5), (1;9).
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, вершины которого имеют координаты (1;7), (5;5), (5;7), (1;9).
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, вершины которого имеют координаты (1; 7), (4; 6), (4; 8), (1; 9).
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, вершины которого имеют координаты (4; 4), (10; 4), (8; 9), (2; 9).
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображенного на рисунке.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см
1см. Ответ дайте в квадратных сантиметрах.
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Найдите площадь параллелограмма, изображённого на рисунке.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора, 5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве
Всего: 589 1–20 | 21–40 | 41–60 | 61–80 …
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
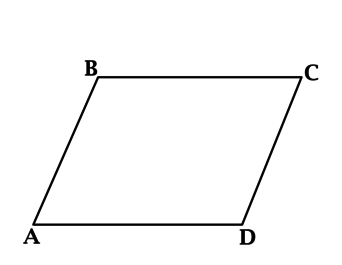
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
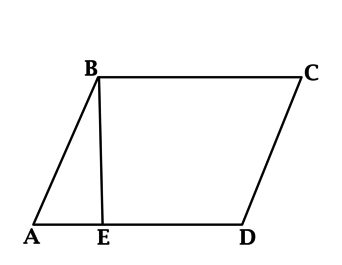
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
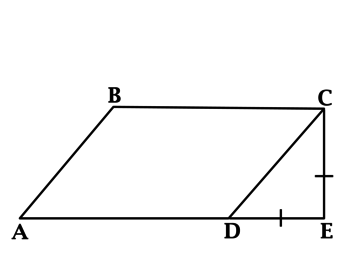
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Четырехугольники
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.
$АВ││CD;BC││AD.$
Свойства параллелограмма:
1. В параллелограмме противоположные стороны и углы попарно равны.
$АВ=CD;BC=AD$
$∠А=∠С; ∠В=∠D$.
2. Диагональ делит параллелограмм на два равных треугольника.
$∆ABD=∆BCD.$
3. Диагонали точкой пересечения делятся пополам.
$BO=OD; AO=OC.$
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
$BD^2+AC^2=2(AB^2+AD^2)$
5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
$∆АВК$ — равнобедренный.
6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
Площадь параллелограмма:
- Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними. $S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
- Площадь параллелограмма равна произведению основания на высоту. $S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.
Пример:
Определите синус острого угла параллелограмма, если его большая высота равна $7$, а стороны $10$ и $14$.
Решение:
Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
$S=a·b·sinα$, из этой формулы можем выразить синус угла.
$sinα={S}/{a·b}$
Стороны параллелограмма нам известны, осталось вычислить площадь. Площадь параллелограмма можно вычислить как произведение высоты на основание. Нам известна большая высота параллелограмма, а большая высота опускается к меньшей стороне параллелограмма, следовательно, $S=7·10=70$.
Подставим все известные данные в формулу синуса:
$sinα={S}/{a·b}={70}/{14·10}=0.5$
Ответ: $0.5$
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
- Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтму у него присутствуют все свойства параллелограмма).
- Диагонали прямоугольника равны. $BD=AC$.
Площадь прямоугольника равна половине произведения смежных (соседних) сторон.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб — это параллелограмм, у которого все стороны равны.
Свойства ромба:
- Все свойства параллелограмма.
- Диагонали ромба пересекаются под прямым углом. $BD⊥AC$.
- Диагонали ромба являются биссектрисами углов.
Площадь ромба:
- Площадь ромба равна половине произведения его диагоналей. $S={d_1·d_2}/2$, где $d_1$ и $d_2$ — диагонали ромба
- Площадь ромба равна произведению квадрата стороны на синус острого угла ромба. $S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все свойства прямоугольника.
- Все свойства ромба.
Площадь квадрата:
- $S=a^2$, где $а$ — сторона квадрата.
- $S={d^2}/{2}$, где $d$ — диагональ квадрата.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет.
Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания.
Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Свойства средней линии трапеции:
1. Средняя линия параллельна основаниям трапеции.
$MN││BC; MN││AD.$
2. Средняя линия равна полусумме оснований.
$MN={BC+AD}/{2}$
3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников.
$МК$ — средняя линия треугольника $ABD; MK={AD}/{2}$.
$KN$ — средняя линия треугольника $BCD; KN={BC}/{2}$.
Трапеция, у которой боковые стороны равны, называется равнобедренной.
Свойства равнобедренной трапеции:
1. Углы при основаниях равны.
$∠А=∠D; ∠B=∠C.$
2. Диагонали в равнобедренной трапеции равны.
$BD=AC.$
3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований.
$АС_1={BC+AD}/{2}.$
4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.
$BC=B_1C_1;$
$AB_1=C_1 D={AD-BC}/{2}.$
5. Если трапеция является равнобедренной, то около неё можно описать окружность.
6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор площади параллелограмма
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S=a⋅hS=acdot h
aa — основание;
hh — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S=a⋅b⋅sin(α)S=acdot bcdotsin(alpha)
a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.
Теперь решим другой пример и воспользуемся вышеописанной формулой.
Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.
Решение
a=20a=20
p=100p=100
α=30∘alpha=30^{circ}
Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30
Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)
Ответ: 300 (см. кв.)
Формула площади параллелограмма по диагоналям и углу между ними
S=12⋅D⋅d⋅sin(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)
DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.
Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.
Решение
D=10D=10
d=5d=5
α=30∘alpha=30^{circ}
S=12⋅10⋅5⋅sin(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)
Ответ: 12.5 (см. кв.)
Решение контрольной работы по геометрии онлайн — от профильных экспертов Студворк!