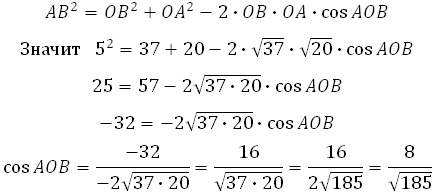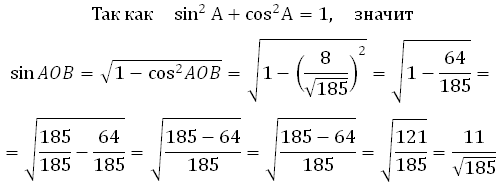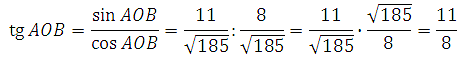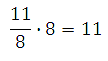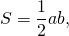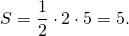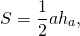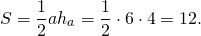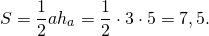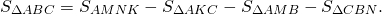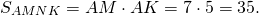Как найти синус угла по клеточкам егэ - Exhelper.top

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Многоугольники: вычисление длин и углов

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д4 № 27449

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на 

Аналоги к заданию № 27450: 27449 26065 316033 316035 316037 509830 512346 512388 519799 525367 … Все

Методы геометрии: Теорема косинусов

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Задания Д4 № 27450

На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.

Аналоги к заданию № 27450: 27449 26065 316033 316035 316037 509830 512346 512388 519799 525367 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Задания Д4 № 27451

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Аналоги к заданию № 27451: 27452 27453 510060 Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Задания Д4 № 27456

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

Аналоги к заданию № 27456: 26074 26077 26080 27454 27455 513703 Все

Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

2 комментария · Сообщить об ошибке · Помощь

Задания Д4 № 27459

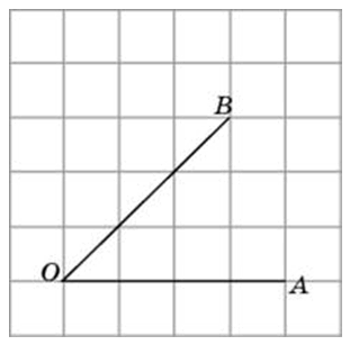
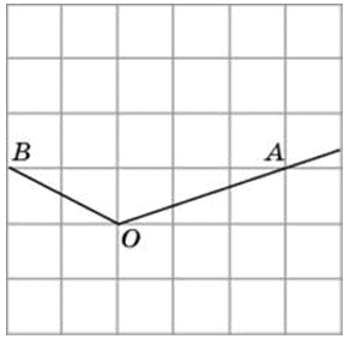
Найдите тангенс угла AOB. Сторона одной клетки равна 1.

Аналоги к заданию № 27459: 27457 27458 Все

Методы геометрии: Теорема косинусов

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.

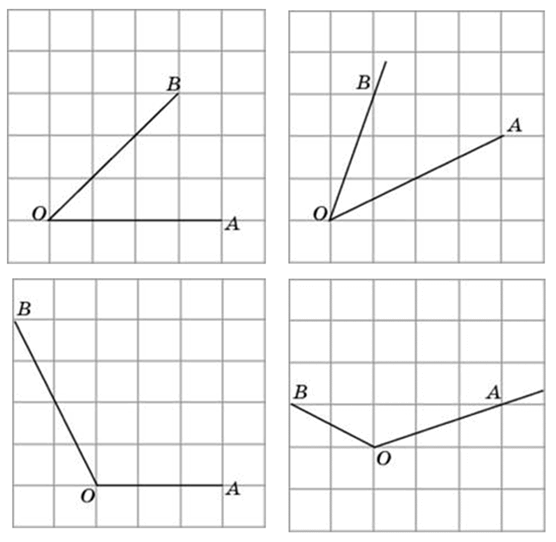
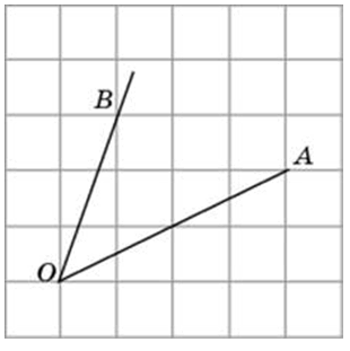
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):

Итак, рассмотрим задание:

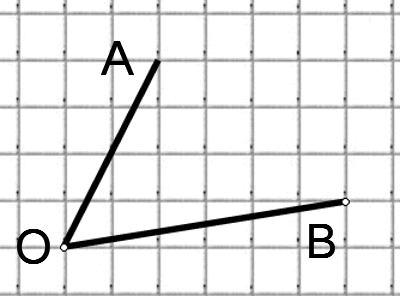
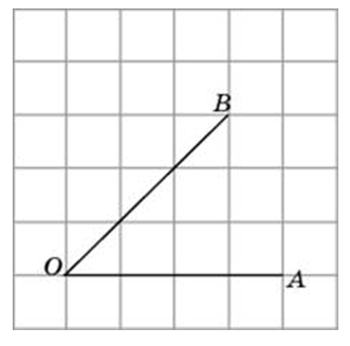
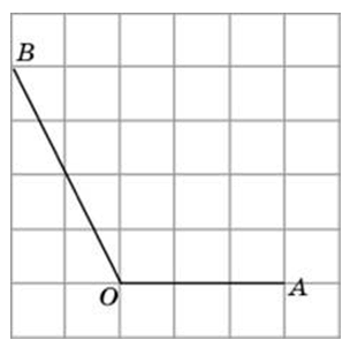
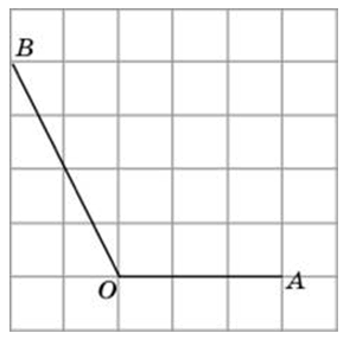
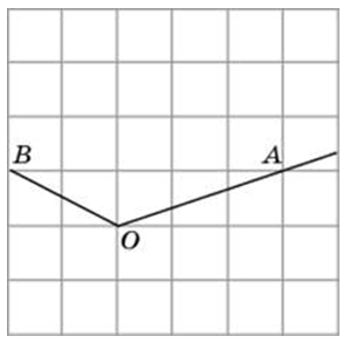
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.

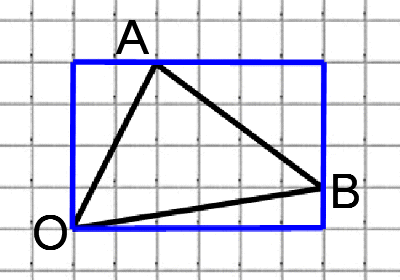
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.

Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).

АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,

ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,

OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.

Из основного тригонометрического тождества можем найти sin AOB:

*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.

Теперь можем найти тангенс:

Умножим результат на 8 и запишем ответ:

Ответ: 11

Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.

Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.

Посмотреть решение

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

С уважением, Александр Крутицких.

*Делитесь информацией в социальных сетях )

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

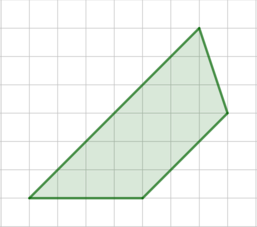
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

(blacktriangleright) Помним, что каждая клетка представляет собой квадрат.

(blacktriangleright) В равных прямоугольниках равны диагонали.

(blacktriangleright) Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

(blacktriangleright) В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
И наоборот: катет, равный половине гипотенузы, лежит против угла (30^circ) (рис. 1).

(blacktriangleright) Медиана, проведенная к основанию в равнобедренном треугольнике, является высотой и биссектрисой (рис. 2).

Задание
22

#3721

Уровень задания: Равен ЕГЭ

Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки (1) см (times) (1) см. Ответ дайте в квадратных сантиметрах.

Опишем вокруг трапеции прямоугольник, как показано на рисунке:

Тогда для того, чтобы найти площадь трапеции, нужно из площади этого прямоугольника вычесть площади трех прямоугольных треугольников: [S=6cdot 7-left(dfrac12cdot 6cdot 6+dfrac12cdot 1cdot 3+dfrac12
cdot 3cdot 3right)=18]

Ответ: 18

Задание
23

#3958

Уровень задания: Равен ЕГЭ

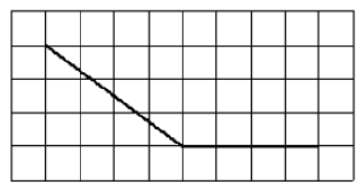
На клетчатой бумаге с размером клетки (1times 1) изображен угол. Найдите синус этого угла.

Продлим одну из сторон тупого угла (A) на отрезок (AC) так, чтобы (BCperp
AC):

Заметим, что все вершины треугольника (ABC) находятся в узлах решетки, причем (AC=3, BC=4). Тогда (AB=sqrt{3^2+4^2}=5). Так как синус острого угла (в прямоугольном треугольнике) – это отношение противолежащего катета к гипотенузе, то [sin angle BAC=dfrac{BC}{AB}=dfrac45=0,8] Угол (BAC) с тупым углом (A) – смежные, следовательно, их синусы равны, значит, синус тупого угла (A) равен также (0,8).

Ответ:

0,8

Задание
24

#4000

Уровень задания: Легче ЕГЭ

На клетчатой бумаге с размером клетки (1times1) изображен треугольник (ABC). Найдите длину его биссектрисы, проведенной из вершины (B).

Из рисунка видно, что треугольник равнобедренный ((BA=BC)). Следовательно, биссектриса, опущенная из вершины (B), будет также являться медианой и высотой. Тогда биссектриса (BH) равна (3):

Ответ:

Задание
25

#4020

Уровень задания: Легче ЕГЭ

На клетчатой бумаге с размером клетки (1times1) изображен угол. Найдите тангенс этого угла.

Проведем перпендикуляр (BH) к стороне (OA). Получим прямоугольный треугольник (OBH). Из него (mathrm{tg},angle O=BH:OH=3:5=0,6).

Ответ:

0,6

Задание
26

#3713

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с размером клетки (1times1) изображен угол. Найдите его градусную величину.

Отметим точки (A, B, C, D) и рассмотрим прямоугольный (triangle ABC):

(AC=BC=3) – катеты, следовательно, треугольник равнобедренный, значит, [angle BAD=angle BAC=45^circ]

Ответ: 45

Задание
27

#3712

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с размером клетки (1) см (times) (1) см отмечены точки (A) и (B). Найдите длину отрезка (AB) в сантиметрах.

Рассмотрим прямоугольный (triangle ABC):

Катеты (AC) и (BC) равны соответственно (9) и (12), следовательно, по теореме Пифагора гипотенуза (AB) равна [AB=sqrt{9^2+12^2}=15]

Ответ: 15

Задание
28

#3711

Уровень задания: Равен ЕГЭ

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки (1) см (times) (1) см. Ответ дайте в квадратных сантиметрах.

Отметим точки (A, B, C) и проведем отрезок (CH), как показано на рисунке:

Заметим, что (CHperp AB). Следовательно, площадь треугольника равна [S=dfrac12cdot ABcdot CH=dfrac12cdot 9cdot 5=22,5]

Ответ: 22,5

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

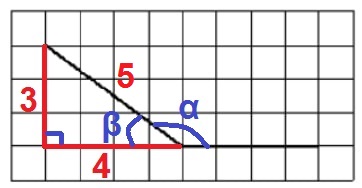
На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите синус этого угла.

Источник задания: alexlarin.net

Решение:

α + β = 180º
sin α = sin(180 – β) = sin β

Найдём синус смежного угла β, из прямоугольного треугольника, со сторонами 3 и 4, гипотенуза тогда равна 5, т.к. это египетский треугольник:

Ответ: 0,6.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

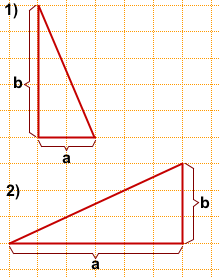
Начнем с прямоугольных треугольников.

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Площадь прямоугольного треугольника будем искать с помощью формулы

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

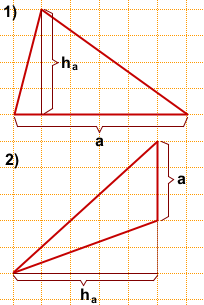
Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

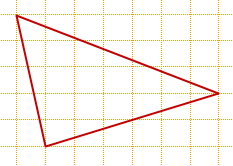
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

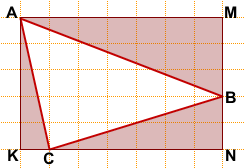
Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

Площади прямоугольных треугольников найдём по формуле

Как найти треугольник по клеткам

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому

см 2 .

Приведём другое решение:

Воспользуемся формулой для нахождения площади треугольника

Одна из сторон данного треугольника является диагональю квадрата со стороной 6, а высота, проведённая к этой стороне, является диагональю квадрата со стороной 2. Тогда

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

Площадь трапеции равна произведению полусуммы оснований на высоту:

Нахождение площадей многоугольников сложной формы

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

14. Найдите площадь четырехугольника, вершины которого имеют координаты

источники:

http://ege.sdamgia.ru/search?search=%D0%BD%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D0%BF%D0%BB%D0%BE%D1%89%D0%B0%D0%B4%D1%8C%20%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0%20%D0%BD%D0%B0%20%D0%BA%D0%BB%D0%B5%D1%82%D1%87%D0%B0%D1%82%D0%BE%D0%B9

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-3-zadachi-na-kletchatoj-bumage-ili-koordinatnoj-ploskosti/

Источник

Площадь треугольника, изображённого на клетчатой бумаге

Как найти треугольник по клеткам

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Новое и интересное на сайте: