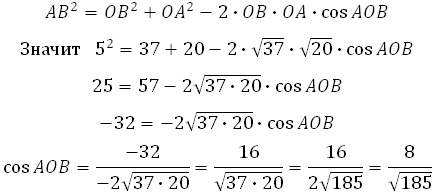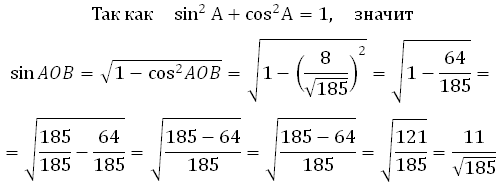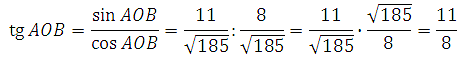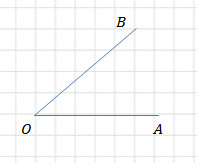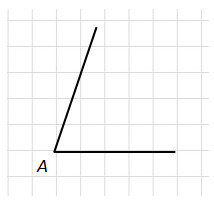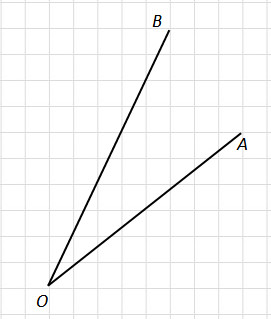Как найти тангенс острого угла по клеточкам егэ - Exhelper.top

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Поиск

Всего: 15 1–15

Добавить в вариант

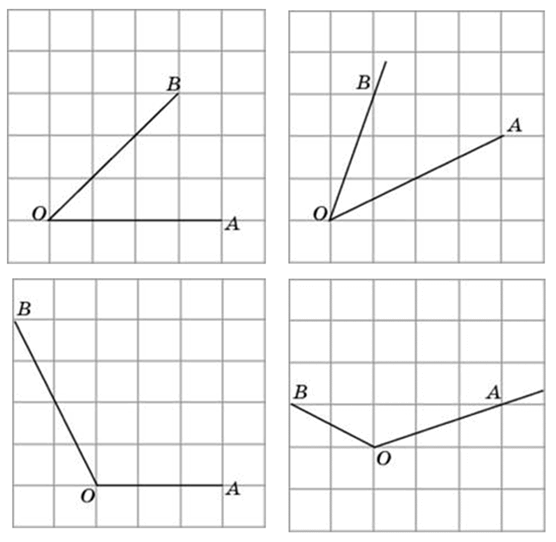
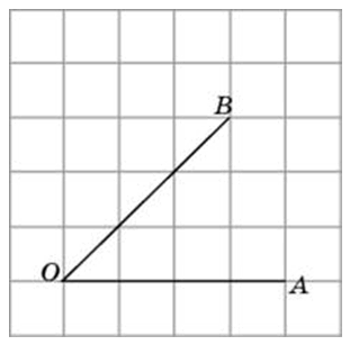
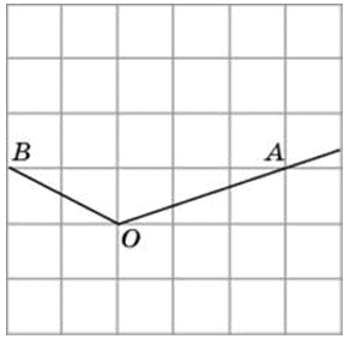
Найдите тангенс угла AOB. Сторона одной клетки равна 1.

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

Источник: ЕГЭ по математике 10.04.2019. Досрочная волна, резервная волна

На клетчатой бумаге с размером клетки 1 × 1 изображён острый угол. Найдите тангенс этого угла.

Источник: ЕГЭ по математике 2021 года. Досрочная волна.

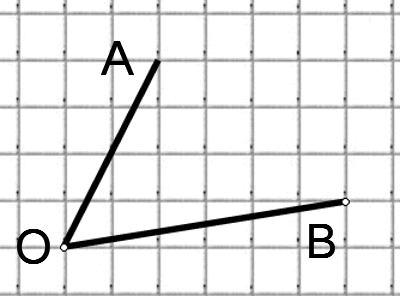
Найдите тангенс угла AOB.

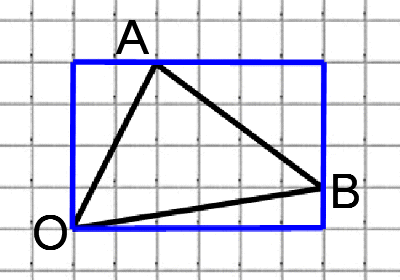
Трапеция ABCD с основаниями AD и BC вписана в окружность с центром O. Найдите высоту трапеции, если её средняя линия равна 3 и

Всего: 15 1–15

Источник

Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.

Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):

Итак, рассмотрим задание:

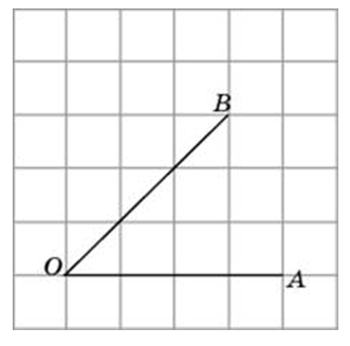
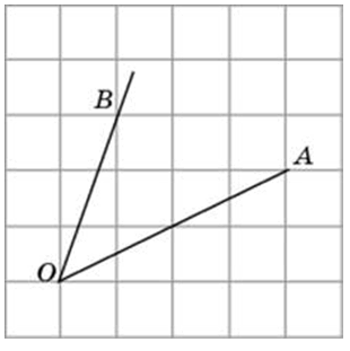
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.

Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.

Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).

АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,

ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,

OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.

Из основного тригонометрического тождества можем найти sin AOB:

*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.

Теперь можем найти тангенс:

Умножим результат на 8 и запишем ответ:

Ответ: 11

Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.

Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):

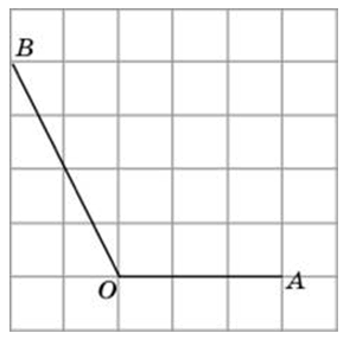
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Посмотреть решение

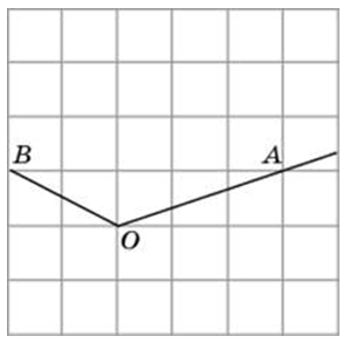
Найдите тангенс угла AOB.

Посмотреть решение

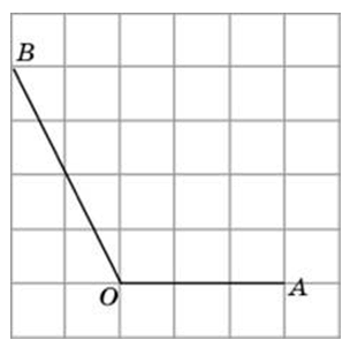
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.

Посмотреть решение

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

С уважением, Александр Крутицких.

*Делитесь информацией в социальных сетях )

Источник

Задание 18 в ОГЭ — это задачи на квадратной решётке, которые, в свою очередь, объединяют в себе очень много геометрического материала. Здесь и нахождение длин отрезков (медиан, биссектрис, средних линий, радиусов, расстояний до прямой), и вычисление площадей, и нахождение тригонометрических функций углов.

Рассмотрим задачи последнего типа. Стороны квадратных клеток равны 1
.

Задача 1. Найдите тангенс угла АОВ.

Эта задача легко решится, если увидеть прямоугольный треугольник и вспомнить, что тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Опустим из точки В перпендикуляр ВН на сторону ОА.

Из рисунка видно, что катет ВН = 4, а катет ОН = 5. Значит,

Ответ: 0,8.

Теперь решим задачу посложней.

Задача 2. Найдите тангенс угла АОВ.

Казалось бы, условие тоже, но посмотрите на расположение угла. Можно ли здесь увидеть прямоугольный треугольник? Можно и нужно.

Что мы знаем? Из любой точки к прямой можно провести перпендикуляр, и притом только один. Перпендикуляр — это кратчайшее расстояние от точки до прямой.

Вполне достаточно.

Из точки В к прямой ОА можно провести отрезки (важно: проводить надо в узлы клеток).

Однако, только один из отрезков перпендикулярен прямой ОА. На рисунке он красного цвета. Уберём с чертежа ненужные элементы.

Перед нами треугольник ОВН. Но, чтобы не было никаких сомнений, проверим, будет ли он прямоугольным. Найдём каждую из сторон треугольника, используя теорему Пифагора.

Для этого достроим наш чертёж.

Используя рисунок, получим

По теореме, обратной теореме Пифагора, если для треугольника выполняется равенство a² + b² = c², то треугольник прямоугольный.

В нашем случае,

Теперь ответим на вопрос задачи (не забыли ещё?).

Ответ: 1,5.

Эти две задачи показывают, что одинаковые условия не гарантируют ещё, что решения также будут один в один. В каждом случае нужно «нащупать» свой путь. Наверное, это самое трудное в этих задачах.

Решите самостоятельно.

1. На квадратной сетке изображён угол . Найдите .

2. Найдите тангенс угла . Размер клетки 1 × 1.

Желаю вам успешной и плодотворной работы по подготовке к экзамену!

Источник

№8. Найдите тангенс угла AOB, изображенного на рисунке.

Решение:

Опустим перпендикуляр AH на сторону OB.

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

Ответ: 2

№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

Ответ: 0,4

№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем AB по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

A B = 5

sin ∠ A = B H A B = 4 5 = 0,8

Ответ: 0,8

№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

Ответ: 0,75

№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

A B = 10

cos ∠ A B H = B H A B = 8 10 = 0,8

Ответ: 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

Ответ: -3

№14. Найдите тангенс угла AOB.

Решение:

Опустим высоту BH на сторону OA.

Рассмотрим прямоугольный △ O B H :

tg ∠ O = B H O H

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

B H = 2 17

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

O H = 17

tg ∠ O = B H O H = 2 17 17 = 2

Ответ: 2

Источник

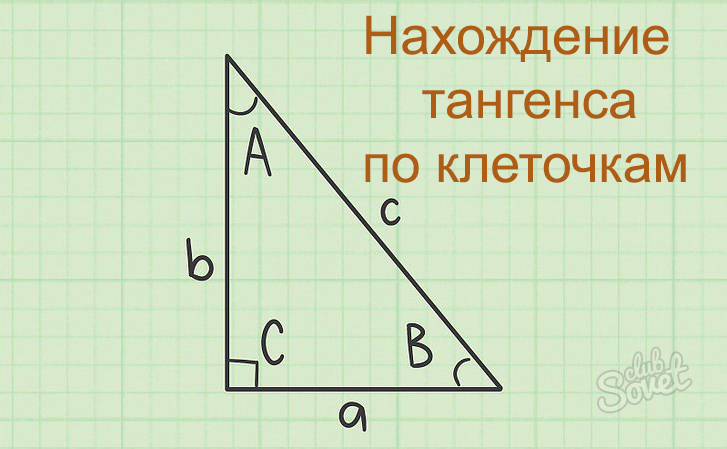
Как найти тангенс угла по клеточкам

Вычисление такой величины как тангенс может потребоваться как в ходе решения тригонометрических уравнений, так и при поиске ответа задачи по геометрии. Именно во втором случае хорошим подспорьем может оказаться наличие графического изображения угла, тангенс которого необходимо найти, на разлинованной в клеточку бумаге. Как это сделать – читайте в данной статье.

1

Работа с прямоугольными треугольниками

Прежде, чем приступить к нахождению такой величины как тангенс, необходимо определиться с терминологией. Так понятие “тангенс угла” характеризует отношение противолежащего данному угла катета к прилежащему. Т. о. работа ведется в пределах прямоугольного треугольника.

Суть описанного далее алгоритма заключается в работе с прямоугольными треугольниками в рамках непосредственно определения тангенса.

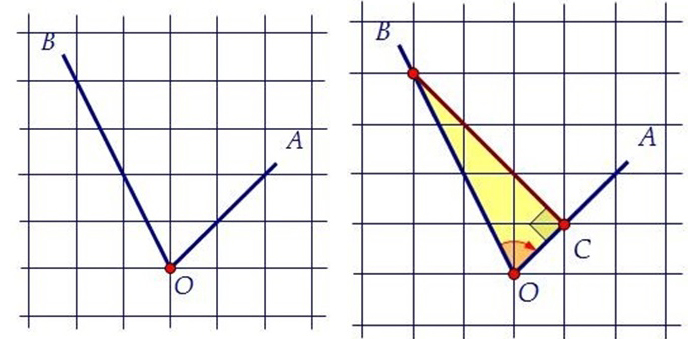
Задача – определить тангенс ∠AOB.

Установите т. B на луче OB в месте его прохождения через вершину клетки.
Из т. B опускаете перпендикуляр на луч OA. Место пересечения отмечаете как т. C.
В результате получается прямоугольный ΔBOC, в котором находится угол ∠AOB (очевидно, что ∠BOC = ∠AOB), тангенс которого необходимо найти.
Исходя из определения тангенса, tg∠AOB = BC / OC. Глядя на рисунок, несложно заметить что длина катета BC складывается из трех диагоналей клеток. При этом длина катета OC соответствует диагонали одной клетки. Следовательно, BC = 3OC.
tg∠AOB = 3OC/OC = 3.

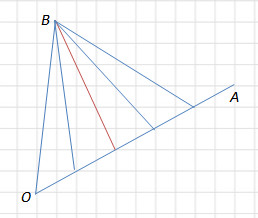
Задача – определить тангенс ∠AOB.

Расчет tg∠AOB будет основан на том, что tg(η – λ) = (tgη – tgλ) / (1 + tgη*tgλ).

В одной из точек прохождения лучами OA и OB вершин клеток-квадратов отмечаете т. A и т. B соответственно.
Опускаете из них перпендикуляры. В результате вы получаете 2 прямоугольных треугольника – ΔOMB и ΔOLA.
“Расчетный” ∠AOB является разностью углов ∠AOL и ∠BOM: ∠AOB = ∠AOL – ∠BOM.
tg∠AOB = tg(∠AOL – ∠BOM) = (tg∠AOL – tg∠BOM) / (1 + tg∠AOL*tg∠BOM). Т. о. нахождение искомой величины сводится к нахождению тангенсов углов в построенных прямоугольных треугольниках.
tg∠AOL = AL / OL. Обратившись к рисунку заметно, что AL = 2OL. Поэтому tg∠AOL= 2OL / OL = 2.
tg∠BOM = BM / OM. Обратившись к рисунку видно, что OM=6BM. Поэтому tg∠BOM = BM / 6BM = 1/6.

tg∠AOB = (2 – 1/6) / (1 + 2/6) = 11*3 / 6*4 = 11/8 ⇒ tg∠AOB = 1,375.

2

Использование теоремы косинусов

Задача – определить тангенс ∠AOB.

т. A и т. B устанавливаете в точках прохождения лучей заданного угла через вершины клеток-квадратов. Опускаете из них перпендикуляры. Также отрезком соединяете между собой т. A и т. B.
Ваша задача – вычислить длины сторон получившегося ΔAOB. Для этого обращаемся к теореме Пифагора.

AO = √OK²+ AK², установив длину стороны клетки как условную 1, получаем AO = √9 + 1=√10.
OB = √BP²+ OP², т. к. длина стороны клетки равна 1, получаем OB = √4 + 1 = √5.

Согласно теореме косинусов, AB²= AO²+ OB²– 2AO*OB*cos∠AOB ⇒ cos∠AOB = (AO²+ OB²– AB²) / 2AO*OB. Подставив числовые значения, получаем:

cos∠AOB = (10 + 5 – 25) / 2√5√10;

cos∠AOB = -10/2√5√10;

cos∠AOB = -1/√2.

Далее воспользуемся основным тождеством тригонометрии: sinβ²+ cosβ²= 1.

sin∠AOB = √1-1/2 = 1/√2.

Известно, что tg∠AOB = sin∠AOB / cos∠AOB = -√2 / √2 ⇒ tg∠AOB = -1.

В зависимости от угла, тангенс которого необходимо найти, выбирайте наиболее подходящий, а главное “рабочий” алгоритм.

Источник

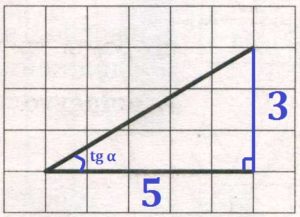
На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите тангенс этого угла.

Источник: ОГЭ 2021 Ященко 36 вариантов.

Решение:

Дорисуем угол до прямоугольного треугольника:

Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

tgalpha=frac{3}{5}=0,6

Ответ: 0,6.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 24

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

За третьим заданием негласно закрепилось название «фигура на бумаге в клетку». В задании представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.

Проверяется знание основ планиметрии: определений, наиболее известных теорем и формул.

Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты

В заданиях встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг.

При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки — надо внимательно читать задание.

По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.

Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.

При подготовке полезно пользоваться прилагающимися к билету справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку.

Определения, а также свойства фигур и их элементов, в справочных материалах не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.

Сложных вычислений в третьем задании нет. Бываю задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще.

Большинство задач можно решить несколькими способами.

Пример №1

Найдите большую диагональ ромба.

Решение: Собственно, все, что нужно знать – определение диагонали и понятие больше-меньше.

Ответ: 4 см.

Удивительно, что в профильной математике встречаются такие задания. И в них тоже допускают ошибки. Видимо, от неожиданности уровня сложности.

Далее для разбора выбраны наиболее сложные задачи, встречавшиеся в третьем задании на экзаменах прошлых лет.

Пример №2

Найдите площадь треугольника.

Решение:

1) Достроим фигуру до прямоугольника. Его площадь равна 6*4=24

2) Найдем площади «лишних» прямоугольных треугольников

(4*4)/2=8 (зеленый)
(2*2)/2=2 (синий)
(6*2)/2=6 (красный)

3) Вычтем из площади прямоугольника лишние площади треугольников: 24-8-2-6=8

Ответ: 8.

Эту же задачу можно решить другим способом.

1) Треугольник является прямоугольным, так как его катеты расположены под углом 45 градусов к вертикальной линии.

2) Катеты найдем из прямоугольных треугольников

Sqrt(4^2+4^2)=4sqrt2 (четыре корня из двух)
Sqrt(2^2+2^2)=2sqrt2 (два корня из двух)

3) Площадь искомого треугольника равна половине произведения катетов: (4sqrt2*2sqrt2)/2=(4*2*2)/2=8

Ответ: 8.

Пример №3

Найдите площадь многоугольника

Решение: Разобьем многоугольник на удобные фигуры и найдем их площади.

Площадь зеленого треугольника 1*3/2=1,5
Площадь синего треугольника 2*1/2=1
Площадь красного треугольника 1*2/2=1
Площадь квадрата 2*2=4
Площадь многоугольника равна их сумме: 1,5+1+1+4=7,5

Ответ: 7,5.

Эту задачу можно решить и вычитанием из площади прямоугольника.

Ответ: 7,5.

Пример №4

Найти площадь многоугольника.

Решение: Можно найти площадь вычитанием, как и в предыдущих заданиях.

Но быстрее можно получить результат с помощью формулы Пика. Для этого нужно сосчитать точки с целыми координатами внутри фигуры (синие) и точки с целыми координатами на контуре фигуры (красные).

Далее к числу точек внутри многоугольника прибавить половину точек на контуре и вычесть единицу.

7+9/2-1=10,5

Ответ: 10,5

Формула Пика не указана в кодификаторе, применять ее при решении заданий с развернутым ответом нельзя. Но в заданиях с кратким ответом она позволяет сэкономить время. Проверьте справедливость формулы на предыдущих примерах.

Пример № 5

Найдите градусную меру угла АВС.

Решение: Точка А имеет нецелые координаты, однако теорема о вписанном и центральном углах позволяет легко решить задачу.

Проведем радиусы в точки А и С.

По рисунку видно, что центральный угол АОС равен 135 градусам. Вписанный угол АВС опирается на те же точки окружности А и С. Согласно теореме, он в два раза меньше центрального.

135/2=67,5

Ответ: 67,5.

Пример №6

Найдите тангенс угла.

Решение: Выделим смежный острый угол.

Выделим прямоугольный треугольник с целочисленными координатами вершин, содержащий этот угол. Найдем тангенс острого угла как отношение противолежащего (зеленого) катета к прилежащему (синему).

tgA=4/1=4

Тангенс смежного тупого угла противоположен по знаку.

Ответ: -4.

В завершении хочется еще раз напомнить: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.

Профессиональный преподаватель также сделал подробный разбор 1 и 2 задания, с которыми можно ознакомиться по ссылкам.

Источник

Как найти тангенс угла по клеточкам

1 Работа с прямоугольными треугольниками

2 Использование теоремы косинусов

Пример №1

Пример №2

Пример №3

Пример №4

Пример № 5

Пример №6

Новое и интересное на сайте:

1

Работа с прямоугольными треугольниками

2

Использование теоремы косинусов