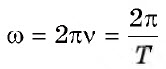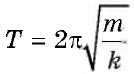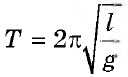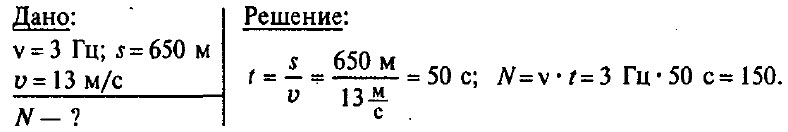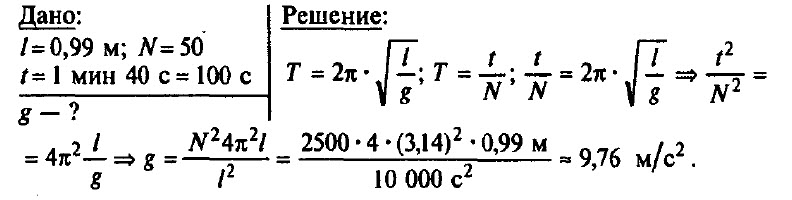Математический маятник егэ - Exhelper.top

Механические колебания.

Гармонические колебания.
Уравнение гармонических колебаний.
Пружинный маятник.
Математический маятник.
Свободные и вынужденные колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: nu =1/T . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение x=0 . Основная задача механики в данном случае состоит в нахождении функции x(t) , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на pi /2 , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина alpha , равная значению фазы при t=0 , называется начальной фазой. Начальная фаза отвечает начальной координате тела: $x_{0}=Acos alpha$ .

Величина называется omega циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное 2 pi радиан: , откуда

$omega = frac{displaystyle 2pi }{displaystyle T}$ (2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

$x=Acos(frac{displaystyle 2pi t }{displaystyle T}+ alpha), x=Acos(2 pi nu t + alpha)$ .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину $x_{0}$ и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае $x_{0}=A$ , поэтому можно положить alpha=0 . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае $x_{0}=0$ , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

$v_{x}=dot{x}=-Aomega sin(omega t+alpha )$ . (4)

Теперь дифференцируем полученное равенство (4):

$a_{x}=ddot{x}=-Aomega^{2} cos(omega t+alpha )$ . (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем $-omega^{2}$ :

$a_{x}=-omega^{2}x$ . (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

$ddot{x}+omega^{2}x=0$ . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой omega и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате x=0 отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости vec F со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

$ma_{x}=F_{x}$ . (8)

Если x>0 (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и $F_{x}<0$ . Наоборот, если x<0 , то $F_{x}>0$ . Знаки и $F_{x}$ всё время противоположны, поэтому закон Гука можно записать так:

$F_{x}=-kx$

Тогда соотношение (8) принимает вид:

$ma_{x}=-kx$

или

$a_{x}=-frac{displaystyle k}{displaystyle m}x$ .

Мы получили уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle k}{displaystyle m}$ .

Циклическая частота колебаний пружинного маятника, таким образом, равна:

$omega =sqrt{frac{displaystyle k}{displaystyle m}}$ . (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

$T=2 pi sqrt{frac{displaystyle m}{displaystyle k}}$ . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

$ma_{x}=T_{x}$ .

Если маятник занимает положение как на рисунке (т. е. x>0 ), то:

$T_{x}=-Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Если же маятник находится по другую сторону от положения равновесия (т. е. x<0 ), то:

$T_{x}=Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Итак, при любом положении маятника имеем:

$ma_{x}=-Tfrac{displaystyle x}{displaystyle l}$ . (11)

Когда маятник покоится в положении равновесия, выполнено равенство T=mg . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

$ma_{x}=-mgfrac{displaystyle x}{displaystyle l}$ ,

или

$a_{x}=-frac{displaystyle g}{displaystyle l}x$ .

Это — уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle g}{displaystyle l}$ .

Следовательно, циклическая частота колебаний математического маятника равна:

$omega =sqrt{frac{displaystyle g}{displaystyle l}}$ . (12)

Отсюда период колебаний математического маятника:

$T=2pi sqrt{frac{displaystyle l}{displaystyle g}}$ . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы F(t) , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна $omega_{0}$ , а вынуждающая сила зависит от времени по гармоническому закону:

$F(t)=F_{0}cos omega t$ .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
omega вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты $omega=omega_{r}$ наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: $omega_{r} approx omega_{0}$ , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, $omega_{r} = omega_{0}$ , а амплитуда колебаний возрастает до бесконечности при $omega Rightarrow omega_{0}$ .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 66 1–20 | 21–40 | 41–60 | 61–66

Добавить в вариант

Математический маятник, частота колебаний которого равна 0,125 Гц, отклонили на небольшой угол от положения равновесия и отпустили без начальной скорости (см. рис.). Выберите все верные утверждения из 5:

1)  Кинетическая энергия маятника в первый раз достигла максимума через 4 секунды.

2)  Полная механическая энергия маятника стала возрастать сразу после начала опыта.

3)  Потенциальная энергия маятника второй раз достигла минимума через 8 секунд.

4)  Кинетическая энергия маятника второй раз достигла максимума через 6 секунд.

5)  Полная механическая энергия маятника оставалась постоянной в течение наблюдения.

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1

Математический маятник совершает колебания в вязкой среде. Нить маятника лёгкая и нерастяжимая. Как в процессе этих колебаний изменяются модуль силы натяжения нити в момент максимального отклонения маятника и полная механическая энергия маятника?

Для каждой величины определите соответствующий характер изменения:

1)  увеличивается

2)  уменьшается

3)  не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Модуль силы натяжения нити в момент

максимального отклонения маятника

Полная механическая энергия

маятника

Задания Д4 B4 № 4519

Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили с начальной скоростью, равной нулю (см. рисунок). Через какое время после этого потенциальная энергия маятника в первый раз вновь достигнет максимума? Сопротивлением воздуха пренебречь.

4)  T

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 2.

Задания Д4 B4 № 4589

Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили c начальной скоростью равной нулю (см. рисунок). Через какое время после этого кинетическая энергия маятника во второй раз достигнет максимума? Сопротивлением воздуха пренебречь.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 4.

Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили с начальной скоростью, равной нулю (см. рисунок). Через какое время (в долях периода) после этого потенциальная энергия маятника в первый раз вновь достигнет максимума? Сопротивлением воздуха пренебречь.

Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили с начальной скоростью равной нулю (см. рисунок). Через какое время (в долях периода) после этого кинетическая энергия маятника во второй раз достигнет максимума? Сопротивлением воздуха пренебречь.

Задания Д4 B4 № 4484

Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили без начальной скорости (см. рис.). Через какое время после этого кинетическая энергия маятника в первый раз достигнет минимума? Сопротивлением воздуха пренебречь.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 1.

Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили без начальной скорости (см. рис.). Через какое время (в долях периода) после этого кинетическая энергия маятника в первый раз достигнет минимума? Сопротивлением воздуха пренебречь.

Задания Д12 B23 № 6314

Необходимо экспериментально выяснить зависимость периода малых колебаний математического маятника от вещества, из которого изготовлен груз. Какую пару маятников можно взять для этой цели? Грузы маятников  —  полые шарики из меди и алюминия одинаковой массы и одинакового внешнего диаметра.

1)  1

2)  2

3)  3

4)  4

Источник: ЕГЭ по физике 05.05.2014. Досрочная волна. Вариант 4.

Время четырёх полных колебаний математического маятника, измеренное с помощью секундомера, равно 18 секундам. Погрешность измерения времени с использованием секундомера равна 1 с. Чему равен период колебаний этого маятника с учётом погрешности измерений? Выразите обе величины в секундах и округлите их до десятых долей.

Время четырёх полных колебаний математического маятника, измеренное с помощью секундомера, равно 22 секундам. Погрешность измерения времени с использованием секундомера равна 1 с. Чему равен период колебаний этого маятника с учётом погрешности измерений? Выразите обе величины в секундах и округлите их до десятых долей.

При свободных колебаниях груза на нити математического маятника его кинетическая энергия изменяется от 0 Дж до 50 Дж, максимальное значение потенциальной энергии 50 Дж. Чему равна полная механическая энергия груза при таких колебаниях? (Ответ выразите в джоулях.)

Школьник, изучая механические колебания, изготовил два маятника – математический с периодом малых колебаний T₁  =  1 c и пружинный с периодом колебаний T₂  =  2T₁. Второй маятник был подвешен в вертикальном положении за свободный конец пружины. Найдите деформацию x₀ пружины для второго маятника в состоянии равновесия.

Школьник, изучая механические колебания, изготовил два маятника  — математический с периодом малых колебаний T₁  =  1 c и пружинный с периодом колебаний T₂  =  T₁/2. Второй маятник был подвешен в вертикальном положении за свободный конец пружины. Найдите деформацию x₀ пружины для второго маятника в состоянии равновесия.

Необходимо при помощи маятника экспериментально определить ускорение свободного падения. Для этого школьник взял штатив с муфтой и лапкой, нить и секундомер.

Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?

1)  электронные весы

2)  алюминиевый шарик

3)  динамометр

4)  линейка

5)  мензурка

В ответ запишите номера выбранного оборудования.

Источник: ЕГЭ по физике. Вариант 114, ЕГЭ по физике 2022. Досрочная волна. Вариант 2

При помощи нитяного маятника необходимо экспериментально определить ускорение свободного падения. Для этого школьник взял штатив с муфтой и лапкой, нить и стальной шарик. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?

1)  электронные весы

2)  мензурка

3)  линейка

4)  динамометр

5)  секундомер

В ответе запишите номера выбранного оборудования.

Источник: ЕГЭ по физике 2022. Досрочная волна

Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?

Какие законы Вы используете для описания движения маятника? Обоснуйте их применение.

Равносторонний треугольник, состоящий из трех жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплен массивный грузик (см. рис.). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?

Какие законы Вы используете для описания движения маятника? Обоснуйте их применение.

Всего: 66 1–20 | 21–40 | 41–60 | 61–66

Источник

Свободные колебания математического и пружинного маятников

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.

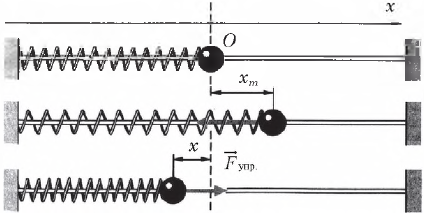
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины, входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник. В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия. Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;
отсутствие трения в системе.

Динамика свободных колебаний

Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости $F_{упр}$ может быть получено с учетом второго закона Ньютона ($F=ma$) и закона Гука ($F_{упр}=-kx$), где $m$ — масса шарика, $а$ — ускорение, приобретаемое шариком под действием силы упругости, $k$ — коэффициент жесткости пружины, $х$ — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось $Ох$). Приравнивая правые части этих уравнений и учитывая, что ускорение $а$ — это вторая производная от координаты $х$ (смещения), получим:

$x»=-{k}/{m}x$

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени {ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

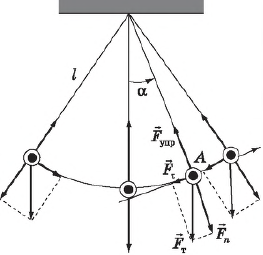
Колебания математического маятника. Для получения уравнения колебания математического маятника необходимо разложить силу тяжести $F_т=mg$ на нормальную $F_n$ (направленную вдоль нити) и тангенциальную $F_τ$ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести $F_n$ и сила упругости нити $F_{упр}$ в сумме сообщают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меняющее ее направление, а тангенциальная составляющая $F_τ$ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения — $ma_τ=F_τ$ и учитывая, что $F_τ=-mgsinα$, получим:

$a_τ=-gsinα$

Знак минус появился потому, что сила и угол отклонения от положения равновесия $α$ имеют противоположные знаки. Для малых углов отклонения $sinα≈α$. В свою очередь, $α={s}/{l}$, где $s$ — дуга $ОА$, $l$ — длина нити. Учитывая, что $a_τ=s»$, окончательно получим:

$s»={g}/{l}s$

Вид уравнения $s»={g}/{l}s$ аналогичен уравнению $x»=-{k}/{m}x$. Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений $x»=-{k}/{m}x$ и $s»={g}/{l}s$ является функция вида:

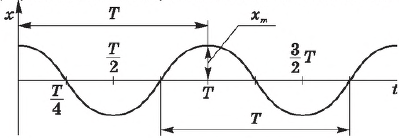
$x=x_{m}cosω_{0}t$(или $x=x_{m}sinω_{0}t$)

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими.

В уравнении $x=x_{m}cosω_{0}t$ хт— амплитуда колебания, $ω_{0}$ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

$ω_0=√{{k}/{m}}; T=2π√{{m}/{k}}$

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

$ω_0=√{{g}/{l}}; T=2π√{{l}/{g}}$

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции $x=x_{m}cosω_{0}t$, получим выражение для скорости:

$x’=υ=-x_{m}·sinω_{0}t=υ_{m}cos(ω_{0}t+{π}/{2})$

где $υ_{m}$ — амплитуда скорости.

Аналогично выражение для ускорения а получим, дифференцируя $x’=υ=-x_{m}·sinω_{0}t=υ_{m}cos(ω_{0}t+{π}/{2})$:

$a=x»=υ’-x_{m}ω_0^{2}cosω_{0}t=a_{m}·cos(ω_{0}t+π)$

где $a_m$ — амплитуда ускорения. Таким образом, из полученных уравнений следует, что амплитуда скорости гармонических колебаний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания:

$υ_{m}=ω_{0}x_m; a_m=ω_0^{2}x_m$

Источник

В данной теме разговор пойдёт
о математическом и пружинном маятниках и их важных характеристиках.

Рассмотрим для начала
математический маятник. Математическим маятником называется находящаяся
в гравитационном поле материальная точка, подвешенная на невесомой и
нерастяжимой нити, прикрепленной к подвесу. Математический маятник
— это модель малых реальных колебаний тела под действием силы тяготения
при условии, что можно пренебречь:

1) размерами подвешенного
тела, по сравнению с длиной нити;

2) сопротивлением движению
тела;

3) массой нити и ее
деформацией.

Рассмотрим подробно колебания
математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса движется
прямолинейно и равномерно или же покоится. И так, пусть в начальный момент
времени маятник покоится в положении равновесия. Тогда, действующие на маятник
сила упругости нити и сила тяжести материальной точки взаимно компенсируются.

Теперь отклоним маятник на
некоторое расстояние от точки равновесия и отпустим его. В этом случае, сила
тяжести и сила упругости нити уже не будут компенсировать друг друга. Разложим
вектор силы тяжести на две составляющих — тангенциальную и нормальную.

Как видим, тангенциальная
составляющая силы тяжести направлена к положению равновесия, то есть она
является возвращающей силой. При этом она сообщает материальной точке
тангенциальное ускорение и маятник начнет двигаться к положению равновесия с
возрастающей по модулю скоростью. А нормальная составляющая силы тяжести, как
видно из рисунка, направлена вдоль нити против силы упругости. Их
равнодействующая сообщает маятнику нормальное ускорение, которое изменяет
направление вектора скорости. В результате маятник начинает двигаться по дуге.

Чем ближе маятник будет
подходить к положению равновесия, тем меньше становиться значение возвращающей
силы и тем больше становиться скорость движения маятника. Дойдя до положения
равновесия, возвращающая сила становится равной нулю.

При этом скорость движения
маятника достигает своего максимума и, не останавливаясь, маятник продолжает
свое движение дальше уже по инерции, поднимаясь по дуге вверх. При этом вновь
возникает возвращающая сила, которая становится тем больше, чем выше
поднимается маятник. Но так как возвращающая сила теперь направлена против
движения маятника, то его скорость убывает и в точке D
скорость маятника становится равной нулю.

Маятник на мгновение
останавливается, а затем начинает двигаться в обратном направлении к положению
равновесия. Опять пройдя его по инерции, маятник, замедляя свое движение,
дойдет до точки А, тем самым совершив одно полное колебание. А так как
силы сопротивления отсутствуют, то после этого движение маятника будет
повторяться в уже описанной последовательности.

Получим уравнение, описывающее
свободные колебания математического маятника. Пусть маятник в данный момент
времени находится в точке B.

Его смещение от положения
равновесия в этот момент равно длине дуги CB.

Пусть длина нити подвеса
маятника равна l, а его масса m. Из
рисунка видно, что значение возвращающей силы (то есть тангенциальной
составляющей силы тяжести), можно найти как произведение модуля силы тяжести на
синус угла отклонения маятника от вертикали.

Из геометрии известно, что по
определению синус острого угла есть отношение противолежащего катета к
гипотенузе. Также из геометрии известно, что при малых углах (то есть когда
острый угол меньше десяти градусов) синус угла можно заменить его градусной мерой.

Перепишем уравнение для
тангенциальной составляющей силы тяжести с учетом последнего равенства.

Обратите внимание на знак «минус»
в этой формуле. Его здесь ставят потому, что тангенциальная составляющая силы
тяжести направлена к положению равновесия, а смещение отсчитывают от положения
равновесия. Теперь применим второй закон Ньютона для нашего маятника, в
проекциях на направление касательной к траектории движения математического
маятника.

Таким образом, имеются два
уравнения, в которых равны их левые части. А раз равны левые, то и правые части
этих равенств также должны быть равными. Сократив полученное равенство на массу
маятника, приходим к тому, что тангенциальное ускорение математического
маятника прямо пропорционально его смещению и направлено к положению равновесия.

Эту формулу называют динамическим
уравнением движения математического маятника.

Теперь перепишем это уравнение
следующим образом

А теперь сравним его с уравнением гармонических
колебаний.

Из такой записи видно, что колебания
математического маятника являются гармоническими. А так как рассмотренные
колебания происходили только под действием внутренних сил, то это
были свободные колебания. Таким образом, можно сделать важный
вывод о том, что при малых углах отклонения свободные колебания
математического маятника являются гармоническими.

Также из анализа формул
следует, что циклическая частота колебаний маятника равна квадратному корню из
отношения ускорения свободного падения к длине маятника.

Помня о том, что период
колебаний и циклическая частота связаны друг с другом обратной
пропорциональностью, получим формулу, по которой можно рассчитать период свободных
колебаний математического маятника.

Полученная формула называется формулой
Гюйгенса, так впервые была получена нидерландским физиком Христианом Гюйгенсом.

Следует обратить внимание на
то, что эту формулу можно использовать для расчета периода при
выполнении одновременно двух условий:

1) колебания маятника
должны быть малыми, так как эта формула дает результаты приемлемой
точности (ошибка менее одного процента) при углах, не превышающих 4º;

2) точка подвеса
маятника должна покоиться или двигаться прямолинейно и равномерно относительно
инерциальной системы отсчета, в которой находится маятник.

Дело в том, что если точка
подвеса математического маятника движется с некоторым ускорением, то изменяется
сила натяжения нити. Это приводит к изменению возвращающей силы, а,
следовательно, частоты и периода колебаний. В этом случае в формуле периода
математического маятника ускорение свободного падения следует заменить на
так называемое «эффективное» ускорение маятника в неинерциальной системе
отсчета.

«Эффективное» ускорение
можно найти, как векторную сумму ускорения свободного падения и вектора,
противоположного вектору ускорения, с которым движется маятник.

Теперь рассмотрим колебания
пружинного маятника. Пружинным маятником называется система,
состоящая из пружины жесткостью k и материальной точки массой m.

В простейшей модели
пружинного маятника рассматривают только упругую деформацию пружины и пренебрегают:

1) любыми силами сопротивления;

2) размерами тела, то есть
тело принимают за материальную точку;

3) массой пружины.

Различают два вида
пружинных маятников — горизонтальный и вертикальный.

В горизонтальном
пружинном маятнике, колебания тела происходят вдоль горизонтальной прямой.

У вертикального
пружинного маятника колебания происходят вдоль вертикальной прямой.

Рассмотрим более подробно
колебания идеального горизонтального пружинного маятника. Пусть в начальный
момент времени пружина не деформирована, и тело находится в положении
равновесия.

Теперь выведем тело из
положения равновесия, например, сжав пружину на некоторую величину, и отпустим
его. И так, со стороны деформированной пружины на тело начнет действовать сила
упругости, которая всегда будет направленна к положению равновесия, и под
действием этой силы тело начнет ускоренно двигаться. При этом в самом крайнем
положении на тело действует максимальная сила упругости, так как здесь
абсолютное удлинение пружины наибольшее. Значит и ускорение тела в этом
положении максимальное.

При движении тела к положению
равновесия абсолютное удлинение пружины начинает уменьшаться, а, следовательно,
уменьшается и ускорение, сообщаемое силой упругости. Но так как ускорение
сонаправлено со скоростью, то скорость маятника увеличивается и в положении
равновесия, как и в случае с математическим маятником, она будет максимальна.

Достигнув положения
равновесия, тело не остановится (хотя в этом положении пружина не
деформирована), а будет по инерции двигаться дальше, растягивая пружину.
Возникающая при этом сила упругости направлена теперь против движения тела и
тормозит его. В точке D тело
на мгновение остановится, так как его скорость окажется равной нулю. Но
ускорение в этой точке максимально, так как максимальна действующая сила
упругости и под действием этой силы тело начнет двигаться в обратную сторону, к
положению равновесия.

Вновь пройдя его по инерции,
тело, сжимая пружину и замедляя движение, дойдет до точки A,
то есть совершит одно полное колебание. После этого движение маятника будет
повторяться в описанной последовательности.

Таким образом, причинами
свободных колебаний пружинного маятника являются действие силы упругости,
возникающей при деформации пружины, и инертность тела.

Получим уравнение, описывающее
движение пружинного маятника. И так, согласно второму закону Ньютона,
единственный результат действия силы упругости — это сообщение телу ускорения.

По закону Гука, сила упругости
прямо пропорциональна смещению тела и противоположно ему направлена.

Перепишем второй закон Ньютона
с учетом определения силы упругости пружины.

Как видно из уравнения, ускорение
маятника прямо пропорционально смещению и противоположно ему по направлению.

Перепишем уравнение следующим
образом

Полученное равенство является динамическим
уравнением движения пружинного маятника.

Сравнивая его с уравнением
гармонических колебаний, видим, что пружинный маятник совершает
гармонические колебания с циклической частотой равной

Учитывая, что период колебаний
и циклическая частота связаны друг с другом обратной пропорциональностью,
получим формулу, по которой можно рассчитать период свободных колебаний
пружинного маятника.

По этой же формуле можно
рассчитывать и период колебаний вертикального пружинного маятника.

Основные выводы:

Рассмотрели математический и
пружинный маятники. Рассмотрели условия возникновения свободных гармонических
колебаний в таких системах. А также вспомнили формулы, по которым можно
рассчитать период свободных колебаний математического и пружинного маятников.

Источник

Главная > ЕГЭ по физике > Математический маятник

Математический маятник — видеоурок

На этом видео уроке для подготовке к экзамену в 11 классе по физике — ЕГЭ физике. Объясняется что такое математический маятник приводится уравнение колебаний математического маятника. Решается КИМ Демидовой по физике на нахождение периода колебаний, частоты и амплитуды колебаний математического маятника.

Источник

Математические маятники: задачки посложнее

В задачах этой статьи мы столкнемся с необходимостью вспомнить формулу ускорения свободного падения, наши маятники будут подниматься в лифтах и скатываться по наклонным плоскостям.

Математический маятник

Задача 1. Одно из самых высоких мест на Земле, где постоянно проживают люди, находится на высоте м над уровнем моря. На сколько будут уходить за сутки маятниковые часы, выверенные на этой высоте, если их перенести на уровень моря? Радиус Земли известен.
Можно установить, на сколько будут уходить часы, если сопоставить два периода: период маятника фактический (на фактической высоте в м над уровнем моря) и период, каким бы он был, спусти мы этот маятник с гор на уровень моря.

Период фактический:

Откуда

Тогда на уровне моря у маятника был бы период , и

То есть

А так как ускорение свободного падения зависит от высоты над уровнем моря, то можно записать, что

Тогда

Или

Когда маятник был на вершине, он совершал колебаний в сутки, и получалось, что часа.

Теперь, на уровне моря, колебаний уже не есть 24 часа, поэтому маятник уйдет на определенное время, равное :

Ответ: 70 с

Задача 2.

Какую длину должен иметь маятник Фуко, если представить себе, что он установлен на планете, плотность которой равна плотности Земли, а радиус в 2 раза меньше? Маятник совершает три колебания в минуту.

Период маятника равен с. По периоду можно установить длину такого маятника, если известно ускорение свободного падения. Но на планете с радиусом меньшим, чем земной, ускорение будет равно

Тогда длина маятника равна

Ответ: м.

Задача 3.

Вблизи рудного месторождения период колебаний маятника изменился на % . Плотность руды в месторождении г/см. Оценить радиус месторождения , если средняя плотность Земли г/см.

Очевидно, что в районе месторождения средняя плотность породы больше, следовательно, больше и ускорение свободного падения, ведь оно прямо зависит от плотности:

Поскольку зависимость периода математического маятника от ускорения свободного падения обратная: , то очевидно, что период с увеличением плотности уменьшается. Тогда можно записать период маятника вдали от месторождения:

Период маятника вблизи месторождения:

Отношение периодов:

С другой стороны, так как период уменьшился вблизи месторождения, то

То есть

Теперь нужно записать ускорение свободного падения и его изменение в районе месторождения:

А в районе месторождения

Теперь вычтем из последнего равенство предыдущее:

И разделим на :

Подставим отношение ускорений:

Выразим радиус месторождения:

В числителе можно пренебречь величиной , в знаменателе можно можно приближенно заменить на , получим:

Подставим числа и рассчитаем радиус месторождения. При этом радиус земли подставим в км, при этом результат тоже получится в км, а плотности можно подставить в любых единицах – эти единицы сократятся при делении:

Ответ: радиус месторождения около 30 км.

Задача 4.

Один конец нити прикреплен к потолку лифта, а на другом укреплен груз пренебрежимо малого размера. Лифт начинает опускаться с ускорением м/с. Каков период малых колебаний груза, если длина нити м?

Так как лифт спускается с ускорением, то в формулу для вычисления периода нужно подставить не ускорение свободного падения, а то результирующее ускорение, которое действует на груз, а именно :

Ответ: с

Источник

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

Название величины	Обозначение	Единица измерения	Формула
*Амплитуда колебаний*	A	м
*Период колебаний*	T	с	T = 1 / v ; T = t / N
*Частота колебаний*	v	Гц	*v = 1 / T ;* *v = N / t*
*Число колебаний за какое-то время*	N		*N = t /T ;* *N = vt*
*Время*	t	с	t = NT ; t = N / v
*Циклическая частота колебаний*	ω	Гц
*Период колебаний пружинного маятника*	T	c
*Период колебаний математического маятника*	T	c
*Уравнение гармонических колебаний*			x(t) = Asin(ωt+φ₀)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

Задача № 8.
Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на
Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Механические колебания.

Гармонические колебания.

Уравнение гармонических колебаний.

Пружинный маятник.

Математический маятник.

Свободные и вынужденные колебания.

Свободные колебания математического и пружинного маятников

Динамика свободных колебаний

Главная > ЕГЭ по физике > Математический маятник

Математический маятник — видеоурок

Математические маятники: задачки посложнее

Задачи на Механические колебания с решениями

Название величины

Обозначение

Единица измерения

Формула

Амплитуда колебаний

A

м

Период колебаний

T

с

T = 1 / v ;

T = t / N

Частота колебаний

v

Гц

v = 1 / T ;

v = N / t

Число колебаний за какое-то время

N

N = t /T ;

N = vt

Время

t

с

t = NT ;

t = N / v

Циклическая частота колебаний

ω

Гц

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/12/2018-12-11_19-48-01.jpg" alt width="166" height="69" />

Период колебаний пружинного маятника

T

c

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/12/2018-12-11_19-50-53.jpg" alt width="134" height="74" />

Период колебаний математического маятника

T

c

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/12/2018-12-11_19-51-08.jpg" alt width="128" height="77" />

Уравнение гармонических колебаний

x(t) = Asin(ωt+φ0)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения Задачи на Механические колебания.

Новое и интересное на сайте:

x(t) = Asin(ωt+φ₀)