Материальная точка егэ математика - Exhelper.top

Поиск

Всего: 23 1–20 | 21–23

Добавить в вариант

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?

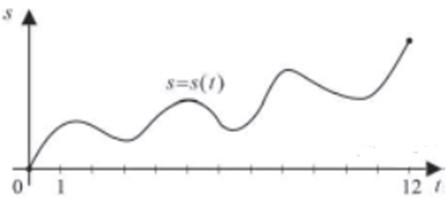
Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат  — расстояние s.

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат  — расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t  =  9 с.

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t  =  6 с.

Материальная точка движется прямолинейно по закону (где x  —расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t  =  3 с.

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t  =  4 с.

Материальная точка движется прямолинейно по закону где х  — расстояние от точки отсчёта (в метрах), t  — время движения (в секундах). Найдите её скорость (в метрах в секунду) в момент времени t  =  6 с.

Всего: 23 1–20 | 21–23

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №6. Физический смысл производной

ЕГЭ Профиль №6. Физический смысл производнойadmin2022-08-16T20:33:21+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №6. Физический смысл производной

Задача 1. Материальная точка движется прямолинейно по закону (xleft( t right) = — frac{1}{3}{t^2} + 4t + 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 3;{text{c}}). Ответ ОТВЕТ: 2.
Задача 2. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + 2{t^2} — 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 2;{text{c}}). Ответ ОТВЕТ: 12.
Задача 3. Материальная точка движется прямолинейно по закону (xleft( t right) = {t^4} + 9{t^2} — 3t + 23), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 1;{text{c}}{text{.}}) Ответ ОТВЕТ: 19.
Задача 4. Материальная точка движется прямолинейно по закону (xleft( t right) = — frac{1}{6}{t^2} + 5t — 19), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с? Ответ ОТВЕТ: 3.
Задача 5. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + {t^2} — 9t + 12), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 15 м/с? Ответ ОТВЕТ: 4.
Задача 6. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние S. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте). Ответ ОТВЕТ: 6.

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Физический смысл производной»

Открытый банк заданий по теме физический смысл производной. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №1148

Тип задания: 7
Тема:
Физический смысл производной

Условие

Материальная точка движется прямолинейно по закону x(t)=frac14t^3-4t^2+t, где x —расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была 13 м/с?

Показать решение

Решение

Согласно физическому смыслу производной необходимо решить уравнение x'(t)=13.

x'(t)=frac34t^2-8t+1. Решаем уравнение:

frac34t^2-8t+1=13,

frac34t^2-8t-12=0,

3t^2-32t-48=0,

t_{1,2}= frac{16pmsqrt{256+3cdot48}}{3}= frac{16pmsqrt{400}}{3}= frac{16pm20}{3}.

t_1=-frac43, t_2=12.

Так как tgeqslant0, то t=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1138

Тип задания: 7
Тема:
Физический смысл производной

Условие

Материальная точка движется прямолинейно по закону x(t)=-t^4+7t^3+6t+16, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=5 с.

Показать решение

Решение

Согласно физическому смыслу производной необходимо найти x'(5).

x'(t)=-4t^3+21t^2+6.

x'(5)= -4cdot 5^3+21cdot 5^2+6= -500+525+6= 31.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №899

Тип задания: 7
Тема:
Физический смысл производной

Условие

Материальная точка движется прямолинейно по закону x(t)=frac14t^3-4t^2+t, где

х — расстояние от точки отсчёта в метрах,

t — время в секундах, измеренное с начала движения.

Найдите её скорость (в метрах в секунду) в момент времени t = 12 с.

Показать решение

Решение

Согласно физическому смыслу производной необходимо найти x'(12).

x'(t) = frac34t^2-8t+1,

x'(12) = frac34cdot12^2-8cdot12+1= 108-96+1=13.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №304

Тип задания: 7
Тема:
Физический смысл производной

Условие

Материальная точка движется прямолинейно по закону x(t)=frac13 t^3-t^2-5t+18, где

x — расстояние от точки отсчета в метрах,

t — время в секундах, измеряемое с начала движения.

В какой момент времени (в секундах) ее скорость была равна 10 м/с?

Показать решение

Решение

Найдем скорость движения точки: v(t)=x'(t)=t^2-2t-5.

По условию v(t)=10 м/с, значит, t^2-2t-5=10,

t^2-2t-15=0,

t_1=5,;t_2=-3.

По смыслу задачи tgeq 0, следовательно, t=5 с.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №89

Тип задания: 7
Тема:
Физический смысл производной

Условие

Закон прямолинейного движения материальной точки равен x(t)=-frac13t^4+4t^3-7t^2-5t-5, где

x – расстояние от точки отсчета (м);

t – время с начала движения (с).

Найдите скорость точки в момент времени t = 6 с. Ответ выразите в метрах в секунду

Показать решение

Решение

Скорость точки в определенный момент времени определяется как производная ее координаты в этот момент времени:

V(t)=frac{dx(t)}{dt}=-frac43t^3+12t^2-14t-5.

Найдем скорость в момент времени t = 6:

V(6)=-frac43cdot 216+12cdot 36-14cdot 6-5=-377+432=55 м/с

Ответ

Задание №88

Тип задания: 7
Тема:
Физический смысл производной

Условие

Закон прямолинейного движения материальной точки равен x(t)=frac12t^2+2t-15, где

x – расстояние от точки отсчета (м);

t – время с начала движения (с).

Найдите скорость точки в момент времени t = 7 с. Ответ выразите в метрах в секунду

Показать решение

Решение

V(t)=frac{dx(t)}{dt}=t+2.

Найдем скорость в момент времени t = 7:

V (7) = 7 + 2 = 9 м/с

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Материальная точка движется прямолинейно по закону

x(t) = –frac{1}{3}t³ + 4t² – 3t + 15,

где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 7 с.

Источник: Ященко ЕГЭ 2022 (36 вар)

Решение:

Скорость – это производная от расстояния:

v(t) = x′(t) = –frac{1}{3}·3·t^3–1 +4·2·t^2–1 – 3·1·t^1–1+ 0 = –t² + 8t – 3

Находим скорость в момент времени t = 7 c:

v(7) = –(7)² + 8·7 – 3 = –49 + 56 – 3 = 4

Ответ: 4.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.8 / 5. Количество оценок: 91

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.

Геометрический смысл производной

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке x_0 равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции f(x) в точке x_0 равна тангенсу угла наклона касательной, проведенной в точке x_0 .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке x_0 функция убывает, следовательно, её производная отрицательна. Касательная в точке x_0 образует тупой угол alpha с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла varphi , смежного с углом alpha .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку $alpha + varphi = 180^{circ}$ , имеем:

$tg alpha = tg(180^{circ} -varphi ) = - tg varphi = -0, 25.$

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой y=kx+b в точке x_0 .

При x= x_0 значения выражений и kx+b равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

$left{ begin{array}{c}fleft(xright)=kx+b \f^{$

$left{ begin{array}{c}x^3+{7x}^2+7x-6=-4x-11 \{3x}^2+14x+7=-4 end{array}right..$

Из второго уравнения находим x = -1 или $x=-frac{11}{3}.$ Первому уравнению удовлетворяет только x = -1 .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени t = 3 с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени t=3 получим:

Ответ: 3.

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция f (x) возрастает.

Если , то функция f (x) убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

	возрастает	точка максимума	убывает	точка минимума	возрастает
		0		0

5. На рисунке изображен график функции y=f(x) , определенной на интервале Найдите количество точек, в которых производная функции f(x) равна 0.

Производная функции f { в точках максимума и минимума функции f(x). Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график y = f — производной функции f(x) , определённой на интервале (-6; 5) . В какой точке отрезка [-1; 3] функция f(x) принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке [-1;3] производная функции f(x) положительна.

Значит, функция f(x) возрастает на этом отрезке. Большим значениям х соответствует большее значение f(x). Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции y= f(x) , определённой на интервале (-3; 8) . Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 1.

Прямая y=1 параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции f(x) , определенной на интервале Найдите количество точек максимума функции f(x) на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке [-6; 9] такая точка всего одна! Это x=7.

Ответ: 1.

9. На рисунке изображен график производной функции f(x) , определенной на интервале Найдите точку экстремума функции f(x) на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке x = -2. В этой точке производная меняет знак с минуса на плюс.

Значит, x= -2 является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция F(x) , для которой f(x) является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции f(x) , определённой на интервале Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке

Функция F(x), для которой f(x) является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку [-4; 4] , в которых производная функции F(x) равна нулю. Это точки максимума и минимума функции F(x). На отрезке [-4; 4] таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

ЕГЭ Профиль №6. Физический смысл производной

ЕГЭ Профиль №6. Физический смысл производной

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Физический смысл производной»

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Новое и интересное на сайте: