Мти вступительный экзамен математика - Exhelper.top

Вступительный тест по математике в МОИ (МТИ, ВТУ)

Решите уравнение

0 и 3
2 и 5
1 и 2
-1 и 0

Основное логарифмическое тождество

Расстояние между двумя точками на координатной плоскости находится по формуле… Выберите один ответ:

(x2-x1)2+(y2-y1)2

Признак делимости … на 9

Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 3

Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9
Число делится на 9 тогда и только тогда, когда две последние цифры … составляют число, кратное 9
Число делится на 9 тогда и только тогда, когда последняя цифра … делится на 9

Множество значений функции

[1;3]

Чему равен объем конуса?

1/3п*r2*h

Сумма логарифмов по одинаковому основанию

loga(bc)

Чему равна площадь поверхности правильного тетраэдра со стороной а? Выберите один ответ:

a2*3корень3/4

Найдите , если ; .

-3
0,1
3
1

Определение хорды… Выберите один ответ:

Хордой называется отрезок, проходящий через центр окружности.
Хордой называется отрезок, соединяющий 2 точки окружности.
Хордой называется отрезок, соединяющий вершины четырехугольника.
Хордой называется отрезок, соединяющий вершину треугольника и середину противоположной стороны

Какая функция называется периодической? Выберите один ответ:

Функция называется периодической, если существует такое число Т, что при выполняется равенство.
Функция называется периодической, если существует такое число Т, что на всей области определения выполняется равенство.
Функция называется периодической, если существует такое число Т (Т>0), что на всей области определения выполняется равенство.
Функция называется периодической, если существует такое число Т (Т>0), что при выполняется равенство.

Чему равен?

p*loga*b

Найдите область определения функции

Какие прямая и плоскость называются параллельными?

Прямая и плоскость называются параллельными, если они не имеют общих точек.
Прямая и плоскость называются параллельными, если они могут иметь общие точки на бесконечности.
Прямая и плоскость называются параллельными, если прямая не лежит в этой плоскости.
Прямая и плоскость называются параллельными, если прямая лежит в этой плоскости.

В институте учится 20 000 студентов. 65% из них – работают. Среди неработающих студентов 25% получают второе высшее образование. Сколько неработающих студентов получают второе высшее образование?

1750
7000
5000
3250

В . Найти .

Цена упаковки кофе – 200 рублей. Какое наибольшее число таких упаковок можно купить на 900 рублей после снижения цены на 15%?

Бросают 2 игральных кости. Найти вероятность того, что в результате выбрасывания на первой кости выпадет число очков 3, а на второй 5.

1/36

Чему равняется ?

sinasinb+cosacosb

Из множества натуральных чисел от 21 до 34 случайным образом выбирают одно число. Какова вероятность того, что оно делится на 4? Ответ округлите до сотых.

0,28
0,29
0,21
0,35…

Другие статьи

Налоги и налогообложение — тесты МТИ, МОИ
Налоговый учет и отчетность (2)- тесты МТИ (МОИ, ВТУ)
Налоговый учет и отчетность- тесты МТИ (МОИ)
Обществознание — тесты МТИ (МОИ)
Ответы МТИ по предмету «Философия»

Источник

Программы вступительных испытаний, проводимых организацией самостоятельно

Если у вас остались вопросы

заполните форму и консультант приемной комиссии свяжется с вами

Позвонить

Подать заявку на обучение

Источник

Вопрос 1

Множеством значений функции y = sin x является …

*[0;1]

*(-∞; + ∞)

*[0; +∞)

*[-1;1]

Вопрос 2

Определение параллелограмма.

*Параллелограмм – четырехугольник, у которого равны все стороны

*Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны

*Параллелограмм – четырехугольник, у которого две стороны параллельны

*Параллелограмм – шестиугольник, у которого противоположные стороны попарно параллельны

Вопрос 3

Модуль числа |a|= …

Вопрос 4

Чему равно отношение площадей подобных фигур, если отношение их сторон равно 2/3?

*4/9

*3/2

*2/3

*1/3

Вопрос 5

Чему равна площадь поверхности правильного тетраэдра со стороной a?

Вопрос 6

Чему равен косинус двойного угла?

Вопрос 7

Чему равняется (a^m)^n=…?

*a^m+n

*a^m^n

*a^m-n

*a^mn

Вопрос 8

Найдите значение выражения

*36

*18

Вопрос 9

Достаточное условие убывания функции на промежутке.

Вопрос 10

Вычислите:

*√ 5

*2 √ 5

Вопрос 11

Признак делимости числа на 9

*Число делится на 9 тогда и только тогда, когда последняя цифра числа делится на 9

*Число делится на 9 тогда и только тогда, когда две последние цифры числа составляют число, кратное 9

*Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9

*Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 3

Вопрос 12

Окружность вписана в трапецию ABCD. Известно, что AD = 12; BC = 18.

Найдите периметр ABCD.

*60

*90

*30

*50

Вопрос 13

Чему равен объем параллелепипеда?

Вопрос 14

Найдите tga, если sina=

*0,1

*-3

Вопрос 15

На складе 120 деталей, из них 15 бракованных.

Найдите вероятность того, что при случайном выборе деталь окажется бракованной.

*0,875

*0,08

*0,125

Вопрос 16

Какие прямые называются скрещивающимися?

*Прямые называются скрещивающимися, если они пересекаются

*Прямые называются скрещивающимися, если они не параллельны

*Прямые называются скрещивающимися, если они не лежат в одной плоскости

*Прямые называются скрещивающимися, если они перпендикулярны

Вопрос 17

В январе горные лыжи стоили 40 000 рублей, в марте цена снизилась на 10%, а в апреле еще на 15%. Сколько рублей стали стоить горные лыжи после снижения цены в апреле?

Выберите один ответ:

*30600

*30000

*34000

*36000

Вопрос 18

Радиус окружности, вписанной в треугольник, равен 4. Периметр этого треугольника равен 8.Найдите площадь треугольника.

*12

*16

*32

Вопрос 19

Что называется сектором круга?

*Сектор круга — это часть круга, ограниченная дугой и двумя радиусами, проведенными к концам дуги

*Сектор круга — это часть круга, ограниченная двумя хордами

*Сектор круга — это часть круга, ограниченная дугой и хордой

*Сектор круга — это часть круга, ограниченная дугой и касательной

Вопрос 20

Достаточное условие убывания функции на интервале.

Источник

Добрый день .я запулся .где можно найти тесты с ответами ?

Добавлено через 1 минуту

Цитата:

Сообщение от Ольга

…

сдесь нету ответов!

Добавлено через 4 минуты
Красотуля, рямые и При каком значении a они перпендикулярны?
Выберите один ответ:

a= 2

a=-2

a= 1

a= 4
Вопрос 2
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Даны вершины треугольника ABC: A(3; -1),B(4; 2) и C(-2; 0). Напишите уравнения его сторон
Выберите один ответ:

3x-y- 10 = 0, x- 3y+ 2 = 0, x+ 5y+ 2 = 0

3x-y= 0, x+ 3y- 6 = 0, x- 5y+ 3 = 0

x-y+ 10 = 0, 3x- 3y+ 2 = 0, x+ 5y+ 2 = 0
Вопрос 3
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол j= 45°
Выберите один ответ:

y= 2x- 2

y=x+ 2

y= 2x+ 2

y=x- 2
Вопрос 4
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Найдите уравнение прямой, проходящей через точки M1(3; 2), M2(4;-1)
Выберите один ответ:

3x-y+ 11 = 0

x+y- 12 = 0

3x+ 2y- 11 = 0

3x+y- 11 = 0
Вопрос 5
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Установите взаимное расположение прямых и
Выберите один ответ:

прямые параллельны

прямые скрещиваются

прямые перпендикулярны

прямые пересекаются, но не перпендикулярны
Вопрос 6
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Уравнение 3x- 4y+ 12 = 0 преобразуйте к уравнению в отрезках
Выберите один ответ:

Вопрос 7
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Укажите канонические уравнения прямой, проходящей через точки M1(3; 2; 5) и M2(-1; 3; -2)
Выберите один ответ:

Вопрос 8
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Найдите координаты точки K пересечения прямой с плоскостью 2x+ 5y- 3z= 0
Выберите один ответ:

Вопрос 9
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M1(-2; 3)
Выберите один ответ:

5x+ 13y- 9 = 0

5x+ 13y- 29 = 0

5x+ 3y- 29 = 0

3x+ 8y- 18 = 0
Вопрос 10
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Составьте уравнение плоскости, проходящей через параллельные прямые и
Выберите один ответ:

6x- 20y- 11z+ 1 = 0

x- 20y- 10z+ 1 = 0

6x- 20y- 11z= 0

6x+ 20y- 11z+ 1 = 0
Вопрос 11
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Укажите канонические уравнения прямой
Выберите один ответ:

Вопрос 12
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Найдите острый угол между прямыми и
Выберите один ответ:

45°

60°

30°

90°
Вопрос 13
Пока нет ответа
Балл: 1
Отметить вопрос
Текст вопроса

Найдите координаты точки пересечения прямых 2x-y- 3 = 0 и 4x+ 3y- 11 = 0
Выберите один ответ:

(1; 3)

(2; 1)

(1; 2)

(2; 2)

Источник

Абитуриентам
Одним из главных принципов уникальной «системы Физтеха», заложенной в основу образования в МФТИ, является тщательный отбор одаренных и склонных к творческой работе представителей молодежи. Абитуриентами Физтеха становятся самые талантливые и высокообразованные выпускники школ всей России и десятков стран мира.
- Приемная комиссия
- Физтех-центр
- ЗФТШ
- Школы
- Олимпиады и конференции
Студентам
Аспирантам
Выпускникам

О Физтехе
Образование
Наука и инновации
Новости науки

МФТИ
Образование
Институтские кафедры
Кафедра высшей математики
Экзамены (контроль успеваемости)
Вступительные экзамены по математике

Программа по математике для восстанавливающихся и переводящихся в МФТИ из других вузов в 2020 г.
Порядок проведения дистанционного устного экзамена для переводников 2020 г.
Письменные работы по математике для переводащихся в МФТИ из других вузов и поступающих в магистратуру в 2007 году
Варианты вступительных заданий для поступающих в магистратуру и восстанавливающихся

Если вы заметили в тексте ошибку, выделите её и нажмите Ctrl+Enter.

Источник

ПРОГРАММА ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ В БАКАЛАВРИАТ И СПЕЦИАЛИТЕТ

Процедура проведения вступительного испытания

1. Вступительное испытание проводится в соответствии с действующими Правилами приема в бакалавриат и специалитет и Положением о порядке проведения вступительных испытаний МФТИ.

2. Вступительное испытание по математике проводится с совмещением письменной и устной форм.

3. Вступительное испытание состоит из четырех частей.

4. Первые три части вступительного испытания – решение задач с численным ответом. Длительность каждой части – 45 минут.

5. Первая часть вступительного испытания вступительного испытания, проводимого с использованием дистанционных технологий, проверяется программно-аппаратным способом.

6. Допуск ко второй письменной части и последующим частям вступительного испытания проводится по результатам проверки первой письменной части. Недопущенным ко второй и последующим частям вступительного испытания выставляется балл на основании проверки первой части вступительного испытания.

7. Четвертая часть вступительного испытания – устный опрос по задачам и программе вступительного испытания. Длительность устной части – до 30 минут.

Программа вступительного испытания

1. Натуральные числа. Делимость. Простые и составные числа. Признаки делимости. Наибольший общий делитель и наименьшее общее кратное.

2. Целые, рациональные, действительные числа и операции с ними.

3. Преобразование арифметических и алгебраических выражений. Формулы сокращённого умножения.

4. Числовые неравенства и их свойства.

5. Функция. Область определения и множество значений. График функции. Чётность, нечётность, периодичность функций. Линейная, квадратичная, степенная, дробно-рациональная функции и их свойства.

6. Линейные уравнения. Квадратные уравнения. Рациональные уравнения. Уравнения с модулем. Уравнения высших степеней. Разложение многочленов на множители.

7. Линейные неравенства. Квадратные неравенства. Рациональные неравенства. Неравенства с модулем.

8. Корень из числа и его свойства. Арифметический корень. Иррациональные уравнения. Иррациональные неравенства.

9. Арифметическая и геометрическая прогрессии и их свойства.

10. Комбинаторика. Правила суммы и произведения. Перестановки, размещения, сочетания.

11. Задачи на составление уравнений (задачи на движение, на проценты, на совместную работу, на смеси и пр.).

12. Тригонометрические формулы. Тригонометрические и обратные тригонометрические функции и их свойства. Преобразование тригонометрических выражений. Тригонометрические уравнения и неравенства.

13. Свойства степеней. Логарифмы и их свойства. Показательная и логарифмическая функции и их свойства. Показательные и логарифмические уравнения и неравенства.

14. Производная. Исследование функций с помощью производных.

15. Задачи с параметром.

16. Системы уравнений и неравенств.

17. Множества точек на координатной плоскости.

18. Планиметрия:

— смежные и вертикальные углы,

— признаки и свойства равнобедренного треугольника, признаки равенства треугольников,

— теоремы о параллельных прямых, сумма углов треугольника, сумма углов выпуклого многоугольника,

— геометрические места точек (множество внутренних точек угла, равноудалённых от его сторон, множество точек, равноудалённых от концов отрезка),

— медианы, биссектрисы, высоты треугольника и их свойства,

— подобие треугольников, теорема Фалеса, теорема о пропорциональных отрезках,

— четырёхугольники; параллелограмм, прямоугольник, ромб, квадрат, трапеция и их свойства,

— пропорциональные отрезки в прямоугольном треугольнике, теорема Пифагора,

— площадь и её свойства,

— формулы площади треугольника, параллелограмма, трапеции,

— точки пересечения высот, медиан, биссектрис, серединных перпендикуляров треугольника,

— теоремы синусов, косинусов и Менелая для треугольника,

— окружность и её свойства,

— касательная к окружности и её свойства,

— теоремы о пропорциональных отрезках в окружности,

— теоремы об углах, связанных с окружностью (вписанный угол, центральный угол, угол между касательной и хордой),

— окружность, описанная около треугольника; окружность, вписанная в треугольник,

— окружность, описанная около четырёхугольника; окружность, вписанная в четырёхугольник,

— правильные многоугольники и их свойства,

— длина окружности, площадь круга и его частей,

— векторы, скалярное произведение векторов,

— метод координат на плоскости.

19. Стереометрия. Параллельность прямых и плоскостей, перпендикулярность прямых и плоскостей. Объём фигуры; площадь поверхности фигуры. Куб, параллелепипед, призма, пирамида, шар, цилиндр, конус и их свойства. Векторы и координаты в пространстве. Сечения многогранников. Углы и расстояния в пространстве.

Литература

1. Шабунин М.И. Математика. Пособие для поступающих в вузы. М.: – 2016.

2. Гордин Р.К. ЕГЭ 2020. Математика. Геометрия. Планиметрия. Задача 16 (профильный уровень), М.: – 2020.

Источник

В данной статье разобран пример вступительного экзамена по математике в МФТИ (бакалавриат). Если вас интересует разбор вступительного экзамена по физике, вы можете найти его на этой странице. Все решения выполнены профессиональным репетитором по математике и физике, осуществляющим подготовку абитуриентов к вступительным экзаменам в МФТИ (ФизТех).

Разбор вступительного экзамена по математике в МФТИ

1. Решите уравнение:

Используем формулу «синус двойного угла»:

Переносим слагаемые, находящиеся справа от знака равенства, в левую сторону, меняя при этом их знак на противоположный, и выносим за скобки:

Преобразуем теперь выражение, стоящее в скобках, используя формулу «косинус двойного угла»:

$[ sin x(4+2sqrt{3}cos x-2(2cos^2x-1))=0 ]$

$[ sin x(6+2sqrt{3}cos x-4cos^2x)=0. ]$

Произведение равно нулю, если хотя бы один из множителей равен нулю. То есть возможны два случая:

1) .

2) $6+2sqrt{3}cos x-4cos^2x=0.$

Умножим обе части последнего уравнения на и введём замену :

$[ 4t^2-2sqrt{3}t-6=0Leftrightarrowleft[ begin{array}{l} t_1 = -frac{sqrt{3}}{2} \ t_2=sqrt{3}. end{array} ]$

Примечание. Последнее уравнение является квадратным и решается по стандартному алгоритму с помощью дискриминанта.

Возвращаемся к исходной переменной. Получаем, что либо (это уравнение не имеет решений в действительных числах, так как ), либо $cos x = -frac{sqrt{3}}{2}$ . Из последнего уравнения получаем $x = pmfrac{5pi}{6}+2pi n,, nin Z$ .

Ответ: $x=pi n,,x=pmfrac{5pi}{6}+2pi n,, nin Z$ .

2. Решите систему уравнений:

$[ begin{cases} x^3+y^3=19 \ (xy+8)(x+y)=2. end{cases} ]$

Преобразуем выражение с суммой кубов:

В скобках заменим член на разность . От этого равенство не нарушится. В результате получим:

Итак, исходную систему можно представить в следующем виде:

$[ begin{cases} (x+y)((x+y)^2-3xy)=19 \ (xy+8)(x+y)=2. end{cases} ]$

Теперь используем замену: и . Тогда система принимает вид:

$[ begin{cases} a(a^2-3b)=19 \ a(b+8)=2 end{cases}Leftrightarrow begin{cases} a^3-3ab = 19 \ 3ab+24a=6. end{cases} ]$

Теперь складываем почленно оба уравнения и приходим к следующему уравнению:

Корень этого уравнения угадывается автоматически: . Других корней не будет, так как справа стоит возрастающая функция, поскольку она является суммой возрастающих функций, поэтому нулевое значение она может принимать только при каком-то одном значении .

Итак, , значит . Возвращаясь к исходным переменным, получаем следующую систему:

$[ begin{cases} x+y = 1 \ xy=-6. end{cases} ]$

В результате приходим к окончательному ответу: и .

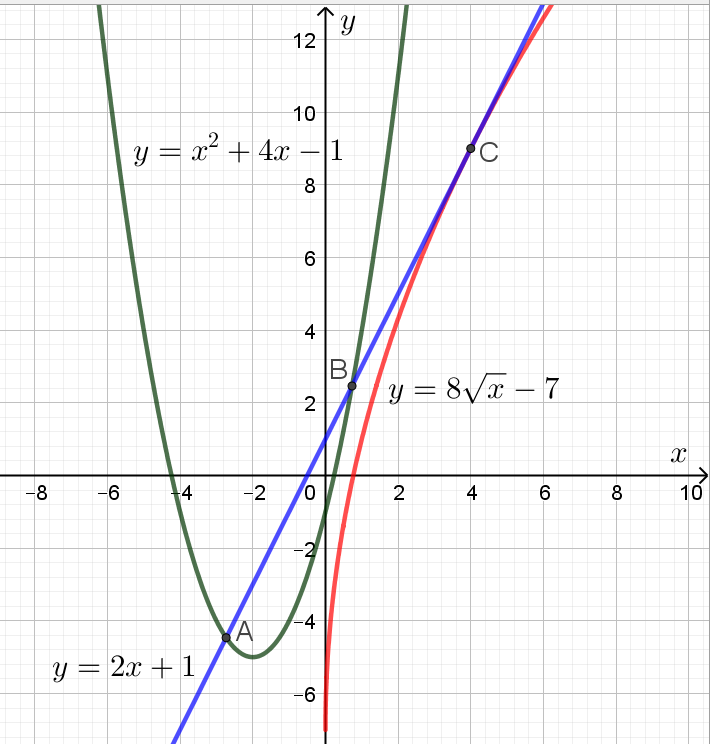
В общем виде уравнение прямой может быть записано следующим образом: . Известно, что эта прямая проходит через точку , то есть имеет место равенство:

(1)

Кроме того, прямая касается графика функции . Значит уравнение

должно иметь ровно один корень. Введём замену . Тогда последнее условие эквивалентно тому, что дискриминант квадратного уравнения

(2) $begin{equation*} kt^2-8t+7+b =0 end{equation*}$

равен нулю, и корень при этом неотрицателен. То есть получаем:

Таким образом с учётом уравнения (1) приходим к следующей системе:

$[ begin{cases} k+b = 3 \ 16-7k-kb=0. end{cases} ]$

Решая эту систему методом подстановки, получаем следующие результаты: ( и ) или ( и ). При и уравнение (2) имеет один неотрицательный корень . При и уравнение (2) имеет один неотрицательный корень $x=frac{1}{2}$ .

То есть из двух прямых и нужно выбрать такую, которая пересекает график функции в двух различных точках.

Решаем сперва уравнение:

Дискриминант последнего уравнения положителен. Значит, оно имеет два различных корня. Этот случай нам подходит.

Решаем теперь уравнение:

Дискриминант этого уравнения равен нулю. Значит, решение в этом случае будет одно. Этот случай нам не подходит.

Ответ: .

Примечание. Для наглядности изобразим ситуацию на графике, хотя делать это необязательно, поскольку в задании этого не требуют:

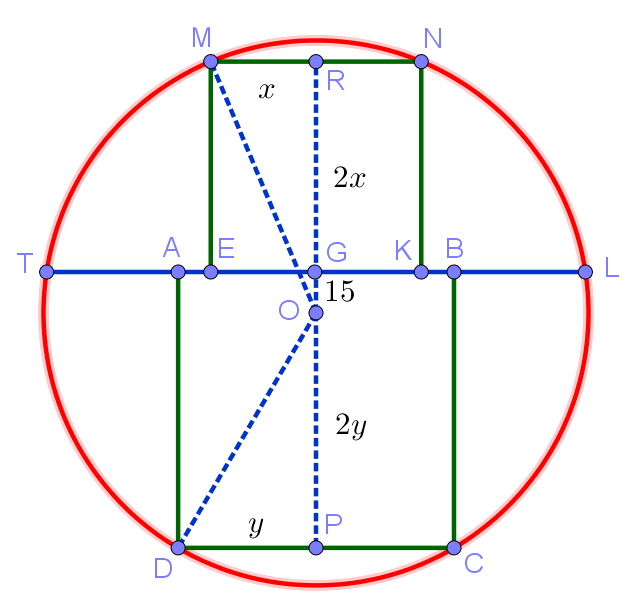
4. Хорда окружности, удалённая от центра на расстояние 15, разбивает окружность на два сегмента, в каждый из которых вписан квадрат. Найдите разность сторон этих квадратов.

Пусть радиус окружности равен . Рассмотрим прямоугольные треугольники OMR и ODP. С учётом введённых на рисунке обозначений распишем теорему Пифагора для этих треугольников:

$[ begin{cases} x^2 = R^2-(2x+15)^2 \ y^2 = R^2 - (2y-15)^2. end{cases} ]$

Вычтем почленно второе уравнение из первого:

Преобразуем полученное выражение, используя формулу «разность квадратов»:

Поделим обе части этого уравнения на и обозначит разность за . В результате приходим к следующему уравнению:

Искомая разность сторон квадратов в наших обозначениях будет равна .

Ответ: 24.

5. Решите неравенство

$[ log_4left(5-3^xright)cdotlog_2left(frac{5-3^x}{8}right)geqslant -1. ]$

Введём замену: . Тогда неравенство принимает вид:

$[ log_{2^2} tcdotlog_2left(frac{t}{8}right)geqslant -1. ]$

Теперь, используя стандартные свойства логарифмов, представим логарифмическое выражение слева от знака неравенства следующим образом:

$[ frac{1}{2}log_2 tleft(log_2 t - 3right)geqslant -1. ]$

Введём ещё одну замену: . Тогда после умножения обеих частей неравенства на положительное число неравенство принимает вид:

$[ z^2-3z+2geqslant 0Leftrightarrow left[ begin{array}{l} zleqslant 1\ zgeqslant 2. end{array} ]$

Последовательно возвращаемся к исходной переменной :

$[ left[ begin{array}{l} log_2 tleqslant 1\ log_2 tgeqslant 2. end{array}Leftrightarrow left[ begin{array}{l} 0< tleqslant 2\ tgeqslant 4. end{array}Leftrightarrow ]$

$[ left[ begin{array}{l} 0< 5-3^xleqslant 2\ 5-3^xgeqslant 4. end{array}Leftrightarrow left[ begin{array}{l} 3leqslant 3^x < 5\ 3^xleqslant 1. end{array} ]$

Окончательно получаем следующий ответ: $xin(-mathcal{1};0]cup[1;log_3 5).$

Пусть в первую бочку долили кг воды, а во вторую — кг. Пусть в первой бочке находится кг, а во второй кг соли.

Тогда изначально в первой бочке процентное содержание соли составляло:

$[ frac{a}{16}times 100%, ]$

а после доливания воды оно стало равно:

$[ frac{a}{x+16}times 100%. ]$

Аналогично, во второй бочке изначально процентное содержание соли составляло:

$[ frac{b}{25}times 100%, ]$

а после доливания воды оно стало равно:

$[ frac{b}{y+25}times 100%. ]$

Тогда справедливы равенства:

(3) $begin{equation*} frac{a}{16}:frac{a}{x+16}=frac{x+16}{16}=1+frac{x}{16} = k end{equation*}$

(4) $begin{equation*} frac{b}{25}:frac{b}{y+25}=frac{y+25}{25} = 1+frac{y}{25} = m. end{equation*}$

Из уравнения (3) выражаем , из уравнения (4) выражаем , а из уравнения выражаем $k=frac{m+3}{m-1}$ . Мы ищем минимальное значение суммы . Проще всего найти его, используя неравенство Коши:

$[ =40sqrt{left(frac{m+3}{m-1}-1right)(m-1)}= ]$

Итак, наименьшее количество воды, которое могло быть долито в обе бочки вместе равно 80 кг.

Этот случай реализуется при , когда неравенство Коши преобразуется в равенство. То есть при $k = dfrac{25}{16}m-dfrac{9}{16}$ . Подставляя это в выражение , получаем после преобразований, что $m = dfrac{13}{5}$ . Отрицательный корень мы в расчёт не берём.

Ответ: 80 кг.

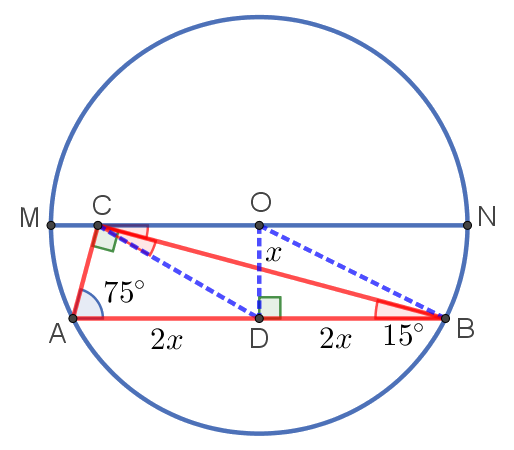
7. Вершина прямого угла C прямоугольного треугольника ABC расположена на диаметре окружности, параллельном хорде AB. Найдите площадь треугольника ABC, если ∠BAC = 75°, а радиус окружности равен 10.

Выполним следующие дополнительные построения:

проведём высоту OD к хорде AB. Тогда D — середина AB, так как OD — высота и медиана, проведённая к основанию равнобедренного треугольника AOB;
проведём отрезок CD. Он является медианой прямоугольного треугольника ACB, проведённой из вершины прямого угла. Значит, CD = AD = BD.

Переходим к решению:

сумма углов в любом треугольнике равна 180°. Значит, ∠CBA = 15°;
так как CD = BD, то треугольник CDB — равнобедренный и ∠CBD = ∠DCB = 15°;
∠CBD = ∠BCO = 15°, поскольку они являются накрест лежащими при параллельных прямых и секущей. Значит, ∠DСO = 30°;
значит, в прямоугольном треугольнике COD против угла в 30° лежит катет OD, который равен половине гипотенузы CD. Пусть DO = x, а CD = AD = DB = 2x;
из теоремы Пифагора для треугольника ODB получаем, что , то есть ;
тогда искомая площадь треугольника ABC равна половине произведения его высоты, проведённой к стороне AB, которая по длине равна x, на основание AB, которое по длине равно 4x. То есть искомая площадь равна .

Ответ: 40.

8. Найдите все значения параметра

, для каждого из которых неравенство

выполняется для всех значений .

Преобразуем данное неравенство, раскрыв в нём скобки и использовав основное тригонометрическое тождество. В результате после всех преобразований получаем следующее неравенство:

Ведём замену , причём . Тогда получим следующее неравенство:

Задача свелась к тому, чтобы найти все значения параметра , при котором последнее неравенство выполняется при всех .

Для решения этой задачи представим последнее неравенство в виде:

Легко видеть, что при любых значениях , так как дискриминант соответствующего квадратного уравнения отрицателен, и ветви соответствующей параболы направлены вверх. Поэтому мы можем разделить обе части последнего неравенства на положительное выражение , при этом знак неравенства не поменяется:

(5) $begin{equation*} a <frac{t+3}{t^2-6t+11}. end{equation*}$

Исследуем функцию $y=dfrac{t+3}{t^2-6t+11}$ на возрастание. Для этого определим при каких значениях её производная положительна:

$[ y'=-frac{t^2+6t-29}{(t^2-6t+11)^2}>0Leftrightarrow ]$

Так как , а , то на промежутке данная функция возрастает. Поэтому неравенство (5) будет выполняться при любом при условии, что , то есть $a<dfrac{3}{11}$ .

Ответ: $ainleft(-mathcal{1};dfrac{3}{11}right)$ .

Подготовка к вступительному экзамену по математике в МФТИ

Если вам требуется подготовка к вступительному экзамену по математике в МФТИ, обращайтесь к опытному профессиональному репетитору в Москве Сергею Валерьевичу. Возможны как очные, так и удаленный занятия через интернет с использованием интерактивной доски. Как показывает практика, в условиях ограниченности во времени именно занятия с репетитором обеспечивают наиболее эффективную подготовку к вступительным экзаменам. Подробную информацию о занятиях с репетитором вы можете найти на этой странице. Успехов вам в подготовке к экзаменам!

Источник

Вступительный тест по математике в МОИ (МТИ, ВТУ)

Программы вступительных испытаний, проводимых организацией самостоятельно

ПРОГРАММА ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ В БАКАЛАВРИАТ И СПЕЦИАЛИТЕТ

Разбор вступительного экзамена по математике в МФТИ

Подготовка к вступительному экзамену по математике в МФТИ

Новое и интересное на сайте: