Оформление 15 номера егэ математика профильный уровень - Exhelper.top

: ЕГЭ по математике профиль

В презентации: консультация по математике «Подготовка к ЕГЭ по профильной математике 2020» показаны примеры и анализ решения заданий повышенного уровня с развернутым ответом заданий профильного уровня 13, 15 и 17.

На слайдах представлен примерный ход решения с ответом. Также даны рекомендации и задания на повторение.

Автор: Козляковская Л. С.

→ Скачать примеры

Пример заданий:

Задача №13

Суть задачи №13 сводится к решению уравнения (в 95% случаев – тригонометрического) с использованием различных формул и методов преобразования и упрощения выражений.

В задаче №15 нужно решить неравенство (т.е. найти множество всех значений х, при которых это неравенство выполняется), подробно изложив ход решения.

Задачи №17 — это текстовые задачи экономического содержания, в которой усилена практическая составляющая условия.

Данные задачи можно разделить на два типа: задачи, использующие дискретные модели (проценты, кредиты, вклады, вклады с пополнением и др.), и задачи, использующие непрерывные модели (производство, объемы выпускаемой продукции, протяженные во времени, и др.).

В любом случае, данные задачи требуют построения математической модели, введения переменных и решения составленных уравнений или системы уравнений.

Связанные страницы:

Источник

9 октября 2019

В закладки

Обсудить

Жалоба

У многих учеников есть вопрос: как оформлять неравенство на ЕГЭ? Можно ли писать ОДЗ и как сделать это правильно?

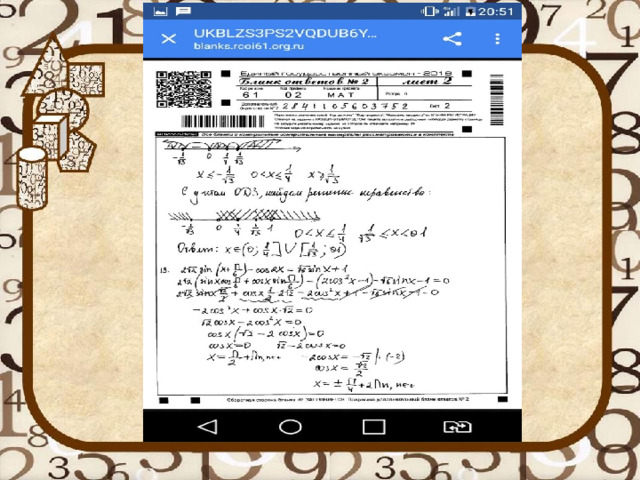
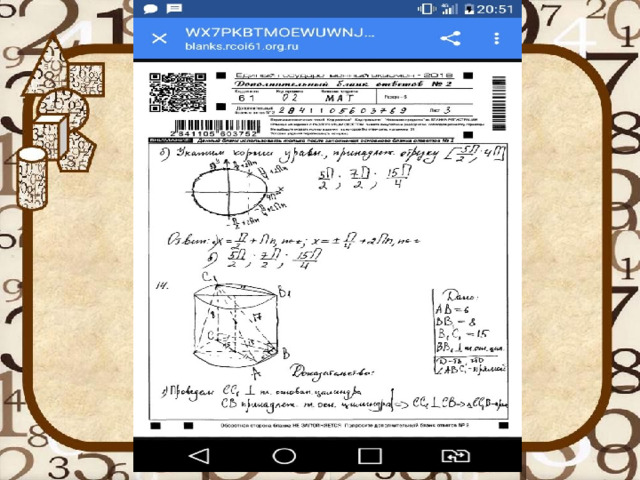
Ниже представлено оформление задания №15 на максимальные 2 первичных балла. Изучите внимательно каждую строку преобразований.

Автор: Артур Шарафиев | vk.com/art_umsch

o15.pdf

Источник

» Разбор и оформление 13 и 15 задания ЕГЭ(профильный уровень)»

Докладчик: учитель МБОУ СОШ № 5

Кугатова Ирина Романовна

Раньше и трава была зеленее

Всю жизнь все при решении неравенств и уравнений в ЕГЭ по профильной математике писали ОДЗ (Область Допустимых Значений), понимая под этим ограничения, накладываемые на аргумент «непростыми» функциями типа квадратного корня или логарифма. И не было проблем.

За ТАКОЕ точно снизят

Семинар Трушкиной Т.П., методиста из Кемеровской области, наделал много шума. Оказалось, что на ЕГЭ по математике можно получит 0 баллов за задачу, даже имея верный ответ и верную последовательность рассуждений. Все из-за неправильного использования понятия «ОДЗ». Первое, что ясно совершенно точно: если вы выписали «ОДЗ» «не полностью» — прощайтесь с баллами за задачу. Если вы решили выписать лишь ограничения, вносимые логарифмической функцией, а условие отличия знаменателя от нуля оставить на потом («ну они ведь и далее сохранятся, «переход равносилен»»), и назвали эти «неполные» ограничения словом ОДЗ — то это 0 баллов. И можно было даже не браться за задачу.

За ТАКОЕ точно снизят

А что говорят интернет-гуру?

Специалисты в области подготовки к ЕГЭ по профильной математике разделились во взглядах. Многие известные Ютуб-блогеры (Борис Трушин, Wild Mathing) придерживаются того мнения, что полностью выписанная ОДЗ ни в коем случае к снижению баллов не приведет . Однако выписаны ограничения, действительно, должны быть полностью. То есть если у вас, например, имеется неравенство с логарифмом, да который ещё и стоит в знаменателе дроби — будьте любезны, потребуйте, чтобы аргумент логарифма был положителен, основание положительно и отлично от единицы, а также чтобы знаменатель вашей дроби был отличен от нуля.

А что говорят интернет-гуру?

То, что за верно выписанную ОДЗ вам не снизят баллы, подтверждают и официальные методические рекомендации по оцениванию выполнения заданий с развернутым ответом ЕГЭ по профильной математике от РосОбрНадзора. Ниже приведен пример работы с верно выписанной ОДЗ. Работа оценена на максимальный балл. К ОДЗ никто не придирался.

И как же быть?

1.Если Вы привыкли использовать ОДЗ — используйте, но пишите его полностью. Если снизят — идите на апелляцию. Методичка по оцениванию — вам в помощь. 2.Если Вы умеете работать с равносильными переходами — вы красавчик =) Это самый безопасный вариант. Но писанины будет… Запасайтесь бланками заранее. 3.Если не устраивают предыдущие два пункта — озаглавьте ОДЗ словом «ограничения» или вообще никак не называйте. Это безопасно, даже если забудете какое-то важное условие.

И как же быть?

Скажите детям — пусть они ОДЗ выбросят!

Но даже при правильной, полностью выписанной ОДЗ, есть риск нарваться на неприятности. Эксперт заявляет: в школьных учебниках по математике понятие области допустимых значений (ОДЗ) определен лишь для функций. Поэтому использовать это понятие при решении уравнений и неравенств не рекомендуется. Однако использование ОДЗ в неравенствах и уравнениях активно использовалось преподавателями ВУЗов, в том числе при работе со школьниками, постепенно «мигрировало» в методички и сборники по подготовке к ЕГЭ, и теперь уже прочно укоренилось в умах репетиторов, учителей и абитуриентов. Как показывает практика, полностью выписанные ограничения на переменную под заголовком «ОДЗ» не ведут к снижению баллов на ЕГЭ по профильной математике. Тем не менее, эксперт не рекомендует использовать эту конструкцию.

«Коллеги, лучше вообще ничего не писать; Скажите детям — пусть они ОДЗ выбросят!» — столько эмоций на пустом, казалось бы, месте.

Эксперт рекомендует накладывать ограничения на переменную, при этом никак это не «озаглавливать». При это заголовки типа «ограничения», «условия», «важные замечания» и т.п. возбраняться не должны.

Спасибо за внимание!

Источник

Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.

В этой статье:

Как научиться решать «экономические» задачи. С чего начать.

Две схемы решения задач на кредиты и как их распознать.

Комбинированные задачи.

В чем основная сложность «экономической» задачи.

Задания на оптимальный выбор. В том числе — с применением производной.

Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.

Надеемся, что вы уже сейчас сможете ответить на такие вопросы:

Что принимается за 100%?
Величина х увеличилась на p%. Как это записать?
Величина y дважды уменьшилась на р%. Как это записать?

Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.

Запомним, что есть всего две схемы решения задач на кредиты

Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.

Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга. Подробно здесь.

В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа — формула суммы арифметической прогрессии.

Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.

Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.

Давайте потренируемся.

1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?

Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.

Введем обозначения:

S=6902 тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.

— процент банка,

$k=1+frac{{ p}}{100}=1+frac{125}{1000}=1+frac{1}{8}=frac{9}{8}$ — коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,

— сумма ежегодного платежа.

Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:

— сумма долга увеличивается в раз;

— Аристарх вносит на счет сумму в счет погашения кредита, и сумма долга уменьшается на .

Вот что получается:

Раскроем скобки:

$S{{ k}}^4-{ X}left({{ k}}^3+{{ k}}^2+{ k}+1right)=0.$

Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как

$1+{{ k}+{{ k}}^2+{ k}}^3$ . В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.

Применим формулу суммы геометрической прогрессии:

${{ Sk}}^4={ X}cdot frac{{{ k}}^4-1}{{ k}-1}=0.$ И выразим из этой формулы .

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}.$ Что же, можно подставить численные данные. Стараемся, чтобы наши вычисления были максимально простыми. Поменьше столбиков! Например, коэффициент k лучше записать не в виде десятичной дроби 1,125 — а в виде обыкновенной дроби $frac{9}{8}$ , Иначе у вас будет 12 знаков после запятой!

И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}=frac{{ S}cdot 9^4left(frac{9}{8}-1right)}{8^4cdot left(frac{9^4}{8^4}-1right)}=frac{{ S}cdot 9^4}{8cdot left(9^4-8^4right)}=frac{{ S}cdot 9^4}{8cdot left(9^2-8^2right)left(9^2+8^2right)}=frac{{ S}cdot 9^4}{8cdot left(9+8right)left(9^2+8^2right)}=$

$=frac{6902cdot {81}^2}{8cdot 17cdot 145}=frac{406cdot {81}^2}{8cdot 145}=frac{203cdot {81}^2}{4cdot 145}=frac{29cdot 7cdot {81}^2}{4cdot 29cdot 5} = 2296,35$ тыс.руб.

Ответ: 2296350 рублей.

Вот следующая задача.

2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

В этой задаче сумма долга уменьшается равномерно — задача второго типа.

Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.

Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.

Как обычно, ${ k}=1+frac{{ p}}{100}.$

Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна $frac{1}{24}{ S}.$ После первой выплаты сумма долга равна $frac{23}{24}{ S},$ после второй $frac{22}{24}{ S}.$

Тогда первая выплата ${{ X}}_1={ kS}-frac{23}{24}{ S},$ вторая выплата ${{ X}}_2={ k}cdot frac{23}{24}{ S}-frac{22}{24}{ S}$ ,

dots

Последняя в году выплата ${{ X}}_{12}={ k}cdot frac{13}{24}{ S}-frac{12}{24}{ S}.$

Сумма всех выплат в течение первого года:

${ X}={{ X}}_1+{{ X}}_2+dots +{{ X}}_{12}={ kS}left(1+frac{23}{24}+dots frac{13}{24}right)-{ S}left(frac{23}{24}+frac{22}{24}+dots +frac{12}{24}right).$

В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой ${{ a}}_1=frac{13}{24};{{ a}}_{{ n}}=frac{24}{24}=1.$ Обозначим эту сумму ${{ S}}_1.$

${{ S}}_1=frac{{{ a}}_1+{{ a}}_{12}}{2}cdot 12=frac{13+24}{2cdot 24}cdot 12=frac{37}{4}.$

Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой ${{ b}}_1=frac{12}{24};{{ b}}_{{ n}}=frac{23}{24}.$ Эту сумму обозначим ${{ S}}_{2.}$

${{ S}}_2=frac{{{ b}}_1+{{ b}}_{12}}{2}cdot 12=frac{12+23}{2cdot 24}cdot 12=frac{35}{4}.$

Общая сумма выплат за год:

$small X= S left({ kS}_1-{{ S}}_2right)=frac{1800}{4}left({ 1,01}cdot 37-35right)=$
$=frac{1800cdot { 2,37}}{4}={ 2,37}cdot 450= 1066,5$ тыс. рублей.

Ответ: 1066500 рублей.

Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.

3. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:

− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить часть долга;

− в июле 2017, 2018 и 2019 долг остаётся равным S тыс. рублей;

− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;

− к июлю 2021 долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

Введем переменные: ${ k}=1+frac{25}{100}=frac{5}{4},Y=625$ тысяч рублей. Рисуем схему погашения кредита:

Общая сумма выплат: Кроме того, долг был полностью погашен последней выплатой .

Это значит, что и тогда

${ S}=frac{left({ k}+1right){ Y}}{{{ k}}^2}{ X}=3cdot frac{left({ k}+1right){ Y}}{{{ k}}^2}left({ k}-1right)+2{ Y}=3{ y}left(frac{{{ k}}^2-1}{{{ k}}^2}right)+2{ Y}=$
$={ Y}left(5-frac{3}{{{ k}}^2}right)=625left(5-frac{3cdot 16}{25}right)=frac{625cdot 77}{25}=77cdot 25=1925$ тысяч рублей.

Ответ: 1925 тыс. рублей.

Но не только задачи на кредиты и вклады могут встретиться в задании 15 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары	Себестоимость, 1 центнера	Отпускная цена, 1 центнера
стеклянная	1500 руб	2100 руб
жестяная	1100 руб	1750 руб

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.

Пусть x — доля мощностей завода, занятых под поизводство компотов в стеклянных банках, а y — доля мощностей, занятых под производство компотов в жестяных банках, Тогда x+y=1. (Например, х=0,3 и у = 0,7 — то есть 30% производства — это компот в стеклянных банках, а 70% — компот в жестяных банках).

Если бы завод выпускал только компот в стеклянных банках, их бы получилось 90 центнеров в сутки. Однако выпускаются и те, и другие, и компотов в стеклянных банках производится 90x центнеров, а в жестяных банках — 80y центнеров в сутки.

Составим таблицу.

Вид тары	Доля в общем количестве	Производится в сутки	Прибыль за 1 центнер
стеклянная			2100 — 1500 = 600 руб
жестяная			1750 — 1100 = 650 руб

Общая прибыль завода за сутки равна

По условию, и , то есть $xge frac{2}{9}$ и $yge frac{1}{4}.$

Нужно найти наибольшее значение выражения при выполнении следующих условий:

$left{begin{matrix} x+y=1\ {{2}over{9}}leq x textless 1, \ {1over4}leq y textless 1 end{matrix}right. Leftrightarrow left{begin{matrix} y=1-x\ {2over9}leq x leq {3over4} end{matrix}right. .$

Подставим y=1-x в выражение для прибыли завода за сутки. Получим, что она равна Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при $x=frac{3}{4}.$ Тогда $y=frac{1}{4}$ и максимально возможная прибыль завода за день равна

$2000cdot left(27cdot frac{3}{4}+26cdot frac{1}{4}right)=2000cdot frac{107}{4}=53500$ руб.

Ответ: 53500 руб.

Больше задач по финансовой математике на нахождение наибольших и наименьших значений функций и применение производной — здесь:

Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная

Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 15. Финансовая математика u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Глава 1. Вебинар по оформлению задач второй части ЕГЭ по математике (3 часа, 10 минут)

Почему важно начать учиться оформлять задачи второй части за 30 дней до ЕГЭ? Потому что вам нужно выработать привычку это делать.

Привычка формируется 30 дней (есть исследования). Если вы узнаете о том, как оформлять задачи за неделю до экзамена, будет поздно.

Поэтому читайте материал первой главы, смотрите наше первый вебинар и потом применяйте на практике то, что вы узнаете при решении задач постоянно в течение 30 ДНЕЙ!

И прекратите терять баллы на ровном месте!

Научиться правильно оформлять задачи 2 части ЕГЭ по математике намного проще, чем научиться их решать!

Но тем не менее, каждый год огромное количество людей теряют десятки баллов из-за неправильного оформления.

Если вы посмотрите видео, вы научитесь оформлять задачи так, что гарантированно 100% экспертов ЕГЭ поставят вам полный балл (если вы правильно решите задачу, конечно же;)

На этом видео мы очень подробно разберем все задачи второй части профильного ЕГЭ по математике, и вы узнаете все нюансы оформления:

Что такое критерии, как их понимать?
Что считается опиской, что – арифметической ошибкой, а что – грубой «смысловой» ошибкой?
Нужно ли делать проверку ответов (да), и как её делать?
Тригонометрия: нужно ли писать разные буквы (n, m, k) в ответах или можно использовать одну для всех формул?
Какие способы отбора корней лучше использовать в задаче 13 б), а какие лучше не трогать?
Как правильно показывать отбор на единичной окружности и не потерять при этом балл?
В каких случаях предпочтительно пользоваться окружностью, а в каких – двойным неравенством?
Насколько подробно нужно расписывать решения уравнений и неравенств?
Нужно ли на чистовике полностью прописывать дискриминант и поиск корней, или достаточно вычислить их устно «по теореме Виета»?
Как не запутаться в «значках»: где использовать равносильность, а где следствие, как не перепутать систему и совокупность и прочее?
Можно ли использовать метод рационализации: мифы и реальность Вспомним, что такое ОДЗ, и всегда ли его нужно писать, и как его правильно писать?
Экономическая задача – это вообще отдельная история. Как могут давать аж 3 первичных балла за простую задачу на проценты? А оказывается, что их за саму задачу и не дают: их дают за правильное оформление! И снимают за каждую мелочь. Многие получают 0 баллов, даже получив правильный ответ. Я очень подробно разберу, что же именно от нас нужно, и как не упустить халявные 3 балла.
Задачи с параметром чаще всего тоже требуют довольно подробных объяснений, особенно, если мы выбираем графический метод решения. Геометрия.
Можно ли не решать пункт а, но пользоваться им в решении пункта б? Обязательно ли делать рисунок?
Как в стереометрии показывать построение сечений? Какими теоремами можно пользоваться без доказательства?
Обязательно ли писать название каждой теоремы? Задача 19 – в каких случаях достаточно примера, а в каких – обязательно писать полное доказательство?
И много других нюансов, которые уже не помещаются в этот длинный список!

Если вам понравилось видео, подписывайтесь, ставьте лайки – это поможет тому, чтобы его увидели другие:

Тайм-коды для просмотра этого видео на YouTube:

Для тех, кто предпочитает смотреть видео на YouTube, вы можете перейти по этим тайм-кодам на наш канал на YouTube.

0:00 Вступление
2:52 Как выглядят критерии
4:09 Задача 13
5:59 ОДЗ
7:37 Можно ли не писать ОДЗ для логарифма?
9:00 Записали ОДЗ, но получили 0 баллов – как же так:(
12:23 Задача 13 (а)
14:00 Подписи осей единичной окружности
17:46 Разные или одинаковые буквы использовать в сериях корней (тригонометрия)?
26:30 Задача 13 (б) – первый способ, через двойное неравенство
32:35 Второй способ, через окружность
35:32 Система, совокупность – что это и что делать, если вы их путаете
37:11 Лайфхак – как быстро расставить корни на окружности
41:06 Третий способ – подбором
50:38 Замена переменных – как описывать
51:10 Квадратные уравнения – дискриминант или Виет?
58:13 Задача 15
1:02:26 Упрощаем себе вычисления ОДЗ
1:03:50 Пользуемся ОДЗ – упрощаем себе решение неравенства
1:04:55 Смешанное неравенство – первый способ (как лучше не делать)
1:07:47 Второй способ – обобщённый метод интервалов (и его подводные камни)
1:13:32 Метод рационализации – можно ли пользоваться и нужно ли доказывать?
1:18:50 Вывод по 15 задаче, критерии
1:21:35 Ответ, отличающийся на конечное число точек
1:25:42 Проверка ответов в неравенствах – как?
1:29:00 значок равносильности
1:40:30 Задача 17
1:49:50 Критерии; что такое мат. модель?
1:52:00 Четыре фразы, которые нужно обязательно написать
1:56:00 Умножать на проценты можно? А складывать?
2:03:28 Задача 18
2:09:46 Обязательно ли нужен красивый рисунок? Как потерять баллы из-за рисунка
2:14:05 Полностью обоснованное решение
2:15:40 Разбор критериев на 4, 3, 2 и 1 балл
2:20:11 Можно ли решать не через окружности, а аналитически?
2:21:13 Задача 19: подбор в пункте (а) и “оценка + пример” в пункте (в)
2:27:00 Задача 14
2:27:40 Координатный метод
2:30:33 Можно ли брать числа из пункта (б), когда решаем пункт (а)?
2:35:13 Построение сечения (с обоснованием)
2:39:05 Значки “лежит”, “принадлежит” – в чём отличие и важно ли не перепутать?
2:44:35 В пункте (б) пользуемся недоказанным пунктом (а) – в задачах 14 и 16
2:48:15 Использование “необычных” теорем – можно ли без доказательства?
2:51:30 Если забыл название теоремы
2:53:54 Элементарные вещи можно не выводить
2:57:05 Теорема Фалеса или обратная теорем Фалеса?
2:58:35 Что будет на Марафоне и кому он нужен
3:00:16 Призы

Источник

Раньше и трава была зеленее

Всю жизнь все при решении неравенств и уравнений в ЕГЭ по профильной математике писали ОДЗ (Область Допустимых Значений), понимая под этим ограничения, накладываемые на аргумент “непростыми” функциями типа квадратного корня или логарифма. И не было проблем. Пока в сеть не попали разъяснения методиста из Кемеровской области.

Писать ли “ОДЗ”?

За ТАКОЕ точно снизят

Семинар Трушкиной Т.П., методиста из Кемеровской области, наделал много шума. Оказалось, что на ЕГЭ по математике можно получит 0 баллов за задачу, даже имея верный ответ и верную последовательность рассуждений. Все из-за неправильного использования понятия “ОДЗ”. Первое, что ясно совершенно точно: если вы выписали “ОДЗ” “не полностью” – прощайтесь с баллами за задачу. Если вы решили выписать лишь ограничения, вносимые логарифмической функцией, а условие отличия знаменателя от нуля оставить на потом (“ну они ведь и далее сохранятся, “переход равносилен””), и назвали эти “неполные” ограничения словом ОДЗ – то это 0 баллов. И можно было даже не браться за задачу =(

Пример неверного оформления

Если хотите пользоваться равносильными переходами – пользуйтесь, никто это не запрещает. Но тогда ОДЗ вам вообще ни к чему – работайте спокойно через систему условий, и будет вам счастье.

Пример верного оформления равносильным переходом, без использования ОДЗ

Скажите детям – пусть они ОДЗ выбросят!

Но даже при правильной, полностью выписанной ОДЗ, есть риск нарваться на неприятности. Эксперт заявляет: в школьных учебниках по математике понятие области допустимых значений (ОДЗ) определен лишь для функций. Поэтому использовать это понятие при решении уравнений и неравенств не рекомендуется. Однако использование ОДЗ в неравенствах и уравнениях активно использовалось преподавателями ВУЗов, в том числе при работе со школьниками, постепенно “мигрировало” в методички и сборники по подготовке к ЕГЭ, и теперь уже прочно укоренилось в умах репетиторов, учителей и абитуриентов. Как показывает практика, полностью выписанные ограничения на переменную под заголовком “ОДЗ” не ведут к снижению баллов на ЕГЭ по профильной математике. Тем не менее, эксперт не рекомендует использовать эту конструкцию.

“Коллеги, лучше вообще ничего не писать; Скажите детям – пусть они ОДЗ выбросят!” – столько эмоций на пустом, казалось бы, месте.

Эксперт рекомендует накладывать ограничения на переменную, при этом никак это не “озаглавливать”. При это заголовки типа “ограничения”, “условия”, “важные замечания” и т.п. возбраняться не должны.

Наша бесплатная Игра-тренажер “ударения на ЕГЭ”

А что говорят интернет-гуру?

Специалисты в области подготовки к ЕГЭ по профильной математике разделились во взглядах. Многие известные Ютуб-блогеры (Борис Трушин, Wild Mathing) придерживаются того мнения, что полностью выписанная ОДЗ ни в коем случае к снижению баллов не приведет. Однако выписаны ограничения, действительно, должны быть полностью. То есть если у вас, например, имеется неравенство с логарифмом, да который ещё и стоит в знаменателе дроби – будьте любезны, потребуйте, чтобы аргумент логарифма был положителен, основание положительно и отлично от единицы, а также чтобы знаменатель вашей дроби был отличен от нуля.

Пример верного и неверного оформления

Пример верно выполненной работы из методички РосОбрНадзора

Если Вам нужна методичка для экспертов по оцениванию работ ЕГЭ по профильной математике – можете написать нам в сообщения сообщества ВК. Подскажем, где скачать.

И как же быть?

Если Вы привыкли использовать ОДЗ – используйте, но пишите его полностью. Если снизят – идите на апелляцию. Методичка по оцениванию – вам в помощь.
Если Вы умеете работать с равносильными переходами – вы красавчик =) Это самый безопасный вариант. Но писанины будет… Запасайтесь бланками заранее.
Если не устраивают предыдущие два пункта – озаглавьте ОДЗ словом “ограничения” или вообще никак не называйте. Это безопасно, даже если забудете какое-то важное условие.

О наших курсах ЕГЭ

А где пруфы?

Ну, если вам мало всего выше написанного – смотрите полную запись вебинара

Источник

Глава 1. Вебинар по оформлению задач второй части ЕГЭ по математике (3 часа, 10 минут)

Тайм-коды для просмотра этого видео на YouTube:

Раньше и трава была зеленее

За ТАКОЕ точно снизят

Скажите детям – пусть они ОДЗ выбросят!

Наша бесплатная Игра-тренажер “ударения на ЕГЭ”

А что говорят интернет-гуру?

И как же быть?

А где пруфы?

Новое и интересное на сайте: