Первая часть егэ математика профиль подготовка - Exhelper.top

7 сентября 2017

В закладки

Обсудить

Жалоба

Теория к заданиям первой части ЕГЭ по математике

Задачи 1-12 профильного уровня.

→ Решение задач на проценты: 1.pdf
→ Чтение графиков: 2.pdf
→ «Теория вероятностей»: 4.pdf
→ «Уравнения»: 5.pdf
→ Планиметрия: 6.pdf
→ «Производная»: 7.pdf
→ «Стереометрия»: 8.pdf
→ «Преобразование выражений»: 9.pdf
→ Задачи с физическим содержанием: 10.pdf
→ Движение. Работа. Смеси. Прогрессия: 11.pdf
→ Максимум (минимум) функции. Наибольшее (наименьшее): 12.pdf

Авторы: Александр и Наталья Крутицких | matematikalegko.ru

Источник

: ЕГЭ по математике профиль

10 вариантов с заданиями первой части (1-11) профильного ЕГЭ по математике в новом формате 2022.

→ скачать варианты

Правильное решение каждого из заданий 1–11 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби.

Максимальный первичный балл за выполнение первой части ЕГЭ 2022 по профильной математике — 11 (за всю работу 31 балл)

Ко всем заданиям есть разбор, для перехода нажмите на номер.

Источник: vk.com/wildmathing

Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях b проверяют следующий учебный материал.

1. Математика, 5–6 классы.

2. Алгебра, 7–9 классы.

3. Алгебра и начала анализа, 10–11 классы.

4. Теория вероятностей и статистика, 7–9 классы.

5. Геометрия, 7–11 классы

Часть 1 содержит 6 заданий базового уровня (задания 1-6) и 5 заданий повышенного уровня (задания 7–11).

Связанные страницы:

Источник

Если вы участвуете в конкурсе от Максима Олеговича
— решайте задачи
в полном тестировании ЭГЭ с бланком ответов.

1. Прикладные задачи (задачи из повседневной жизни)

В магазине продаются ручки, карандаши и фломастеры — всего 1000 предметов. Ручки составляют 35(%) от всех предметов, а карандаши — 45(%). Известно, что 76(%) фломастеров — синего цвета, а остальные — красные. Сколько красных фломастеров?

Ответ:

Добавить задание в избранное

2. Анализ данных по графикам и диаграммам

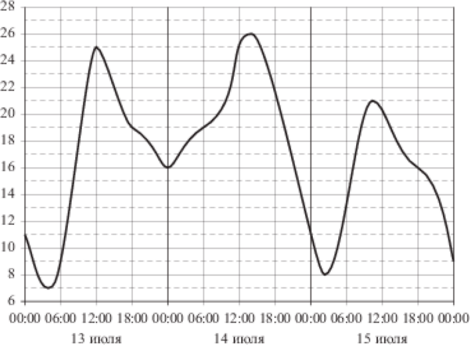
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия.

Ответ:

Добавить задание в избранное

3. Геометрия на плоскости (планиметрия). Часть I

Площадь четырехугольника, вершины которого являются серединами сторон квадрата, равна (1). Найдите площадь квадрата.

Ответ:

Добавить задание в избранное

Найдите корень уравнения (log_{3}(2x + 1) = log_{3}(3 — x) + 1).

Ответ:

Добавить задание в избранное

6. Геометрия на плоскости (планиметрия). Часть II

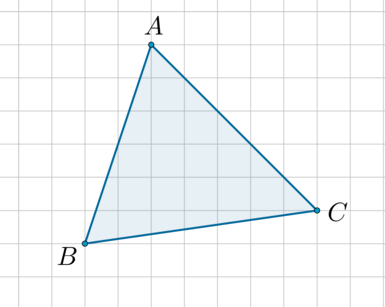
На клетчатой бумаге изображен треугольник (ABC). Найдите его высоту, опущенную из вершины (C), если длина стороны (AB) равна 7.
Вершины треугольника лежат в узлах решетки.

Ответ:

Добавить задание в избранное

7. Взаимосвязь функции и ее производной

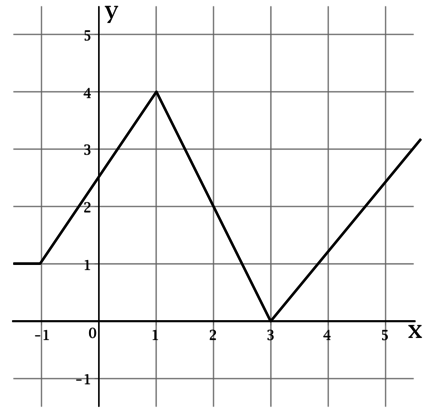
На рисунке изображён график функции (y = f(x)). Вычислите по рисунку (F(3) — F(-1)), где (F(x)) – одна из первообразных функции (y = f(x)).

Ответ:

Добавить задание в избранное

8. Геометрия в пространстве (стереометрия)

Дана правильная четырехугольная пирамида, объем которой равен (7). Найдите объем пирамиды, вершина которой совпадает с вершиной исходной пирамиды, а вершины основания совпадают с серединами сторон основания исходной пирамиды.

Ответ:

Добавить задание в избранное

9. Преобразование числовых и буквенных выражений

Найдите значение выражения (displaystylefrac{1 — 2cos^2{73^circ}}{2sin^2{73^circ} — 1}).

Ответ:

Добавить задание в избранное

10. Задачи прикладного характера

Совершенный газ описывается законом Менделеева-Клапейрона: (pV = nu RT), где (p) – давление в Паскалях, (V) – объем в м(^3), (nu) – количество вещества в молях, (T) – температура в градусах Кельвина, (R) – универсальная газовая постоянная, равная (8,31) Дж/(К(cdot)моль). Во сколько раз надо увеличить температуру совершенного газа, чтобы при неизменном давлении его объем вырос в 3 раза?

Ответ:

Добавить задание в избранное

11. Сюжетные текстовые задачи

Поезд едет с постоянной скоростью 60 км/ч. Он проезжает мимо столба за 45 секунд. За сколько секунд он полностью переедет мост длиной 1500 метров?

Ответ:

Добавить задание в избранное

12. Исследование функций с помощью производной

Найдите наименьшее значение функции (y = (2 — x)cdot e^{-x}cdot e^3 — 2).

Ответ:

Добавить задание в избранное

a) Решите уравнение

[begin{aligned}
dfrac{cos x}{1 — sin^2 x — cos x} = dfrac{sin (2x)}{1 — sin^2 x — cos x}
end{aligned}]

б) Найдите все его корни, принадлежащие промежутку (left(-2pi; -dfrac{3pi}{2}right)).

Добавить задание в избранное

Источник

Задача 3. Начала теории вероятностей

Задача 4. Вероятности сложных событий

Задача 5. Простейшие уравнения

Задача 5. Простейшие уравнения

Задача 6. Вычисления и преобразования

Задача 7. Производная и первообразная

Задача 8. Задачи с прикладным содержанием

Задача 9. Текстовые задачи

Задача 10. Графики функций

Задача 11. Наибольшее и наименьшее значение функций

Источник

Курс посвящен решению прототипов заданий из открытого банка заданий профильного ЕГЭ. Основные цели – устранение пробелов в знаниях, а также подготовка учеников к сдаче ЕГЭ по математике.

About this course

Курс охватывает все темы, необходимые для успешного решения любого задания из первой части профильного ЕГЭ по математике.

Курс разбит на 11 модулей. На каждом занятии слушателям предлагаются видеолекции и конспекты, а также задачи, которые позволят понять, насколько хорошо усвоен материал.

Модули курса:

Простейшие текстовые задачи;
Чтение графиков и диаграмм;
Квадратная решётка, координатная плоскость;
Начала теории вероятностей;
Простейшие уравнения;
Планиметрия;
Производная;
Стереометрия;
Вычисления и преобразования;
Задачи с прикладным содержанием;
Наибольшее и наименьшее значение функций.

Возникшие вопросы по заданиям курса вы всегда можете обсудить с однокурсниками и преподавателями в комментариях к задачам.

Whom this course is for

Курс рассчитан на всех, кто хочет решить первую часть профильного ЕГЭ на максимальный балл.

Initial requirements

Для усвоения материала потребуются базовые знания из школьной программы по математике.

Meet the Instructors

Course content

Certificate

Stepik certificate

Share this course

https://stepik.org/course/9737/promo

Источник

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

1. B треугольнике ABC угол C равен 90^circ , BC = 15, . Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

$AC=frac{BC}{tgA}=frac{15}{0,75}=20.$

Ответ: 20.

2. B треугольнике ABC угол C равен $90^circ, , tgA=frac{9}{40}, , AC=20$ . Найдите AB.

По определению косинуса угла, $cosA=frac{AC}{AB},AB=frac{AC}{{cos A}}.$

Найдем косинус угла A с помощью формулы:

${tg}^2angle { A+1=}frac{{ 1}}{{cos}^2angle { A}}.$

Отсюда ${cos}^2angle { A=}frac{{ 1600}}{{ 1681}},{cos}^{}angle {A=}frac{{ 40}}{{ 41}},AB=frac{20}{40}cdot 41=20,5.$

Ответ: 20,5.

Треугольники. Формулы площади треугольника.

3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен 58^circ , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, ${ S}vartriangle { =}frac{{1}}{{2}}{ a}cdot {b}cdot { sin}angle { C}$ . Получим:

$S=frac{1}{2}cdot 10^2 cdot sin30^circ=25$ см2.

Ответ: 25.

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен 90^circ , угол B равен 58^circ , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

Углы ACD и DCB в сумме дают 90^circ . Отсюда

6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны 90^circ . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен

7. Острые углы прямоугольного треугольника равны 24^circ и 66^circ . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

Тогда

$angle MCH=angle C-angle ACM-angle BCH{ =90^circ -24^circ -}left({ 90^circ -66^circ }right){=42^circ }.$

8. B треугольнике ABC угол A равен 60^circ угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 30^circ и

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен $frac{1}{2}cdot (180^circ -x)$ .

C другой стороны, этот угол равен углу BAC, то есть 2x.

Получим:

$2x=frac{1}{2}cdot (180^circ -x).$
Отсюда ${x }= 36^circ.$

Ответ: 36.

Параллелограмм

10. B параллелограмме ABCD AB=3, AD=21, $sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

Получим:

$DH=ADsinA=21cdot frac{6}{7}=3cdot 6 =18.$

Ответ: 18.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен 2 (a+b) , его площадь равна ab, а квадрат диагонали равен

Получим: , тогда a+b = 4 ,

По формуле квадрата суммы,

Отсюда квадрат диагонали , и длина диагонали AC = 3.

Ответ: 3.

13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит, $HG = EF = frac{5}{2}.$

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны $frac{5}{2}.$ Тогда HGFE — ромб, и его периметр равен $4cdot frac{5}{2}=10$ .

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции: $AH=frac{AB-CD}{2}=frac{26-14}{2}=6.$

Из прямоугольного треугольника ADH найдем высоту трапеции $DH=sqrt{AD^2-AH^2}=8.$

Площадь трапеции равна произведению полусуммы оснований на высоту:

$S=frac{left ( AB+CD right )cdot DH}{2}=160.$

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

Тогда

Ответ: 0,5.

17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

$OF=FC=frac{1}{2}DC,$

$OE=AE=frac{1}{2}AB.$

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Ответ: 9.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру 80^circ . Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть

Ответ: 40.

19. Угол ACB равен. 3^circ Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен 62^circ — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

Ответ: 59.

Касательная, хорда, секущая

20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 90^circ , и тогда угол ОBA равен Угол ОAB также равен 58^circ , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна

Ответ: 64.

21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна

Bписанные и описанные треугольники

22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника $S_{ABC}=sqrt{8cdot 3cdot 3cdot 2}=sqrt{16cdot 9}=12.$

Тогда

$r=frac{2cdot 12}{16}=frac{3}{2}=1,5.$

Ответ: 1,5.

23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна

Периметр треугольника:

Ответ: 22.

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

Угол C может быть равен 30^circ или — ведь синусы этих углов равны $frac{1}{2}.$ Однако по рисунку угол C — острый, значит, он равен

Ответ: 30.

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

По условию, угол C — тупой. Значит, он равен

Ответ: 150.

26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: $r=frac{a+b-c}{2}.$ Гипотенуза равнобедренного прямоугольного треугольника в sqrt{2} раз больше катета. Получим:

$newline r=frac{a+b-c}{2}=frac{2left(82+41sqrt{2}right)-sqrt{2}(82+41sqrt{2})}{2}= newline frac{164+82sqrt{2}-82sqrt{2}-82}{2}=frac{82}{2}=41.$

Ответ: 41.

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, AB=10 , CD=16. Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

Тогда периметр четырехугольника равен

Ответ: 52.

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен $frac{1}{2}cdot left ( 145^circ + 71^circ right )=108^circ.$

Ответ: 108.

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 84^circ . Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,

$angle AOB=180^circ -angle ABO - angle BAO = 12^circ, , n=frac{360^circ}{angle AOB}=frac{360^circ}{12^circ}=30.$

Ответ: 30.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Профильный ЕГЭ по математике состоит из двух частей.

Первая часть – это 12 простых задач, за которые дают 1 первичный балл, а вторая часть это 7 задач повышенной сложности, за которые дают разное количество баллов.

В этом посте мы подробно разберем каждую задачу первой части отдельно.

Поехали!

Примечание. Этот разбор относится к ЕГЭ 2021 года. В 2022 году из ЕГЭ первой части убрали простые задачи и сделали акцента на теории вероятностей.

ЕГЭ по математике профильный. Разбор 1-й части пробного ЕГЭ 2020

В этом видео мы разберем 12 задач первой части профильного ЕГЭ. И это чаще всего ПРОСТЫЕ задачи. Не надо их боятся!

Вы можете переходить от одной задачи к другой, используя таймкоды на самом видео или перейти в наш канал YouTube по ссылкам ниже:

00:00 Начало
00:40 Задача №1. Найти наименьшее количество бумаги, которую можно купить в офис.
03:20 Задача №2. Задача на понимание графика.
05:50 Задача №3. Найти площадь треугольника на клетчатой бумаге.
09:30 Задача №4. Теория вероятностей.
16:17 Задача №5. Показательное уравнение
18:30 Задача №6. Вписанный угол. Два угла вписанного в окружность четырехугольника равны 82 и 58 градусов. Найдите больший из оставшихся углов.
24:30 Задача №7. Производная. Найти наименьшее значение производной по графику функции.
30:30 Задача №8. Стереометрия. Найти объем.
35:27 Задача №9. Тригонометрия. Нужно знать таблицы значений синусов, косинусов и тангенсов.
39:20 Задача №10. Задача на подстановку чисел в формулу.
41:28 Задача №11. Задача на движение по течению. Одна из самых сложных задач первой части.
49:33 Задача №12. Производная. Исследование функции. Найти точку минимума функции. Самая сложная задача.
59:40 Выводы

ЕГЭ 3. Длины, площади. Геометрия на клетчатой бумаге.

Клетчатая бумага очень удобная для геометрии. В основном тем, что на ней очень легко рисовать прямые углы.

А если прямой угол достроить к какому-то отрезку, то получится прямоугольный треугольник. А для прямоугольного треугольника можно записать теорему Пифагора – и вот уже мы определили длину нашего отрезка.

И хотя в 2021 году задача на геометрию на клечатой бумаге не будет входить в ЕГЭ, она очень полезна для того, чтобы начать изучать геометрию, для понимания планиметрии.

Площадь фигуры на клетчатой бумаге – это, по сути, сколько клеточек находится внутри фигуры. Да, конечно часть клеток туда попадают не целиком.

На этом уроке мы научимся находить длины отрезков; вспомним формулы площади треугольника, параллелограмма и трапеции. И не только вспомним, но и научимся применять в задаче №3 из ЕГЭ.

А также мы узнаем ещё два универсальных способа нахождения площадей любых многоугольников – с помощью прямоугольной рамки и с помощью разрезания.

00:00 Вступление
00:39 Решение простейших задач на основы геометрии (что такое биссектриса)
07:52 Найти длину медианы, доказательство равенства двух отрезков через признак равенства треугольников (две стороны и угол между ними)
13:37 Найти длину большей высоты параллелограмма
18:30 Найти длину средней линии трапеции
22:42 Найти среднюю линию треугольника
28:13 Найти высоту треугольника
30:15 Найти расстояние от точки до прямой
32:30 Найти медиану равнобедренного прямоугольного треугольника
37:10 Найти длину отрезка
40:20 Найти гипотенузу прямоугольного треугольника (пифагоровы тройки, египетский треугольник)
43:45 Далее более сложные задачи, где стороны квадратов на клечатой бумаге не равны единице.
50:45 Найти периметр 4-угольника (стороны квадратов на клечатой бумаге не равны единице)
54:35 Еще одна задача на периметр (стороны квадратов на клечатой бумаге не равны единице)
59:25 Найти высоту трапеции (стороны квадратов на клечатой бумаге не равны единице)
01:03:50 Задача на самостоятельную работу
01:04:40 Радиус описанной окружности
01:06:46 Найти площадь четырехугольника
01:07:45 Найти площадь прямоугольного треугольника
01:09:05 Найти площадь непрямоугольного треугольника (2 способа)
01:14:25 Найти площадь непрямоугольного треугольника
01:16:20 Найти площадь непрямоугольного тупого треугольника
01:19:30 Найти площадь непрямоугольного треугольника (неудобный треугольник), с помощью описанного прямоугольника.
01:23:43 Найти площадь “неудобного” квадрата (2 способа)
01:27:20 Найти площадь “неудобного” прямоугольника (2 способа)
01:30:10 Найти площадь ромба (2 способа)
01:33:40 Найти площадь произвольной фигуры (3 способа)
01:35:20 Найти площадь трапеции (3 способа)
01:37:30 Найти площадь трапеции (через две высоты)
01:40:05 Найти площадь трапеции по формуле
01:41:08 Найти площадь параллелограмма
01:42:55 Найти площадь ромба
01:45:10 Найти площадь “некрасивого” четырехугольника
01:47:15 Не стесняйтесь отказываться от способа, который вызывает большие расчеты!

ЕГЭ 4. Теория вероятностей

20% видео – теория

Мы разберём, что такое вероятность; –
Узнаем, что можно называть случайным событием;
Рассмотрим, на какие типы можно разделить события ( Что такое совместные и несовместные события. Что такое зависимые и независимые события);
Выучим формулы, которые нужно применять для разных типов событий.

80% видео – решение задач

Мы решим 54 задачи на первом уроке и ещё 22 (посложнее) на втором.
Мы отработаем все 6 типов задач, которые могут встретиться в ЕГЭ.

00:00 Вступление
00:58 Отношение благоприятных исходов ко всем возможным исходам
01:06:15 Выводы
01:06:40 Произведение вероятностей совместных независимых событий
01:32:38 Сумма вероятностей несовместных событий
01:53:50 Комбинация правил сложения и произведения

ЕГЭ 5, 9. Логарифм и его свойства

В этом видео мы разобрали свойства логарифмов на примере решения 35 задач. Начиная от самых простых логарифмов и заканчивая сложными.

00:00 Вступление
00:34 Что такое логарифм определение логарифма
05:00 8 простых задач вида log {5}{0,2} + log {0,5}{4}
09:09 Найти значение выражения: 7*5^(log {5}{4})
29:50 Сумма логарифмов с одинаковым основанием log {3}{8,1} + log {03}{10}
35:10 Сумма логарифмов с одинаковым основанием – правило №1
35:50 Еще пример на сумму логарифмов log {5}{40} + log {5}{1/8}
37:20 Разность логарифмов log {5}{60} – log {5}{12}
38:55 Разность логарифмов в общем виде
40:00 Логарифм от 1 с любым основанием = 0
40:50 Найти значение выражения log {0,3}{10} – log {0,3}{3}
43:00 Усложняем… деление логарифмов (log {3}{18} /(2 + log {3}{2})
47:30 Сумма и разность логарифмов (правило №2 и №3)
48:25 Правило №4 степень аргумента…
50:10 Три примера на логарифм, где аргумент находится в степени. log {2}{2^3}, lg {10}
53:50 Несколько более сложных задач из ЕГЭ на логарифмы
01:36:20 Найдите значение выражения: (1 – log {2}{12} )(1 – log {5}{12} )

ЕГЭ 5,9 Свойства степеней и логарифмов – продвинутый уровень

Решая логарифмические и показательные неравенства, почти всегда приходится упрощать сложные выражения.

А для этого нужно хорошо знать (и уметь применять) свойства степеней и логарифмов.

На этом видео мы повторим все эти свойства (которые мы выучили в предыдущем видео).

ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия

Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.

Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.

Но на этом видео мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой – почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую – прямоугольными.

В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.

ЕГЭ 7. Геометрический смысл производной

Задачи по производной на ЕГЭ считаются сложными, но на самом деле это не так. Они будут сложными в институте. А пока, на этой теме можно получить легкие баллы на ЕГЭ. Но для этого нужно разобраться.

Чем мы и сейчас займемся! Это видео – первый вебинар нашего курса по производной.

На нем мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.

Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ.

Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.

Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.

ЕГЭ 8. Куб. Параллелепипед. Призма – углы, расстояния. Комбинированные тела

На этом видео мы на примере самых простых объемных фигур научимся находить важнейшие вещи в стереометрии – расстояния и углы в пространстве.

ЕГЭ 9. Тригонометрическая окружность, табличные значения

На этом видео мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии.

Мы увидим, что она – основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.

Мы поймем, как “работает” окружность – а значит, поймём тригонометрию в целом.

ЕГЭ 11. Задачи на проценты и задачи на растворы, смеси и сплавы

В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы – на все, что содержит разные вещества в каком-то соотношении.

Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).

Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.

Также мы научимся решать сложные задачи на проценты – в основном они на банковские вклады и кредиты и прочие финансовые штуки.

Это, в том числе, даст нам очень большой задел для “ экономической” задачи №17 (которая стоит аж 3 первичных балла).

Линейные уравнения. 65 решенных уравнений

Цель урока – научиться решать линейные уравнения любого уровня сложности.

Линейные уравнения – основа всей алгебры. Поэтому, эта тема настолько важна: научитесь решать линейные уравнения, и вам будет намного проще осваивать всё остальное.

Приёмы, которые мы узнаем на этом уроке, применяются не только в линейных, но во всех типах уравнений, от квадратных до логарифмических. Все приёмы будем разбирать на конкретных примерах и сразу же отрабатывать.

Мы решим 65 разных уравнений, разберём все возможные типы линейных уравнений.

Мы научимся:

приводить подобные слагаемые;
“переносить” слагаемые через знак равно;
избавляться от коэффициентов (и заодно узнаем, что это такое – коэффициент:);
раскрывать скобки (в том числе, если перед скобками минус);
справляться с дробями в уравнениях

Выделение полного квадрата

Это самое сложное и важное умение, относящееся к формулам сокращенного умножения.

Этот навык поможет вам решать квадратные уравнения, раскладывать выражение на множители, разобраться с с уравнением окружности в задаче с параметром (18-я задача), которая дает целых 4 первичных балла..

В общем, метод выделения полного квадрата – бесценный навык.

Формулы сокращенного умножения. Разбор 119 задач

Цель этого видео в том, чтобы вы тему “Формулы сокращенного умножения” закрыли полностью, чтобы научились решать любую задачу на ЕГЭ.

Эти формулы нужны для задачи №9 – на преобразование выражений. Также они нужны для решения уравнений и неравенств, очень часто пригождаются в задачах №13 и 15.

А в 18 задаче без них вообще нечего делать.

Для этого вы, вместе с репетитором Алексеем Шевчуком, решите 119 задач, просматривая это видео.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж – c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

Источник

Теория к заданиям первой части ЕГЭ по математике

About this course

Whom this course is for

Initial requirements

Meet the Instructors

Course content

Certificate

Share this course

ЕГЭ по математике профильный. Разбор 1-й части пробного ЕГЭ 2020

ЕГЭ 3. Длины, площади. Геометрия на клетчатой бумаге.

ЕГЭ 4. Теория вероятностей

ЕГЭ 5, 9. Логарифм и его свойства

ЕГЭ 5,9 Свойства степеней и логарифмов – продвинутый уровень

ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия

ЕГЭ 7. Геометрический смысл производной

ЕГЭ 8. Куб. Параллелепипед. Призма – углы, расстояния. Комбинированные тела

ЕГЭ 9. Тригонометрическая окружность, табличные значения

ЕГЭ 11. Задачи на проценты и задачи на растворы, смеси и сплавы

Линейные уравнения. 65 решенных уравнений

Выделение полного квадрата

Формулы сокращенного умножения. Разбор 119 задач

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Новое и интересное на сайте: