План подготовки к егэ по математике базовый уровень 2022

План

подготовки обучающихся 11 класса

к Государственной Итоговой Аттестации

 по математике в форме ЕГЭ

МБОУ «Средняя общеобразовательная русско-татарская школа № 150»

Приволжского района города Казани

Габдуллиной Альбины Рафиковны

учителя первой категории

на 2021-2022 учебный год

Единый государственный экзамен по математике в настоящее время совмещает два экзамена — выпускной за среднюю школу и вступительный в высшие учебные заведения и имеет два уровня: базовый и профильный. Поэтому в рамках ЕГЭ осуществляется проверка овладения материалом курса алгебры и начал анализа, геометрии, усвоение которых должно проверяться на выпускном школьном экзамене, а также материалом некоторых тем курса алгебры основной школы и геометрии основной и средней школы, которые традиционно даются на вступительных экзаменах в вузы. Поэтому успешная сдача к экзамену позволит ученику поступить в ВУЗ.

      Цель: создание условий для систематизации полученных знаний, овладение приемами и методами решения задач, подготовка к итоговой аттестации в форме ЕГЭ.

        Задачи:

• повторить и закрепить знания, умения и навыки, полученные в 5- 9,10 классах;
• развить способность самоконтроля: времени, поиска ошибок в планируемых проблемных заданиях;
• сформировать спокойное, уравновешенное отношение к экзамену;
• вести планомерную подготовку к экзамену;
• знакомство с новыми методами и приемами решения задач;
• формирование специальных умений и навыков обучающихся: алгоритмических умений и вычислительных навыков;
• освоение нестандартных приемов и методов решения задач;
• формирование умений применять полученные знания при решении «нетипичных», нестандартных задач.
• закрепить математические знания, которые пригодятся в обычной жизни и при продолжении образования.

Требования (умения), проверяемые заданиями экзаменационной работы:

1. Уметь выполнять вычисления и преобразования

1.1. Выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма;

1.2. Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

1.3. Проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

2. Уметь решать уравнения и неравенства:

2.1. Решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы;

2.2. Решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод;

2.3. Решать рациональные, показательные и логарифмические неравенства, их системы.

3. Уметь выполнять действия с функциями

3.1. Определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций;

3.2. Вычислять производные и первообразные элементарных функций;

3.3. Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции;

4. Уметь выполнять действия с геометрическими фигурами,

координатами и векторами

4.1. Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);

4.2. Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов);использовать при решении стереометрических задач планиметрические факты и методы;

4.3. Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.

5. Уметь строить и исследовать простейшие математические модели:

5.1. Моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры;

5.2. Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать

практические задачи, связанные с нахождением геометрических величин;

5.3. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения;

5.4. Моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.

6. Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

6.1. Анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчеты по формулам; пользоваться оценкой и прикидкой при практических расчетах;

6.2. Описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках;

6.3. Решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

Организуемая деятельность

ПЛАН ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ БАЗОВОГО УРОВНЯ

ПЛАН ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ

Особое внимание уделять проработке и решению таких заданий, как 1-12 (как ни странно, наиболее подготовленные учащиеся часто ошибаются в простых заданиях по небрежности). Необходимо научить выполнять (может быть, с некоторыми недочётами) задания 13, 15, 17. Основной объект внимания обучающихся — задание 18, требующее умения комбинировать геометрические и алгебраические идеи, видеть за уравнением фигуру, за рисунком решение уравнений и их систем; умения вообразить взаимное расположение двигающихся по плоскости линий и фигур.

Задание 19 требует высокой математической культуры, но не очень много специальных знаний. Все необходимые сведения о целых числах и делимости изучаются в 5-7 классах. Вопрос не в знаниях, а в том, как их применить.  Здесь важно сочетание опыта, фантазии и подготовки.

Необходима постоянная работа с математической терминологией, работа с формулами.

Контроль знаний и умений выпускников при подготовке к ЕГЭ

1. Проведение зачётных занятий в форме тренировочных и диагностических работ по математике в форме ЕГЭ по линии СтатГрад.
2. Проведение постоянного мониторинга качества обученности и успешности выполнения заданий ЕГЭ базового и профильного уровней

В ЕГЭ базового уровня 21 задание с кратким ответом, задания с развернутым ответом отсутствуют. Соответственно, работу проверяет не эксперт, а компьютер. Представляем ТОП-5 ошибок, которые выпускники чаще всего допускают на ЕГЭ базового уровня.

Ошибка 1. Ученик выполняет задания по порядку

Напоминайте ученикам, что самое сложное и самое легкое задание в этой работе оцениваются одинаковым количеством баллов. Ученик решит первый и двадцать первый номер — и за каждый из них получит лишь один балл. Поэтому номера лучше решать по уровню сложности от самого простого к самому затруднительному для ученика. Так ученик решит наибольшее количество заданий.

Ошибка 2. Ученик округляет ответ «не в ту сторону»

В простейших текстовых задачах нужно научится различать задачи с недостатком и с избытком.

Ошибка 3. Ученик не проверяет ответы

Обязательно перепроверить все задания! Лучше проверять задания после того, как решили все возможные задачи. Важно проверить не только вычисления, но и реалистичность ответа.

Какие ошибки часто допускают по невнимательности:

1. Не учитывают единицы измерения.
2. В бланке записывают ответ не в той строке.
3. Записывают символы не по образцу. Часто в бланках запятая похожа на 9.

Ошибка 4. Ученик неверно воспринимает смысл задачи

Ученики часто делят 291 на 300. Ответ неверный. Всего 309 деталей, поэтому 291 будем делить на 309. Ошибка возникла из-за того, что ученик неверно истолковал данные в задаче.

В чемпионате по гимнастике участвуют 40 спортсменок: 14 из Аргентины, 8 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая восьмой, окажется из Парагвая.

Ученики часто делят 8 (порядковый номер спортсмена) на общее количество. Ответ неверный. Номер выступления не важен, главное, что восьмым может выступать только один участник и он должен оказаться из Парагвая.

Ответ: 18 :40 = 0,45.

Ошибка 5. Ученик записывает промежуточный ответ

Часто промежуточные ответы встречаются в задачах по стереометрии, в задачах на концентрацию и движение.

Как этого избежать?

1. Перед записью ответа перечитать вопрос.
2. При составлении уравнения переменной обозначать то, что нужно найти в задаче. Например, необходимо найти диаметр, ученик обозначает радиус за x, велика вероятность что он значение x и запишет в ответ.

Вот такие частые ошибки в ЕГЭ по математике мы разобрали. Желаем успешной сдачи экзамена вашим ученикам!

Другие статьи автора:

Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.

В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.

Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.

Какие задания решать, чтобы сдать базовую математику

Задание 1: обязательно делать

Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:

100 : 14,6 = 6, 849…

Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.

Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:

63 : 6 = 10,5. 

Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.

Ответ: 11.

Задание 2: обязательно делать

Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.

Давайте вместе подберем значения.

• Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
• Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
• Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
• А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.

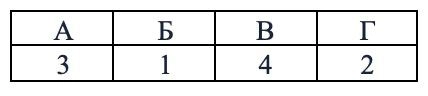
Ответ:

Главное — внимательно перенести ответы в бланк: 3142.

Задание 3: обязательно делать

Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.

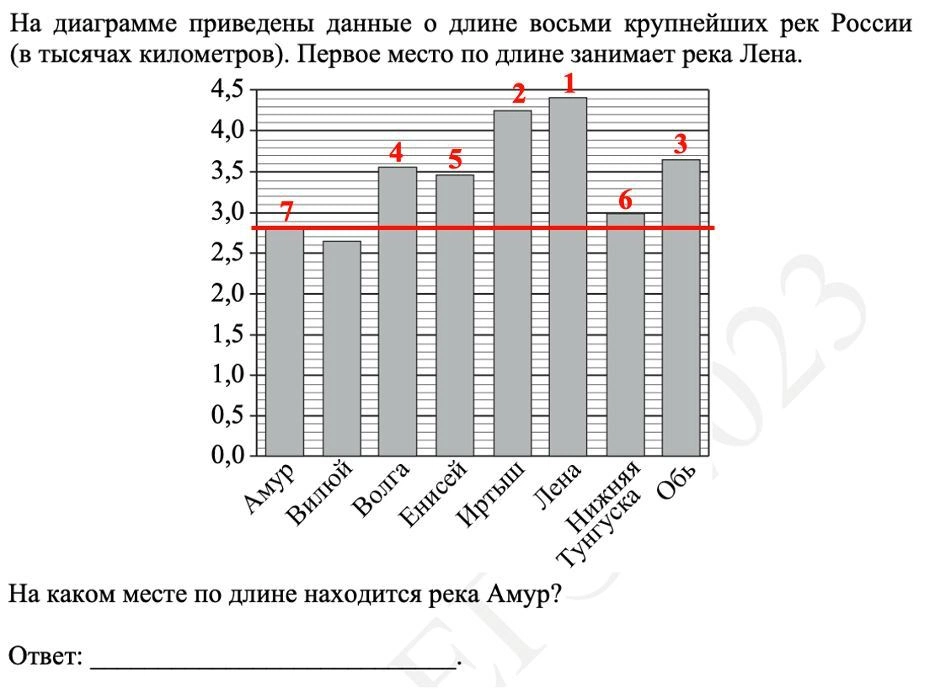
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!

Ответ: 7.

Задание 4: обязательно делать

Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:

• Выписываем формулу из условия.
• Определяем, что нужно найти: единственную букву, значение которой не дано.
• Выражаем искомую величину.
• Подставляем значения из условия в формулу.
• Ищем неизвестное.

Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.

И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.

Задание 5: обязательно делать

Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.

Решаем с помощью формулы:

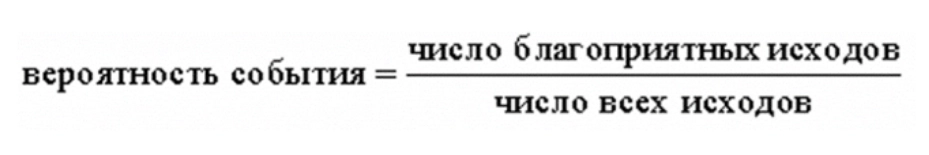
Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.

97 : 100 = 0,97.

Ответ: 0,97.

Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.

Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.

Задание 6: обязательно делать

Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.

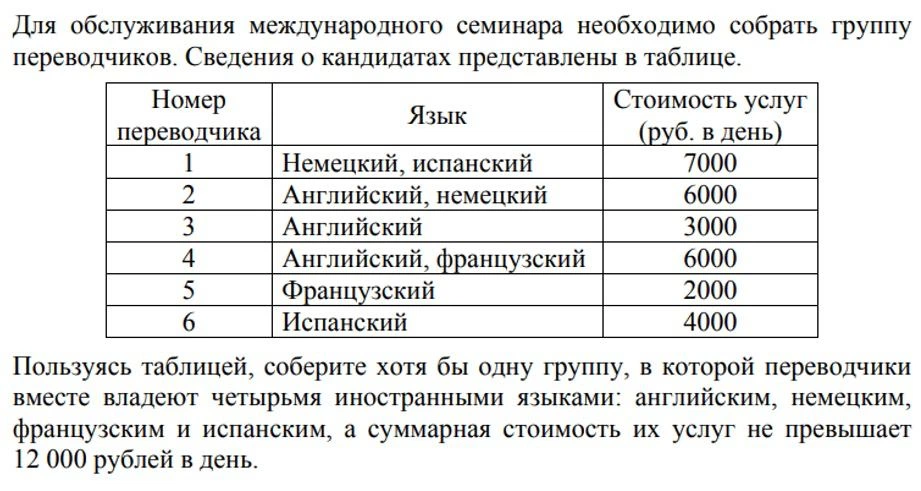
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.

Ответ: 135.

Задание 7

Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.

Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.

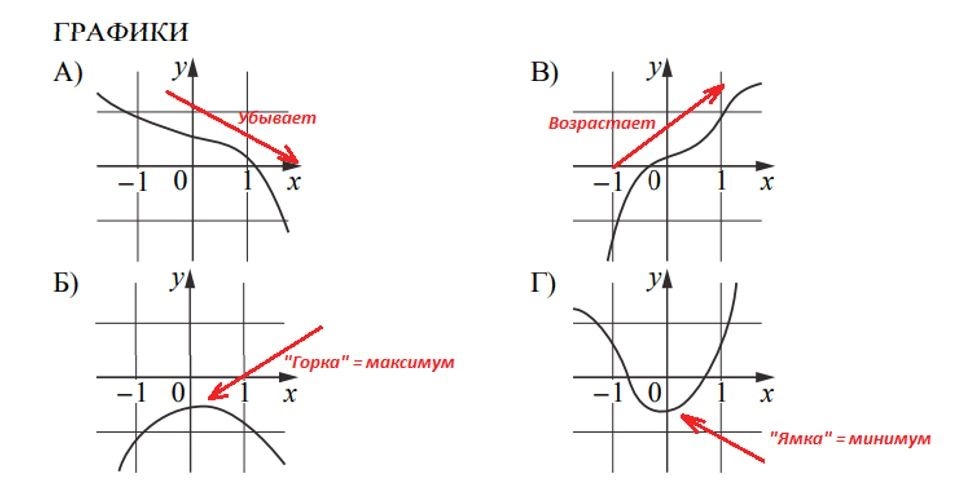
Если не повезет, то придется вспомнить азы теории по производной.

Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.

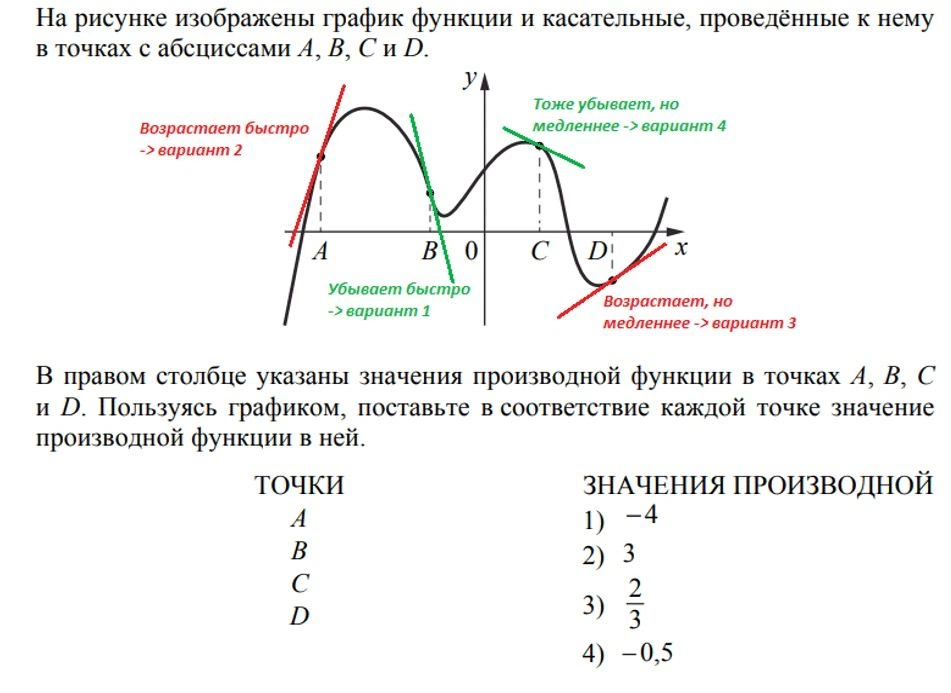
Ответ: 2143.

Задание 8: обязательно делать

Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.

Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.

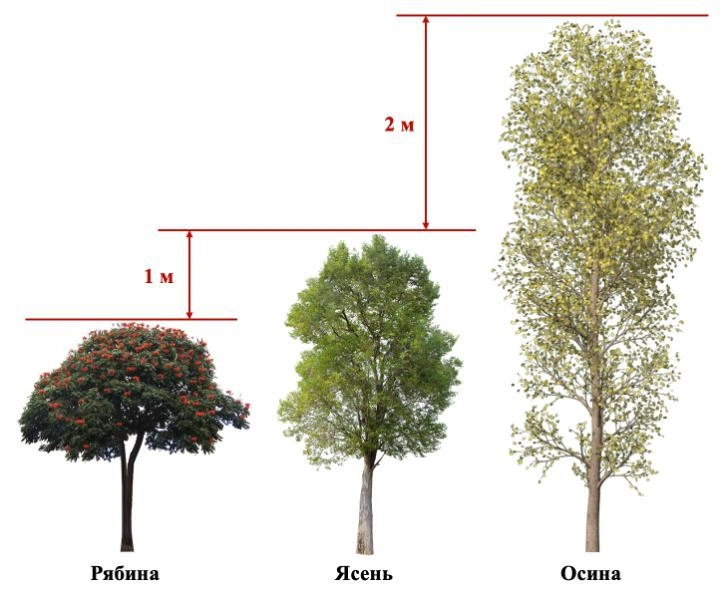
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.

Ответ: 14.

А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.

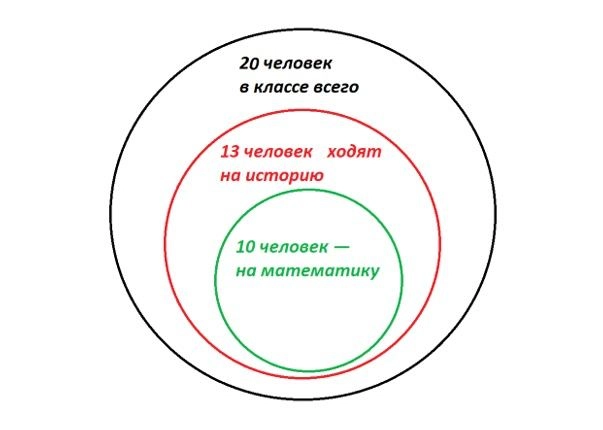
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.

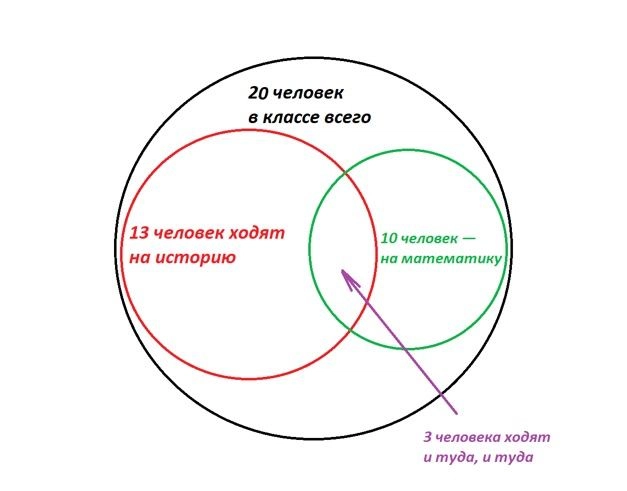
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.

Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.

1. Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
2. Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
3. Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
4. Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек. 

Ответ: 24.

Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.

Задание 14: обязательно делать

Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:

• уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
• правильно расставлять порядок действий;
• быть предельно внимательными.

Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.

Задание 15

Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.

Тип 1. Найти часть от числа

Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.

Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.

Чтобы ответить на вопрос задачи, нужно сделать три шага:

1. Перевести процент в десятичную дробь.

Для этого всегда надо количество процентов поделить на 100.

13 : 100 = 0,13.

2. Найти, сколько это от зарплаты в рублях.

Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.

12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.

3. Ответить на вопрос задачи.

У нас просили зарплату после вычета налога, а не сам налог.

12 500 – 1625 = 10 875 (руб.).

Ответ: 10 875.

Будьте внимательны: многие совершают ошибку именно на последнем шаге!

Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.

1. Переводим процент в десятичную дробь:

25 : 100 = 0,25.

2. Находим, сколько учеников всего.

Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.

124 : 0,25 = 496 (уч.) — всего.

Ответ: 496.

Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.

1. Находим, какую долю новая цена составляет от первоначальной.

Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.

680 : 800 = 0,85.

2. Переводим долю в процент.

В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.

0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.

3. Отвечаем на вопрос задачи.

Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:

100 – 85 = 15%.

Ответ: 15%.

Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.

Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.

1. Считаем общее количество частей:

3 + 2 = 5.

2. Узнаем, сколько голосов составляет одна такая часть.

Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»

100 : 5 = 20%.

3. Отвечаем на вопрос задачи.

За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.

20 ∙ 2 = 40%.

Ответ: 40%.

Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.

Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике. 

Задание 16: обязательно делать

Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:

• выражения со степенями,
• иррациональные выражения,
• логарифмические выражения,
• тригонометрические выражения.

Ваша задача, соответственно, — знать:

• свойства степеней

• свойства корней

• свойства логарифмов

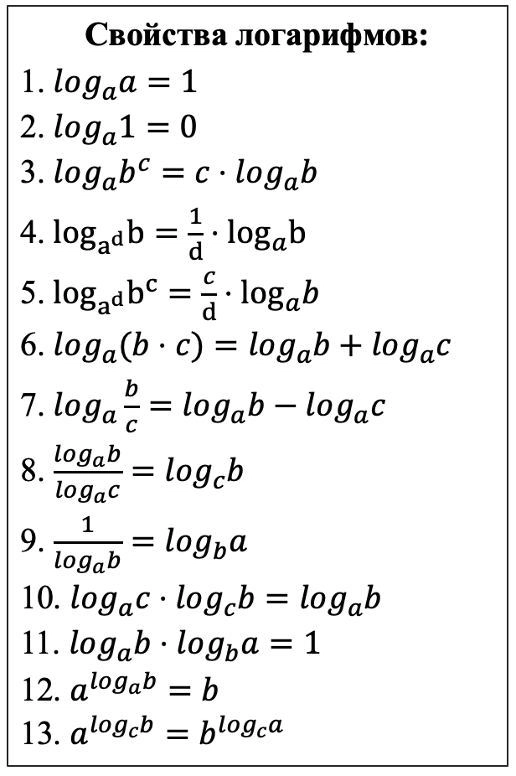
• формулы тригонометрии

Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.

Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!

Задание 17: обязательно делать

В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:

• линейные уравнения

Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.

• квадратные уравнения

Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.

• иррациональные уравнения

Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.

• показательные уравнения

Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.

• логарифмические уравнения

С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.

Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.

Задание 19

Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.

Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть. 

• На 3: сумма всех цифр делится на 3.
• На 4: число, образованное последними двумя цифрами, делится на 4.

Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.

Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.

Ответ: 75576.

Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.

Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.

Ответ: 390.

Какие задания мы не разобрали и почему

Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.

Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.

Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3  больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!

Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:

• на производительность,
• движение (по прямой, воде, окружности),
• сплавы и смеси,
• проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
• прогрессии.

В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.

Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!

Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!