План сечение егэ - Exhelper.top - портал для учащихся

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A₁C₁.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а)  Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б)  Найдите площадь сечения.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.

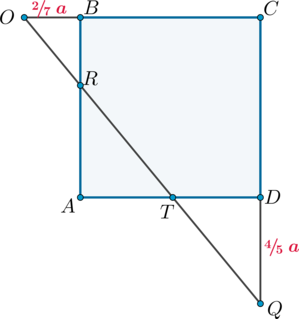
На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 5 : 3, на ребре BB₁  — точка F так, что B₁F : FB = 5 : 11, а точка T − середина ребра B₁C₁. Известно, что AD = 10, AA₁  =  16.

а)  Докажите, что плоскость EFT проходит через вершину D₁.

б)  Найдите площадь сечения параллелепипеда плоскостью EFT.

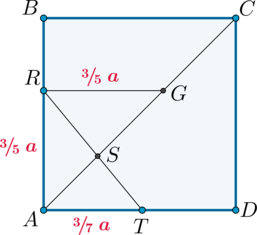
На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E  =  6EA. Точка T  — середина ребра B₁C₁. Известно, что AD  =  12, AA₁  =  14.

а)  Докажите, что плоскость ETD₁ делит ребро BB₁ в отношении 4 : 3.

б)  Найдите площадь сечения параллелепипеда плоскостью ETD₁.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

Пройти тестирование по этим заданиям

Источник

14. Задачи по стереометрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на построение сечений

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Важные факты и теоремы, необходимые для построения сечений

(blacktriangleright) Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются.
Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.

(blacktriangleright) Теорема о параллельности трех прямых: если (aparallel b, bparallel c), то и (aparallel c).

(blacktriangleright) Определение: прямая и плоскость параллельны, если они не имеют общих точек.

Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.

(blacktriangleright) Определение: две плоскости параллельны, если они не имеют общих точек.

Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.

(blacktriangleright) Если две плоскости пересекаются, то их линия пересечения — прямая.

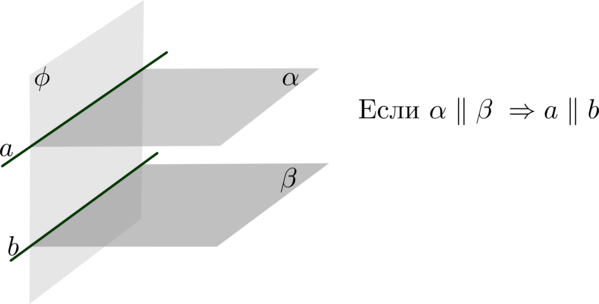
(blacktriangleright) Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)

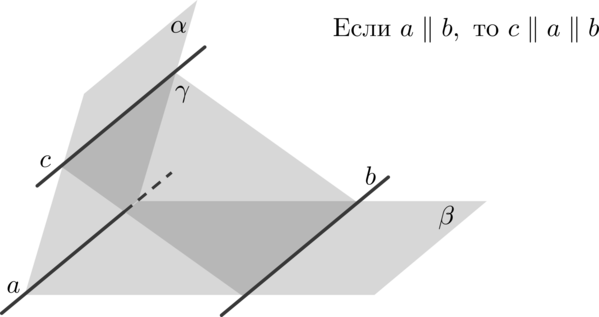
(blacktriangleright) Если плоскости (alpha) и (beta) пересекаются по прямой (a), а плоскости (beta) и (gamma) пересекаются по прямой (b), причем (aparallel b), то плоскости (alpha) и (gamma) пересекутся по прямой (cparallel aparallel b).

Задание
1

#999

Уровень задания: Легче ЕГЭ

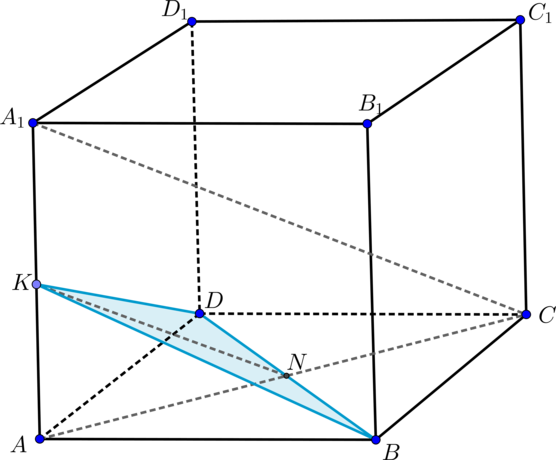
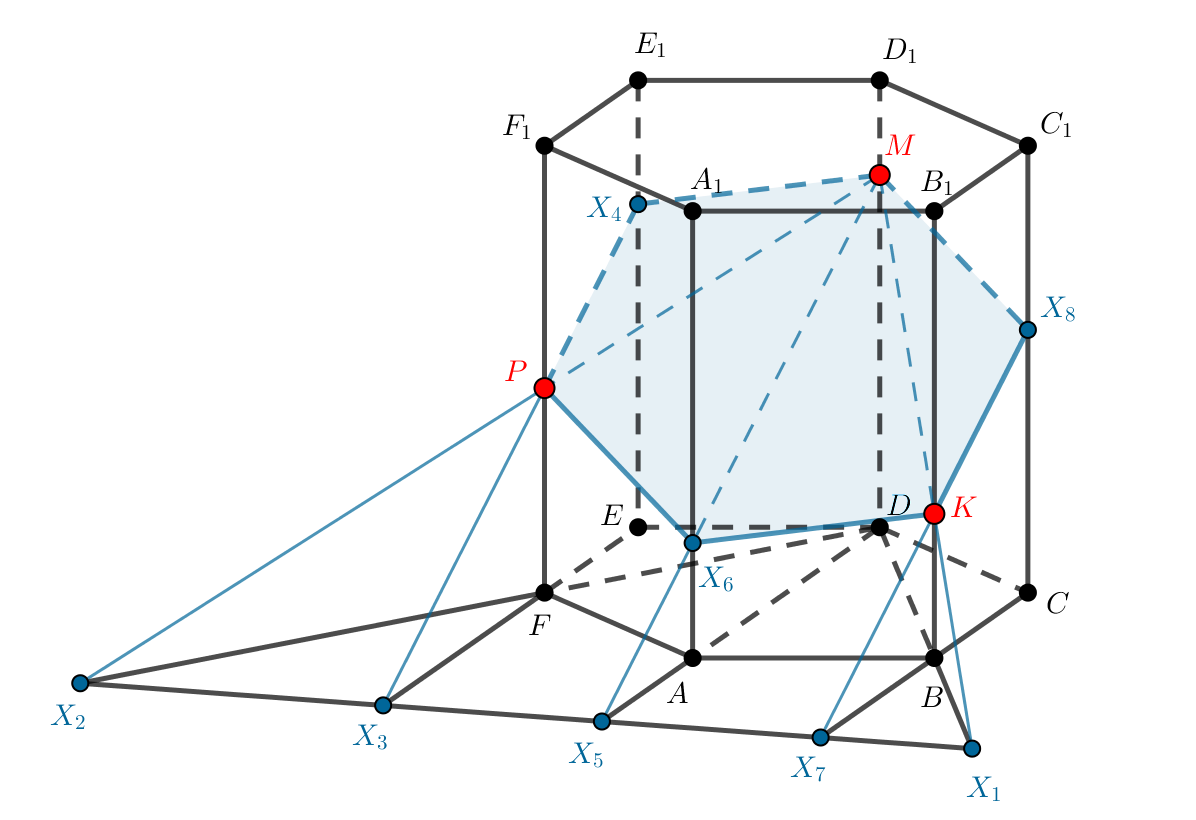
Дан куб (ABCDA_1B_1C_1D_1). Через точку (K), середину ребра (AA_1), и точку (B) проведите плоскость (alpha) параллельно диагонали (A_1C).

Т.к. (A_1Cparallel alpha Rightarrow A_1C) параллельна некоторой прямой, содержащейся в (alpha). Рассмотрим плоскость (AA_1C_1C), в которой находится (A_1C). Т.к. точка (Kin AA_1C_1C), то проведем в этой плоскости (KN parallel A_1C) (по теореме Фалеса (N) – середина (AC)).

Т.к. (ABCDA_1B_1C_1D_1) – куб, то (N) – точка пересечения диагоналей квадрата (ABCD), следовательно, (Nin BD). Таким образом, получили сечение (KBD) куба плоскостью (alpha).

Ответ:

Рисунок.

Задание
2

#3981

Уровень задания: Легче ЕГЭ

Дан куб (ABCDA_1B_1C_1D_1). На ребрах (AA_1) и (BC) отмечены точки (M) и (N) соответственно, причем (AM:MA_1=2:1), а (N) – середина (BC). Найдите сечение куба плоскостью (DMN).

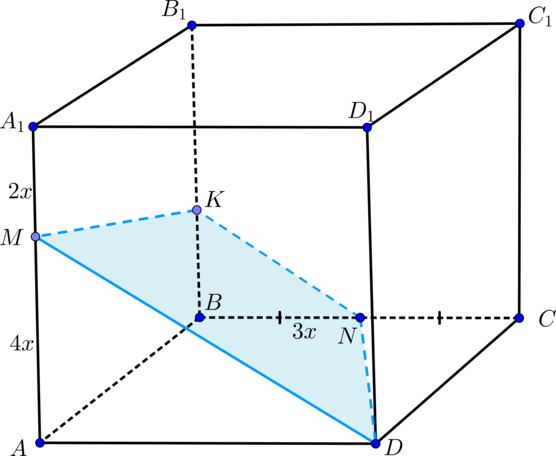
Т.к. грани (ADD_1A_1) и (BCC_1B_1) куба параллельны, то плоскость (DMN) пересечет их по параллельным прямым. Таким образом, проведем (NKparallel DM). Таким образом, (DNKM) – искомое сечение.

Необходимо найти точное расположение точки (K).

Обозначим ребро куба за (6x). Т.к. (bigtriangleup ADM sim
bigtriangleup BNK Rightarrow dfrac{BK}{AM}=dfrac{BN}{AD}
Rightarrow BK=2x). Таким образом, (BK:KB_1=1:2).

Ответ:

Рисунок.

Задание
3

#3804

Уровень задания: Равен ЕГЭ

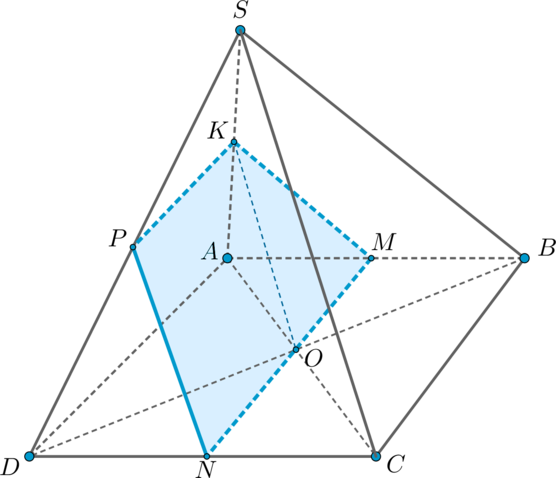
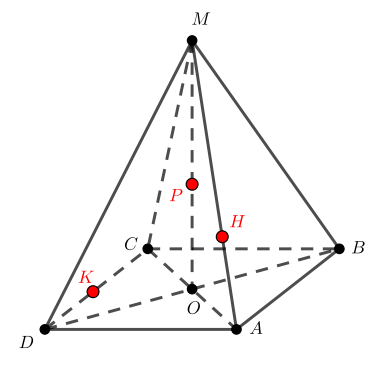
(SABCD) – четырехугольная пирамида, в основании которой лежит квадрат (ABCD), а две боковые грани (SAB) и (SAD) представляют собой прямоугольные треугольники с прямым углом (angle A).

1) Проведите плоскость (alpha) через точку пересечения диагоналей основания параллельно грани (SBC).

2) Найдите площадь сечения пирамиды плоскостью (alpha), если (SA=AB=a).

1) Пусть (ACcap BD=O). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Заметим, что т.к. (angle SAB=angle SAD=90^circ Rightarrow
SAperp
(ABC)).

Проведем в плоскости (SAC) прямую (OKparallel SC). Т.к. (O) – середина (AC), то по теореме Фалеса (K) – середина (SA). Через точку (K) в плоскости (SAB) проведем (KMparallel SB) (следовательно, (M) – середина (AB)). Таким образом, плоскость, проходящая через прямые (OK) и (KM), и будет искомой плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки (O) и (M), получим прямую (MN).

Т.к. (alphaparallel (SBC)),то (alpha) пересечет плоскость (SCD) по прямой (NPparallel SC) (если (NPcap SC ne varnothing), то (alphacap (SBC)ne varnothing), что невозможно ввиду их параллельности).

Таким образом, (KMNP) – искомое сечение, причем (KPparallel
ADparallel MN Rightarrow) это трапеция.

2) Т.к. все точки (K,M,N,P) – середины отрезков (SA, AB, CD, SD) соответственно, то:

а) (MN=AD=a)

б) (KP=dfrac{1}{2}AD=dfrac{a}{2})

в) (KM=dfrac{1}{2}SB=dfrac{asqrt2}{2})

Заметим, что по теореме о трех перпендикулярах (SBperp BC
Rightarrow KMperp MN). Таким образом, (KMNP) – прямоугольная трапеция.

(S_{KMNP}=dfrac{KP+MN}{2}cdot KM=dfrac{3sqrt2}{8}a^2)

Ответ:

1) Рисунок.

2) (dfrac{3sqrt2}{8}a^2)

Задание
4

#1003

Уровень задания: Равен ЕГЭ

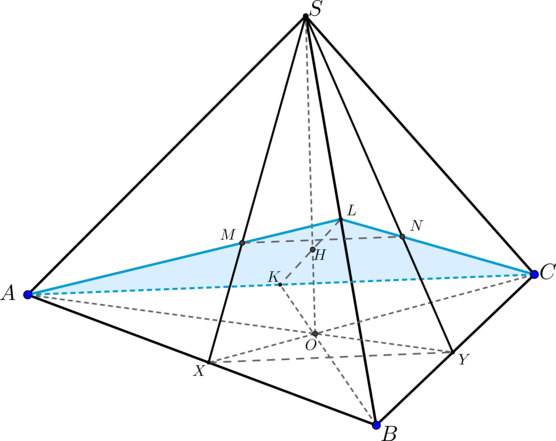
Дана правильная треугольная пирамида (SABC) с вершиной (S). Проведите плоскость через середину ребра (AC) и точки пересечения медиан граней (ASB) и (CSB). Найдите площадь сечения пирамиды этой плоскостью, если (AB=21, AS=12sqrt2).

1) Пусть(K) – середина (AC), (SX, AL) – медианы грани (ASB), (CL,
SY) – медианы грани (CSB), (ALcap SX=M, CLcap SY=N). (SO) – высота пирамиды.

Найдем сечение пирамиды плоскостью (MNK).
Т.к. пирамида правильная, то (triangle SXY) – равнобедренный, (SM=SN=dfrac{2}{3}SX Rightarrow MNparallel XY Rightarrow
MNparallel (ABC)). Таким образом, плоскость (MNK) содержит прямую (MN), параллельную (ABC), следовательно, плоскость (MNK) пересечет плоскость (ABC) по прямой, параллельной (MN) (если это не так, то линия пересечения этих плоскостей (lcap MN=E Rightarrow Ein
(ABC)) и (Ein MN Rightarrow MN) не может быть параллельна ((ABC))).

Прямая, проходящая через точку (K) и параллельная (MN) (или (XY)) – это (AC). Следовательно, сечением является равнобедренный треугольник (ALC).

2) Пусть (LKcap SO=H). Тогда по теореме о трех перпендикулярах (HKperp AC) как наклонная ((HOperp (ABC), OKperp AC) как проекция). Следовательно, и (LKperp AC).

Тогда (S_{ALC}=dfrac{1}{2}ACcdot LK).

Рассмотрим (triangle SKB: BK=ABcdot
dfrac{sqrt3}{2}=dfrac{21sqrt3}{2} Rightarrow cos
B=dfrac{7sqrt3}{12sqrt2}).

Тогда по теореме косинусов для (triangle KLB):

(KL^2=dfrac{729}{4} Rightarrow KL=dfrac{27}{2})

Значит, (S_{ALC}=dfrac{567}{4}).

Ответ:

(dfrac{567}{4}).

Задание
5

#3792

Уровень задания: Сложнее ЕГЭ

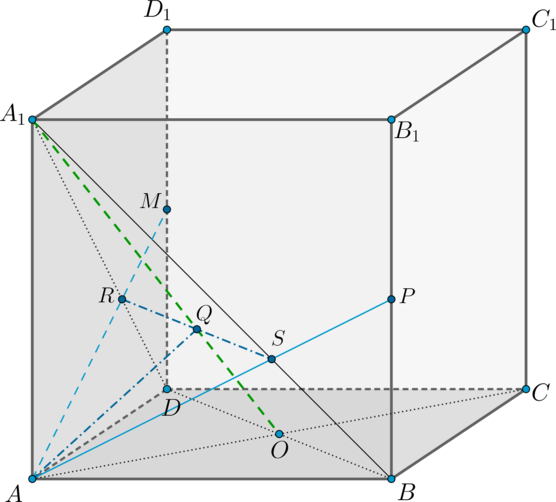
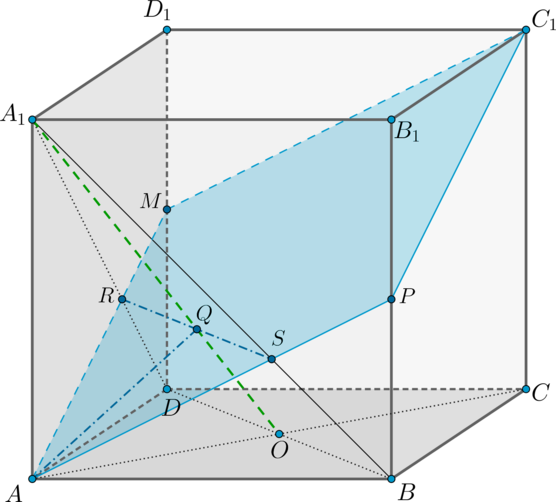
Дан куб (ABCDA_1B_1C_1D_1). Диагонали основания (AC) и (BD) пересекаются в точке (O). Найдите сечение куба плоскостью (alpha), проходящей через точку (A) перпендикулярно прямой (A_1O).

1) Если (A_1Operp alpha), то (A_1O) перпендикулярно двум пересекающимся прямым, лежащим в плоскости (alpha). Построим эти две прямые.

Рассмотрим плоскость (AA_1C_1C) ((A_1O) лежит в этой плоскости). Проведем в ней (AQperp A_1O). Теперь необходимо через их точку пересечения (точку (Q)) провести еще одну прямую перпендикулярно (A_1O).

Рассмотрим для этого плоскость (A_1BD) ((A_1O) лежит в этой плоскости). Проведем через точку (Q) прямую (RSperp A_1O). Т.к. по теореме о трех перпендикулярах (A_1Operp BD) как наклонная ((A_1Aperp (ABC), AOperp BD) – проекция), то (RSparallel BD).

2) Проведем прямые (AR) и (AS). Они могут пересечь либо сами ребра (DD_1) и (BB_1), либо их продолжения. Т.к. от этого зависит вид сечения, определим расположение точек (R) и (S).

Обозначим ребро куба за (a). Тогда (AO=dfrac{asqrt2}{2}=dfrac
a{sqrt2}). Рассмотрим прямоугольный (triangle AA_1O). Так как (AQperp A_1O), то по свойству прямоугольного треугольника (triangle AA_1Qsim triangle AA_1O). Следовательно, [dfrac{A_1Q}{AA_1}=dfrac{AA_1}{A_1O}] Так как по теореме Пифагора (A_1O=sqrt{a^2+frac{a^2}2}=dfrac{sqrt6 a}2), то [A_1Q=dfrac{AA_1^2}{A_1O}=dfrac{sqrt6}3a]

Так как (RSparallel BD), то (triangle A_1DOsim triangle A_1RQ), следовательно, [dfrac{A_1R}{A_1D}=dfrac{A_1Q}{A_1O}=dfrac{sqrt6}3:dfrac{sqrt6}2=
dfrac23] Аналогично (A_1S:A_1B=2:3).

Заметим, что (triangle AA_1Rsim triangle MDR) с коэффициентом подобия (2) ((A_1R:RD=2:1)), следовательно, (MD=frac12AA_1).
Аналогично (PB=frac12AA_1).

Таким образом, получили линии пересечения плоскостей (AA_1D_1) и (AA_1B_1) с плоскостью (alpha) – прямые (AM) и (AP).

3) Так как плоскости (AA_1B_1) и (DD_1C_1) параллельны, то плоскость (alpha) пересечет их по параллельным прямым. Следовательно, в плоскости (DD_1C_1) через точку (M) нужно провести прямую, параллельную (AP).
Так как (M) и (P) – середины (DD_1) и (BB_1), то (MC_1parallel
AP).

Таким образом, сечение куба плоскостью (alpha) – это четырехугольник (AMC_1P) (который, вообще говоря, является ромбом, так как (AM=AP=MC_1) и (MC_1parallel AP)).

Ответ:

Рисунок.

Задание
6

#2451

Уровень задания: Сложнее ЕГЭ

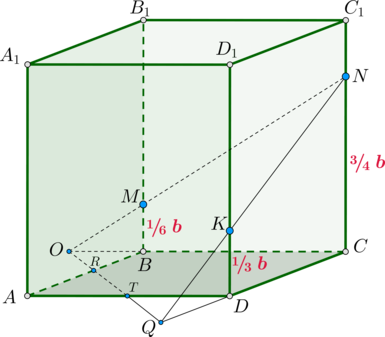
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1), в основании которого лежит квадрат (ABCD). На ребрах (BB_1), (CC_1), (DD_1) отмечены точки (M, N, K) соответственно так, что (BM:MB_1=1:5), (CN:NC_1=3:1), (DK:KD_1=1:2).
Найдите отношение отрезков, на которые делит плоскость (MNK) диагональ (AC).

Обозначим ребро основания за (a), а боковое ребро за (b). Тогда из условия задачи следует, что (BM=frac16b), (CN=frac34b), (DK=frac13b).

Найдем положение точек (R) и (T), в которых плоскость пересекает ребра (AB) и (AD) соответственно.

1) Продлим отрезки (NK) и (CD) до пересечения в точке (Q). Тогда (triangle QDKsim triangle QNC). Следовательно,

[dfrac{QD}{QC}=dfrac{KD}{NC} quad Rightarrow quad
dfrac{QD}{QD+a}=dfrac{frac13b}{frac34b}=dfrac49 quad
Rightarrow quad QD=dfrac45a.]

Аналогично из (triangle OMBsim triangle ONC) получаем, что [OB=dfrac27a.]

Соединив точки (Q) и (O), получим точки пересечения плоскости с ребрами (AB) и (AD).

2) Рассмотрим основание.

(triangle OBRsim triangle OCQ), следовательно,

[dfrac{OB}{OC}=dfrac{BR}{CQ} quad Rightarrow quad
dfrac{frac27a}{frac97a}=dfrac{BR}{frac95a} quad Rightarrow
quad BR=dfrac25a.]

(triangle OBRsim triangle TAR), следовательно,

[dfrac{OB}{AT}=dfrac{BR}{AR}quad Rightarrow quad
dfrac{frac27a}{AT}=dfrac{frac25a}{frac35a} quad Rightarrow
quad AT=dfrac37a.]

3) Для того, чтобы найти, в каком отношении (RT) поделит (AC), проведем прямую (RGparallel AD), (Gin AC).

Тогда (triangle ARG) – прямоугольный и (angle RAG=45^circ), то есть он равнобедренный и (RG=frac35a). Тогда по теореме Фалеса (AG:AC=AR:AB=3:5), следовательно, т.к. (AC=asqrt2), то (AG=frac{3sqrt2}5a).

(triangle ASTsim triangle RSG), следовательно,

[dfrac{AT}{RG}=dfrac{AS}{SG} quad Rightarrow quad
dfrac{frac37a}{frac35a}=dfrac{AS}{frac{3sqrt2}5a-AS} quad
Rightarrow quad AS=dfrac{sqrt2}4a.]

Тогда (SC=asqrt2-frac{sqrt2}4a=frac{3sqrt2}4a) и (AS:SC=1:3).

Ответ:

(1:3)

Теме «Построение сечения» в ЕГЭ по математике профильного уровня посвящается, как правило, несколько заданий. Они могут требовать от школьника как краткого ответа, так и полного развернутого решения. Если одним из ваших слабых мест являются именно задачи на сечения (в ЕГЭ при этом вы хотите получить конкурентные баллы), непременно стоит повторить или вновь разобраться в материале.

Сделать это наиболее эффективно вам поможет образовательный математический проект «Школково». Наши специалисты подготовили теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко справиться с решением задач на сечение.

Полезная информация

Для того чтобы выполнить построение сечений в ЕГЭ, нужно отметить точки пересечения пространственной фигуры с ребрами и произвести их соединение, начертив отрезки.

Необходимо запомнить

Производится соединение только двух точек, которые лежат в плоскости одной грани. Прежде чем приступить к решению задачи на построение сечений, полезно повторить материал о параллельных прямых. Сделать это вы можете, посетив раздел «Теоретическая справка».

Также необходимо запомнить, что пересечение секущей плоскости параллельных граней возможно только по параллельным отрезкам.

В том случае, когда в плоскости грани обозначена только одна точка, которая принадлежит плоскости сечения, следует отметить еще одну дополнительную. Для того чтобы это сделать, нужно определить точки пересечения прямых, которые уже построены, с теми, которые лежат в тех же гранях.

Выполнив построение сечений многогранников в задачах, которые представлены в нашем «Каталоге», вы сможете закрепить изученный материал и успешно справиться с подобным заданием на ЕГЭ в Москве.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.

Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.

Как вы думаете — может ли восьмиугольник быть сечением куба?

И может ли правильный пятиугольник быть сечением куба?

Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.

А вообще сечение — это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.

Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.

При построении сечений мы часто используем следующие теоремы:

1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.

Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.

2. Теорема о прямой и параллельной ей плоскости:

Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.

Эта теорема помогает, например, при построении сечений пирамиды.

Разберем несколько задач на построение сечений.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.

Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.

Продлим отрезки MN и АС;

Проведем РК в плоскости нижней грани; четырехугольник MNLK — искомое сечение.

2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.

Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,

Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.

3. Постройте сечение куба проходящее через вершину D_1 и середины ребер и BC.

Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;

Треугольники АМР и KCN — прямоугольные равнобедренные, причем $AP = CK = frac{AB}{2}.$

Проведем D_1K — в плоскости задней грани и D_1P — в плоскости левой грани куба;

$D_1Kcap {CC}_1=F,{D}_1Pcap AA_1=T,$

Пятиугольник $MNFD_{1}T$ — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.

4. Постройте сечение куба проходящее через вершину В и середины ребер AA_1 и CC_1.

Пусть М — середина ребра $AA{}_{1}$ , N — середина ребра $CC_{1}.$

Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб $BND{}_{1}M.$

5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.

Пусть SH — апофема грани SBC; N—середина SH.

Проведем MN в плоскости ASH;

Четырехугольник KMEF — искомое сечение.

Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.

Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.

Из подобия треугольников SMT и SEH получим, что Значит

По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ. Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.

где — середина ;

— искомое сечение.

7. Постройте сечение куба , проходящее через точку М, лежащую на ребре DD_1 и точки Т и К, принадлежащие граням АВС и $DCC_{1}$ .

Точки М и К лежат в плоскости задней грани $DCC{}_{1}D{}_{1}$ . Соединив М и К, получим, что

$MKcap CC{}_{1}=E,(MK)cap (DC)=P.$

Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;

. Трапеция FMEN — искомое сечение.

8. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.

Пусть точки $M{}_{1}$ и $N{}_{1}$ — проекции точек M и N на плоскость нижней грани

Плоскость $(MNN{}_{1})$ проходит через параллельные прямые $MM{}_{1}$ и $NN{}_{1}$ .

Проведем в этой плоскости MN и $M{}_{1}N{}_{1};$

$(MN )cap ( M{}_{1}N{}_{1})=P$ .

Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Стереометрия. Задачи на построение сечений» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Инфоурок

›

Геометрия

›Презентации›Подготовка к ЕГЭ. Построение сечений.

Подготовка к ЕГЭ. Построение сечений.

Скачать материал

Дудников Ю. А.
МБОУ Качалинская СОШ
Тацинского района
Сечения

Скачать материал

Сейчас обучается 94 человека из 37 регионов

Описание презентации по отдельным слайдам:

1 слайд

Дудников Ю. А.
МБОУ Качалинская СОШ
Тацинского района

Сечения
2 слайд

Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника. Итак, сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.
3 слайд

Вершины многоугольника всегда лежат на ребрах многогранника.

Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении.

Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника.

Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Правило для самоконтроля.
4 слайд

Процесс построения сечений многогранников сложен тем, что в каждом конкретном случае он различен. И никакая теория не описывает его от начала и до конца. На самом деле есть только один верный способ научиться быстро и безошибочно строить сечения любых многогранников – это постоянная практика. Чем больше сечений вы построите, тем легче в дальнейшем вам будет это делать.
6 слайд

E
T
С
Д
Д1
С1
А
А1
В
В1
K
F
O1
O2
O
7 слайд

А

М
Д
В
С
E
К
Т
О
N
F
Правильная пирамида
8 слайд

Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры

Метод следов.
9 слайд

Строим прямую а, которая является линией пересечения плоскости основания и плоскости сечения. Для этого находим две точки, которые являются пересечением прямых плоскости сечения и их проекций на плоскость основания. Находим дополнительные точки, как точки пересечения прямых, содержащих ребра основания, с прямой а.

Метод следов.
10 слайд

O
T2
Д
Метод проекций.
Построение сечения в шестиугольной призме.
В
С
F1
Е1
Д1
Е
F
А1
С1
В1
А
T4
T3
O3
O1
O2
T
T1
T5
11 слайд

С
O
F
М
L
А
E
K
Треугольная пирамида
В
12 слайд

О
А
М
Д
В
С
Четырехугольная пирамида
F
E
K
О1
R
N
13 слайд

T
O1
С
Д
Д1
С1
А
А1
В
В1
M
O2
O3
K
E
F
N
КУБ
14 слайд

R
O3
F
M
T
С
Д
Д1
С1
А
А1
В
В1
K
Тяжелый случай
O1
N
O2
E
15 слайд

Найти расстояние между скрещивающимися прямыми.
16 слайд

K
H
А
М
Д
В
С
T
Задача ЕГЭ 2013
В правильной четырехугольной пирамиде МАВСД С вершиной М, стороны основания равны 3, а боковые ребра 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку Д и середину ребра МВ, параллельно прямой АС
P
E
О
18 слайд

M
K
R
K
E
В правильной четырехугольной призме АВСДА1В1С1Д1, сторона основания равны 4, а высота равны 3 Найдите площадь сечения призмы плоскостью, проходящей через вершину Д1 и середину ребер АВ и ВС.

А1
В
В1
С1
Д1
С
Д
А
N
T
O
20 слайд

R
X
Д
С
Сторона основания правильной четырехугольной пирамиды равна 4, а боковое ребро 6. Через середины двух смежных сторон основания проведено сечение параллельно пересекающему их боковому ребру. Найдите площадь сечения.

E
В
А
М
Т
O
K
E
N
H
21 слайд

С
ЕГЭ 2014.
В треугольной пирамиде МАВС основанием является правильный
треугольник АВС, ребро МВ перпендикулярно плоскости основания,
стороны основания равны 3, а ребро МА равно 6. На ребре АC находится
точка D, на ребре АВ находится точка Е, а на ребре АМ точка L. Известно,
что АD = АL = 2, и ВЕ = 1. Найдите площадь сечения пирамиды плоскостью,
проходящей через точки Е, D и L.
В
М
А
L
Д
E
4
1
3
1
2
2
2
6

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 154 962 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

Рейтинг:
1 из 5

24.12.2017
4425
23

24.12.2017
2117
44

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Страхование и актуарные расчеты»
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»

Настоящий материал опубликован пользователем Дудников Юрий Алексеевич. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 5 лет и 2 месяца
- Подписчики: 2
- Всего просмотров: 22958
- Всего материалов:
  
  16

Источник

Тема 13.

Задачи по стереометрии

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

задачи по стереометрии

13.01Задачи из ЕГЭ прошлых лет

13.02Задачи из сборника И.В. Ященко ЕГЭ 2023

13.03Задачи формата ЕГЭ на многогранники. Пирамида, призма

13.04Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

13.05Аксиомы. Доказательство базовых фактов

13.06Параллельность. Доказательство базовых фактов

13.07Перпендикулярность. Доказательство базовых фактов

13.08Тела вращения. Доказательство базовых фактов

13.09Задачи на построение

13.10Упрощенные задачи

13.11Построение сечений

13.12Нахождение площади сечения

13.13Расстояние от точки до прямой

13.14Расстояние от точки до плоскости

13.15Угол между прямой и плоскостью

13.16Угол между плоскостями

13.17Нахождение объема или площади поверхности

13.18Угол между скрещивающимися прямыми

13.19Расстояние между скрещивающимися прямыми

13.20Метод объемов

Решаем задачи

Показать ответ и решение

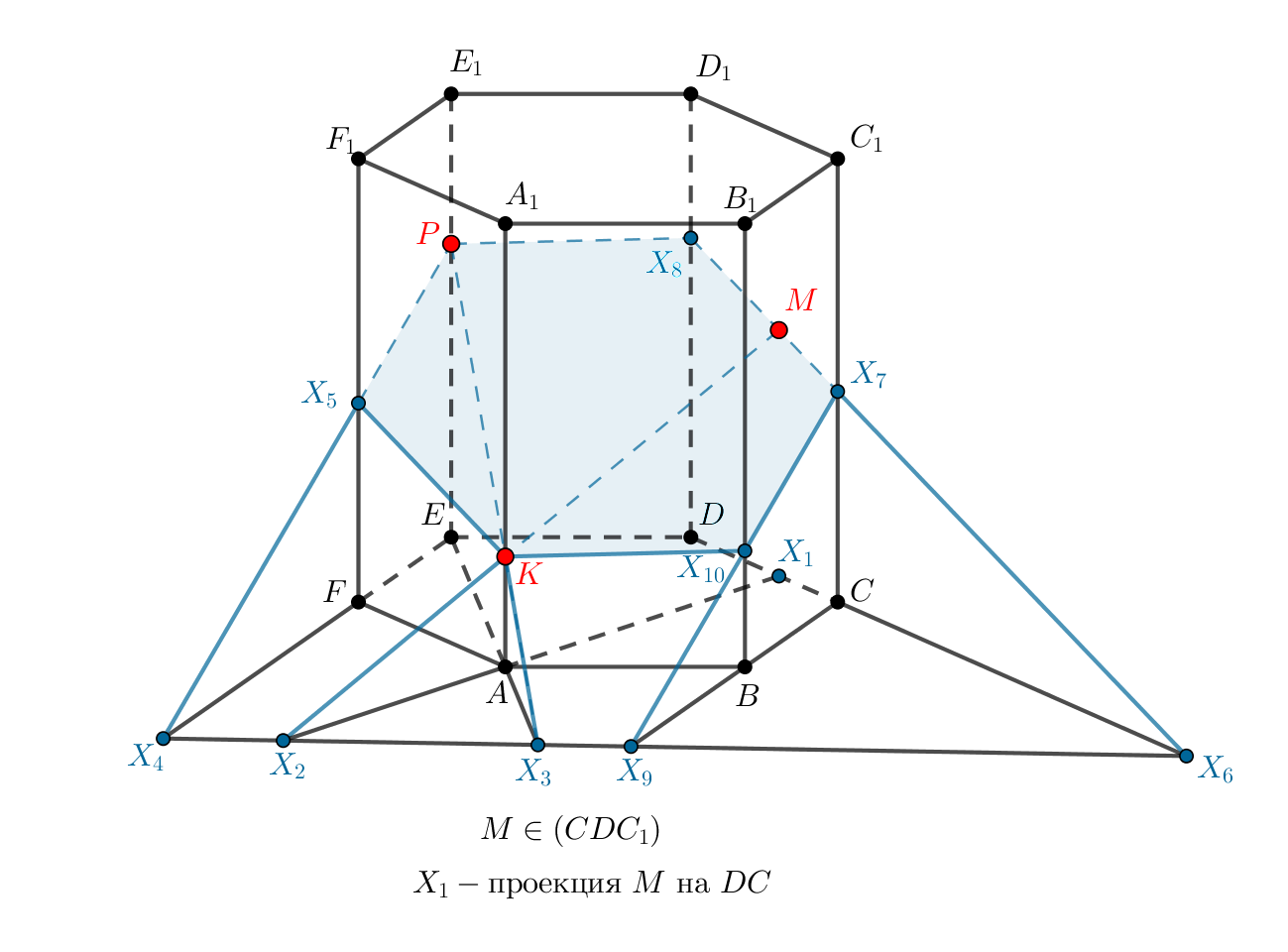
Назовем плоскость (MP K ) плоскостью

Пусть — ортогональная проекция точки на плоскость (ABC ). Тогда
пересекает (ABC ) в точке X2, в которой прямая пересекает прямую
X1C (так как — проекция точки на плоскость ABC ). Плоскость
также пересекает (ABC ) в точке X3, в которой прямая пересекает
прямую X1F (так как — проекция точки на плоскость ABC ). Таким
образом, пересекает (ABC ) по прямой X X .
2 3

Пусть тогда X4X5 — сторона сечения
призмы плоскостью

Пусть Тогда — точка, лежащая в следовательно,
KX7 — еще одна сторона сечения, где

Пусть Тогда — точка, лежащая в следовательно,
P X9 — еще одна сторона сечения, где

Получаем еще одну сторону сечения X7X9. Тогда сечение призмы плоскостью
— шестиугольник

X2X3 могла пересечь не стороны и , а их продолжения (либо
продолжение только одной из этих сторон), тогда сечение получилось бы
другим.

KX6 могла бы пересечь не F1E1, а ребро EE1, тогда сечение выглядело
бы по-другому.

Заметим, что P X8 в нашем случае пересечет именно ребро C1D1, так
как точка лежит на ребре E1F1, следовательно, плоскость пересекает
плоскость по прямой MX7, которая пересекает в результате
положения отрезок C1D1, а не его продолжение.

Все зависит от положения точек

Ответ:

Постройте сечение правильной шестиугольной призмы плоскостью, проходящей
через точки и (точка лежит на грани CDD1C1 ).

Показать ответ и решение

Ответ:

Постройте сечение правильной шестиугольной призмы плоскостью, проходящей
через точки и

Показать ответ и решение

Ответ:

Постройте сечение правильной шестиугольной призмы плоскостью, проходящей
через точки и

Показать ответ и решение

Ответ:

Постройте сечение правильной шестиугольной призмы плоскостью (MKP ).

Показать ответ и решение

Пусть точка — середина BB1 , точка — середина .

Тогда как средняя линия в треугольнике DBB1.

Далее, как средняя линия в треугольнике ABD . Кроме того, , так как и — середины
противоположных сторон квадрата AA1B1B .

Тогда , следовательно, точки , , и лежат в одной плоскости .

Плоскость проходит через прямую и содержит прямую , параллельную B1D , следовательно, и есть
плоскость искомого сечения.

Продлив до пересечения с , получим точку и сечение MNKF .

Показать ответ и решение

1.: Обозначим плоскость сечения через . По условию , а значит, пересекает плоскость по прямой,
параллельной и проходящей через точку , так как и . Тогда точка
такая, что , принадлежит .
2.: В параллелепипеде плоскости и параллельны. Тогда прямые их пересечения с плоскостью
должны быть параллельны между собой и параллельны прямой , так как . Таким образом,
прямая пересечения плоскостей и должна быть параллельна прямой , а также должна
проходить через точку , так как и . Тогда точка такая, что ,
принадлежит .
3.: Искомое сечение .

Показать ответ и решение

б) Запишем теорему Менелая для треугольника ADB и прямой M K , учитывая, что и
BK = 1KA
2

Ответ:

б) 1 : 2

Постройте сечение куба, проходящее через точки , и .

а)

б)

в) (точка М находится в верхней грани)

г)

Показать ответ и решение

Точки сечения всюду обозначены синим и пронумерованы в том порядке, в котором мы их получаем.

Показать ответ и решение

а) Обозначим через плоскость сечения.

По условию , следовательно, пересекает плоскость , содержащую прямую , по прямой,
проходящей через точку и параллельной . Проведем через прямую, параллельную , точки
и — ее пересечения с и соответственно — лежат в плоскости .
По условию , следовательно, пересекает плоскости и , содержащие , по прямым,
параллельным . Проведем через и прямые, параллельные , тогда и — точки пересечения
этих прямых с и соответственно, эти точки также принадлежат .
Все точки прямой принадлежат , при этом . Тогда принадлежит
.
Все точки прямой принадлежат , при этом . Тогда принадлежит .

Получили, что — искомое сечение.

б) По построению плоскость сечения параллельна прямой . Отрезок X6M лежит как в плоскости сечения, так и в
плоскости (SCA ) , значит, он параллелен . Тогда по теореме Фалеса

Отрезок равен четверти диагонали параллелограмма, следовательно, искомое отношение равно
3 :1 .

Ответ:

б) 3 :1

Показать ответ и решение

Ответ:

б) 1 :2

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Показать ответ и решение

а) Обозначим плоскость сечения через

Все точки прямой принадлежат при этом Тогда принадлежит

Все точки прямой X1K принадлежат при этом Тогда принадлежит

Искомое сечение MKX2L.

б) Запишем теорему Менелая для треугольника ADC и прямой X1X2, учитывая, что

Запишем теорему Менелая для треугольника ABC и прямой X L,
1 учитывая, что и

CL- BM-- AX1- AX1-
1= LB ⋅MA ⋅X1C = 2⋅X1C

Поделим первое на второе, получим

pict

Ответ:

б) 2 :1

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

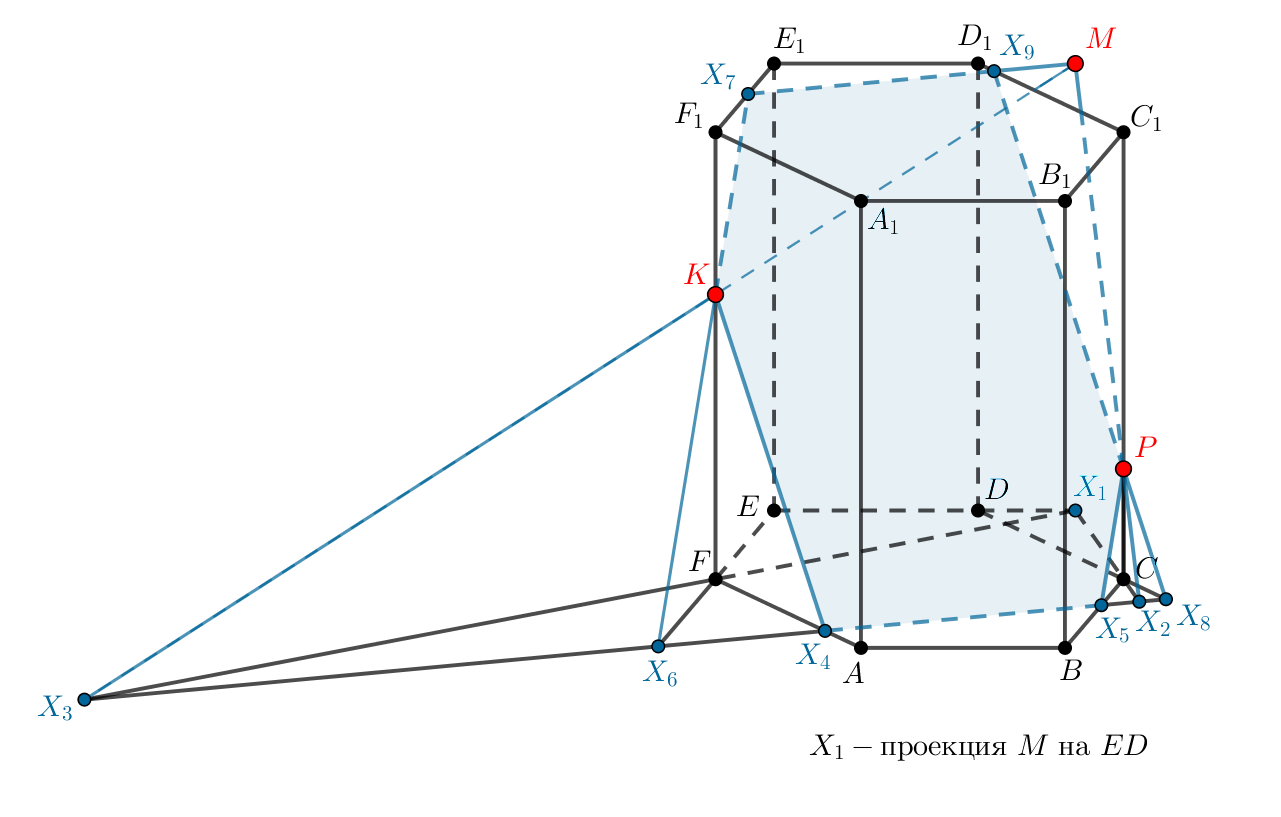
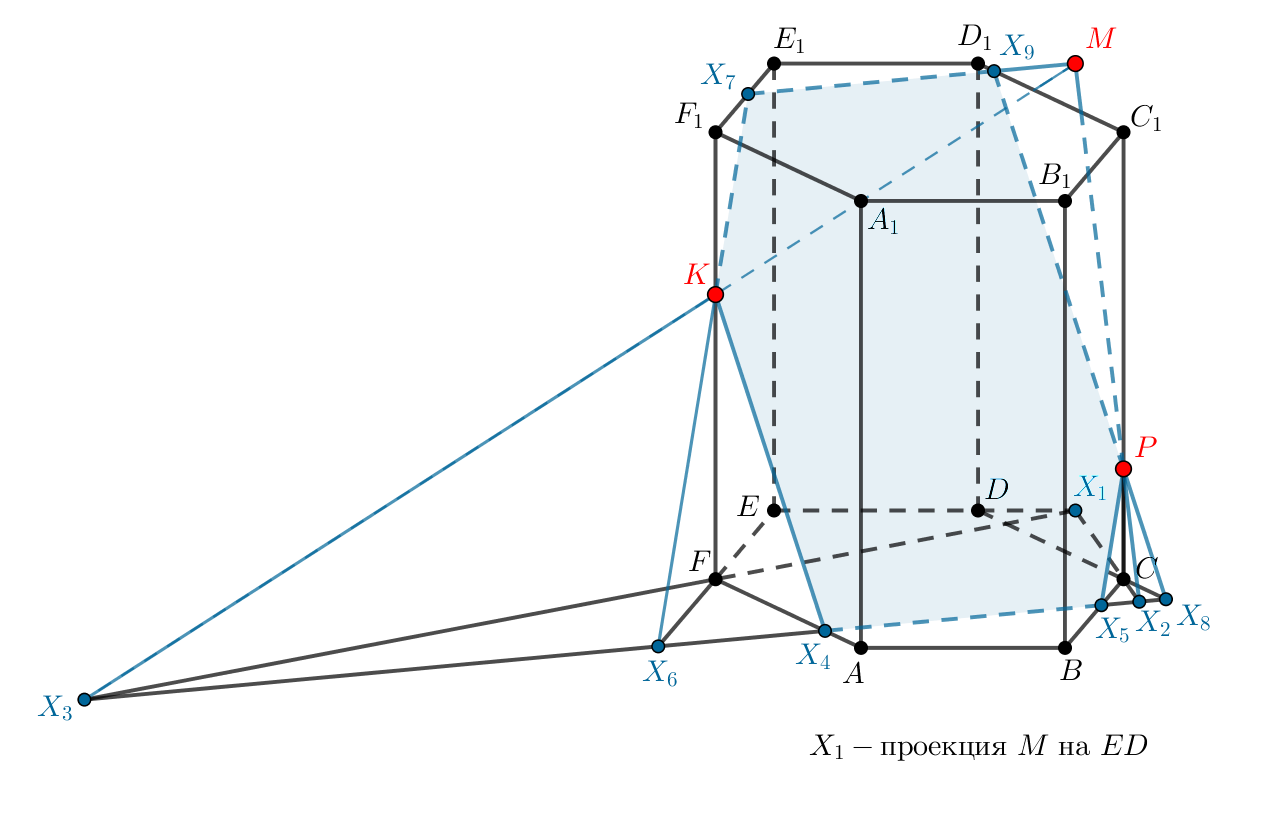
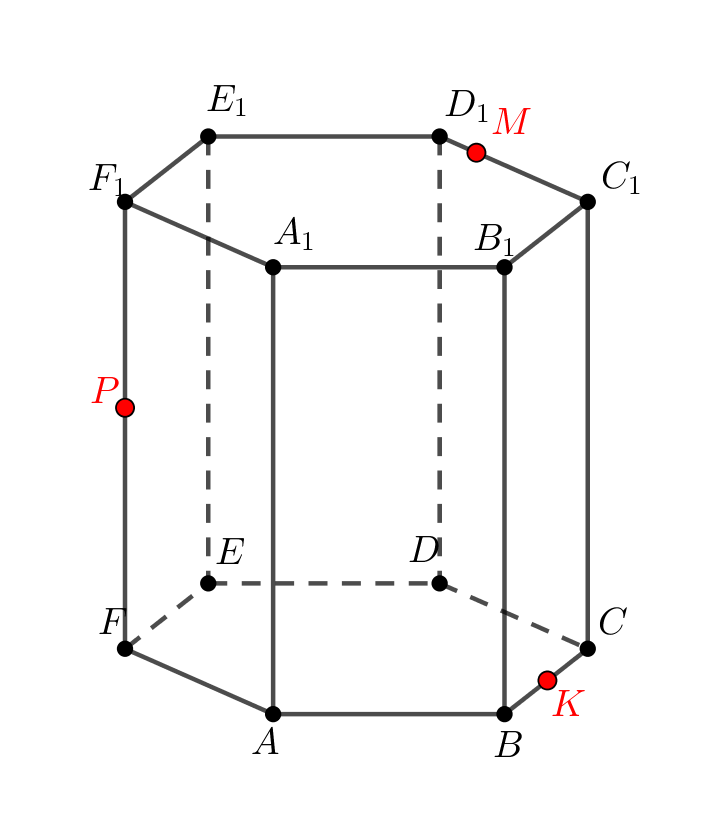
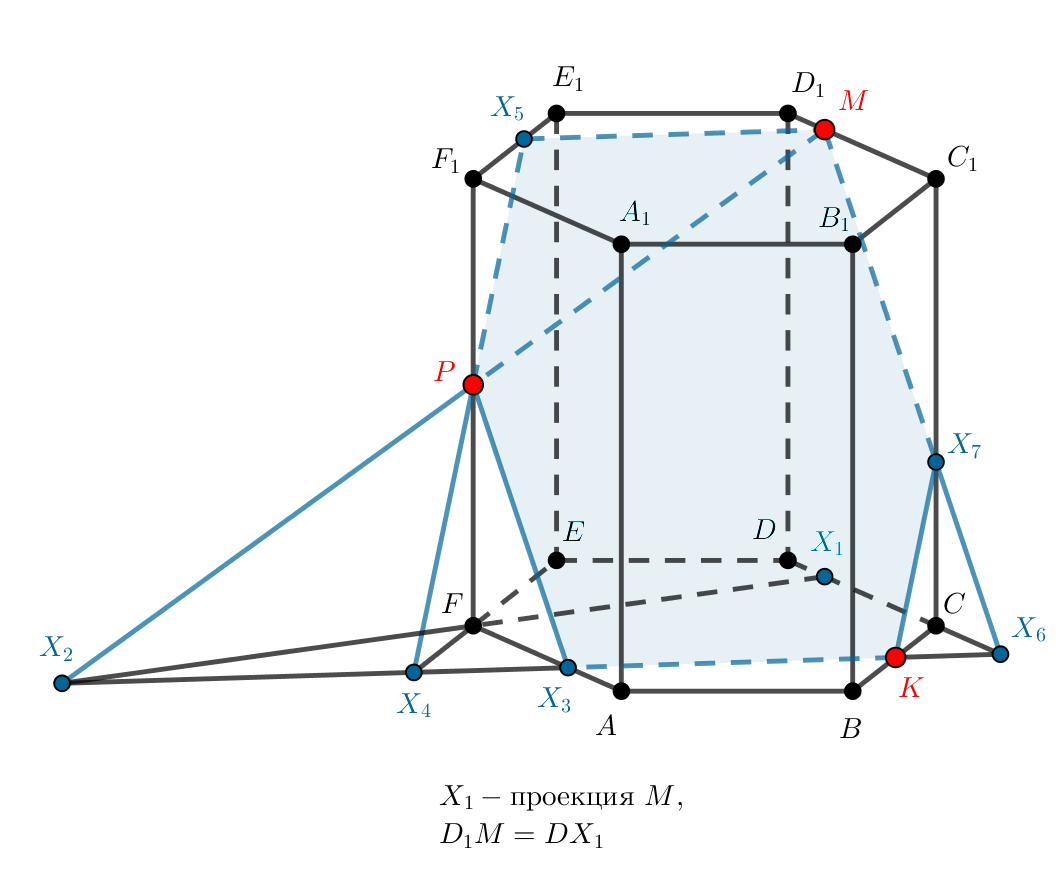
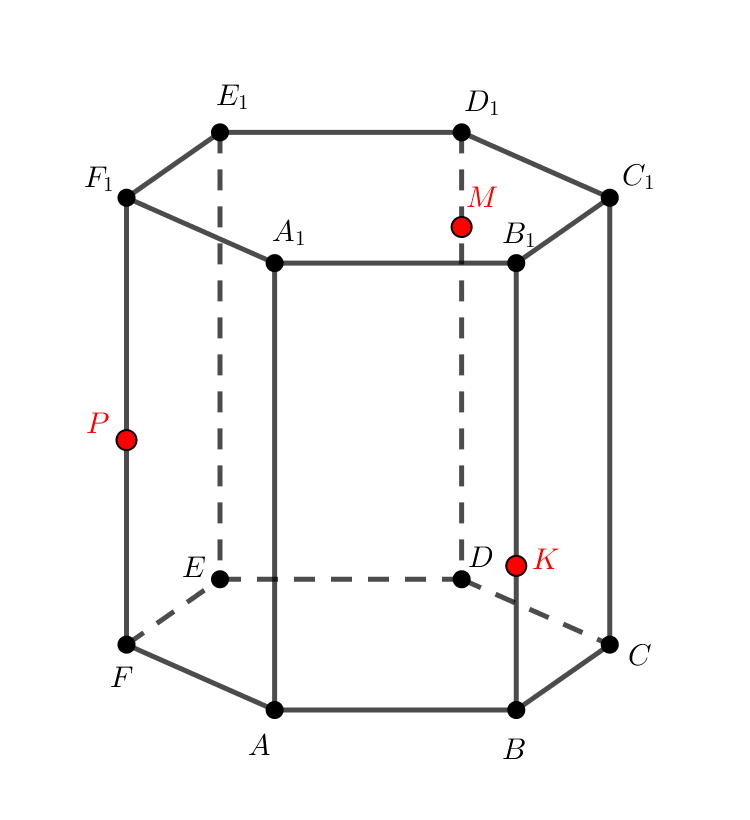
Постройте сечение правильной шестиугольной призмы, проходящее через точки , и точку бокового ребра
EE1 .

Показать ответ и решение

Точки сечения, которые мы строим, всюду обозначены синим и пронумерованы в том порядке, в котором мы их
строим!

Обозначим через плоскость сечения.

1.: Все точки прямой принадлежат , при этом . Тогда ,
и принадлежат .
2.: Все точки прямой принадлежат , при этом . Тогда
принадлежит .
3.: Все точки прямой принадлежат , при этом . Тогда
принадлежит .
4.: В правильной шестиугольной призме противолежащие
грани и параллельны, следовательно, прямые их пересечения с плоскостью
параллельны. , тогда прямая через , параллельная ,
принадлежит и лежит в плоскости . Ее точки пересечения и с ребрами и
соответственно принадлежат .
5.: Искомое сечение .