МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«АЛТЫНЖАРСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА ИМЕНИ КУРМАНГАЗЫ САГЫРБАЕВА»
ПЛАН
подготовки обучающихся 11 класса
к Государственной Итоговой Аттестации
по математике в форме ЕГЭ
2020-2021 учебный год
Единый государственный экзамен по математике в настоящее время совмещает два экзамена — выпускной за среднюю школу и вступительный в высшие учебные заведения и имеет два уровня: базовый и профильный. Поэтому в рамках ЕГЭ осуществляется проверка овладения материалом курса алгебры и начал анализа, геометрии, усвоение которых должно проверяться на выпускном школьном экзамене, а также материалом некоторых тем курса алгебры основной школы и геометрии основной и средней школы, которые традиционно даются на вступительных экзаменах в вузы. Поэтому успешная сдача к экзамену позволит ученику поступить в ВУЗ.
Цель: создание условий для систематизации полученных знаний, овладение приемами и методами решения задач, подготовка к итоговой аттестации в форме ЕГЭ.
Задачи:
- повторить и закрепить знания, умения и навыки, полученные в 5- 9,10 классах;
- развить способность самоконтроля: времени, поиска ошибок в планируемых проблемных заданиях;
- сформировать спокойное, уравновешенное отношение к экзамену;
- вести планомерную подготовку к экзамену;
- знакомство с новыми методами и приемами решения задач;
- формирование специальных умений и навыков обучающихся: алгоритмических умений и вычислительных навыков;
- освоение нестандартных приемов и методов решения задач;
- формирование умений применять полученные знания при решении «нетипичных», нестандартных задач.
- закрепить математические знания, которые пригодятся в обычной жизни и при продолжении образования.
Требования (умения), проверяемые заданиями экзаменационной работы:
1. Уметь выполнять вычисления и преобразования
1.1. Выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма;
1.2. Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
1.3. Проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
2. Уметь решать уравнения и неравенства:
2.1. Решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы;
2.2. Решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод;
2.3. Решать рациональные, показательные и логарифмические неравенства, их системы.
3. Уметь выполнять действия с функциями
3.1. Определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций;
3.2. Вычислять производные и первообразные элементарных функций;
3.3. Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции;
4. Уметь выполнять действия с геометрическими фигурами,
координатами и векторами
4.1. Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);
4.2. Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов);использовать при решении стереометрических задач планиметрические факты и методы;
4.3. Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.
5. Уметь строить и исследовать простейшие математические
модели:
5.1. Моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры;
5.2. Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать
практические задачи, связанные с нахождением геометрических величин;
5.3. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения;
5.4. Моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
6. Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
6.1. Анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчеты по формулам; пользоваться оценкой и прикидкой при практических расчетах;
6.2. Описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках;
6.3. Решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Организуемая деятельность
|
Сроки |
Мероприятие |
|
сентябрь |
изучение демоверсии ЕГЭ-2020 (цель – понять особенности заданий, которые будут предложены учащимся в этом году) |
|
сентябрь |
формирование на основе подготовленного аналитического материала понимания у обучающихся специфики ЕГЭ |
|
сентябрь |
оценка готовности учащихся к ЕГЭ, выявление проблем, типичных как для данного класса, так и индивидуально для каждого ученика; |
|
сентябрь |
планирование работы по развитию навыков выполнения первой части экзаменационного задания |
|
сентябрь |
формирование справочного материала для подготовки к ЕГЭ |
|
в течение года |
ознакомление с литературой по подготовке к ЕГЭ |
|
в течение года |
психологическая подготовка обучающихся к ЕГЭ, оказание помощи в выработке индивидуального способа деятельности в процессе выполнения экзаменационных заданий |
|
в течение года |
а) ознакомление учащихся с правилами заполнения бланков ответов. б) репетиция с учащимися заполнения бланков ответов. |
|
в течение года |
знакомство учащихся с информацией по регламенту проведения ЕГЭ |
|
в течение года |
проведение индивидуально-групповых занятий по математике |
|
в течение года |
индивидуальная работа с учащимися «группы риска» |
|
в течение года |
индивидуальная работа с мотивированными учащимися |
|
в течение года |
Информирование родителей учеников 11 класса о результатах тренировочных, диагностических и репетиционных работ и индивидуальных достижениях обучающихся |
|
в течение года |
оформление информационных стендов «Готовимся к ЕГЭ» |
ПЛАН ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ БАЗОВОГО УРОВНЯ
|
№ |
Тема |
|
|
Структура вариантов КИМ 2020. Спецификация. Типы заданий. |
|
|
Практикум по заполнению бланков ЕГЭ |
|
|
Действия с рациональными числами (Задание №1Б). |
|
|
Действия со степенями (Задание №2 Б) |
|
|
Практические задачи на процентные расчеты (Задание №3Б) |
|
|
Вычисление значения величины по формуле (Задание №4Б) |
|
|
Нахождение значения выражения (Задание №5 Б) |
|
|
Практические арифметические задачи (Задание №6Б) |
|
|
Решение уравнений (Задание №7Б) |
|
|
Практические задачи с геометрическим содержанием (Задание №8 Б) |
|
|
Анализ и сопоставление данных (Задание №9 Б) |
|
|
Задачи на вычисление вероятности события (Задание №10Б) |
|
|
Чтение данных по графику, диаграмме, таблице (Задание №11Б) |
|
|
Практические задачи на оптимальный выбор (Задание №12 Б) |
|
|
Задачи на вычисление площади поверхности, объема, количества ребер и граней (Задание №13 Б) |
|
|
Анализ и сопоставление данных, представленных в таблице, графике (Задание №14 Б) |
|
|
Нахождение элементов планиметрических фигур (Задание №15 Б) |
|
|
Зависимость объема и площади стереометрических тел от величины их элементов (Задание №16 Б) |
|
|
Решение неравенств с указанием соответствия (Задание №17 Б) |
|
|
Задания на умение исследовать простейшие математические модели (Задание №18 Б) |
|
|
Задания на применение признаков делимости (Задание №19 Б) |
|
|
Задания на умение строить и исследовать простейшие математические модели (Задание №20 Б) |
|
|
Решение вариантов ЕГЭ |
ПЛАН ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ
|
№ |
Тема |
|
|
Структура вариантов КИМ 2020. Спецификация. Типы заданий. |
|
|
Практикум по заполнению бланков ЕГЭ |
|
|
Практические задачи на процентные расчеты, арифметические задачи (Задание №1). Решение тригонометрических уравнений с отбором корней |
|
|
Чтение данных по графику, диаграмме, таблице (Задание №2). Решение тригонометрических уравнений с отбором корней |
|
|
Нахождение элементов и площади плоских фигур (Задание №3). Решение стереометрических задач |
|
|
Задачи на вычисление вероятности события (Задание №4). Решение стереометрических задач |
|
|
Решение уравнений (Задание №5). Решение стереометрических задач |
|
|
Нахождение элементов плоских фигур (Задание №6). Решение неравенств |
|
|
Чтение графика производной, первообразной (Задание №7). Решение неравенств. |
|
|
Нахождение элементов, объема и площади стереометрических тел (Задание №8). Решение неравенств |
|
|
Нахождение значения выражения (Задание №9). Решение планиметрических задач |
|
|
Вычисление значения величины по формуле (Задание № 10). Решение планиметрических задач |
|
|
Решение задач на движение, смеси, сплавы, работу, производительность (Задание №11) |
|
|
Задачи на нахождение точек максимума, минимума, наибольшего и наименьшего значений функции (Задание №12) |
|
|
Решение тригонометрических уравнений с отбором корней. Задачи на оптимальный выбор |
|
|
Решение тригонометрических уравнений с отбором корней. Задачи на оптимальный выбор |
|
|
Решение стереометрических задач. Банки, вклады, кредиты |
|
|
Решение стереометрических задач. Банки, вклады, кредиты |
|
|
Решение неравенств |
|
|
Задачи на оптимальный выбор |
|
|
Банки, вклады, кредиты |
|
|
Решение вариантов ЕГЭ |
Особое внимание уделять проработке и решению таких заданий, как 1-12 (как ни странно, наиболее подготовленные учащиеся часто ошибаются в простых заданиях по небрежности). Необходимо научить выполнять (может быть, с некоторыми недочётами) задания 13, 15, 17. Основной объект внимания обучающихся — задание 18, требующее умения комбинировать геометрические и алгебраические идеи, видеть за уравнением фигуру, за рисунком решение уравнений и их систем; умения вообразить взаимное расположение двигающихся по плоскости линий и фигур.
Задание 19 требует высокой математической культуры, но не очень много специальных знаний. Все необходимые сведения о целых числах и делимости изучаются в 5-7 классах. Вопрос не в знаниях, а в том, как их применить. Здесь важно сочетание опыта, фантазии и подготовки.
Необходима постоянная работа с математической терминологией, работа с формулами.
Контроль знаний и умений выпускников при подготовке к ЕГЭ
- Проведение зачётных занятий в форме тренировочных и диагностических работ по математике в форме ЕГЭ по линии СтатГрад.
- Проведение постоянного мониторинга качества обученности и успешности выполнения заданий ЕГЭ базового и профильного уровней
Пособия и интернет – ресурсы для подготовки к ЕГЭ
- Сборники тестовых заданий ЕГЭ, 2019-2020 гг. Изд. МНЦМО, Экзамен, Национальное образование и др.
- Видео-репетиторы по математике ЕГЭ.
3. Интернет ресурсы: http://reshuege.ru http://www.alleng.ru, http://shpargalkaege.ru, http://mirege.ru, http://www.egetrener.ru, http://www.ege-ok.ru, http://www.alexlarin.net, http://www.egeigia.ru, http://ege-study.ru и др.
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
Задание 16
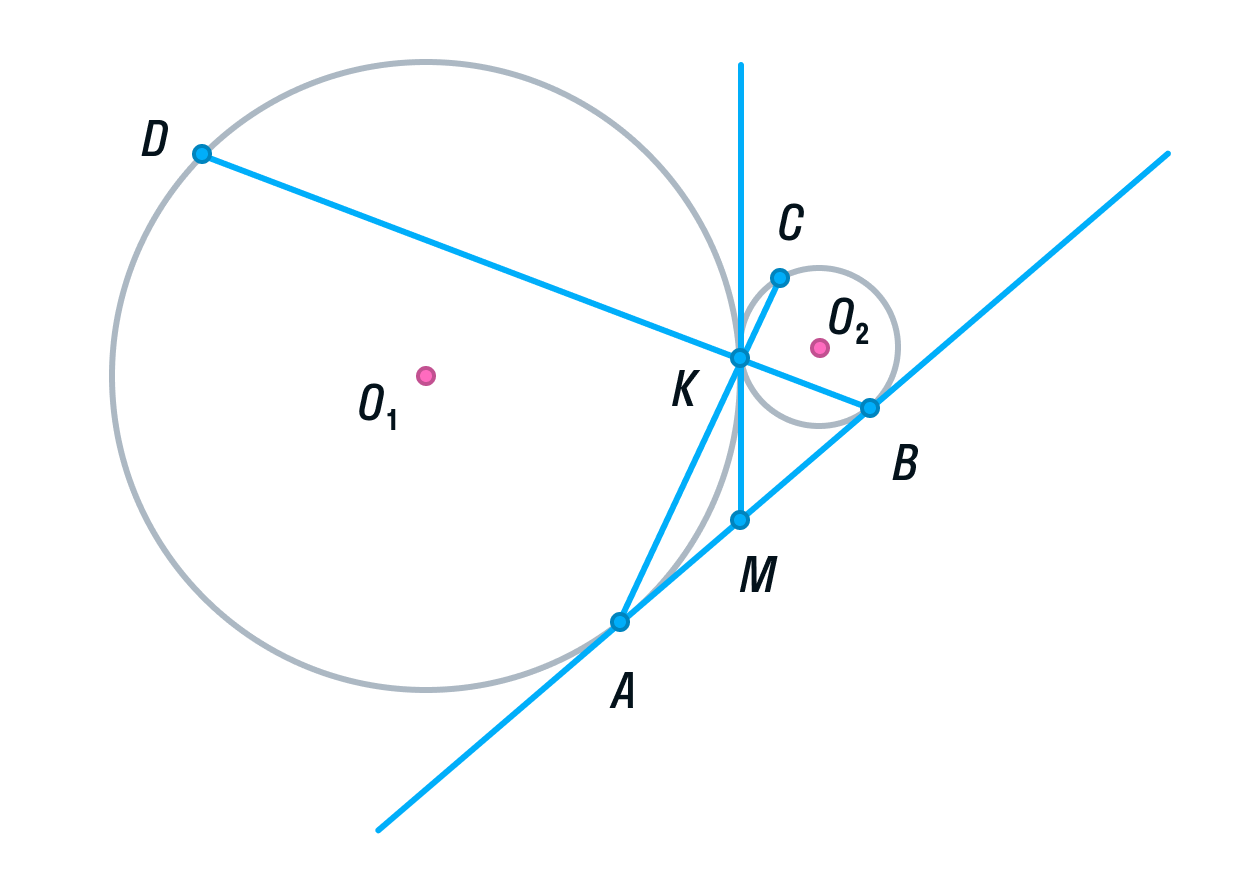
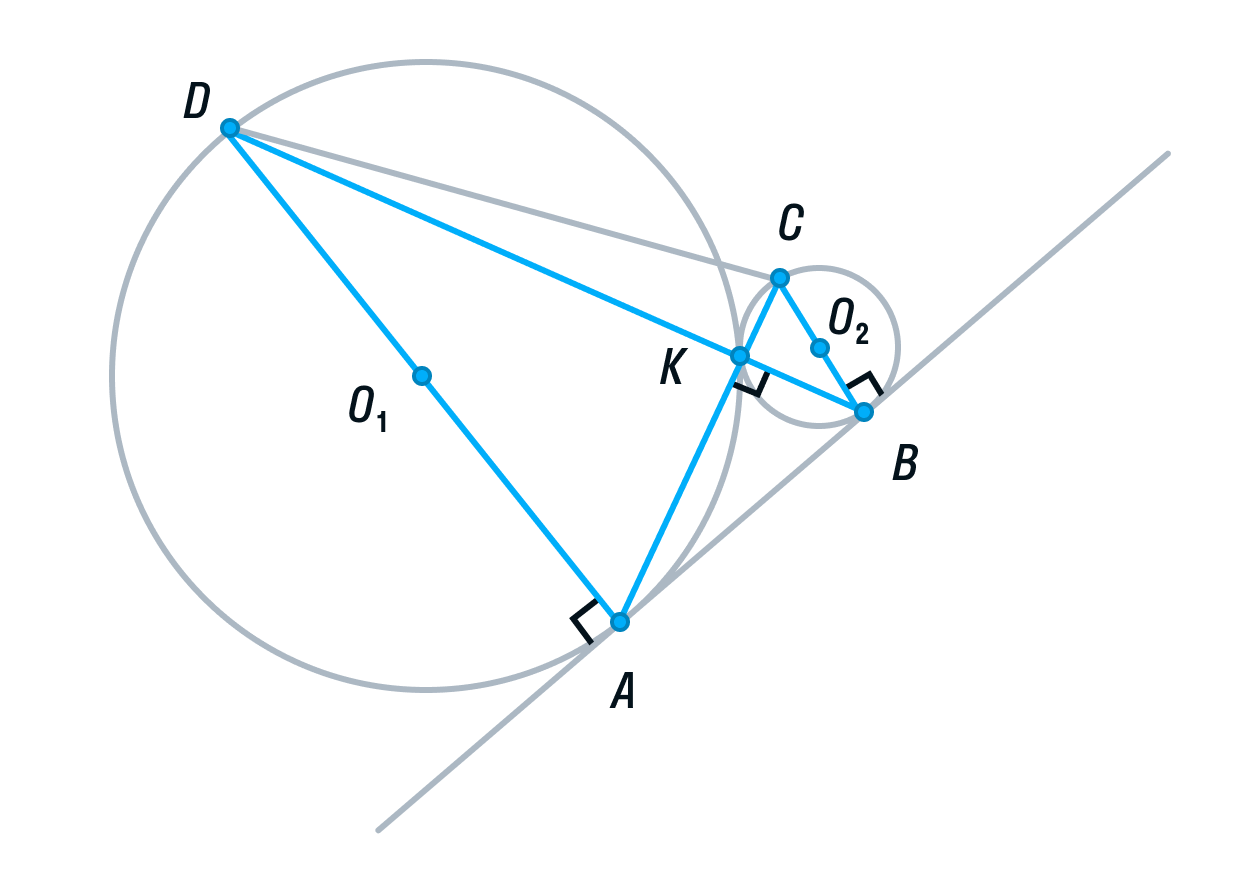
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
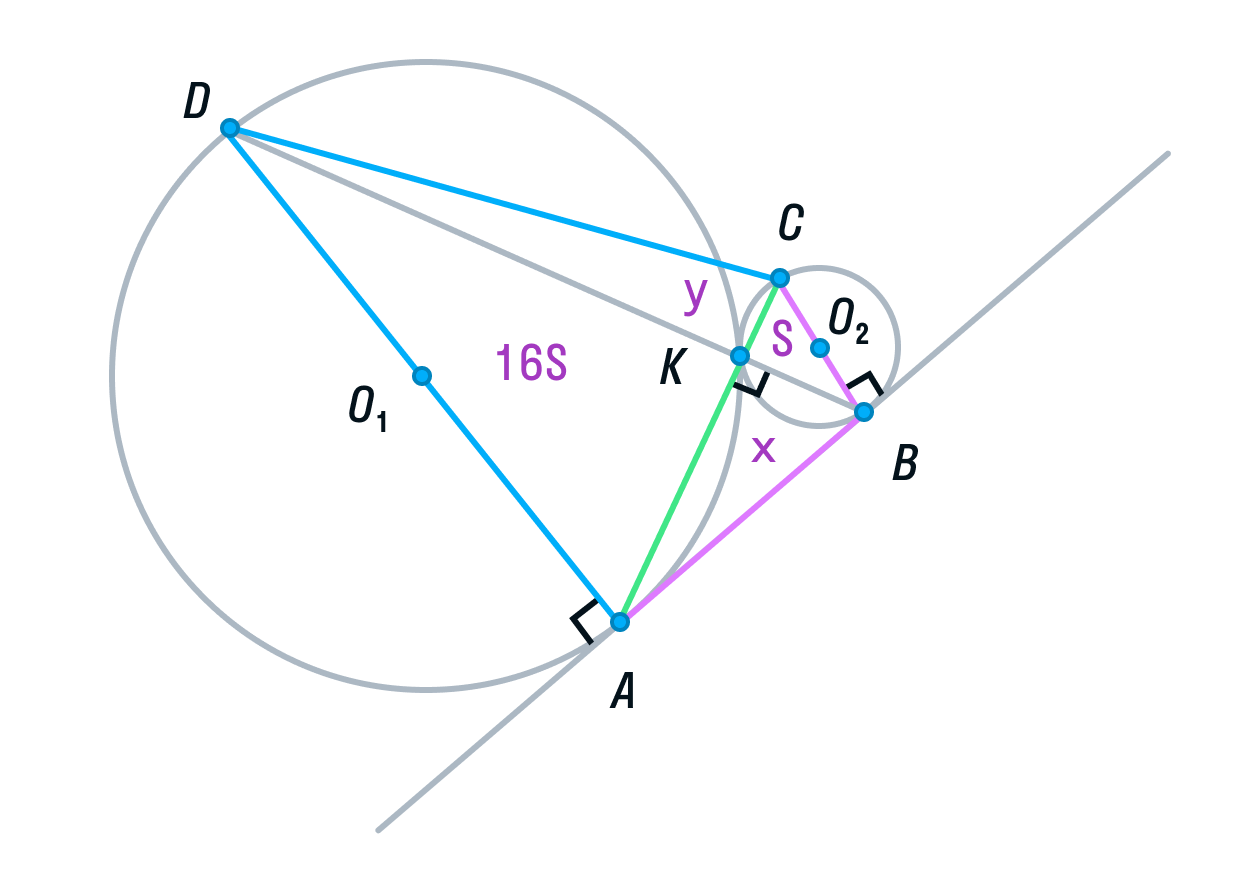
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
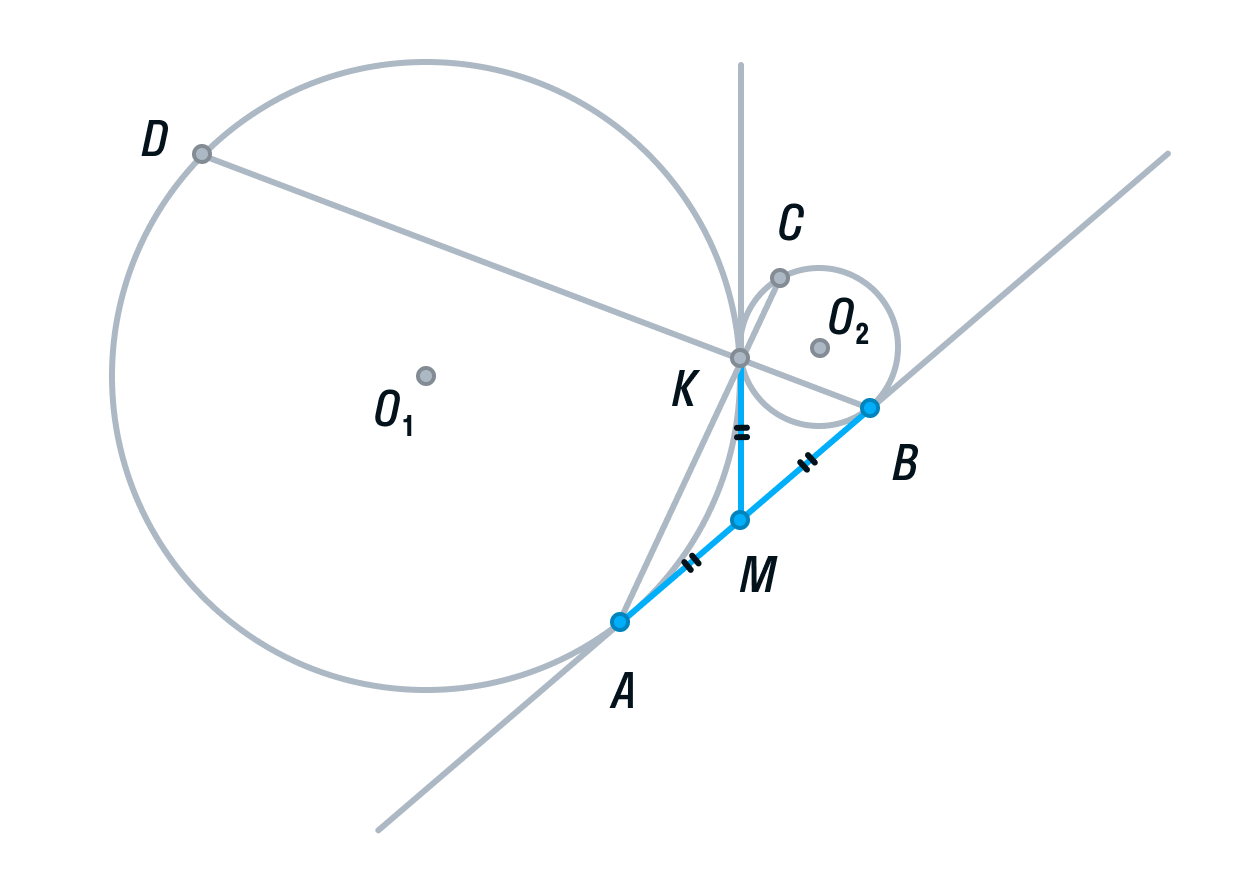
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
-
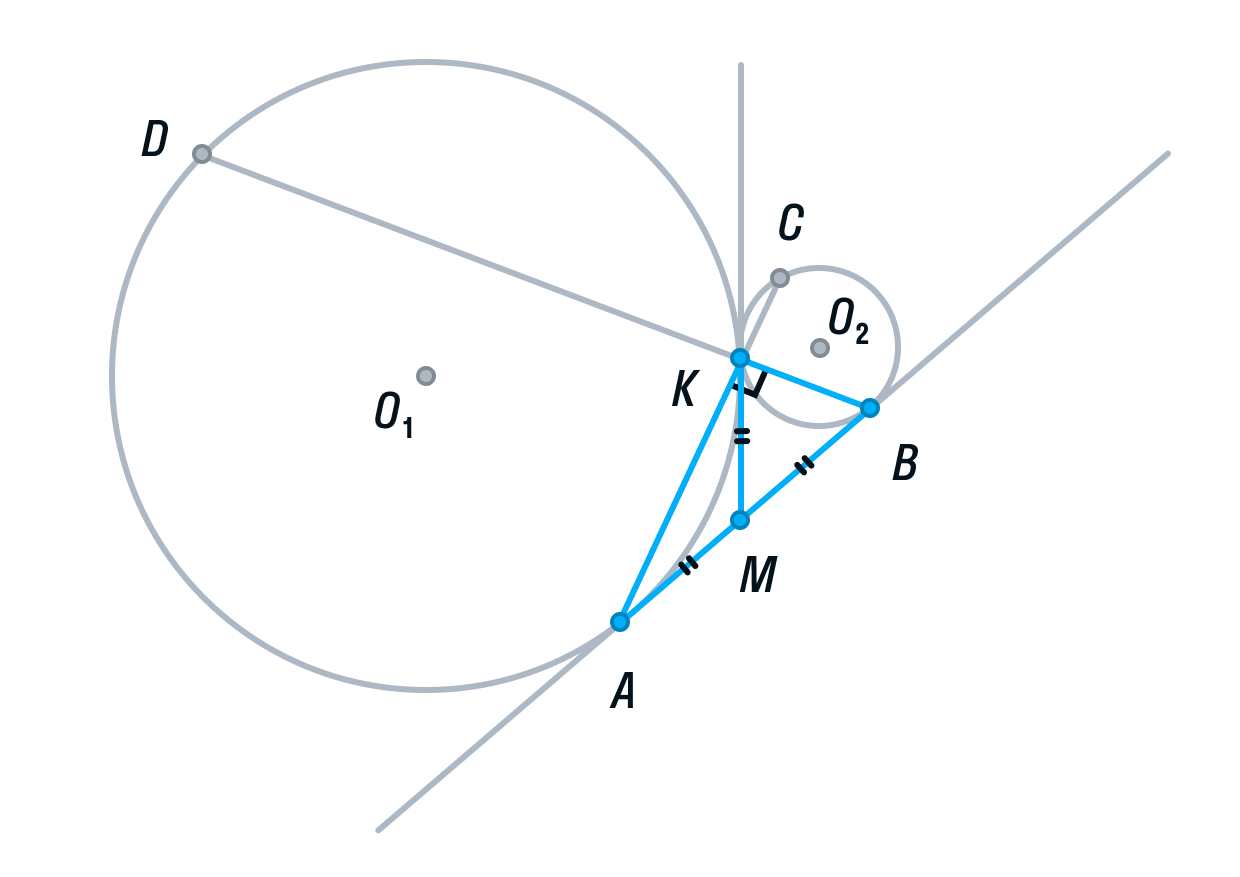
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
-
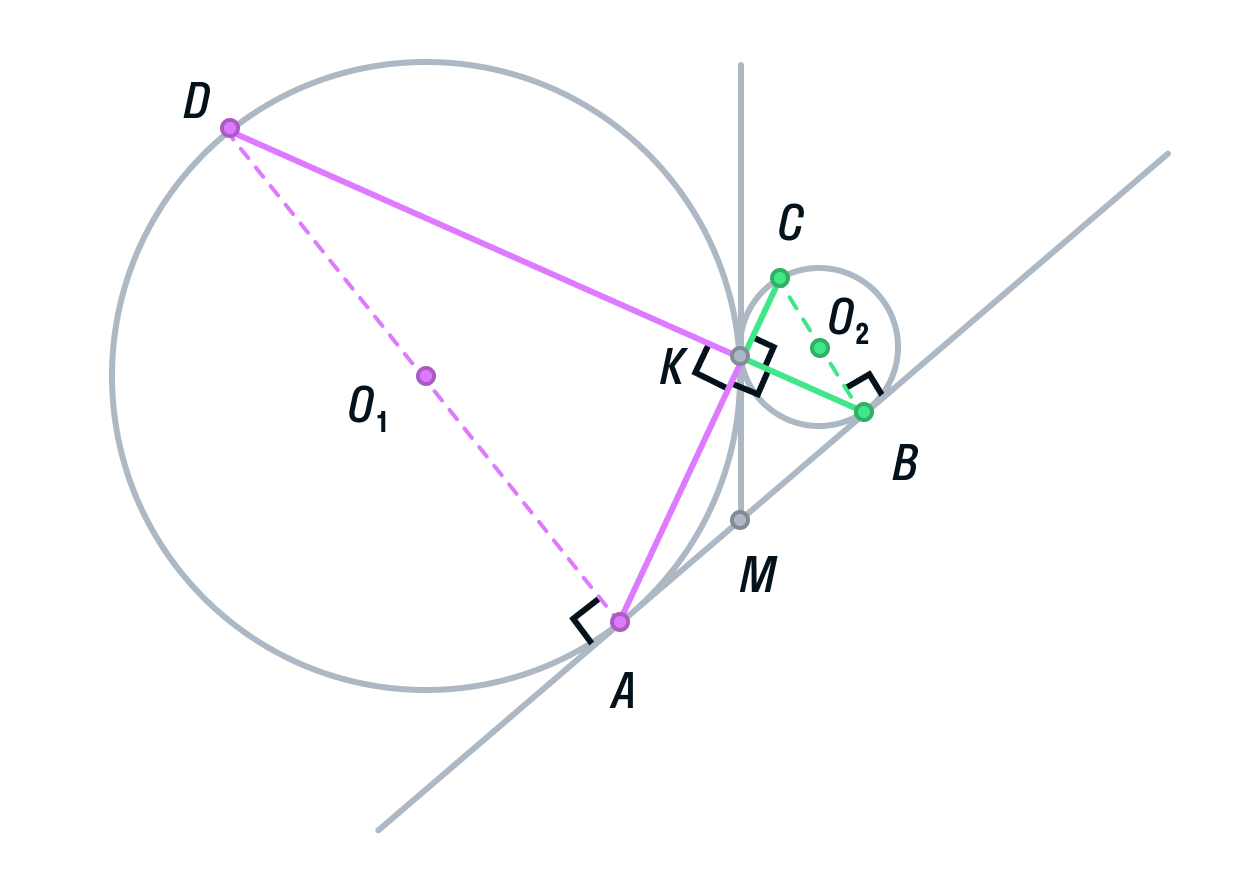
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
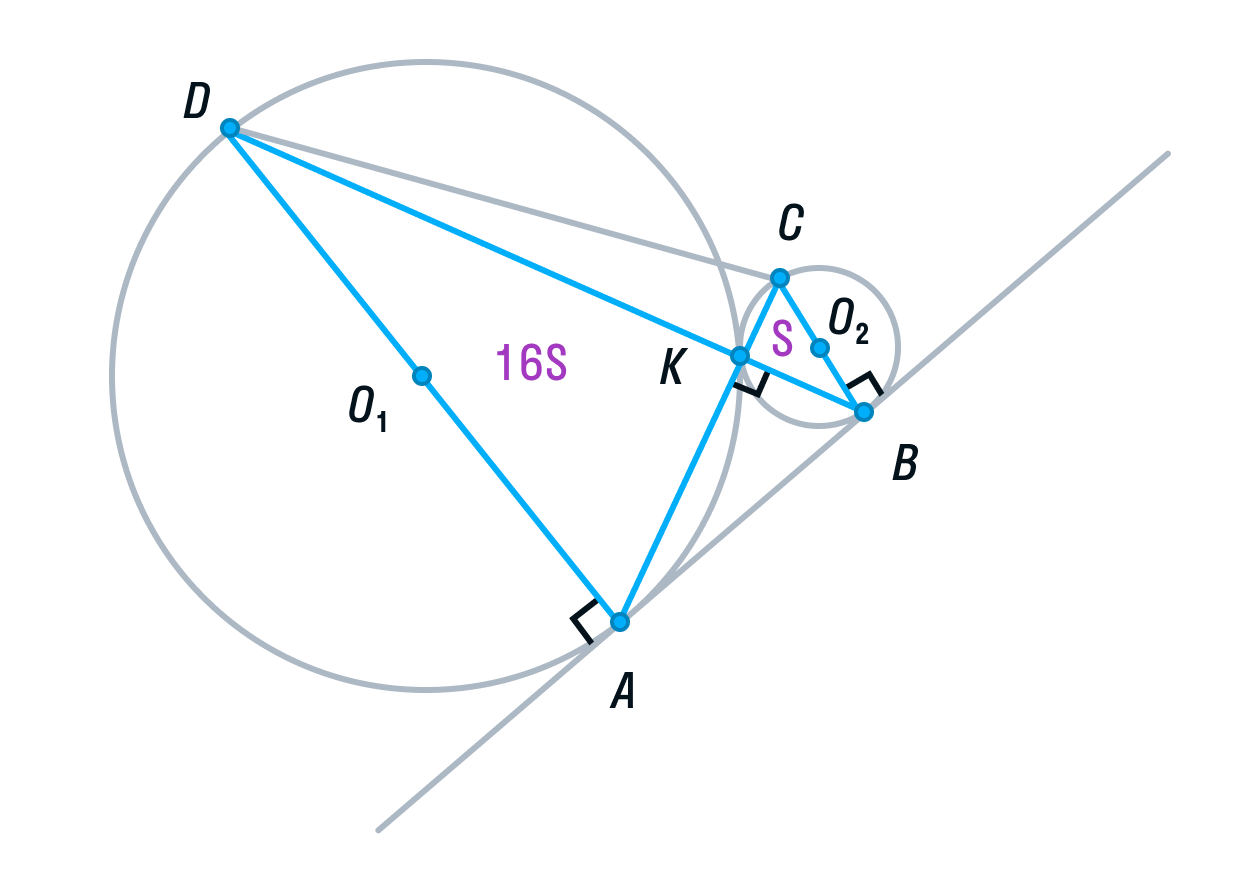
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
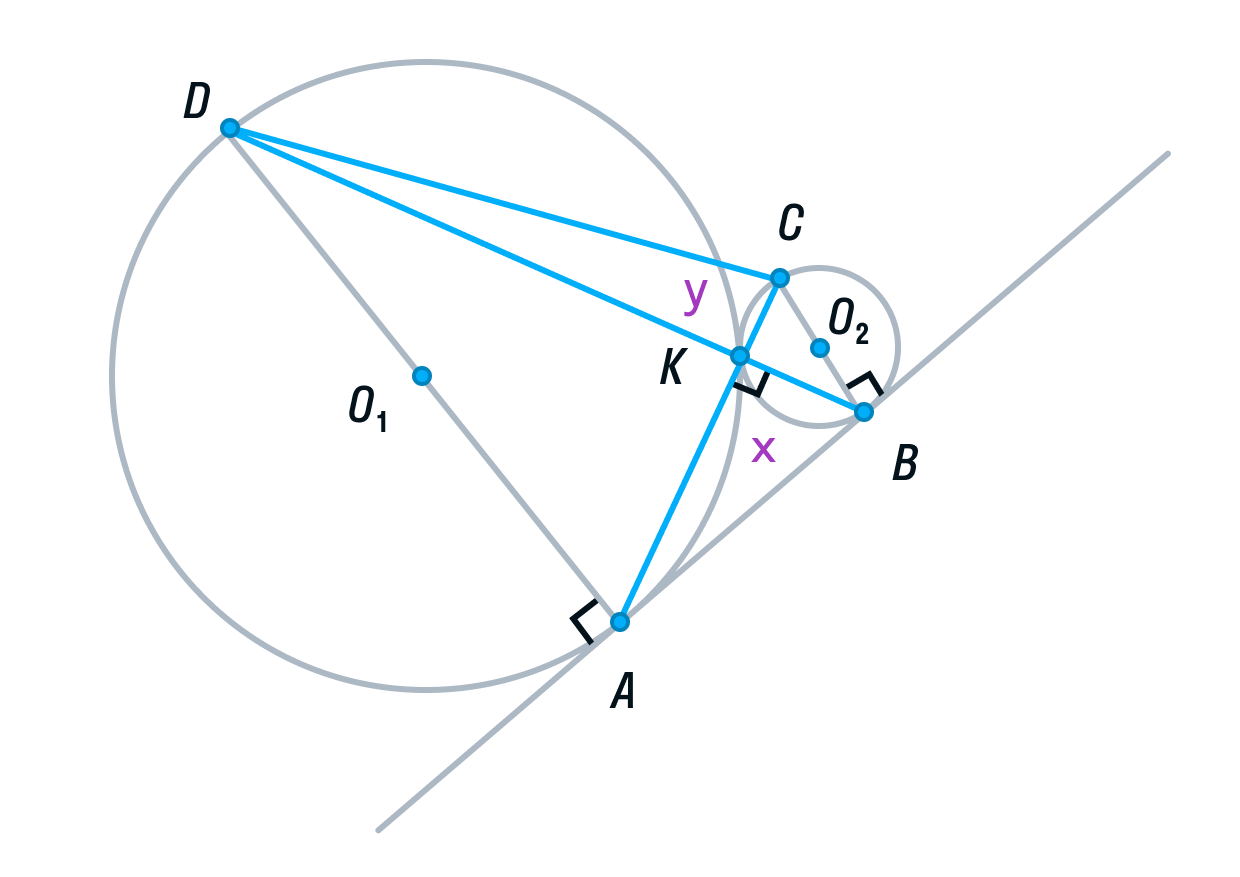
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
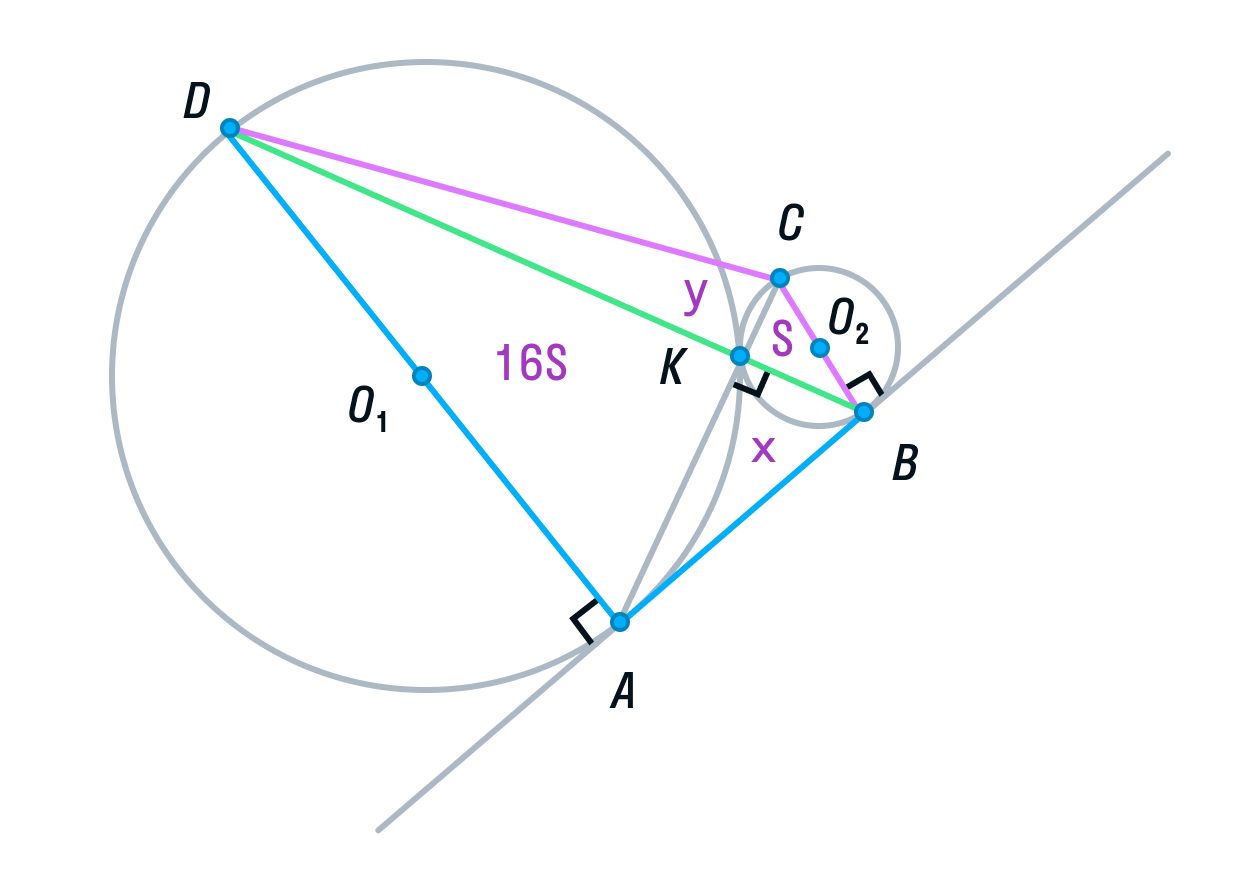
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
-
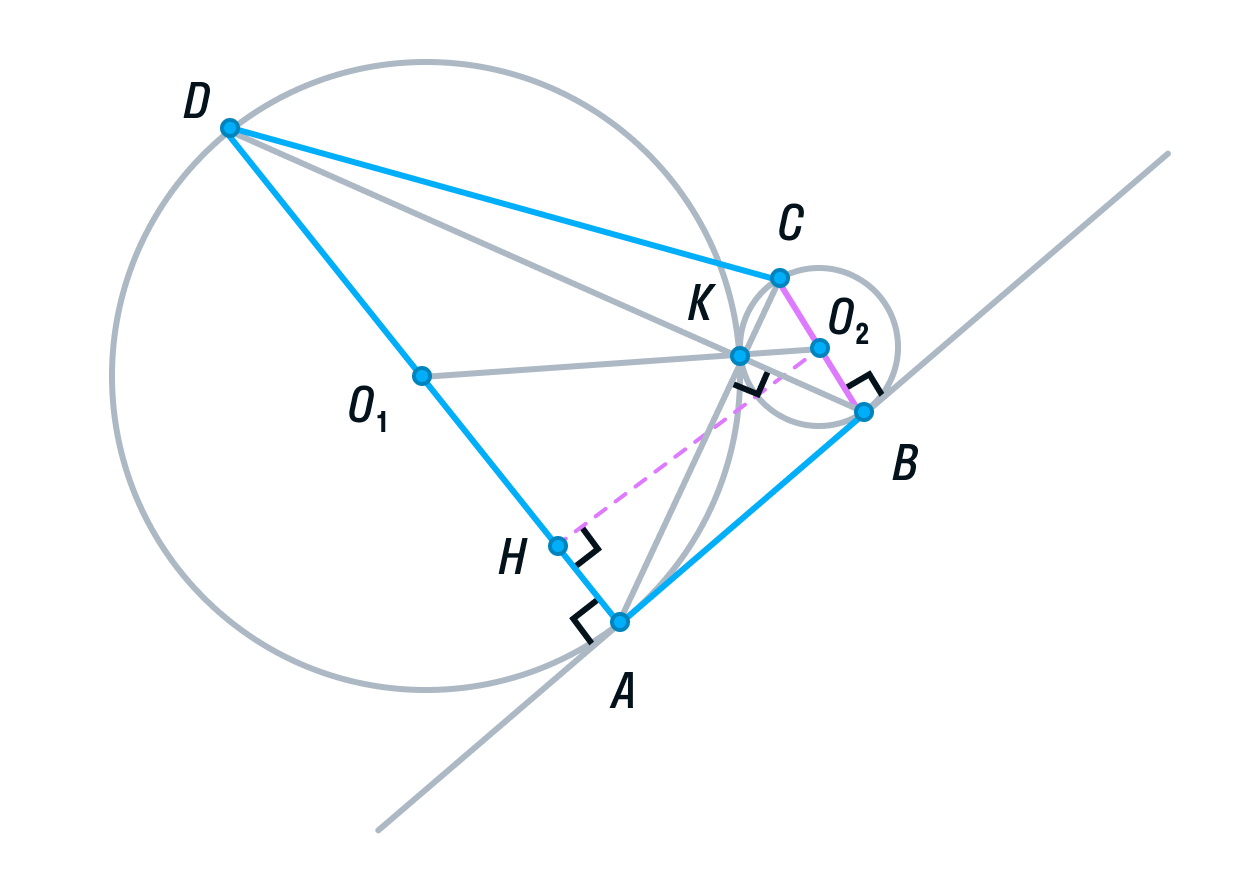
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
-
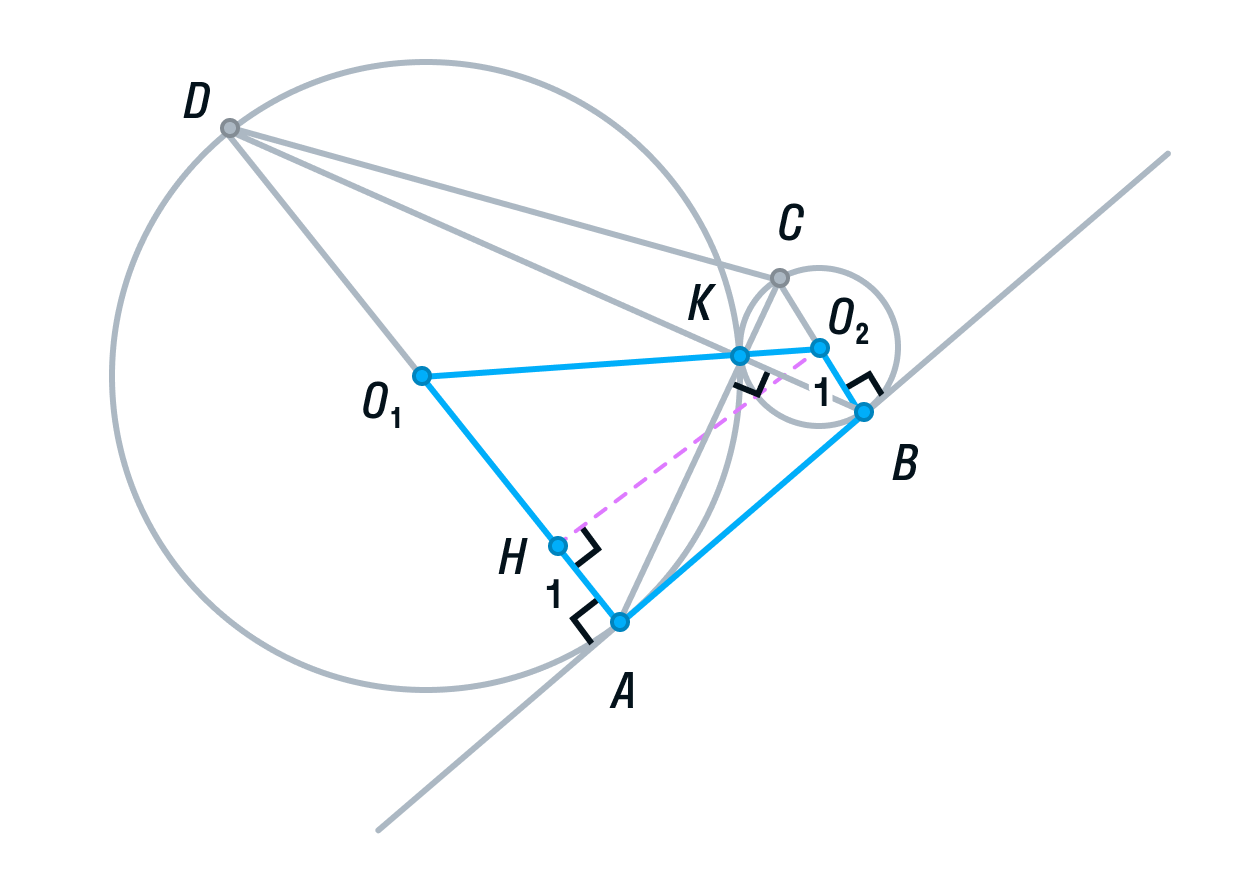
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!
Календарно-тематическое
планирование консультаций «Подготовка к ЕГЭ по математике
профильного уровня» 2022-2023
учебный год в 11 классе
|
|
Тема |
Дата |
|
|
план |
факт |
||
|
|
Структура |
16.09 |
|
|
|
. |
23.09 |
|
|
|
Преобразование |
30.09 |
|
|
|
Преобразование |
07.10 |
|
|
|
Решение |
14.10 |
|
|
|
Решение линейных |
21.10 |
|
|
|
Решение |
11.11 |
|
|
|
Решение |
18.11 |
|
|
|
Решение |
25.11 |
|
|
|
Чтение |
02.12 |
|
|
|
Применение |
09.12 |
|
|
|
Графики |
16.12 |
|
|
|
Графики |
23.12 |
|
|
|
Решение |
13.01 |
|
|
|
Решение |
20.01 |
|
|
|
Решение |
27.01 |
|
|
|
Решение |
03.02 |
|
|
|
Решение |
10.02 |
|
|
|
Решение |
17.02 |
|
|
|
Решение |
24.02 |
|
|
|
Решение |
03.03 |
|
|
|
Решение |
03.03 |
|
|
|
Решение |
10.03 |
|
|
|
Решение |
17.03 |
|
|
|
Задачи. |
24.03 |
|
|
|
Задачи. |
07.04 |
|
|
|
Решение |
14.04 |
|
|
|
Решение |
21.04 |
|
|
|
Решение |
28.04 |
|
|
|
Решение |
05.05 |
|
|
|
Решение |
12.05 |
|
|
|
Решение |
19.05 |
|
|
|
Решение |
26.05 |
|
|
|
Решение |
26.05 |
Привет тебе, будущий студент/-ка! Это — твой план подготовки к ЕГЭ по профильной математике по демо-версии 2023 года. Его составили мы, Константин и Виктория Кос, репетиторы и авторы: сайта cos-cos.ru и группы vk.com/cos_cos_ru.
Зачем этот план нужен?
Мы не понаслышке знаем, что у ребят, которые готовятся сами к ЕГЭ (без репетиторов и курсов) есть два больших вопроса: в какой последовательности проходить темы и как распределить свое время. План дает ответ на оба:
— в нем продуманная последовательность прохождения задач ЕГЭ по математике, выстроенная логически (по темам),
— задачи распределены по неделям, так, чтобы нагрузка была примерно одинаковой, и ты всё успел и ничего не забыл.
ВАЖНО! Тебе может показаться, что это не так, и некоторые недели сложнее, чем другие. Это нормально – у разных людей разные темы идут легче или, наоборот, труднее, — кроме того, в плане занятий заложено время на повторение пройденного + решение контрольного варианта – каждые 2-3 месяца.
Как пользоваться?
Распечатываешь план и вешаешь на стенку. Каждую неделю проходишь темы, указанные в плане. Пройденные темы отмечаешь галочкой и радуешься четко заметным результатам.
Что надо знать на старте?
— линейные и квадратные уравнения (часть задачи 1)
— простые задачи на теорию вероятность (часть задачи 2)
Как видишь, требования совсем невысокие. Если уж эти задачи вызывают затруднения, то стоит подумать, надо ли тебе сдавать профиль вообще?
Что будешь знать в итоге?
Первые 12 задач, 14 задача (неравенства), 15 задача (экономическая), 18 задача, пункты а, б (на логику и числа). По баллам это до 80 (максимум), реальный ориентир — 70 — 75.



.
Скачать статью
Математика — обязательный предмет на ЕГЭ. При этом, если он не нужен для поступления, вы можете сдать упрощенный экзамен. Он позволит проверить, насколько хорошо усвоена школьная программа. У медали есть и обратная сторона: если не перейти порог по базовой математике, то аттестат не получаешь.
Структура экзамена
По демоверсии 2021 года, серьезных изменений в структуре экзамена не предвидится. Количество заданий, система их оценивания и предоставленные формулы остались прежними.
На решение КИМ дается 3 часа.
Взять с собой на экзамен предложено можно простую линейку. Однако подготовка к ЕГЭ по математике, базовый уровень которой предполагает отсутствие номеров с развернутым ответом, не требует специального оборудования.
Навыки, необходимые для решения экзамена:
- выполнять вычисления и преобразования,
- решать уравнения и неравенства,
- выполнять действия с функциями,
- выполнять действия с геометрическими фигурами,
- строить и исследовать математические модели,
- решать простые текстовые задачи, в том числе на комбинаторику.
Количество заданий — 20.
Вторая часть отсутствует.
Оценка заданий ЕГЭ по базовой математике
Точная шкала перевода первичных баллов в оценку будет известна только после проверки экзаменационных работ. Подготовка к ЕГЭ по математике (базовый уровень в том числе) необходима, чтобы после экзамена не возникло неприятного сюрприза.
На данный момент нет оснований предполагать, что шкала перевода изменится в сравнении с прошлым годом:
- 0-6 баллов — «2»,
- 7-11 баллов — «3»,
- 12-16 баллов — «4»,
- 17-20 баллов — «5».
Все задания имеют одинаковый вес — один балл.
План подготовки к ЕГЭ по математике базового уровня
Когда в школе начинается подготовка к ЕГЭ по математике, базовый уровень экзамена часто игнорируют. Это может привести к досадным ошибкам. Чтобы их избежать, нужно разработать план подготовки.
Во-первых, стоит повторить основы, то есть математику 5-6 класса. Для этого можно использовать учебники, рекомендованные ФГОС, которые легко получить в школьной библиотеке или найти в интернете. От основ зависит успешная подготовка к ЕГЭ по математике: базовый уровень знаний обрести просто необходимо.
Во-вторых, прорешивайте задания каждого типа, не пропуская. Экзамен — всегда лотерея, поэтому никогда не предугадаешь, что тебе попадется. При решении некоторых заданий может оказаться бесполезна вся подготовка к ЕГЭ по математике: базовый уровень, несмотря на название, не предполагает, что все номера составлены без подводных камней.
В-третьих, не игнорируйте программу одиннадцатого класса. Структура экзамена редко совпадает с тем, что изучается в школе, но есть и исключения из правила. Когда начинается специализированная подготовка к ЕГЭ по математике, базовый уровень стереометрии, комбинаторики и некоторых других разделов, заложенный именно в одиннадцатом классе, позволяет успешно решать часть заданий КИМ.
Разбор заданий ЕГЭ по базовой математике
Когда в школах начинается подготовка к ЕГЭ по математике, базовый уровень предмета просто нарешивают, не пытаясь разобрать задания. Чтобы разобраться в решении номеров, следует помнить основные типы встречающихся задач:
- Текстовые задачи — сюда входят задачи на проценты, округление и смелкалку. Задачи на проценты решаются через умножение (процент принимается за десятичную дробь — 15% = 0,15). Задачи на округление решаются через деление с помощью логики. Задача №20 решается методом подбора.
- Вычисления и преобразования — блок заданий, проверяющих умение обращаться с дробями и степенями, а также с тригонометрическими и иррациональными выражениями. Предполагается, что когда начинается подготовка к ЕГЭ по математике, базовый уровень знаний и умение обращаться с формулами, данными в начале КИМ, у вас уже имеется. В заданиях важно уметь подставлять необходимые значения в формулы и производить вычисления по этим формулам, а также записывать числа в разных видах.
- Размеры и единицы измерения — чтобы решить задания этого раздела, необходимо знать порядок возрастания величин времени, длины, массы, объема, площади и уметь сопоставлять их с реальными объектами.
- Фигуры — для решения заданий данного блока нужно знать основные понятия (единицы измерения и части фигур), а также уметь сопоставлять их с реальными фигурами и использовать эти данные при решении задач. Например, когда идет подготовка к ЕГЭ по математике, базовый уровень владения стереометрией должен позволять определить объем фигур, площадь их боковых граней и тому подобное.
- Анализ информации — на экзамене информация представлена в виде графиков, диаграмм и текста. Для решения заданий нужно пронаблюдать за изменениями величин, а также найти наибольшую из них. Проверяется умение анализировать информацию или выбирать оптимальный вариант, опираясь на логическое мышление.
- Уравнения и неравенства — проверяется умение использовать данные формулы, выводить из них другие, а также отмечать значения на числовой прямой. Все это обеспечит хорошая подготовка к ЕГЭ по математике: базовый уровень заданий раздела предполагает, что они с большей вероятностью будут типовыми и без подводных камней, к которым привыкают выпускники, сдающие профиль, и учителя.
- Теория вероятностей (1 задание) — задание, решающееся с помощью определения нужной формулы комбинаторики (их всего три) и подставления в нее значений из задачи.
Материалы для подготовки к базе по математике ЕГЭ
Решение актуальных заданий экзамена — это почти гарантированно хорошая подготовка к ЕГЭ по математике: базовый уровень предмета также имеет демоверсию, кодификатор и спецификатор, опубликованные на сайте ФИПИ.
Найти дополнительный практический материал можно в открытом банке заданий также на сайте ФИПИ.
Также можно использовать дополнительные пособия:
- комплекс материалов для подготовки учащихся от ФИПИ,
- «Математика в схемах и таблицах» (И.В. Третьяк),
- типовые варианты от разработчиков (И.В. Ященко) и др.
Одно из самых важных дел одиннадцатиклассника — подготовка к ЕГЭ по математике, базовый уровень или профильный, при этом, не важно. От экзамена любого уровня сложности зависит получение аттестата и возможность поступить в вуз, поэтому откладывать подготовку на потом не стоит.
Населенный пункт: Иркутская область, рп. Видим
Цель:
Успешно пройти ЕГЭ (ГИА) по математике в 2022-2023 учебном году.
Задачи:
-Осуществить информационное, методическое, психолого-педагогическое обеспечение итоговой аттестации выпускников 11 класса;
-Выявить соответствие подготовки выпускников требованиям образовательных стандартов;
-Обеспечить психологический комфорт и правовую защищенность всех участников образовательного процесса в ходе проведения итоговой аттестации.
Система работы по подготовке к ЕГЭ по математике на 2022 -2023 учебном году в 11 классе
- Включать в изучение текущего учебного материала задания, соответствующие экзаменационным заданиям.
- В содержание текущего контроля включать экзаменационные задачи.
- Изменить систему контроля над уровнем знаний учащихся по математике
- Итоговое повторение построить исключительно на отработке умений и навыков, требующихся для получения положительной отметки на экзамене.
- Подготовка ко второй части работы осуществляется как на уроках, так и во внеурочное время на элективных курсах. Используется сборники для подготовки к экзаменам, рекомендованные ФИПИ.
- Важным условием успешной подготовки к экзаменам является тщательность в отслеживании результатов учеников по всем темам и в своевременной коррекции уровня усвоения учебного материала.
План работы по подготовке учащихся к ЕГЭ (ГИА) на 2022-2023 учебный год по математике
|
№ п/п |
Мероприятия |
Сроки проведения |
|
1 |
Работа по изучению индивидуальных особенностей учащихся (с целью выработки оптимальной стратегии подготовки к ЕГЭ (ГИА) по математике). |
В течение года |
|
2 |
Психологическая подготовка к ЕГЭ (ГИА). Индивидуальное консультирование учащихся. |
В течение года |
|
3 |
Использование современных образовательных технологий, новых форм организации учебно- воспитательного процесса, способствующих повышению качества подготовки школьников к итоговой аттестации, формированию предметной компетенции. |
В течение года |
|
4 |
Беседа с учащимися: «Подготовка к ЕГЭ (ГИА) по математике» |
1 четверть |
|
5 |
Пополнение классной библиотеки методической и информационной литературой по подготовке к ЕГЭ (ГИА) -2020. Обеспечение участников ЕГЭ (ГИА) учебно-тренировочными материалами, обучающими программами, методическими пособиями, информационными и рекламными материалами. |
В течение года |
|
6 |
Проведение с учащимися цикла бесед: « Знакомство с Положением о формах и порядке проведения ЕГЭ (ГИА)» |
2 четверть |
|
7 |
Работа с учащимися:
|
В течение года Сентябрь Сентябрь-октябрь Ноябрь Ноябрь 2 четверть 3 четверть В течение года |
|
8 |
Разбор заданий демонстрационного варианта экзамена по математике (ЕГЭ-2023) |
1 четверть |
|
9 |
Подготовка, оформление информационного стенда «Подготовка к ЕГЭ (ГИА) -2023» для учащихся и их родителей |
2 четверть |
|
10 |
Индивидуальные консультации родителей |
В течение года |
|
11 |
Работа с заданиями различной сложности. Практикум по решению заданий экзаменационной работы |
Индивидуальная работа по группам в течение года |
|
12 |
Подготовка материалов для проведения пробной внутришкольной ГИА-2023 |
3четверть |
|
13 |
Регулярное участие в диагностических работах |
В течение года |
|
14 |
Регулярное участие в тренировочных работах |
В течение года |
|
15 |
Мониторинг качества подготовки учащихся к ЕГЭ (ГИА) |
В течение года |
|
16 |
Информирование по вопросам подготовки к ЕГЭ (ГИА): -знакомство с инструкцией по подготовке к ЕГЭ (ГИА); -правила поведения на ЕГЭ (ГИА); -КИМы; -инструктирование учащихся; проведения ЕГЭ (ГИА); -официальные сайты ЕГЭ (ГИА). Индивидуальное информирование и консультирование по всем вопросам, связанных с ЕГЭ (ГИА) |
В течение года |
|
17 |
Индивидуальные консультации для учащихся и их родителей по вопросам подготовки и проведения ЕГЭ (ГИА) -2023 Анализ работы учителя «О порядке подготовки и проведения ЕГЭ (ГИА)» (нормативные документы, КИМы, сайты) |
В течение года Май — июнь |
Календарно тематический план консультаций для учащихся11 класса по подготовке к ГИА (в форме ЕГЭ профильный уровень)
|
№ п/п |
Тема консультации |
Примерные сроки |
Примечание |
|
1 |
Задания 1,2,3,4 |
Сентябрь |
|
|
2 |
Задания 5,6,7,8 |
Октябрь |
|
|
3 |
Задания 9,10,11 |
Ноябрь |
|
|
4 |
Задания 12 |
Декабрь |
|
|
5 |
Задание 12 |
Январь |
|
|
6 |
Решение типовых тестов ЕГЭ-2023 |
Февраль |
|
|
7 |
Решение типовых тестов ЕГЭ-2023 |
Март |
|
|
8 |
Решение типовых тестов ЕГЭ-2023 |
Апрель |