B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии.
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.
Решения заданий № 16 Профильного ЕГЭ по математике.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
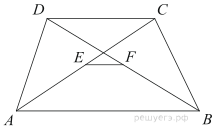
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
.
Посмотреть решение
3. (ЕГЭ-2020, Демовариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
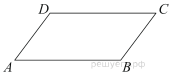
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
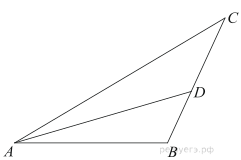
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Планиметрия. Стрим 10 марта. Разбор домашнего задания
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Вариант 1 6. Планиметрия
1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
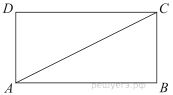
2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.
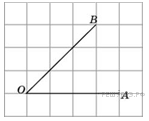
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2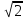
4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
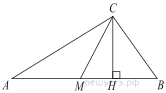
5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
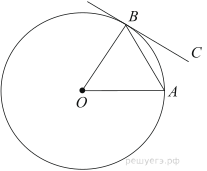
6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.
8. Найдите величину угла АВС. Ответ дайте в градусах.
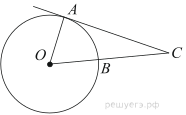
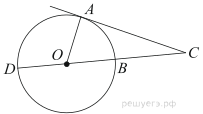
9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Вариант 2 6. Планиметрия
В 1. Сторона правильного треугольника равна 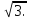
2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.
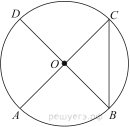
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.
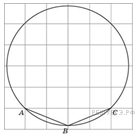
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.
Вариант 3 6. Планиметрия
1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.
2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.
4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.
5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.
6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите
8. Найдите площадь ромба, если его диагонали равны 4 и 12.
9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.
10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
Вариант 4 6. Планиметрия
1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.
2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.
3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.
6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41
Найдите радиус окружности, вписанной в этот треугольник.
8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите
10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
Вариант 5 6. Планиметрия
1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2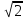
2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.
4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.
6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.
7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.
9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.
Вариант 6 6. Планиметрия
1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.
2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите
4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.
6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.
7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.
8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
10. В треугольнике ABC угол ACB равен °, угол B равен
°, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Вариант 7 6. Планиметрия
1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.
4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.
10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Вариант 8 6. Планиметрия
1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.
3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.
6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.
7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.
9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.
10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2
Вариант 9 6. Планиметрия
1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на
4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.
5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту
7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.
8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.
Вариант 10 6. Планиметрия
1. Найдите величину угла АВС. Ответ дайте в градусах.
2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.
3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.
4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.
5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.
6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.
7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
9. В треугольнике известно, что , , угол
равен 90°. Найдите радиус вписанной окружности.
10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС =
. Найдите
|
6. Планиметрия |
||||
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
Всё варианты 16 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 13 ЕГЭ по математике профильного уровня 2022 год (планиметрия)
1) (28.03.2022 досрочная волна) В треугольник АВС вписана окружность, которая касается АВ в точке Р. Точка М – середина стороны АВ.
а) Докажите, что (MP = frac{{left| {,BC — AC,} right|}}{2}.)
б) Найдите углы треугольника АВС, если известно, что длина отрезка МР равна половине радиуса вписанной в треугольник АВС окружности, BC > AC, а отрезки МС и МА равны.
ОТВЕТ: (angle C = {90^ circ };,,angle A = arctgfrac{4}{3};,,angle B = arctgfrac{3}{4}.)
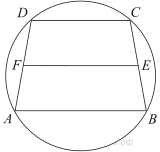
2) (28.03.2022 досрочная волна) Дана равнобедренная трапеция ABCD. На боковой стороне AB и большем основании AD взяты соответственно точки F и E так, что FE параллельно CD, а FC = ED.
а) Докажите, что (angle BCF = ,angle AFE;)
б) Найдите площадь трапеции ABCD, если ED = 3 BF, FE = 5 и площадь трапеции FCDE равна (14sqrt {35} .)
ОТВЕТ: (frac{{73sqrt {35} }}{4}.)
3) (28.03.2022 досрочная волна) На сторонах AB и BC треугольника ABC отмечены точки M и N так, что АМ : МВ = CN : NB = 1 : 2. Прямая MN касается окружности, вписанной в треугольник ABC в точке L.
a) Докажите, что AB+ BC= 5 AC.
б) Найдите радиус окружности, вписанной в треугольник ABC, если ML = 1 и LN = 3.
ОТВЕТ: (frac{{3sqrt 2 }}{2}.)
4) (02.06.2022 основная волна) В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE = CE.
а) Докажите, что (AL cdot BC = AB cdot AC;)
б) Найдите EL, если AC = 12, (tgangle BCA = frac{1}{4}.)
5) (02.06.2022 основная волна) На стороне BC параллелограмма ABCD выбрана точка M такая, что АМ = МС.
а) Докажите, что центр вписанной в треугольник AMD окружности лежит на диагонали AC.
б) Найдите радиус вписанной в треугольник AMD окружности, если АВ = 7, ВС = 21, а (angle DAB = ,{60^ circ }.)
ОТВЕТ: (frac{{sqrt 3 left( {34 — sqrt {127} } right)}}{{14}}.)
6) (02.06.2022 основная волна) На стороне острого угла с вершиной A отмечена точка B. Из точки B на биссектрису и другую сторону угла опущены перпендикуляры BC и BD соответственно.
а) Докажите, что (A{C^2} + C{D^2} = A{D^2} + D{B^2}.)
б) Прямые AC и BD пересекаются в точке T. Найдите отношение AT : TC, если (cos angle ,ABC = frac{3}{8}.)
7) (02.06.2022 основная волна) В остроугольном треугольнике ABC проведены высоты АА1, ВВ1 и СС1, которые пересекаются в точке H. Через точку С1 провели прямую, параллельную ВВ1. Данная прямая пересекает АА1 в точке К.
а) Докажите, что (AB cdot HK = {C_1}H cdot BC.)
б) Найдите отношение площадей треугольников АВС и C1HK, если известно, что АВ = 5, ВС = 6,
(AC = sqrt {31} .)

а) Докажите, что CN = BМ.
б) Пусть MN и ВС пересекаются в точке D. Найти площадь треугольника BDN, если его высота ВН равна 7.
9) (02.06.2022 основная волна) В квадрате ABCD точки M и N – середины сторон АВ и ВС, соответственно. Отрезки СМ и DN пересекаются в точке К.
а) Докажите, что (angle BKM = ,{45^ circ }.)
б) Найдите радиус окружности, описанной около треугольника АВК, если (AB = ,2sqrt {20} .)
ОТВЕТ: (frac{{10sqrt 2 }}{3}.)
10) (02.06.2022 основная волна) В треугольнике ABC на стороне BC отметили точку D так, что AB = BD. Биссектриса BF пересекает AD в точке E. Из точки C на прямую AD опущен перпендикуляр CK.
a) Докажите, что АВ: ВС= АЕ : ЕК.
б) Найдите отношение площади треугольника ABE к площади четырёхугольника CDEF, если известно, что BD : DC = 3 : 2.
11) (02.06.2022 основная волна) В треугольнике ABC точки M и N — середины сторон AB и BC соответственно. Известно, что около четырехугольника AMNC можно описать окружность.
а) Докажите, что треугольник ABC — равнобедренный.
б) На стороне AС отмечена точка F, такая что (angle AFB = ,{135^ circ }.) Отрезок BF пересекает отрезок MN в точке E. Найдите радиус окружности, описанной около четырёхугольника AMNC, если (angle ABC = ,{120^ circ }) и (EF = 6sqrt 2 .)
12) (27.06.2022 резервная волна) Точка D лежит на основании AC равнобедренного треугольника ABC. Точки I и J — центры окружностей, описанных около треугольников ABD и CBD соответственно.
а) Докажите, что прямые BI и DJ параллельны.
б) Найдите IJ, если AC = 16, (cos angle BDC = ,frac{1}{9}.)
ОТВЕТ: (frac{{18sqrt 5 }}{5}.)
13) (27.06.2022 резервная волна) Две окружности пересекаются в точках А и В. Общая касательная к этим окружностям касается их с точках С и D. Прямая АВ пересекает отрезок CD в точке М, центры окружностей лежат в разных полуплоскостях относительно прямой АВ, точка В лежит между точками А и М.
а) Докажите, что CM = MD.
б) Найдите расстояние между центрами данных окружностей, если их радиусы равны 1 и 3 соответственно, а точка В является серединой отрезка АМ.
ОТВЕТ: (frac{{8sqrt 2 }}{3}.)
14) (27.06.2022 резервная волна) В трапеции ABCD с основанием AD диагонали пересекаются в точке O, AD = 2 BC. Через вершину A проведена прямая параллельная диагонали BD, а через вершину D проведена прямая параллельная диагонали AC, и эти прямые пересекаются в точке E.
а) Докажите, что BO : AE = 1 : 2.
б) Прямые BE и CE пересекают сторону AD в точках M и N соответственно. Найдите MN, если AD = 10.