16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по планиметрии прошлых лет
Задание
1
#6325
Уровень задания: Равен ЕГЭ
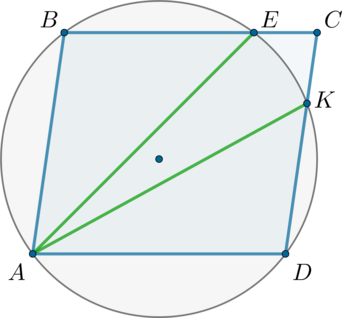
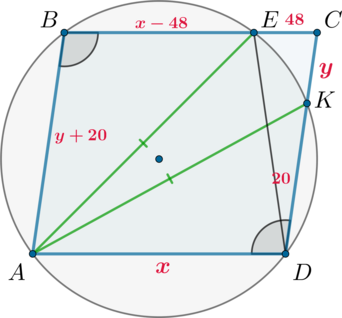
Окружность проходит через вершины (A, B) и (D) параллелограмма (ABCD). Эта окружность пересекает (BC) в точке (E), а (CD) в точке (K).
а) Докажите, что отрезки (AE) и (AK) равны.
б) Найдите (AD), если известно, что (EC=48), (DK=20), а косинус угла (BAD) равен (0,4).
(ЕГЭ 2018, основная волна)
а)
Так как противоположные углы параллелограмма равны, то (angle
ABE=angle ADK). Так как равные вписанные углы опираются на равные дуги и на равные хорды, то (AE=AK), чтд.
б) Введем обозначения: (AD=x), (CK=y). Проведем отрезок (ED). Тогда (ABED) – трапеция, причем, так как она вписана в окружность, она равнобедренная. Следовательно, (ED=y+20).
Запишем теорему косинусов для (triangle ECD): [(y+20)^2=48^2+(y+20)^2-2cdot 48cdot (y+20)cdot 0,4
quadRightarrowquad y=40] Следовательно, (AB=60).
Так как (angle B+angle C=180^circ) по свойству параллелограмма, то их косинусы противоположны, следовательно, (cos angle
B=-0,4).
Так как (AE=AK), то найдем (AE^2) и (AK^2) по теореме косинусов из (triangle ABE) и (triangle ADK) и приравняем: [60^2+(x-48)^2-2cdot 60cdot (x-48)cdot (-0,4)=x^2+20^2-2cdot 20cdot x
cdot (-0,4) quadRightarrowquad x=50] Следовательно, (AD=50).
Ответ:
б) 50
Задание
2
#3983
Уровень задания: Равен ЕГЭ
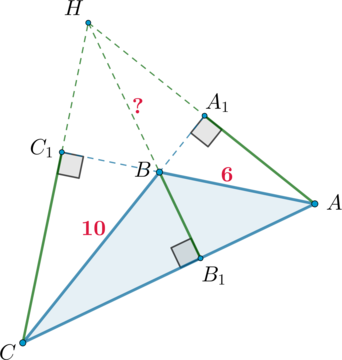
Дан тупоугольный треугольник (ABC) с тупым (angle ABC). Продолжения высот этого треугольника пересекаются в точке (H). (angle AHC=60^circ).
а) Докажите, что (angle ABC=120^circ).
б) Найдите (BH), если (AB=6), (BC=10).
(ЕГЭ 2018, досрочная волна)
а) Заметим, что в тупоугольном треугольника в одной точке пересекаются продолжения высот. Рассмотрим чертеж:
Рассмотрим четырехугольник (A_1BC_1H). В нем (angle A_1=angle
C_1=90^circ). Следовательно, (angle A_1BC_1=180^circ-angle
A_1HC_1=180^circ-60^circ=120^circ).
Так как (angle A_1BC_1) и (angle ABC) – вертикальные, то они равны, значит, (angle ABC=120^circ).
б) Рассмотрим прямоугольный (triangle CHA_1). Так как (angle
CHA_1=60^circ), то (angle HCA_1=30^circ).
Аналогично (angle HAC_1=30^circ).
Тогда из прямоугольного (triangle C_1CB) катет (C_1B) равен половине гипотенузы (CB), так как лежит против угла в (30^circ), значит, (C_1B=5).
Аналогично (A_1B=0,5cdot AB=3).
Рассмотрим снова (triangle HCA_1). Так как [dfrac{sqrt3}3=mathrm{tg},30^circ=dfrac{HA_1}{CA_1}quadrightarrowquad
HA_1=dfrac{13}{sqrt3}] Тогда по теореме Пифагора из прямоугольного (triangle HA_1B): [BH=sqrt{3^2+left(dfrac{13}{sqrt3}right)^2}=dfrac{14}{sqrt3}]
Ответ:
б) (frac{14}{sqrt3})
Задание
3
#4030
Уровень задания: Равен ЕГЭ
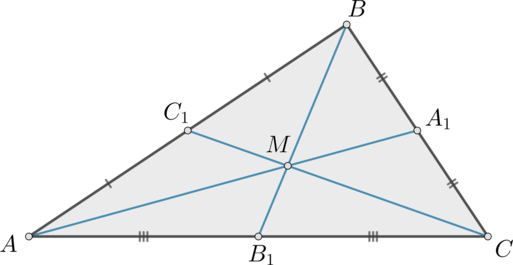
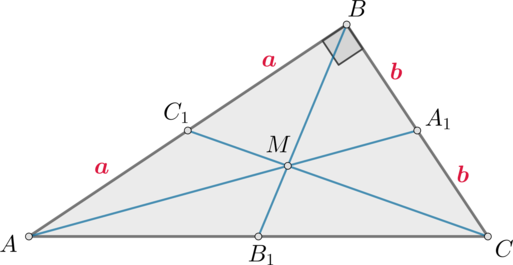
Медианы (AA_1, BB_1, CC_1) треугольника (ABC) пересекаются в точке (M). Известно, что (AC=3MB).
а) Докажите, что треугольник (ABC) прямоугольный.
б) Найдите сумму квадратов медиан (AA_1) и (CC_1), если известно, что (AC=12).
(ЕГЭ 2018, СтатГрад, 19 апреля 2018)
а) Пусть (BM=x), тогда (AC=3x). Так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (MB_1=0,5x), следовательно, (BB_1=1,5x). Следовательно, (AB_1=B_1C=BB_1=1,5x). Следовательно, (triangle ABC) прямоугольный с (angle B=90^circ).
б) Обозначим (AB=2a), (BC=2b).
Тогда по теореме Пифагора [begin{aligned}
&AA_1^2=4a^2+b^2\
&CC_1^2=a^2+4b^2 end{aligned}] Отсюда (AA_1^2+CC_1^2=5(a^2+b^2)).
Так как по теореме Пифагора из (triangle ABC): (4a^2+4b^2=12^2), то (a^2+b^2=36). Следовательно, [AA_1^2+CC_1^2=5(a^2+b^2)=5cdot 36=180]
Ответ:
б) 180
Задание
4
#3982
Уровень задания: Равен ЕГЭ
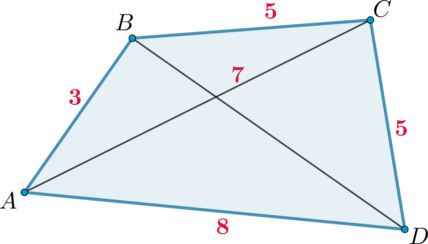
В выпуклом четырехугольнике (ABCD): (AB=3), (BC=5), (CD=5), (AD=8), (AC=7).
а) Докажите, что около этого четырехугольника можно описать окружность.
б) Найдите диагональ (BD).
(ЕГЭ 2018, досрочная волна, резерв)
а) Если в выпуклом четырехугольнике сумма противоположных углов равна (180^circ), то около него можно описать окружность. Докажем, что (angle B+angle D=180^circ).
По теореме косинусов для (triangle ABC): [cosangle B=
dfrac{AB^2+BC^2-AC^2}{2cdot ABcdot BC}=-dfrac12] По теореме косинусов для (triangle ADC): [cosangle D=dfrac{AD^2+CD^2-AC^2}{2cdot ADcdot CD}=dfrac12] Так как (alpha+beta=180^circ) равносильно (cosalpha=-cosbeta), то из (cosangle B=-cos angle D) следует, что (angle B+angle
D=180^circ).
б) Если около (ABCD) можно описать окружность, то и (angle A+angle
C=180^circ).
Обозначим (BD=x). Тогда, также используя теорему косинусов для (triangle ABD) и (triangle CBD), можно сказать: [begin{cases}
cos angle A=dfrac{9+64-x^2}{2cdot 3cdot 8} \[2ex]
cos angle C=dfrac{25+25-x^2}{2cdot 5cdot 5} end{cases}]Также имеем, что (cosangle A=-cosangle C), следовательно, [begin{aligned}
&dfrac{9+64-x^2}{2cdot 3cdot 8}=-dfrac{25+25-x^2}{2cdot 5cdot
5} quadLeftrightarrowquad dfrac{73-x^2}{24}=dfrac{x^2-50}{25}
quadLeftrightarrow\[2ex]
&Leftrightarrowquad 73cdot 25-25x^2=24x^2-50cdot 24
quadLeftrightarrow\[2ex]
&Leftrightarrowquad x^2=dfrac{73cdot 25+50cdot 24}{49}=
dfrac{25(73+48)}{49}=dfrac{25cdot 121}{49} end{aligned}] Отсюда [x=dfrac{5cdot 11}{7}=dfrac{55}7]
Ответ:
б) (frac{55}7)
Задание
5
#4011
Уровень задания: Равен ЕГЭ
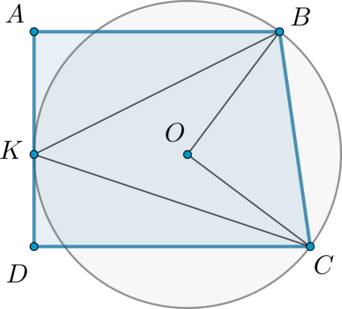
Окружность с центром (O) проходит через вершины (B) и (C) большей боковой стороны прямоугольной трапеции (ABCD) и касается боковой стороны (AD) в точке (K).
а) Докажите, что угол (BOC) вдвое больше угла (BKC).
б) Найдите расстояние от точки (K) до прямой (BC), если основания трапеции (AB) и (CD) равны 4 и 9 соответственно.
(ЕГЭ 2018, СтатГрад, 26 января 2018)
а) Угол (BOC) – центральный, опирающийся на дугу (BC); угол (BKC) – вписанный и опирающийся на ту же дугу, следовательно, (angle
BOC=2angle BKC), чтд.
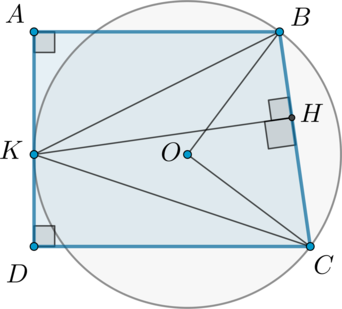
б) Проведем (KHperp BC). Так как угол между касательной и хордой, выходящей из точки касания, равен половине дуги, заключенной между ними, то (angle DKC=0,5buildrelsmileover{KC}=angle KBC). Аналогично (angle AKB=angle KCB):
Следовательно, (triangle AKBsim triangle KHC, triangle KDCsim
triangle KHB) как прямоугольные по острому углу. Тогда: [begin{aligned}
&dfrac{KB}{KC}=dfrac{KH}{CD}\[2ex]
&dfrac{KC}{KB}=dfrac{KH}{AB}end{aligned}] Отсюда [1=dfrac{KH^2}{CDcdot AB}quadRightarrowquad KH=sqrt{CDcdot AB}=sqrt{
4cdot 9}=6]
Ответ:
б) 6
Задание
6
#3276
Уровень задания: Равен ЕГЭ
Прямая, проходящая через середину (M) гипотенузы (AB) прямоугольного треугольника (ABC), перпендикулярна (CM) и пересекает катет (AC) в точке (K). При этом (AK:KC=1:2).
а) Докажите, что (angle BAC=30^circ).
б) Пусть прямые (MK) и (BC) пересекаются в точке (P), а прямые (AP) и (BK) – в точке (Q). Найдите (KQ), если (BC=2sqrt3).
(ЕГЭ 2017, официальный пробный 21.04.2017)
а) Пусть (AK=x, KC=2x). Проведем (BLparallel MK). Тогда по теореме Фалеса [dfrac{BM}{MA}=dfrac11=dfrac{LK}{KA}
quadRightarrowquad LK=KA=x quadRightarrow quad CL=x.]
Тогда также по теореме Фалеса: [dfrac{CL}{LK}=dfrac11=dfrac{CO}{OM} quadRightarrowquad CO=OM.] Следовательно, (BO) – медиана и высота ((MKperp CM, BOparallel
MK quadRightarrowquad BOperp CM)), следовательно, (triangle
CBM) равнобедренный и (CB=BM). Следовательно, (CB=frac12BA). Так как катет, равный половине гипотенузы, лежит против угла в (30^circ), то (angle BAC=30^circ).
б) Рассмотрим (triangle PMC): (angle PMC=90^circ). Так как (BM=BC), то (BM=BC=BP), то есть (B) – середина (CP) ((angle
BCM=angle BMC=60^circ), следовательно, (angle CPM=30^circ=angle
PMB), следовательно, (BP=BM)).
Проведем (BSparallel AP). Тогда (BS) – средняя линия треугольника (APC). Значит, (CS=SA).
Из прямоугольного (triangle ABC): [mathrm{tg},30^circ=dfrac{BC}{AC} quadRightarrowquad AC=
BCcdot sqrt3=6.] Следовательно, (CS=SA=3), а так как (CK:KA=2:1), то (KA=2) и (SK=1).
Заметим, что (triangle BKSsim triangle QKA) по двум углам ((angle BKS=angle QKA) как вертикальные, (angle BSK=angle QAK) как накрест лежащие при (AQparallel BS) и (SA) секущей). Следовательно, [dfrac{SK}{AK}=dfrac12=dfrac{BK}{KQ} quadRightarrowquad KQ=2BK.] Найдем (BK).
По теореме Пифагора из (triangle BKC): [BK=sqrt{BC^2+KC^2}=sqrt{(2sqrt3)^2+4^2}=2sqrt{7}] Следовательно, [KQ=4sqrt7.]
Ответ:
б) (4sqrt7)
Задание
7
#3249
Уровень задания: Равен ЕГЭ
В трапецию (ABCD) с основаниями (AD) и (BC) вписана окружность с центром в (O).
а) Докажите, что (sin angle AOD=sinangle BOC).
б) Найдите площадь трапеции, если (angle BAD=90^circ), а основания равны (5) и (7).
(ЕГЭ 2017, резервный день)
а) Так как окружность вписана в трапецию, то ее центр лежит на пересечении биссектрис углов трапеции.
Так как (angle A+angle B=180^circ), то (frac12cdot (angle
A+angle B)=90^circ). Следовательно, (angle
AOB=180^circ-90^circ=90^circ).
Аналогично доказывается, что (angle COD=90^circ).
Следовательно, (angle BOC+angle
AOD=360^circ-90^circ-90^circ=180^circ). Следовательно, (sin
angle BOC=sin angle AOD).
б) Так как в трапеции (angle A=angle B=90^circ), то (angle
BAO=angle ABO=45^circ), следовательно, (triangle AOB) – прямоугольный и равнобедренный.
Пусть (M, N, K, L) – точки касания окружности со сторонами (AB, BC,
CD, AD) соответственно.
Следовательно, (OMperp AB) как радиус, проведенный в точку касания. Так как (triangle AOB) равнобедренный, то (OM) – медиана, следовательно, (AM=MB). Как отрезки касательных (AM=AL, BM=BN). Следовательно, (AL=AM=BM=BN=x). Пусть также (NC=CK=y), (DL=DK=z). Тогда (x+y=5), (x+z=7).
Тогда (AB=2x) – высота трапеции. Следовательно, нужно найти (x).
Проведем (CHperp AD). Тогда (HD=AD-BC=2), а (CH=AB=2x). Тогда по теореме Пифагора из (triangle GHD): [(2x)^2+2^2=(y+z)^2] Так как (y=5-x), (z=7-x), то получаем уравнение [4x^2+4=(12-2x)^2quadRightarrowquad x=dfrac{35}{12}] Следовательно, площадь трапеции равна [S=dfrac{5+7}2cdot 2x=35.]
Ответ:
б) 35

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии.
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.
Решения заданий № 16 Профильного ЕГЭ по математике.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
.
Посмотреть решение
3. (ЕГЭ-2020, Демовариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Планиметрия. Стрим 10 марта. Разбор домашнего задания
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Планиметрия – профильный ЕГЭ по математике (оглавление)
Планиметрия плохо дается многим ученикам. На ЕГЭ эта задача №16 – одна из самых сложных задач и многие даже не пытаются за нее браться.
Весь секрет в том, что понимание планиметрии приходит не постепенно, а сразу. Вчера не получалось, а сегодня уже все понятно. Большинству просто не хватает терпения дойти до этого момента.
Надеемся, что ты не такой и не бросишь занятия на полпути. И вот тебе в помощь все, что нужно знать по планиметрии + несколько вебинаров для отработки навыков!
Планиметрия – часть 1. ЕГЭ №3 (бывшая №6)
Если вы плохо знаете планиметрию, начинайте с этой части и смотрите вебинар за вебинаром, ставьте на паузу и решайте задачи вместе с ведущим вебинаров Алексеем Шевчуком.
Помните, планиметрия требует нарешенности. Чтобы научиться решать любую задачу по планиметрии, нужно решать много задач.
Начните с самого начала.
Планиметрия – прямоугольный треугольник
Итак, прямоугольный треугольник, его свойства, площадь и углы прямоугольного треугольника, теорема Пифагора, тригонометрический функции острых углов, медиана и высота.
Планиметрия – равнобедренный треугольник и произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и “обычные” треугольники.
Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках – очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие ее свойства. В какие фигуры можно, а в какие нельзя вписать окружность.
Научимся решать задачи на вписанную окружность – очень важный навык в понимании планиметрии.
Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Что приблизит нас к умению решать любые задачи по планиметрии.
Теорема косинусов и синусов
Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов.
Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Планиметрия – часть 2. ЕГЭ №16
Эта часть планиметрии – для продвинутых, для тех, кто уже хорошо усвоил планиметрию из первой части.
Принцип тот же – смотрите вебинар за вебинаром и, самое главное, ставьте на паузу и решайте задачи.
Планиметрия. Подобие треугольников. Задачи на доказательство. ЕГЭ №16
Подобие треугольников. Это одна из самых сложных задачи планиметрии в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности – это очень классный метод, используемый в планиметрии но, к сожалению, он не всегда очевиден. Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы – те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод – но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
Теорема Менелая и Чевы. “Секретный” метод решения самой сложной задачи ЕГЭ по математике
Задача №16. Планиметрия. Одна из самых сложных задач на ЕГЭ. Редко кто (менее 1% учеников!) набирает полные баллы по ней и поэтому грех не воспользоваться шорткатами и лайфхаками, если они есть.
Теорема Менелая и Чевы – один из таких шорткатов. Эти теоремы не входят в стандартную школьную программу, но они невероятно мощный инструмент! Они могут очень-очень упростить решение и сами по себе они красивые и легко запоминаются.
Итак, смотрите видео, учите теорему Менелая и Чевы, используйте ее на ЕГЭ.
Теорема Менелая и Чевы — её уже запретили, наконец, или нет?
Каждый год начинают ходить слухи, что теоремами Менелая и Чевы В ЭТОМ ГОДУ НЕЛЬЗЯ будет пользоваться на ЕГЭ. Правда ли это? Чтобы понять это, достаточно заглянуть в обычный…
Впрочем, смотрите это видео и узнаете, как понять, какими теоремами можно, а какими нельзя пользоваться. А также, на этом вебе мы разберём, что это за теоремы такие, и как ими пользоваться.
Вы узнаете, насколько они крутые и мощные, и насколько экономят нам время в некоторых задачах.
Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом. Никуда не деться от окружностей – остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше – разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче). Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники.
Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Разбор задачи №16 (б) из реального варианта ЕГЭ 2021 по профильной математике
Продолжение предыдущего видео. Разбор части (б):
Теперь слово вам…
Как вам наш гид по планиметрии? Что нового вы узнали? Что еще хотите узнать?
Как вам теорема Менелая и Чевы? Один из моих знакомых сказал: “В школе ее от нас утаивали!”. Шутка, в которой есть доля… шутки.
Готовьтесь к планиметрии и забирайте свои 3 балла на ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
- Читаю
- Хочу прочитать
- Прочитал
Жанр: Учебная литература
Серия: ЕГЭ 2016. Математика
Год издания: 2016
Издательство: МЦНМО
Фрагмент книги
О книге «ЕГЭ 2016. Математика. Геометрия. Планиметрия. Задача 16»
Пособия по математике серии «ЕГЭ 2016. Математика» ориентированы на подготовку учащихся старшей школы к успешной сдаче единого государственного экзамена по математике. В данном учебном пособии представлен материал для подготовки к решению задачи 16 профильного уровня. На различных этапах обучения пособие поможет обеспечить уровневый подход к организации повторения, осуществить контроль и самоконтроль знаний по планиметрии. Пособие предназначено для учащихся старшей школы, учителей математики, родителей. Издание соответствует новому Федеральному государственному образовательному стандарту (ФГОС).
На нашем сайте вы можете скачать книгу «ЕГЭ 2016. Математика. Геометрия. Планиметрия. Задача 16» Р. К. Гордин в формате pdf, читать книгу онлайн или купить книгу в интернет-магазине.
Скачать книгу
247 скачиваний
Читать онлайн
Отзывы читателей
Подборки книг
Похожие книги
Другие книги автора
Информация обновлена: 20.02.2022