B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии.
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.
Решения заданий № 16 Профильного ЕГЭ по математике.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
.
Посмотреть решение
3. (ЕГЭ-2020, Демовариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Планиметрия. Стрим 10 марта. Разбор домашнего задания
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Теоремы и определения по Планиметрии
Теоремы и определения по Планиметрии. Справочник по геометрии для 7-11 классов, для подготовки к ОГЭ и ЕГЭ. Часть 1 «Планиметрия». Автор: Нелин Е.П. Использованы цитаты из пособия «Геометрия. 7-11 классы. Определения, свойства, методы решения задач в таблицах / М.: Илекса, 2018» из серии «Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). Цитаты использованы в учебных целях.
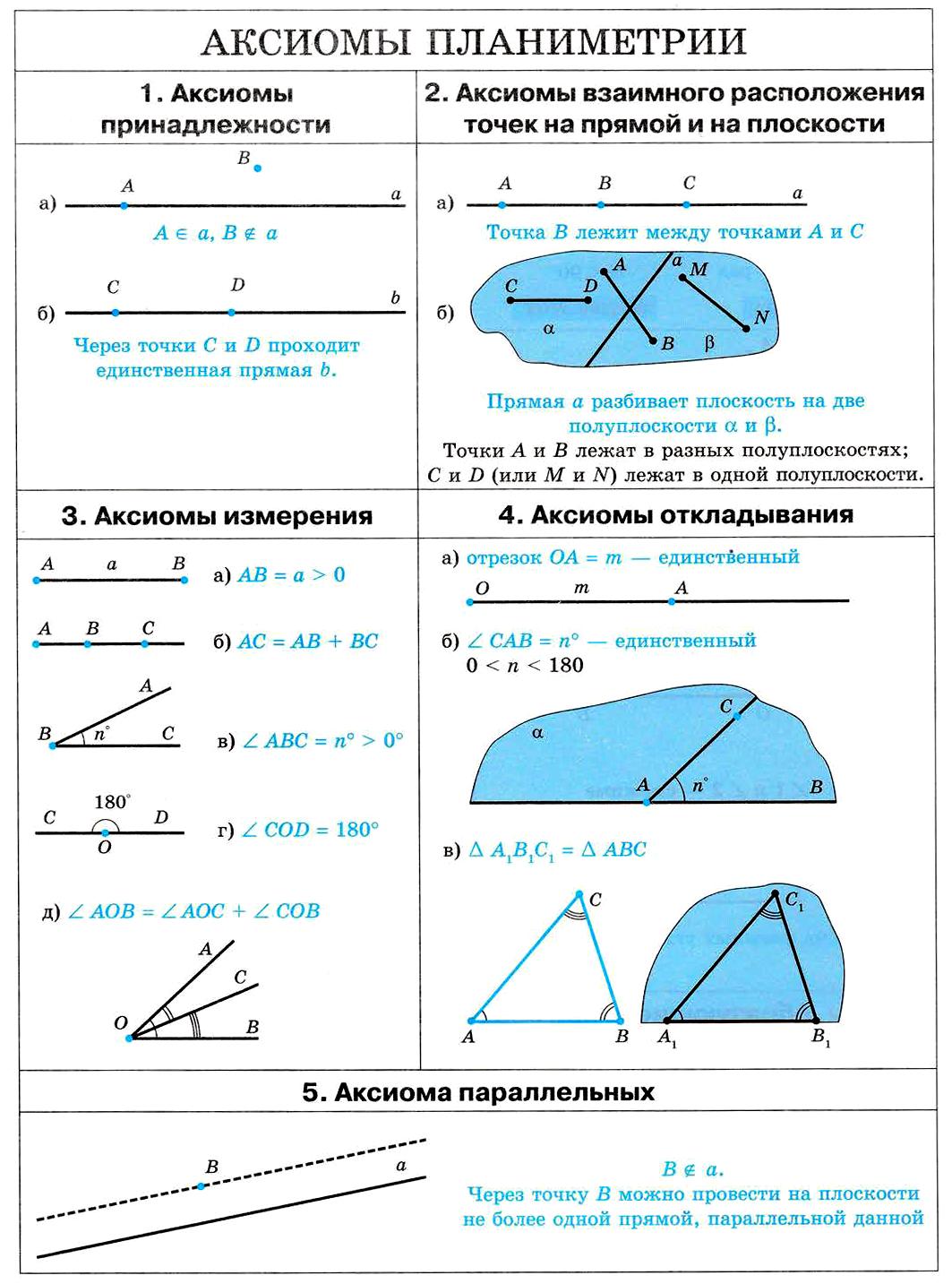
01. Аксиомы планиметрии.
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
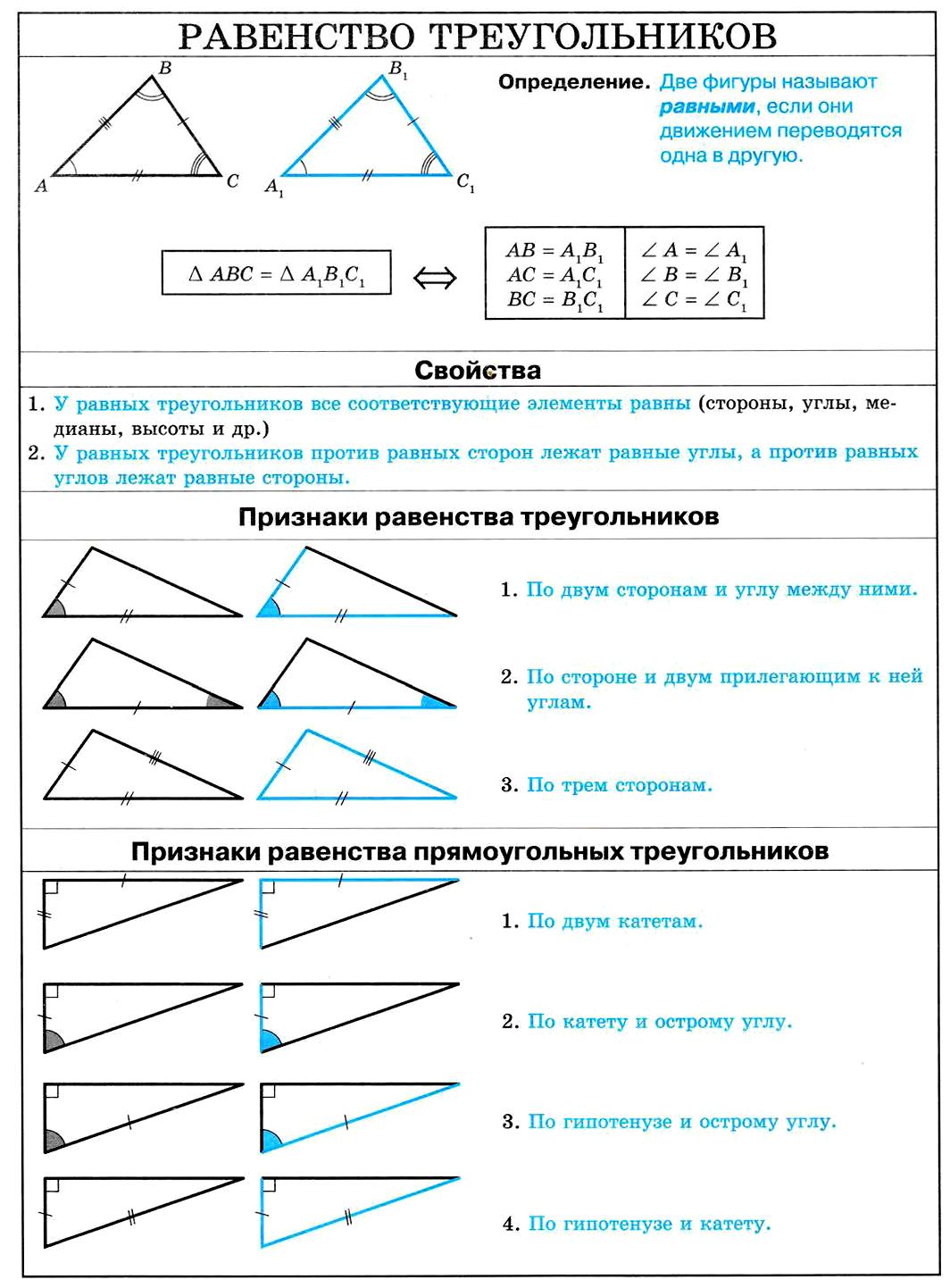
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
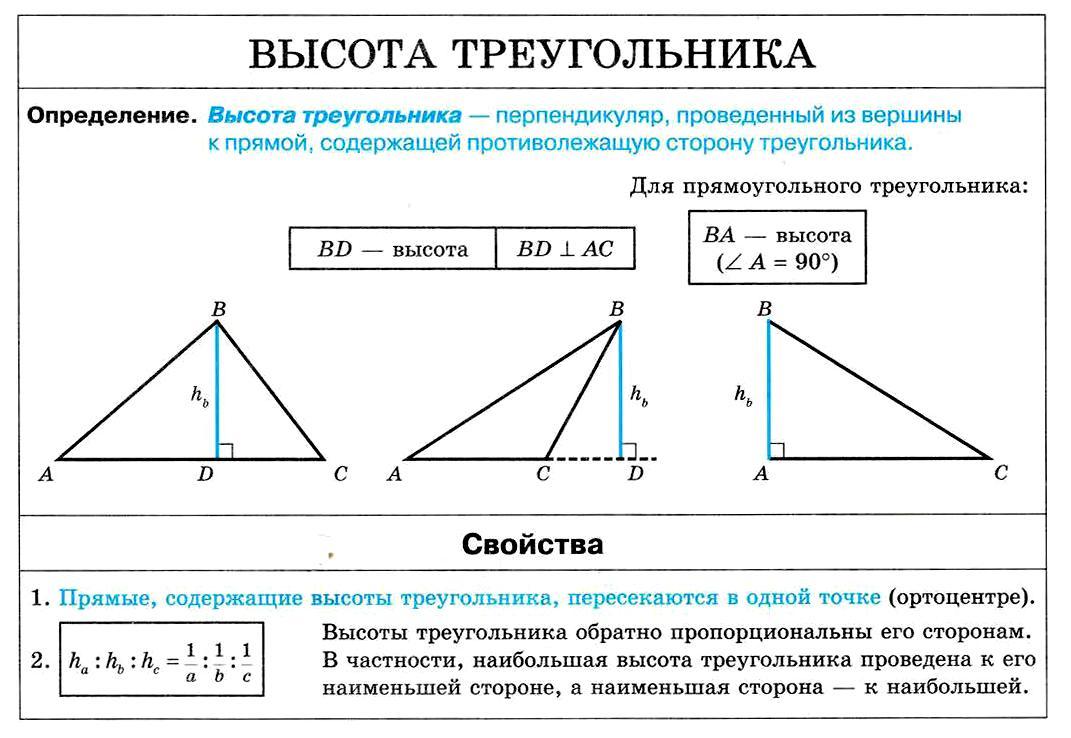
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
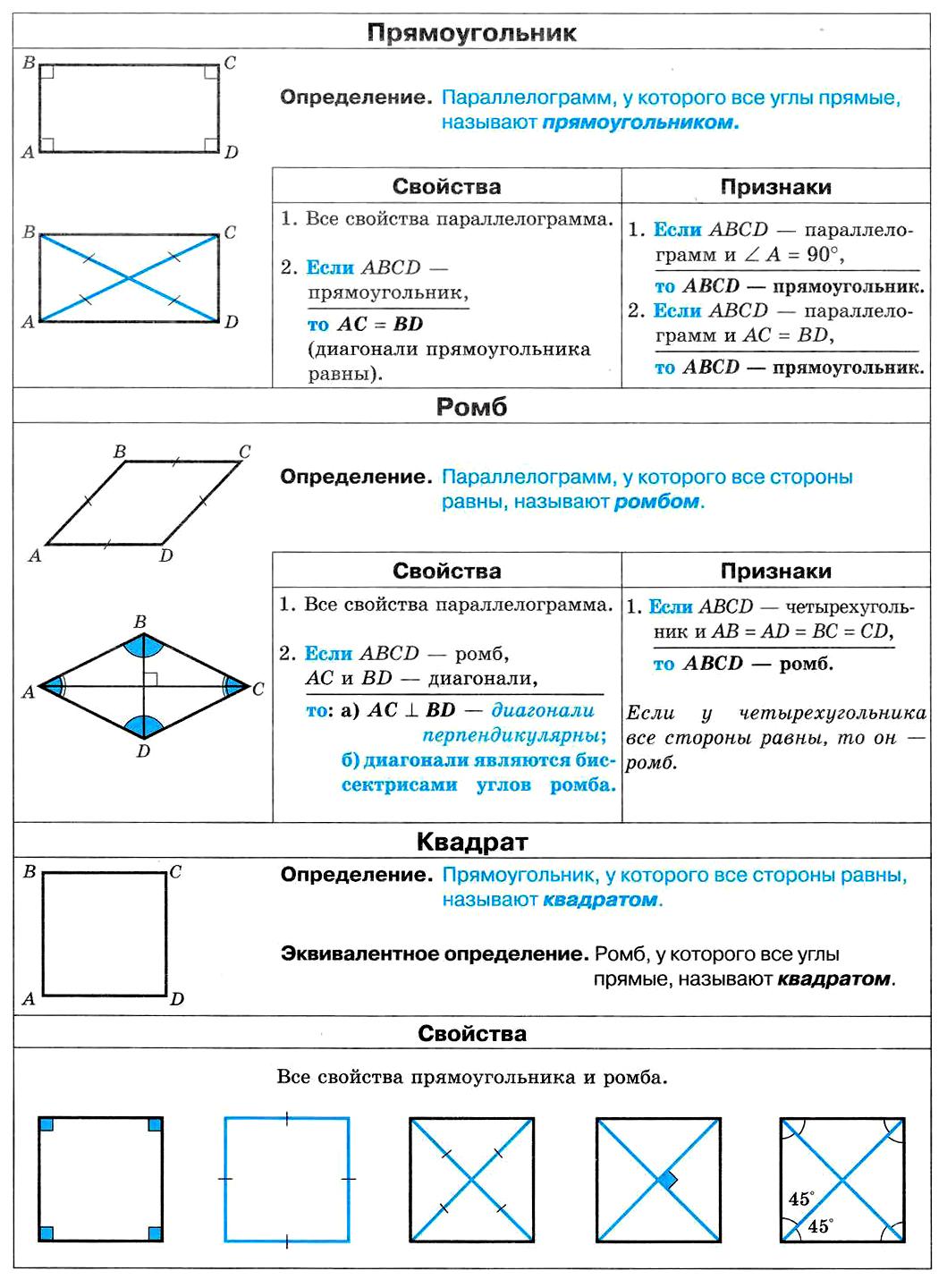
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
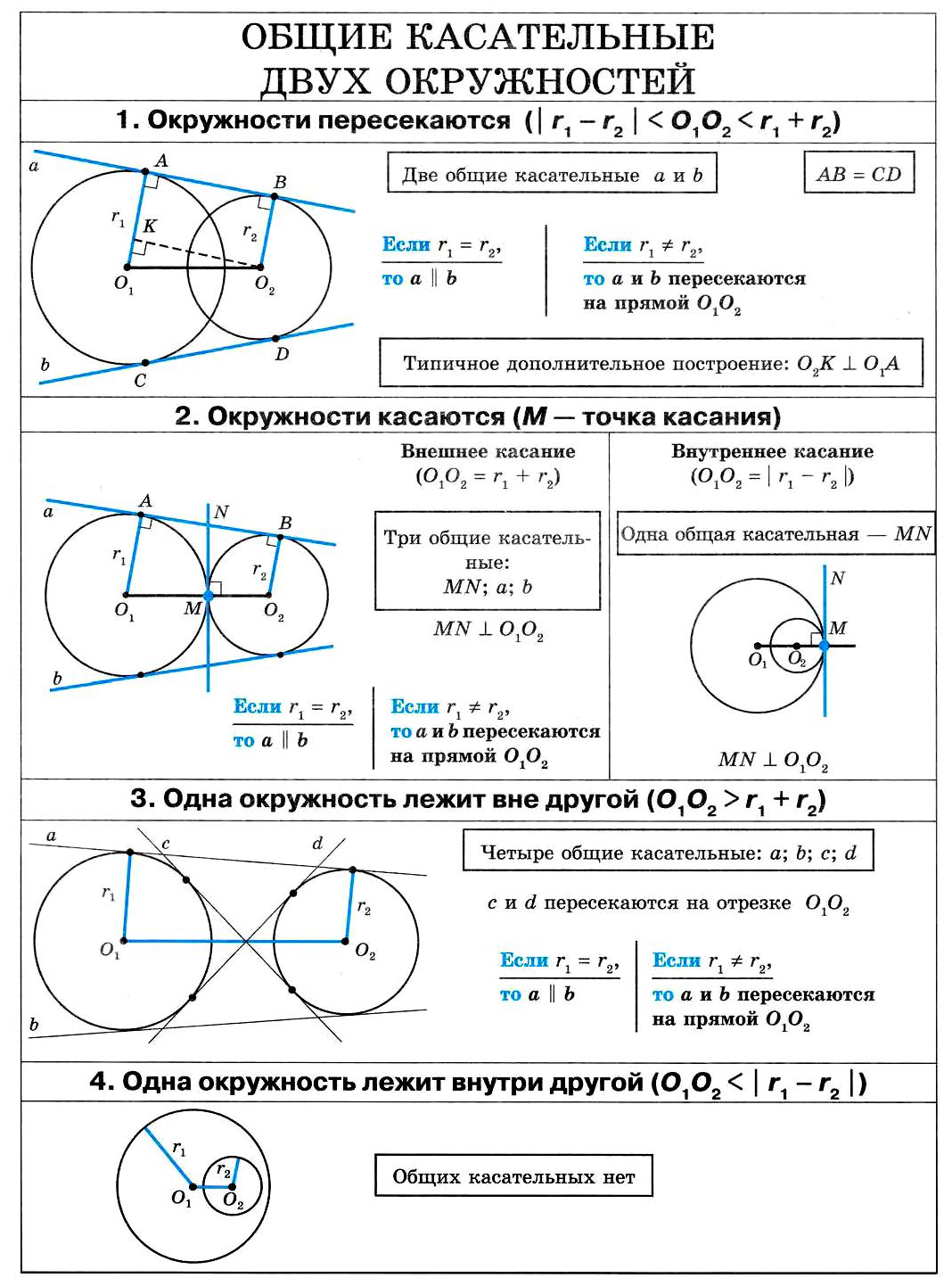
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
Углы в окружности.
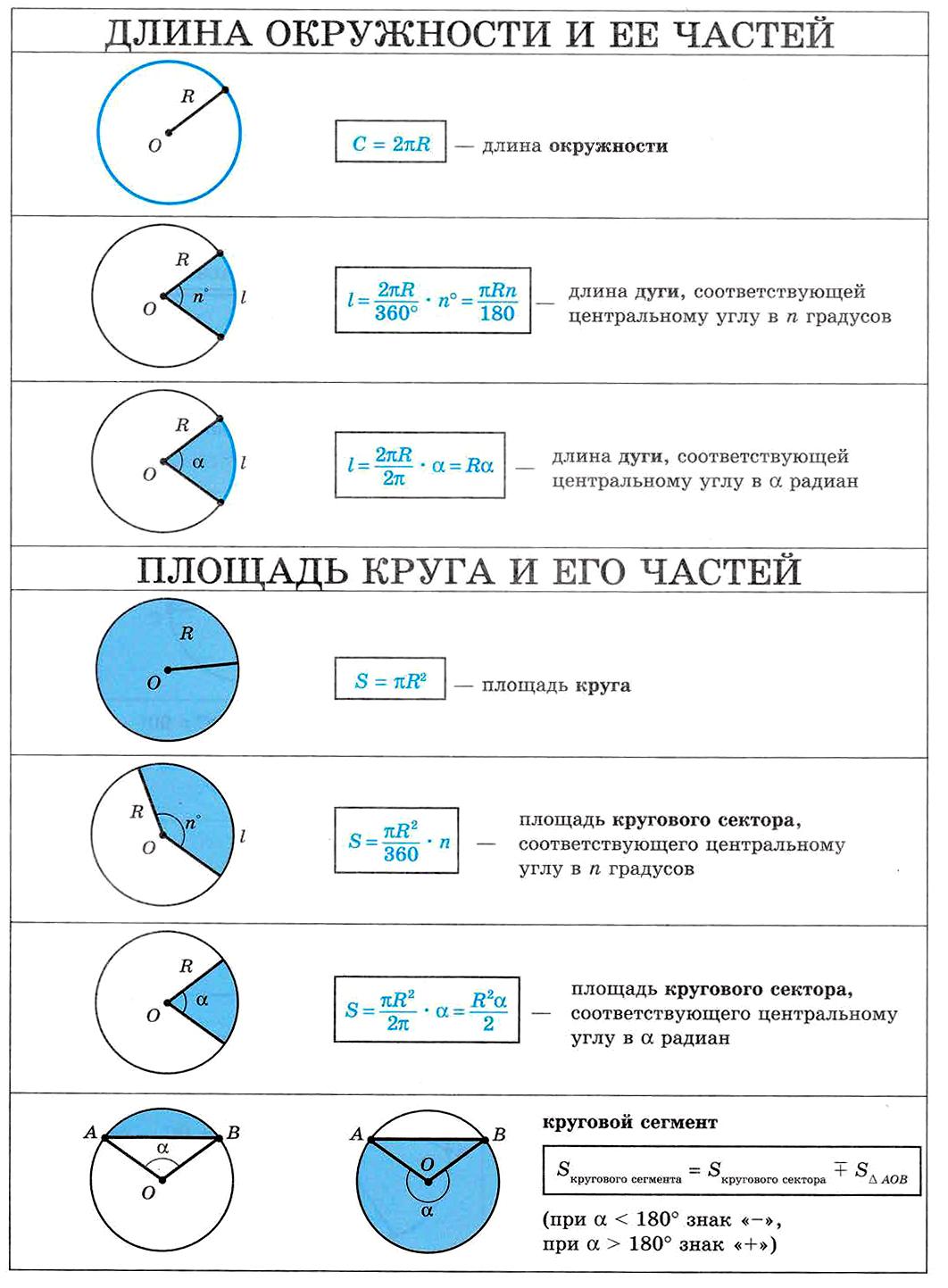
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
Площади треугольников.
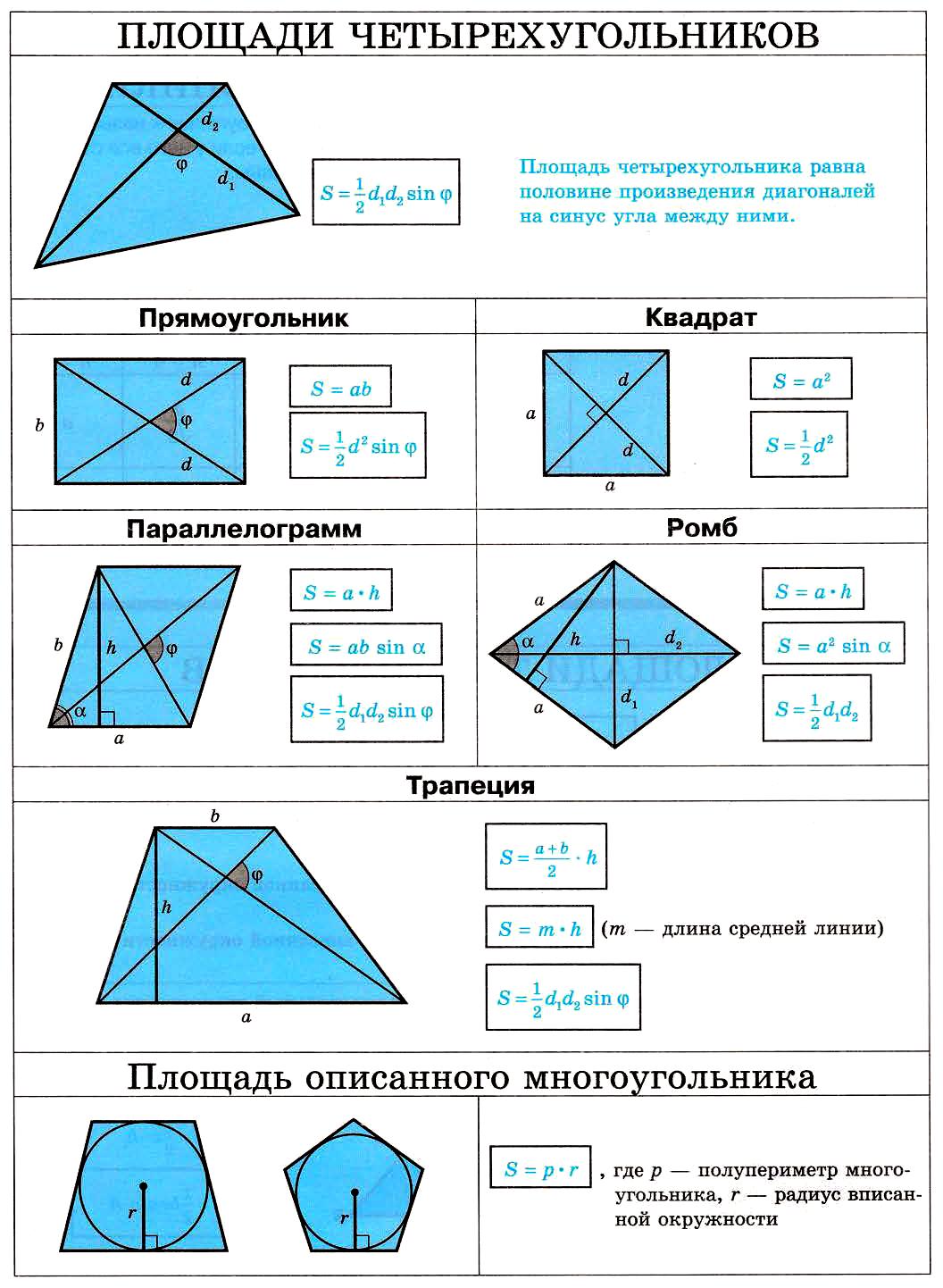
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».
Справочный материал по планиметрии
Планиметрия – профильный ЕГЭ по математике (оглавление)
Планиметрия плохо дается многим ученикам. На ЕГЭ эта задача №16 – одна из самых сложных задач и многие даже не пытаются за нее браться.
Весь секрет в том, что понимание планиметрии приходит не постепенно, а сразу. Вчера не получалось, а сегодня уже все понятно. Большинству просто не хватает терпения дойти до этого момента.
Надеемся, что ты не такой и не бросишь занятия на полпути. И вот тебе в помощь все, что нужно знать по планиметрии + несколько вебинаров для отработки навыков!
Планиметрия – часть 1. ЕГЭ №3 (бывшая №6)
Если вы плохо знаете планиметрию, начинайте с этой части и смотрите вебинар за вебинаром, ставьте на паузу и решайте задачи вместе с ведущим вебинаров Алексеем Шевчуком.
Помните, планиметрия требует нарешенности. Чтобы научиться решать любую задачу по планиметрии, нужно решать много задач.
Начните с самого начала.
Планиметрия – прямоугольный треугольник
Итак, прямоугольный треугольник, его свойства, площадь и углы прямоугольного треугольника, теорема Пифагора, тригонометрический функции острых углов, медиана и высота.
Планиметрия – равнобедренный треугольник и произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и “обычные” треугольники.
Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках – очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие ее свойства. В какие фигуры можно, а в какие нельзя вписать окружность.
Научимся решать задачи на вписанную окружность – очень важный навык в понимании планиметрии.
Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Что приблизит нас к умению решать любые задачи по планиметрии.
Теорема косинусов и синусов
Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов.
Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Планиметрия – часть 2. ЕГЭ №16
Эта часть планиметрии – для продвинутых, для тех, кто уже хорошо усвоил планиметрию из первой части.
Принцип тот же – смотрите вебинар за вебинаром и, самое главное, ставьте на паузу и решайте задачи.
Планиметрия. Подобие треугольников. Задачи на доказательство. ЕГЭ №16
Подобие треугольников. Это одна из самых сложных задачи планиметрии в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности – это очень классный метод, используемый в планиметрии но, к сожалению, он не всегда очевиден. Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы – те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод – но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
Теорема Менелая и Чевы. “Секретный” метод решения самой сложной задачи ЕГЭ по математике
Задача №16. Планиметрия. Одна из самых сложных задач на ЕГЭ. Редко кто (менее 1% учеников!) набирает полные баллы по ней и поэтому грех не воспользоваться шорткатами и лайфхаками, если они есть.
Теорема Менелая и Чевы – один из таких шорткатов. Эти теоремы не входят в стандартную школьную программу, но они невероятно мощный инструмент! Они могут очень-очень упростить решение и сами по себе они красивые и легко запоминаются.
Итак, смотрите видео, учите теорему Менелая и Чевы, используйте ее на ЕГЭ.
Теорема Менелая и Чевы — её уже запретили, наконец, или нет?
Каждый год начинают ходить слухи, что теоремами Менелая и Чевы В ЭТОМ ГОДУ НЕЛЬЗЯ будет пользоваться на ЕГЭ. Правда ли это? Чтобы понять это, достаточно заглянуть в обычный…
Впрочем, смотрите это видео и узнаете, как понять, какими теоремами можно, а какими нельзя пользоваться. А также, на этом вебе мы разберём, что это за теоремы такие, и как ими пользоваться.
Вы узнаете, насколько они крутые и мощные, и насколько экономят нам время в некоторых задачах.
Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом. Никуда не деться от окружностей – остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше – разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче). Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники.
Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Разбор задачи №16 (б) из реального варианта ЕГЭ 2021 по профильной математике
Продолжение предыдущего видео. Разбор части (б):
Теперь слово вам…
Как вам наш гид по планиметрии? Что нового вы узнали? Что еще хотите узнать?
Как вам теорема Менелая и Чевы? Один из моих знакомых сказал: “В школе ее от нас утаивали!”. Шутка, в которой есть доля… шутки.
Готовьтесь к планиметрии и забирайте свои 3 балла на ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
1.Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.
1 − 0,81 = 0,19.
2.Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
P(A) = 0,97 − 0,89 = 0,08.
3.Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
0,3·0,3 = 0,09. 1 − 0,09 = 0,91.
4.В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
0,3 + 0,3 − 0,12 = 0,48. 1 − 0,48 = 0,52.
5.При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24.
Р(3) = Р(2)·0,4 = 0,096. Р(4) = Р(3)·0,4 = 0,0384;
Р(5) = Р(4)·0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.
6.Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
0,45 · 0,03 = 0,0135. 0,55 · 0,01 = 0,0055.
0,0135 + 0,0055 = 0,019.
7. В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе. Пусть один из близнецов находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников 12 : 25 = 0,48.
8.В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение.
Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО
P(XXO) = 0,8·0,8·0,2 = 0,128;
P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008;
P(OOO) = 0,2·0,8·0,8 = 0,128.
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.
9.Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение.
0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52.
10.Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Ответ 0,75
11. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
0,7+(1-0,7) ·0,7=0,91
12.Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
0,6·0,8·(1 –(1-0,7)(1-0,5)) =0,48·(1-0,3·0,5)=0,408
13. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
0,1·0,8=0,08, 1-0,08=0,92 0,9 : 0,92=0,98
14.Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
0,05·0,9+0,95·0,01 =0,0545
15. У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Решение.
У Вити в копилке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Больше 70 рублей останется, если достать из копилки либо рублёвую, либо двухрублёвую монету. Искомая вероятность равна 18 : 25 = 0,72.
16.В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах. Всего 6 монет. Вероятность того, что Петя взял пятирублевую монету, затем десятирублевую, и затем еще одну десятирублевую (в указанном порядке) равна 2/6·4/5·3/4=0,2 Поскольку Петя мог достать пятирублевую монету не только первой, но и второй или третьей, вероятность достать набор из одной пятирублевой и двух десятирублевых монет в 3 раза больше. Тем самым, она равна 0,6.
17. За круглый стол на 101 стул в случайном порядке рассаживаются 99 мальчиков и 2 девочки. Найдите вероятность того, что между двумя девочками будет сидеть один мальчик.
Решение.
Пусть первой за стол сядет девочка, тогда для каждого из оставшихся ребят (в том числе и для второй девочки ) вероятность оказаться на любом из оставшихся стульев равна 0,01 . А мест, удовлетворяющих условию задачи, только два. Таким образом вероятность, что между двумя девочками будет сидеть один мальчик равна 2·0,01 = 0,02
18. За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Решение.
Пусть первой за стол сядет девочка, тогда рядом с ней есть два места, на каждое из которых претендует 16 человека, из которых только одна девочка. Таким образом, вероятность, что девочки будут сидеть рядом равна 2·1/16 =1/8 =0,125
Не будут сидеть рядом 1-0,125=0,875
19. Про паука.
На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.
Содержание
Формулы для ЕГЭ по профильной математике. Алгебра
Формулы сокращенного умножения
Квадрат суммы: (a + b)² = a² + 2ab + b²
Квадрат разности: (a – b)² = a² – 2ab + b²
Разность квадратов: a² – b² = (a + b)(a – b)
Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)
Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)
Прогрессия
Арифметическая
Геометрическая
Таблица степеней
Свойства степеней
Таблица квадратов
Интенсивы по подготовке к региональному этапу ВсОШ
Все, что нужно знать
для победы, за 7 дней!
Свойства корней
Тригонометрия
Таблица значений тригонометрических функций
Тригонометрическая окружность
Тригонометрические формулы
Обратные тригонометрические функции
Преобразование суммы и разности в произведение
Регулярные курсы по подготовке к олимпиадам и ЕГЭ
Поступаем в вуз мечты без проблем!
Вероятность
Вероятность события А: m – благоприятные, n – общее число событий
P(A) = m/n
События А и В происходят одновременно: A · B
Независимые события: P(A · B) = P(A) · P(B)
Зависимые события: P(A · B) = P(A) · P(B | A)
Происходит или А, или В: A + B
Несовместные события: P(A + B) = P(A) + P(B)
Совместные события: P(A + B) = P(A) + P(B) – P(A · B)
Свойства модуля
Производные
Основные правила дифференцирования
Таблица производных
Первообразные
Логарифмы
Квадратные уравнения
Дискриминант
Теорема Виета
Разложение на множители
Формулы для ЕГЭ по профильной математике. Геометрия
Планиметрия
Треугольник
Следствие из теоремы косинусов:
Длина биссектрисы (через угол):
Длина биссектрисы (через отрезки):
Прямоугольный треугольник
24 декабря – 20 января
5-11 классы
Онлайн-олимпиада Коалиции
Равносторонний треугольник
Аргументы для итогового сочинения
Подборка лучших аргументов
Равносторонний шестиугольник
Площадь внутреннего треугольника:
Площадь внутреннего прямоугольника:
Ромб
Трапеция
Произвольный четырёхугольник
Окружность
Стереометрия
Выводы
Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.
А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.
Поделиться в социальных сетях
Какими формулами вам приходится пользоваться чаще всего?
Межтекстовые Отзывы
Посмотреть все комментарии
Читайте также
От Мои ответы и задания 18 июня, 2020 Сборники ЕГЭ и ОГЭ
Полезная шпаргалка для 11 класса по математике профильный уровень ЕГЭ. Справочные материалы и все формулы для решения заданий. Можно взять на ЕГЭ, чтобы было легче решать задания на экзамене.
Ссылка для скачивания шпаргалки ЕГЭ: скачать в формате PDF
Шпаргалка ЕГЭ по математике профильный уровень онлайн:
Смотрите также на нашем сайте полезные материалы:
МА1900201-МА1900212 статград математика 10 класс ответы и задания 6 февраля 2020
29 января 2020 ответы и задания по математике 11 класс статград МА1910301-МА1910312
Метки: ЕГЭматематика 11 классшпаргалка