Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 1.
1.
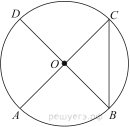
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
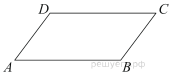
Сторона ромба равна 58, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 3
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
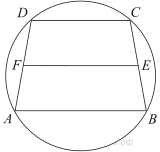
Основания равнобедренной трапеции равны 240 и 70. Радиус описанной окружности равен 125.
Найдите высоту трапеции.
5.
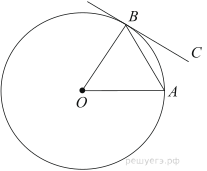
Касательные CA и CB к окружности образуют угол ACB, равный 34°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
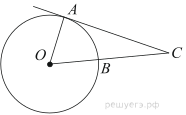
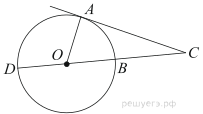
Угол ACO равен 58°. Его сторона CA касается окружности. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 48, средняя линия равна 19. Найдите боковую сторону трапеции.
8.
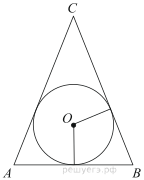
Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 88. Найдите радиус описанной окружности этой трапеции.
Проверочная работа по № 1ЕГЭ «Окружность». ВАРИАНТ – 2.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 100, острый угол равен 
2.
Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.
10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 19 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 4
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 72 и 30. Радиус описанной окружности равен 39.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 76, средняя линия равна 6. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 7, описан многоугольник, периметр которого равен 30. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ –3.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 24, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 20 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 4
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 144 и 60. Радиус описанной окружности равен 78.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 88, средняя линия равна 12. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 4.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 46, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 6
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 288 и 84. Радиус описанной окружности равен 150.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 104, средняя линия равна 20. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 4, описан многоугольник, периметр которого равен 63. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 5.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 50, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 3
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 104, средняя линия равна 20. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 35. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 6.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 94, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 3
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 192 и 56. Радиус описанной окружности равен 100.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 100, средняя линия равна 18. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 62. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 7.
1.
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.
9.
Сторона ромба равна 20, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 2
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 78°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.
6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Вариант 1 6. Планиметрия
1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2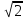
4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
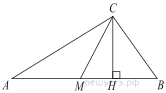
5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.
8. Найдите величину угла АВС. Ответ дайте в градусах.
9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Вариант 2 6. Планиметрия
В 1. Сторона правильного треугольника равна 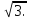
2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.
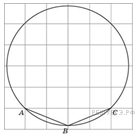
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.
Вариант 3 6. Планиметрия
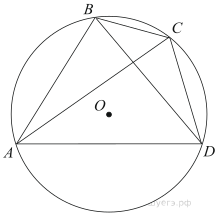
1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.
2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.
4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.
5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.
6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите
8. Найдите площадь ромба, если его диагонали равны 4 и 12.
9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.
10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
Вариант 4 6. Планиметрия
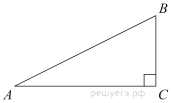
1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.
2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.
3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.
6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41
Найдите радиус окружности, вписанной в этот треугольник.
8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите
10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
Вариант 5 6. Планиметрия
1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2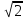
2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.
4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.
6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.
7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.
9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.
Вариант 6 6. Планиметрия
1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.
2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите
4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.
6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.
7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.
8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
10. В треугольнике ABC угол ACB равен °, угол B равен
°, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Вариант 7 6. Планиметрия
1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.
4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.
10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Вариант 8 6. Планиметрия
1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.
3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.
6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.
7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.
9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.
10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2
Вариант 9 6. Планиметрия
1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на
4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.
5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту
7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.
8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.
Вариант 10 6. Планиметрия
1. Найдите величину угла АВС. Ответ дайте в градусах.
2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.
3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.
4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.
5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.
6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.
7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
9. В треугольнике известно, что , , угол
равен 90°. Найдите радиус вписанной окружности.
10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС =
. Найдите
|
6. Планиметрия |
||||
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
18 июня 2021
В закладки
Обсудить
Жалоба
Тесты по планиметрии
Сборник тестов по всем разделам планиметрии. Проработка этих задач будет служить первым этапом подготовки к успешному решению задачи 16 ЕГЭ. Тесты можно использовать как для работы на спецкурсах по планиметрии, домашней работы, так и итогового контроля.
t1.docx
t2.docx
t3.docx
t4.docx
t5.docx
Автор: Марина Владимировна Авраменко.
|
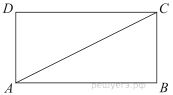
Вариант 1 1) Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 2) Найдите абсциссу середины отрезка, соединяющего точки A(3;7) и B(12;4). 3) В треугольнике ABC угол C равен 90°,AB=20,BC=15. Найдите sinA. 4) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 5) В треугольнике АВС, AC=BC=8, косинус внешнего угла при вершине A равен –0,5. Найдите AB. |
Вариант 2 1) Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 2) Найдите абсциссу середины отрезка, соединяющего точки A(-2;7) и B(-13;2). 3) В треугольнике ABC угол C равен 90°,AB=20,BC=16. Найдите sinA. 4) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 5) В треугольнике АВС, AC=BC=20, косинус внешнего угла при вершине A равен –0,8. Найдите AB. |
|
Вариант 3 1) Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 2) Найдите абсциссу середины отрезка, соединяющего точки A(-2;9) и B(2;-8). 3) В треугольнике ABC угол C равен 90°,AB=20,BC=15. Найдите sinA. 4) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 5) В треугольнике АВС, AC=BC=12, косинус внешнего угла при вершине A равен –0,25. Найдите AB. |
Вариант 4 1) Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 2) Найдите абсциссу середины отрезка, соединяющего точки A(3;7) и B(12;4). 3) В треугольнике ABC угол C равен 90°,AB=15,BC=9. Найдите sinA. 4) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 5) В треугольнике АВС, AC=BC=20, косинус внешнего угла при вершине A равен –0,7. Найдите AB. |
|
Вариант 5 1) Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 2) Найдите абсциссу середины отрезка, соединяющего точки A(1;-3) и B(3;2). 3) В треугольнике ABC угол C равен 90°,AB=10,BC=6. Найдите sinA. 4) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 5) В треугольнике АВС, AC=BC=10, косинус внешнего угла при вершине A равен –0,6. Найдите AB. |
Вариант 6 1) Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 2) Найдите абсциссу середины отрезка, соединяющего точки A(-3;5) и B(10;4). 3) В треугольнике ABC угол C равен 90°,AB=15,BC=3. Найдите sinA. 4) Четырёхугольник ABCD вписан в окружность. Угол ABC равен 5) В треугольнике АВС, AC=BC=4, косинус внешнего угла при вершине A равен –0,75. Найдите AB. |
Вариант 1
№1
А) Показания счётчика электроэнергии 1 апреля
составляли 79 621 кВт/ч, а 1 мая — 79 821 кВт/ч. Сколько нужно заплатить за
электроэнергию за апрель, если 1 кВт/ч электроэнергии стоит 4 руб. 50 коп.?
Ответ дайте в рублях.
Б) В среднем за день во время конференции расходуется
90 пакетиков чая. Конференция длится 4 дня. В пачке чая 100 пакетиков. Какого
наименьшего количества пачек чая хватит на все дни конференции?
В) В летнем лагере на каждого участника полагается 40
г сахара в день. В лагере 160 человек. Сколько килограммовых пачек сахара
понадобится на весь лагерь на 6 дней?
№2
А) На диаграмме показано распределение выплавки меди в
10 странах (в тысячах тонн) за 2006 год. Среди представленных стран первое
место по выплавке меди занимали США, десятое место — Казахстан. Какое место
занимала Австралия?
Б) При работе фонарика батарейка постепенно
разряжается и напряжение в электрической цепи фонарика падает. На рисунке
показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной
оси отмечается время работы фонарика в часах, на вертикальной оси —напряжение в
вольтах. Определите по рисунку, на сколько вольт упадёт напряжение с 6-го по
56-й час работы фонарика.
В) На рисунке жирными точками показано суточное
количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По
горизонтали указываются числа месяца, по вертикали — количество осадков,
выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на
рисунке соединены линией. Определите по рисунку, сколько дней из данного
периода не выпадало осадков.
№3
А) На клетчатой бумаге с размером клетки 1×1
изображён ромб. Найдите его площадь.
Б) Найдите площадь четырехугольника, изображенного на
клетчатой бумаге с размером клетки 1×1.
В) На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите длину средней линии этой трапеции.
№4
В треугольнике ABC CD — медиана,
угол C равен 90°, угол B равен 35°. Найдите угол ACD.
Ответ дайте в градусах.
Вариант 2
№1
А) В летнем лагере 246 детей и 29 воспитателей. В
автобус помещается не более 45 пассажиров. Какое наименьшее количество
автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Б) Блокнот в магазине стоит 22 рубля. Сколько рублей
заплатит покупатель за 70 блокнотов, если при покупке больше 50 блокнотов
магазин делает скидку 5% от стоимости всей покупки?
В) Килограмм орехов стоит 75 рублей. Маша купила 4 кг
400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей?
№2
А) На диаграмме показана среднемесячная температура
воздуха за месяц. По горизонтали указываются месяцы, по вертикали — температура
в градусах Цельсия. Определите по приведённой диаграмме наименьшую
среднемесячную температуру.
Б) При работе фонарика батарейка постепенно
разряжается и напряжение в электрической цепи фонарика падает. На графике
показана зависимость напряжения в цепи от времени работы фонарика. На
горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси
— напряжение в вольтах. Определите по рисунку, за сколько часов напряжение
упадёт с 1,2 вольта до 1 вольта.
В) На рисунке показано изменение температуры воздуха
на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали
— значение температуры в градусах Цельсия. Определите по рисунку разность между
наибольшей и наименьшей температурами воздуха 18 декабря. Ответ дайте в
градусах Цельсия.
№3
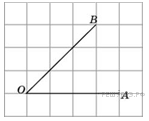
А) На клетчатой бумаге с размером клетки
1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой
из вершины C.
Б) На клетчатой бумаге с размером клетки 1×1 изображён
треугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.
В) Найдите площадь трапеции, изображенной на клетчатой
бумаге с размером клетки 1×1.
№4
В прямоугольном треугольнике угол между высотой и
биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший
угол прямоугольного треугольника. Ответ дайте в градусах
|
Вариант 1 |
Вариант 2 |
|
№1 |
№1 |
|
900, 4, 39 |
7, 1463, 20 |
|
№2 |
№2 |
|
4, 0,4, 4 |
-2, 6, 6,5 |
|
№3 |
№3 |
|
24, 6, 7,5 |
3, 18, 2 |
|
№4 550 |
№4 310 |
Самостоятельная работа по геометрии 11 класс
по заданиям ЕГЭ «Планиметрия. Треугольники».
1. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 26 °. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
2. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 3 и 5.
3. Площадь прямоугольного треугольника равна 264. Один из его катетов на 2 больше другого. Найдите меньший катет.
4. Один острый угол прямоугольного треугольника в раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
5. В треугольнике ABC угол ACB равен 90°, угол B равен 68°, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
6. Острый угол прямоугольного треугольника равен 34°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
7. В треугольнике ABC Найдите AC.
8. В треугольнике ABC AH — высота, Найдите BH.
9. В треугольнике ABC AH — высота, Найдите BH.
10. В треугольнике ABC угол A равен внешний угол при вершине B равен Найдите угол C. Ответ дайте в градусах.
11. В треугольнике ABC AD — биссектриса, угол C равен 50°, угол BAD равен 63°. Найдите угол ADB. Ответ дайте в градусах.
12. В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения CH и AD, угол BAD равен 10°. Найдите угол AOC. Ответ дайте в градусах.
13. В треугольнике ABC DE — средняя линия. Площадь треугольника ADE равна 5. Найдите площадь треугольника АВС.
14. В треугольнике ABC угол B — тупой, AB = 7, BC = 8. Найдите величину угла, противолежащего стороне AC, если площадь треугольника равна Ответ дайте в градусах.
15. В треугольнике ABC угол A равен 135°. Продолжения высот BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
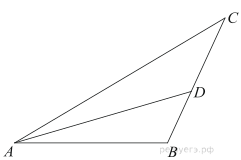
1
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям

















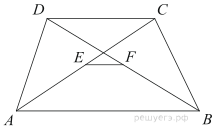



 .
.
 угол
угол  Найдите угол
Найдите угол 


 угол
угол  Найдите угол
Найдите угол 
 угол
угол  Найдите угол
Найдите угол 
 угол
угол  Найдите угол
Найдите угол 
 угол
угол  Найдите угол
Найдите угол 
 угол
угол  Найдите угол
Найдите угол 











