Практика по заданию №15 ЕГЭ по математике базового уровня — планиметрия.
Для выполнения задания №15 необходимо уметь выполнять действия с геометрическими фигурами .
Практика
| Источник | Задания |
| time4math.ru | Скачать задания |
| math100.ru | Планиметрия |
Коды проверяемых элементов содержания (по кодификатору) — 5.1.1–5.1.5, 5.5.1, 5.5.3, 5.5.5
Уровень сложности задания — базовый
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 8
Связанные страницы:
Задание 1 ЕГЭ по математике база — действия с дробями
Задание 2 ЕГЭ по математике база — простейшие текстовые задачи
Задание 3 ЕГЭ по математике база — размеры и единицы измерения
Задание 6 ЕГЭ по математике база — простейшие текстовые задачи
Задание 14 ЕГЭ по математике база — анализ графиков и таблиц
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий
Задания 12. Планиметрия . Треугольники и их элементы
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 27289
В треугольнике ABC
Найдите
Аналоги к заданию № 27289: 520479 520499 520520 520543 31891 31893 31895 31897 31899 31901 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
1 комментарий · Сообщить об ошибке · Помощь
2
Тип 12 № 27290
В треугольнике ABC
Найдите
Аналоги к заданию № 27290: 19283 19285 19287 19289 19291 19293 19295 19297 19299 19301 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 12 № 27303
высота CH равна 4,
Найдите
Аналоги к заданию № 27303: 32499 32501 32503 32505 32507 32509 32511 32513 32515 32517 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 12 № 27309
В треугольнике ABC
высота CH равна 20. Найдите
Аналоги к заданию № 27309: 4563 4565 4567 4569 4571 4573 Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 12 № 27619
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Аналоги к заданию № 27619: 26342 56555 56557 56559 56561 56563 56565 56567 56569 56571 … Все
Раздел кодификатора ФИПИ: Треугольники и их элементы
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Планиметрия
В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.
Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня
Вариант 15МБ1
[su_note note_color=”#defae6″]
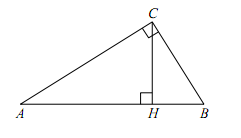
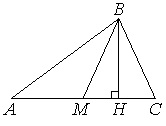
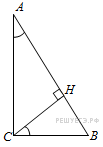
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.
[/su_note]
Алгоритм выполнения:
- Вспомнить определение косинуса угла.
- Записать выражение для нахождения косинуса угла.
- Выразить неизвестную величину.
- Вычислить.
Решение:
Вспомним определение косинуса угла.
Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.
Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.
Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.
Прилежащий к углу А катет – АН.
Получим cos A = АН/АС.
Выразим неизвестную величину.
АН = АС · cos A
Вычислим.
АН = АС · cos A = 4 · 0,8 = 3,2
Ответ: 3,2.
Вариант 15МБ2
[su_note note_color=”#defae6″]
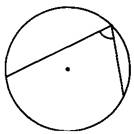
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.
[/su_note]
Алгоритм выполнения:
- Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
- Вычислить градусную меру угла, на который опирается дуга.
- Вычислить вписанный угол.
Решение:
Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.
Вычислим градусную меру угла, на который опирается дуга.
Весь круг составляет 360°, а 5/18 от его длины это
Вычислим вписанный угол.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
100°:2 = 50°.
Ответ: 50.
Вариант 15МБ3
[su_note note_color=”#defae6″]
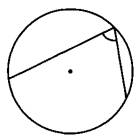
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.
[/su_note]
Алгоритм выполнения:
- Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
- Вычислить градусную меру угла, на который опирается дуга.
- Вычислить вписанный угол.
Решение:
Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.
Вычислим градусную меру угла, на который опирается дуга.
Весь круг составляет 360°, а 11/36 от его длины это
Вычислим вписанный угол.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
110°:2 = 55°.
Ответ: 55.
Вариант 15МБ4
[su_note note_color=”#defae6″]
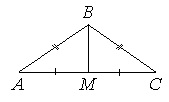
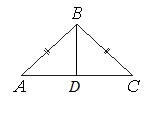
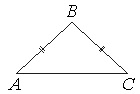
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.
[/su_note]
Алгоритм выполнения
- Определяем вид треугольника.
- Доказываем, что медиана ВМ является и высотой.
- Из прямоугольного треугольника АМВ по т.Пифагора находим медиану ВМ.
Решение:
Если АВ=ВС, то ∆АВС – равнобедренный.
В равнобедр.треугольнике медиана, опущенная на основание, является еще и высотой. Тогда угол АМВ=900, и ∆АМВ – прямоугольный с катетами АМ и ВМ и гипотенузой АВ.
По т.Пифагора АМ2+ВМ2=АВ2. Отсюда: .
Т.к. АМ медиана, то
AM=АС:2=24:2=12.
Тогда:
.
Вариант 15МБ5
[su_note note_color=”#defae6″]
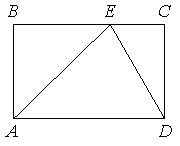
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.
[/su_note]
Алгоритм выполнения
- Находим ЕС.
- Определяем значение СD.
- Из прямоугольного треугольника АСD по т.Пифагора находим ЕD.
Решение:
Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.
Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.
ЕС=ВС–ВЕ=17–12=5.
Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=900, и ∆ЕСD прямоугольный.
Тогда по т.Пифагора ЕD2=ЕC2+СD2. Получаем:
Вариант 15МБ6
[su_note note_color=”#defae6″]
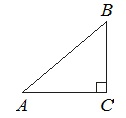
В треугольнике АВС угол С равен 900, АВ=25, АС=24. Найдите cos B.
[/su_note]
Алгоритм выполнения
- По т.Пифагора находим величину катета ВС.
- По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.
Решение:
Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ2=АС2+ВС2.
Отсюда: .
Вариант 15МБ7
[su_note note_color=”#defae6″]
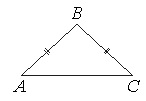
В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.
[/su_note]
Алгоритм выполнения
- Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB.
- Из ∆ADB находим катет ВD, используя sin A.
- Находим АD из ∆ADB по т.Пифагора. Далее определяем АС как 2AD.
- Находим площадь ∆АВС по формуле S=ah/2.
Решение
В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.
Из ∆ADB по т.Пифагора имеем: AB2=AD2+BD2 →
Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.
Площадь ∆АВС равна:
Вариант 15МБ8
[su_note note_color=”#defae6″]
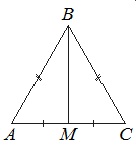
В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.
[/su_note]
Алгоритм выполнения
- Доказываем, что ∆АВМ прямоугольный.
- Из ∆АВМ, используя формулу-определение для тангенса, находим АМ.
- Из ∆АВМ по теореме Пифагора находим АВ.
Решение:
Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.
Из ∆АВМ имеем:
Из ∆АВМ по теореме Пифагора АВ2=АМ2+ВМ2 →
Вариант 15МБ9
[su_note note_color=”#defae6″]
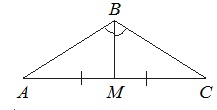
В треугольнике АВС угол В равен 1200. Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.
[/su_note]
Алгоритм выполнения
- Определяем величину угла АВМ.
- Доказываем, что ∆АМВ прямоугольный.
- Находим АВ, используя формулу-определение для косинуса.
Решение:
По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет
1200:2=600.
Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.
В прямоугольного ∆АМВ:
Отсюда:
Вариант 15МБ10
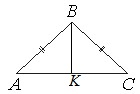
[su_note note_color=”#defae6″]
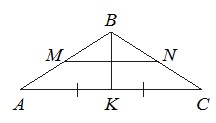
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.
[/su_note]
Алгоритм выполнения
- Доказываем, что ∆АКВ прямоугольный.
- Из ∆АКВ по т.Пифагора находим АК.
- Находим АС как 2АК.
- Находим МN как среднюю линию.
Решение:
Т.к. ∆АВС равнобедренный, то медиана ВК, опущенная на основание АС, является и высотой. Поэтому угол АКВ равен 900, и ∆АКВ прямоугольный.
Из прямоугольного ∆АКВ по т.Пифагора АВ2=АК2+ВК2.
Отсюда:
Поскольку ВК медиана, то АС=2АК=2·24=48.
Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).
Значит, MN=AC:2=48:2=24.
Вариант 15МБ11
[su_note note_color=”#defae6″]
В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.
[/su_note]
Алгоритм выполнения
- Находим длину отрезков АМ и МС как половину от АС.
- Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС.
- Находим АН как сумму АМ и МН.
Решение:
Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.
По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.
АН=АМ+МН=28+14=42.
Вариант 15МБ12
[su_note note_color=”#defae6″]
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.
[/su_note]
Алгоритм выполнения
- Находим величину 2-го (неизвестного) катета по т.Пифагора.
- Определяем площадь треугольника как полупроизведение катетов.
Решение:
Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.
По т.Пифагора a2+b2=c2. Отсюда:
Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.
Вариант 15МБ13
[su_note note_color=”#defae6″]
В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.
[/su_note]
Алгоритм выполнения
- Используя формулу для площади треугольника S=ah/2 и зная величину а (по условию – основание АС), найдем высоту ∆АВС. Отображаем высоту на рисунке, обозначив ее пересечение с основанием буквой К.
- Доказываем, что высота ВК является и его медианой. Отсюда находим АК.
- Из ∆АКВ по т.Пифагора находим АВ.
Решение:
Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.
Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.
Из прямоугольного ∆АКВ по т.Пифагора АВ2=АК2+ВК2. Получаем:
Даниил Романович | Просмотров: 10.3k
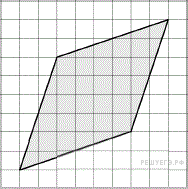
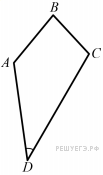
1. Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
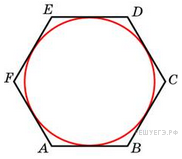
2. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
3. Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (8; 4), (8; 8), (2; 10).
4. В треугольнике угол
равен 90°,
– высота,
,
. Найдите
.
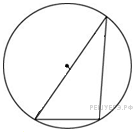
5. Найдите хорду, на которую опирается угол , вписанный в окружность радиуса 3.
.
6. Сумма трёх углов выпуклого четырёхугольника равна 322°. Найдите его четвёртый угол. Ответ дайте в градусах
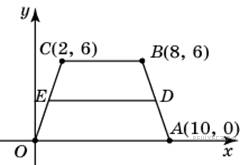
7. Точки O(0; 0), A(10; 0), B(8; 6), C(2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
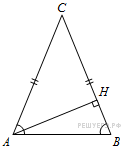
8. В треугольнике
,
– высота,
. Найдите
.
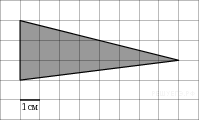
9. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
10. В треугольнике
, высота
равна 4, угол
равен
. Найдите
.
11.Острые углы прямоугольного треугольника равны 85° и 5°. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
12.
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см 1 см (см. рис.). В ответе запишите
.
13. На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
14.
В треугольнике проведены медиана
и высота
. Известно, что и . Найдите
.
15. Найдите угловой коэффициент прямой, проходящей через точки с координатами и
16. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
17.
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см 1 см (см. рис.). В ответе запишите
.
18. Точки O(0; 0), A(6; 8), B(6; 2), C(0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
19. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
20. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
21. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
23. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Инфоурок
›
Геометрия
›Презентации›Презентация по математике на тему «ЕГЭ по математике. Базовый уровень. Планиметрия»№20»
Скачать материал

Скачать материал


- Сейчас обучается 899 человек из 81 региона


- Сейчас обучается 21 человек из 14 регионов


- Сейчас обучается 20 человек из 12 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
2019
Выполнила:
Ученица 10 «А» класса
Сазонова А.А.2019
ЕГЭ по математике
Базовый уровень Планиметрия -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 154 984 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Больше материалов по этому УМК
Другие материалы

Площади поверхностей в ЕГЭ
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- 14.05.2019
- 739
- 7

Площадь поверхности цилиндра и конуса
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- 13.05.2019
- 430
- 0

Конспект урока по теме «Цилиндр, конус,шар»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 6. Цилиндр, конус, шар
- 12.05.2019
- 1536
- 31



Решение задач по теме «Цилиндр. Конус»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- 08.05.2019
- 847
- 29

Решение задач по теме «Пирамида»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: § 2. Пирамида
- 08.05.2019
- 1968
- 85

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс профессиональной переподготовки «Экскурсоведение: основы организации экскурсионной деятельности»
-
Курс повышения квалификации «Этика делового общения»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Скачать материал
-
16.05.2019
606
-
PPTX
821.3 кбайт -
25
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Ваулина Марина Николаевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 1 месяц
- Подписчики: 1
- Всего просмотров: 23601
-
Всего материалов:
33
16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по планиметрии
Задание
1
#2436
Уровень задания: Легче ЕГЭ
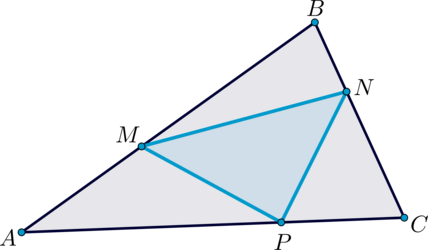
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).
(triangle ABC) и (triangle MBN) имеют общий угол (B), при этом (BM=frac23BA), (BN=frac13BC).
Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то
[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]
Аналогично рассуждая, получаем, что
[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]
Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]
Ответ: 45
Задание
2
#2444
Уровень задания: Легче ЕГЭ
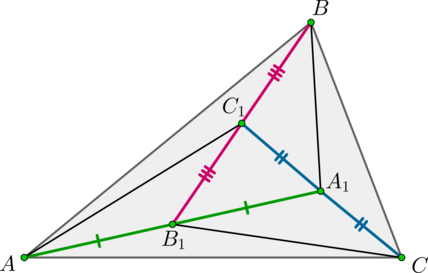
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).
Соединим точки (A) и (C_1), (B) и (A_1), (C) и (B_1).
Т.к. медиана делит треугольник на два равновеликих треугольника, то
[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]
Аналогично,
[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]
Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,
[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]
Ответ:
(1:7)
Задание
3
#1760
Уровень задания: Равен ЕГЭ
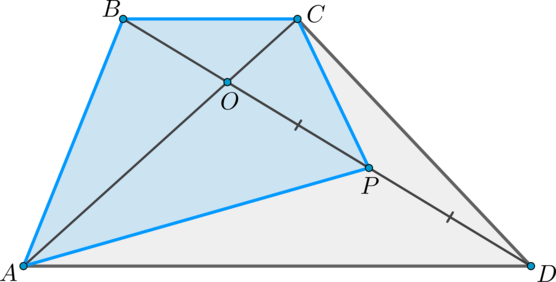
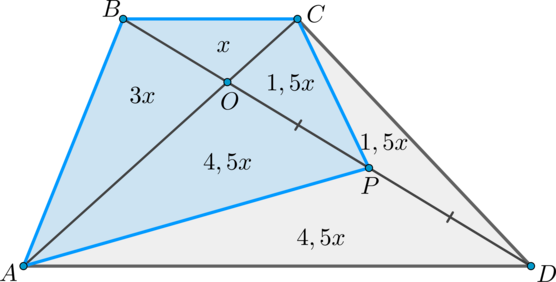
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).
Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.
Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]
(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).
(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).
Ответ: 30
Задание
4
#2441
Уровень задания: Равен ЕГЭ
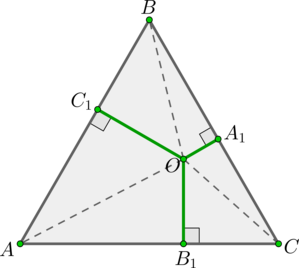
Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.
Рассмотрим равносторонний (triangle ABC), (AB=m), (O) – точка внутри треугольника, (OA_1, OB_1, OC_1) — перпендикуляры на стороны (BC, AC, AB) соответственно.
Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:
[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]
Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.
Ответ:
(dfrac{sqrt3}2m)
Задание
5
#1287
Уровень задания: Равен ЕГЭ
Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.
а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.
б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.
а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.
Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).
В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.
б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).
Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).
Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.
При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).
Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).
Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.
Ответ:
б) (21).
Задание
6
#1288
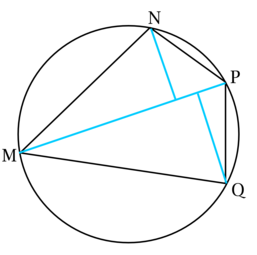
Уровень задания: Равен ЕГЭ
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).
а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).
б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).
а) Так как (dfrac{MN}{PQ} = dfrac{QM}{PN}), то (MNcdot PN = QMcdot PQ).
Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).
В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]
С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).
б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).
Ответ:
б) (2).
Задание
7
#1289
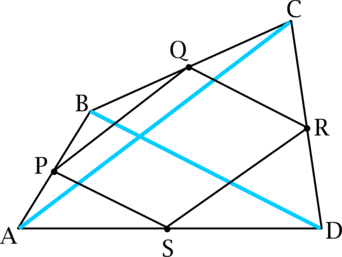
Уровень задания: Равен ЕГЭ
(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).
а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.
б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).
а) Проведём диагонали (AC) и (BD).
Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).
Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).
Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.
б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.
Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]
Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]
Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).
В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]
Ответ:
б) (1).

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
| НАЧАЛЬНАЯ ШКОЛА |
ДОШК. ОБРАЗОВАНИЕ
• Все дошкольное обр.
• Занятия c дошколь.
• Методика воспитания
• Рабочие программы
• Работа с родителями
• Игры для дошкольников
• ОБЖ и ЗОЖ
• Праздники
• Обобщение опыта
УЧИТЕЛЮ 1-4 КЛАСС
• Кружки и факультативы
• Методика преподавания
• Обобщение опыта
• Классные часы
• Воспитательная работа
• Рабочие программы
• Родительские собрания
• Физминутки на уроках
• Здоровьесбережение
• Оформление кабинета
• Проекты учащихся
КОНТРОЛЬ ЗНАНИЙ
• Проверочные (ВПР)
• Итоговые работы
ПРАЗДНИКИ
• Игры и викторины
• Сценарии праздников
• Спортивные меропр-я
• Линейки и выпускные
ЛОГОПЕДУ
• Весь материал
• Дошкольникам
• Школьникам
• Планы, методики
МАТЕМАТИКА
• Вся математика
• Математика 1 класс
• Математика 2 класс
• Математика 3 класс
• Математика 4 класс
• Внеклас. мероприятия
ИНФОРМАТИКА
• Вся информатика
• Информатика 1 класс
• Информатика 2 класс
• Информатика 3 класс
• Информатика 4 класс
• Внеклас. мероприятия
АНГЛИЙСКИЙ ЯЗЫК
• Весь английский
• Английский 2 класс
• Английский 3 класс
• Английский 4 класс
• Внеклас. мероприятия
ОРКСЭ
• Всё ОРКСЭ
• Православная культура
• Светская этика
• Буддийская культура
• Иудейская культура
• Исламская культура
• Мировые культуры
• Методика преподавания
ОКРУЖАЮЩИЙ МИР
• Весь окр. мир
• Окр. мир 1 класс
• Окр. мир 2 класс
• Окр. мир 3 класс
• Окр. мир 4 класс
• Игры и викторины
ЛИТЕРАТУРНОЕ ЧТЕНИЕ
• Все литератур. чтение
• Литература 1 класс
• Литература 2 класс
• Литература 3 класс
• Литература 4 класс
• Внеклас. мероприятия
РУССКИЙ ЯЗЫК
• Весь русский язык
• Обучение грамоте
• Русский 1 класс
• Русский 2 класс
• Русский 3 класс
• Русский 4 класс
• Внеклас. мероприятия
ОБЖ
• Все ОБЖ
• ОБЖ 1 класс
• ОБЖ 2 класс
• ОБЖ 3 класс
• ОБЖ 4 класс
• Внеклас. мероприятия
ИЗО ИСКУССТВО
• Всё ИЗО
• ИЗО 1 класс
• ИЗО 2 класс
• ИЗО 3 класс
• ИЗО 4 класс
ТЕХНОЛОГИЯ
• Вся технология
• Технология 1 класс
• Технология 2 класс
• Технология 3 класс
• Технология 4 класс
МУЗЫКА
• Вся музыка
• Материалы для уроков
• Разработки уроков
• Методика преподавания
ФИЗКУЛЬТУРА
• Материалы для уроков
• Спортивные мероприятия
• Рабочие программы
ПОДПИСКА НА МАТЕРИАЛЫ САЙТА
|
ОСНОВНАЯ И СРЕДНЯЯ |
МАТЕМАТИКА
• Вся математика
• Математика 5 класс
• Математика 6 класс
• Математика 7 класс
• Математика 8 класс
• Математика 9 класс
• Математика 10 класс
• Математика 11 класс
• ГИА по математике
• ЕГЭ по математике
• Игры и викторины
• Олимпиады по матема.
• Методика преподавания
ФИЗИКА
• Вся физика
• Физика 7 класс
• Физика 8 класс
• Физика 9 класс
• Физика 10 класс
• Физика 11 класс
• ЕГЭ по физике
• Игры и викторины
• Проекты учащихся
• Методика преподавания
ИНФОРМАТИКА
• Вся информатика
• Информатика 5 класс
• Информатика 6 класс
• Информатика 7 класс
• Информатика 8 класс
• Информатика 9 класс
• Информатика 10 класс
• Информатика 11 класс
• Игры и викторины
• ЕГЭ по информатике
• Проекты учащихся
• Факультативы по инфо.
ХИМИЯ
• Вся химия
• Химия 7 класс
• Химия 8 класс
• Химия 9 класс
• Химия 10 класс
• Химия 11 класс
• ЕГЭ по химии
• Факультативы по химии
• Игры и викторины
• Проекты учащихся
• Методика преподавания
АСТРОНОМИЯ
• Вся астрономия
• Уроки и презентации
АНГЛИЙСКИЙ ЯЗЫК
• Весь английский
• Английский 5 класс
• Английский 6 класс
• Английский 7 класс
• Английский 8 класс
• Английский 9 класс
• Английский 10 класс
• Английский 11 класс
• ЕГЭ по английскому
• Игры и викторины
• Топики (Topics)
• Статьи (Article)
• Методика преподавания
НЕМЕЦКИЙ ЯЗЫК
• Весь немецкий
• Немецкий 2 класс
• Немецкий 5 класс
• Немецкий 6 класс
• Немецкий 7 класс
• Немецкий 8 класс
• Немецкий 9 класс
• Немецкий 10 класс
• Немецкий 11 класс
• Игры и викторины
ФРАНЦУЗСКИЙ ЯЗЫК
• Весь французский
• Французский 4 класс
• Французский 5 класс
• Французский 6 класс
• Французский 9 класс
• Французский 10 класс
БИОЛОГИЯ
• Вся биология
• Природовед. 5 класс
• Биология 6 класс
• Биология 7 класс
• Биология 8 класс
• Биология 9 класс
• Биология 10 класс
• Биология 11 класс
• Факультативы
• ГИА по биологии
• ЕГЭ по биологии
• Игры и викторины
• Методика преподавания
• Проекты учащихся
• Плакаты и схемы
• Экологическая культура
ГЕОГРАФИЯ
• Вся география
• География 5 класс
• География 6 класс
• География 7 класс
• География 8 класс
• География 9 класс
• География 10 класс
• География 11 класс
• Игры и викторины
• ЕГЭ по географии
• Методика преподавания
• Проекты учащихся
ИСТОРИЯ
• Вся история
• История 4 класс
• История 5 класс
• История 6 класс
• История 7 класс
• История 8 класс
• История 9 класс
• История 10 класс
• История 11 класс
• Игры и викторины
• Проекты учащихся
• Методика преподавания
КРАЕВЕДЕНИЕ
ЭКОНОМИКА
• Вся экономика
• Экономика 7 класс
• Экономика 8 класс
• Экономика 9 класс
• Экономика 10 класс
• Экономика 11 класс
• Игры и викторины
ОБЩЕСТВОЗНАНИЕ
• Всё обществознание
• Обществ. 5 класс
• Обществ. 6 класс
• Обществ. 7 класс
• Обществ. 8 класс
• Обществ. 9 класс
• Обществ. 10 класс
• Обществ. 11 класс
• ЕГЭ по обществознанию
• Игры и викторины
• Проекты учащихся
РУССКИЙ ЯЗЫК
• Весь русский
• Русский 5 класс
• Русский 6 класс
• Русский 7 класс
• Русский 8 класс
• Русский 9 класс
• Русский 10 класс
• Русский 11 класс
• ГИА по русскому
• ЕГЭ по русскому
• Плакаты и схемы
• Проекты учащихся
• Игры и викторины
• Методика преподавания
ЛИТЕРАТУРА
• Вся литература
• Литература 5 класс
• Литература 6 класс
• Литература 7 класс
• Литература 8 класс
• Литература 9 класс
• Литература 10 класс
• Литература 11 класс
• ЕГЭ по литературе
• Школьные сочинения
• Плакаты и схемы
• Проекты учащихся
• Игры и викторины
• Методика преподавания
ФИЗКУЛЬТУРА
• Вся физкультура
• Физкультура
• Методика преподавания
ОБЖ
• Всё ОБЖ
• ОБЖ 5 класс
• ОБЖ 6 класс
• ОБЖ 7 класс
• ОБЖ 8 класс
• ОБЖ 9 класс
• ОБЖ 10 класс
• ОБЖ 11 класс
• Олимпиады по ОБЖ
• Рабочие программы
• Игры и викторины
• Методика преподавания
• Проекты учащихся
ТЕХНОЛОГИЯ
• Вся технология
• Технология 5 класс
• Технология 6 класс
• Технология 7 класс
• Технология 8 класс
• Технология 9 класс
• Технология 10-11 класс
• Игры и викторины
• Методика преподавания
• Проекты учащихся
• Факультативы
ИЗО, МХК
• Разработки уроков
• Методика преподавания
МУЗЫКА
• Разработки уроков
• Методика преподавания
| ОБОБЩЕНИЕ ОПЫТА |
КЛАССНЫЙ ЧАС
• Все классные часы
• Разговоры о важном
• Отечество
• Общение
• Гражданственность
• Солидарность
• Труд и творчество
• Искусство и литература
• Человечество
• Природа
• Семья
• ЗОЖ
• Религия
• Наука
• Финансовая грамотность
• Разные КЧ
КЛ. РУКОВОДСТВО
• Все кл. руководство
• Обобщение опыта
• Род. собрания
• Планы работы
• Характеристики
• Анкеты и тесты
ПРАЗДНИКИ
• Каталог праздников
• День рождения
• Выпускные 9 класс
• Выпускные 11 класс
• Спортивные
• Разные праздники
УЧИТЕЛЮ
• Общая методика
• Полезные программы
• Интерактивная доска
• Инклюзивное обучение
• Аттестация
• Педсовет
• Полезные статьи
• Мастер-класс
• Технологические приемы
• Педагог-библиотекарь
• Комплексы уроков
• Универсальное видео
ШАБЛОНЫ И НАГРАДЫ
• Шаблоны презентаций
• Оформление
• Медали
ДОПОЛНИТЕЛЬНОЕ ОБР.
• Музыкальное
• Художественное
• Танцевальная
• Театральная
• Туристическое
• Общее ДО
РУКОВОДИТЕЛЯМ
ВОСПИТАТЕЛЮ
• Все для воспитателя
• Программы лагерей
• Программы продленок
• Полезные статьи
ПСИХОЛОГУ
• Все для психолога
• Работа с родителями
• Работа с детьми
• Общая психология
| ГОРЯЧИЙ ФОРУМ еще… |
Видео для подготовк…
11.03.2023 (ответов: 7)
Грамота активности и …
10.03.2023 (ответов: 444)
Куда уходит зарплата?
09.03.2023 (ответов: 168)
Оценка ученика
09.03.2023 (ответов: 59)
Что должно быть у с…
09.03.2023 (ответов: 1)
Гибкие учебные план…
08.03.2023 (ответов: 1)
Выполняют ли учащие…
08.03.2023 (ответов: 4)
18 задача ЕГЭ
08.03.2023 (ответов: 0)
Задач второй части …
08.03.2023 (ответов: 0)
Нужно ли называть чел…
07.03.2023 (ответов: 25)
В БЛОГАХ…
еще…
С праздником! (3)
С Прощеным воскресе… (1)
Любим! Верим! Ждем … (2)
Вновь про шахты и к… (2)
Поэт Есенин (8)
Открытие Спартакиад… (6)
Потомки Данилы-маст… (10)
Пора учить язык гра… (3)
Моя. Фестиваль варе… (25)
Моя. Несмотря и воп… (4)
еще…
Интерактивная игра &quo…
Очень благодарна Вам, Зоя Андреевна, что находите время посмотреть и оценить рес…
ФГ. Читательская грамот…
Татьяна Владимировна, большое спасибо за очередной ресурс по функциональной грам…
Поиграем с юбиляром. С….
Ирина Александровна, Вы подготовили очень интересный материал, посвящённый творч…
Презентация «Литер…
Наталья Александровна, спасибо за замечательный ресурс! Ну, ОЧЕНЬ эмоциональный!
Интерактивный тренажёр …
Зоя Андреевна, спасибо за очередной тренажёр по теме «Основное свойство дро…
sergeevasya, Кориневская, ромашка5975
|
Материалы » Математика » ЕГЭ по математике 39592 ЕГЭ по математике
|
||||||||||||||||||
|
Работа предназначена для учащихся 11 класса обучающихся по учебнику геометрии любого автора для проверки и систематизации знаний учащихся по заданиям ЕГЭ базового уровня. Работа состоит из двух разделов: в первом разделе данной работы приведено решение 23 задач по теме «Треугольник», а во втором разделе подобраны похожие задачи для самостоятельного решения.
Данную работу можно применить при организации уроков итогового повторения так и при проведении консультаций. Практикум №1 по решению стереометрических задач базового уровня (куб) Практикум №2 по решению планиметрических задач базов (вычисление углов равнобедренного треугольника) © Мишарина Альбина Геннадьевна Мишарина Альбина Геннадьевна
Понравилось? Сохраните и поделитесь:
По кнопке ниже вы можете скачать методическую разработку «Практикум №1 по решению планиметрических задач базового уровня (треугольник)» категории «ЕГЭ по математике» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Характеристики документа: «презентация».
Загрузка началась… Понравился сайт? Получайте ссылки Подарок каждому подписчику!
|
||||||||||||||||||
Порядок вывода комментариев:
|
БУДЬТЕ С НАМИ
• Регистрация
• Подписка
• Вход на сайт
еще…
Презентация «Сергей Владимирович Михалков»
Интерактивная познавательная викторина по произведениям С.В.Михалкова
Презентация к уроку по теме «Какая бывает промышленность»
Презентация к уроку по теме «Животноводство»
Видеоролик к песне «Азбука»




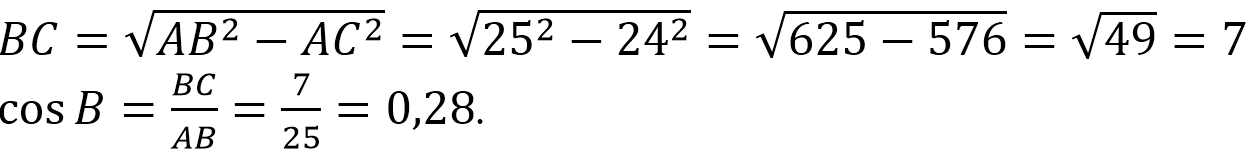






























 0
0




