Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник- описанным около этой окружности.
В любой треугольник можно вписать окружность. Центром вписанной окружности (точка $О$) является точка пересечения биссектрис внутренних углов треугольника.
$OD$ – это радиус $(r)$ вписанной окружности
$r={2S_{ABC}}/{a+b+c}$
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
В равнобедренном треугольнике вписанная окружность точкой касания делит основание пополам
В равностороннем треугольнике радиус вписанной окружности равен трети высоты данного треугольника.
$r={h}/{3}$
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Пример:
В прямоугольном треугольнике $АВС$ катет и гипотенуза соответственно равны $8$ и $10$. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Нам неизвестен один из катетов, найдем его по теореме Пифагора:
$a^2+b^2=c^2$
$8^2+b^2=10^2$
$64+b^2=100$
$b^2=100-64$
$b^2=36$
$b=6$
Теперь подставим все величины в формулу нахождения радиуса вписанной окружности в прямоугольном треугольнике:
$r={6+8-10}/{2}={4}/{2}=2$
Ответ: $2$
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
В трапеции и ромбе центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов, радиус вписанной окружности равен половине высоты.
$r={h}/{2}$
В квадрате радиус вписанной окружности равен половине стороны.
$r={a}/{2}$
Площадь любого многоугольника можно найти как произведение полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник- вписанным в эту окружность.
Около любого треугольника можно описать окружность, причем только одну. Центром описанной окружности является точка $(О)$ пересечения серединных перпендикуляров к сторонам треугольника.
$ОА$ — радиус описанной окружности $(R)$
В равностороннем треугольнике радиус описанной окружности равен две трети высоты данного треугольника.
$R={2h}/{3}$
Центр описанной окружности может находиться в различных положениях относительно треугольника:
1. В остроугольном треугольнике центр описанной окружности лежит внутри треугольника.
2. В тупоугольном треугольнике центр описанной окружности лежит снаружи треугольника.
3. В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.
$R={c}/{2}$
Радиус описанной окружности можно найти как:
$R={a}/{2sinA}={b}/{2sinB}={c}/{2sinC};$
$R={a∙b∙c}/{4S}$, где $S$ — это площадь заданного треугольника.
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.
$R={d}/{2}$
Только вокруг равнобедренной трапеции можно описать окружность.
Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей:
$АВ=an$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2∙R∙sin{180°}/{n};$
$r=R∙cos{180°}/{n};$
$a_n=2∙r∙tg{180°}/{n}.$
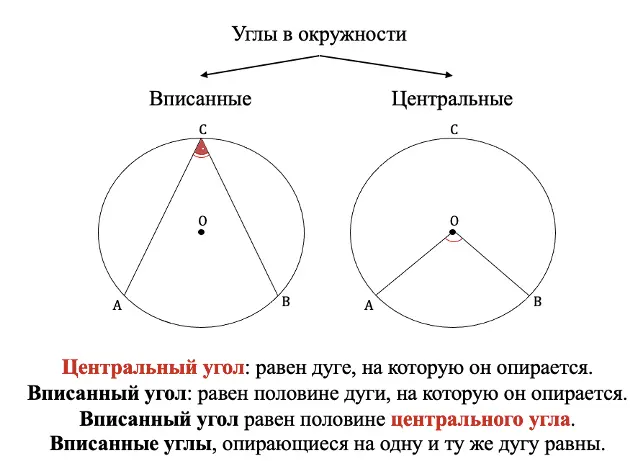
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
$∠B={∪AmC}/{2}$
3. Угол между хордой и касательной равен половине дуги, заключенной внутри него.
$∠B={∪BmC}/{2}$
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Окружность
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 27864
Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
Аналоги к заданию № 27864: 507940 507963 508006 508047 514748 514768 514792 514815 51281 51283 … Все
Раздел кодификатора ФИПИ: Окружность
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 12 № 27865
Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
Раздел кодификатора ФИПИ: Окружность
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 12 № 27870
В окружности с центром O AC и BD − диаметры. Центральный угол AOD равен
Найдите вписанный угол
Ответ дайте в градусах.
Аналоги к заданию № 27870: 511011 514642 26216 51500 51501 51502 51503 51504 51505 51506 … Все
Раздел кодификатора ФИПИ: Окружность
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 12 № 27874
Четырехугольник ABCD вписан в окружность. Угол ABC равен
угол CAD равен
Найдите угол
Ответ дайте в градусах.
Аналоги к заданию № 27874: 51783 512677 26220 51731 51732 51733 51734 51735 51736 51737 … Все
Раздел кодификатора ФИПИ: Окружность
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 12 № 27875
Четырехугольник ABCD вписан в окружность. Угол ABD равен
угол CAD равен
Найдите угол
Ответ дайте в градусах.
Аналоги к заданию № 27875: 26221 51788 51789 51790 51791 51792 51793 51794 51795 51796 … Все
Раздел кодификатора ФИПИ: Окружность
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
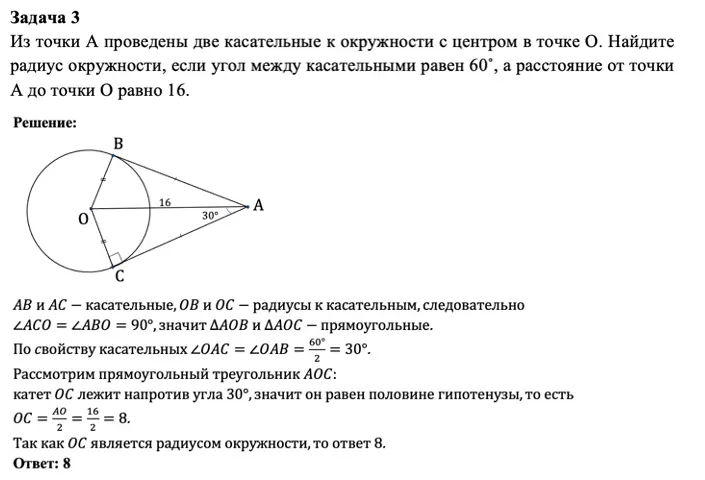
Окружность на ЕГЭ и ОГЭ — сложно. Все потому, что эта фигура не похожа на остальные: у неё нет углов и сторон, зато есть совсем другие элементы. В этой статье мы подробно поговорим про элементы окружности, углы, отрезки и прямые, которые с ней связаны, а также обсудим длину окружности и площадь круга. Ну и разберем основные задания ЕГЭ и ОГЭ, конечно же!
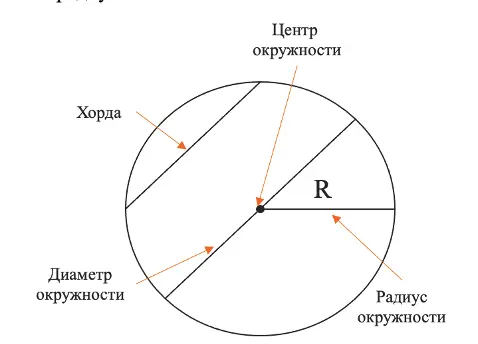
Для начала давайте разберёмся, что же такое окружность. Окружность — это замкнутая линия, состоящая из множества точек, которые равноудалены от центра окружности. Основной элемент окружности — это радиус, он соединяет центр с любой точкой на окружности.
Углы у окружности на ЕГЭ и ОГЭ
У окружности есть 2 вида углов:
- вписанные (их вершина лежит на окружности);
- центральные (тут всё понятно из названия, у них вершина в центре окружности).
Расположение и свойства углов в окружности можно увидеть на схеме ниже:
Давайте отработаем это на практике:
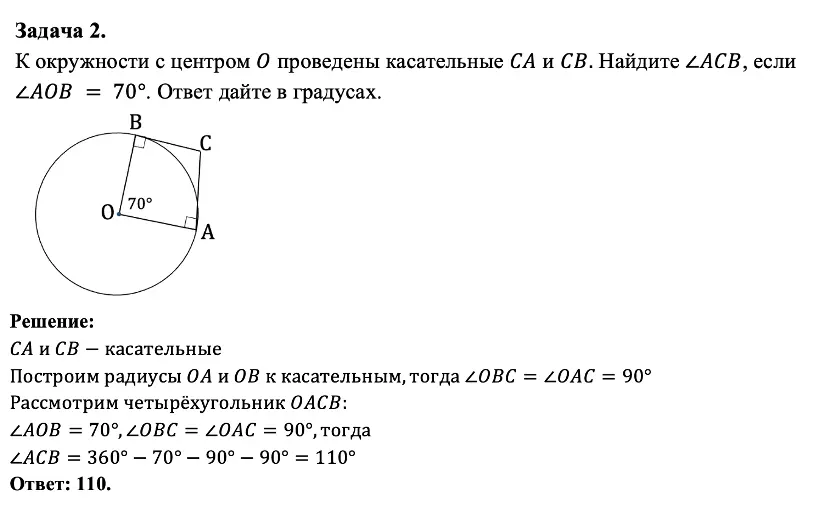
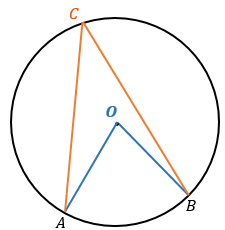
Решение
Можно заметить, что угол АСВ — вписанный и опирается на дугу АВ, соответственно, центральный угол АОD, опирающийся на ту же дугу будет в 2 раза больше, то есть 70 градусов. Теперь рассмотрим развёрнутый угол ВОD, он состоит из углов АОВ и АОD. Градусная мера развёрнутого угла 180 градусов, следовательно искомый угол АОD будет равен 180 – 70 = 110 градусов.
Отрезки и прямые в окружности на ЕГЭ и ОГЭ
Теперь рассмотрим отрезки и прямые в окружности. Приготовьтесь, их будет много!
Есть хорда — это отрезок, который соединяет 2 любые точки на окружности. Если хорда пройдёт через центр окружности, то она превратится в диаметр. Кстати, если внимательно посмотреть, то можно увидеть, что диаметр — это 2 радиуса!
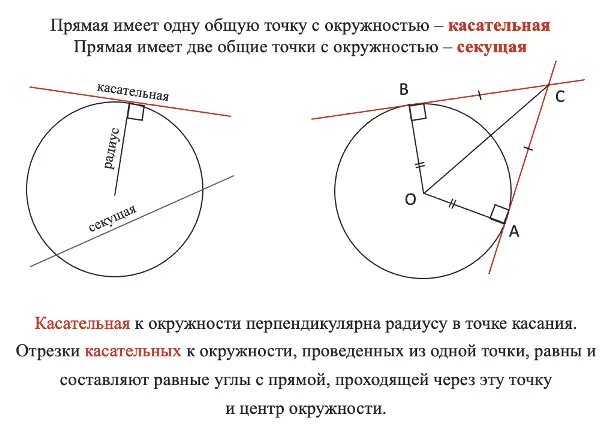
Теперь продлим хорду в обе стороны за пределы окружности, получим прямую, которая переСЕКает нашу окружность, отсюда и её название — секущая. Можно заметить, что секущая имеет 2 общих точки пересечения с окружностью. А ещё мы можем провести прямую так, чтобы она имела с окружностью только 1 точку пересечения, то есть касалась её, такая прямая будет называться касательная.
Подробнее со свойствами касательной и секущей можно ознакомиться на рисунке:
Рассмотрим на примерах заданий про окружность в ЕГЭ и ОГЭ:
4 теоремы про окружность в ЕГЭ и ОГЭ
Теперь я предлагаю ознакомиться с теоремами, которые появляются в комбинациях различных прямых и отрезков в окружности.
Теорема № 1: теория и задания из ЕГЭ и ОГЭ
Первая теорема про хорду и касательную звучит так:
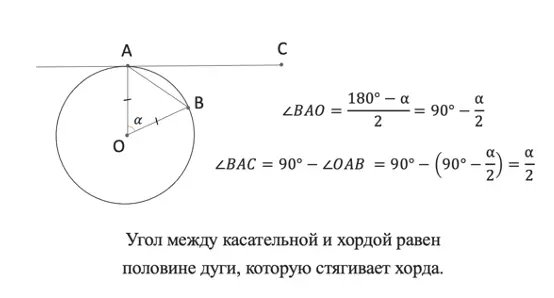
Угол между касательной и хордой равен половине дуге, которую стягивает хорда.
Подробнее с выведением вы можете ознакомиться на рисунке:
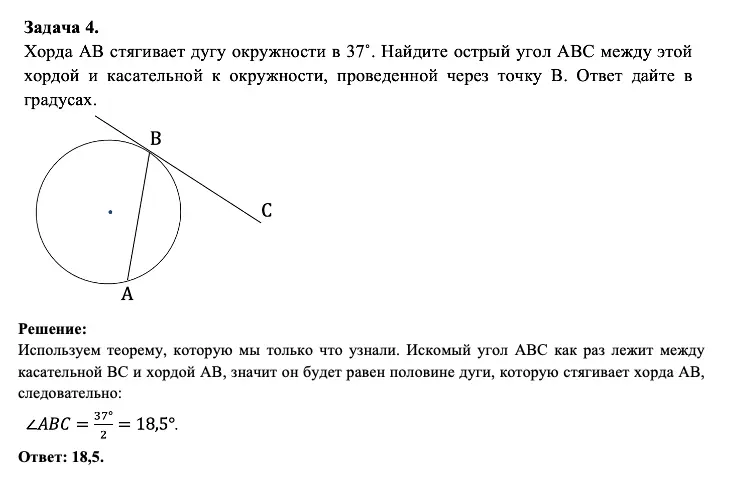
Однако хочу обратить ваше внимание, что если вы просто запомните формулировку, то многие задачи на окружность в ЕГЭ и ОГЭ покажутся вам супер-простыми и будут решаться в 1 действие. Давайте в этом убедимся:
Вот так просто и быстро в 1 действие мы справились с задачей. Правда здорово?!
Теорема № 2: теория и задания из ЕГЭ и ОГЭ
А теперь давайте посмотрим на одну из моих самых любимых теорем. А любимая она, потому что без неё некоторые задачи кажутся практически нерешаемыми, а с ней их можно решить быстро и просто! Звучит она так:
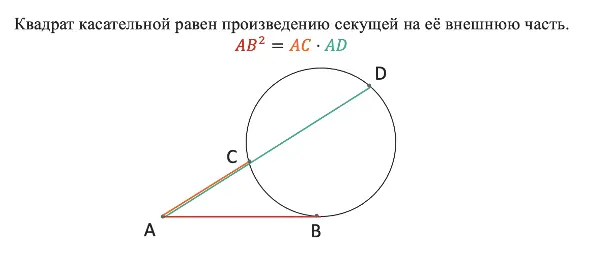
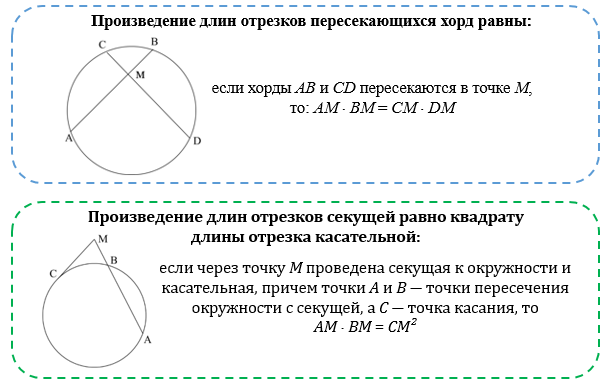
Квадрат касательной равен произведению секущей на её внешнюю часть.
Я советую запоминать именно словесную формулировку, так как чертежи и буквы на них могут быть разными, и есть риск всё перепутать.
Наглядно познакомиться с теоремой можно на рисунке ниже:
И конечно же давайте отработаем на практике!
Если бы мы не знали ту теорему, которую только что прошли, то было бы много версий, как можно решить задачу. Кто-то начал бы строить радиус к касательной и рассматривать треугольники, а кто-то просто не стал бы решать, однако у нас есть формула: давайте её используем!
Решение:
Теорема № 3: теория и задания из ЕГЭ и ОГЭ
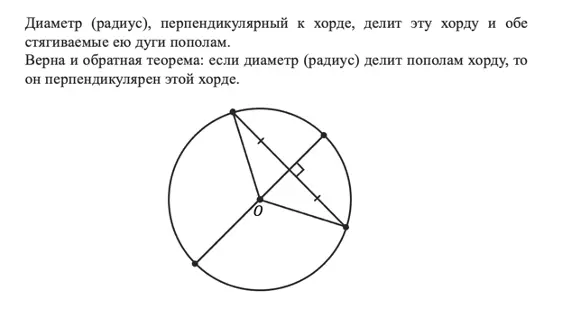
Если вы ещё не устали от теорем, то давайте познакомимся с ещё одной, которая связывает хорду с диаметром (радиусом).
Эта теорема интересна тем, что работает в обе стороны:
Конечно же я не могу оставить вас без тренировки, поэтому посмотрим на следующую задачу:
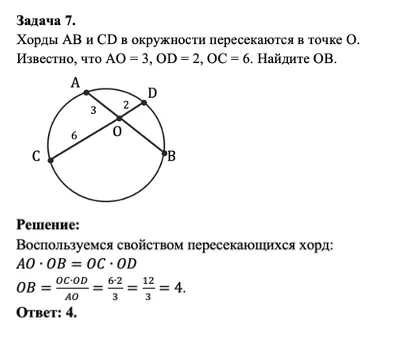
Теорема № 4: пересекающиеся хорды
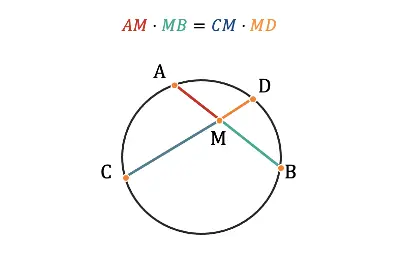
Последнее, с чем я вас познакомлю в контексте прямых и отрезков в окружности будет свойство пересекающихся хорд:
Произведения отрезков пересекающихся хорд равны.
Для наглядности отрезки выделены разными цветами, так вам будет проще запомнить свойство.
А теперь отработаем его на практике:
Длина окружности и площадь круга
Вот мы и подошли с вами к самому интересному, формулам длины окружности и площади круга, давайте их запишем:
Эти формулы очень походы, в них есть двойка, число Pi и радиус, однако можно заметить, что у формулы длины окружности двойка слева, а у площади круга справа в степени.
Так как же их не путать? Очень просто: запомните, что вторая степень (или квадрат) должна быть у площади, значит двойка слева будет у длины.
Давайте это закрепим:
Вот так просто и быстро мы закрепили сразу обе формулы.
Как находить площадь и длину дуги сектора круга: задачи
А теперь перейдём к самому интересному — нахождению площади и длины дуги сектора круга. Многие ученики думаю, что это сложно, но на самом деле это не так. Я предлагаю записать 2 коротких алгоритма, с помощью которых вы сможете легко найти площадь или длину дуги сектора.
И конечно же давайте закрепим эти алгоритмы на практике:
Теперь вы умеете решать задания на поиск площади сектора. Согласитесь, что с алгоритмом всё намного понятнее и проще?
Что нужно иметь в виду для ЕГЭ и ОГЭ
На самом деле это всё, что я хотела вам рассказать в данной статье. Давайте ещё раз повторим, что вы узнали.
- Сначала мы познакомились с понятием окружность, потом посмотрели, какие бывают углы в окружности.
- Затем увидели множество отрезков и прямых в окружности, записали их свойства, а также несколько теорем с ними.
- В завершение мы поговорили про длину окружности, площадь круга, а также поиск площади и длины дуги сектора.
Самое ценное, что всю теорию мы закрепили на реальных заданиях из ОГЭ и ЕГЭ. Конечно, это далеко не всё, что вам может встретиться. Если вы хотите хорошо разбираться в окружности и в других темах, которые встречаются на экзаменах, записывайтесь на наши курсы подготовки к ОГЭ и ЕГЭ. На них мы подробно изучаем всю теорию, решаем много заданий, запоминаем удобные лайфхаки и решаем пробные экзамены, чтобы не стрессовать на реальном. Присоединяйтесь!
16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с окружностями
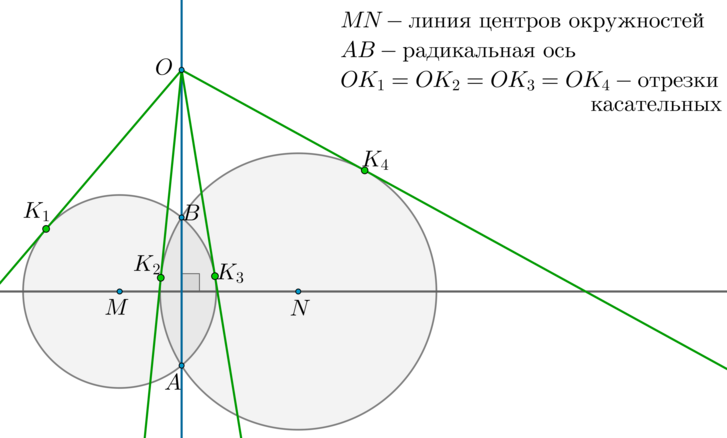
(blacktriangleright) Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Радикальная ось перпендикулярна линии центров окружностей. Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
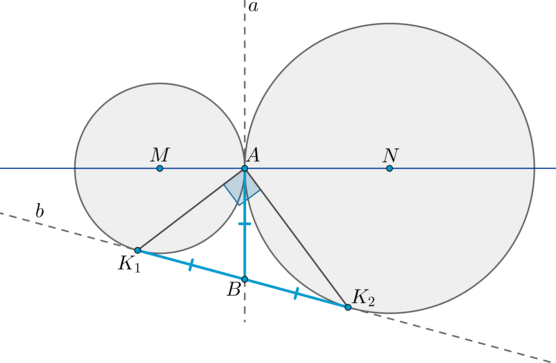
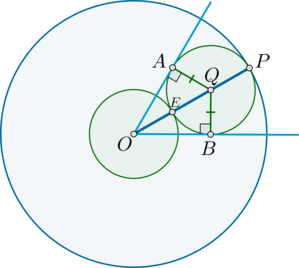
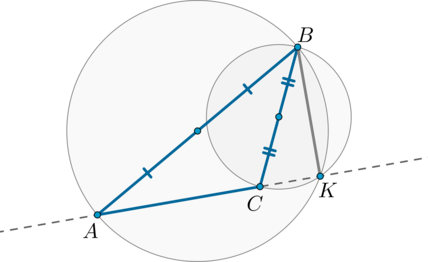
(blacktriangleright) Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A). Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B). Точки касания — точки (A, K_1, K_2). Тогда [{large{K_1B=AB=K_2B}}] [{large{angle K_1AK_2=90^circ}}]
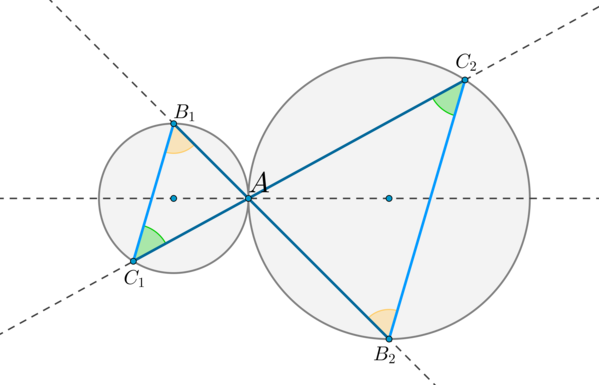
(blacktriangleright) Пусть две окружности касаются внешним образом в точке (A). Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [{large{triangle AB_1C_1 sim triangle
AB_2C_2}}] [{large{B_1C_1parallel B_2C_2}}]
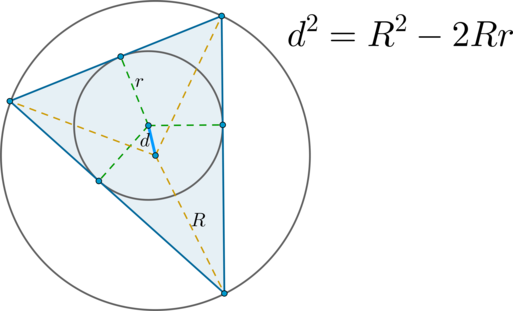
(blacktriangleright) Формула Эйлера: Пусть (R) — радиус описанной около треугольника окружности, (r) — радиус вписанной окружности. Тогда расстояние между центрами этих окружностей вычисляется по формуле:
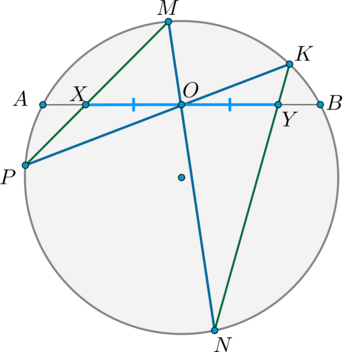
(blacktriangleright) Теорема о бабочке: Пусть через середину хорды (AB) — точку (O), проведены две хорды (MN) и (KP). Пусть (MPcap AB=X, KNcap AB=Y). Тогда [{large{OX=OY}}]
Задание
1
#2378
Уровень задания: Легче ЕГЭ
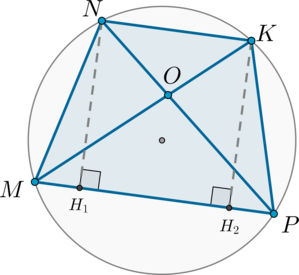
В окружность вписан четырехугольник (MNKP), причем площади треугольников (MNP) и (MKP) равны.
Докажите, что треугольник (NOK) – равнобедренный, где (O) – точка пересечения отрезков (MK) и (NP).
Т.к. (S_{triangle MNP}=S_{triangle MKP}) и эти треугольники имеют общее основание (MP), то [frac12cdot MPcdot NH_1=frac12cdot MPcdot KH_2 quad Rightarrow quad
NH_1=KH_2]
Таким образом, точки (N) и (K) находятся на одинаковом расстоянии от прямой (MP), следовательно, (NKparallel MP). Таким образом, (MNKP) – трапеция, вписанная в окружность. Т.к. параллельные прямые отсекают от окружности равные дуги, то меньшие полуокружности дуги (buildrelsmileover{MN}=buildrelsmileover{KP}). Т.к. равные дуги стягиваются равными хордами, то отрезки (MN) и (KP) равны. Следовательно, трапеция (MNKP) является равнобедренной.
В равнобедренной трапеции (triangle MOP) и (triangle NOK) являются равнобедренными, чтд.
Действительно, вписанные углы (angle NKM) и (angle KNP) равны, т.к. опираются на равные дуги, следовательно, (triangle NOK) – равнобедренный.
Ответ:
Доказательство
Задание
2
#2379
Уровень задания: Легче ЕГЭ
Две хорды окружности взаимно перпендикулярны. Найдите расстояние от точки их пересечения до центра окружности, если расстояние между их серединами равно (2).
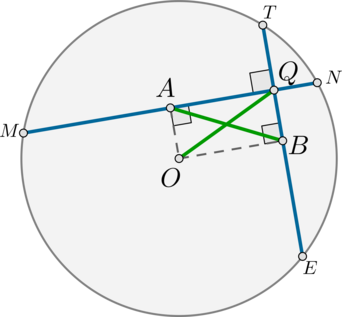
Пусть (Q) – точка пересечения взаимно перпендикулярных хорд (MN) и (TE), (O) – центр окружности. Тогда необходимо найти (OQ).
Пусть (A) и (B) – середины этих хорд, то есть (AB=2). Тогда (OA) и (OB) – перпендикуляры к этим хордам.
Действительно, (triangle MON) – равнобедренный ((OM=ON) – радиусы), поэтому медиана (OA) в нем является и высотой. Аналогично доказывается, что (OBperp TE).
Таким образом, в четырехугольнике (OAQB) три угла – прямые ((angle
A=angle Q=angle B=90^circ)), следовательно, этот четырехугольник по признаку является прямоугольником. Т.к. в прямоугольнике диагонали равны, то (AB=OQ=2).
Ответ: 2
Задание
3
#2380
Уровень задания: Легче ЕГЭ
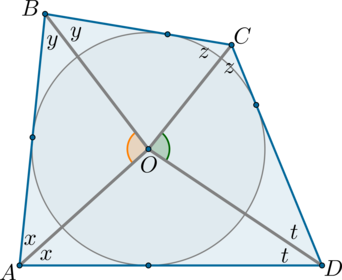
Четырехугольник (ABCD) описан около окружности с центром (O). Докажите, что (angle AOB+angle COD=180^circ).
Если окружность вписана в многоугольник, то ее центр лежит на пересечении биссектрис углов этого многоугольника. Действительно, окружность вписана в угол (A), следовательно, центр окружности лежит на биссектрисе этого угла. Аналогично можно сказать и про остальные углы.
Введем обозначения: (angle A=2x, angle B=2y, angle C=2z, angle
D=2t). Сумма углов четырехугольника равна (360^circ), следовательно, [2x+2y+2z+2t=360^circ quad Rightarrow quad
x+y+z+t=180^circ.] Из (triangle AOB): (angle AOB=180^circ-x-y);
из (triangle
COD): (angle COD=180^circ-z-t).
Таким образом, [angle AOB+angle COD=180^circ-x-y+180^circ-z-t=
360^circ-(x+y+z+t)=360^circ-180^circ=180^circ.]
Ответ:
Доказательство
Задание
4
#2381
Уровень задания: Легче ЕГЭ
Даны две концентрические окружности радиусов (1) и (3) с общим центром (O). Третья окружность касается их обеих. Найдите угол между касательными к третьей окружности, проведенными из точки (O).
Если две окружности касаются, то их центры и точка касания лежат на одной прямой. Таким образом, для первой и третьей окружности точки (O), (Q) и (P) лежат на одной прямой, для второй и третьей — точки (O), (Q) и (E) лежат на одной прямой. Таким образом, все эти четыре точки лежат на одной прямой.
Значит, (OP=3), (OE=1), следовательно, (EP=3-1=2) — диаметр третьей окружности, следовательно, ее радиус (EQ=1).
Пусть касательные к третьей окружности касаются ее в точках (A) и (B). Тогда радиусы (QA) и (QB) перпендикулярны к касательным (OA) и (OB) соответственно. Таким образом, (triangle AOQ=triangle BOQ) по катету и гипотенузе, следовательно, (angle AOQ=angle BOQ).
Найдем (angle AOQ). Заметим, что в (triangle AOQ) катет (AQ=1), гипотенуза (OQ=2). Следовательно, (angle AOQ=30^circ) как угол, лежащий против катета, равного половине гипотенузы.
А значит весь (angle AOB=30^circ+30^circ=60^circ).
Ответ:
(60^circ)
Задание
5
#2382
Уровень задания: Легче ЕГЭ
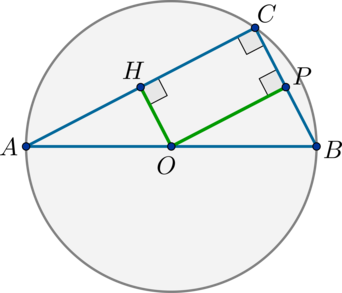
Через концы диаметра окружности проведены две хорды, пересекающиеся на окружности, сумма длин которых равна (14). Найдите сумму длин расстояний от центра окружности до этих хорд.
Пусть (AB) – диаметр, (O) – центр окружности, (AC) и (BC) – хорды, (AC+BC=14).
Т.к. (angle ACB) – вписанный и опирающийся на диаметр, то (angle
ACB=90^circ). Проведем (OHperp AC, OPperp BC). В четырехугольнике (OHCP) три угла прямые, следовательно, по признаку он является прямоугольником. Таким образом, (OH=CP), (OP=HC).
Заметим, что т.к. радиус, перпендикулярный к хорде, делит ее пополам, то (AH=HC), (CP=PB). Таким образом, [OH+OP=CP+HC=frac12BC+frac12AC=dfrac12left(BC+ACright)=
frac12cdot 14=7.]
Ответ: 7
Задание
6
#2383
Уровень задания: Легче ЕГЭ
Докажите, что отличная от (B) точка пересечения окружностей, построенных на сторонах (BA) и (BC) треугольника (ABC) как на диаметрах, лежит на прямой (AC).
Пусть (K) – вторая точка пересечения окружностей.
(angle AKB=90^circ) как вписанный угол, опирающийся на диаметр (AB). Аналогично (angle CKB=90^circ) как вписанный угол, опирающийся на диаметр (BC). Таким образом, через точку (K) к прямой (BK) проведены две прямые (AK) и (CK), перпендикулярные (BK). Следовательно, эти прямые либо совпадают, либо параллельны. Но т.к. они имеют общую точку (K), то они не могут быть параллельны, то есть они совпадают. Значит, точки (A, C) и (K) лежат на одной прямой, чтд.
Ответ:
Доказательство
Задание
7
#2385
Уровень задания: Легче ЕГЭ
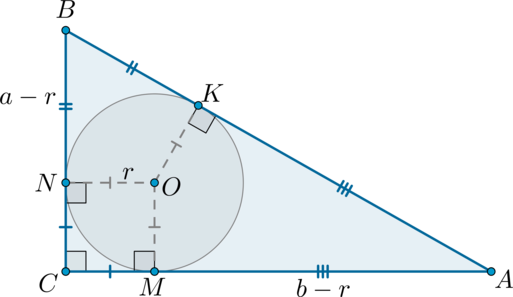
Катеты прямоугольного треугольника равны (a) и (b), а гипотенуза равна (c). Докажите, что радиус вписанной окружности равен [dfrac{a+b-c}2]
1 способ
Рассмотрим прямоугольный (triangle ABC), пусть (BC=a, AC=b, AB=c). Проведем радиусы (ON, OK, OM) в точки касания. Обозначим также радиус (ON=r).
Рассмотрим четырехугольник (CNOM). У него 3 угла прямые, следовательно, по признаку он является прямоугольником. Также соседние стороны ((ON=OM=r)) у него равны. Следовательно, все его стороны равны (r) (то есть это квадрат). Таким образом, (CN=CM=r).
Значит, (BN=a-r), (AM=b-r). Т.к. отрезки касательных, проведенные из одной точки к окружности, равны, то (BK=BN=a-r), (AK=AM=b-r).
Таким образом, гипотенуза (AB=a-r+b-r=a+b-2r). Но с другой стороны гипотенуза равна (c). Таким образом, [a+b-2r=c quad Rightarrow
quad r=dfrac{a+b-c}2]
2 способ
Как известно, площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. Т.к. (S=frac12ab), (p=frac12left(a+b+cright)), то
[frac12ab=frac12left(a+b+cright)cdot r quad Rightarrow quad
r=dfrac{ab}{a+b+c}]
По теореме Пифагора (a^2+b^2=c^2), следовательно, (a^2+b^2-c^2=0). Сделаем преобразования:
(r=dfrac{ab}{a+b+c}=dfrac{ab(a+b-c)}{(a+b+c)(a+b-c)}=
dfrac{ab(a+b-c)}{(a+b)^2-c^2}=)
(=dfrac{ab(a+b+c)}{a^2+2ab+b^2-c^2}=
dfrac{ab(a+b-c)}{2ab}=dfrac{a+b-c}2.)
Ответ:
Доказательство
Планиметрические задачи с окружностями в ЕГЭ по математике традиционно встречаются из года в год. Находить правильное решение в подобных заданиях нужно уметь каждому ученику вне зависимости от того, базовый или профильный уровень экзамена ему предстоит сдавать. Освоив задачи по теме «Геометрия окружности», учащиеся смогут успешно выполнить ЕГЭ по математике и рассчитывать на получение достойных баллов по итогам прохождения аттестационного испытания.
Готовьтесь к экзамену вместе с образовательным порталом «Школково»
Приступая к решению задач с окружностями в ЕГЭ, рекомендуем освежить в памяти параметры и свойства вписанных и описанных фигур. Кроме того, в некоторых заданиях понадобится применить базовые теоремы.
Всю необходимую теоретическую информацию, которая поможет вам в решении задач на окружность в ЕГЭ по математике, вы найдете на образовательном портале «Школково». Наши специалисты подготовили материал и представили его в максимально доступной форме. Ознакомиться с ним можно в разделе «Теоретическая справка».
Закрепить полученные знания и отточить навык выполнения задач на окружности при подготовке к ЕГЭ вам помогут соответствующие упражнения. Подборка простых и более сложных заданий представлена в блоке «Каталог». Раздел регулярно обновляется и дополняется.
Попрактиковаться в решении задач по планиметрии с окружностями, подобным тем, которые встречаются в ЕГЭ математике, можно в режиме онлайн, находясь в Москве или любом другом городе России.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Планиметрия – профильный ЕГЭ по математике (оглавление)
Планиметрия плохо дается многим ученикам. На ЕГЭ эта задача №16 – одна из самых сложных задач и многие даже не пытаются за нее браться.
Весь секрет в том, что понимание планиметрии приходит не постепенно, а сразу. Вчера не получалось, а сегодня уже все понятно. Большинству просто не хватает терпения дойти до этого момента.
Надеемся, что ты не такой и не бросишь занятия на полпути. И вот тебе в помощь все, что нужно знать по планиметрии + несколько вебинаров для отработки навыков!
Планиметрия – часть 1. ЕГЭ №3 (бывшая №6)
Если вы плохо знаете планиметрию, начинайте с этой части и смотрите вебинар за вебинаром, ставьте на паузу и решайте задачи вместе с ведущим вебинаров Алексеем Шевчуком.
Помните, планиметрия требует нарешенности. Чтобы научиться решать любую задачу по планиметрии, нужно решать много задач.
Начните с самого начала.
Планиметрия – прямоугольный треугольник
Итак, прямоугольный треугольник, его свойства, площадь и углы прямоугольного треугольника, теорема Пифагора, тригонометрический функции острых углов, медиана и высота.
Планиметрия – равнобедренный треугольник и произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и “обычные” треугольники.
Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках – очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие ее свойства. В какие фигуры можно, а в какие нельзя вписать окружность.
Научимся решать задачи на вписанную окружность – очень важный навык в понимании планиметрии.
Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Что приблизит нас к умению решать любые задачи по планиметрии.
Теорема косинусов и синусов
Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов.
Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Планиметрия – часть 2. ЕГЭ №16
Эта часть планиметрии – для продвинутых, для тех, кто уже хорошо усвоил планиметрию из первой части.
Принцип тот же – смотрите вебинар за вебинаром и, самое главное, ставьте на паузу и решайте задачи.
Планиметрия. Подобие треугольников. Задачи на доказательство. ЕГЭ №16
Подобие треугольников. Это одна из самых сложных задачи планиметрии в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности – это очень классный метод, используемый в планиметрии но, к сожалению, он не всегда очевиден. Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы – те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод – но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
Теорема Менелая и Чевы. “Секретный” метод решения самой сложной задачи ЕГЭ по математике
Задача №16. Планиметрия. Одна из самых сложных задач на ЕГЭ. Редко кто (менее 1% учеников!) набирает полные баллы по ней и поэтому грех не воспользоваться шорткатами и лайфхаками, если они есть.
Теорема Менелая и Чевы – один из таких шорткатов. Эти теоремы не входят в стандартную школьную программу, но они невероятно мощный инструмент! Они могут очень-очень упростить решение и сами по себе они красивые и легко запоминаются.
Итак, смотрите видео, учите теорему Менелая и Чевы, используйте ее на ЕГЭ.
Теорема Менелая и Чевы — её уже запретили, наконец, или нет?
Каждый год начинают ходить слухи, что теоремами Менелая и Чевы В ЭТОМ ГОДУ НЕЛЬЗЯ будет пользоваться на ЕГЭ. Правда ли это? Чтобы понять это, достаточно заглянуть в обычный…
Впрочем, смотрите это видео и узнаете, как понять, какими теоремами можно, а какими нельзя пользоваться. А также, на этом вебе мы разберём, что это за теоремы такие, и как ими пользоваться.
Вы узнаете, насколько они крутые и мощные, и насколько экономят нам время в некоторых задачах.
Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом. Никуда не деться от окружностей – остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше – разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче). Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники.
Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Разбор задачи №16 (б) из реального варианта ЕГЭ 2021 по профильной математике
Продолжение предыдущего видео. Разбор части (б):
Теперь слово вам…
Как вам наш гид по планиметрии? Что нового вы узнали? Что еще хотите узнать?
Как вам теорема Менелая и Чевы? Один из моих знакомых сказал: “В школе ее от нас утаивали!”. Шутка, в которой есть доля… шутки.
Готовьтесь к планиметрии и забирайте свои 3 балла на ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
ЕГЭ Профиль №16. Окружности
Скачать ЕГЭ Профиль №16. Окружности в формате pdf.
Окружность ― множество всех точек плоскости, равноудаленных от данной точки на плоскости (то есть замкнутая линия).
Круг ― часть плоскости, ограниченная окружностью (то есть площадь).
Элементы окружности:
Центр окружности ― точка O.
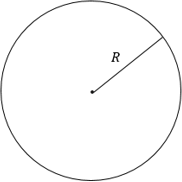
Радиус окружности (r) ― отрезок, соединяющий точку окружности с центром. Все радиусы одной окружности равны.
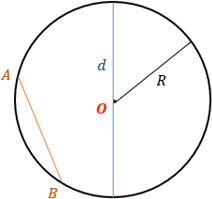
Диаметр (d) ― хорда, проходящая через центр окружности. Диаметр равен двум радиусам.
Хорда (AB) ― отрезок, соединяющий любые две точки окружности.
Площадь круга и длина окружности:
Дуга и сектор:
|
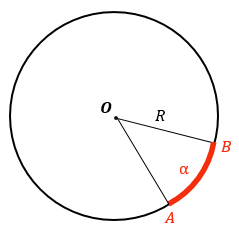
Дуга окружности — участок окружности между двумя точками на ней. |
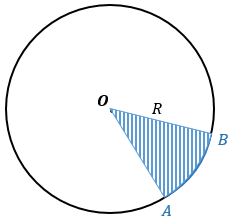
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности. |
|
|
|
|
Длина дуги окружности: |
Площадь сектора: |
|
Чтобы найти длину дуги АВ, нужно понять, какую часть она занимает от всей окружности. Это можно сделать через градусную меру дуги (угол между отрезками ОА и ОB). Если окружности — R, а градусная мера дуги АВ — α, то длина всей окружности = 2ℼR, а дуга занимает от всей окружности α/360°. То есть: $l_{AB} = 2pi R cdot displaystylefrac{alpha}{360^{circ}} = frac{pialpha R}{180^{circ}}$ |
Чтобы найти площадь сектора ОАВ, нужно понять, какую часть он занимает от всего круга, что можно сделать через градусную меру дуги АВ. Если окружности — R, а градусная мера дуги АВ — α, то площадь всего круга = πR2, а дуга занимает от всей окружности α/360°. То есть: $S_{OAB} = pi R^2 cdot displaystylefrac{alpha}{360^{circ}} = frac{pialpha R^2}{360^{circ}}$ |
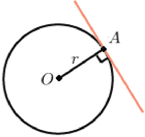
Касательная к окружности:
Касательная ― прямая, имеющая с окружностью ровно одну общую точку.
СВОЙСТВА КАСАТЕЛЬНОЙ:
|
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. |
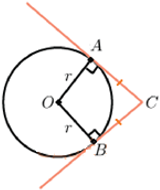
Отрезки касательных, проведенных из одной точки, равны до точек касания. |
|
|
|
Центральные и вписанные углы:
|
Вписанный угол (ACB) ― угол, вершина которого лежит на окружности, а стороны являются ее хордами |
|
Центральный угол (AOB) ― угол, образованный двумя радиусами: |
|
1. Измеряется половиной дуги, на которую он опирается; 2. Вписанные углы, опирающиеся на одну и ту же дугу, равны; 3. Вписанный угол, опирающийся на диаметр — прямой. |
1. Измеряется дугой, на которую опирается; 2. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу. |
Хорды и секущие: