Планиметрия прямоугольный треугольник егэ профиль - Exhelper.top

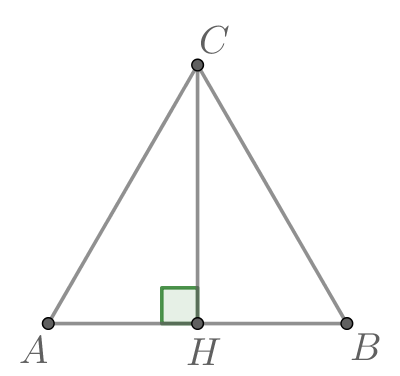
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

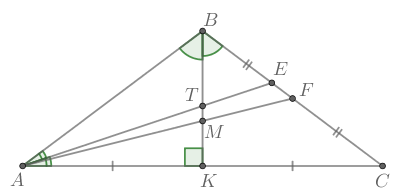
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

$sin⁡B={AC}/{AB};$

$cos⁡B={BC}/{AB};$

$tgB={AC}/{BC};$

$ctgB={BC}/{AC}.$

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$sin BOA=sin BOC;$

$cos BOA=-cos BOC;$

$tg BOA=-tg BOC;$

$ctg BOA=-ctg BOC.$

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Площадь прямоугольного треугольника равна половине произведения его катетов

$S={AC∙BC}/{2}$

Пример:

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.

Решение:

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

$cosABD=-cosABC$

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

$cosABC={ВС}/{АВ}$

Катет $ВС$ мы можем найти по теореме Пифагора:

$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$

Подставим найденное значение в формулу косинуса

$cos ABC = {3}/{10}=0,3$

$cos ABD = — 0,3$

Ответ: $-0,3$

Пример:

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A={4}/{5}, AC=9$. Найдите $АВ$.

Решение:

Распишем синус угла $А$ по определению:

$sin⁡A={ВС}/{АВ}={4}/{5}$

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

$АС^2+ВС^2=АВ^2$

$9^2+(4х)^2=(5х)^2$

$81+16х^2=25х^2$

$81=25х^2-16х^2$

$81=9х^2$

$9=х^2$

$х=3$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

Ответ: $15$

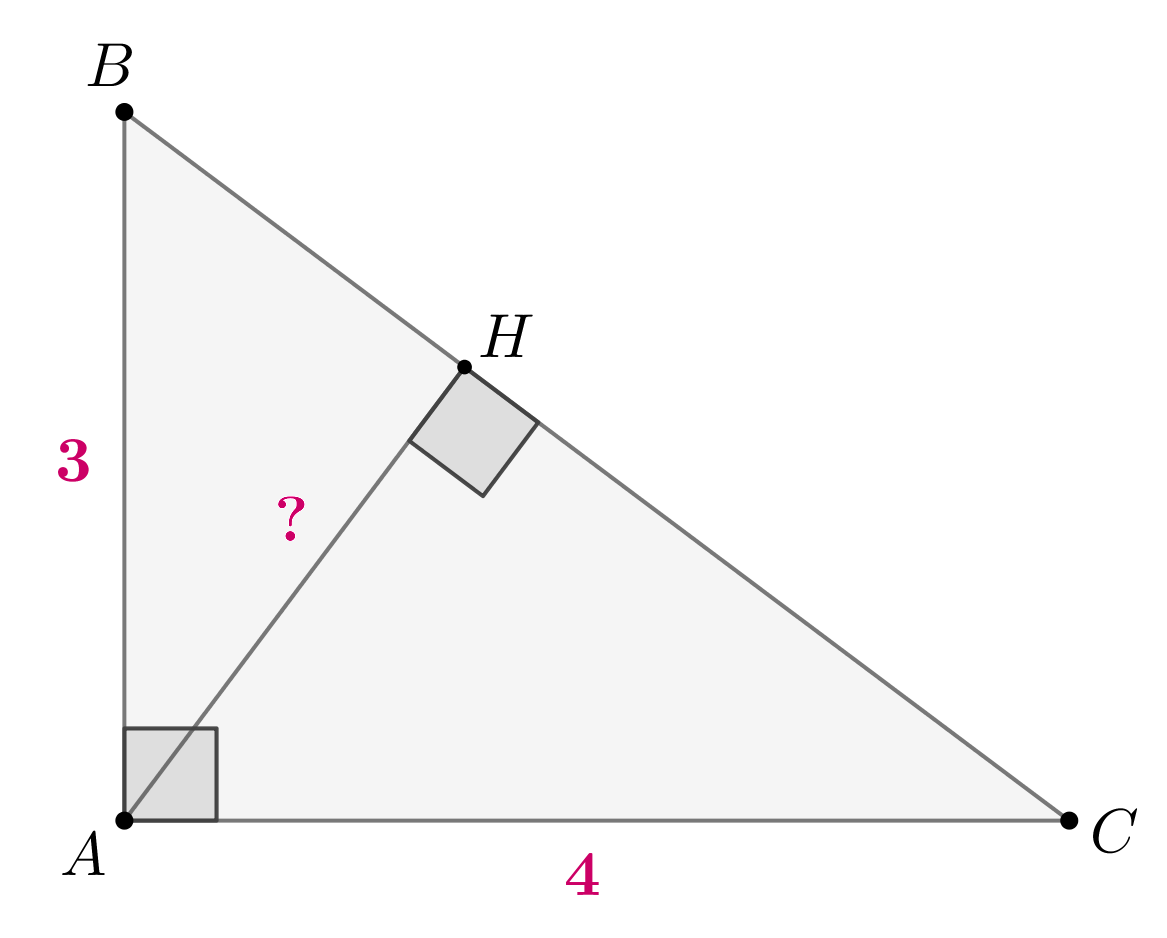
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

$CD^2=DB∙AD$

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

$CB^2=AB∙DB$

$AC^2=AB∙AD$

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

$AC∙CB=AB∙CD$

Источник

Каталог заданий.
Решение прямоугольного треугольника

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 1 № 27238

В треугольнике ABC угол C равен 90°, Найдите AB.

Аналоги к заданию № 27238: 4583 19737 635953 4584 4585 4586 4587 4588 4589 4590 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 1 № 27239

В треугольнике ABC угол C равен 90°, AC = 2, Найдите  BC.

Аналоги к заданию № 27239: 4651 4787 4653 4655 4657 4659 4661 4663 4665 Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 1 № 27240

В треугольнике ABC угол C равен 90°, АС  =  4, Найдите АВ.

Аналоги к заданию № 27240: 26095 29575 29579 500952 29538 29539 29540 29541 29542 29543 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 1 № 27242

В треугольнике ABC угол C равен 90°, АС  =  4. Найдите АВ.

Аналоги к заданию № 27242: 29651 29747 530665 530685 29650 29652 29653 29654 29655 29656 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 1 № 27243

В треугольнике ABC угол C равен 90°, АС  =  8, Найдите BC.

Аналоги к заданию № 27243: 29749 29791 29750 29751 29752 29753 29754 29755 29756 29757 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №1. Прямоугольный треугольник

ЕГЭ Профиль №1. Прямоугольный треугольникadmin2022-08-28T09:25:51+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №1. Прямоугольный треугольник

Задача 1. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (sin A = frac{7}{{25}}). Найдите АС.

Ответ

ОТВЕТ: 4,8.

Задача 2. В треугольнике ABC угол C равен ({90^ circ }), (AB =

, (sin A = 0,5). Найдите ВС.

Ответ

ОТВЕТ: 4.

Задача 3. В треугольнике ABC угол C равен ({90^ circ }), (AB =

, (cos A = 0,5). Найдите AС.

Ответ

ОТВЕТ: 4.

Задача 4. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (cos A = frac{7}{{25}}). Найдите ВС.

Ответ

ОТВЕТ: 4,8.

Задача 5. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{33}}{{4sqrt {33} }}). Найдите AС.

Ответ

ОТВЕТ: 4.

Задача 6. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите BС.

Ответ

ОТВЕТ: 4.

Задача 7. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4,8), (sin A = frac{7}{{25}}). Найдите АB.

Ответ

ОТВЕТ: 5.

Задача 8. В треугольнике ABC угол C равен ({90^ circ }), (AC = 2), (sin A = frac{{sqrt {17} }}{{17}}). Найдите BC.

Ответ

ОТВЕТ: 0,5.

Задача 9. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (cos A = 0,5). Найдите АB.

Ответ

ОТВЕТ: 8.

Задача 10. В треугольнике ABC угол C равен ({90^ circ }), (AC = 0,5), (cos A = frac{{sqrt {17} }}{{17}}). Найдите BC.

Ответ

ОТВЕТ: 2.

Задача 11. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (tgA = frac{{33}}{{4sqrt {33} }}). Найдите АB.

Ответ

ОТВЕТ: 7.

Задача 12. В треугольнике ABC угол C равен ({90^ circ }), (AC =

, ({text{tg}},A = 0,5). Найдите BC.

Ответ

ОТВЕТ: 4.

Задача 13. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), (sin A = 0,5). Найдите АB.

Ответ

ОТВЕТ: 8.

Задача 14. В треугольнике ABC угол C равен ({90^ circ }), (BC = 0,5), (sin A = frac{{sqrt {17} }}{{17}}). Найдите AC.

Ответ

ОТВЕТ: 2.

Задача 15. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4,8), (cos A = frac{7}{{25}}). Найдите AB.

Ответ

ОТВЕТ: 5.

Задача 16. В треугольнике ABC угол C равен ({90^ circ }), (BC = 2), (cos A = frac{{sqrt {17} }}{{17}}). Найдите AC.

Ответ

ОТВЕТ: 0,5.

Задача 17. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите AB.

Ответ

ОТВЕТ: 7.

Задача 18. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = 0,5). Найдите AC.

Ответ

ОТВЕТ: 8.

Задача 19. В треугольнике ABC угол C равен ({90^ circ }), (AC = 24,;;BC = 7.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,28.

Задача 20. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;;BC = 24.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,28.

Задача 21. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;;BC = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.

Задача 22. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;BC = 4.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,5.

Задача 23. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;BC = 20.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,6.

Задача 24. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;BC = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.

Задача 25. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;AC = 20.) Найдите (sinA.)

Ответ

ОТВЕТ: 0,6.

Задача 26. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;AC = 4.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,5.

Задача 27. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;AC = 8.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.

Задача 28. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 15.

Задача 29. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 12.

Задача 30. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;sin A = 0,25.) Найдите высоту СH.

Ответ

ОТВЕТ: 3,75.

Задача 31. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 12.

Задача 32. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 15.

Задача 33. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;cos A = 0,25.) Найдите высоту СH.

Ответ

ОТВЕТ: 3,75.

Задача 34. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите AH.

Ответ

ОТВЕТ: 12,5.

Задача 35. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 13,;;{text{tg}},A = 5). Найдите BH.

Ответ

ОТВЕТ: 12,5.

Задача 36. В треугольнике ABC угол C равен ({90^ circ }), (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите высоту CH.

Ответ

ОТВЕТ: 2,5.

Задача 37. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 3,;;sin ,A = frac{1}{6}). Найдите AH.

Ответ

ОТВЕТ: 17,5.

Задача 38. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;sin ,A = 0,5.) Найдите BH.

Ответ

ОТВЕТ: 4.

Задача 39. В треугольнике ABC угол C равен ({90^ circ }), (BC = 5,;;sin ,A = frac{7}{{25}}.) Найдите высоту CH.

Ответ

ОТВЕТ: 4,8.

Задача 40. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 3,;;cos ,A = frac{{sqrt {35} }}{6}.) Найдите AH.

Ответ

ОТВЕТ: 17,5.

Задача 41. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 5,;;cos ,A = frac{7}{{25}}.) Найдите BH.

Ответ

ОТВЕТ: 4,8.

Задача 42. В треугольнике ABC угол C равен ({90^ circ }), (BC = 8,;;cos ,A = 0,5.) Найдите высоту CH.

Ответ

ОТВЕТ: 4.

Задача 43. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите BH.

Ответ

ОТВЕТ: 4.

Задача 44. В треугольнике ABC угол C равен ({90^ circ }), (BC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.

Задача 45. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;sin ,A = frac{{sqrt {35} }}{6}.) Найдите BH.

Ответ

ОТВЕТ: 17,5.

Задача 46. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;sin A = 0,5.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.

Задача 47. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 8,;;cos ,A = 0,5.) Найдите AH.

Ответ

ОТВЕТ: 4.

Задача 48. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;cos ,A = frac{1}{6}.) Найдите BH.

Ответ

ОТВЕТ: 17,5.

Задача 49. В треугольнике ABC угол C равен ({90^ circ }), (AC = 5,;cos A = frac{7}{{25}}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4,8.

Задача 50. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите AH.

Ответ

ОТВЕТ: 4.

Задача 51. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.

Задача 52. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;BH = 4.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,5.

Задача 53. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 25,;;BH = 20.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,6.

Задача 54. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 4sqrt 5 ,;;BH = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.

Задача 55. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 20, (BC = 25.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,6.

Задача 56. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = 8.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,5.

Задача 57. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = sqrt {17} .) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,25.

Задача 58. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 24, (BH = 7.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,28.

Задача 59. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 7, (BH = 24.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,28.

Задача 60. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 8, (BH = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.

Задача 61. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AH = 27,;;{text{tg}},A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 12.

Задача 62. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BH = 12,;;{text{tg}},A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 27.

Задача 63. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BH = 12,;;sin A = frac{2}{3}.) Найдите AB.

Ответ

ОТВЕТ: 27.

Задача 64. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AH = 12,;;cos A = frac{2}{3}.) Найдите AB.

Ответ

ОТВЕТ: 27.

Задача 65. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

Ответ

ОТВЕТ: 24.

Задача 66. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Ответ

ОТВЕТ: 6.

Задача 67. В треугольнике ABC угол C равен ({90^ circ }), угол В равен ({58^ circ }), CD медиана. Найдите угол ACD. Ответ дайте в градусах.

Ответ

ОТВЕТ: 32.

Задача 68. Острый угол прямоугольного треугольника равен ({32^ circ }). Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Ответ

ОТВЕТ: 61.

Задача 69. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

Ответ

ОТВЕТ: 45.

Задача 70. Один из углов прямоугольного треугольника равен ({29^ circ }). Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ

ОТВЕТ: 16.

Задача 71. В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.

Задача 72. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Задача 73. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Задача 74. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Задача 75. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

Задача 76. В треугольнике ABC угол C равен 90°, угол A равен 30°, (AB = 2sqrt 3 ). Найдите высоту CH.

Задача 77. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, угол A равен 30°, (AB = 2). Найдите AH.

Задача 78. В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, (AB = 4). Найдите BH.

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

Прямоугольный треугольник и теорема Пифагора

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

1.01Треугольник: внутренние и внешние углы

1.02Треугольник: высота, биссектриса, медиана

1.03Треугольник: задачи на подобие

1.04Прямоугольный треугольник и теорема Пифагора

1.05Треугольник: площадь и периметр

1.06Параллелограмм и его свойства

1.07Параллелограмм и свойство его биссектрисы

1.08Прямоугольник и его свойства

1.09Ромб и его свойства

1.10Квадрат и его свойства

1.11Трапеция и ее свойства

1.12Равнобедренная трапеция

1.13Окружность: центральный и вписанный углы

1.14Окружность: углы, образованные хордами, секущими, касательными

1.15Окружность: отрезки хорд, секущих, касательных

1.16Окружность: описанная около многоугольника

1.17Окружность: вписанная в многоугольник или угол

1.18Длина окружности или дуги и площадь круга или сектора

1.19Правильный шестиугольник и его свойства

1.20Площадь многоугольника: различные формулы

1.21Внешние углы многоугольника и тригонометрия

1.22Решение треугольника и других фигур с помощью тригонометрии

1.23Теорема синусов и теорема косинусов

1.24Координатная плоскость

1.25Векторы: сложение, вычитание, координаты

1.26Задачи на клетчатой бумаге

Решаем задачи

Найдите высоту прямоугольного треугольника с катетами и проведенную к
гипотенузе.

Показать ответ и решение

Пусть дан △ABC с и проведена

Тогда

AH-⋅BC- = S△ABC = AB-⋅AC- ⇔
2 2
AB-⋅AC-
AH = BC

По теореме Пифагора BC =5. Следовательно,

AH = 3⋅4= 12 = 2,4
5 5

Тем самым мы вывели формулу: высота прямоугольного треугольника с
катетами и проведенная к гипотенузе равна

ab
h = c

Показать ответ и решение

Рассмотрим прямоугольный треугольник AHB.

Так как и то

180∘-− 120∘ ∘
∠A = ∠B = 2 =30

Катет, лежащий против угла ∘
30 , равен половине гипотенузы, следовательно, в прямоугольном треугольнике
AHB

√-
HA = 1AB = 3
2

Рассмотрим прямоугольный треугольник ACH. Так как то

Так как в прямоугольном треугольнике сумма острых углов равна 90∘, то

Следовательно, Тогда по теореме Пифагора

2 2 2 2 AC2
AC = HC + HA ⇒ AC = --4-+ 3 ⇒ AC =2

В треугольнике ABC Найдите высоту AH.

Показать ответ и решение

Рассмотрим прямоугольный треугольник ACH. Катет, лежащий против угла 30∘, равен половине гипотенузы,
следовательно,

Заметим, что условие BC = 4 в данной задаче является лишним.

Показать ответ и решение

Так как катет, лежащий против угла 30∘, равен половине гипотенузы, то

BC = 1AB = 2
2

По свойству прямоугольного треугольника следовательно, в треугольнике BCH :

1
HB = 2BC = 1

Показать ответ и решение

Так как катет, лежащий против угла 30∘, равен половине гипотенузы, то

BC = 1AB = 1
2

Тогда по теореме Пифагора в треугольнике ABC :

В прямоугольном треугольнике AHC :

1 √3
HC = 2AC = 2--

Тогда по теореме Пифагора

∘ -----
∘ ---2-----2 3
AH = AC − HC = 3− 4 = 1,5

Показать ответ и решение

По теореме Пифагора в треугольнике из BCH :

∘---------- √ ------
BH = BC2 − HC2 = 17− 16 = 1

Следовательно,

tg∠BCH = BH--= 0,25
CH

По свойству прямоугольного треугольника следовательно,

Найдите основание равнобедренного треугольника, если угол при основании равен 30∘, а взятая внутри треугольника точка
находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 2√3- от основания.

В равнобедренном треугольнике ABC, в котором найти расстояние между точкой пересечения медиан и
точкой пересечения биссектрис.

Показать ответ и решение

Т.к. треугольник ABC равнобедренный, то — медиана, высота и биссектриса. Значит, 1
AK = 2 AC = 24.

По теореме Пифагора в треугольнике ABK :

∘ ---------- √--------
BK = AB2 − AK2 = 900− 576= 18

Пусть точка — точка пересечения медиан и BK. По свойству медиан точка делит медианы в отношении 2:1,
считая от вершины, тогда

Пусть точка — точка пересечения биссектрис и BK. В треугольнике ABK по свойству биссектрис делит отрезок
на части, пропорциональные прилежащим сторонам, то есть:

Найдем TM :

В прямоугольном треугольнике CAT из вершины прямого угла опущена высота CH. Известно, что
Найдите

Показать ответ и решение

По свойству прямоугольного треугольника и высоты, опущенной из его прямого угла, Значит,
Поэтому будем искать

В треугольнике HCT :

TH
sin ∠HCT = TC-

По теореме Пифагора из этого же треугольника мы можем найти TC :

∘ ---------- ∘ -------
T C = TH2 + CH2 = 122+ 52 = 13

Следовательно,

Показать ответ и решение

Проведем

Так как треугольник ABC равнобедренный, то также является медианой и биссектрисой, следовательно, и
∘
∠ACK = 120- =60∘.
2

Так как сумма острых углов прямоугольного треугольника равна 90∘, то

∘ ∘ ∘
∠CAK = 90 − 60 =30

Катет, лежащий против угла 30∘, равен половине гипотенузы, то есть Тогда по теореме
Пифагора:

∘ ---2-----2
AK = AC − CK = 3 ⇒ AB = 2AK = 6

В треугольнике ABC Найдите высоту AH.

Показать ответ и решение

Рассмотрим прямоугольный треугольник ACH. Так как то

∘ ∘ ∘
∠ACH = 180 − 120 = 60

Так как сумма острых углов прямоугольного треугольника равна 90∘, то

∘ ∘ ∘
∠HAC = 90 − 60 = 30

Катет, лежащий против угла 30∘, равен половине гипотенузы, следовательно, Тогда по теореме
Пифагора

∘ ---2-----2
AH = AC − HC = 3

Показать ответ и решение

Рассмотрим прямоугольный треугольник ACH. Катет, лежащий против угла 30∘, равен половине гипотенузы, следовательно,
откуда

В равностороннем треугольнике ABC высота равна 2√3. Найдите AB.

В треугольнике ABC Найдите высоту CH.

Показать ответ и решение

Так как катет, лежащий против угла 30∘, равен половине гипотенузы, то

√ -
BC =0,5AB = 3

По свойству прямоугольного треугольника следовательно, в треугольнике BCH :

√ -
HB = 0,5BC = --3
2

Тогда по теореме Пифагора в треугольнике BCH :

∘---------- ∘ --
CH = BC2 − BH2 = 9 = 1,5
4

Показать ответ и решение

В треугольнике BCH :

sin∠BCH = BH--= 0,5
BC

По свойству прямоугольного треугольника следовательно,

В треугольнике ABC угол BC = 7. Найдите

Показать ответ и решение

Так как по определению BC-
sin ∠A = AB , то нужно найти AB. По теореме Пифагора

∘ ---------- ∘------- √ ---
AB = AC2 + BC2 = 242+ 72 = 625 = 25

Значит,

sin ∠A = 7-= 0,28
25

Показать ответ и решение

В прямоугольном треугольнике катет, лежащий против угла в 30∘, равен половине гипотенузы. В данном случае известно, что в
треугольнике ABC сторона, лежащая против угла в 30∘, равна половине другой стороны. Значит ли это, что треугольник ABC
обязательно прямоугольный? Подобного рода умозаключения в общем случае очень опасны, так как часто попросту
неверны.

Но в данном конкретном случае нам повезло: докажем, что треугольник ABC — прямоугольный. В самом деле, если
опустить перпендикуляр из точки на прямую, содержащую AC, то окажется, что

Но если при этом и не совпадают, то HBC — прямоугольный треугольник, у которого гипотенуза равна катету
BH, чего быть не может, следовательно, и совпадают и треугольник ABC — прямоугольный.

По теореме Пифагора в треугольнике ABC :

2
AB2 = BC2 + AC2 ⇔ 4BC2 = BC2 + AC2 ⇔ AC2 = 3BC2 ⇔ AC2-= 3
BC

Две вершины квадрата расположены на гипотенузе равнобедренного прямоугольного треугольника, а две другие — на катетах.
Найдите сторону квадрата, если гипотенуза равна 9.

Показать ответ и решение

В прямоугольном треугольнике сумма острых углов равна 90∘. Так как треугольник равнобедренный, то

∘
∠CBA = ∠BCA = 90-= 45∘
2

Квадрат образует с гипотенузой углы

В прямоугольных треугольниках DBE и GF C

∠BDE = 90∘− ∠DBE = 45∘
∘ ∘
∠F GC = 90 − ∠F CG = 45

Значит, треугольники DBE и GFC — равнобедренные, то есть Так как по свойству
квадрата, то

Пусть сторона квадрата равна тогда длину гипотенузы можно выразить через сторону квадрата:

Катеты прямоугольного треугольника относятся как 5:4, а площадь равна 4,1. Найдите гипотенузу этого треугольника.

Показать ответ и решение

Т.к. катеты относятся как 5:4, то их можно обозначить за и 5x. Тогда необходимо найти гипотенузу, по теореме Пифагора
равную

∘---------- √ ----
25x2+ 16x2 = 41x2

Т.к. площадь прямоугольного треугольника равна полупроизведению катетов, то

2
S = 0,5 ⋅5x⋅4x= 10x = 4,1

Следовательно,

Значит, гипотенуза равна

∘ ------- ∘ ----------
41⋅0,41= 41⋅41⋅0,01 =41 ⋅0,1 =4,1.

Источник

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$<1>/<2>$	$<√2>/<2>$	$<√3>/<2>$
$cosα$	$<√3>/<2>$	$<√2>/<2>$	$<1>/<2>$
$tgα$	$<√3>/<3>$	$1$	$√3$
$ctgα$	$√3$	$1$	$<√3>/<3>$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√<91>$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=<4>/<5>, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Прямоугольный треугольник

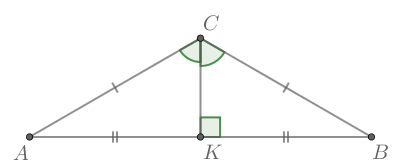
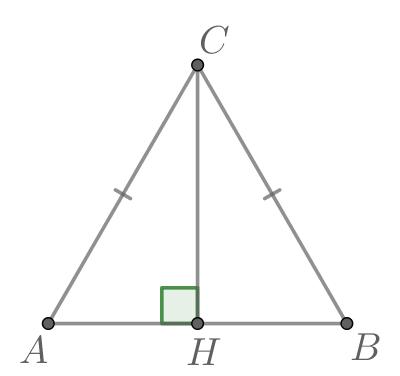
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Задание 3 Профильного ЕГЭ по математике. Планиметрия

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №3 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №3 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

1. B треугольнике ABC угол C равен , BC = 15, . Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

2. B треугольнике ABC угол C равен . Найдите AB.

По определению косинуса угла,

Найдем косинус угла A с помощью формулы:

Треугольники. Формулы площади треугольника.

3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, . Получим:

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен , угол B равен , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

Углы ACD и DCB в сумме дают . Отсюда

6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O . Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен

7. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

8. B треугольнике ABC угол A равен угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть и

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен .

C другой стороны, этот угол равен углу BAC, то есть

Параллелограмм

10. B параллелограмме ABCD AB=3, AD=21, Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен , его площадь равна ab, а квадрат диагонали равен

По формуле квадрата суммы,

Отсюда квадрат диагонали , и длина диагонали

13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит,

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны Тогда HGFE — ромб, и его периметр равен .

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции:

Из прямоугольного треугольника ADH найдем высоту трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту:

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

17. Диагонали равнобедренной трапеции диагонали перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру . Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть

19. Угол ACB равен Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

Касательная, хорда, секущая

20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен , и тогда угол ОBA равен Угол ОAB также равен , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна

21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна

Bписанные и описанные треугольники

22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника

23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, Тогда

Угол C может быть равен или — ведь синусы этих углов равны Однако по рисунку угол C — острый, значит, он равен

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, Тогда

По условию, угол C — тупой. Значит, он равен

26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: Гипотенуза равнобедренного прямоугольного треугольника в раз больше катета. Получим:

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, , Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

Тогда периметр четырехугольника равен

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,

источники:

http://egemaximum.ru/pryamougolnyj-treugolnik/

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-6-profilnogo-ege-po-matematike-planimetriya/

Источник

31
Июл 2013

Категория: Справочные материалы

Прямоугольный треугольник

2013-07-31
2019-09-30

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами.

Признаки равенства прямоугольных треугольников

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и острому углу).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

$S=frac{1}{2}ab$

$h=frac{ab}{c}$

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

$R=frac{c}{2}$

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

$r=frac{a+b-c}{2}$

cvb

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

И, думаю, будет полезна таблица формул для треугольника

Автор: egeMax |

комментария 3

Печать страницы

Источник

3. Геометрия на плоскости (планиметрия). Часть I

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Прямоугольный треугольник. Теорема Пифагора

Прямоугольный треугольник – это треугольник, один из углов которого равен (90^circ) (прямой).
Сторона, лежащая напротив прямого угла, называется гипотенузой ((AB)), а две другие стороны — катетами ((AC) и (BC)).

(bullet) Катет, лежащий против угла (30^circ), равен половине гипотенузы.
Следовательно, если, например, (angle A=30^circ), то (BC=dfrac12AB).

(bullet) Сумма острых углов прямоугольного треугольника равна (90^circ): (angle A+angle B=90^circ).
Следовательно, если в прямоугольном треугольнике один из острых углов равен (45^circ), то такой треугольник является равнобедренным.

(bullet) Если в прямоугольном треугольнике (ABC) провести высоту (CH) из прямого угла, то (angle BAC=angle BCH) и (angle
ABC=angle
ACH):

(bullet) Теорема Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов: [AB^2=AC^2+BC^2]

(bullet) (triangle ABCsim triangle AHCsim triangle BHC)

(bullet) Высота, проведенная из вершины прямого угла, есть среднее геометрическое (среднее пропорциональное) отрезков, на которые делится гипотенуза этой высотой: [CH=sqrt{AHcdot HB}]

Задание
1

#3770

Уровень задания: Равен ЕГЭ

В треугольнике (ABC) угол (C) равен (90^circ), угол (A) равен (30^circ), (AB=2sqrt3). Найдите высоту (CH).

Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=sqrt3).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=sqrt3:2).
Тогда по теореме Пифагора из (triangle BCH): [CH=sqrt{BC^2-BH^2}=sqrt{dfrac94}=1,5]

Ответ: 1,5

Задание
2

#3771

Уровень задания: Равен ЕГЭ

В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (AH), если (AB=2).

Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=1).
Тогда по теореме Пифагора из (triangle ABC): [AC=sqrt{AB^2-BC^2}=sqrt3] Из прямоугольного (triangle AHC): (HC=0,5AC=sqrt3:2). Тогда по теореме Пифагора [AH=sqrt{AC^2-HC^2}=1,5]

Ответ: 1,5

Задание
3

#3772

Уровень задания: Равен ЕГЭ

В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (BH), если (AB=4).

Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=2).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=1).

Ответ: 1

Задание
4

#3773

Уровень задания: Равен ЕГЭ

В треугольнике (ABC) ( AB=BC=AC=2sqrt3). Найдите высоту (CH).

Так как (AC=BC), то (CH) также является медианой, следовательно, (AH=0,5 AB=sqrt3). Тогда по теореме Пифагора из (triangle ACH): [CH=sqrt{AC^2-AH^2}=3]

Ответ: 3

Задание
5

#3774

Уровень задания: Равен ЕГЭ

В равностороннем треугольнике (ABC) высота (CH) равна (2sqrt3). Найдите (AB).

Так как (AC=BC), то (CH) также является медианой. Следовательно, если (AH=a), то (AB=AC=2a). Тогда по теореме Пифагора из (triangle
ACH): [AC^2=AH^2+CH^2quadRightarrowquad 4a^2=a^2+12quadRightarrowquad
a=2quadRightarrowquad AB=2a=4]

Ответ: 4

Задание
6

#3775

Уровень задания: Равен ЕГЭ

В треугольнике (ABC) (AC=BC=4), (angle C=30^circ). Найдите высоту (AH).

Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (AH=0,5AC=2).

Заметим, что условие (BC=4) в данной задаче является лишним.

Ответ: 2

Задание
7

#3776

Уровень задания: Равен ЕГЭ

В треугольнике (ABC) (AC=BC), высота (AH) равна (4), угол (C) равен (30^circ). Найдите (BC).

Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (4=AH=0,5AC), откуда (8=AC=BC).

Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Некоторые свойства прямоугольного треугольника:

Соотношение между сторонами и углами в прямоугольном треугольнике:

Значения тригонометрических функций некоторых углов:

ЕГЭ Профиль №1. Прямоугольный треугольник

ЕГЭ Профиль №1. Прямоугольный треугольник

Прямоугольные треугольники

Некоторые свойства прямоугольного треугольника:

Соотношение между сторонами и углами в прямоугольном треугольнике:

Значения тригонометрических функций некоторых углов:

Прямоугольный треугольник

Признаки равенства прямоугольных треугольников

Свойства прямоугольного треугольника

Задание 3 Профильного ЕГЭ по математике. Планиметрия

Прямоугольный треугольник

Признаки равенства прямоугольных треугольников

Свойства прямоугольного треугольника

Прямоугольный треугольник. Теорема Пифагора

Новое и интересное на сайте: