Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Контрольная мониторинговая работа ЕГЭ 2022 по математике 11 класс профильный уровень 3 варианта заданий с ответами за 1 полугодие 56 регион Оренбургская область, официальная дата проведения работы 4 декабря 2021 год.
-
Скачать задания 1 варианта
-
Скачать задания 2 варианта
-
Скачать задания 3 варианта
-
Скачать ответы и решения 1 вариант
-
Скачать ответы и решения 2 вариант
-
Скачать ответы и решения 3 вариант
Контрольная работа ЕГЭ 2022 по математике профиль за 1 полугодие 11 класс вариант №1
Вариант №2
Вариант №3
1)В соревновании по биатлону участвуют спортсмены из 25 стран, одна из которых — Россия. Всего на старт вышло 60 участников, из которых 6 — из России. Порядок старта определяется жребием, стартуют спортсмены друг за другом. Какова вероятность того, что десятым стартовал спортсмен из России?
2)Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
3)На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
4)Теплоход проходит по течению реки до пункта назначения 255 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 1 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 34 часа после отплытия из него. Ответ дайте в км/ч.
5)Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
6)Для перевозки 500 маленьких и 26 больших блоков был выделен автомобиль грузоподъемностью 9,75 т. По техническим условиям он может перевозить не более 38 маленьких блоков. Габариты блоков таковы, что перевозка одного большого блока приравнивается к перевозке 18 маленьких. Большой блок весит 3,5 т, а маленький 0,25 т. Какое минимальное количество перевозок потребуется для перемещения всех блоков?
7)В нескольких одинаковых бочках налито некоторое количество литров воды (необязательно одинаковое). За один раз можно перелить любое количество воды из одной бочки в другую. а) Пусть есть четыре бочки, в которых 29, 32, 40, 91 литров. Можно ли не более чем за четыре переливания уравнять количество воды в бочках? б) Пусть есть семь бочек. Всегда ли можно уравнять количество воды во всех бочках не более чем за пять переливаний? в) За какое наименьшее количество переливаний можно заведомо уравнять количество воды в 26 бочках?
8)Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, перейдя отметку 10 часов, но не дойдя до отметки 1 час.
9)Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
10)Имеется два сплава. Первый содержит 10% меди, второй — 30% меди. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% меди. На сколько килограммов масса первого сплава была меньше массы второго?
11)Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
12)В июле 2016 года планируется взять кредит в размере 4,2 млн. руб. Условия возврата таковы: — каждый январь долг возрастает на r% по сравнению с концом предыдущего года. — с февраля по июнь необходимо выплатить часть долга. — в июле 2017, 2018 и 2019 годов долг остается равным 4,2 млн. руб. — суммы выплат 2020 и 2021 годов равны. Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 6,1 млн. рублей.
13)Агата добиралась от дома до института на своем автомобиле с постоянной скоростью 100 км/ч. Обратно она ехала с постоянной скоростью, которая измерялась целым числом километров в час, причем путь до дома занял у нее больше времени, чем путь до института. а) Могла ли ее средняя скорость за эти две поездки составить 90 км/ч? б) Могла ли ее средняя скорость за эти две поездки оказаться равной целому числу километров в час? в) Какое наименьшее целое число километров в час могла составлять ее средняя скорость за эти две поездки?
14)У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
15)Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите тупой угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
16)На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].
17)Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.
18)При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? В ответе укажите наименьшее необходимое количество выстрелов.
19)В аграрной стране А производство пшеницы на душу населения в 2015 году составляло 192 кг и ежегодно увеличивалось на 20%. В аграрной стране В производство пшеницы на душу населения в 2015 году составляло 375 кг. В течение трех лет производство зерна в стране В увеличивалось на 14% ежегодно, а ее население увеличивалось на m% ежегодно. В 2018 году производство зерна на душу населения в странах А и В стало одинаковым. Найдите m.
20)На сторонах АВ, ВС и АС треугольника АВС отмечены точки C1, A1 и B1 соответственно, причём АC1 : С1B = 21 : 10, ВА1 : A1C = 2 : 3, АВ1:В1С = 2 : 5. Отрезки BB1 и CC1 пересекаются в точке D. а) Докажите, что четырёхугольник ADA1B1 — параллелограмм. б) Найдите CD, если отрезки AD и ВС перпендикулярны, АС = 63, ВС = 25.
21)Первый набор чисел состоит из чисел 2, 4, 8, …, . Второй набор состоит из чисел 3, 9, 27, …, . Числа разбиты на пары. В каждой паре на первом месте — число из первого набора, а на втором — число из второго. В каждой паре два числа умножили друг на друга и полученные произведения сложили. а) Может ли полученная сумма делиться на 9? б) Может ли полученная сумма быть больше 1 000 000? в) Найдите наименьшее возможное значение полученной суммы.
Тренировочные варианты ЕГЭ 2022 по математике 11 класс:
-
Пробный вариант №211122 ЕГЭ 2022 по математике профиль 11 класс 100 баллов с ответами
-
Тренировочный вариант №152 ЕГЭ 2022 по математике 11 класс профильный уровень
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Пробный ЕГЭ № 1 по математике. 11 класс
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Ответы
Скачать:
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №1
Профильный уровень. 2022г.
Вариант 1
Часть 1
1. Найдите корень уравнения 
Ответ: ___________________
2. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом все три раза.
Ответ: ___________________
3. В треугольнике АВС СD – медиана, угол С равен 900, угол В равен 350. Найдите угол АСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите значение выражения 
Ответ: ___________________
5. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 28. Найдите площадь боковой поверхности исходной призмы.
Ответ: ___________________
6. На рисунке изображён график функции 

Ответ: ___________________
7. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле 


Ответ: ___________________
8. Имеется два сплава. Первый сплав содержит 5% никеля, второй – 20% никеля. Из этих двух сплавов получили третий сплав массой 225кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Ответ: ___________________
9. На рисунке изображён график функции 

Ответ: ___________________
10. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: ___________________
11. Найдите наибольшее значение функции


Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
б) Найдите корни этого уравнения, принадлежащие отрезку 
13. На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СС1.
б) Найдите расстояние от точки С1 до плоскости А1РQ.
14. Решите неравенство 
15. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.
17. Найдите значения a, при каждом из которых уравнение
имеет ровно два различных корня.
18. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №1
Профильный уровень. 2022г.
Вариант 2
Часть 1
1. Найдите корень уравнения 
Ответ: ___________________
2. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом ровно один раз.
Ответ: ___________________
3. В треугольнике АВС СD – медиана, угол С равен 900, угол В равен 410. Найдите угол АСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите значение выражения 
Ответ: ___________________
5. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 32. Найдите площадь боковой поверхности исходной призмы.
Ответ: ___________________
6. На рисунке изображён график функции 

Ответ: ___________________
7. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле 


Ответ: ___________________
8. Имеется два сплава. Первый сплав содержит 10% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 270кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Ответ: ___________________
9. На рисунке изображён график функции 

Ответ: ___________________
10. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35% этих стекол, вторая – 65%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: ___________________
11. Найдите наибольшее значение функции


Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
б) Найдите корни этого уравнения, принадлежащие отрезку 
13. На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СС1.
б) Найдите расстояние от точки С1 до плоскости А1РQ.
14. Решите неравенство 
15. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.
17. Найдите значения a, при каждом из которых уравнение
имеет ровно два различных корня.
18. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №1
Профильный уровень. 2022г.
Вариант 3
Часть 1
1. Найдите корень уравнения 
Ответ: ___________________
2. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом ровно два раза.
Ответ: ___________________
3. В треугольнике АВС СD – медиана, угол С равен 900, угол В равен 370. Найдите угол АСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите значение выражения 
Ответ: ___________________
5. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 36. Найдите площадь боковой поверхности исходной призмы.
Ответ: ___________________
6. На рисунке изображён график функции 

Ответ: ___________________
7. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле 


Ответ: ___________________
8. Имеется два сплава. Первый сплав содержит 5% никеля, второй – 20% никеля. Из этих двух сплавов получили третий сплав массой 240кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Ответ: ___________________
9. На рисунке изображён график функции 

Ответ: ___________________
10. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 40% этих стекол, вторая – 60%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: ___________________
11. Найдите наибольшее значение функции


Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
б) Найдите корни этого уравнения, принадлежащие отрезку 
13. На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СС1.
б) Найдите расстояние от точки С1 до плоскости А1РQ.
14. Решите неравенство 
15. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.
17. Найдите значения a, при каждом из которых уравнение
имеет ровно два различных корня.
18. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №1
Профильный уровень. 2022г.
Вариант 4
Часть 1
1. Найдите корень уравнения 
Ответ: ___________________
2. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» ни разу не начнёт игру с мячом.
Ответ: ___________________
3. В треугольнике АВС СD – медиана, угол С равен 900, угол В равен 390. Найдите угол АСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите значение выражения 
Ответ: ___________________
5. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 35. Найдите площадь боковой поверхности исходной призмы.
Ответ: ___________________
6. На рисунке изображён график функции 

Ответ: ___________________
7. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле 


Ответ: ___________________
8. Имеется два сплава. Первый сплав содержит 10% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 210кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Ответ: ___________________
9. На рисунке изображён график функции 

Ответ: ___________________
10. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 6% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: ___________________
11. Найдите наибольшее значение функции


Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
б) Найдите корни этого уравнения, принадлежащие отрезку 
13. На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СС1.
б) Найдите расстояние от точки С1 до плоскости А1РQ.
14. Решите неравенство 
15. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.
17. Найдите значения a, при каждом из которых уравнение
имеет ровно два различных корня.
18. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №1
Профильный уровень. 2022г.
Ответы
Часть 1
Вариант 1
1) 7; 2) 0,125; 3) 55; 4) – 10; 5) 56; 6) 5; 7) 6 
Вариант 2
1) 11; 2) 0,375; 3) 49; 4) – 6; 5) 64; 6) 3; 7) 7 
Вариант 3
1) 8; 2) 0,375; 3) 53; 4) – 20; 5) 72; 6) 5; 7) 5 
Вариант 4
1) 3; 2) 0,125; 3) 51; 4) – 16; 5) 70; 6) 3; 7) 8 
Часть 2
12) а) 


14) 


18) а) 1, 2, 4 (1,1,1,1,1,1,1; 1,1,2,3); б) нет; в) 7, 7, 7, 9, 11 или 7, 9, 11, 14.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 1.
1. Найдите корень уравнения 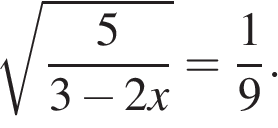
2. В сборнике билетов по философии всего 50 билетов, в 11 из них встречается вопрос по теме «Пифагор». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Пифагор».
3.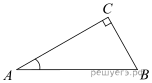
В треугольнике ABC угол C равен 90°, АС = 20, Найдите BC.
4.
Найдите значение выражения
5. 
6.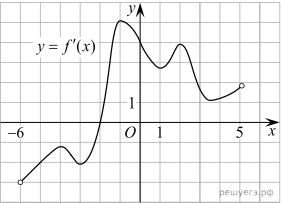
На рисунке изображен график производной функции f(x), определенной на интервале (−6; 5). Найдите точку экстремума функции f(x) на отрезке [−5; 4].
7. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.
Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Каким должно быть число A, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
8. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 90 км/ч, а последнюю — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
9.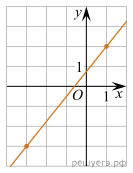
На рисунке изображён график функции Найдите
10. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 8 очков в двух играх. Если команда выигрывает, она получает 5 очков, в случае ничьей — 3 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
11. Найдите наименьшее значение функции на отрезке
12. а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
13. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.
а) Докажите, что SA — высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
14. Решите неравенство:
15. Тимофей хочет взять в кредит 1,1 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Тимофей взять кредит, чтобы ежегодные выплаты были не большее 270 тысяч рублей?
16. Четырёхугольник ABCD вписан в окружность, причем сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке Е, а окружность — в точке F, причем H — середина AE.
а) Докажите, что четырёхугольник BCFE — параллелограмм.
б) Найдите площадь четырёхугольника ABCD, если известно, что AB = 3 и
17. Найдите все значения параметра а, при каждом из которых множество решений неравенства
содержит отрезок
18. Десять мальчиков и семь девочек пошли в лес за грибами. Известно, что любые две девочки набрали больше грибов, чем любые три мальчика, но любые пять мальчиков набрали больше грибов, чем любые три девочки.
а) Может ли так случиться, что какая-то девочка набрала меньше грибов, чем какой-нибудь мальчик?
б) Может ли так случиться, что количество найденных грибов у всех детей будет различным?
в) Найдите минимальное возможное количество грибов, собранное всеми детьми суммарно.
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 2.
1.
Решите уравнение 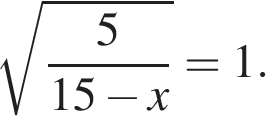
2. В сборнике билетов по философии всего 50 билетов, в 11 из них встречается вопрос по теме «Пифагор». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Пифагор».
3.
Острые углы прямоугольного треугольника равны 62° и 28°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
4. Найдите значение выражения
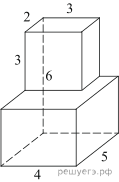
5. 
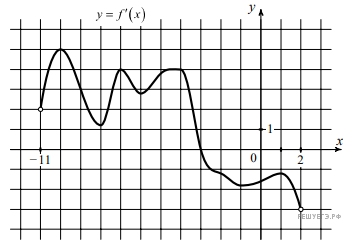
6. На рисунке изображён график — производной функции
определенной на интервале (−11; 2). В какой точке отрезка [−9; 1] функция
принимает наибольшее значение?
7. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением где p (атм.) — давление газа, V — объeм газа в литрах. Изначально объeм газа равен 243,2 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
8. Первый и второй насосы наполняют бассейн за 10 минут, второй и третий — за 15 минут, а первый и третий — за 24 минуты. За сколько минут три эти насоса заполнят бассейн, работая вместе?
9. 
где числа a, b и c — целые. Найдите значение дискриминанта уравнения
.
10. В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру дня кофе останется в обоих автоматах.
11.
Найдите точку минимума функции
12. Решите уравнение
13. ABCA1B1C1 — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.
а) Докажите что периметр сечения призмы плоскостью α больше 40.
б) Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.
14. Решите неравенство
15. Вася мечтает о собственной квартире, которая стоит 2 млн руб. Вася может купить ее в кредит, при этом банк готов выдать эту сумму сразу, а погашать кредит Васе придется 20 лет равными ежемесячными платежами, при этом ему придется выплатить сумму, на 260% превышающую исходную. Вместо этого, Вася может какое-то время снимать квартиру (стоимость аренды – 14 тыс. руб. в месяц), откладывая каждый месяц на покупку квартиры сумму, которая останется от его возможного платежа банку (по первой схеме) после уплаты арендной платы за съемную квартиру. За сколько месяцев в этом случае Вася сможет накопить на квартиру, если считать, что стоимость ее не изменится?
16. Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A. Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон.
а) Докажите, что треугольник OLO1 прямоугольный.
б) Найдите радиус второй окружности, если известно, что радиус первой равен 15 и AK = 32.
17. Найдите все значения a, при каждом из которых уравнение
имеет более одного корня.
18. На листочке записано 13 различных натуральных чисел. Среднее арифметическое семи наименьших из них равно 7, среднее арифметическое семи наибольших из них равно 16.
а) Может ли наименьшее из 13 чисел равняться 5?
б) Может ли среднее арифметическое всех 13 чисел равняться 12?
в) Пусть P — среднее арифметическое всех 13 чисел, Q — седьмое по величине число. Найдите наибольшее значение выражения P − Q.
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 3.
1. Найдите корень уравнения
2. На экзамене 40 вопросов, Коля не выучил 4 из них. Найдите вероятность того, что ему попадется выученный вопрос.
3.
Радиус окружности, описанной около прямоугольного треугольника, равен 2. Найдите гипотенузу этого треугольника.
4. Найдите если
5. 
6.
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
7.
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке.
В этой системе координат линия, по которой провисает цепь моста, имеет уравнение где x и y измеряются в метрах. Найдите длину ванты, расположенной в 70 метрах от пилона. Ответ дайте в метрах.
8. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
9. 
где числа a, b, c и d — целые. Найдите
10. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °C, равна 0,91. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °C или выше.
11. Найдите точку максимума функции
12. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
13. В основании прямой треугольной призмы ABCA1B1C1 лежит равнобедренный треугольник ABC с основанием AC. Точка K — середина ребра A1B1, а точка M делит ребро AC в отношении AM : MC = 1 : 3.
а) Докажите, что KM перпендикулярно AC.
б) Найдите угол между прямой KM и плоскостью ABC, если AB = 12, AC = 16 и AA1 = 6.
14. Решите неравенство:
15. У фермера есть два поля, каждое площадью 15 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 400 ц/га.
Фермер может продавать картофель по цене 2000 руб. за центнер, а свёклу — по цене 3000 руб. за центнер. Какой наибольший доход может получить фермер?
16. Основания трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
17. Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
18. Будем называть четырёхзначное число интересным, если среди четырёх цифр в его десятичной записи нет нулей, а одна из этих цифр равна сумме трёх других из них. Например, интересным является число 6321.
а) Приведите пример двух интересных четырёхзначных чисел, разность между которыми равна пяти.
б) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна 91?
в) Найдите наименьшее нечётное число, для которого не существует кратного ему интересного четырёхзначного числа.
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 4.
1.
Решите уравнение Если уравнение имеет более одного корня, в ответе запишите больший из корней.
2. Вероятность того, что новый ноутбук в течение года поступит в гарантийный ремонт, равна 0,091. В некотором городе из 1000 проданных ноутбуков в течение года в гарантийную мастерскую поступило 96 штук. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
3.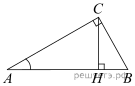
В треугольнике ABC угол C равен 90°, CH – высота, угол A равен
Найдите
4. Найдите значение выражения
5. 
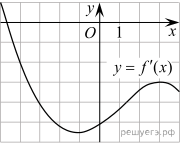
6. 
7. Груз массой 0,2 кг колеблется на пружине. Его скорость v меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.
8. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 77 км. На следующий день он отправился обратно в A со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
9.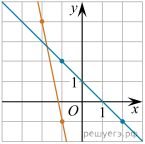
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
10. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 5 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 8 апреля в Волшебной стране будет отличная погода.
11. Найдите наименьшее значение функции на отрезке
12. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
13. Дана правильная четырёхугольная пирамида MABCD, все рёбра которой равны 12. Точка N — середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2 : 1, считая от вершины M.
а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
14. Решите неравенство
15. По бизнес-плану предполагается вложить в четырёхлетний проект целое число млн рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 15 млн рублей в первый и второй годы, а также по 10 млн в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика к началу третьего года станет больше 110 млн, а к концу проекта — больше 190 млн рублей.
16. В треугольнике MPK биссектриса угла K пересекает сторону MP в точке A. Окружность, описанная около треугольника AMK пересекает сторону PK в точке B.
а) Докажите, что треугольник ABM равнобедренный.
б) Найдите площадь треугольника ABM, если MK = 9, PK = 6, MP = 5.
17. Найдите все значения a, при каждом из которых уравнение
имеет единственный корень на отрезке [−1; 1].
18. На доске написаны числа 2 и 3. За один ход два числа a и b, записанных на доске заменяется на два числа: a + b и 2a − 1 или a + b и 2b − 1.
Пример: числа 2 и 3 заменяются на 3 и 5, на 5 и 5, соответственно.
а) Приведите пример последовательности ходов, после которых одно из чисел, написанных на доске, окажется числом 19.
б) Может ли после 50 ходов одно из двух чисел, написанных на доске, оказаться числом 100.
в) Сделали 2015 ходов, причём на доске никогда не было написано одновременно двух равных чисел. Какое наименьшее значение может принимать разность большего и меньшего из полученных чисел?
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 5.
1. Найдите корень уравнения 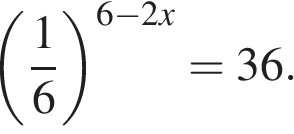
2.
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Китая будет выступать после группы из Канады и после группы из Англии? Результат округлите до сотых.
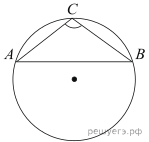
3. 
4. Найдите значение выражения
5. 
B, C,
прямоугольного параллелепипеда
у которого
6. 
определенной на интервале
Найдите точку экстремума функции
на отрезке
7. Рейтинг R интернет-магазина вычисляется по формуле где
rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 49, их средняя оценка равна 0,88, а оценка экспертов равна 0,38.
8. Смешали некоторое количество 13-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
9. 
где числа a, b и c — целые. Найдите значение дискриминанта уравнения
.
10. Игральную кость бросили два раза. Известно, что шесть очков не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 5».
11.
Найдите наименьшее значение функции на отрезке
12. а) Решите уравнение 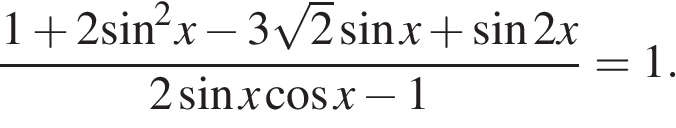
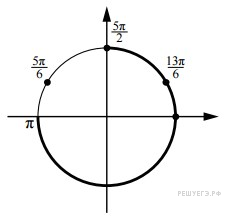
б) Укажите корни этого уравнения, принадлежащие отрезку
13. Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA1 и AB1 перпендикулярны.
а) Докажите, что AA1 = AС.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 7, BC = 8.
14. Решите неравенство:
15. 5 января 2020 года Андрей планирует открыть вклад на сумму 3 миллиона рублей. Первые три года 2 января банк будет начислять 10% на сумму вклада, а в последующие годы банк будет начислять 5% на сумму вклада.
4 января каждого года Андрей будет делать дополнительный взнос на вклад так, чтобы после этого величина вклада на 5 января была больше величины вклада на 5 января прошлого года на одно и то же число. Определите общий размер начислений банка, если 3 января 2031 года на вкладе будет лежать 24,15 миллиона рублей.
16. В каждый угол равнобедренного треугольника ABC, в котором AB = 10, AC = BC = 13, вписана окружность единичного радиуса, точки О1, О2 и О3 центры этих окружностей. Найдите:
а) радиус окружности, вписанной в треугольник ABC;
б) площадь треугольника О1, О2, О3.
17. Найдите все значения параметра a, при каждом из которых система уравнений

имеет ровно четыре различных решения.
18. Натуральные числа a, b, c и d удовлетворяют условию a b c d.
а) Найдите числа a, b, c и d, если a + b + с + d = 15 и a2 − b2 + с2 − d2 = 19.
б) Может ли быть a + b + с + d = 23 и a2 − b2 + с2 − d2 = 23?
в) Пусть a + b + с + d = 1200 и a2 − b2 + с2 − d2 = 1200. Найдите количество возможных значений числа a.
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 6.
1. Найдите корень уравнения
2.
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет 1?
3.
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
4.
Найдите значение выражения 
5.
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 8, а объем равен
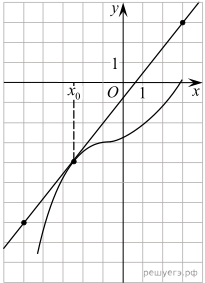
6. 
и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
7. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель − целое число от –2 до 2.
Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.
8. Первая труба наполняет резервуар на 27 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 18 минут. За сколько минут наполняет этот резервуар одна вторая труба?
9. 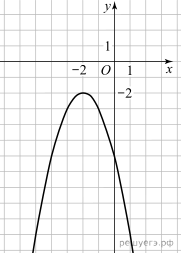
где числа a, b и c — целые. Найдите значение дискриминанта уравнения
.
10. Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».
11.
Найдите наибольшее значение функции на отрезке
12. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
13. На рёбрах DD1 и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP = 10, а B1Q = 4. Плоскость A1PQ пересекает ребро CC1 в точке М.
а) Докажите, что точка М является серединой ребра CC1.
б) Найдите расстояние от точки С1 до плоскости A1PQ.
14. Решите неравенство
15. Строительство нового завода стоит 192 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x2 + 4x + 18 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px − (0,5x2 + 4x + 18). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 6 лет?
16. Окружность с центром O, вписанная в треугольник ABC, касается стороны BC в точке K. К этой окружности проведена касательная, параллельная биссектрисе AP треугольника и пересекающая стороны AC и BC в точках M и N соответственно.
а) Докажите, что угол MOC равен углу NOK.
б) Найдите периметр треугольника ABC, если отношение площадей трапеции AMNP и треугольника ABC равно 2:7, MN = 1, AM + PN = 3 .
17. Найдите все значения a, при которых неравенство выполняется для всех действительных значений
18. Бесконечная арифметическая прогрессия a1, a2, …, an, … состоит из различных натуральных чисел.
а) Существует ли такая прогрессия, в которой среди чисел a1, a2, …, a7 ровно три числа делятся на 36?
б) Существует ли такая прогрессия, в которой среди чисел a1, a2, …, a30 ровно 9 чисел делятся на 36?
в) Для какого наибольшего натурального n могло оказаться так, что среди чисел a1, a2, …, a2n больше кратных 36, чем среди чисел a2n + 1, a2n + 2, …, a5n?
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 7.
1. Найдите корень уравнения
2. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 спортсмена из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России.
3.
В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите
4. Найдите значение выражения 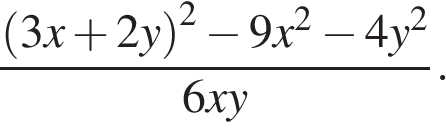
5. 
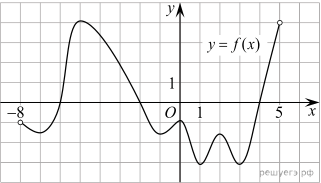
6. 
7. Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле 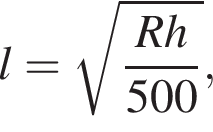
8. Рабочие прокладывают тоннель длиной 39 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 4 метра туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 6 дней.
9. 
где числа a, b и c — целые. Найдите
10. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
11. Найдите наименьшее значение функции на отрезке
12. а) Решите уравнение 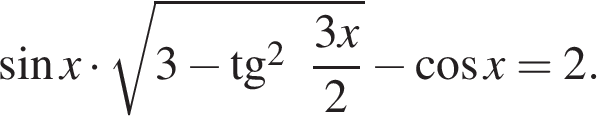
б) Укажите корни этого уравнения, принадлежащие отрезку
13. В основании правильной треугольной призмы ABCA1B1C1лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
14. Решите неравенство:
15. В двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи y кг никеля в день требуется y2 человеко-часов труда.
Для нужд промышленности можно использоваться или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую суммарную массу металлов можно добыть в двух областях за сутки?
16. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что
а) Докажите, что точка I лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OIH, если
17. Найдите все значения параметра a, при каждом из которых наименьшее значение функции
меньше 2.
18. Возрастающие арифметические прогрессии и
состоят из натуральных чисел.
а) Приведите пример таких прогрессий, для которых
б) Существуют ли такие прогрессии, для которых ?
в) Какое наибольшее значение может принимать произведение если
?
ТРЕНИРОВОЧНАЯ РАБОТА ЕГЭ профильный уровень
ДЕКАБРЬ 2021
Вариант 8.
1. Найдите корень уравнения
2. На конференцию приехали 6 ученых из Швейцарии, 3 из Болгарии и 6 из Австрии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что третьим окажется доклад ученого из Болгарии.
3.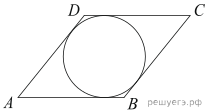
Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 9. Найдите сторону ромба.
4. Найдите значение выражения:
5. 
у которого
6. 
7. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле где
(км) — радиус Земли. С какой высоты горизонт виден на расстоянии 16 километров? Ответ выразите в километрах.
8.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
9. 
где числа a, b и c — целые. Найдите
10. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?
11. Найдите точку минимума функции
12.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
13. В правильной четырехугольной пирамиде MABCD через середины сторон АВ и AD параллельно боковому ребру АМпроведена плоскость. Сторона основания пирамиды равна 20, а боковое ребро —
а) Докажите, что сечение пирамиды этой плоскостью является пятиугольником с тремя прямыми углами.
б) Найдите площадь этого сечения.
14. Решите неравенство:
15. В июле планируется взять кредит на сумму 2 320 500 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
16. Основания трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.
17. Найдите все значения a, при каждом из которых уравнение
имеет единственный корень.
18. Последовательность a1, a2, …,an,… состоит из натуральных чисел, причем an+2 = an+1 + an при всех натуральных n.
а) Может ли выполняться равенство 4a5 = 7a4?
б) Может ли выполняться равенство 5a5 = 7a4?
в) При каком наибольшем натуральном n может выполняться равенство
Ответы Вариант 1
|
№ п/п |
№ задания |
Ответ |
|
1 |
523392 |
-201 |
|
2 |
286325 |
0,78 |
|
3 |
29749 |
16 |
|
4 |
90983 |
64 |
|
5 |
74663 |
2,5 |
|
6 |
9049 |
-2 |
|
7 |
319859 |
35 |
|
8 |
525066 |
60 |
|
9 |
508896 |
-10,5 |
|
10 |
321163 |
0,28 |
|
11 |
26691 |
-1 |
|
12 |
505547 |
а) |
|
13 |
513097 |
|
|
14 |
508423 |
|
|
15 |
515690 |
6. |
|
16 |
519685 |
|
|
17 |
507235 |
|
|
18 |
548484 |
а) нет, б) да, в) 106 |
Вариант 2
|
№ п/п |
№ задания |
Ответ |
|
1 |
102379 |
10 |
|
2 |
286325 |
0,78 |
|
3 |
502085 |
34 |
|
4 |
26847 |
1,5 |
|
5 |
27210 |
78 |
|
6 |
561723 |
-3 |
|
7 |
42963 |
7,6 |
|
8 |
504259 |
9,6 |
|
9 |
562294 |
20 |
|
10 |
509531 |
0,65 |
|
11 |
127993 |
-5 |
|
12 |
511289 |
|
|
13 |
559408 |
б) |
|
14 |
507661 |
|
|
15 |
513717 |
125 месяцев. |
|
16 |
513368 |
б) 240. |
|
17 |
512996 |
|
|
18 |
528993 |
а) нет, б) нет, в) |
Вариант 3
|
№ п/п |
№ задания |
Ответ |
|
1 |
26651 |
4 |
|
2 |
1004 |
0,9 |
|
3 |
52649 |
4 |
|
4 |
26786 |
-2,5 |
|
5 |
519535 |
29 |
|
6 |
6041 |
-4 |
|
7 |
325728 |
8,39 |
|
8 |
5913 |
10 |
|
9 |
564589 |
-0,5 |
|
10 |
541813 |
0,09 |
|
11 |
77465 |
9 |
|
12 |
522094 |
а) |
|
13 |
526591 |
б) |
|
14 |
511539 |
|
|
15 |
517222 |
30 млн рублей. |
|
16 |
517535 |
б) 30. |
|
17 |
526679 |
|
|
18 |
513371 |
а) Да, например, 7124 и 7119; б) нет; в) 11. |
Вариант 4

Вариант 5

Вариант 6
|
№ п/п |
№ задания |
Ответ |
|
1 |
39003 |
226 |
|
2 |
320849 |
0,1 |
|
3 |
27615 |
3 |
|
4 |
541256 |
2 |
|
5 |
73945 |
0,75 |
|
6 |
525690 |
42 |
|
7 |
319860 |
10 |
|
8 |
119153 |
27 |
|
9 |
562293 |
8 |
|
10 |
508778 |
0,16 |
|
11 |
70537 |
23 |
|
12 |
519828 |
а) |
|
13 |
514631 |
|
|
14 |
507667 |
|
|
15 |
530903 |
14. |
|
16 |
525748 |
б) 14. |
|
17 |
513452 |
а) Да, например, прогрессия 18, 36, 54, 72, 90, 108, 126, …; б) нет; в)23 |
Вариант 7
|
№ п/п |
№ задания |
Ответ |
|
1 |
511021 |
-3 |
|
2 |
286209 |
0,08 |
|
3 |
27337 |
0,6 |
|
4 |
26987 |
2 |
|
5 |
73455 |
2 |
|
6 |
520183 |
-7 |
|
7 |
525065 |
4,8 |
|
8 |
110543 |
9 |
|
9 |
564649 |
-61 |
|
10 |
509569 |
0,06 |
|
11 |
77445 |
-25 |
|
12 |
546982 |
а) |
|
13 |
510460 |
19. |
|
14 |
508353 |
|
|
15 |
515652 |
165 кг. |
|
16 |
513627 |
б) 175°. |
|
17 |
526018 |
|
|
18 |
517186 |
а) 1, 3, 5,… и 1, 4, 7,…; б) нет; в) 98. |
Вариант 8
|
№ п/п |
№ задания |
Ответ |
|
1 |
510900 |
8,75 |
|
2 |
286125 |
0,2 |
|
3 |
53471 |
36 |
|
4 |
16125 |
425 |
|
5 |
245335 |
30 |
|
6 |
530551 |
1,25 |
|
7 |
263803 |
0,02 |
|
8 |
99619 |
6 |
|
9 |
564647 |
61 |
|
10 |
509078 |
0,192 |
|
11 |
124267 |
9 |
|
12 |
517746 |
а) |
|
13 |
552931 |
б) 250. |
|
14 |
508509 |
|
|
15 |
519832 |
254 100 рублей. |
|
16 |
517535 |
б) 30. |
|
17 |
501693 |
|
|
18 |
520501 |
а) да; б) нет; в) при |
Сборники тренировочных тестов по математике профильного уровня для ЕГЭ в 2023 году и для ЕГЭ прошлых лет. Все тренировочные варианты/пробники содержат ответы и решения ко 2-й части кима. Обсудить решение и задания каждого варианта вы можете в комментариях под ними. РЕШАТЬ ТЕСТЫ
Обращайте внимание на уровень пробника — здесь только профильный! Базовый уровень смотрите здесь.
- Всё про ЕГЭ 2023
- Демоверсия 2023 + изменения 2023
Что почитать?
- Из актуального: рекомендации от ФИПИ по профильной математике
Что изменилось в ЕГЭ 2023 по математике
Представляете — ничего 
Теория для подготовки к ЕГЭ 2023 по математике
Для теории у нас создан особый раздел «Теория для ЕГЭ по математике». Отдельно может порекомендовать посмотреть сборник шпаргалок для ЕГЭ по математике и на проекте ЕГЭ100Баллов целая ветка, посвященная шпаргалкам.
Что можно брать с собой на ЕГЭ по профильной математике?
На ЕГЭ по математике как всегда с собой можно взять только линейку. Никаких калькуляторов и мобильных телефонов, конечно же. Вода и шоколадка разрешаются 
Выбирайте вариант, сверяйте с ответами, оставляйте комментарии НИЖЕ
Проверочная работа по математике в 11 классе
Инструкция по выполнению работы
На выполнение работы отводится 90 минут.
Работа состоит из двух частей, включающих в себя 15 заданий.
Часть 1 (1-12 задание) содержит задания базового уровня с кратким ответом.
Часть 2 (13-15 задание) содержат задания повышенного уровня. При выполнении этих заданийнеобходимо записать полное обоснованное решение и ответ.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаѐтся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении работы запрещается пользоваться вычислительной техникой.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
|
Вариант 1 Часть 1 Ответами к заданиям 1–12 являются цифра, число или последовательность цифр, которые следует записать в специальном поле |
|
|
1 |
Для ремонта квартиры требуется 37 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов? |
|
2 |
На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия. |
|
3 4 |
Найдите значение выражения Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. |
|
5 |
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. |
|
6 |
Решите уравнение: |
|
7 |
Упростите выражение и найдите его значение при |
|
8 9 10 11 12 |
В треугольнике АВС угол С равен 90°, АС=9,sinА= Найдите значение выражения Площадь поверхности куба равна 18. Найдите его диагональ. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: (считайте |
|
Часть 2 При выполнении заданий 13 –15 необходимо записать полное обоснованное решение и ответ. 13 а) Решите уравнение б) Найдите все корни уравнения, принадлежащие отрезку 14 В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD. |
|
|
15 |
Решите неравенство: |
Проверочная работа в 11 классе
Инструкция по выполнению работы
На выполнение работы отводится 90 минут.
Работа состоит из двух частей, включающих в себя 15 заданий.
Часть 1 (1-12 задание) содержит задания базового уровня с кратким ответом.
Часть 2 (13-15 задание) содержат задания повышенного уровня. При выполнении этих заданий необходимо записать полное обоснованное решение и ответ.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаѐтся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении работы запрещается пользоваться вычислительной техникой.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
|
Вариант 2 Часть 1 Ответами к заданиям 1–12 являются цифра, число или последовательность цифр, которые следует записать в специальном поле |
|
|
1 |
Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов? |
|
2 |
На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия. |
|
3 4 |
Найдите значение выражения Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. |
|
5 |
В фирме такси в данный момент свободно 16 машин: 4 черных, 3 синих и 9 белых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет черное такси. |
|
6 |
Решите уравнение: |
|
7 |
Упростите выражение и найдите его значение при |
|
8 9 10 11 12 |
В треугольнике АВС угол С равен 90°, АС=4,sinА= Найдите значение выражения:
Площадь поверхности куба равна 8. Найдите его диагональ. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27 км/ч, а вторую половину пути — со скоростью, на 18 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах. |
|
Часть 2 При выполнении заданий 13 –15 необходимо записать полное обоснованное решение и ответ. |
|
|
13 |
а) Решите уравнение б) Укажите корни этого уравнения, принадлежащее отрезку |
|
14 |
В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD. |
|
15 |
Решите неравенство: |
Ответы и решения
Вариант 1
Часть 1:
|
№ п/п |
Ответ |
|
1 |
7 |
|
2 |
20 |
|
3 |
-1,3 |
|
4 |
6 |
|
5 |
0,4 |
|
6 |
5 |
|
7 |
5 |
|
8 |
15 |
|
9 |
6 |
|
10 |
3 |
|
11 |
32 |
|
12 |
2,5 |
Часть 2:
13. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решение.
а) Преобразуем уравнение:
Получаем или
откуда
или
где
б) На отрезке корни отберём с помощью единичной окружности.
Получаем и
Ответ: а)
б)
|
Баллы |
Критерии оценки выполнения задания |
|
3 |
Обоснованно получен правильный ответ |
|
2 |
Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку |
|
1 |
Тригонометрическое уравнение решено, но допущена вычислительная ошибка |
|
0 |
Решение не соответствует ни одному из критериев |
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая AD параллельна прямой BC. Следовательно, искомый угол — SBC. В равнобедренном треугольнике SBC проведём медиану и высоту SM. Имеем:
Из прямоугольного треугольника SBM
получаем:
Ответ:
|
Баллы |
Критерии оценки выполнения задания |
|
2 |
Обоснованно получен верный ответ |
|
1 |
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
|
0 |
Другие случаи, не соответствующие указанным критериям |
|
2 |
Максимальный балл |
15. Решите неравенство:
Решение.
Перепишем неравенство в виде:
Множество решений исходного
неравенства:
Ответ:
|
Баллы |
Критерии оценки выполнения задания |
|
2 |
Обоснованно получен верный ответ |
|
1 |
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
|
0 |
Другие случаи, не соответствующие указанным критериям |
|
2 |
Максимальный балл |
Вариант 2
Часть 1:
|
№ п/п |
Ответ |
|
1 |
11 |
|
2 |
-14 |
|
3 |
4 |
|
4 |
6 |
|
5 |
0,25 |
|
6 |
45 |
|
7 |
3 |
|
8 |
5 |
|
9 |
2 |
|
10 |
2 |
|
11 |
36 |
|
12 |
2 |
Часть 2:
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащее
отрезку
Решение.
Сведём уравнение к квадратному относительно синуса, используя
формулу Имеем:
б) С помощью числовой окружности отберём корни, принадлежащие
отрезку , получим число
Ответ:
а) б)
|
Баллы |
Критерии оценки выполнения задания |
|
3 |
Обоснованно получен правильный ответ |
|
2 |
Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку |
|
1 |
Тригонометрическое уравнение решено, но допущена вычислительная ошибка |
|
0 |
Решение не соответствует ни одному из критериев |
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая параллельна прямой
Следовательно, искомый угол — В равнобедренном треугольнике
проведём
медиану и высоту
Имеем:
Из прямоугольного треугольника
получаем:
Ответ:
|
Баллы |
Критерии оценки выполнения задания |
|
2 |
Обоснованно получен верный ответ |
|
1 |
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
|
0 |
Другие случаи, не соответствующие указанным критериям |
|
2 |
Максимальный балл |
15. Решите неравенство:
Решение.
Перепишем неравенство в виде:
Таким образом, множество решений исходного неравенства:
Ответ:
|
Баллы |
Критерии оценки выполнения задания |
|
2 |
Обоснованно получен верный ответ |
|
1 |
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
|
0 |
Другие случаи, не соответствующие указанным критериям |
|
2 |
Максимальный балл |
Критерии оценки выполнения
Общий балл формируется путем суммирования баллов, полученных учащимися за выполнение заданий. За каждое верно выполненное задание части 1 начисляется 1 балл, за каждое задание части 2 – 2 балла.
Оценка работы:
|
Балл |
Отметка |
|
14-18 |
5 |
|
9-13 |
4 |
|
6-8 |
3 |
|
0-5 |
2 |






































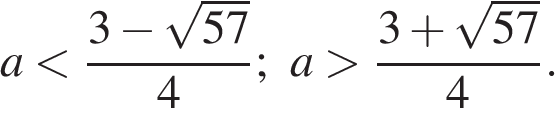
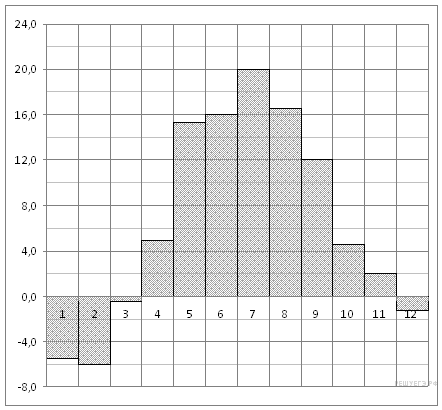
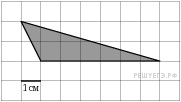
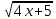 = 5
= 5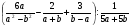
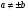 .
.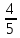 . Найдите АВ.
. Найдите АВ. 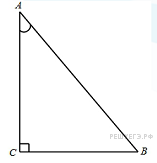
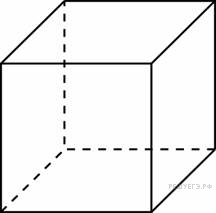
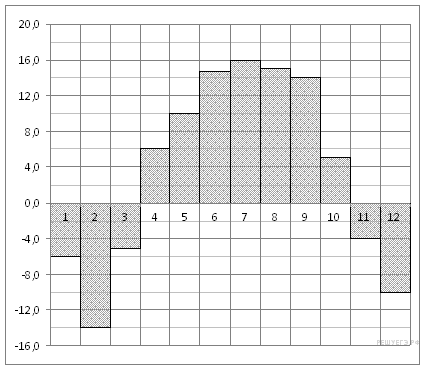
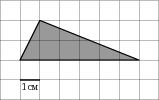
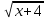 = 7
= 7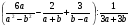
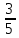 . Найдите АВ.
. Найдите АВ.