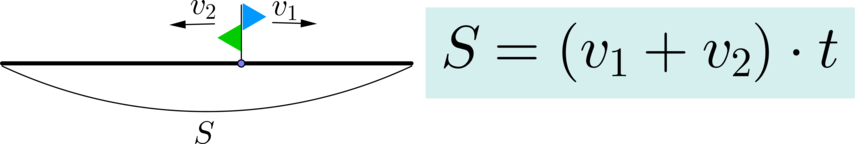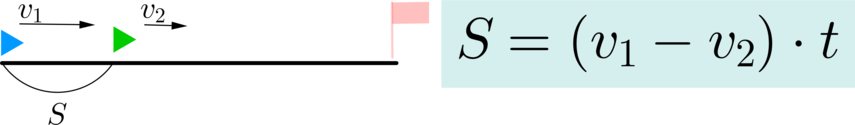в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 56 1–20 | 21–40 | 41–56
Добавить в вариант
Школьник летом на даче жил недалеко от военного аэродрома, на который постоянно садились военно-транспортные самолеты, которые летели всегда по одной и той же траектории («глиссаде»), проекция которой на землю являлась прямой линией, отстоящей на расстояние L = 800 м от дачи школьника. Он вооружился секундомером и точным угломерным инструментом, провел многократные измерения некоторых времен и углов и усреднил их для однотипных марок самолетов. Оказалось, что когда самолет находился на минимальном расстоянии от школьника, угол между горизонталью и направлением на самолет составлял а а звук его двигателей был слышен в месте нахождения школьника спустя время
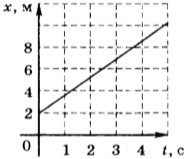
За это время самолет успевал удалиться от точки максимального сближения со школьником на угловое расстояние
Исходя из этих данных, школьник определил скорость
самолета. Чему она оказалась равна?
Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.
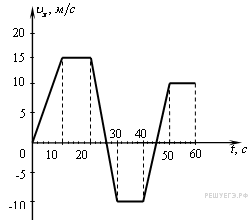
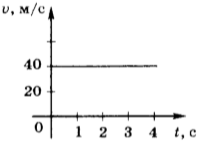
Небольшое тело движется вдоль оси OX. На рисунке показан график зависимости проекции скорости Vx этого тела на указанную ось от времени t. Выберите все верные утверждения на основании анализа графика.
1) За первые 30 секунд движения тело проходит такой же путь, как и за последние 30 секунд движения
2) В интервале времени от t = 20 с до t = 35 с тело движется равномерно
3) В момент времени t = 30 с тело останавливается
4) Тело оказывается на максимальном расстоянии от своего начального положения через 60 секунд после начала движения
5) В моменты времени t = 23 с и t = 33 с тело имеет одинаковое ускорение
На рисунке изображены графики зависимостей скоростей V двух точечных тел от времени t. Известно, что в начальный момент времени координата второго тела равна нулю, и в момент времени t = 10 с тела встретились. Определите начальную координату первого тела. Ответ дайте в метрах.
На рисунке изображены графики зависимостей скоростей V двух точечных тел от времени t. Известно, что в начальный момент времени координата первого тела равна 15 м, и в момент времени t = 10 с тела встретились. Определите начальную координату второго тела. Ответ дайте в метрах.
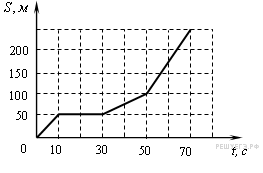
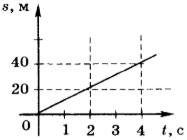
При проведении эксперимента исследовалась зависимость пройденного телом пути S от времени t. График полученной зависимости приведён на рисунке.
Выберите все утверждения, соответствующие результатам этих измерений.
1) Скорость тела равна 6 м/с.
2) Ускорение тела равно 2 м/с2.
3) Тело движется равномерно.
4) За вторую секунду пройден путь 6 м.
5) За пятую секунду пройден путь 30 м.
Источник: Практикум по выполнению типовых тестовых заданий ЕГЭ. С. Б. Бобошина.
В эксперименте по измерению пути, пройденному телом, заполнена таблица зависимости пути от времени. Анализируя данные таблицы, выберите из приведённых ниже утверждений три правильных и укажите их номера.
| t, с | s, м |
| 0 | 0 |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
| 4 | 40 |
1) За каждый из четырёх интервалов времени пройденный телом путь увеличивался на 10 м.
2) Движение тела равномерное.
3) Движение тела равноускоренное.
4) Ускорение тела было постоянным и равным 10 м/с2.
5) Скорость тела была постоянной и равной 10 м/с.
Задания Д1 B1 № 122
Автомобиль движется по прямой улице. На графике представлена зависимость его скорости от времени.
На каком интервале времени модуль ускорения автомобиля максимален?
1) от 0 с до 10 с
2) от 10 с до 20 с
3) от 20 с до 30 с
4) от 30 с до 40 с
К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рис.). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?
Какие законы Вы использовали для описания движения шарика? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 13.12.2017, вариант ФИ10203
Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
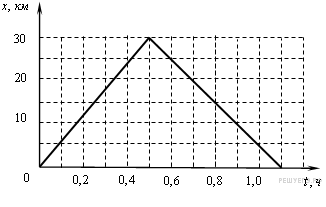
На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке а пункт Б — в точке
Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Задания Д28 C1 № 4500
Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с постоянным ускорением, и догоняет грузовик на расстоянии 150 м от остановки. Чему равно ускорение мотоцикла? Ответ приведите в метрах на секунду в квадрате.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 1.
Задания Д28 C1 № 4640
Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением Сколько времени потребуется мотоциклисту, чтобы догнать грузовик? Ответ приведите в секундах.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 5.
Задания Д28 C1 № 4675
Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через некоторое время t от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с постоянным ускорением 3 м/с Он догоняет грузовик на расстоянии 150 м от остановки. Чему равно t? Ответ приведите в секундах.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 6.
Задания Д28 C1 № 5375
Мимо остановки по прямой улице с постоянной скоростью проезжает грузовик. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с и догоняет грузовик на расстоянии 150 м от остановки. Чему равна скорость грузовика? Ответ приведите в метрах в секунду.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 1.
Задания Д1 B1 № 7172
Координата тела меняется с течением времени согласно закону x = 4 − 2t, где все величины выражены в СИ. Какой из графиков отражает зависимость проекции скорости движения тела от времени?
1) 1
2) 2
3) 3
4) 4
Источник: Демонстрационная версия ЕГЭ—2016 по физике.
Электрон влетает в пространство между пластинами плоского конденсатора со скоростью V0 = 4 · 107 м/с (на рисунке показан вид сверху) на расстоянии d/2 от пластин. Расстояние между пластинами d = 4 мм, длина пластин L = 6 см, напряжение между ними 10 В.
Выберите все верные утверждения.
1) Модуль напряжённости электрического поля в конденсаторе равен 2,5 кВ/м.
2) На электрон внутри конденсатора со стороны электрического поля будет действовать сила, всегда направленная вдоль отрицательного направления оси 0y.
3) В процессе движения электрона внутри конденсатора действующая на него со стороны поля электрическая сила не будет изменяться.
4) Траектория движения электрона в конденсаторе представляет собой прямую линию, направленную под углом к оси 0x.
5) Время, которое потребуется электрону для того, чтобы вылететь из конденсатора, равно 0,0015 мкс.
При постановке первого опыта маленький шарик массой m, несущий заряд q > 0, отпускают с высоты h вблизи поверхности земли без начальной скорости в области, в которой создано однородное электрическое поле. Линии напряжённости этого поля направлены параллельно поверхности земли, сопротивление воздуха пренебрежимо мало. При постановке второго опыта бросают в аналогичных условиях с высоты 2h шарик массой 2m, который несёт заряд q/2. Определите, как изменяются время полёта и горизонтальное смещение шарика при постановке второго опыта по сравнению с первым опытом. Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Время полёта | Горизонтальное смещение |
Задания Д1 B1 № 101
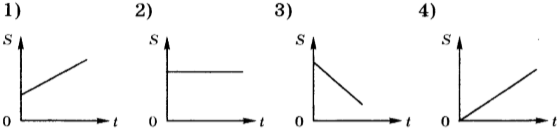
Может ли график зависимости пути от времени иметь следующий вид?
1) да
2) нет
3) может, если траектория прямолинейная
4) может, если тело возвращается в исходную точку
Отрицательно заряженная частица влетает в однородное электрическое поле между пластинами плоского конденсатора (см. рис.). Начальная скорость частицы параллельна пластинам, при вылете из конденсатора скорость частицы направлена под углом α к первоначальному направлению движения. Как изменятся модуль ускорения частицы и время пролёта частицей конденсатора при увеличении напряжённости электрического поля в конденсаторе?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Модуль ускорения частицы | Время пролёта конденсатора |
На рисунке представлен график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t. Чему равна проекция скорости тела υx в интервале времени от 30 до 50 секунд?
Всего: 56 1–20 | 21–40 | 41–56
ЗАДАЧИ на Прямолинейное равномерное
движение с решениями
Формулы, используемые в 9 классе на уроках
«Задачи на прямолинейное равномерное движение».
Название величины |
Обозначение |
Единица измерения (в СИ) |
Связь с другими величинами |
Начальная координата |
х0 |
м |
х0 = х – Sхх0 = х – νxt |
Координата в любой момент времени |
х |
м |
х = х0 + Sхх = х0 + νxt |
Проекция скорости |
νx |
м/с |
|
Проекция перемещения |
Sх |
м |
Sх = νxtSх = х – х0 |
Время |
t |
с |
|
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1.
В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2.
Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.
Типовая задача «График координаты»
Задача № 3.
Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.
Типовая задача «График координаты. Движение нескольких тел»
Задача № 4.
На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.
ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5.
На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.
РЕШЕНИЕ:
Задача № 6.
По графикам на рисунке напишите уравнения движения x = x(t). Из уравнений и графиков найдите координаты тел через 5 с, скорости движения тел, время и место встречи второго и третьего тел.
РЕШЕНИЕ:
Задача № 7.
ОГЭ
Расстояние (S) между городами М и К = 250 км. Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч, из города К — со скоростью ν2 = 40 км/ч. Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.
Задача № 8.
ЕГЭ
Скорость течения реки vp = 1 м/с, скорость лодки относительно воды v0 = 2 м/с. Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м?
Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями
- Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к Списку конспектов по Физике.
- Проверить свои знания по Физике (ОНЛАЙН-ТЕСТЫ)
Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.
В. З. Шапиро
Первое задание ЕГЭ по физике проверяет ваши знания по разделу «Кинематика». Оно относится к базовому уровню, и в нем нет возможности выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.
Определение кинематических величин по графику
1. На рисунке приведён график зависимости проекции скорости тела от времени t.
Определите проекцию ускорения тела в промежутке времени от 15 до 20 с.
Ответ: _________________________ м/с2.Решение:
На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, причем проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:
Проведем расчет:
(м/с2).Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.
Ответ: -4 м/с2.
Секрет решения: Долгое время в учебниках физики движение с переменной скоростью делилось на равноускоренное и равнозамедленное
Но в последнее время в основном применяют термин «равноускоренное движение», подразумевая постоянство ускорения. Только знак проекции ускорения определяет возрастание или убывание скорости движения тела.
Необходимая теория: Равноускоренное движение
2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.
Определите проекцию скорости тела в промежутке времени от 25 до 30 с.
Ответ: ___________________________ м/с.
Согласно представленному графику, зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Чтобы решить задачу, необходимо воспользоваться формулой для определения скорости при равномерном движении:
Проведем расчет:
(м/с)
Ответ: -2 м/с.
Проекция скорости получилась отрицательной, и это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.
Необходимая теория: Вычисление перемещения по графику проекции скорости
3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.
Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.
Ответ: _________________________ м.
Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.).
Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).
(м);
(м);
(м).
Ответ: 450 м.
Полученный пятиугольник можно разбить не только на две трапеции. Здесь можно выделить трапецию, прямоугольник и треугольник. Тогда необходимо рассчитывать площади трех фигур и так же их суммировать.
4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени.
Определите проекцию перемещения тела за 10 с от начала наблюдения.
Ответ: ________________________ м.
Так же, как в задаче №3, модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.
(м);
(м);
(м).
Ответ: 20 м.
При расчете можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с тело движется в направлении, противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.
Относительность движения
5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?
Ответ: ________________________ м/с.
Формула для нахождения относительной скорости в векторной форме имеет вид:
Если два тела движутся навстречу друг другу, то в проекциях на ось оХ это уравнение выглядит следующим образом:
С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.
, скорость первого автомобиля
Ответ: 15 м/с.
В курсе математики при изучении движения двух тел вводятся понятия «скорость сближения» и «скорость удаления». В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.
6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?
Ответ: ___________________________ м.
Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.
(м);
(м).
Знак «минус» для показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.
(м).
Ответ: 40 м.
Секрет решения:. Самое главное в этой задаче – выяснить, в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.
7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?
Ответ: ___________________________ км/ч
Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо. Тогда катеру необходимо держать курс немного левее, чтобы двигаться перпендикулярно береговой линии.
Векторы собственной скорости катера, скорости течения реки и скорости катера относительно береговой линии образуют прямоугольный треугольник. Запишем для него теорему Пифагора:
Ответ: 7,5 км/ч.
Равномерное движение тел по окружности
Необходимая теория: Равномерное движение по окружности
8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.
Ответ: ___________________________ м/с2.
Так как тело движется равномерно по окружности, то найти требуется центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением
Подставляя это выражение в первое уравнение и проводя сокращения, получим
При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.
Проведем расчет:
Ответ: 118 м/с2.
В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.
9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?
Ответ: ___________________________ Гц.
Так как шестерни касаются друг друга, это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.
Приравняем скорости и проведем сокращения.
с учетом того, что период и частота величины обратные, запишем следующее равенство:
Проведем расчет: (Гц).
Ответ: 4 Гц.
В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В данной задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.
10. Волчок, вращаясь с частотой 20 с-1, свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?
Ответ: ___________________________ оборотов.
Вначале определим время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость будет равна 0. Тогда высота и время падения будут связаны формулой отсюда
Проведем расчет времени падения:
(с). Так как волчок вращается с частотой 20
то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.
Ответ: 20.
Секрет решения: Эта задача — комбинированная. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.
Если вы хотите разобрать большее количество заданий — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 1 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на прямолинейное движение
Если тело движется с постоянной скоростью, то пройденное им расстояние удовлетворяет следующей формуле: [{large{S=vcdot t}}] где (v) — его скорость, (t) — время, в течение которого оно двигалось.
Другие вариации данной формулы: (v=dfrac St) и (t=dfrac Sv)
Некоторые частные случаи:
(blacktriangleright) Когда два тела движутся навстречу друг другу со скоростями (v_1) и (v_2) соответственно, то (v_1+v_2) — их скорость сближения. Если (S) — расстояние между ними на момент начала движения, (t) — время, через которое они встретились, то:
(blacktriangleright) Когда тела движутся в противоположном направлении (например, из одной точки), то (v_1+v_2) — их скорость удаления. Тогда расстояние (S) между ними через время (t):
(blacktriangleright) Когда тела движутся друг за другом, то:
((1) quad v_1>v_2). Тогда первое тело догонит второе через некоторой время (t).
(v_1-v_2) — скорость сближения. Если (S) — расстояние между ними в начале движения, то:
((2) quad v_1<v_2). Тогда первое тело никогда не догонит второе и расстояние между ними будет только увеличиваться.
(v_2-v_1) — скорость удаления. Если (S) — расстояние между ними на момент начала движения, то через время (t) расстояние между ними будет:
((3) quad v_1=v_2). Тогда первое тело никогда не догонит второе, но расстояние между ними всегда будет оставаться одинаковым.
Задание
1
#3013
Уровень задания: Легче ЕГЭ
Катер движется по стоячей воде. Собственная скорость катера — (35) км/ч. Навстречу катеру дует ветер, который за каждый час сносит катер на (3) км назад. За сколько часов катер доберется в назначенный пункт, если он находится на расстоянии (144) км от места начала движения катера?
Так как за час катер проходил бы 35 км, но ветер сносит его назад на 3 км, то в итоге за час катер проходит 32 км. Следовательно, 144 км катер пройдет за (144:32=4,5) часа.
Ответ: 4,5
Задание
2
#3014
Уровень задания: Легче ЕГЭ
Яхта движется по стоячей воде, ее собственная скорость — (30) км/ч, встречный ветер каждую минуту сносит яхту на (20) метров. За сколько часов яхта пройдет (259,200) метров?
За каждый час яхта проходила бы 30 км, или 30000 метров, значит, за минуту она проходила бы (30,000:60=500) метров. Так как за каждую минуту ветер сносит ее на 20 метров, то в итоге за минуту яхта проходит 480 метров. Следовательно, ей понадобится (259,200:480=540) минут или (540:60=9) часов.
Ответ: 9
Задание
3
#3017
Уровень задания: Легче ЕГЭ
Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?
Заметим, что за каждый час второй велосипедист будет проходить на (18-10=8) км больше, чем первый. Следовательно, 8 км/ч – скорость удаления. Изначально между велосипедистами было расстояние 0 км, стало – 104 км, следовательно, расстояние между ними изменилось на 104 км. Значит, прошло (104:8=13) часов.
Ответ: 13
Задание
4
#3018
Уровень задания: Легче ЕГЭ
Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?
Заметим, что за каждый час второй велосипедист будет проходить на (17-12=5) км больше, чем первый. Следовательно, 5 км/ч – скорость удаления. Изначально между велосипедистами было расстояние 13 км, стало – 58 км, следовательно, расстояние между ними изменилось на (58-13=45) км. Значит, прошло (45:5=9) часов.
Ответ: 9
Задание
5
#3012
Уровень задания: Легче ЕГЭ
Альпинистка Маша начала ползти по стене, находясь на высоте (2,75) м от пола. За каждую минуту она поднималась бы на (1,5) м, но ветер тут же сносит ее вниз на (0,25) м. Сколько минут она ползет, если теперь она находится на высоте (14) м от пола?
Так как Маша уже находилась на высоте 2,75 м, то проползла она за время наблюдения (14-2,75=11,25) метров. Заметим, что в итоге за каждую минуту она поднимается на 1,25 метров. Следовательно, время, которое она затратила на подъем, равно [11,25:1,25=9 {small{text{минут.}}}]
Ответ: 9
Задание
6
#818
Уровень задания: Легче ЕГЭ
Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.
Пусть (v) км/ч – скорость медленного туриста.
Тогда расстояние, которое прошёл медленный турист, равно (3v), а расстояние, которое прошёл быстрый турист, равно (2v cdot 3 = 6v).
Так как быстрый турист прошёл на 9 км больше, то:
[6v — 3v = 9,] откуда находим (v = 3) км/ч, значит скорость быстрого туриста (2cdot 3 = 6) км/ч.
Ответ: 6
Задание
7
#2128
Уровень задания: Легче ЕГЭ
Лыжник планировал проехать (4, км) с горы с постоянной скоростью (v). Вместо этого первые два километра он проехал в два раза быстрее, чем планировал, а оставшиеся два километра он проехал в два раза медленнее, чем планировал. Во сколько раз больше времени ушло у лыжника на самом деле, чем должно было бы уйти, если бы всё в его жизни было по плану?
Пусть по плану на весь маршрут лыжника должно было уйти (t) часов, тогда на первые два километра (которые составляют половину пути) у лыжника ушло [tcdotdfrac{1}{2}cdotdfrac{1}{2} = 0,25t, ч,,] а на оставшиеся два километра ушло [tcdotdfrac{1}{2}cdot 2 = t, ч,,] следовательно, на весь путь ушло (1,25t, ч), то есть в (1,25) раза больше, чем было запланировано изначально.
Ответ: 1,25
Задачи на прямолинейное движение в ЕГЭ по математике могут быть как совсем простыми, без необходимости вводить переменную, так и более сложными, где требуется свести задание к решению квадратного уравнения. Для успешного выполнения подобного упражнения школьнику необходимо прежде всего запомнить следующую формулу:
[{large{S=Vcdot t}}] где (S) — пройденное расстояние, (V) — скорость, (t) — время, в течение которого двигалось тело.
Для того чтобы решить задачи на прямолинейное движение в ЕГЭ, учащимся из Москвы и других городов также для большей наглядности стоит выполнить чертеж. На нем нужно отметить все векторы, о которых идет речь в условии упражнения.
Для того чтобы правильно решить задачи на прямолинейное движение в ЕГЭ и получить заветные баллы, многим школьникам необходимо восполнить пробелы в знаниях по данной теме. Поможет в этом образовательный проект «Школково». Наш ресурс предоставляет возможность не только повторить теоретический материал, но и познакомиться с различными вариантами решения заданий по данной теме.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задание 1 № 101. Может ли график зависимости пути от времени иметь следующий вид?
1) да
2) нет
3) может, если траектория прямолинейная
4) может, если тело возвращается в исходную точку
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем, так что представленный график не может изображать зависимость пути от времени.
Правильный ответ: 2.
Задание 1 № 125. Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Решение.
В системе отсчета, связанной с винтом, точка на конце лопасти не двигается. Следовательно, ее траектория в данной системе отсчета представляет собой точку.
Правильный ответ: 1.
Задание 1 № 126. Два автомобиля движутся по прямому шоссе: первый — со скоростью ν, второй — со скоростью -3 ν. Какова скорость второго автомобиля относительно первого?
|
1) |
2) |
3) |
4) |
Решение.
Скорость второго автомобиля относительно первого равна ν2 — ν 1=-3 ν- ν= -4ν
Правильный ответ: 2.
Задание 1 № 131. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды ν . Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Решение.
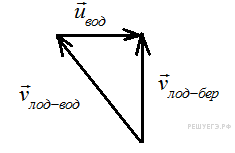
2 способ:
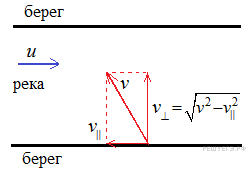
Правильный ответ: 4.
Задание 1 № 133. На рисунке представлен график зависимости пути S велосипедиста от времени t.
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью 5 м/с.
1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Решение.
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
.
На других интервалах скорость была иная.
Правильный ответ: 4.
Задание 1 № 134. На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке х=0, а пункт Б — в точке х=30 км. Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Решение.
Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна: 30-0/0,5=60 км/ч.
Задание 1 № 138. На рисунке приведен график зависимости проекции скорости тела от времени.
Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Задание 1 № 317. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки:. Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение: 0,4 + 0,3 =0,7 м/с.
Задание 1 № 3354. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.
|
t, с |
0 |
1 |
2 |
3 |
4 |
5 |
|
x1, м. |
0 |
2 |
4 |
6 |
8 |
10 |
|
x2, м |
0 |
0 |
0 |
0 |
0 |
0 |
|
x3, м |
0 |
1 |
4 |
9 |
16 |
25 |
|
x4, м |
0 |
2 |
0 |
-2 |
0 |
2 |
У какого из тел скорость могла быть постоянна и отлична от нуля?
Решение.
Таблица содержит информацию о положениях тел только в отдельные моменты времени. В промежутках между указанными временами тела могли двигаться абсолютно произвольно. Определим тело, скорость которого могла бы быть постоянной и отличной от нуля. При движении с постоянной скоростью координата тела за равные промежутки времени изменяется одинаково. Из таблицы видно, что этому свойству удовлетворяет только первое тело. Значит, скорость первого тела могла быть постоянной и не равной нулю.
Задание 1 № 3357. Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Решение.
Крайняя точка лопасти вертолета двигается по окружности вокруг оси вращения винта. Поскольку ось вращения жестко связана с корпусом вертолета, такую же траекторию описывает эта точка и относительно любой точки корпуса. Правильный ответ 3.
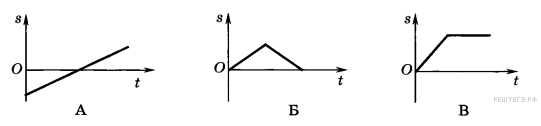
Задание 1 № 3539. На каком из графиков изображена возможная зависимость пройденного пути от времени?
1) А
2) Б
3) В
4) Такой график отсутствует
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем. Этому требованию удовлетворяет только график В.
Правильный ответ: 3.
Задание 1 № 3540. Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Решение.
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: . То есть, буквально, надо весь пройденный телом путь разделить на все время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберемся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: . В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через ? тогда весь путь пройденный велосипедистом равен . На первую половину пути велосипедист затратил время . На обратную дорогу — время . Все время пути составило . Окончательно, находим, что средняя путевая скорость велосипедиста равна
.
Задание 1 № 3541. Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
Решение.
Из графика видно, что начальная координата тела равна . Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: . Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при и равен 20 м.
Ответ: 6 с
Задание 1 № 3544. Движение двух велосипедистов заданы уравнениями x1 =2 t и x2 =100- 8 t . Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Решение.
Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение . Теперь не составляет труда определить координату места встречи:
Задание 1 № 3545.
На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t1 = 1 c до t2 = 4 c. (Ответ дайте в метрах.)
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от до электрокар двигался в положительном направлении оси . При этом его координата изменилась на . Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно . Таким образом, путь, пройденный машинкой за интервал времени от до равен .
Задание 1 № 3548. Пешеход идет по прямолинейному участку дороги со скоростью v. Навстречу ему движется автобус со скоростью 10v. С какой скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
1)
2)
3)
4)
Решение.
Обозначим искомую скорость велосипедиста через . Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью , а к автобусу — со скоростью .
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Правильный ответ: 1.
Задание 1 № 3549. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Обозначим искомую скорость течения реки через , а скорость парохода в стоячей воде — через . Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна . Скорость парохода вверх по течению: . Решая систему из двух этих уравнений, для скорости течения воды имеем .
Задание 1 № 3734.
Материальная точка движется вдоль оси OX. На рисунке представлен график зависимости проекции скорости этой материальной точки на ось OX от времени. Какой из приведенных ниже графиков может соответствовать зависимости координаты материальной точки от времени?
1) 1
2) 2
3) 3
4) 4
Решение.
Из графика видно, что проекция скорости материальной точки на ось OX положительна и постоянна, а значит, точка движется равномерно и в положительном направлении оси OX. Единственный график, удовлетворяющий обоим этим требованиям, — это график под номером 1.
Правильный ответ: 1.
Задание 1 № 3783. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
Решение.
Из графика видно, что для обоих тел пройденный путь линейно зависит от времени, а значит, оба тела двигались с постоянными по величине скоростями. Модуль скорости первого тела равен . Скорость же второго тела: . Следовательно, скорость второго тела больше скорости первого тела на величину
Задание 1 № 3867.
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Решение.
Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем
Для тела 2:
Таким образом модуль скорости одного тела относительно другого равен
Задание 1 № 4077. Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Решение.
Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» связана со скоростью этого тела относительно «подвижной системы отсчёта» и скоростью движения «подвижной с. о.» относительно «неподвижной» при помощи следующего соотношения: В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:
Ответ: 11 м/с
Задание 1 № 4186. Координата материальной точки изменяется с течением времени по закону x=3-2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1) 1
2) 2
3) 3
4) 4
Решение.
Из зависимости видно, что координата убывает со временем, при этом в начальный момент времени координата равна а в начало координат материальная точка попадает в момент времени: Таким образом, зависимости соответствует график под номером 4.
Правильный ответ: 4.
Задание 1 № 4221. Координата материальной точки изменяется с течением времени по закону . x=3+ 2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1)
2)
3)
4)
Решение.
Из зависимости видно, что координата возрастает со временем, при этом в начальный момент времени координата равна , а в момент времени координата равна . Таким образом, зависимости соответствует график под номером 3.
Правильный ответ: 3.
Задание 1 № 4409. По плоскости движутся четыре точечных тела —А, Б, В, Г. x=1+t., y=2 t, и , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид и . Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая .
Правильный ответ: 3
Задание 1 № 4444. По плоскости движутся четыре точечных тела — А,Б В, и Г, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид x=2t.и . y=1+ t. Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая A.
Правильный ответ: 1
Задание 1 № 4934. Два автомобиля движутся по прямому шоссе: первый со скоростью , второй со скоростью относительно шоссе. Скорость первого автомобиля относительно второго равна
1)
2)
3)
4)
Решение.
Скорость первого автомобиля относительно второго равна
.
Правильный ответ: 2.
Равномерное прямолинейное движение
1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.
Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.
2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.
Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.
Если за время ( t ) тело совершило перемещение ( vec{s} ), то скорость его движения ( vec{v} ) равна ( vec{v}=frac{vec{s}}{t} ).
Единица скорости: ( [,v,]=frac{[,s,]}{[,t,]} ); ( [,v,]=frac{1,м}{1,с}=1frac{м}{с} ). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.
Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: ( vec{s}=vec{v}t ). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.
3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.
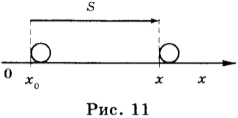
Пусть ( vec{s} ) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ( x_0 ) — координата начальной точки перемещения, ( x ) — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: ( vec{s}_x=x-x_0 ). С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. ( vec{s}_x=vec{v}_xt ). Откуда ( x-x_0=vec{v}_xt ) или ( x=x_0+vec{v}_xt ). Если начальная координата ( x_0 ) = 0, то ( x=vec{v}_xt ).
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.
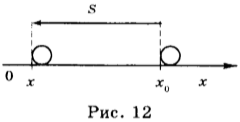
Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ( x>x_0 ). Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае ( x<x_0 ).
4. Зависимость координаты от времени можно представить графически.
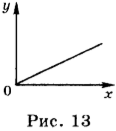
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ( x ) = 4 м/с · ( t ). Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).
Для того чтобы её построить, необходимо иметь две точки: одна из них ( t ) = 0 и ( x ) = 0, а другая ( t ) = 1 с, ( x ) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.
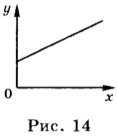
Если в начальный момент времени координата тела ( x_0 ) = 2 м, а проекция его скорости ( v_x ) = 4 м/с, то уравнение движения имеет вид: ( x ) = 2 м + 4 м/с · ( t ). Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ( t ) = 0, ( x ) = 2 м (рис. 14).
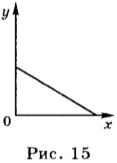
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: ( x ) = 2 м – 4 м/с · ( t ). График зависимости координаты такого движения от времени представлен на рисунке 15.
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.
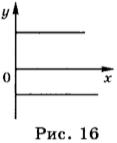
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.
Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.
При решении задачи целесообразно придерживаться следующей последовательности действий:
- Кратко записать условие задачи.
- Проанализировать ситуацию, описанную в условии задачи:
— выяснить, можно ли принять движущиеся тела за материальные точки;
— сделать рисунок, изобразив на нём векторы скорости;
— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела. - Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
- Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
- Решить задачу в общем виде.
- Подставить в формулу значения величин и выполнить вычисления.
- Проанализировать ответ.
Применим эту последовательность действий к приведённой выше задаче.
Дано: ( v_1 ) = 15 м/с ( v_2 ) = 12 м/с ( l ) = 270 м. Найти: ( t ) – ? ( x) – ?
Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь
Система отсчёта связана с Землёй, ось ( Ox ) направлена в сторону движения первого тела, начало отсчёта координаты — т. ( O ) — положение первого тела в начальный момент времени.
Начальные условия: ( t ) = 0; ( x_{01} ) = 0; ( x_{02} ) = 270.
Уравнение в общем виде: ( vec{s}=vec{v}t ); ( x=x_0+v_xt ).
Уравнения для каждого тела с учётом начальных условий: ( x_1=v_1t ); ( x_2=l-v_2t ). В месте встречи тел ( x_1=x_2 ); следовательно: ( v_1t=l-v_2t ). Откуда ( t=frac{l}{v_1+v_2}cdot t ). Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ( x ) = 150 м.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?
1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с
2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?
1) 0,25 м
2) 6 м
3) 10 м
4) 150 м
3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ( v_1 ) и скорости «Пежо» — ( v_2 ).
1) ( v_1=v_2 )
2) ( v_1=2v_2 )
3) ( 2v_1=v_2 )
4) ( 1,2v_1=10v_2 )
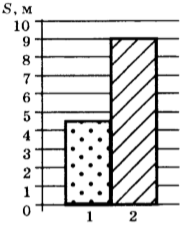
4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ( v_1 ) и ( v_2 ).
1) ( v_1=v_2 )
2) ( v_1=2v_2 )
3) ( 3v_1=v_2 )
4) ( 2v_1=v_2 )
5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен
1) 20 м
2) 40 м
3) 80 м
4) 160 м
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ( v_1 ), ( v_2 ) и ( v_3 ) движения этих тел.
1) ( v_1=v_2=v_3 )
2) ( v_1>v_2>v_3 )
3) ( v_1<v_2<v_3 )
4) ( v_1=v_2 ), ( v_3<v_1 )
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м
10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид
1) ( x=1t ) (м)
2) ( x=2+3t ) (м)
3) ( x=2-1t ) (м)
4) ( x=4+2t ) (м)
11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость
ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит
12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось
Часть 2
13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?
Ответы
Равномерное прямолинейное движение
3 (59.44%) 144 votes