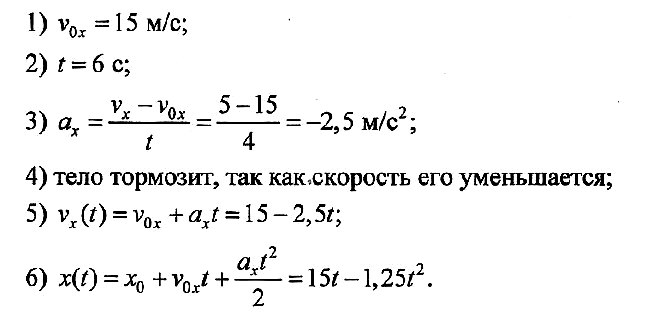Равнопеременное движение ускорение тела решу егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

В этой статье разобраны задачи на движение тела с постоянным ускорением. Начинать решать задачи на новую тему нужно всегда с простых, постепенно увеличивая сложность, поэтому следующая статья будет включать в себя уже действительно интересные задачи. Падение тел также происходит с постоянным ускорением, поэтому можно просмотреть и статью на эту тему, там тоже собраны интересные задачи.

Задача 1.

Известно, что материальная точка за время с  прошла путь м, причем ее скорость увеличилась в раз. Определить ускорение, считая его постоянным.

Пусть начальная скорость точки , тогда конечная — .

Ускорение равно .

Тогда ускорение равно

Ответ: начальная скорость тела 2 м/с, а ускорение м/c

Задача 2.

Автомобиль движется с постоянным ускорением м/с. Мимо наблюдателя он проезжает со скоростью м/с. На каком расстоянии от наблюдателя он был секунду назад?

Первый способ решения: найдем скорость автомобиля секунду назад (м/с):

Тогда путь, пройденный автомобилем за секунду с начальной скоростью 9,5 м/с с данным ускорением, равен, м:

Второй способ решения: представим обратный процесс, процесс торможения автомобиля, начальная скорость которого равна 10,5 м/с и ускорение 1 м/с. Тогда он пройдет точно такой же путь, как и при разгоне:

Ответ: автомобиль находился в 10 метрах от наблюдателя.

Задача 3.

Водитель автомобиля, движущегося со скоростью км/ч, подъезжая к закрытому железнодорожному переезду, начал тормозить за 50 м до него. У переезда машина стояла с. После того как шлагбаум открыли, водитель набрал прежнюю скорость на том же отрезке пути. На сколько ближе к месту назначения оказался бы водитель автомобиля, если бы он ехал с прежней скоростью без остановки? Движение при разгоне и торможении считать равнопеременным.

Скорость в 72 км/ч – это 20 м/с. Обычно удобно сразу все величины перевести в СИ.

Найдем время торможения автомобиля и ускорение при торможении.

Конечная скорость по окончании торможения равна 0, поэтому

Тогда время торможения мы найдем из выражения для скорости:

Очевидно, что разгон с таким же ускорением будет длиться столько же, то есть 5 с. Тогда вместе со временем стоянки на переезде водитель потерял минуту. Если бы он не останавливался, то проехал бы за эту минуту   м. А из-за задержки он преодолел только 100: 50 при разгоне и 50 при торможении. Таким образом, водитель оказался бы дальше на 1100 м, если бы не переезд.

Ответ: 1100 м

Другой, более лаконичный вариант решения здесь.

Задача 4.

Тело начинает двигаться из состояния покоя равноускоренно и за 10-ю секунду проходит путь м. Найти путь, пройденный телом за 12-ю секунду движения.

При постоянном ускорении пути, которые тело проходит за каждую следующую секунду, относятся как ряд последовательных нечетных чисел:

Тогда м, м. А м.

Ответ: 46 м.

Задача 5.

Двигаясь прямолинейно и равноускоренно, тело проходит путь м за первые с, а следующий промежуток длиной м за с. Определить ускорение тела.

Запишем уравнения для пути, пройденного телом. Начальная скорость его нам неизвестна. Поэтому обозначим ее за . Тогда для первого участка пути:

Поскольку за первые 4 с тело изменило свою скорость , то начальной скоростью для второго участка пути будет уже  и тогда путь, пройденный телом на втором участке, равен:

Объединим эти два уравнения в систему и решим совместно:

Решая эту систему, получаем м/c, м/с.

Ответ: м/с см/с

Задача 6.

Автомобиль начинает спускаться с горы без начальной скорости и за время мин приобретает скорость км/ч. Одновременно навстречу ему начинает подъем в гору автомобиль, имеющий начальную скорость м/c. За время мин скорость второго автомобиля уменьшается до м/с. Какое расстояние будет разделять автомобили через с после начала движения, если длина горы км? Движение автомобилей считать равноускоренным.

Переведем все данные задачи в единицы СИ: с, м/с.

Теперь можем определить ускорения автомобилей:

Тогда путь, пройденный первым автомобилем:

А второй пройдет

Таким образом, между автомобилями через 80 с останется расстояние, равное м.

А  интересно, сможет ли второй автомобиль преодолеть подъем? Определим его скорость на вершине:

Получили корень из отрицательного числа, поэтому, если водитель не добавит газу, то второй автомобиль не сможет преодолеть подъем.

Ответ: 640 м.

Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.

Обозначим: — вектор начальной скорости,  — изменение скорости, а Δt — промежуток времени.

Пусть  Δt₁= Δt₂=Δt₃=…, тогда по определению

Следовательно,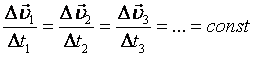

Т.о., это характеристика движения.

Если t₀=0, то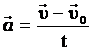    

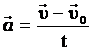
УСКОРЕНИЕ — физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло.

Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ —    м/с².

Например, ускорение равно 5 м/с²  — это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения.

В случае не равнопеременного движения:

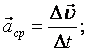
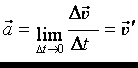
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает.

Условие р.у.д. —.

Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается.

Условие р.з.д. — .

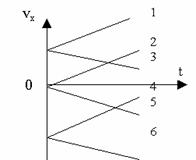
Графики равнопеременного движения.

или  — в проекциях;

или – через модули.

Линейная функция. График — прямая.

Движения, совпадающие с направлением координатной оси:

1. равноускоренноес начальной скоростью

2. равноускоренное без начальной скорости

3. равнозамедленное

4. равнозамедленное

5. равноускоренное без начальной скорости

6. равноускоренное с начальной скоростью

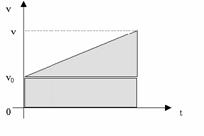
Перемещение при равнопеременном движении.

Площадь под графиком скорости численно равна перемещению.

Следовательно, площадь трапеции численно равна перемещению.

Решение основной задачи механики для р.у.д. :

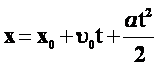
Графики перемещения и координаты.

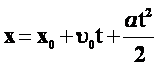
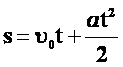
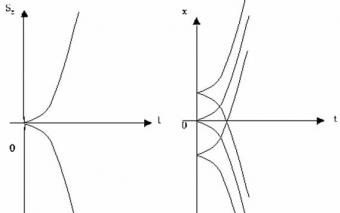
Функции   и   — квадратичные. График – парабола!

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

Формулы, используемые в 9-11 классах по теме
«ЗАДАЧИ на Прямолинейное равноускоренное движение».

Название величины	Обозначение	Единица измерения	Формула
Время	t	с
Проекция начальной скорости	v0x	м/с
Проекция мгновенной скорости	vx	м/с
Проекция ускорения	ax	м/с2
Проекция перемещения	Sx	м
Координата	x	м

1 мин = 60 с;   1 ч = 3600 с;   1 км = 1000 м;   1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача № 1.
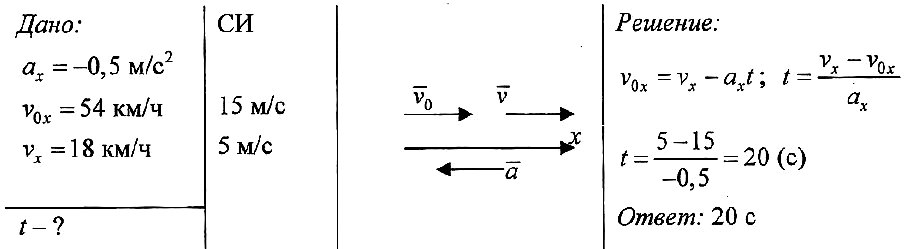
 Автомобиль, двигаясь с ускорением –0,5 м/с², уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?

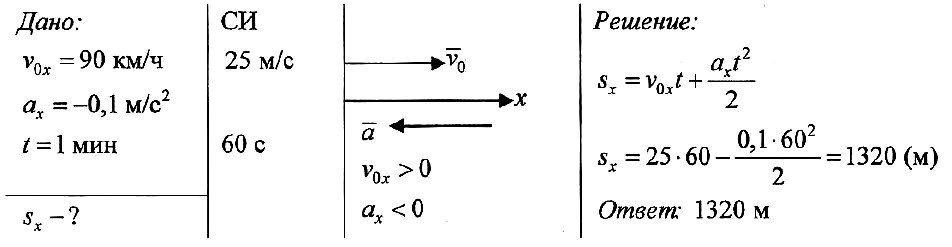
Задача № 2.
 При подходе к станции поезд начал торможение с ускорением 0,1 м/с², имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.

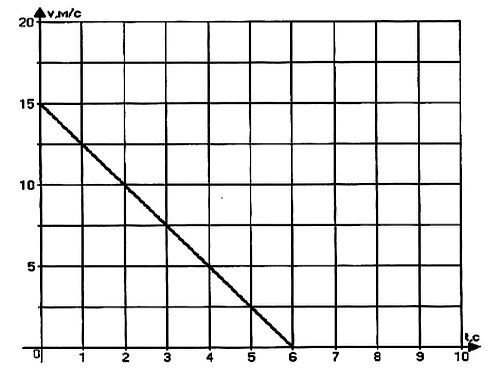
Задача № 3.
 По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит);  5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

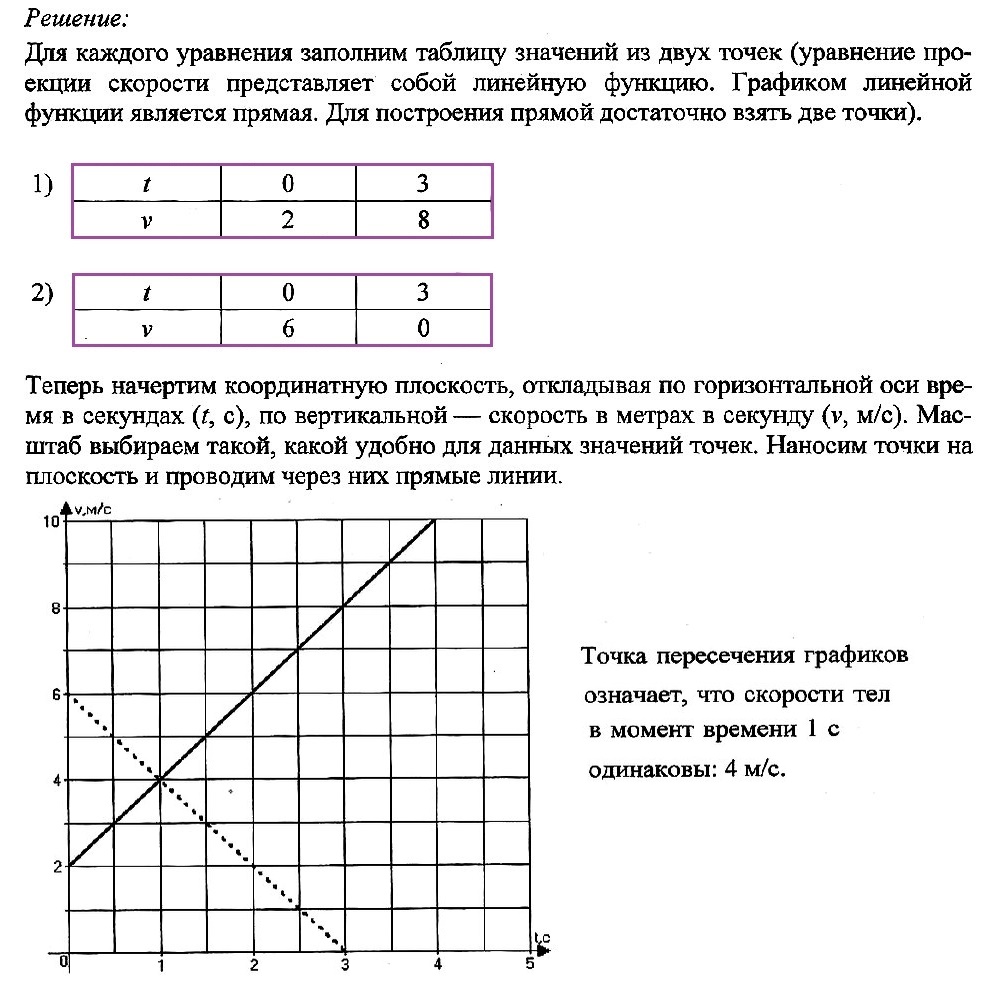
Решение:

Задача № 4.
 Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v_2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Задача № 5.
 Движение тела задано уравнением x(t) = 5 + 10t — 0,5t².  Определите:  1) начальную координату тела;  2) проекцию скорости тела;  3) проекцию ускорения;  4) вид движения (разгоняется тело или тормозит);  5) запишите уравнение проекции скорости;  6) определите значение координаты и скорости в момент времени t = 4 с.  Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.

Решение:

Задача № 6.
 Вагон движется равноускоренно с ускорением -0,5 м/с². Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

Задача № 7.
 Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с² в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Задача № 8.
 Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с². Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

Задача № 9.
 Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м, причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.

Задача № 10. (повышенной сложности)
 Прямолинейное движение описывается формулой х = –4 + 2t – t². Опишите движение, постройте для него графики v_x(t), s_x(t), l(t).

Задача № 11.
  ОГЭ
 Поезд, идущий со скоростью v₀ = 36 км/ч, начинает двигаться равноускоренно и проходит путь S = 600 м, имея в конце этого участка скорость v = 45 км/ч. Определить ускорение поезда а и время t его ускоренного движения.

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на Свободное падение тел с решениями
• Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике (онлайн-тесты).

Равнопеременное
движение, ускорение тела

1. Автомобиль движется по прямой
улице. На графике представлена зависимость скорости автомобиля от времени. Чему
равен максимальный модуль ускорения? Ответ выразите в м/с2.

2. Тело разгоняется на прямолинейном
участке пути, при этом зависимость пройденного телом пути S от
времени t имеет вид:

 Чему равна скорость тела в момент
времени t = 2 c при таком движении? (Ответ дайте в метрах в
секунду.)

3. При прямолинейном движении
зависимость координаты тела x от времени t имеет вид:

 Чему равна скорость тела в момент
времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)

4.Зависимость координаты x тела
от времени t имеет вид:

Чему равна проекция скорости тела на
ось Ox в момент времени t = 3 с при таком движении? (Ответ
дайте в метрах в секунду.)

5. Зависимость
координаты x тела от времени t имеет вид:

 Чему равна проекция скорости тела на
ось Ox в момент времени t = 1 с при таком движении? (Ответ
дайте в метрах в секунду.)

6. Зависимость координаты x тела
от времени t имеет вид: 

Через сколько секунд после начала отсчета
времени t = 0 с проекция вектора скорости тела на
ось Ox станет равной нулю?

7. На рисунке приведен график
зависимости проекции скорости тела от времени. Чему равна проекция ускорения
тела в момент времени 16 с? Ответ выразите в м/с2. 

8.На рисунке приведен график зависимости
проекции скорости тела от времени. Чему равна проекция ускорения тела в момент
времени 6 с? Ответ выразите в м/с2.

9. На рисунке приведен график
зависимости проекции скорости тела от времени. Чему равна проекция ускорения
тела в момент времени 26 с? Ответ выразите в м/с2.

10. На рисунке приведен график
зависимости проекции скорости тела от времени. Чему равна проекция ускорения
тела в момент времени 54 с? Ответ выразите в м/с2. 

11. На рисунке приведен график
зависимости проекции скорости тела от времени. Чему равна проекция ускорения
тела в момент времени 45 с? Ответ выразите в м/с2.

12. Тело брошено вертикально вверх.
Через 0,5 с после броска его скорость 20 м/с. Какова начальная скорость
тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)

13. Автомобиль движется прямолинейно.
На графике представлена зависимость скорости автомобиля от времени. Чему равен
минимальный модуль ускорения? Ответ выразите в м/с2 

14. Тело брошено вертикально вверх с
начальной скоростью 20 м/с. Чему равен модуль скорости тела через 0,5 c
после начала отсчета времени? Сопротивление воздуха не учитывать. (Ответ дайте
в метрах в секунду.)

15. Велосипедист съезжает с горки,
двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста
увеличилась на 10 м/с. Ускорение велосипедиста — 0,5 м/с2. Сколько секунд
длился спуск?

16. 

Тело начинает
двигаться из начала координат вдоль оси Ox, причем проекция
скорости vx меняется с течением времени по закону, приведенному на
графике. Чему будет равна проекция ускорения тела ax через 2 c?
(Ответ дайте в метрах в секунду в квадрате.)

17. 

На графике
приведена зависимость скорости прямолинейно движущегося тела от времени.
Определите модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)

18. Небольшое тело движется вдоль
оси Ox. Его координата x изменяется с течением
времени t по закону

 где  выражено
в секундах, а  —
в метрах. Чему равна проекция ускорения этого тела на ось Ox в момент
времени ?
(Ответ дайте в метрах в секунду в квадрате.)

19. Точечное тело начинает движение
из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой
горизонтальной поверхности. Используя таблицу, определите значение проекции на
ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в
квадрате.) 

20. Точечное тело начинает движение
из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой
горизонтальной поверхности. Используя таблицу, определите значение проекции на
ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в
квадрате.) 

21. На графике приведена зависимость
скорости тела от времени при прямолинейном движении. Определите по графику
ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)

 22. 

На графике
приведена зависимость скорости тела от времени при прямолинейном движении.
Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в
квадрате.)

23.

На графике
приведена зависимость проекции скорости vx тела от времени.
Определите ускорение тела ax. (Ответ дайте в метрах в секунду в квадрате.)

24.

На графике
приведена зависимость проекции скорости тела от времени. Определите по графику
модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)

25. Мальчик съезжает на санках
равноускоренно со снежной горки. Скорость санок в конце спуска 10 м/с.
Ускорение равно 1 м/с2, начальная скорость равна нулю. Какова длина горки?
(Ответ дайте в метрах.)

26. Автомобиль трогается с места и
движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его
скорость в конце пути оказалась равной 15 м/с? (Ответ дайте в метрах.)

27. При равноускоренном движении
автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему
равно ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)

28. Велосипедист съезжает с горки,
двигаясь равноускоренно. Начальная скорость велосипедиста равна нулю. У
основания горки длиной 100 м скорость велосипедиста 10 м/с. Чему равно его
ускорение? (Ответ дайте в метрах в секунду в квадрате.)

29. На рисунке приведён график
зависимости проекции скорости тела vx от времени. Чему равна проекция
ускорения этого тела ax в интервале времени от 6 с до 10 с? Ответ
выразите в м/с2.

30. На рисунке приведен график
зависимости проекции скорости тела от времени. Чему равна проекция ускорения
этого тела ax в интервале времени от 5 с до 10 с? Ответ выразите в
м/с2.

31.На рисунке приведён график зависимости
проекции скорости тела  от
времени. Чему равна проекция ускорения этого тела  в
интервале времени от 0 до 10 с? Ответ выразите в м/с2.

32. Автомобиль движется по прямой
улице. На графике представлена зависимость проекции его скорости от времени.
Чему равна проекция ускорения автомобиля ax в интервале времени от 10
до 20 с? Ответ выразите в м/с2.

33. Небольшое тело движется вдоль
горизонтальной оси Ox. В момент времени  координата
этого тела равна  На
рисунке приведена зависимость проекции скорости  этого
тела на ось Ox от времени  Чему
равна координата тела в момент времени ?

34. Небольшое тело движется вдоль
горизонтальной оси Ox. В момент времени  координата
этого тела равна  На
рисунке приведена зависимость проекции скорости  этого
тела на ось Ox от времени  Чему
равна координата тела в момент времени ?

35. Тело движется равноускоренно, не
изменяя направления движения. За две секунды модуль скорости тела увеличился от
4 м/с до 5 м/с. Какой путь прошло тело за это время?

36.Тело движется равнозамедленно, не
изменяя направления движения. За две секунды модуль скорости тела уменьшился от
4 м/с до 3 м/с. Какой путь прошло тело за это время?

Ответы:

Равноускоренное движение.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение — это движение с постоянным вектором ускорения . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

к оглавлению ▴

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

. (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор ? Разумеется, функцию . Но не только: к ней можно добавить ещё произвольный постоянный вектор (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы ? В начальный момент времени скорость равна своему начальному значению: . Поэтому, полагая в формуле (2), получим:

.

Итак, константа — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

. (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

, (4)

. (5)

Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)

к оглавлению ▴

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

Подставляем сюда выражение для скорости, даваемое формулой (3):

(6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить , надо продифференцировать функцию . Чтобы получить , нужно продифференцировать . Не забудем добавить и произвольную константу :

.

Ясно, что — это начальное значение радиус-вектора в момент времени . В результате получаем искомый закон равноускоренного движения:

. (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

. (8)

. (9)

. (10)

Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что — перемещение тела. Тогда
получаем зависимость перемещения от времени:

.

к оглавлению ▴

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

,

,

,

где — проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

и подставим в формулу для перемещения:

.

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

.

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

к оглавлению ▴

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения , направленным вертикально вниз. Почти во всех задачах при расчётах полагают м/с.

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

.

Имеем: — искомая скорость приземления, . Получаем: , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

.

Здесь , так что . Вычисляем: м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

.

Имеем: так что , или . Решая квадратное уравнение, получим c.

к оглавлению ▴

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат так, как показано на рис. 1.

Рис. 1. Горизонтальный бросок

Используем формулы:

В нашем случае . Получаем:

. (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

.

Дальность полёта — это значение координаты в момент времени :

.

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

.

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

к оглавлению ▴

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью , направленной под углом к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

,

.

В нашем случае . Получаем:

.

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

,

,

.

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

.