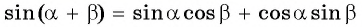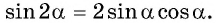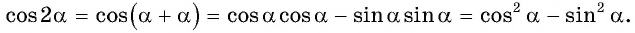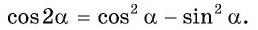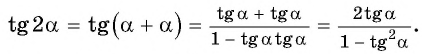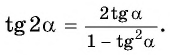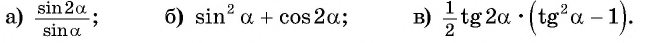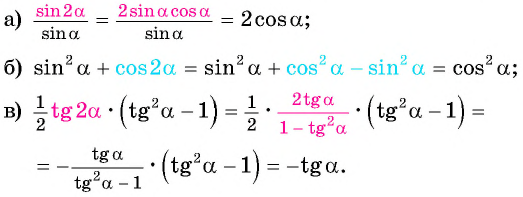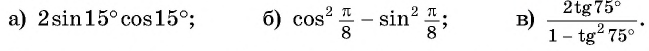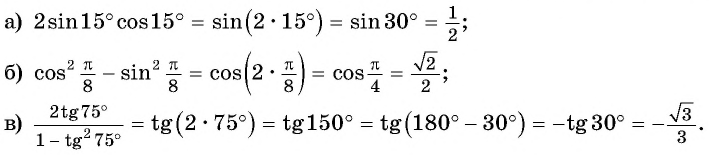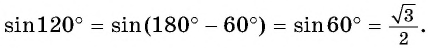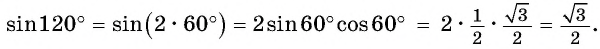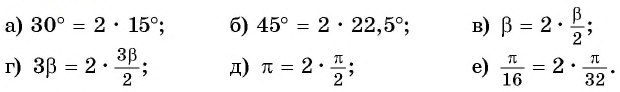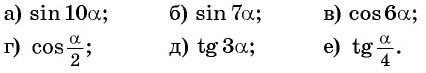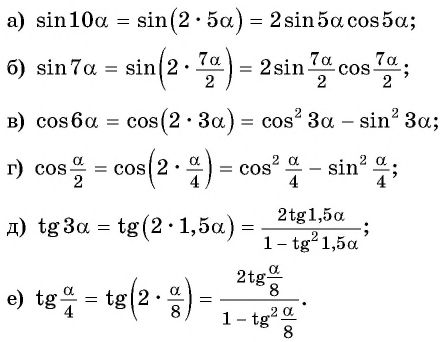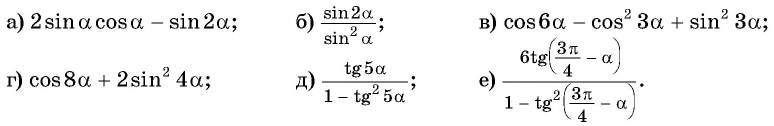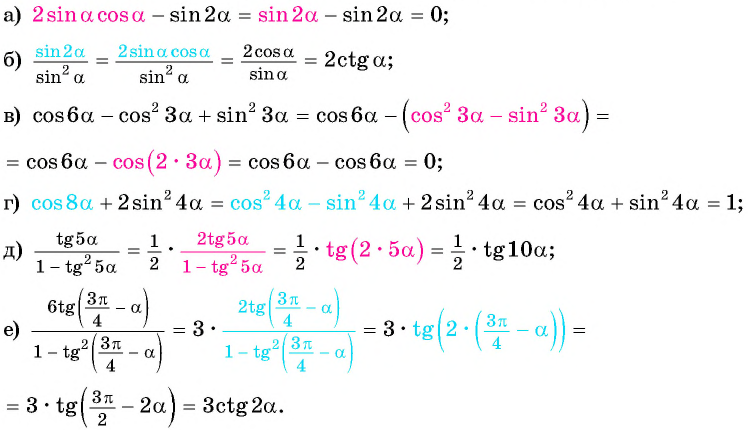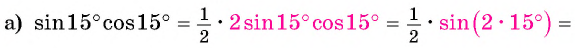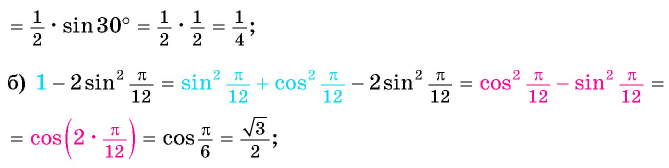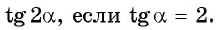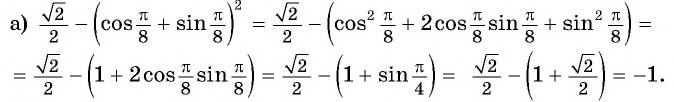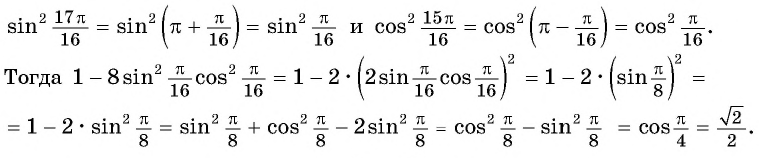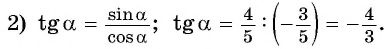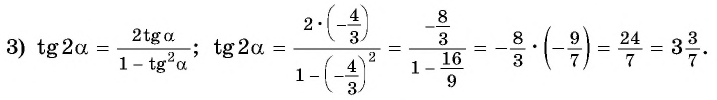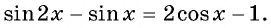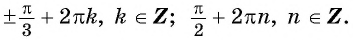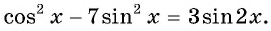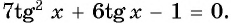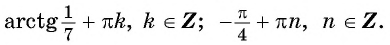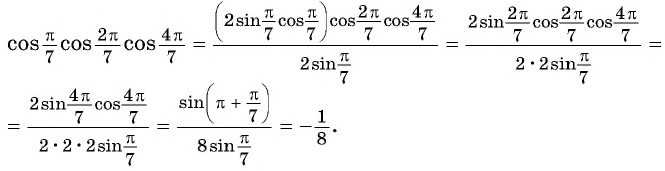Синус косинус двойного угла егэ - Exhelper.top

Поиск

Всего: 150 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите значение выражения:

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.3 Синус, косинус, тангенс и котангенс числа, 1.2.4 Основные тригонометрические тождества, 1.4.4 Преобразования тригонометрических выражений, 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 1.2.2 Радианная мера угла, 1.2.5 Формулы приведения, 1.2.6 Синус, косинус и тангенс суммы и разности двух углов, 1.2.7 Синус и косинус двойного угла

Найдите значение выражения

Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.

Найдите значение выражения

Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 2

Найдите значение выражения

Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 4

Найдите значение выражения:

Найдите значение выражения

Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018

Найдите значение выражения

Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2.

Источник: Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2019 по математике. Профильный уровень.

Найдите значение выражения

Источник: ЕГЭ по математике 02.06.2022. Основная волна. Восток

Найдите значение выражения

Найдите  если

Найдите значение выражения

Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 2.

Найдите значение выражения

Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1., ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть).

Найдите значение выражения

Всего: 150 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Видеоурок 1: Косинус и синус двойного угла, часть 1

Видеоурок 2: Косинус и синус двойного угла, часть 2

Лекция: Синус и косинус двойного угла

Если произвольный аргумент тригонометрической функции можно записать в виде произведения некоторого угла на 2, то для таких углов можно использовать формулы двойного угла.

Итак, давайте воспользуемся некоторой формулой для суммы аргументов:

А теперь давайте предположим, что углы α и β равны, то получим cos (2 β) = cos² β — sin² β.

Если данное предположение мы сделаем относительно синуса, то получим:

Если сделать аналогичные преобразования, то можно получить:

Все перечисленные формулы применимы для двойного аргумента.

Источник

Примеры:

(2 sin⁡15^° cos⁡15^°=sin⁡(2·15^°)=sin⁡30^° =frac{1}{2})
(cos⁡6α=cos^2⁡3α-sin^2⁡3α)
(sin⁡α=2 sin⁡frac{α}{2}cos⁡frac{α}{2})
(2 cos^2⁡frac{π}{12}-1=cos⁡frac{2π}{12}=cos⁡frac{π}{6}=frac{sqrt{3}}{2})

Примеры решения задач из ЕГЭ на формулы двойного угла

Пример (ЕГЭ). Найдите значение выражения (frac{12 sin⁡11^° cdot, cos⁡11^°}{sin ⁡22^° }).
Решение. (frac{12 sin⁡11^° cdot, cos⁡11^°}{sin⁡22^°})(=)(frac{12 sin⁡11^° cdot,cos⁡11^°}{2 sin⁡11^° cdot, cos⁡11^° })(=)(frac{12}{2})(=6).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}).
Решение. (sqrt{3}cos^2frac{5π}{12}-sqrt{3}sin^2frac{5π}{12}=sqrt{3}(cos^2frac{5π}{12}-sin^2frac{5π}{12})=sqrt{3}cos(2cdotfrac{5π}{12})=sqrt{3}cosfrac{5π}{6})

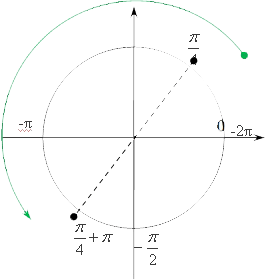
Вычислим (cos⁡frac{5π}{6}) с помощью тригонометрического круга. Сначала найдем (frac{5π}{6}) на круге:

(frac{5π}{6}=frac{6π-π}{6}=π-frac{π}{6})

Теперь видно, что (cos⁡frac{5π}{6}=-frac{sqrt{3}}{2})
(sqrt{3}cos⁡ frac{5π}{6}=sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{3}{2}=-1,5).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (frac{24(sin^2 17^°- cos^2⁡ 17^°)}{cos⁡34^°}).
Решение. (frac{24(sin^2 17^°- cos^2⁡ 17^°)}{cos⁡34^°})(=)(frac{-24(cos^2⁡ 17^°- sin^2 17^° )}{cos⁡34^°})(=)(frac{-24 cos⁡2cdot 17^°}{cos⁡34^° }) (=)(frac{-24 cos⁡34^° }{cos⁡34^° })(=-24).

Пример (ЕГЭ).

Пример (ЕГЭ). Найдите значение выражения (5sinfrac{11π}{12}cos⁡frac{11π}{12}).
Решение. (5 sinfrac{⁡11π}{12}cos⁡frac{11π}{12}=frac{5}{2}cdot2sin⁡frac{11π}{12}cos⁡frac{11π}{12}=frac{5}{2}sinfrac{⁡2cdot 11π}{12}=frac{5}{2} sin⁡frac{11π}{6}=frac{5}{2}sin⁡frac{12π-π}{6}=frac{5}{2}sin⁡(frac{12π}{6}-frac{π}{6})=)
(=frac{5}{2}sin⁡(2π-frac{π}{6})=frac{5}{2}sin⁡(-frac{π}{6})=-frac{5}{2}sin⁡frac{π}{6}=-frac{5}{2}cdot frac{1}{2}=-frac{5}{4}=-1,25).

Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{5sin⁡98^°}{sin⁡49^° sin⁡ 41^°}).

Решение:

(frac{5sin⁡98^°}{sin⁡49^° sin⁡ 41^°})		Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.
(frac{10sin⁡49^°cos49^°}{sin⁡49^° sin⁡ 41^°})		Одинаковые синусы можно сократить.
(frac{10cos49^°}{sin⁡ 41^°})		Теперь обратите внимание на то, что (49^°=90^°-41^°). Поэтому мы можем заменить (49^°) на (90^°-41^°).
(frac{10cos(90^°-41^°)}{sin⁡ 41^°})		Теперь применим к косинусу формулу приведения: ((90^°-41^°)) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс; (90^°)- находится на «вертикали» — функция меняется на кофункцию. (cos⁡ (90^°-41^°)=sin⁡41^°)
(=frac{10 sin⁡41^° }{sin⁡41^°})( =10)

Ответ: (10).

Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt{12}cos^2⁡frac{5π}{12}-sqrt{3}).

Решение:

(sqrt{12}cos^2⁡frac{5π}{12}-sqrt{3}=)		С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt{12}). (sqrt{12}=sqrt{4cdot 3}=2sqrt{3}).
(=2sqrt{3}cos^2⁡frac{5π}{12}-sqrt{3}=)		Теперь можно вынести (sqrt{3}) за скобки.
(=sqrt{3}(2 cos^2⁡frac{5π}{12}-1)=)		Вот теперь видно, что перед нами формула косинуса двойного угла.
(=sqrt{3}cos(2cdotfrac{5π}{12})=)		Сокращаем (2) и (12).
(=sqrt{3}cos(frac{5π}{6})=)		Разложим (frac{5π}{6}): (frac{5π}{6}=frac{6π-π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6})
(=sqrt{3}cos(π-frac{π}{6})=)		Теперь применим к косинусу формулу приведения: ((π-frac{π}{6})) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус; (π) — находится на «горизонтали» — функция не меняется на кофункцию. (cos⁡(π-frac{π}{6})=-cos frac{π}{6})
(=-sqrt{3}cos⁡frac{π}{6}=-sqrt{3}cdotfrac{sqrt{3}}{2}=) (=-frac{3}{2}=-1,5.)

Ответ: (-1,5).

Смотрите также:
Формулы тригонометрии с примерами

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Формулы двойного аргумента с примерами решения

Содержание:

Преобразования тригонометрических выражений можно упростить, если рассмотреть частные случаи общих формул. Рассмотрим формулу синуса суммы

Формула синуса двойного аргумента

Получили формулу синуса двойного аргумента:

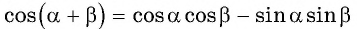
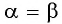
Выведем формулу косинуса двойного аргумента. Используем формулу косинуса суммы для случая и получим:

Формула косинуса двойного аргумента

Формула косинуса двойного аргумента:

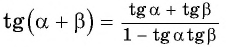
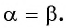
Для вывода формулы тангенса двойного аргумента рассмотрим формулу тангенса суммы при В этом случае имеем:

Формула тангенса двойного аргумента

Получили формулу тангенса двойного аргумента:

Пример №1

Упростите выражение:

Решение:

Применим формулы двойного аргумента:

Пример №2

Вычислите:

Решение:

Применим формулы двойного аргумента «справа налево»:

Пример №3

Найдите значение выражения 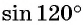двумя способами.

Решение:

Первый способ. Применим формулы приведения:

Второй способ. Применим формулу синуса двойного аргумента:

Пример №4

Представьте данный угол в виде

Решение:

Пример №5

Преобразуйте каждое из выражений с помощью формул двойного угла:

Решение:

Представим угол в каждом из выражений в виде 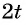и применим формулу двойного аргумента:

Пример №6

Упростите выражение:

Решение:

Применим формулы двойного аргумента и получим:

Пример №7

Найдите значение выражения:

Решение:

Пример №8

Вычислите

Решение:

Применим формулу тангенса двойного аргумента и получим:

Пример №9

Вычислите:

Решение:

б) По формулам приведения

Пример №10

Вычислите 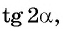если

Решение:

Так как или Поскольку

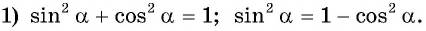
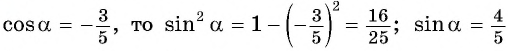
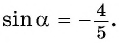
Ответ: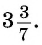

Заказать решение задач по высшей математике

Пример №11

Решите уравнение

Решение:

Используем формулу синуса двойного аргумента:

Ответ:

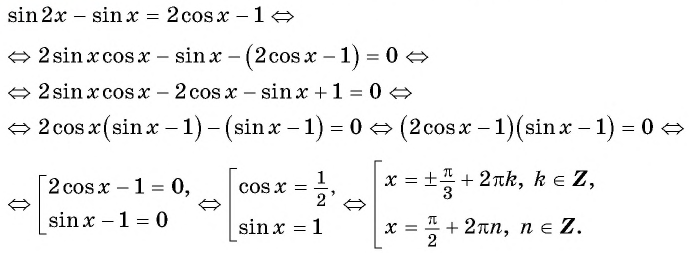
Пример №12

Решите уравнение

Решение:

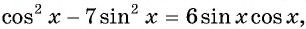
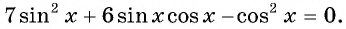
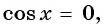
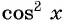
Воспользуемся формулой синуса двойного угла и получим или Так как значения переменной, при которых не являются корнями данного уравнения, то разделим обе части уравнения на и получим

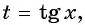
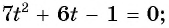
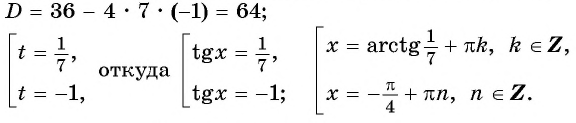
Пусть тогда уравнение примет вид Ответ:

Пример №13

Докажите тождество

Решение:

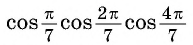
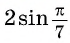
Умножим и разделим выражение на и применим формулу синуса двойного аргумента:

Формулы преобразования суммы и разности синусов (косинусов) в произведение
Корень n-й степени из числа и его свойства
Свойства и график функции y=ⁿ√x (n>1, n∈N)
Иррациональные уравнения
Тригонометрические уравнения
Тригонометрические неравенства
Формулы приведения
Синус, косинус, тангенс суммы и разности

Источник

Самые необходимые тригонометрические формулы

Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!

Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.

Эти формулы применяются и в заданиях 1 части ЕГЭ по математике, и в заданиях 2 части.

Эта полезная табличка – только одна из многих страниц Справочника Анны Малковой для подготовки к ЕГЭ. Скачай Справочник бесплатно здесь.

Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.

Первые 3 блока формул из нашей таблицы часто встречаются в заданиях 1 части ЕГЭ и в задаче из второй части, где надо решить тригонометрическое уравнение.

В первую очередь это основное тригонометрическое тождество:

sin ${}^2 alpha +$ cos ${}^2 alpha =1.$

Это формулы, которые показывают, как выразить тангенс через косинус и котангенс через синус угла.

tg ${}^2alpha +1=displaystyle frac{1}{{{cos}^2 alpha }};$

1 + ctg ${}^2alpha =displaystyle frac{1}{{{sin}^2 alpha }}.$

Формулы синуса и косинуса двойного угла, формулы синуса суммы, косинуса разности, – все это надо знать, чтобы без ошибок решать тригонометрические уравнения.

А вот формулы суммы синусов и косинусов, а также преобразование произведения в сумму могут пригодиться при решении задач с параметрами.

Где же могут встретиться формулы из двух последних блоков, внизу таблицы?

Формулы понижения степени могут присутствовать и в тригонометрических уравнениях, и в «параметрах». И даже в задачах с физическим содержанием из 1 части ЕГЭ, если там вдруг попадется тригонометрия.

А универсальная тригонометрическая замена, когда мы выражаем синус и косинус угла альфа через тангенс половинного угла? А формулы синуса и косинуса тройных углов? Где же они применяются? Оказывается, они помогают решать задачи по геометрии из 2 части ЕГЭ. Так что их тоже стоит знать, если хотите сдать на высокий балл.

Обратите внимание, что в этой таблице нет формул приведения. О них мы рассказываем в отдельной статье нашего сайта.

Как же выучить тригонометрические формулы?

1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.

2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.

3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.

4. Еще один отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!

5. И конечно, решаем задания ЕГЭ на применение этих формул. Начнем с задач 1 части, преобразование тригонометрических выражений.

Задача 1.

Найдите tg alpha , если cos $alpha =displaystyle frac{sqrt{10}}{10}$ и $alpha in left(displaystyle frac{3pi }{2};2pi right).$

Решение:

Воспользуемся формулой:

tg ${}^2x+1=displaystyle frac{1}{{cos}^2x} Rightarrow$ tg x $=pm sqrt{displaystyle frac{1}{{cos}^2x}-1}.$

Какой знак будет у тангенса, «плюс» или «минус»?

В условии дано, что $alpha in left(displaystyle frac{3pi }{2};2pi right)$ , то есть это угол из четвертой четверти, значит tgx

tgx $=-sqrt{displaystyle frac{100}{10}-1}=-3.$

Ответ: -3.

Задача 2.

Найдите $displaystyle frac{10{sin 6alpha }}{3{cos 3alpha }},$ если sin

Решение:

Воспользуемся формулой синуса двойного угла: sin2 alpha = 2sin alpha cos alpha :

$displaystyle frac{10{sin 6alpha }}{3{sin 3alpha }}=displaystyle frac{10cdot 2{sin 3alpha }{cos 3alpha }}{3{sin 3alpha }}=displaystyle frac{20cdot {cos 3alpha }}{3}=displaystyle frac{20cdot 0,6}{3}=4.$

Ответ: 4.

Задача 3.

Найдите 24cos если sin

Решение:

Воспользуемся формулой косинуса двойного угла: cos 2 alpha = 1 — 2sin ${}^2$ alpha :

24cos2 alpha = 24(1 — 2sin ${}^2 alpha )=24left(1-2{left(-0,2right)}^2right)=$

Ответ: 22,08.

Задача 4.

Найдите $displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }},$ если tg alpha =3.

Решение:

Вынесем косинус альфа за скобки в числителе и знаменателе:

$displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }}=displaystyle frac{{cos alpha }left(3-4tgalpha right)}{{cos alpha }left(2tgalpha -5right)}=displaystyle frac{3-4cdot 3}{2cdot 3-5}=displaystyle frac{-9}{1}=-9.$

Ответ: -9.

Задача 5.

Найдите значение выражения: $displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ }cdot {sin 41{}^circ }}.$

Решение:

Воспользуемся формулой синуса двойного угла:

sin2 alpha = 2sin alpha cos alpha ; тогда sin alpha cos alpha = $displaystyle frac{1}{2}{sin 2alpha } .$

$displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 49{}^circ }cdot {cos 49{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 41{}^circ }}{{sin 41{}^circ }}=10.$

Ответ: 10.

Задача 6.

Найдите значение выражения: sqrt{3} cos ${}^2 displaystyle frac{5pi }{12}-sqrt{3}$ sin ${}^2 displaystyle frac{5pi }{12} .$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos alpha = cos ${}^2$ alpha — sin ${}^2$ alpha.

$sqrt{3}{{cos}^2 displaystyle frac{5pi }{12} }-sqrt{3}{{sin}^2 displaystyle frac{5pi }{12}=sqrt{3}left({{cos}^2 displaystyle frac{5pi }{12} }-{{sin}^2 displaystyle frac{5pi }{12} }right) }=$

cos $displaystyle frac{5pi }{6}=sqrt{3}cdot left(-displaystyle frac{sqrt{3}}{2}right)=-1,5.$

Ответ: -1,5.

Задача 7.

Найдите значение выражения: $-50tg 9{}^circ cdot$ tg $81{}^circ +31.$

Решение:

Используя формулы приведения, получим: tg $81{}^circ$ = tg $left(90{}^circ -9{}^circ right)$ = ctg $9{}^circ.$

Пользуемся также тем, что тангенс и котангенс угла альфа — взаимно обратные величины,

Получим:

-50tg $9{}^circ cdot$ ctg $9{}^circ +31=-50+31 = - 19.$

Ответ: -19.

Задача 8.

Найдите значение выражения: sin ${}^2 displaystyle frac{21pi }{8}.$

Решение:

sin ${}^2 displaystyle frac{21pi }{8}=6sqrt{2}-12sqrt{2}$ sin ${}^2 displaystyle frac{21pi }{8}=6sqrt{2}cdot left(1-2{}^2 displaystyle frac{21pi }{8} right)=$

cos $(2cdot displaystyle frac{21pi }{8})=6sqrt{2}$ cos $displaystyle frac{21pi }{4}=6sqrt{2}$ cos $displaystyle frac{5pi }{4}=6sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=6.$

Мы вынесли за скобки множитель и применили формулу косинуса двойного угла, выразив его через квадрат синуса угла.

Ответ: 6.

Задача 9.

Найдите значение выражения: 5sin $displaystyle frac{11pi }{12}cdot$ cos $displaystyle frac{11pi }{12}.$

Решение:

Воспользуемся формулой синуса двойного угла: sin alpha = 2sin alpha cos alpha . Также применим одну из формул приведения: sin = -sin alpha .

5sin $displaystyle frac{11pi }{12}$ cos $displaystyle frac{11pi }{12}=displaystyle frac{5}{2}cdot$ sin $displaystyle frac{11pi }{6}=displaystyle frac{5}{2}cdot$ sin $left(2pi -displaystyle frac{pi }{6}right)=-displaystyle frac{5}{2}cdot$ sin $displaystyle frac{pi }{6}=-displaystyle frac{5}{2}cdot displaystyle frac{1}{2}=-1,25.$

Ответ: -1,25.

Задача 10.

Найдите значение выражения: $2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}}.$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2 alpha = 1 — 2 ${sin}^2 alpha.$

$2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}= }2sqrt{3}(1-2{{sin}^2 displaystyle frac{7pi }{12})= }$

cos $displaystyle frac{7pi }{6}=2sqrt{3}cdot$ cos $left(pi +displaystyle frac{pi }{6}right)=-2sqrt{3}cdot$ cos $displaystyle frac{pi }{6}=-2sqrt{3}cdot displaystyle frac{sqrt{3}}{2}=-3.$

Ответ: -3.

Задача 11.

Найдите значение выражения: $sqrt{108}{{cos}^2 displaystyle frac{pi }{12} }-sqrt{27}.$

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2 alpha = ${cos}^2 alpha -sin{}^2 alpha = 2cos{}^2 alpha -1.$

cos ${}^2 displaystyle frac{pi }{12}-sqrt{27}=6sqrt{3}$ cos ${}^2 displaystyle frac{pi }{12}-3sqrt{3}=3sqrt{3}left(2{{cos}^2 displaystyle frac{pi }{12} }-1right)=3sqrt{3}cdot$ cos $displaystyle frac{pi }{6}=$

$=3sqrt{3}cdot displaystyle frac{sqrt{3}}{2} =4,5.$

Ответ: 4,5.

Задача 12.

Найдите значение выражения: $-displaystyle frac{6{sin 374{}^circ }}{{sin 14{}^circ }}.$

$displaystyle frac{-6{sin 374{}^circ }}{{sin 14{}^circ }}=displaystyle frac{-6{sin 14{}^circ }}{{sin 14{}^circ }}=-6.$

Мы воспользовались периодичностью функции синус: sinsin alpha . В нашей задаче 374 = 360 + 14.

Ответ: — 6.

Задача 13.

Найдите значение выражения: $7sqrt{2}{sin displaystyle frac{15pi }{8}cdot {cos displaystyle frac{15pi }{8} } }.$

Решение:

Воспользуемся формулой синуса двойного угла: sin2 alpha = 2sin alpha cos alpha.

sin $displaystyle frac{15pi }{8}cdot$ cos $displaystyle frac{15pi }{8}=displaystyle frac{7sqrt{2}}{2}cdot$ sin $displaystyle frac{15pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot$ sin $left(4pi -displaystyle frac{pi }{4}right)=displaystyle frac{7sqrt{2}}{2}cdot$ sin $displaystyle frac{pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=3,5.$

Ответ: 3,5.

Заметим, что если в задаче нам встретилось произведение синуса альфа на косинус альфа, то, скорее всего, нужно будет применять формулу синуса двойного угла.

Задача 14.

Найдите tg alpha , если cos alpha $=-displaystyle frac{5sqrt{41}}{41}$ и $alpha in left(pi ;displaystyle frac{3pi }{2}right).$

Решение:

Вспомним основное тригонометрическое тождество: ${{cos}^2 alpha }+ {{sin}^2 alpha }=1.$ Выразим из этой формулы синус альфа:

sin alpha $=pm sqrt{1-{{cos}^2 alpha }}.$

Какой же знак выбрать, «плюс» или «минус»?

Угол альфа в третьей четверти, значит, его синус отрицателен.

sin alpha $=-sqrt{1-{left(-displaystyle frac{5sqrt{41}}{41}right)}^2}=-sqrt{1-displaystyle frac{25}{41}}=-sqrt{displaystyle frac{16}{41}}=-displaystyle frac{4}{sqrt{41}}.$

tg $alpha =displaystyle frac{{sin alpha }}{{cos alpha }}=left(-displaystyle frac{5sqrt{41}}{41}right):left(-displaystyle frac{4}{sqrt{41}}right)=displaystyle frac{5}{4}=1,25.$

Ответ: 1,25.

Задача 15.

Найдите sin alpha , если cos alpha $=-displaystyle frac{sqrt{19}}{10}$ и $alpha in left(displaystyle frac{pi }{2};pi right).$

Решение:

Как и в предыдущей задаче, выразим синус альфа из основного тригонометрического тождества:

sin $alpha =pm sqrt{1-{{cos}^2 alpha }}.$

Дан угол альфа, принадлежащий второй четверти, значит, его синус положителен.

sin $alpha =sqrt{1-{left(displaystyle frac{sqrt{19}}{10}right)}^2}=sqrt{displaystyle frac{81}{100}}=0,9.$

Ответ: 0,9.

Задача 16.

Найдите tg alpha , если sin alpha $=-displaystyle frac{4sqrt{41}}{41}$ и $alpha in left(pi ;displaystyle frac{3pi }{2}right).$

Решение:

Аналогично предыдущим задачам, выразим косинус альфа из основного тригонометрического тождества:

cos alpha $=pm sqrt{1-{{sin}^2 alpha }}.$

Угол альфа в третьей четверти, значит, его косинус отрицателен.

cos alpha $=-sqrt{1-displaystyle frac{16}{41}}=-sqrt{displaystyle frac{25}{41}}=-displaystyle frac{5}{sqrt{41}}$ , тогда tg $alpha =displaystyle frac{{sin alpha }}{{cos alpha }}=-displaystyle frac{4}{sqrt{41}}div left(-displaystyle frac{5}{sqrt{41}}right)=displaystyle frac{4}{5}=0,8.$

Ответ: 0,8.

Задача 17.

Найдите значение выражения: — 42tg $34{}^circ cdot$ tg $56{}^circ +6.$

Решение:

-42tg $34{}^circ cdot$ tg ${56}^circ =$ -42tg $34{}^circ cdot$ tg $left(90{}^circ -34{}^circ right)=$ -42tg $34{}^circ cdot$ ctg $34{}^circ =-42.$

Мы применили формулу приведения, а также то, что тангенс и котангенс угла альфа — взаимно обратные величины, и их произведение равно единице.

Ответ: -42.

Задача 18.

Найдите значение выражения: $displaystyle frac{24}{{{sin}^2 127{}^circ }}+4+$ sin ${}^2 217{}^circ .$

Решение:

Воспользуемся формулами приведения:

$displaystyle frac{24}{{{sin}^2 127+4+sin{}^2 217}}=displaystyle frac{24}{{{sin}^2 left(90{}^circ +37{}^circ right)+4+{{sin}^2 left(180{}^circ +37{}^circ right) } }}=$

$=displaystyle frac{24}{{{cos}^2 37{}^circ +4+{{sin}^2 37{}^circ } }}=displaystyle frac{24}{5}=4,8.$

Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.

Ответ: 4,8.

Задача 19.

Найдите значение выражения: $displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }cdot {sin 22{}^circ }}.$

Решение:

Так как $68{}^circ +22{}^circ =90{}^circ ,$ то заменим ${sin 68{}^circ }$ на ${cos 22 }^circ$ по формуле приведения и воспользуемся формулой синуса двойного угла:

sin2 alpha = 2sin alpha cos alpha.

$displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }{sin 22{}^circ }}=displaystyle frac{2{sin 136{}^circ }}{{cos 22{}^circ }{sin 22{}^circ }}=displaystyle frac{4{sin left(180{}^circ -44{}^circ right) }}{{sin 44{}^circ }}=$

$=displaystyle frac{4{sin 44{}^circ }}{{sin 44{}^circ }}=4.$

Ответ: 4.

Задача 20.

Найдите значение выражения: $displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}.$

Решение:

Воспользуемся формулой косинуса двойного угла:

${cos 2alpha ={{cos}^2 alpha }-{{sin}^2 alpha } }.$

$displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}=displaystyle frac{-21{cos 132{}^circ }}{{cos 132{}^circ }}=-21.$

Ответ: -21.

Задача 21.

Найдите значение выражения: $sqrt{2}{sin displaystyle frac{7pi }{8}cdot {cos displaystyle frac{7pi }{8}} }.$

Решение:

Воспользуемся формулой синуса двойного угла:

$sqrt{2}{sin displaystyle frac{7pi }{8} }cdot {cos displaystyle frac{7pi }{8}=displaystyle frac{sqrt{2}}{2}{sin displaystyle frac{7pi }{4} } }=displaystyle frac{sqrt{2}}{2}{sin left(2pi -displaystyle frac{pi }{4}right) }=-displaystyle frac{sqrt{2}}{2}sin displaystyle frac{pi }{4}=$

$= -displaystyle frac{sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=-0,25.$

Ответ: -0,25.

Задача 22.

Найдите значение выражения: $3sqrt{2}{{cos}^2 displaystyle frac{9pi }{8} }-3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }.$

Решение:

$3sqrt{2}{cos}^2 displaystyle frac{9pi }{8} -3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }=3sqrt{2}left({{cos}^2 displaystyle frac{9pi }{8} }-{{sin}^2 displaystyle frac{9pi }{8} }right)=3sqrt{2}{cos displaystyle frac{9pi }{4} }=$

$=3sqrt{2}cos left(2pi +displaystyle frac{pi }{4}right)=3sqrt{2}cos displaystyle frac{pi }{4}=3sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=3.$

И здесь тоже была формула косинуса двойного угла, но только в другой форме.

Ответ: 3.

Задача 23.

Найдите значение выражения: $26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{3} }.$

Решение:

$26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{4} }=26sqrt{2}cdot displaystyle frac{sqrt{2}}{2}cdot left(-displaystyle frac{1}{2}right)=-13.$

А здесь мы просто вычислили косинус и синус табличного угла $displaystyle frac{pi }{4}.$

Ответ: -13.

Задача 24.

Найдите значение выражения: $18sqrt{2}tgdisplaystyle frac{pi }{4}{sin displaystyle frac{pi }{4} }.$

Решение:

$18sqrt{2}cdot tgdisplaystyle frac{pi }{4}{cdot sin displaystyle frac{pi }{4}= }18sqrt{2}cdot 1cdot displaystyle frac{sqrt{2}}{2}=18.$

Это задача на вычисление тригонометрических функций для табличного угла $displaystyle frac{pi }{4}.$ Если этот угол выразить в градусах, то он равен 45 градусов.

Ответ: 18.

Задача 25.

Найдите значение выражения: $displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}.$

Решение:

Используя формулы приведения, получим:

$displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}=displaystyle frac{2{cos beta }+3{cos beta }}{-2{cos beta }}=$

$=-displaystyle frac{5{cos beta }}{2{cos beta }}=-2,5.$

Лайфхак: если вам сложно запомнить формулы приведения, вы можете вместо них использовать формулы косинуса разности и синуса суммы.

Ответ: -2,5.

Посмотрим, как формулы тригонометрии применяются при решении уравнений.

Задача 26.

Решите уравнение: ${{sin}^2 left(displaystyle frac{pi }{4}-xright) }={{sin}^2 left(displaystyle frac{pi }{4}+xright) }.$

Решение:

Воспользуемся формулой понижения степени: sin ${}^2 x=displaystyle frac{1-{cos 2x }}{2}.$

$displaystyle frac{1-{cos left(displaystyle frac{pi }{2}-2xright) }}{2}=displaystyle frac{1-{cos left(displaystyle frac{pi }{2}+2xright) }}{2}Leftrightarrow {cos left(displaystyle frac{pi }{2}-2xright) }={cos left(displaystyle frac{pi }{2}+2xright)Leftrightarrow }$

$Leftrightarrow {cos 2x=-{cos 2xLeftrightarrow 2 } }{cos 2x=0 }Leftrightarrow 2x=displaystyle frac{pi }{2}+pi kLeftrightarrow x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.$

Ответ: $x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.$

Задача 27.

Решите уравнение: ${{cos}^2 3x }+{{cos}^2 4x }+{{cos}^2 5x }=displaystyle frac{3}{2}.$

Решение:

Воспользуемся формулой понижения степени: ${{cos}^2 x }=displaystyle frac{1+{cos 2x }}{2}.$

${cos}^2 3x+{cos}^2 4x+{cos}^2 5x=displaystyle frac{3}{2}Leftrightarrow displaystyle frac{1+{cos 6x }}{2}+$

$+displaystyle frac{1+{cos 8x }}{2}+displaystyle frac{1+{cos 10x }}{2}=displaystyle frac{3}{2}.$

Умножим обе части на два:

Воспользуемся формулой суммы косинусов: cos alpha + cos beta = 2cos $displaystyle frac{alpha +beta }{2}$ cos $displaystyle frac{alpha -beta }{2};$

cos6x + cos10x = 2cos8x cos2x.

Уравнение примет вид:

2cos8x cos2x + cos8x =0.

Вынесем общий множитель за скобки. Теперь произведение двух множителей равно нулю, а с этим мы умеем работать.

${cos 8xleft(2{cos 2x+1 }right)=0Leftrightarrow left[ begin{array}{c}{cos 8x=0 } \{cos 2x=-displaystyle frac{1}{2} } end{array}Leftrightarrow left[ begin{array}{c}8x=displaystyle frac{pi }{2}+pi k \2x=pm displaystyle frac{2pi }{3}+2pi k;kin Z end{array}right.right. }Leftrightarrow left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .$

Ответ: $left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .$

Все о решении тригонометрических уравнений здесь.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Самые необходимые тригонометрические формулы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.

Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$
Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$
Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$
Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$
Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$
Формулы приведения можно найти в отдельной статье

Зачем нужны тригонометрические формулы?

Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.

Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.

Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.

Обсудим и порешаем примеры на все формулы из таблицы.

Основное тригонометрическое тождество

$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$

Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.

При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:

Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)

Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.

Формула, которая связывает и синус, и косинус — это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.

В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?

В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$

Ответ: (4.)

Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.

Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.

Основные связи тригонометрических функций

А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:

$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$

Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.

Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).

Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$

Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)

Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$

Вывод связи тангенса с косинусом и котангенса с синусом

Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство — формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).

Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$

Формулы суммы и разности тригонометрических функций

Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$
Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$
Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$
Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$

Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.

Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:

Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).

Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$

Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:

Пример 4
Найдите значение (sin(15^o)=?)

(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.

Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)

Пример 5
Найдите значение (cos(75^o)=?)

(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.

Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)

Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.

Формулы двойного угла

$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$

Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :

$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$

Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$

Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$

В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:

Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)

Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$

Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)

Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$

Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)

Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$

Формулы тройного угла

Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$

Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$

Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$

Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$

Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.

Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.

Формулы половинного угла (двойного аргумента)

$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$

Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$

Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$

Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$

Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):

$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$

Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$

Формулы понижения степени

$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$

Формулы понижения второй степени на самом деле дублируют формулы половинного угла.

Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.

Преобразование суммы и разности тригонометрических функций:

$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$

Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.

Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.

Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:

$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$

Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.

Аналогично выводятся все остальные формулы.

Пример 10
Вычислить (sin(165)+sin(75)=?)

(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$

Преобразование произведения тригонометрических функций

$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$

В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.

Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$

Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:

$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.

Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.

Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$

Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)

Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$

Источник

cos2a, sin2a. Формулы двойного угла. Примеры на ЕГЭ

Примеры решения задач из ЕГЭ на формулы двойного угла

Вычислим (cos⁡frac<5π><6>) с помощью тригонометрического круга. Сначала найдем (frac<5π><6>) на круге:

Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что (98^°)ровно в два раза больше (49^°). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.

Одинаковые синусы можно сократить.

Теперь обратите внимание на то, что (49^°=90^°-41^°).
Поэтому мы можем заменить (49^°) на (90^°-41^°).

((90^°-41^°)) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс;

(90^°)- находится на «вертикали» — функция меняется на кофункцию. (cos⁡ (90^°-41^°)=sin⁡41^°)

Пример. (Задание из ЕГЭ) Найдите значение выражения (sqrt<12>cos^2⁡frac<5π><12>-sqrt<3>).

С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать (sqrt<12>).
(sqrt<12>=sqrt<4cdot 3>=2sqrt<3>).

Теперь можно вынести (sqrt<3>) за скобки.

Вот теперь видно, что перед нами формула косинуса двойного угла.

Сокращаем (2) и (12).

Теперь применим к косинусу формулу приведения:

((π-frac<π><6>)) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус;

(π) — находится на «горизонтали» — функция не меняется на кофункцию.

Формулы двойного угла в тригонометрии

Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.

Список формул двойного угла

Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .

Ниже приведены формулы двойного угла:

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α

Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .

Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.

Доказательство формул двойного угла

Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:

sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что

sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α

Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .

Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .

Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:

t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α

Примеры использования формул двойного угла

Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .

Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .

Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и

sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что

2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3

и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3

Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.

Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .

Представить sin 2 α 3 через тригонометрические функции, при α 6 .

Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6

Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .

Формулы тройного, четверного и т.д. угла

Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.

sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α

При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .

Так же приводится формула косинуса тройного угла:

cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α

При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .

При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:

t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1

Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.

Задача C1: тригонометрические уравнения и формула двойного угла

Очень часто в задачах C1 из ЕГЭ по математике ученикам предлагают решить тригонометрическое уравнение, содержащее формулу двойного угла.

Сегодня мы вновь будем разбирать задачу С1 и, в частности, разберем довольно нестандартный пример, который одновременно вместил в себе и формулу двойного угла, и даже однородное уравнение. Итак:

Решите уравнение. Найдите корни этого уравнения, принадлежащие промежутку:

sinx+ sin 2 x 2 − cos 2 x 2 ,x∈ [ −2 π ;− π 2 ]

Полезные формулы для решения

Прежде всего, хотел бы напомнить, что все задания С1 решаются по одной и той же схеме. В первую очередь, исходную конструкцию нужно преобразовать в выражении, в котором содержится синус, косинус или тангенс:

Именно в этом состоит основная сложность задания С1. Дело в том, что для каждого конкретного выражения требуются свои выкладки, с помощью которых можно перейти от исходника к таким простейшим конструкциям. В нашем случае это формула двойного угла. Давайте я запишу ее:

cos2x= cos 2 x− sin 2 x

Однако в нашем задании нет cos 2 x <<cos >^<2>>x или sin 2 x <<sin >^<2>>x, зато есть sin 2 x 2 frac<<<sin >^<2>>x> <2>и cos 2 x 2 frac<<<cos >^<2>>x><2>.

Решаем задачу

Что же делать с этими выкладками? Давайте мы немножко схитрим, и в наши формулы синуса и косинуса двойного угла введем новую переменную:

Мы запишем такую конструкцию с синусом и косинусом:

cos2⋅ t 2 = cos 2 t 2 − sin 2 t 2

Или другими словами:

cost= cos 2 t 2 − sin 2 t 2

Возвращаемся к нашему исходному заданию. Давайте sin 2 x 2 frac<<<sin >^<2>>x> <2>перенесем вправо:

sinx= cos 2 x 2 − sin 2 x 2

Справа стоит именно те самые выкладки, которые мы только что записали. Давайте мы преобразуем их:

А теперь внимание: перед нами однородное тригонометрическое уравнение первой степени. Смотрите, у нас нет никаких слагаемых, состоящих просто из чисел и просто из x x, у нас есть только синус и косинус. Также у нас нет квадратных тригонометрических функций, все функции идут в первой степени. Как решаются такие конструкции? В первую очередь, давайте предположим, что cosx=0 cos x=0.

Подставим это значение в основное тригонометрическое тождество:

sin 2 x+ cos 2 x=1

Если эти числа, 0 и ±1, мы подставим в исходную конструкцию, то получим следующее:

Мы получили полный бред. Следовательно, наше предположение, что cosx=0 cos x=0 неверно, cosx cos x не может быть равен 0 в данном выражении. А если cosx cos x не равен 0, то давайте разделим обе стороны на cosx cos x:

И вот мы получили долгожданное простейшее выражение вида tg x=a tgx=a. Прекрасно, решаем его. Это табличное значение:

Мы нашли корень, мы решили первую часть задачи, т. е. честно заработали один первичный балл из двух.

Переходим ко второй части: найдите корни этого уравнения, принадлежащие промежутку, а, точнее, отрезку

[left[ -2text< >!!pi!!text< >;-frac<text< >!!pi!!text< >> <2>right]]. Предлагаю, как и в прошлый раз решать это выражение графически, т. е. нарисовать окружность, отметить в ней начало, т. е. 0, а также концы отрезка:

-2text< >!!pi!!text< >;-frac<pi > <2>нужно найти все значения, которые принадлежат

frac<text< >!!pi!!text< >><text<4>>+text< >!!pi!!text< >n. А теперь самое веселое: дело в том, что сама точка π 4 frac<text< >!!pi!!text< >> <4>не принадлежит отрезку

π 4 ∉ ˜ [ −2 π ;− π 2 ]

Уже хотя бы потому, что оба конца этого отрезка отрицательные, а число π 4 frac<text< >!!pi!!text< >> <4>положительное, но с другой стороны, какие-то значения вида

frac<text< >!!pi!!text< >><4>+text< >!!pi!!text< >n все-таки принадлежат нашему отрезку. Так как же их выделить? Очень просто: берем конец отрезка

-2text< >!!pi!!text < >и прибавляем π 4 frac<text< >!!pi!!text< >><text<4>> , т. е. все происходит то же самое, как если бы мы начали отчет не от 0, а от −2 π -2text< >!!pi!!text< >, и у нас найдется первая точка:

x=−2 π + π 4 =− 7 π 4

Теперь второе число:

x=−2 π + π 4 + π =− 3 π 4

Это и есть второе значение. Других корней нет, потому что мы сами при их разметке и при отметке нашего отрезка ограничения обнаружили, что внутри этого отрезка лежат лишь два вида — π 4 frac<text< >!!pi!!text< >><text<4>> и π 4 + π frac<text< >!!pi!!text< >><4>+text< >!!pi!!text< >. Эти точки мы и наши. Выписываем ответ:

За такое решение вы получите два первичных балла из двух возможных.

Что нужно помнить для правильного решения

Еще раз ключевые шаги, которые необходимо выполнить. В первую очередь, нужно знать выкладки двойного угла синуса или косинуса, в частности, именно в нашей задаче, косинус двойного угла. Кроме того, после его применения необходимо решить простейшее тригонометрическое уравнение. Решается оно довольно просто, однако необходимо написать и проверить, что cosx cos x в нашей конструкции не равен 0. После тригонометрического уравнения мы получаем элементарное выражение, в нашем случае это tg x=1 tgx=1, которое легко решается по стандартным формулам, известным еще с 9-10 класса. Таким образом, мы решим пример и получим ответ на первую часть задания — множество всех корней. В нашем случае это

frac<text< >!!pi!!text< >><text<4>>+text< >!!pi!!text< >n,nin ˜Z. Затем остается лишь отобрать корни, принадлежащие отрезку

left[ -2text< >!!pi!!text< >;-frac<text< >!!pi!!text< >> <2>right]. Для этого мы снова чертим тригонометрический круг, отмечаем на нем наши корни и наш отрезок, а затем отсчитываем от конца то самое π 4 frac<text< >!!pi!!text< >> <4>и π 4 + π frac<text< >!!pi!!text< >><4>+text< >!!pi!!text< >, которые получились во время отметки всех корней вида π 4 + π n frac<text< >!!pi!!text< >><text<4>>+text< >!!pi!!text< >n. После несложного счета мы получили два конкретных корня, а, именно,

-frac<3text< >!!pi!!text< >><4>, которые являются ответом ко второй части задачи, т. е. корнями, принадлежащими отрезку

Ключевые моменты

Чтобы без проблем справиться с задачами C1 такого типа, запомните две основные формулы:

Синус двойного угла:

sin2 α =2sin α cos α

sin 2text< >!!alpha!!text< >=2sin text< >!!alpha!!text< >cos text< >!!alpha!!text < >— эта формула для синусов всегда работает именно в таком виде;

Косинус двойного угла: cos2 α =co s 2 α −si n 2 α cos 2text< >!!alpha!!text< =>co<~~^<2>>text< >!!alpha!!text< >-si<^<2>>text< >!!alpha!!text < >— а вот тут возможны варианты.~~

С первой все понятно. Но что за варианты возможны во втором случае? Дело в том, что косинус двойного угла можно записать по-разному:

~~cos2 α =cos2 α −sin2 α =2cos2 α −1=1−2sin2 α~~

~~cos 2text< >!!alpha!!text< >=cos 2text< >!!alpha!!text< >-sin 2text< >!!alpha!!text< >=2cos 2text< >!!alpha!!text< >-1=1-2sin 2text< >!!alpha!!text~~

Эти равенства следуют из основного тригонометрического тождества. Ну и какое равенство выбрать при решении конкретного примера C1? Все просто: если вы планируете свести конструкцию к синусам, то выбирайте последнее разложение, в котором присутствует только

sin 2text< >!!alpha!!text< >. И наоборот, если хотите свести все выражение к работе с косинусами, выбирайте второй вариант — тот, где косинус является единственной тригонометрической функцией.

~~источники:~~

~~http://zaochnik.com/spravochnik/matematika/trigonometrija/formuly-dvojnogo-ugla-v-trigonometrii/~~

~~http://www.berdov.com/ege/equation-root/trigonometricheskoe-uravnenie-dvoinoi-ugol/~~

Источник

Примеры решения задач из ЕГЭ на формулы двойного угла

Формулы двойного аргумента с примерами решения

Формула синуса двойного аргумента

Формула косинуса двойного аргумента

Формула тангенса двойного аргумента

Пример №1

Пример №2

Пример №3

Пример №4

Пример №5

Пример №6

Пример №7

Пример №8

Пример №9

Пример №10

Пример №11

Пример №12

Пример №13

Самые необходимые тригонометрические формулы

Как же выучить тригонометрические формулы?

Зачем нужны тригонометрические формулы?

Основное тригонометрическое тождество

Основные связи тригонометрических функций

Вывод связи тангенса с косинусом и котангенса с синусом

Формулы суммы и разности тригонометрических функций

Формулы двойного угла

Формулы тройного угла

Формулы половинного угла (двойного аргумента)

Формулы понижения степени

Преобразование суммы и разности тригонометрических функций:

Преобразование произведения тригонометрических функций

cos2a, sin2a. Формулы двойного угла. Примеры на ЕГЭ

Примеры решения задач из ЕГЭ на формулы двойного угла

Формулы двойного угла в тригонометрии

Список формул двойного угла

Доказательство формул двойного угла

Примеры использования формул двойного угла

Формулы тройного, четверного и т.д. угла

Задача C1: тригонометрические уравнения и формула двойного угла

Полезные формулы для решения

Решаем задачу

Что нужно помнить для правильного решения

Ключевые моменты

Новое и интересное на сайте: